中国是世界上自然灾害最严重的国家之一. 据统计，2018年全国共发生地质灾害2966起，其中由降雨引起的滑坡1631起、泥石流339起，共造成近百人伤亡. 在自然灾害频发及“一带一路”等基础设施大规模建设的背景下，边坡工程防灾形势依然严峻. 自然边坡与工程边坡高度多在数十米至百米级别，常重力试验难以再现极端环境下大尺度边坡灾变过程. 利用超重力离心机施加Ng（g为重力加速度，N为重力加速度的倍数）的离心加速度，再现原型边坡应力场进行“降雨”模拟，成为研究降雨条件下边坡稳定性的重要手段^[1-3].

高g值条件下土壤渗流、管涌等过程对降雨均匀性敏感度较高，而降雨覆盖范围的偏差直接影响降雨均匀性、进而导致边坡稳定性研究失真. 系统性地分析离心模拟超重力环境下雨滴受力、运动轨迹和覆盖范围将对保证超重力降雨试验准确性有着重要的意义^[4-6]. 在当前研究背景下，研究者多以模型箱内土体模型为参考进行受力分析，忽略了在离心模拟超重力环境下超重力产生的本质，导致现阶段多数此领域研究成果的受力分析存在不准确的现象. 刘小川^[7]在分析离心模拟超重力环境下雨滴下落受力时，忽略了离心机半径的影响；张敏等^[8-9]忽略了部分科氏力与离心力的影响，造成分析结果存在一定的误差.

本文采用惯性坐标系与随动坐标系相结合的方法，系统分析了离心模拟超重力环境下雨滴下落受力及运动轨迹，比较了推荐方法与现有方法之间的误差，根据实际要求提出离心机降雨模拟试验工况建议，为正确认识离心模拟超重力环境下雨滴运动过程明确了方向.

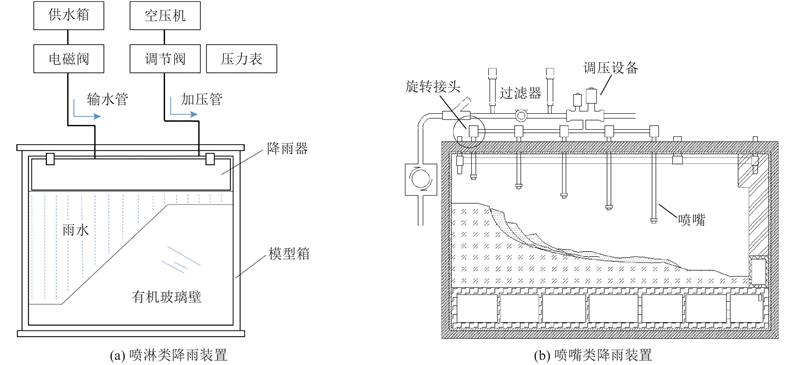
超重力试验通过离心机高速旋转产生的离心加速度在吊篮中模拟超重力环境，使得模型应力与原型相同实现“缩尺”，模型内渗流加快实现“缩时”，从而在实验室中再现与原型相类似的灾变过程，解决实际工程中的“长历时”、“大尺度”问题. 目前，常用的机载降雨模拟装置主要分为滴淋类与喷嘴类2种. 如图1所示，滴淋类降雨装置采用孔径细小的多孔板和渗透性小的布料或膜，施加水压实现滴淋来模拟降雨. 这类降雨模拟装置所形成的液滴粒径可控性差，难以精确控制降雨强度及历时，难以避免滴漏问题. 喷嘴类降雨模拟装置使用特定类型的喷嘴，在一定水压下喷嘴喷射液滴粒径大小可控，结合调压设备和中磁阀等元件，通过标定可以实现定量模拟某一范围内的降雨强度和历时^[7].

剑桥大学、香港科技大学和浙江大学等多数研究机构均使用喷嘴类降雨装置，可以控制降雨的初始速度大小、方向和雨滴粒径. 本文针对喷嘴类降雨模拟装置，开展雨滴下落轨迹分析.

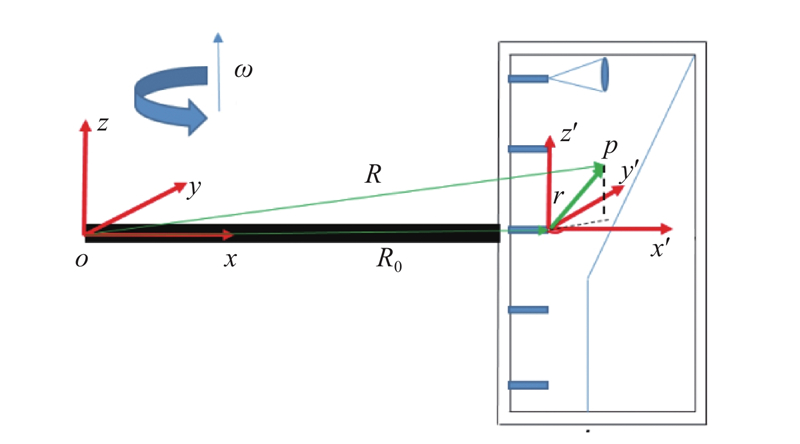
由于离心模拟超重力场下降雨模拟过程中雨滴运动的复杂性，将惯性系与随动坐标系相结合进行分析计算. 如图2所示，惯性系原点在旋转中心，重力的反方向为 $z$轴正方向；随动坐标系指随离心机同步旋转的非惯性系，随动坐标系的坐标原点 $o'$建在模型箱喷嘴端部，离心机转臂的顺臂向为 $x'$正向，离心机旋转切向为 $y'$方向，天地向为 $z'$方向. 惯性系原点到雨滴 $p$的位矢为R，离心机旋转中心到喷嘴端部的位矢为 ${{{R}}_{{0}}}$，喷嘴顶端到雨滴位置的位矢为 ${{r}}$，离心机以 ${{\omega}} $的角速度匀速转动，转动方向如图2所示. 设定试验过程中以喷嘴端部计算得到的离心加速度保持不变，则角速度为

(1) $\omega = \sqrt {\frac{{N{{g}}}}{{{R_0}}}} .$

式中： $N$为重力加速度的倍数，通常取正数； ${R_0}$为R₀的长度.

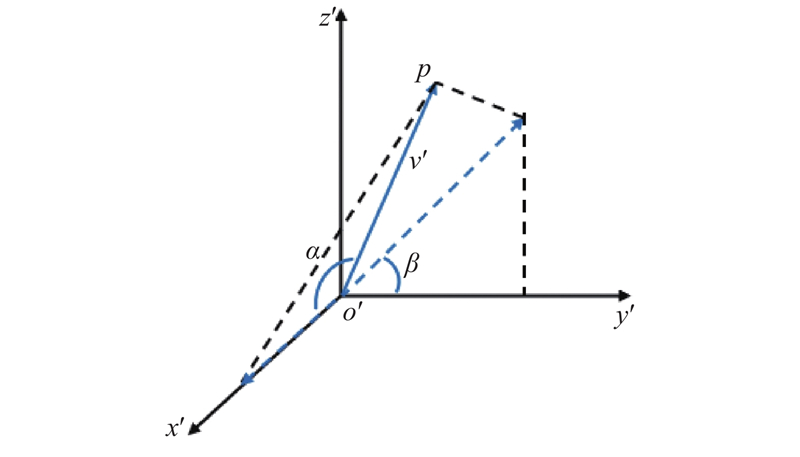
雨滴喷出的速度在惯性坐标系下描述为 ${{v}}$，在 $x$、 $y$、 $z$方向上的分量为 ${v_x}$、 ${v_y}$、 ${v_z}$；雨滴喷出速度在随动坐标系下描述为 ${{v}}'$，其在 $x'$、 $y'$、 $z'$方向上的分量为 ${v_x}'$、 ${v_y}'$、 ${v_z}'$. 如图3所示，雨滴从喷嘴喷出速度 ${{v}}'$与 $x'$轴夹角为 $\alpha $，速度 ${{v}}'$在 $y'z'$平面上的投影与 $y'$轴夹角为 $\beta $. 雨滴喷出速度在2个坐标系下的表达关系式为

(2) ${{v}} = {{{v}}_{{{o}}'}} + {{v}}' .$

式中： ${{{v}}_{{{o}}'}}$为离心机在惯性坐标系下的运动速度.

定义离心机模型箱中雨滴在某一时刻的位置为 $p$，则点 $p$的位矢可以表示为^[10]

(3) ${{R}} = {{{R}}_{{0}}} + {{r}} ,$

(4) ${{R}} = {R_0}{{i}}' + {r_x}{{i}}' + {r_y}{{j}}' + {r_z}{{k}}' .$

式中： ${{i}}'$、 ${{j}}'$、 ${{k}}'$分别为随动坐标系中 $x'$、 $y'$、 $z'$方向上的单位矢量， ${r_x}$、 ${r_y}$、 ${r_z}$为位矢 ${{r}}$在 $x'$、 $y'$、 $z'$方向上的分量大小.

在惯性坐标系下描述质点运动，随动坐标系的各单位矢量将会随离心机转动而变化，对时间的一阶导数为

(5) $\frac{{{\rm{d}}{{i}}'}}{{{\rm{d}}{{t}}}} = \omega {{j}}' ,$

(6) $\frac{{{\rm{d}}{{j}}'}}{{{{{\rm{d}}t}}}} = - \omega {{i}}' ,$

(7) $\frac{{{\rm{d}}{{k}}'}}{{{\rm{d}}t}} = {{0}} .$

式中：t为目标下落距离的运动时间.

根据式（3）~（7）， $p$点的运动速度和加速度可以表示为

(8) $ {{{v}}_{{p}}} = \frac{{{\rm{d}}{{R}}}}{{{\rm{d}}{{t}}}} = \left( {\frac{{{\rm{d}}{R_0}}}{{{\rm{d}}t}} + {v_x}' - \omega {r_y}} \right){{i}}' + \left( {\omega {R_0} + \omega {r_x} + {v_y}'} \right){{j}}' + {v_z}'{{k}}' , $

(9) $\begin{array}{l} {{{a}}_{{p}}} \!=\! \dfrac{{{{\rm{d}}^2}{{R}}}}{{{\rm{d}}{t^2}}} \!=\! \left[ { \!-\! {\omega ^2}\left( {{R_0} \!+\! {r_x}} \right) \!-\! 2\omega {v_y}' \!+\! {a_x}' - \dfrac{{{\rm{d}}\omega }}{{{\rm{dt}}}}{r_y} \!+ \dfrac{{{{\rm{d}}^2}{R_0}}}{{{\rm{d}}{{\rm{t}}^2}}}} \right]{{i}}' + \\ \left[ { - {\omega ^2}{r_y} + 2\omega {v_x}' + {a_y}' + \dfrac{{{\rm{d}}\omega }}{{{\rm{dt}}}}\left( {{R_0} + {r_y}} \right) + 2\omega \dfrac{{{\rm{d}}{R_0}}}{{{\rm{dt}}}}} \right]{{j}}' + {a_z}'{{k}}' . \end{array} $

式中： ${{{v}}_{{p}}}$为 $p$点的绝对速度， ${{{a}}_{{p}}}$为 $p$点的绝对加速度， ${a_x}'$、 ${a_y}'$、 ${a_z}'$分别为 $p$点在 $x'$、 $y'$、 $z'$方向上的相对加速度. 模型箱的绝对加速度可以描述为

(10) ${{{a}}_{{{o}}'}} = \left( { - {\omega ^2}{R_0} + \frac{{{{\rm{d}}^2}{R_0}}}{{{\rm{d}}{{{t}}^2}}}} \right){{i}}' + \left( {\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}}{R_0} + 2\omega \frac{{{\rm{d}}R}}{{{\rm{d}}t}}} \right){{j}}' .$

若不考虑半径 ${R_0}$的影响，即将旋转轴“平移”至喷嘴端部 $o'$，则 $p$点的运动学方程可以描述为

(11) $\begin{array}{l} {{{a}}_{{{o}}'{{p}}}} = {{{a}}_{{p}}} - {{{a}}_{{{o}}'}} = \left( { - {\omega ^2}{r_x} - 2\omega {v_y}' + {a_x}' - \dfrac{{{\rm{d}}\omega }}{{{\rm{dt}}}}{r_y}} \right){{i}}' + \\ \;\;\;\;\;\; \left( { - {\omega ^2}{r_y} + 2\omega {v_x}' + {a_y}' + \dfrac{{{\rm{d}}\omega }}{{{\rm{dt}}}}{r_y}} \right){{j}}' + a_z^{'}{{k}}' .\\[-12pt] \end{array} $

不考虑转速变化及转臂和模型箱变形时，式（9）、（11）可以简化为

(12) $\begin{split} {{{a}}_{{p}}} = &\left[ { - {\omega ^2}\left( {{R_0} + {r_x}} \right) - 2\omega {v_y}' + {a_x}'} \right]{{i}}' + \\ & \left[ { - {\omega ^2}{r_y} + 2\omega {v_x}' + {a_y}'} \right]{{j}}' + {a_z}'{{k}}' , \end{split} $

(13) $\begin{split} {{{a}}_{{{o}}'{{p}}}} =& \left( { - {\omega ^2}{r_x} - 2\omega {v_y}' + {a_x}'} \right){{i}}' + \\ &\left( { - {\omega ^2}{r_y} + 2\omega {v_x}' + {a_y}'} \right){{j}}' + {a_z}'{{k}}' . \end{split} $

式中： $ - {\omega ^2}{R_0}$为目标超重力Ng， $2\omega {v_x}'$、 $2\omega {v_y}'$为科氏加速度， ${\omega ^2}{r_x}$、 ${\omega ^2}{r_y}$为离心加速度.

上述推导结果与文献[10]的结果相同. 刘小川^[7]将式（13）误理解为 $p$点相对于模型箱的相对运动方程. 张敏等^[8]将式（9）简化为

(14) ${{{a}}_{{p}}} = \left( { - N{{g}} + {a_x}'} \right){{i}}' + \left( {2\omega {v_x}' + {a_y}'} \right){{j}}' + {a_z}'{{k}}' .$

式（14）忽略了“雨滴”位置变化引起的离心加速度以及在 $x'$方向上的科氏加速度等因素的影响. 当雨滴下落距离较小时， ${\omega ^2}{r_x}$、 ${\omega ^2}{r_y}$影响可以忽略，但 $x'$方向的科氏加速度的影响不能忽略.

根据上述运动学分析结果，对点 $p$相对于模型箱的运动过程进行动力学分析. 在 $x'$、 $y'$、 $z'$,方向上的动力学方程分别为

(15) $m{a_x}' = {F_x} + m{\omega ^2}\left( {{R_0} + {r_x}} \right) + 2m\omega {v_y}' + m\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}}{r_y} - m\frac{{{{\rm{d}}^2}{R_0}}}{{{\rm{d}}{{{t}}^2}}},$

(16) $m{a_y}' = {F_y} + m{\omega ^2}{r_y} - 2m\omega {v_x}' - m\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}}\left( {{R_0} + {r_x}} \right) - 2m\omega \frac{{{\rm{d}}{R_0}}}{{{\rm{d}}t}},$

(17) $m{a_z}' = {F_z}.$

式中： ${F_x}$、 ${F_y}$、 ${F_z}$为雨滴在点 $p$受到的合力在 $x'$、 $y'$、 $z'$方向上的分量大小.

当离心机半径及角速度不变时，雨滴相对于模型箱的加速度可以简化为

(18) $m{a_x}' = {F_x} + m{\omega ^2}\left( {{R_0} + {r_x}} \right) + 2m\omega {v_y}',$

(19) $m{a_y}' = {F_y} + m{\omega ^2}{r_y} - 2m\omega {v_x}',$

(20) $m{a_z}' = {F_z}.$

由式（18）~（20）两次积分，可以计算出雨滴在模型箱内的运动轨迹方程：

(21) $ \begin{array}{l} x' \!=\! \left( {\left( {{{y'}_0} \!+\! \dfrac{{{F_y}}}{{m\;{\omega ^2}}}} \right) \!+\! \left( {{{v'}_{y0}} \!+\! \omega {{x'}_0} + \omega {R_0} + \dfrac{{{F_x}}}{{m\;\omega }}} \right)t} \right)\sin\;(\omega t) + \\ \!\left(\! {\left( {{{x'}_0} \!\!+\!\! {R_0} \!\!+\!\! \dfrac{{{F_x}}}{{m\;{\omega ^2}}}} \right) \!\!+\!\! \left( {{{v'}_{x0}} \!\!-\!\! \omega {{y'}_0}\! \!-\! \!\dfrac{{{F_y}}}{{m\;\omega }}} \right)t} \right)\cos\;(\omega t) \!\!-\!\! \dfrac{{{F_x}}}{{m\;{\omega ^2}}} \!-\! {R_0}, \end{array} $

(22) $ \begin{array}{l} y' \!=\! \left( {\left( {{{y'}_0} \!+\! \dfrac{{{F_y}}}{{m\;{\omega ^2}}}} \right) \!+\! \left( {{{v'}_{y0}} \!+\! \omega {{x'}_0} + \omega {R_0} + \dfrac{{{F_x}}}{{m\;\omega }}} \right)t} \right)\cos\;(\omega t) - \\ \left( {\left( {{{x'}_0} \!+\! {R_0} \!+\! \dfrac{{{F_x}}}{{m\;{\omega ^2}}}} \right) \!+\! \left( {{{v'}_{x0}} - \omega {{y'}_0} - \frac{{{F_y}}}{{m\;\omega }}} \right)t} \right)\sin\;(\omega t) - \dfrac{{{F_y}}}{{m\;{\omega ^2}}}, \end{array} $

(23) $z' = {z'_0} + {v'_{z0}}t + \frac{{{F_z}}}{{2m}}{t^2}.$

式中： $x{'_0}$、 $y{'_0}$、 $z{'_0}$为雨滴在t=0在 $x'$、 $y'$、 $z'$3个方向上的初始位移分量， $v{'_{x0}}$、 $v{'_{y0}}$、 $v{'_{z0}}$为雨滴t=0时刻的初速度 $v{'_0}$在 $x'$、 $y'$、 $z'$3个方向上的分量.

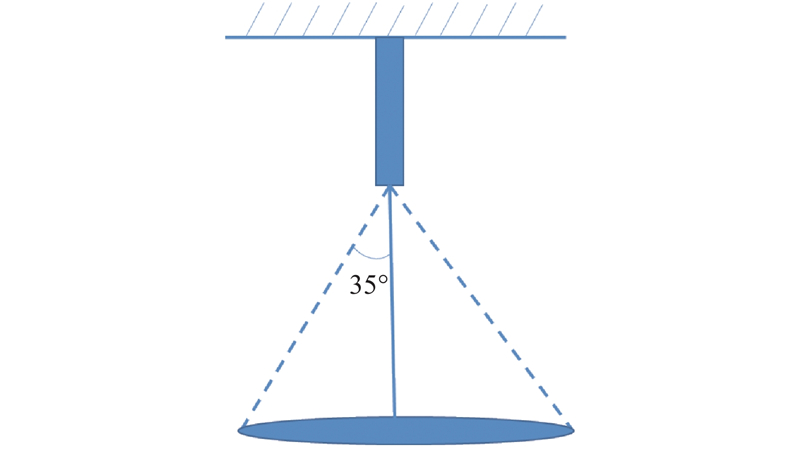
以常用在机载降雨装置上的Hago牌M10型空气雾化喷嘴为例，喷射水滴直径为20~70 µm. 如图4所示，常重力下，喷嘴喷出雨滴范围大致可以描述为以喷嘴出口为顶点的圆锥体，单个雨滴喷出的运动轨迹大致可以描述为沿着初速度方向的一条直线，覆盖范围在理想情况下为以喷嘴的投影点为圆心的圆面，喷射角度 $\delta $为70°. 明确了喷射边界雨滴的轨迹即可确定覆盖范围. 边界雨滴运动的初始条件为 $x{'_0} = 0$、 $y{'_0} = 0$、 $z{'_0} = 0$、 ${v_{x0}}' = v{'_0}\cos\;\alpha $、 ${v_{y0}}' = v{'_0}\sin\;\alpha \cos\;\beta $、 ${v_{z0}}' = v{'_0}\sin\;\alpha \sin\;\beta $，ZJU400超重力离心机半径 ${R_0}$为4 m.

在离心机降雨模拟过程中，雨滴受到空气阻力和重力等外力作用，根据文献[11~13]的研究结果可知，雨滴在下落过程中受到的空气阻力为

(24) $f = \left\{ \begin{array}{l} 3{\text{π}} \eta dv' ,\;\;\;\;\;\; {{Re}} < 1; \\ \dfrac{1}{2}{C_{\rm{D}}}{\rho _{\rm{a}}}sv{^{'2}},\;{{Re}} > 1. \end{array} \right.$

式中： $f$为空气阻力； $\eta $为常温条件下的空气黏滞系数， $\eta = 1.81\; \times 1{0^{ - 5}}\;{\rm{kg/(m \cdot s)}}$； $d$为雨滴直径；C_D为阻力系数， ${C_{\rm{D}}} = $ $ {{24}}/{{{{Re}}}} + {6}/\left( {{{1 + \sqrt {{{Re}}} }}} \right) + 0.4\;$； ${\rho _{\rm{a}}}$为空气密度； $s$为雨滴与空气垂直方向最大截面积； ${{Re}}$为雨滴在空气中运动的雷诺数.

设雨滴脱离喷嘴时的初速度为10 m/s，雨滴下落距离为0.15 m，求得离心模拟超重力环境中降雨覆盖范围随N的变化，如图5所示.

由图5可知，根据2种方法得到的降雨覆盖范围中心位置随着N的增大逐渐向 $y'$轴负方向，即旋转切向速度的反方向偏移. 其中，根据文献[8]方法得到的覆盖范围沿 $y'$轴和 $z'$轴呈现扩大趋势，总体呈现沿 $y'$轴方向“拉长”的趋势；覆盖范围边界均为圆形且半径逐渐变小. 根据推荐方法得到覆盖范围边界呈椭圆形且逐渐变小. 推荐方法覆盖范围边界呈椭圆形，长、短半轴长度 $a$、 $b$均随着N的增加而减小，100g时 $a$、 $b$相对于常重力下的半径分别减少37.5%和39.5%. 覆盖范围形心沿 $y'$轴偏移量 $c$在100 g时可达2.6 cm，为常重力下覆盖范围直径的12.38%.

为了定量评价本文方法与文献[8]方法的差别，给出2种方法得到的 $a$、 $b$和 $c$随N的变化，如图6所示. 文献[8]方法相对于本文方法的误差如表1所示. 表中，e_a、e_b、e_c分别为利用文献[8]方法得到的a、b、c相对于本文方法的误差率.

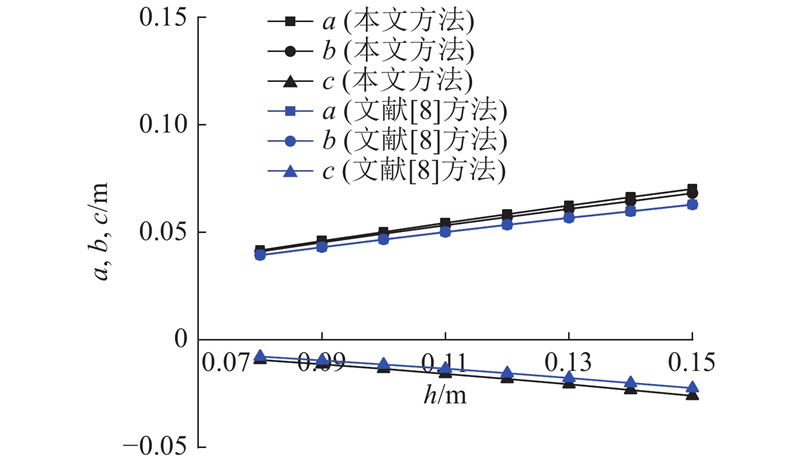
在超重力试验中，边坡模型高度不同使得喷嘴到坡面距离不同，对降雨覆盖范围产生影响. 取N为100、喷出速度为10 m/s，采用不同方法求解的降雨覆盖范围随下落距离的变化如图7所示.

如图7所示，2种方法计算得到的降雨覆盖范围中心位置均会随着下落距离的增加逐渐向 $y'$轴负方向偏移，且覆盖范围边界逐渐增大. 文献[8]方法得到的覆盖范围边界为理想圆形. 推荐方法得到边界覆盖范围边界形状为椭圆形，但椭圆离心率较小. 推荐方法覆盖范围参数 $a$、 $b$相对于常重力下的变化量均随着下落距离增加而增大，下落距离为0.15 m时计算参数 $a$、 $b$相对于常重力下半径减小37.5%和39.5%. $c$在下落距离为0.15 m时可达2.6 cm，为常重力下覆盖范围直径的12.38%.

为了进一步定量评价推荐方法与文献[8]方法的差别，给出2种方法得到的 $a$、 $b$、 $c$随下落距离h的变化，如图8所示. 文献[8]方法相对于本文方法的误差如表1所示.

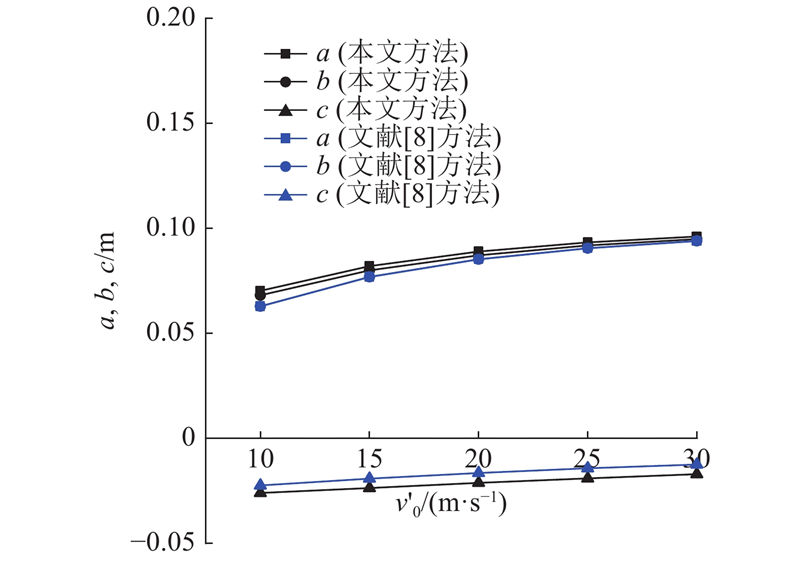
超重力试验中雨滴初速度不同时所受科氏力不同，导致雨滴在落地前的运动时间发生变化，使得离心模拟超重力场下雨滴的运动过程更加复杂. 设雨滴下落高度为0.15 m，N为100，降雨覆盖范围随初始速度变化的计算结果如图9所示.

由图9可知，2种方法计算的覆盖范围形心均会随着初始速度的增加逐渐向坐标原点偏移，且覆盖范围逐渐逼近于理想状态下的覆盖范围. 利用本文方法得到的 $a$、 $b$相对于常重力下的变化量均随着初始速度的增加而减小. 当初始速度达到30 m/s时， $a$、 $b$的相对变化量可以分别减小到8.48%和9.64%；当初始速度为30 m/s时， $c$减小为1.71 cm，为常重力下覆盖范围直径的8.1%.

为了进一步定量评价推荐方法与文献[8]方法的差别，给出2种方法得到的 $a$、 $b$和 $c$随初始速度 $v{'_0}$的变化，如图10所示. 文献[8]方法相对于本文方法的误差如表1所示.

在离心机降雨模拟试验中，雨滴在下落时会对试验模型产生一定的冲击作用，造成边坡模型破坏无法达到试验要求. 降雨的冲击作用在自然环境中和实验室条件下均无法避免，因此在离心机试验时应考虑离心机降雨冲击作用的合理范围.

在自然环境中，雨滴在下落时由于受到空气阻力作用会出现收尾速度，即雨滴下落过程后期将以匀速下落至地面，此收尾速度一般为4~10 m/s^[10]，因此离心机降雨冲击作用的合理范围，应以雨滴下落带来的能量符合自然条件下的情况为参考. 根据计算可知，离心机试验中的能量比尺为 $1/{N^3}$，即试验中雨滴下落的冲击能量应为自然条件下的 $1/{N^3}$.

离心机试验中应满足的试验条件为

(25) ${N^3}{E_{{\rm{ks}}}} \leqslant {E_{{\rm{kz}}}}.$

式中： ${E_{{\rm{ks}}}}$为实验室中雨滴落地动能， ${E_{{\rm{kz}}}}$为自然环境中雨滴落地动能. 假设自然条件下雨滴的粒径为d，根据比尺关系和相关能量公式，雨滴落地速度应有如下关系：

(26) $\frac{1}{2}m{v^2}{N^3} < \frac{1}{2}M{V^2}.$

式中： $m$为模型雨滴质量， $M$为自然环境下雨滴质量， $v$为模型雨滴落地速度， $V$为自然环境下雨滴收尾速度. 将式（26）展开可得

(27) $\frac{2}{3}{\rho _{\rm{w}}}{\left( {\frac{d}{N}} \right)^3}{N^3}{v^2} < \frac{2}{3}{\rho _{\rm{w}}}{d^3}{V^2}.$

式中： ${\rho _{\rm{w}}}$为水的密度.

根据式（12）可知，在考虑空气阻力的离心模拟超重力环境下，雨滴主要受超重力Ng和空气阻力的影响，其他作用力与之相比数量级相差较大，在本节计算中忽略不计.

降雨覆盖范围中心点处的雨滴下落距离最短、落地速度最大，为了保证计算结果的适用性，以此处的雨滴下落过程为研究目标. 根据理论力学相关结论可知，模型雨滴下落速度与所受加速度 ${a_{\rm{p}}}$之间的关系为

(28) ${v^2} - v_0^{'2} = 2{a_{\rm{p}}}h,$

(29) $v = \sqrt {v_0^{'2} + 2{a_{\rm{p}}}h} .$

式中：

(30) ${a_{\rm{p}}} = \frac{{mNg - f}}{m}.$

离心机降雨试验的雨滴冲击作用判据为

(31) $\sqrt {v_0^{'2} + 2{a_{\rm{p}}}h} < V.$

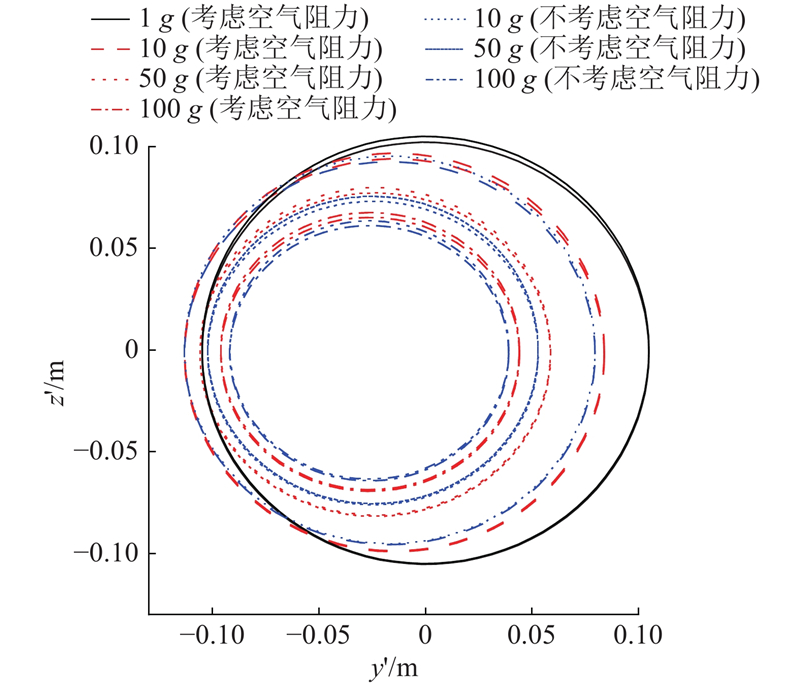
在离心模拟超重力环境下进行降雨模拟试验，由于在高g值下土体模型对降雨的均匀性和降雨强度有着较高的敏感性，研究并预测离心机内降雨模拟覆盖范围的大小变化规律对离心机降雨模拟试验有十分重要的意义. 如图11所示，是否考虑空气阻力作用的降雨模拟覆盖范围相对误差较小且变化规律相似. 为了方便研究变化规律，在计算实验室内降雨覆盖范围时，采用不考虑空气阻力的控制方程.

根据式（22）、（23）可知，离心机降雨模拟覆盖范围可以描述为

(32) $\frac{{{{\left( {y' + c} \right)}^2}}}{a} + \frac{{{{\left( {z'} \right)}^2}}}{b} = 1.$

式中：

(33) $a = v{'_0}t \sin\alpha \cos\;(\omega t),$

(34) $b = v{'_0}t \sin\alpha ,$

(35) $c = (v{'_0}t \cos\alpha + {R_0})\sin\;(\omega t) - \omega {R_0}t \cos\;(\omega t).$

t可由式（21）确定.

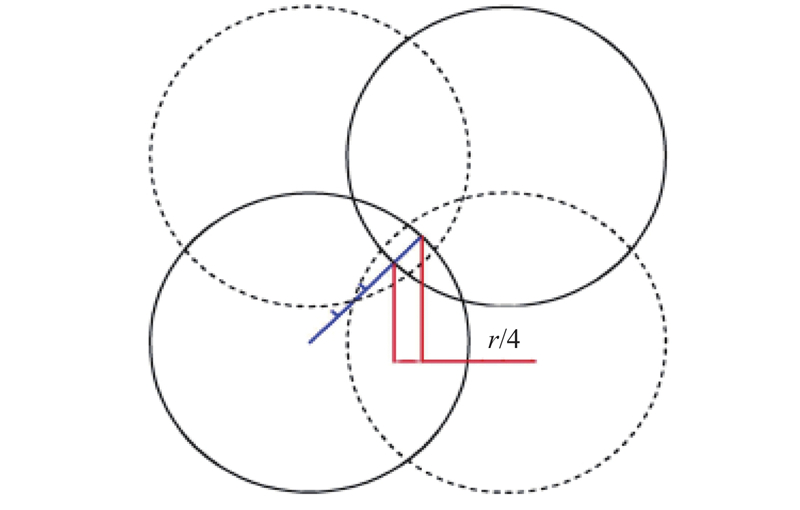
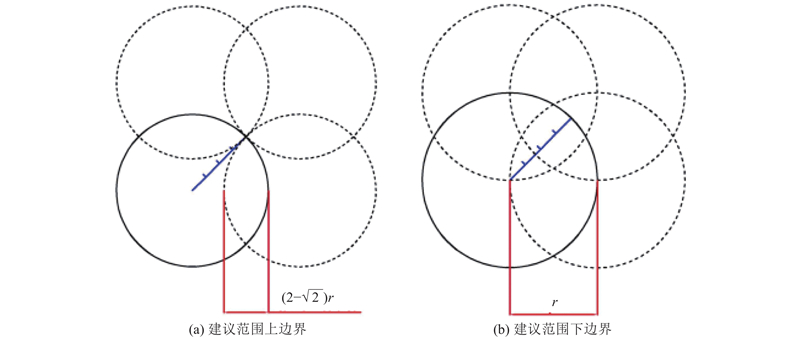
设离心机上降雨模拟的模型箱长、宽、高分别为L、W、H，计算结果表明，当使用多个喷嘴进行降雨试验时，由于喷雾范围为类圆形，为了避免产生明显的盲区，保证更好的降雨均匀性，相邻喷嘴应设置15%~30%的喷雾重叠区. 如图12所示，以相邻“对角线”处的覆盖范围半径重叠 $r/4$（ $r$为理想覆盖范围半径）作为理想重叠面积，以保证降雨覆盖在全区域内的均匀性.

根据前文的分析结果以及几何关系，设喷嘴在模型箱长度方向上排布l个，在宽度方向上排布w个，同时设 $r = \left( {a + b} \right)/2$用来近似代替理想情况下的覆盖范围半径. 离心机内降雨模拟装置喷嘴排布时，应有以下几何限制条件：

(36) $w\left( {2a - r'} \right) + r' = W,$

(37) $l\left( {2b - r'} \right) + r' = L.$

式中： $r'$为相邻覆盖范围沿半径方向重叠长度.

如图13所示，在实际情况中，工况变化较复杂，覆盖范围不能准确满足理想的重叠面积，所以重叠面积应以保证试验过程中不出现降雨“空白”区域和不“过度重叠”（重叠部分不超过相邻覆盖范围圆心）为基准，即“对角线”处覆盖范围圆心距应为 $\sqrt 2 r\sim 2r$. 根据计算可知，此时 $\left( {2 - \sqrt 2 } \right)r < $ $ r' < r$，覆盖范围重叠区域面积占比为18.15%~27.74%，满足均匀性要求.

根据式（36）、（37）可知，离心机内降雨模拟试验工况均匀性判据为

(38) $\left. \begin{array}{l} \dfrac{{W + r\left( {2 - \sqrt 2 } \right)\left( {w - 1} \right)}}{{2w}} < a < \dfrac{{W + r\left( {w - 1} \right)}}{{2w}},\\ \dfrac{{L + r\left( {2 - \sqrt 2 } \right)\left( {l - 1} \right)}}{{2l}} < b < \dfrac{{W + r\left( {w - 1} \right)}}{{2w}}. \end{array} \right\}$

综合分析结果，根据ZJU-400离心机中降雨装置进行建议工况分析. 在ZJU-400中， ${R_0} = 4\;{\rm{m}}$， $L = 1\;{\rm{m}}$， $W = 0.4\;{\rm{m}}$， $l = 5$， $w = 2$，以自然环境中2 mm雨滴为参考，则100 g下ZJU-400的建议试验工况范围为

(39) $\left. \begin{array}{l} 0.13\;{\rm{m}} < h < 0.22\;{\rm{m}} ,\\ 4\;{\rm{m/s}} < v{'_0} < 18\;{\rm{m/s}}. \end{array} \right\}$

开展离心模拟超重力环境下雨滴下落的运动学和动力学分析，得到雨滴下落的加速度，求解不同初始条件下的雨滴运动轨迹和单喷嘴降雨的覆盖范围，对比了不同分析方法，明确了离心模拟超重力环境下雨滴下落时受力及运动过程的求解思路. 讨论了不同计算理论下雨滴下落过程中受N值、下落高度及初始速度影响的覆盖范围以及前人计算方法与推荐计算方法之间的误差：当忽略雨滴位移引起的离心力变化和 $x'$方向上的科氏力时，100 g下e_a、e_b分别为4.16%和1.03%，e_c达到28.22%.

以实际情况下离心机降雨冲击作用和降雨均匀性要求为判据，提出离心机降雨模拟过程的建议试验工况. 雨滴的最终落地速度不应超过降雨冲击能量要求的限制速度；为了保证降雨均匀性，试验中N值、雨滴速度、下落距离等工况应使降雨覆盖范围保持15%~30%的重叠面积.

为了便于计算和求解，将实验室内降雨模拟与自然情况进行类比等效，但是实验室内降雨模拟试验与自然界中的降雨存在诸多不同之处：例如自然界中降雨会改变空气温度和湿度等环境进而影响土体性质，自然界中降雨与渗流管涌等现象关系复杂. 为了分析自然界中降雨对边坡土体的影响效应，应进一步地研究降雨的相关性质及其试验相似性.