定义一个完全对称网络图 ${{G}} = [N,A]$ . $N$ $N = \{ 0,1,2,\cdots n\}$ ${N'} = \{ 1,2,\cdots n\}$ $A$ $A = \{ (i,j)|i,$ $ j \in N,i \ne j\} $ 表1 所示.
(4) ${u_{iJ}} = \left\{ \begin{array}{l} {\rm{ }}\left\lfloor {{{{q_i}} / {{q^{{V_J}}}}}} \right\rfloor ,\;J{\rm{ = 1}} ;\\ \left\lfloor {{{\left( {{q_i} - \displaystyle\sum\limits_{j = 1}^{J - 1} {{u_{ij}}{q^{{V_J}}}} } \right)} / {{q^{{V_J}}}}}} \right\rfloor,\;J = 2,\cdots,m - 1 ; \\ \left\lceil {{{\left( {{q_i} - \displaystyle\sum\limits_{j = 1}^{J - 1} {{u_{ij}}{q^{{V_J}}}} } \right)} / {{q^{{V_J}}}}}} \right\rceil ,\;J = m .\\ \end{array} \right.$
(6) $ f_i^z({x^z}) = \left\{ {\begin{array}{*{20}{l}} {1,}&\!\!\!\!\!\!{{x^z} \in (0,{\lambda ^z}(1));}\\ \!\!\!\!{\dfrac{{{\lambda ^z}(2) - {x^z}}}{{{\lambda ^z}(2) - {\lambda ^z}(1)}},}&\!\!\!\!\!\!{{x^z} \in \!\left[ {{\lambda ^z}(1),\!{\lambda ^z}(2)} \right],z\! =\! 1,2,3,i \in N'\!;\!}\\ {0,}&\!\!\!\!\!\!{{x^z} \in ({\lambda ^z}(2),\infty ).} \end{array}} \right.$
(8) ${\rm{Sa}}(i,k) = \left\{ \begin{array}{l} {\rm{L}}{{\rm{e}}_1}f_i^1\left( {t_i^1 - {t_{ik}} - {t_{0k}}} \right){\vartheta _1}{\rm{ + 10}}{\vartheta _2} + \\ \qquad{\rm{ L}}{{\rm{e}}_1}f_i^3({\rm{Ls}}(i,k)){\vartheta _3}{\rm{, }}\;{S_{1i}} \leqslant {t_{0k}} + {t_{ik}} < t_i^1;\\ 10{\vartheta _1} + {\rm{L}}{{\rm{e}}_1}f_i^2\left( {{t_{ik}} + {t_{0k}} - t_i^2} \right){\vartheta _2} + \\ \qquad{\rm{ L}}{{\rm{e}}_1}f_i^3({\rm{Ls}}(i,k)){\vartheta _3}{\rm{, }}\;t_i^2 < {t_{0k}} + {t_{ik}} \leqslant {S_{2i}};{\rm{ }}\\ 10{\vartheta _1} + 10{\vartheta _2} + \\ \qquad{\rm{ L}}{{\rm{e}}_1}f_i^3({\rm{Ls}}(i,k)){\vartheta _3}{\rm{, }}\;t_i^1 \leqslant {t_{0k}} + {t_{ik}} \leqslant t_i^2;{\rm{ }}\\ {\rm{L}}{{\rm{e}}_1}f_i^3({\rm{Ls}}(i,k)){\vartheta _3}{\rm{, }}\;{S_{1i}} - \psi \leqslant {t_{0k}} + {t_{ik}}{\rm{ < }}{S_{1i}}{\rm{, }}\\ \qquad{S_{2i}} \leqslant {t_{0k}} + {t_{ik}}{\rm{ < }}{S_{2i}}+\psi .{\rm{ }} \end{array} \right.$
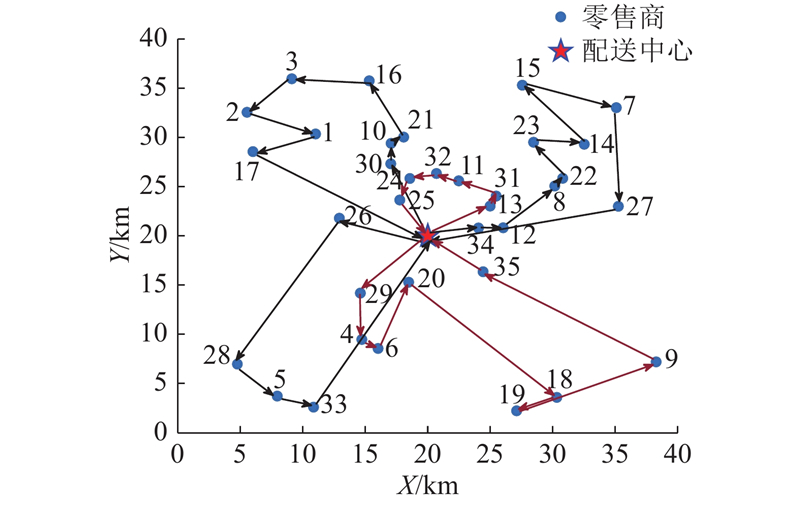
通过资料查阅与实地调研,获取零售商位置相对坐标 $(X,Y)$ ${{\rm{Le}}_1} = 9.5$ ${{\rm{Le}}_2} = 8.0$ ${{\rm{Le}}_3} = 6.0$ $[t_i^1,t_i^2,{S_{2i}}]$ $[17,37,63]$ $[0.028,0.120,0.240]$ . 配送点的基本零售商信息如表2 所示. 运输过程中保温箱种类m =4,参数如表3 所示.
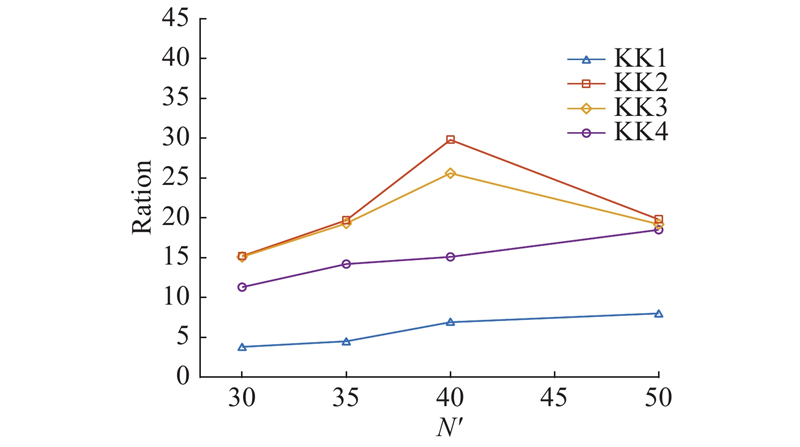
选取12组数值算例,命名为Vxy , 其中x 为零售商人数,y 为货物卸货率. 在3.1节基本案例取值基础上,应用3种算法. 零售商人数为30、35、40、50,货物卸载率为10、14、16 kg/min,进行组合求解. 当零售商人数>35时,零售商需求、零售商位置坐标、零售商时间窗、行驶速度均随机生成,其中 $ {q}_{i}\sim 100+U(\rm{0},\rm{200})$ $X,Y\sim U(0,40)$ $t_i^1\sim {t_{0k}} + U(0,2)$ $t_i^2\sim t_i^1 + U(0.5,4)$ ${S_{2i}}\sim t_i^2 + U(0,2)$ ${v_{ij}}\sim 20 + U(0,20)$ . 如表5 所示为3种算法收敛结果.
[1]
张东. 电子商务环境下冷链物流的顾客满意度研究[D]. 天津: 天津理工大学, 2018.
[本文引用: 1]
ZHANG Dong. Research on customer satisfaction of cold chain logistics in E-commerce environment [D]. Tianjin: Tianjin University of Technology, 2018.
[本文引用: 1]
[2]
杜志平, 胡永彪, 陈永立 基于客户满意度的生鲜农产品末端配送的VRP研究
[J]. 供应链管理 , 2020 , 1 (1 ): 113 - 128
[本文引用: 1]
DU Zhi-ping, HU Yong-biao, CHEN Yong-li Research on the vehicle routing problem in the distribution of fresh agricultural products based on customer satisfaction
[J]. Supply Chain Management , 2020 , 1 (1 ): 113 - 128
[本文引用: 1]
[3]
张亚明, 李娜 基于精英单亲遗传算法的冷链物流VRP模型优化研究
[J]. 数学的实践与认识 , 2016 , 46 (4 ): 87 - 96
[本文引用: 1]
ZHANG Ya-ming, LI Na Research on elite selection based partheno-genetic algorithm under optimized cold chain logistics VRP model
[J]. Mathematics in Practice and Theory , 2016 , 46 (4 ): 87 - 96
[本文引用: 1]
[4]
YANG B, HU ZH, WEI C, et al Routing with time-windows for multiple environmental vehicle types
[J]. Computers and Industrial Engineering , 2015 , 89 : 150 - 161
DOI:10.1016/j.cie.2015.02.001
[本文引用: 1]
[5]
RABBANI M, TAHERI M, RAVANBAKHSH M A bi-objective vehicle routing problem with time window by considering customer satisfaction
[J]. International Journal of Strategic Decision Sciences , 2016 , 7 (2 ): 16 - 39
DOI:10.4018/IJSDS.2016040102
[6]
SIVARAMKUMAR V, THANSEKHAR M R, SARAVANAN R, et al Multi-objective vehicle routing problem with time windows: improving customer satisfaction by considering gap time
[J]. Part B: Journal of Engineering Manufacture , 2017 , 231 (7 ): 1248 - 1263
DOI:10.1177/0954405415586608
[本文引用: 1]
[7]
韩亚娟, 彭运芳, 魏航, 等 超启发式遗传算法求解带软时间窗的车辆路径问题
[J]. 计算机集成制造系统 , 2019 , 25 (10 ): 2571 - 2579
[本文引用: 1]
HAN Ya-juan, PENG Yun-fang, WEI Hang, et al Hyper heuristic genetic algorithm for vehicle routing problem with soft time windows
[J]. Computer Integrated Manufacturing Systems , 2019 , 25 (10 ): 2571 - 2579
[本文引用: 1]
[8]
ZHANG H Z, ZHANG Q W, MA L, et al A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows
[J]. Information Sciences , 2019 , 490 : 166 - 190
DOI:10.1016/j.ins.2019.03.070
[本文引用: 1]
[9]
ZULVIA F E, KUO R J, NUGROHO D Y A many-objective gradient evolution algorithm for solving a green vehicle routing problem with time windows and time dependency for perishable products
[J]. Journal of Cleaner Production , 2020 , 242 : 118428
DOI:10.1016/j.jclepro.2019.118428
[10]
AFSHAR B M, MEHRABI A, SAFARI H, et al A green vehicle routing problem with customer satisfaction criteria
[J]. Journal of Industrial Engineering International , 2016 , 12 (4 ): 529 - 544
DOI:10.1007/s40092-016-0163-9
[本文引用: 1]
[11]
梁承姬, 黄涛, 徐德洪, 等 改进遗传算法求解带模糊时间窗冷链配送问题
[J]. 广西大学学报 , 2016 , 41 (3 ): 826 - 835
[本文引用: 1]
LIANG Cheng-ji, HUANG Tao, XU De-hong, et al A solution for cold chain distribution with fuzzy time window based on improved Genetic Algorithm
[J]. Journal of Guangxi University , 2016 , 41 (3 ): 826 - 835
[本文引用: 1]
[12]
王娇. 基于多目标决策的生鲜电商联合配送车辆路径优化研究[D].重庆: 重庆大学, 2017.
[本文引用: 1]
WANG Jiao. Study on optimization of joint distribution VRP in fresh product E-commerce based on multi-objective decision [D]. Chongqing: Chongqing University, 2017.
[本文引用: 1]
[14]
林清国. 基于混合遗传算法的有时间窗车辆路径问题研究[D]. 济南: 山东大学, 2007.
[本文引用: 1]
LIN Qing-guo. Research of the vehicle routing problem with time windows based on hybrid Genetic Algorithm [D]. Jinan: Shandong University, 2007.
[本文引用: 1]
[15]
高志波, 龙科军, 王倩, 等 车辆路线问题的自适应遗传模拟退火算法
[J]. 中国科技论文 , 2017 , 12 (7 ): 764 - 769
DOI:10.3969/j.issn.2095-2783.2017.07.009
[本文引用: 1]
GAO Zhi-bo, LONG Ke-jun, WANG Qian, et al A self adaptive genetically simulated annealing algorithm of vehicle routing problem
[J]. China Sciencepaper , 2017 , 12 (7 ): 764 - 769
DOI:10.3969/j.issn.2095-2783.2017.07.009
[本文引用: 1]
[16]
RABBANI M, TAHAEI M, FARROKHI A H, et al. Using meta-heuristic algorithms and hybrid of them to solve multi compartment vehicle routing problem [C]// 2017 Proceedings of IEEE International Conference on Industrial Engineering and Engineering Management . Singapore: IEEE, 2017: 1022-1026.
[本文引用: 1]
[17]
XIAO Y Y, ZHAO Q H, KAKU I, et al Development of a fuel consumption optimization model for the capacitated vehicle routing problem
[J]. Computers and Operations Research , 2012 , 39 : 1419 - 1431
DOI:10.1016/j.cor.2011.08.013
[本文引用: 1]
[18]
杨珍花, 赖平仲, 汤洋, 等 冷藏车多车型混合配送调度优化
[J]. 系统工程 , 2015 , 33 (10 ): 28 - 36
[本文引用: 1]
YANG Zhen-hua, LAN Ping-zhong, TANG Yang, et al Mix distribution dispatch optimization by multi-type refrigerated trucks
[J]. Systems Engineering , 2015 , 33 (10 ): 28 - 36
[本文引用: 1]
[20]
韩晓龙. 水果物流网络及节点布局研究[D]. 武汉: 华中农业大学, 2009.
[本文引用: 1]
HAN Xiao-long. Research on fruit logistics network and nodes layout [D]. Wuhan: Huazhong Agricultural University, 2009.
[本文引用: 1]
[21]
EMRAH D, TOLGA B, GILBERT L The bi-objective pollution-routing problem
[J]. European Journal of Operational Research , 2014 , 232 : 464 - 478
DOI:10.1016/j.ejor.2013.08.002
[本文引用: 1]
[22]
康凯, 韩杰, 普玮, 等 生鲜农产品冷链物流低碳配送路径优化研究
[J]. 计算机工程与应用 , 2019 , 55 (2 ): 259 - 265
DOI:10.3778/j.issn.1002-8331.1709-0276
[本文引用: 1]
KANG Kai, HAN Jie, PU Wei, et al Optimization research on cold chain distribution routes considering carbon emissions for fresh agricultural products
[J]. Computer Engineering and Applications , 2019 , 55 (2 ): 259 - 265
DOI:10.3778/j.issn.1002-8331.1709-0276
[本文引用: 1]
[23]
HERRERA F, LOZANO M, VERDEGAY J L Tackling real-coded genetic algorithms: operators and tools for behavioral analysis
[J]. Artificial Intelligence Review , 1998 , 12 (4 ): 265 - 319
DOI:10.1023/A:1006504901164
[本文引用: 1]
[24]
CHEN Z, LU Z X, QIAN J A new non-geometric transmission parameter optimization design method for HMCVT based on improved GA and maximum transmission efficiency
[J]. Computers and Electronics in Agriculture , 2019 , 167 : 105034
DOI:10.1016/j.compag.2019.105034
[本文引用: 1]
[26]
XIN J F, ZHONG J B, LI S X, et al Greedy mechanism based particle swarm optimization for path planning problem of an unmanned surface vehicle
[J]. Sensors , 2019 , 19 (21 ): 4620
DOI:10.3390/s19214620
[本文引用: 1]
[27]
BABIN G, DENEAULT S, LAPORTE G Improvements to the or-opt heuristic for the symmetric travelling salesman problem
[J]. Journal of the Operational Research Society , 2007 , 58 (3 ): 402 - 407
DOI:10.1057/palgrave.jors.2602160
[本文引用: 1]
[28]
OSMAN I H Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem
[J]. Annals of Operations Research , 1993 , 41 (4 ): 421 - 451
DOI:10.1007/BF02023004
[本文引用: 1]
1
... 近年来,随着各界对易耗损产品质量重视程度的提升,我国冷链物流迅速发展. 在冷链物流市场中,生鲜食品是冷链物流的主体. 以果蔬、肉禽和水产为主的生鲜产品接近冷链物流商品总量的60%,是冷链物流运输中的绝对主体[1 ] . 其中果蔬的刚性消费属性使得对果蔬的研究更具现实意义. 从家庭需要的频率和需求量来说,水果的需求量更多,研究发展冷链水果运输的必要性更强. 从水果生命周期来说,水果的生命周期略短于肉禽以及水产,这是由于随着时间的推动,水果的鲜活度逐渐下降,造成水果口感变差,而在顾客决策购买过程中,口感是购买水果的关键指标. 最后,水果品类繁多,配送地区地形各异,不同时节下对恒温冷藏要求较高,同时水果外部易破损. 据2018年数据显示,我国肉类、水产品和果蔬类农产品冷链腐损率分别为8%、10% 和15%[2 ] . 基于水果易腐损的特性,冷链水果运输可以选择保温箱运输方式,减轻因碰撞和温度不恒定造成的腐损. 目前,我国冷链水果运输的发展水平不高,导致冷链水果运输成本消耗巨大. 与传统物流相比,冷链水果运输不仅要降低运输成本,而且对水果的品质要求更高. 由于消费者消费选择增多,顾客黏性降低,如何提高顾客满意度成为企业物流配送考虑的问题之一[3 ] . 针对冷链运输中极易耗损的水果,如何在降低冷链水果运输成本的基础上增加顾客满意度,是冷链水果运输亟待解决的问题. ...
1
... 近年来,随着各界对易耗损产品质量重视程度的提升,我国冷链物流迅速发展. 在冷链物流市场中,生鲜食品是冷链物流的主体. 以果蔬、肉禽和水产为主的生鲜产品接近冷链物流商品总量的60%,是冷链物流运输中的绝对主体[1 ] . 其中果蔬的刚性消费属性使得对果蔬的研究更具现实意义. 从家庭需要的频率和需求量来说,水果的需求量更多,研究发展冷链水果运输的必要性更强. 从水果生命周期来说,水果的生命周期略短于肉禽以及水产,这是由于随着时间的推动,水果的鲜活度逐渐下降,造成水果口感变差,而在顾客决策购买过程中,口感是购买水果的关键指标. 最后,水果品类繁多,配送地区地形各异,不同时节下对恒温冷藏要求较高,同时水果外部易破损. 据2018年数据显示,我国肉类、水产品和果蔬类农产品冷链腐损率分别为8%、10% 和15%[2 ] . 基于水果易腐损的特性,冷链水果运输可以选择保温箱运输方式,减轻因碰撞和温度不恒定造成的腐损. 目前,我国冷链水果运输的发展水平不高,导致冷链水果运输成本消耗巨大. 与传统物流相比,冷链水果运输不仅要降低运输成本,而且对水果的品质要求更高. 由于消费者消费选择增多,顾客黏性降低,如何提高顾客满意度成为企业物流配送考虑的问题之一[3 ] . 针对冷链运输中极易耗损的水果,如何在降低冷链水果运输成本的基础上增加顾客满意度,是冷链水果运输亟待解决的问题. ...
基于客户满意度的生鲜农产品末端配送的VRP研究
1
2020
... 近年来,随着各界对易耗损产品质量重视程度的提升,我国冷链物流迅速发展. 在冷链物流市场中,生鲜食品是冷链物流的主体. 以果蔬、肉禽和水产为主的生鲜产品接近冷链物流商品总量的60%,是冷链物流运输中的绝对主体[1 ] . 其中果蔬的刚性消费属性使得对果蔬的研究更具现实意义. 从家庭需要的频率和需求量来说,水果的需求量更多,研究发展冷链水果运输的必要性更强. 从水果生命周期来说,水果的生命周期略短于肉禽以及水产,这是由于随着时间的推动,水果的鲜活度逐渐下降,造成水果口感变差,而在顾客决策购买过程中,口感是购买水果的关键指标. 最后,水果品类繁多,配送地区地形各异,不同时节下对恒温冷藏要求较高,同时水果外部易破损. 据2018年数据显示,我国肉类、水产品和果蔬类农产品冷链腐损率分别为8%、10% 和15%[2 ] . 基于水果易腐损的特性,冷链水果运输可以选择保温箱运输方式,减轻因碰撞和温度不恒定造成的腐损. 目前,我国冷链水果运输的发展水平不高,导致冷链水果运输成本消耗巨大. 与传统物流相比,冷链水果运输不仅要降低运输成本,而且对水果的品质要求更高. 由于消费者消费选择增多,顾客黏性降低,如何提高顾客满意度成为企业物流配送考虑的问题之一[3 ] . 针对冷链运输中极易耗损的水果,如何在降低冷链水果运输成本的基础上增加顾客满意度,是冷链水果运输亟待解决的问题. ...
基于客户满意度的生鲜农产品末端配送的VRP研究
1
2020
... 近年来,随着各界对易耗损产品质量重视程度的提升,我国冷链物流迅速发展. 在冷链物流市场中,生鲜食品是冷链物流的主体. 以果蔬、肉禽和水产为主的生鲜产品接近冷链物流商品总量的60%,是冷链物流运输中的绝对主体[1 ] . 其中果蔬的刚性消费属性使得对果蔬的研究更具现实意义. 从家庭需要的频率和需求量来说,水果的需求量更多,研究发展冷链水果运输的必要性更强. 从水果生命周期来说,水果的生命周期略短于肉禽以及水产,这是由于随着时间的推动,水果的鲜活度逐渐下降,造成水果口感变差,而在顾客决策购买过程中,口感是购买水果的关键指标. 最后,水果品类繁多,配送地区地形各异,不同时节下对恒温冷藏要求较高,同时水果外部易破损. 据2018年数据显示,我国肉类、水产品和果蔬类农产品冷链腐损率分别为8%、10% 和15%[2 ] . 基于水果易腐损的特性,冷链水果运输可以选择保温箱运输方式,减轻因碰撞和温度不恒定造成的腐损. 目前,我国冷链水果运输的发展水平不高,导致冷链水果运输成本消耗巨大. 与传统物流相比,冷链水果运输不仅要降低运输成本,而且对水果的品质要求更高. 由于消费者消费选择增多,顾客黏性降低,如何提高顾客满意度成为企业物流配送考虑的问题之一[3 ] . 针对冷链运输中极易耗损的水果,如何在降低冷链水果运输成本的基础上增加顾客满意度,是冷链水果运输亟待解决的问题. ...
基于精英单亲遗传算法的冷链物流VRP模型优化研究
1
2016
... 近年来,随着各界对易耗损产品质量重视程度的提升,我国冷链物流迅速发展. 在冷链物流市场中,生鲜食品是冷链物流的主体. 以果蔬、肉禽和水产为主的生鲜产品接近冷链物流商品总量的60%,是冷链物流运输中的绝对主体[1 ] . 其中果蔬的刚性消费属性使得对果蔬的研究更具现实意义. 从家庭需要的频率和需求量来说,水果的需求量更多,研究发展冷链水果运输的必要性更强. 从水果生命周期来说,水果的生命周期略短于肉禽以及水产,这是由于随着时间的推动,水果的鲜活度逐渐下降,造成水果口感变差,而在顾客决策购买过程中,口感是购买水果的关键指标. 最后,水果品类繁多,配送地区地形各异,不同时节下对恒温冷藏要求较高,同时水果外部易破损. 据2018年数据显示,我国肉类、水产品和果蔬类农产品冷链腐损率分别为8%、10% 和15%[2 ] . 基于水果易腐损的特性,冷链水果运输可以选择保温箱运输方式,减轻因碰撞和温度不恒定造成的腐损. 目前,我国冷链水果运输的发展水平不高,导致冷链水果运输成本消耗巨大. 与传统物流相比,冷链水果运输不仅要降低运输成本,而且对水果的品质要求更高. 由于消费者消费选择增多,顾客黏性降低,如何提高顾客满意度成为企业物流配送考虑的问题之一[3 ] . 针对冷链运输中极易耗损的水果,如何在降低冷链水果运输成本的基础上增加顾客满意度,是冷链水果运输亟待解决的问题. ...
基于精英单亲遗传算法的冷链物流VRP模型优化研究
1
2016
... 近年来,随着各界对易耗损产品质量重视程度的提升,我国冷链物流迅速发展. 在冷链物流市场中,生鲜食品是冷链物流的主体. 以果蔬、肉禽和水产为主的生鲜产品接近冷链物流商品总量的60%,是冷链物流运输中的绝对主体[1 ] . 其中果蔬的刚性消费属性使得对果蔬的研究更具现实意义. 从家庭需要的频率和需求量来说,水果的需求量更多,研究发展冷链水果运输的必要性更强. 从水果生命周期来说,水果的生命周期略短于肉禽以及水产,这是由于随着时间的推动,水果的鲜活度逐渐下降,造成水果口感变差,而在顾客决策购买过程中,口感是购买水果的关键指标. 最后,水果品类繁多,配送地区地形各异,不同时节下对恒温冷藏要求较高,同时水果外部易破损. 据2018年数据显示,我国肉类、水产品和果蔬类农产品冷链腐损率分别为8%、10% 和15%[2 ] . 基于水果易腐损的特性,冷链水果运输可以选择保温箱运输方式,减轻因碰撞和温度不恒定造成的腐损. 目前,我国冷链水果运输的发展水平不高,导致冷链水果运输成本消耗巨大. 与传统物流相比,冷链水果运输不仅要降低运输成本,而且对水果的品质要求更高. 由于消费者消费选择增多,顾客黏性降低,如何提高顾客满意度成为企业物流配送考虑的问题之一[3 ] . 针对冷链运输中极易耗损的水果,如何在降低冷链水果运输成本的基础上增加顾客满意度,是冷链水果运输亟待解决的问题. ...
Routing with time-windows for multiple environmental vehicle types
1
2015
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
A bi-objective vehicle routing problem with time window by considering customer satisfaction
0
2016
Multi-objective vehicle routing problem with time windows: improving customer satisfaction by considering gap time
1
2017
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
超启发式遗传算法求解带软时间窗的车辆路径问题
1
2019
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
超启发式遗传算法求解带软时间窗的车辆路径问题
1
2019
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows
1
2019
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
A many-objective gradient evolution algorithm for solving a green vehicle routing problem with time windows and time dependency for perishable products
0
2020
A green vehicle routing problem with customer satisfaction criteria
1
2016
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
改进遗传算法求解带模糊时间窗冷链配送问题
1
2016
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
改进遗传算法求解带模糊时间窗冷链配送问题
1
2016
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
1
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
1
... 在构建顾客满意度模型方面,Yang等[4 -6 ] 解决了硬时间窗下满意度问题. 对早到或迟到间隔施加惩罚系数,通过最小化惩罚成本提高顾客满意度. 韩亚娟等[7 ] 在前人基础上针对不同的间隔时间段,分别设置不同的惩罚系数. Zhang等[8 -10 ] 引入模糊梯形函数表征软时间窗下顾客满意度:在顾客期望时间窗内到达,顾客满意度为最大;在期望时间点与最大容忍时间点内到达,顾客满意度随偏离期待时间窗的时间间隔呈线性递减函数. 梁承姬等[11 ] 在模糊梯度函数基础上,将顾客需求大小作为优先级构建满意度模型. 王娇[12 ] 改变现存论文中满意度与时间呈线性的假设,通过引入个体时间敏感性系数,构造体现个体满意度差异的非线性模型. 然而,现有求解软时间窗下顾客满意度的研究仍然较少,部分文献假设满意度与早到、迟到时间间隔呈线性递减关系;部分提出个体化差异的非线性满意度模型,不过体现个人差异的敏感性系数均为主观设定. 在实际情况下,顾客满意行为更加复杂,满意度感知可能在一定早到/迟到时间间隔下保持不变. 现有论文中基于模糊理论的线性求解满意度感知模型无法正确拟合现实情况,且无法估计早到、迟到对满意度的影响权值. 因此,本研究引入灰度白化权函数构建改进满意度模型. 通过调研获取顾客对于早到、迟到、耗损程度评价指标满意度等级感知节点;建立不同满意度等级的满意度分段函数;输出不同评价指标对满意度影响权值,旨在建立更加准确的顾客满意度模型. ...
带软时间窗的集配货一体化 VRP 改进模拟退火算法优化研究
1
2009
... 路径规划问题是典型的组合优化问题,设计启发式算法可以在较短时间内获得优质解. 邓爱民等[13 ] 综合考虑软时间窗、车辆的固定成本、满载系数等条件,建立集配货一体化车辆路径问题数学模型. 采用模拟退火算法,结合线路内和线路间交换机制,并且增加算法记忆功能,最后依据双终止准则终止求解. 林清国[14 ] 系统性地比较了遗传算法和模拟退火算法的算法性能,根据2种算法设计过程中存在的弊端,提出糅合全局探索与局部优化的遗传模拟退火算法. 高志波等[15 ] 针对多车型、多目标带软时间窗路径优化问题,建立双层目标规划模型,上层求解车辆范围,下层利用自适应遗传模拟退火算法实现路径优化,通过与标准遗传算法的对比,验证了改进算法的有效性. Rabbani等[16 ] 以Pollution Routing Problem (PRP)为背景,以多车厢车辆为运输载体,满足顾客多种产品需求,探索不同速度、不同载重下,碳排放与燃油费用的变化幅度,分别采用标准遗传算法、模拟退火算法和混合遗传模拟退火算法进行算例分析,通过成本与计算时间综合评估算法性能. 以上遗传模拟退火算法以相等概率选择2个父代进行交叉运算,并根据模拟退火Metropolis准则决定子代构成. 现有论文中对父代的选择缺乏针对性,易造成随机交叉,破坏优秀基因,增加算法求解时间. 针对现有遗传模拟退火算法的不足,本研究提出改进遗传算法进行模型求解:定期针对“超级个体”进行局部模拟退火操作,以提高算法求解速率与求解质量;结合不同邻域搜索操作加强优秀基因搜索深度和跳出局优解的能力. ...
带软时间窗的集配货一体化 VRP 改进模拟退火算法优化研究
1
2009
... 路径规划问题是典型的组合优化问题,设计启发式算法可以在较短时间内获得优质解. 邓爱民等[13 ] 综合考虑软时间窗、车辆的固定成本、满载系数等条件,建立集配货一体化车辆路径问题数学模型. 采用模拟退火算法,结合线路内和线路间交换机制,并且增加算法记忆功能,最后依据双终止准则终止求解. 林清国[14 ] 系统性地比较了遗传算法和模拟退火算法的算法性能,根据2种算法设计过程中存在的弊端,提出糅合全局探索与局部优化的遗传模拟退火算法. 高志波等[15 ] 针对多车型、多目标带软时间窗路径优化问题,建立双层目标规划模型,上层求解车辆范围,下层利用自适应遗传模拟退火算法实现路径优化,通过与标准遗传算法的对比,验证了改进算法的有效性. Rabbani等[16 ] 以Pollution Routing Problem (PRP)为背景,以多车厢车辆为运输载体,满足顾客多种产品需求,探索不同速度、不同载重下,碳排放与燃油费用的变化幅度,分别采用标准遗传算法、模拟退火算法和混合遗传模拟退火算法进行算例分析,通过成本与计算时间综合评估算法性能. 以上遗传模拟退火算法以相等概率选择2个父代进行交叉运算,并根据模拟退火Metropolis准则决定子代构成. 现有论文中对父代的选择缺乏针对性,易造成随机交叉,破坏优秀基因,增加算法求解时间. 针对现有遗传模拟退火算法的不足,本研究提出改进遗传算法进行模型求解:定期针对“超级个体”进行局部模拟退火操作,以提高算法求解速率与求解质量;结合不同邻域搜索操作加强优秀基因搜索深度和跳出局优解的能力. ...
1
... 路径规划问题是典型的组合优化问题,设计启发式算法可以在较短时间内获得优质解. 邓爱民等[13 ] 综合考虑软时间窗、车辆的固定成本、满载系数等条件,建立集配货一体化车辆路径问题数学模型. 采用模拟退火算法,结合线路内和线路间交换机制,并且增加算法记忆功能,最后依据双终止准则终止求解. 林清国[14 ] 系统性地比较了遗传算法和模拟退火算法的算法性能,根据2种算法设计过程中存在的弊端,提出糅合全局探索与局部优化的遗传模拟退火算法. 高志波等[15 ] 针对多车型、多目标带软时间窗路径优化问题,建立双层目标规划模型,上层求解车辆范围,下层利用自适应遗传模拟退火算法实现路径优化,通过与标准遗传算法的对比,验证了改进算法的有效性. Rabbani等[16 ] 以Pollution Routing Problem (PRP)为背景,以多车厢车辆为运输载体,满足顾客多种产品需求,探索不同速度、不同载重下,碳排放与燃油费用的变化幅度,分别采用标准遗传算法、模拟退火算法和混合遗传模拟退火算法进行算例分析,通过成本与计算时间综合评估算法性能. 以上遗传模拟退火算法以相等概率选择2个父代进行交叉运算,并根据模拟退火Metropolis准则决定子代构成. 现有论文中对父代的选择缺乏针对性,易造成随机交叉,破坏优秀基因,增加算法求解时间. 针对现有遗传模拟退火算法的不足,本研究提出改进遗传算法进行模型求解:定期针对“超级个体”进行局部模拟退火操作,以提高算法求解速率与求解质量;结合不同邻域搜索操作加强优秀基因搜索深度和跳出局优解的能力. ...
1
... 路径规划问题是典型的组合优化问题,设计启发式算法可以在较短时间内获得优质解. 邓爱民等[13 ] 综合考虑软时间窗、车辆的固定成本、满载系数等条件,建立集配货一体化车辆路径问题数学模型. 采用模拟退火算法,结合线路内和线路间交换机制,并且增加算法记忆功能,最后依据双终止准则终止求解. 林清国[14 ] 系统性地比较了遗传算法和模拟退火算法的算法性能,根据2种算法设计过程中存在的弊端,提出糅合全局探索与局部优化的遗传模拟退火算法. 高志波等[15 ] 针对多车型、多目标带软时间窗路径优化问题,建立双层目标规划模型,上层求解车辆范围,下层利用自适应遗传模拟退火算法实现路径优化,通过与标准遗传算法的对比,验证了改进算法的有效性. Rabbani等[16 ] 以Pollution Routing Problem (PRP)为背景,以多车厢车辆为运输载体,满足顾客多种产品需求,探索不同速度、不同载重下,碳排放与燃油费用的变化幅度,分别采用标准遗传算法、模拟退火算法和混合遗传模拟退火算法进行算例分析,通过成本与计算时间综合评估算法性能. 以上遗传模拟退火算法以相等概率选择2个父代进行交叉运算,并根据模拟退火Metropolis准则决定子代构成. 现有论文中对父代的选择缺乏针对性,易造成随机交叉,破坏优秀基因,增加算法求解时间. 针对现有遗传模拟退火算法的不足,本研究提出改进遗传算法进行模型求解:定期针对“超级个体”进行局部模拟退火操作,以提高算法求解速率与求解质量;结合不同邻域搜索操作加强优秀基因搜索深度和跳出局优解的能力. ...
车辆路线问题的自适应遗传模拟退火算法
1
2017
... 路径规划问题是典型的组合优化问题,设计启发式算法可以在较短时间内获得优质解. 邓爱民等[13 ] 综合考虑软时间窗、车辆的固定成本、满载系数等条件,建立集配货一体化车辆路径问题数学模型. 采用模拟退火算法,结合线路内和线路间交换机制,并且增加算法记忆功能,最后依据双终止准则终止求解. 林清国[14 ] 系统性地比较了遗传算法和模拟退火算法的算法性能,根据2种算法设计过程中存在的弊端,提出糅合全局探索与局部优化的遗传模拟退火算法. 高志波等[15 ] 针对多车型、多目标带软时间窗路径优化问题,建立双层目标规划模型,上层求解车辆范围,下层利用自适应遗传模拟退火算法实现路径优化,通过与标准遗传算法的对比,验证了改进算法的有效性. Rabbani等[16 ] 以Pollution Routing Problem (PRP)为背景,以多车厢车辆为运输载体,满足顾客多种产品需求,探索不同速度、不同载重下,碳排放与燃油费用的变化幅度,分别采用标准遗传算法、模拟退火算法和混合遗传模拟退火算法进行算例分析,通过成本与计算时间综合评估算法性能. 以上遗传模拟退火算法以相等概率选择2个父代进行交叉运算,并根据模拟退火Metropolis准则决定子代构成. 现有论文中对父代的选择缺乏针对性,易造成随机交叉,破坏优秀基因,增加算法求解时间. 针对现有遗传模拟退火算法的不足,本研究提出改进遗传算法进行模型求解:定期针对“超级个体”进行局部模拟退火操作,以提高算法求解速率与求解质量;结合不同邻域搜索操作加强优秀基因搜索深度和跳出局优解的能力. ...
车辆路线问题的自适应遗传模拟退火算法
1
2017
... 路径规划问题是典型的组合优化问题,设计启发式算法可以在较短时间内获得优质解. 邓爱民等[13 ] 综合考虑软时间窗、车辆的固定成本、满载系数等条件,建立集配货一体化车辆路径问题数学模型. 采用模拟退火算法,结合线路内和线路间交换机制,并且增加算法记忆功能,最后依据双终止准则终止求解. 林清国[14 ] 系统性地比较了遗传算法和模拟退火算法的算法性能,根据2种算法设计过程中存在的弊端,提出糅合全局探索与局部优化的遗传模拟退火算法. 高志波等[15 ] 针对多车型、多目标带软时间窗路径优化问题,建立双层目标规划模型,上层求解车辆范围,下层利用自适应遗传模拟退火算法实现路径优化,通过与标准遗传算法的对比,验证了改进算法的有效性. Rabbani等[16 ] 以Pollution Routing Problem (PRP)为背景,以多车厢车辆为运输载体,满足顾客多种产品需求,探索不同速度、不同载重下,碳排放与燃油费用的变化幅度,分别采用标准遗传算法、模拟退火算法和混合遗传模拟退火算法进行算例分析,通过成本与计算时间综合评估算法性能. 以上遗传模拟退火算法以相等概率选择2个父代进行交叉运算,并根据模拟退火Metropolis准则决定子代构成. 现有论文中对父代的选择缺乏针对性,易造成随机交叉,破坏优秀基因,增加算法求解时间. 针对现有遗传模拟退火算法的不足,本研究提出改进遗传算法进行模型求解:定期针对“超级个体”进行局部模拟退火操作,以提高算法求解速率与求解质量;结合不同邻域搜索操作加强优秀基因搜索深度和跳出局优解的能力. ...
1
... 路径规划问题是典型的组合优化问题,设计启发式算法可以在较短时间内获得优质解. 邓爱民等[13 ] 综合考虑软时间窗、车辆的固定成本、满载系数等条件,建立集配货一体化车辆路径问题数学模型. 采用模拟退火算法,结合线路内和线路间交换机制,并且增加算法记忆功能,最后依据双终止准则终止求解. 林清国[14 ] 系统性地比较了遗传算法和模拟退火算法的算法性能,根据2种算法设计过程中存在的弊端,提出糅合全局探索与局部优化的遗传模拟退火算法. 高志波等[15 ] 针对多车型、多目标带软时间窗路径优化问题,建立双层目标规划模型,上层求解车辆范围,下层利用自适应遗传模拟退火算法实现路径优化,通过与标准遗传算法的对比,验证了改进算法的有效性. Rabbani等[16 ] 以Pollution Routing Problem (PRP)为背景,以多车厢车辆为运输载体,满足顾客多种产品需求,探索不同速度、不同载重下,碳排放与燃油费用的变化幅度,分别采用标准遗传算法、模拟退火算法和混合遗传模拟退火算法进行算例分析,通过成本与计算时间综合评估算法性能. 以上遗传模拟退火算法以相等概率选择2个父代进行交叉运算,并根据模拟退火Metropolis准则决定子代构成. 现有论文中对父代的选择缺乏针对性,易造成随机交叉,破坏优秀基因,增加算法求解时间. 针对现有遗传模拟退火算法的不足,本研究提出改进遗传算法进行模型求解:定期针对“超级个体”进行局部模拟退火操作,以提高算法求解速率与求解质量;结合不同邻域搜索操作加强优秀基因搜索深度和跳出局优解的能力. ...
Development of a fuel consumption optimization model for the capacitated vehicle routing problem
1
2012
... 式中:m 为保温箱种类数. 式(1)为车辆总固定使用成本;式(2)中,单位距离燃料消耗量可以表示为依赖货车载货量的线性函数[17 ] ,以空车单位距离燃料消耗量 $U$ ${H_1}$ $\;\rho $ ${H_1}$ $\;\rho $ ${t_{ik}}$ $\Delta \theta $ ${R_1}$ ${s_J}$
冷藏车多车型混合配送调度优化
1
2015
... 同理,设置相同高、中、低三级评分体系 ${\rm{Le}}{_1}$ ${\rm{Le}}{_2}$ ${\rm{Le}}{_3}$ [18 ] 为 ...
冷藏车多车型混合配送调度优化
1
2015
... 同理,设置相同高、中、低三级评分体系 ${\rm{Le}}{_1}$ ${\rm{Le}}{_2}$ ${\rm{Le}}{_3}$ [18 ] 为 ...
基于白化权函数聚类法的航电系统效能评估
2
2012
... 通过白化权函数构造满意度模型. 白化权函数是在已有信息下对灰色朦胧集内部白化规律的数学表达,用来定量描述某指标值属于某灰类的程度[19 ] . 由于提高零售商属于高满意度灰类的概率有利于增加零售商复订几率,利用灰度白化权函数分别计算不同早到、迟到时间以及货损程度属于高满意度等级的概率. 基于白化权函数的满意度计算逻辑如图1 所示. ...
... 对于零售商( $i \in {{{N}}'}$ $f_i^1\left( {{x^1}} \right)$ $f_i^2\left( {{x^2}} \right)$ $f_i^3\left( {{x^3}} \right)$ [19 -20 ] 如下: ...
基于白化权函数聚类法的航电系统效能评估
2
2012
... 通过白化权函数构造满意度模型. 白化权函数是在已有信息下对灰色朦胧集内部白化规律的数学表达,用来定量描述某指标值属于某灰类的程度[19 ] . 由于提高零售商属于高满意度灰类的概率有利于增加零售商复订几率,利用灰度白化权函数分别计算不同早到、迟到时间以及货损程度属于高满意度等级的概率. 基于白化权函数的满意度计算逻辑如图1 所示. ...
... 对于零售商( $i \in {{{N}}'}$ $f_i^1\left( {{x^1}} \right)$ $f_i^2\left( {{x^2}} \right)$ $f_i^3\left( {{x^3}} \right)$ [19 -20 ] 如下: ...
1
... 对于零售商( $i \in {{{N}}'}$ $f_i^1\left( {{x^1}} \right)$ $f_i^2\left( {{x^2}} \right)$ $f_i^3\left( {{x^3}} \right)$ [19 -20 ] 如下: ...
1
... 对于零售商( $i \in {{{N}}'}$ $f_i^1\left( {{x^1}} \right)$ $f_i^2\left( {{x^2}} \right)$ $f_i^3\left( {{x^3}} \right)$ [19 -20 ] 如下: ...
The bi-objective pollution-routing problem
1
2014
... 式中: $I$ $Z_1^j$ $Z_2^j$ [21 ] . 当方案 $j$ $\left( {\mathop {\min }\limits_{i \in I} Z_1^i} \right)/Z_1^j$ $j$ $Z_2^j/(\mathop {\max }\limits_{i \in I} Z_2^i)$
生鲜农产品冷链物流低碳配送路径优化研究
1
2019
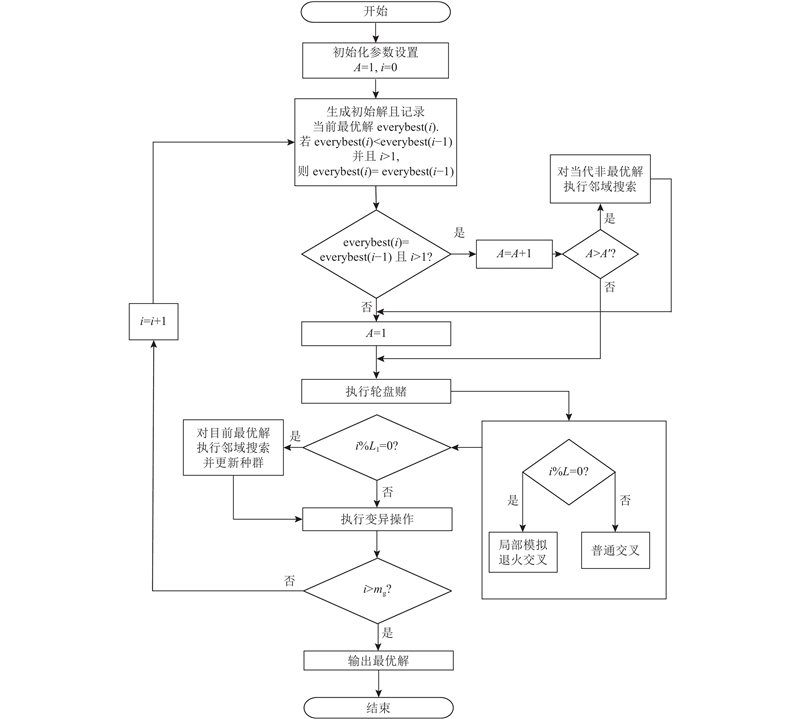
... 传统路径规划问题为NP-hard问题[22 ] ,本研究针对软时间窗下的多目标路径规划问题VRPSTW,求解更为复杂. 目前解决多目标路径规划问题(vehicle routing problem. VRP)最常用的求解方法包括2种:精确算法和启发式算法. 精确算法适用于解决规模较小的线性规划问题,而启发式算法能够在较短时间内获得大规模非线性问题的较优解. 基于模型(M2)非线性的特性,设计改进遗传算法对模型进行求解. ...
生鲜农产品冷链物流低碳配送路径优化研究
1
2019
... 传统路径规划问题为NP-hard问题[22 ] ,本研究针对软时间窗下的多目标路径规划问题VRPSTW,求解更为复杂. 目前解决多目标路径规划问题(vehicle routing problem. VRP)最常用的求解方法包括2种:精确算法和启发式算法. 精确算法适用于解决规模较小的线性规划问题,而启发式算法能够在较短时间内获得大规模非线性问题的较优解. 基于模型(M2)非线性的特性,设计改进遗传算法对模型进行求解. ...
Tackling real-coded genetic algorithms: operators and tools for behavioral analysis
1
1998
... 遗传算法是通用搜索算法,是使用受自然种群遗传学启发的原理来发展问题的解决方案[23 ] ,适用于求解全局优化问题,具有较强的全局寻优能力,但易于陷入局部解;模拟退火算子模仿固体的退火过程,随着温度参数的不断下降,算法中的解趋于稳定. 模拟退火算子会以一定的概率跳出过程中的稳定解,以寻找目标函数的全局最优解. ...
A new non-geometric transmission parameter optimization design method for HMCVT based on improved GA and maximum transmission efficiency
1
2019
... 综合借鉴2种算法的思路,以遗传算法作为主体算法,对“超级个体[24 ] ”引入模拟退火思想,以一定概率接受劣解,避免种群快速收敛至局部解. 在迭代过程中,充分利用优质解的寻优思想,采用邻域搜索生成邻域解,取高适应度的邻域解取代种群中数量冗余的染色体;为了有效跳出局部解,通过差异化思想搜索异于最优解的其他染色体的邻域解,更新当前收敛解. ...
A tabu search heuristicfor the vehicle routing problem
1
1994
... 算法中染色体采用自然数编码,配送中心用0表示,其他自然数表示零售商,其中相邻2个0之间的部分构成一条行驶线路,多条行驶路线构成一条染色体. 定义同时满足车辆载重和最大路长限制,但超出最大容忍时间窗的路径所在的染色体为不可行解. 借鉴Gendreau等[25 ] 的思想,构造有限地接受不可行解的机制,以便通过不可行解的过渡,搜索到更好的可行解,从而提升算法的全局寻优能力. 在设计接受不可行解的机制时,对每一个零售商的最大容忍时间上、下限扩大时间段 $\psi $ $[{S_{1i}} - \psi ,{S_{1i}}]$ $[{S_{2i}},{S_{2i}} + \psi ]$
Greedy mechanism based particle swarm optimization for path planning problem of an unmanned surface vehicle
1
2019
... 为了利用全体染色体信息,迭代采用邻域搜索生成邻域解,邻域搜索是一种高效寻优的搜索方法,文章选用2-opt[26 ] ,or-opt[27 ] ,1-1 interchange[28 ] 3种方式,每次随机选择一种邻域搜索方式进行邻域搜索得到邻域解. ...
Improvements to the or-opt heuristic for the symmetric travelling salesman problem
1
2007
... 为了利用全体染色体信息,迭代采用邻域搜索生成邻域解,邻域搜索是一种高效寻优的搜索方法,文章选用2-opt[26 ] ,or-opt[27 ] ,1-1 interchange[28 ] 3种方式,每次随机选择一种邻域搜索方式进行邻域搜索得到邻域解. ...
Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem
1
1993
... 为了利用全体染色体信息,迭代采用邻域搜索生成邻域解,邻域搜索是一种高效寻优的搜索方法,文章选用2-opt[26 ] ,or-opt[27 ] ,1-1 interchange[28 ] 3种方式,每次随机选择一种邻域搜索方式进行邻域搜索得到邻域解. ...