裂纹是装备和工程结构中常见的缺陷形式. 在交变载荷的作用下,裂纹持续扩展至结构所能承受的极限值将引发结构失效或倒塌,造成严重的经济损失甚至人员伤亡. 譬如,Alexander L. Kielland 号钻井平台单个支撑腿的疲劳裂纹在海洋环境载荷作用下不断扩展,最终导致整座平台倾覆[1]. 因此,探索裂纹的扩展规律并准确预测疲劳裂纹扩展过程,对保障装备和结构的安全运行具有重大的应用价值和科学意义.
断裂力学的Paris公式是当前疲劳裂纹扩展预测的主要手段[2]. 譬如,何文涛等[3]利用Paris公式分析船侧纵骨节点疲劳趋势和裂纹扩展规律;陈飞宇等[4]基于该公式,针对导管架平台管节点,预测其疲劳裂纹扩展过程. 然而,经典的Paris公式主要适用于恒幅载荷下疲劳裂纹扩展的预测,但是在实际工况下变幅载荷广泛存在,此时的裂纹扩展具有高载迟滞和低载加速的特点,Paris公式无法解释这类现象[5]. 因此已有多种Paris修正公式提出,主要有Wheeler疲劳裂纹扩展公式[6]、统一疲劳寿命预测[7](unified fatigue life prediction,UFLP),也称统一疲劳裂纹扩展模型. 修正公式可以对变幅载荷下疲劳试验中的现象予以合理解释,并且在实验环境中取得了较为理想的预测效果. 基于上述断裂力学理论,诸多学者开展了疲劳裂纹扩展评估方法的研究. 譬如,Dirik等[8]基于扩展有限元方法(extended finite element method, XFEM)实现了带孔铝板的疲劳裂纹扩展路径预测;Lesiuk等[9]采用裂纹扩展逐步计算方法预测在混合载荷加载下的疲劳裂纹扩展过程;张宝峰等[10-11]建立K型管节点疲劳裂纹多尺度有限元模型,并且通过疲劳试验验证了模型的准确性. 但是,如果从工程应用的角度出发,不可避免地会遇到多种不确定因素[12](几何、材料和制造等)对裂纹扩展规律产生影响的问题,极大提高了裂纹扩展预测的难度. 除此之外,修正公式较经典Paris公式,一般存在参数众多,拟合难度大的问题,从而加剧了其在应用中的困难. 总之,现阶段变幅载荷作用下的疲劳裂纹扩展预测存在极大挑战.
综上,如果将疲劳裂纹扩展分析理论和监测方法进行有效融合和优势互补,既完成对疲劳裂纹当前位置的有效感知,又可以进行变幅载荷下裂纹扩展趋势的分析和预测,将极大促进疲劳裂纹扩展预测技术的发展,有利于结构安全性的提高[18]. 对于该方法的实现,本质上可以归结于滤波问题,但采用传统的滤波算法难以完成对多项不确定因素的处理. 动态贝叶斯网络(dynamic Bayesian network,DBN)作为描述数据变量之间依赖关系的有向无环图,可以将实时监测数据、可靠性数据以及物理模型有效融合,通过输入数据对多个随机节点进行推理更新以消除不确定因素的对于损伤预测精度的影响[19]. 宋悦等[20]综合考虑多种不确定因素建立了光电探测系统的DBN模型,增强了性能退化预测效果. 杨旗等[21]融合行走时整体以及局部细节信息建立了双尺度步态识别DBN模型,提高了步态识别的准确性. 关于DBN在结构损伤和寿命预测方面的研究较少,如何建立变幅载荷下结构疲劳裂纹扩展的DBN模型问题亟须解决.
本研究提出基于DBN的变幅载荷下疲劳裂纹扩展预测方法. 基于UFLP,建立疲劳裂纹扩展状态方程,分析裂纹扩展过程中的不确定因素,确立不确定因素之间的因果关系;构建面向裂纹扩展的DBN模型,结合观测数据的注入,实现网络节点在时间序列上的传播计算;选取粒子滤波(particle filter,PF)作为DBN推断算法,根据观测到的真实裂纹信息,动态更新网络不确定性因素节点,实现不确定因素在疲劳裂纹扩展过程的不断修正,完成裂纹扩展的动态跟随预测;通过算例,验证该方法是否可以有效消除由裂纹扩展过程中的不确定因素所导致的预测结果不准确.
1. 统一疲劳裂纹扩展模型
应用Cui等[7]提出的UFLP作为理论分析工具,以支撑DBN的构建,该疲劳裂纹扩展模型将横幅载荷和变幅载荷对裂纹扩展的影响纳入公式中进行集成表示:
式中:aT为裂纹长度;
Cui等[22]采用虚拟强度
虚拟强度代表
高载后出现的低载将削弱迟滞效应,但是如果先出现低载,对裂纹扩展无明显影响[23],所以将模型表示为高载产生的塑性区
式中:
2. 面向裂纹扩展的动态贝叶斯网络
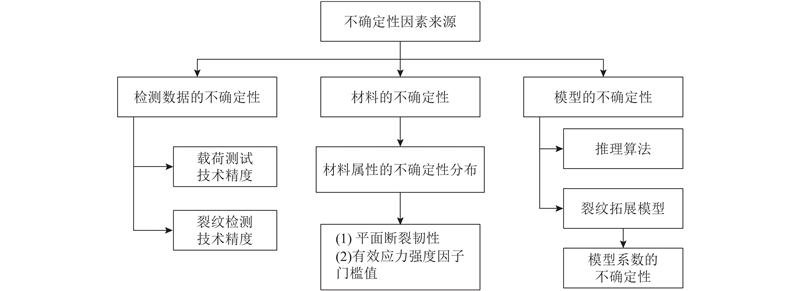
2.1. 疲劳裂纹扩展不确定性因素分析
图 1
1)检测数据的不确定性. 疲劳裂纹扩展DBN模型最重要的是载荷和裂纹信息输入,而结构所受到的载荷和裂纹信息则需要传感器进行信息采集,因此存在由于传感器精度导致的测量误差.
2)材料物理属性的不确定性. 裂纹扩展速率与材料性能有较大的关系,而材料性能受到较多因素的影响,如制造工艺、元素比重. 对于UFLP来说,
3)模型的不确定性. UFLP中模型系数
2.2. 动态贝叶斯网络模型变量选取
模型系数的不确定性是裂纹预测精度不足的重要原因之一. 影响裂纹扩展速率的参数较多,如果全部考虑完全这些参数,会使模型变得臃肿复杂,因此须对模型参数进行敏感度分析,将低敏感度的参数定义为固定值,提高模型整体计算效率.
Wang等[27]根据钛合金TC4-ELI在横幅载荷下的实验数据,在将扩展速率曲线斜率系数
表 1 D16Cz合金板中心裂纹扩展模型参数值
Tab.1
| 参数 | 取值 |
| | 1.42×10−8 |
| | 1.4903 |
| | 6 |
| | 10−6 |
| | 26.72 |
| | 3.6 |
| | 15.93 |
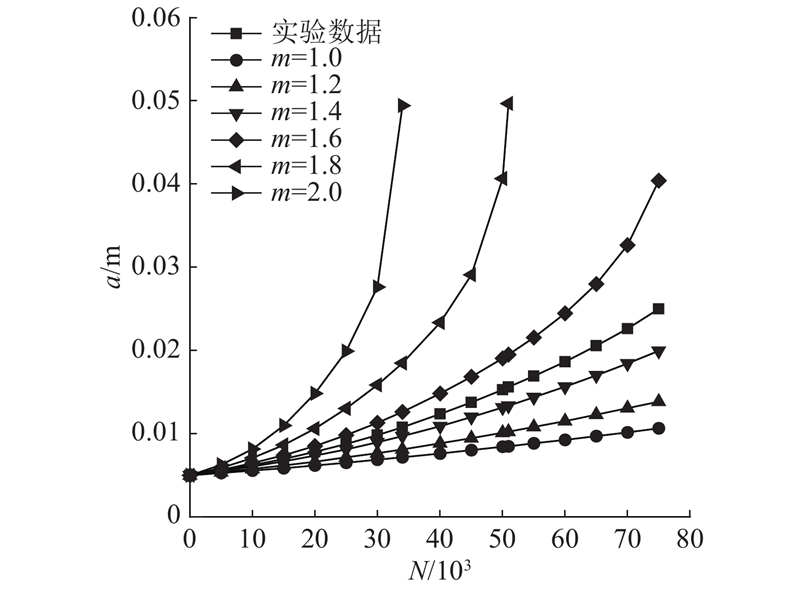
图 2
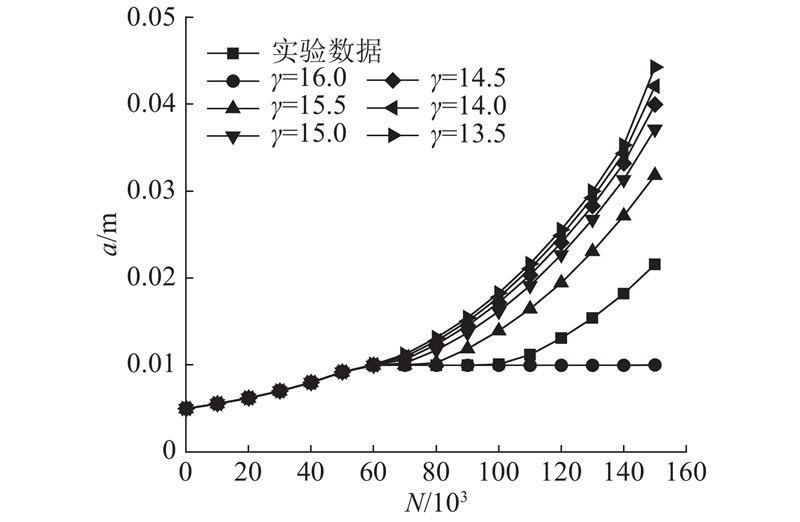
图 3
图 3
参数
Fig.3
Effect of parameters
对于均匀拉伸的中心裂纹板,裂纹几何形状因子表达式[29]如下:
式中:
不同材料几何形状因子计算公式存在一定的误差,所以将公式修改为
式中:
综上,选取
2.3. 动态贝叶斯网络模型的构建
根据UFLP以及上文分析的不确定性因素对于疲劳裂纹预测的敏感度,建立如图4所示的DBN的疲劳裂纹扩展模型. 采用3种不同类型的节点来构造DBN模型:1)函数节点代表确定性函数;2)随机节点表示变量对于父节点是随机的,具有不确定性,即模型的不确参量;3)观测节点为系统的输入部分,即传感器采集到的载荷信息以及检测到的裂纹长度信息. 每个时刻的BN模型节点之间采用实心箭头相连,表示这个时刻内确定性的传播计算,而相邻的时间片节点之间采用虚箭头相连接,表示节点随时间变化的影响. 根据UFLP,由传感器采集的载荷信息
图 4
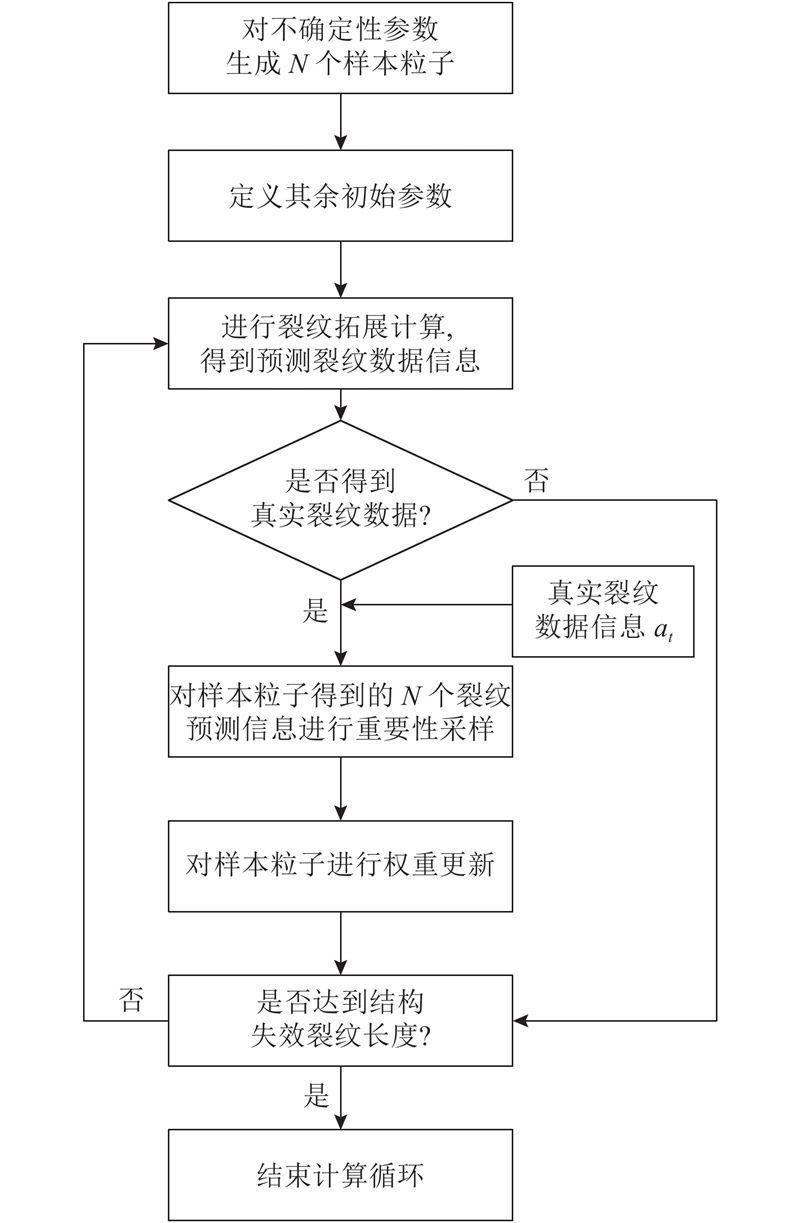
2.4. 动态贝叶斯网络推理
在建立裂纹扩展的DBN模型后,便完成了裂纹在时序过程中的传播计算,但是由于存在多个不确定性变量,原模型预测会逐渐偏离实际值. 因此,须采用合适的推理算法对模型中随机节点进行更新,从而减小状态变量的不确定性带来的影响[30].
采用PF算法作为DBN推理算法. PF主要是在不确定性节点的后验概率中抽取随机状态粒子来表示,通过赋予这些粒子权重,然后根据向模型中输入的观测信息来比较各个粒子计算的偏离程度,迭代更新粒子权重,去除小权重的粒子,逐渐逼近真实后验分布[31].
根据UFLP,如果预测间隔
系统的测量方程为
式中:
DBN中存在多个不确定性因素,这些因素之间可能互相存在影响. 在生成粒子时,首先将S个不确定性因素每个都独立生成N个粒子,将各个不确定因素生成的粒子进行随机组合,形成N个模型参数组合,即
重要性权值
式中:p为后验分布函数,q为重要性分布函数.
随着更新过程的不断迭代,会产生粒子的退化现象. 采用重采样的方法来避免这种情况发生,具体思想为:权值大的粒子会被复制,权值小的粒子会被去除. 重采样后的所有粒子的权值均变为
图 5
3. 算例分析
表 2 AlMgSi1-T6铝合金的化学组成成分
Tab.2
| % | ||||||||
| w(Si) | w(Fe) | w(Cu) | w(Mn) | w(Mg) | w(Cr) | w(Zn) | w(Ti) | 其他 |
| 0.70~1.30 | 0.50 | 0.10 | 0.40~1.00 | 0.60~1.20 | 0.25 | 0.20 | 0.10 | 0.05 |
表 3 AlMgSi1-T6铝合金的物理性能
Tab.3
| | | n′ | | |
| | | 0.064 | 32 | 2.184−1.007R[33] |
采用液压机对初始裂纹长度为
表 4 周期性高载疲劳试验载荷大小
Tab.4
| | | | | | | | |
| 1.5 | 30.0 | 28.5 | 0.05 | 45.0 | 1000 | 500 |
基于DBN的疲劳裂纹扩展模型主要目的是通过推理更新校准不确定性参数的数值,实现对疲劳裂纹扩展的动态跟随和当前时间节点裂纹状态的准确获知. 在执行贝叶斯推理前须由疲劳裂纹扩展实验得到各个参数的先验分布. 本例中假设初始裂纹长度为确定值,而其余各个参数的先验分布被定义为:
图 6
图 7
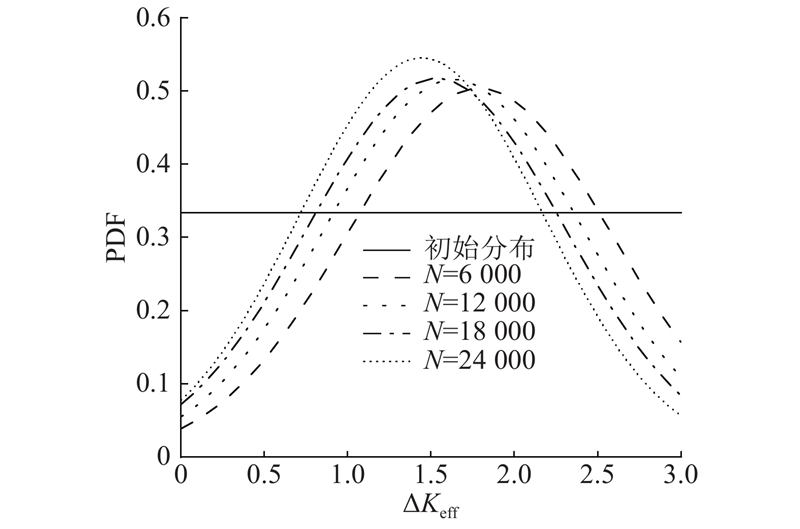
图 8
图 8
每个检查点后的
Fig.8
PDF of parameters
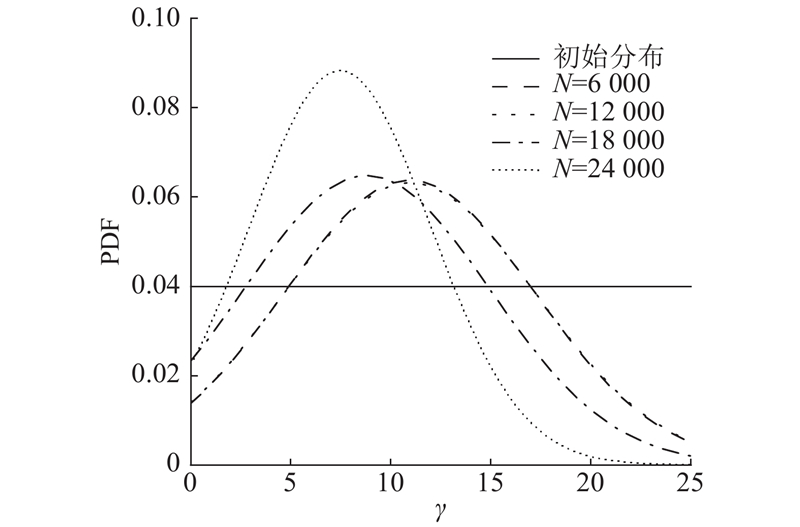
图 9
图 9
每个检查点后的
Fig.9
PDF of parameters
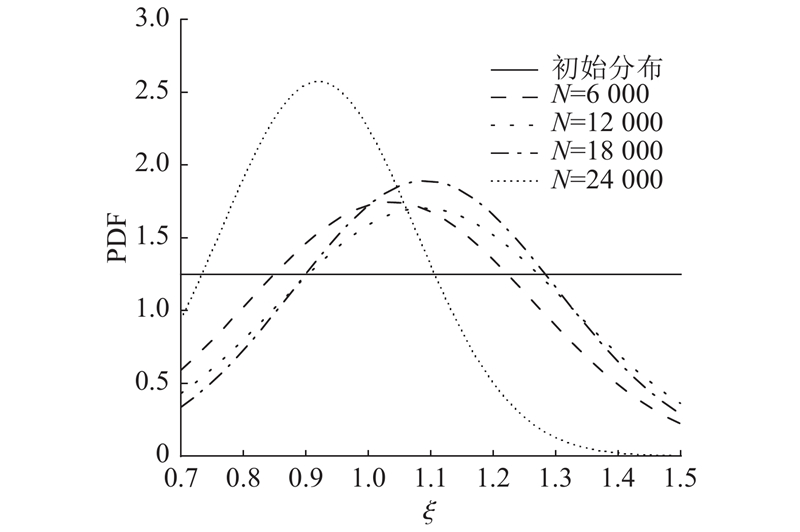
图 10
图 10
每个检查点后的
Fig.10
PDF of parameters
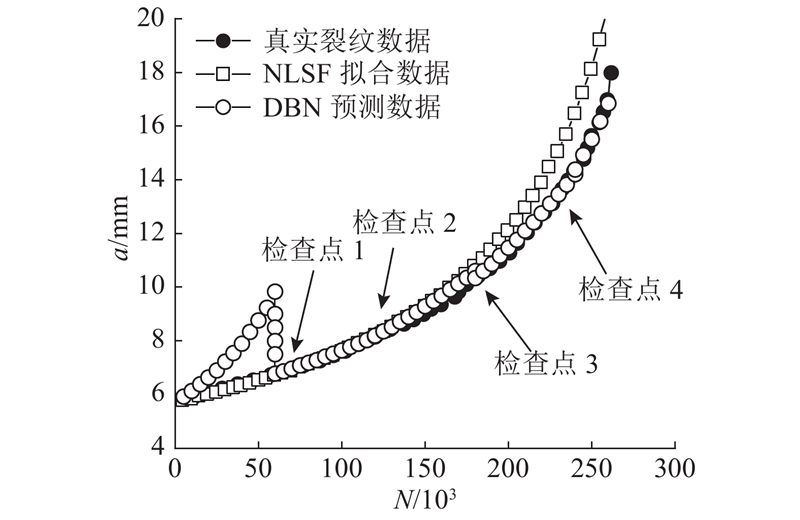
如图11所示为通过非线性最小二乘法拟合(nonlinear least-square fitting,NLSF)得到的参数进行裂纹预测和采用DBN进行裂纹预测的对比图. 结果表明,由于各个参数的不确定性,裂纹长度的误差会在每个检测点间隔内逐渐叠加累积,所以在第1个检测点处,由于参数的先验分布平均值偏离实际值较大,DBN预测的结果比真实值偏离3.14 mm,而NLSF预测结果与真实值相差0.03 mm;在第1个检查点处采用PF算法,参数的不确定度显著降低,所以在之后的2个检查点处2种方法计算得到的预测值基本一致;在第4个检测点处,PF预测结果与真实值相差0.27 mm,而NLSF预测结果与真实值相差2.36 mm. 可以看出,本研究所提方法可以有效减小不确定因素给裂纹扩展预测带来的影响,实现在变幅载荷下对裂纹扩展过程进行实时动态跟随和预测.
图 11
4. 结 语
本研究应用动态贝叶斯网络解决疲劳裂纹预测过程中存在不确定性因素干扰的问题,基于UFLP模型,通过分析不确定因素对于疲劳裂纹扩展过程的敏感度,建立变幅载荷下的疲劳裂纹扩展DBN模型. 通过向DBN模型中输入真实裂纹数据,采用PF算法实现真实数据与预测数据的相互融合,即采用真实数据逐步修正裂纹扩展预测过程中所存在的不确定因素以提高裂纹预测结果的准确度,完成对于结构疲劳裂纹扩展的动态跟随和准确预测. 从算例结果可以看出,采用所提方法可以让裂纹扩展过程中的预测模型相关参量的不确定度随着检查点次数的增加而逐渐减小,因此本研究所提方法与传统的拟合方法相比具有更好的预测精准度.
后续的工作主要有两部分:在变幅载荷下的疲劳裂纹扩展DBN模型基础上考虑实际结构中常受到的混合载荷作用下的疲劳裂纹扩展规律;将混合载荷作用下应力强度因子计算方法与DBN模型进行相互融合,实现对于任意载荷情况下疲劳裂纹的扩展预测.
参考文献
The Alexander L. Kielland disaster revisited: a review by an experienced welding engineer of the catastrophic North Sea platform collapse
[J].DOI:10.1007/s11668-019-00680-4 [本文引用: 1]
复杂载荷作用下潜艇结构疲劳裂纹扩展预报方法
[J].DOI:10.3404/j.issn.1672-7649.2012.02.002 [本文引用: 1]
Procedure to predict fatigue crack growth of submarine structures under complex loading conditions
[J].DOI:10.3404/j.issn.1672-7649.2012.02.002 [本文引用: 1]
船体纵骨典型节点疲劳裂纹扩展寿命评估
[J].
Life assessment of fatigue crack growth of typical details in hull longitudinals
[J].
基于裂纹扩展的海洋平台疲劳可靠性分析
[J].
Reliability assessment and fatigue life of jacket platform based on the theory of crack propagation
[J].
变幅载荷下疲劳裂纹扩展规律试验研究综述
[J].DOI:10.3969/j.issn.1007-7294.2010.05.015 [本文引用: 1]
An overview on experimental investigation on variable amplitude fatigue crack growth rule
[J].DOI:10.3969/j.issn.1007-7294.2010.05.015 [本文引用: 1]
Spectrum loading and crack growh
[J].
A unified fatigue life prediction method for marine structures
[J].DOI:10.1016/j.marstruc.2011.02.007 [本文引用: 2]
Crack path and life prediction under mixed mode cyclic variable amplitude loading through XFEM
[J].DOI:10.1016/j.ijfatigue.2018.04.026 [本文引用: 1]
Analysis of fatigue crack growth under mixed mode (I+II) loading conditions in rail steel using CTS specimen
[J].DOI:10.1016/j.engfailanal.2019.104354 [本文引用: 1]
海洋平台K型管节点的疲劳裂纹扩展分析I: 试验测试
[J].DOI:10.3969/j.issn.1007-4708.2007.05.018 [本文引用: 1]
Fatigue crack propagation analysis of tubular K joints1: experimental test
[J].DOI:10.3969/j.issn.1007-4708.2007.05.018 [本文引用: 1]
海洋平台K型管节点的疲劳裂纹扩展分析II: 数值分析
[J].DOI:10.3969/j.issn.1007-4708.2007.06.016 [本文引用: 1]
Fatigue crack propagation analysis of tubular K-joints1: numerical
[J].DOI:10.3969/j.issn.1007-4708.2007.06.016 [本文引用: 1]
基于视情维修的机队维修决策方法
[J].
Research on maintenance decision-making based on CBM for a fleet
[J].
基于几何与纹理特征相融合的磁粉探伤裂纹提取算法
[J].
Crack detection algorithm for fluorescent magnetic particle inspection based on shape and texture features
[J].
Acousto-ultrasonic based damage characterization: linear versus nonlinear signal features
[J].DOI:10.1016/j.ymssp.2013.10.017 [本文引用: 1]
铝板损伤的超声Lamb波与机磁阻抗集成检测
[J].DOI:10.11973/wsjc201907006 [本文引用: 1]
Damage detection of aluminum plate based on integrated ultrasonic lamb wave and magneto-mechanical impedance
[J].DOI:10.11973/wsjc201907006 [本文引用: 1]
基于声发射技术的海洋平台材料疲劳损伤检测
[J].DOI:10.11973/wsjc201610003 [本文引用: 1]
Fatigue failure detection of the offshore platform materal based on acoustic emission
[J].DOI:10.11973/wsjc201610003 [本文引用: 1]
Dynamic Bayesian network for aircraft wing health monitoring digital twin
[J].DOI:10.2514/1.J055201 [本文引用: 1]
Integration of heterogeneous information in SHM models
[J].DOI:10.1002/stc.1572 [本文引用: 1]
基于数字孪生的光电探测系统性能预测
[J].
Application of digital twin model in performance prediction of electro-optical detection system
[J].
基于双尺度动态贝叶斯网络及多信息融合的步态识别
[J].
Gait recognition based on two-scale dynamic bayesian network and more information fusion
[J].
A general constitutive relation for fatigue crack growth analysis of metal structures
[J].
Fatigue life prediction of engineering structures subjected to variable amplitude loading using the improved crack growth rate model
[J].
Uncertainty quantification and model validation of fatigue crack growth prediction
[J].DOI:10.1016/j.engfracmech.2011.02.017 [本文引用: 1]
A study on the relation between threshold effective stress intensity factor range and load ratio
[J].
Applicability of the improved crack growth rate model and its parameters estimation method
[J].
Fatigue reliability analysis for the manned cabin of deep manned submersibles based on the unified fatigue life prediction method
[J].
Fatigue crack growth in the aluminium alloy D16 under constant and variable amplitude loading
[J].DOI:10.1016/S0142-1123(03)00067-7 [本文引用: 1]
On the engineering approach to estimating the parameters in an improved crack growth rate model for fatigue life prediction
[J].DOI:10.1080/17445300903439207 [本文引用: 1]
贝叶斯网络推理算法综述
[J].DOI:10.3321/j.issn:1001-506X.2008.05.039 [本文引用: 1]
Survey of Bayesian network inference algorithms
[J].DOI:10.3321/j.issn:1001-506X.2008.05.039 [本文引用: 1]
预测结构性能退化的混合粒子滤波方法
[J].DOI:10.6052/0459-1879-18-014 [本文引用: 1]
A combined Particle Filter method for predicting structural performance degradation
[J].DOI:10.6052/0459-1879-18-014 [本文引用: 1]
Fatigue crack growth in thin aluminium alloy sheets under loading sequences with periodic overloads
[J].
Fatigue crack growth and crack closure in an AlMgSi alloy
[J].