焊接构造对T型接头超低周疲劳性能的影响

doi:10.3785/j.issn.1008-973X.2021.01.004

焊接构造对T型接头超低周疲劳性能的影响

余文韬^,, 谢旭^,, 成程

浙江大学建筑工程学院，浙江杭州 310058

Effects of welding details on ultra-low cycle fatigue performance of T-welded joint

YU Wen-tao^,, XIE Xu^,, CHENG Cheng

College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

通讯作者: 谢旭，男，教授，博导. orcid.org/0000-0002-4247-0487. E-mail： xiexu@zju.edu.cn

收稿日期: 2020-01-18

Received: 2020-01-18

作者简介 About authors

余文韬（1995—），男，硕士生，从事结构多尺度分析的研究.orcid.org/0000-0002-6898-1912.E-mail：923864247@qq.com , E-mail：923864247@qq.com

摘要

为了研究焊接细节对钢结构超低周疲劳性能的影响，以T型接头为对象，在通用有限元程序Abaqus平台上，开发基于Arlequin算法的结构多尺度计算程序. 利用多尺度算法，开展焊接接头的局部弹塑性有限元分析. 比较焊趾半径、厚钢板未熔透长度及焊趾表面凹凸对局部塑性应变履历的影响，利用Coffin-Manson模型对T型接头的超低周疲劳特性进行定性讨论. 数值计算结果表明，焊趾位置是焊接接头的超低周疲劳易损位置，厚钢板的未熔透长度对焊接部位局部塑性应变的影响不大；焊趾半径对焊趾局部塑性应变有较大的影响，增大焊趾半径可以有效提升钢结构在循环荷载下的超低周疲劳性能；焊趾表面的平整性是影响焊趾局部塑性应变履历的重要因素，尖锐的凹坑会明显降低焊接接头的超低周疲劳性能，磨平的焊趾表面可以减少局部塑性应变，提高接头的超低周疲劳强度.

关键词： T型焊接接头 ; 多尺度分析方法 ; Arlequin法 ; 局部塑性应变履历 ; 超低周疲劳 ; 参数分析

Abstract

T-welded joint was adopted as a research object and a structural multi-scale calculation program was proposed based on Arlequin algorithm on the general finite element program Abaqus platform in order to analyze the effects of welding details on ultra-low cycle fatigue performance of steel structures. Local elastic-plastic finite element analysis of T-welded joints were conducted, and the local plastic strain characteristics were analyzed. The effects of welding details, such as weld toe radius, unfused length of thick steel plate and unevenness of weld toe surface on local plastic strain history were compared. The ultra-low cycle fatigue characteristics of T-welded joints were discussed by qualitatively using Coffin-Manson model. The numerical calculation results show that weld toe position is the vulnerable position of T-welded joints, and the influence of the unfused length of the steel plates on the local plastic strain history of the welded part is negligible. The local plastic strain history is more sensitive to the change of the weld toe radius, and the increase of the weld toe radius can significantly improve the ultra-low cycle fatigue performance of the structure under cyclic loading. The flatness of weld surfaces is an important factor on the plastic strain history of welding areas. Sharp dents can significantly reduce the ultra-low cycle fatigue performance of welded joints whereas a smoother welding surface is beneficial to reduce the local plastic strain and improve the ultra-low cycle fatigue strength of joints.

Keywords： T-welded joint ; multi-scale analysis method ; Arlequin algorithm ; local plastic strain history ; ultra-low cycle fatigue ; parametric analysis

PDF (1434KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

余文韬, 谢旭, 成程. 焊接构造对T型接头超低周疲劳性能的影响. 浙江大学学报(工学版)[J], 2021, 55(1): 31-37 doi:10.3785/j.issn.1008-973X.2021.01.004

YU Wen-tao, XIE Xu, CHENG Cheng. Effects of welding details on ultra-low cycle fatigue performance of T-welded joint. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(1): 31-37 doi:10.3785/j.issn.1008-973X.2021.01.004

超低周疲劳开裂是钢结构在强地震作用下的主要破坏形式之一^[1-2]. 这类破坏的特点是在应变集中的焊接部位首先萌生裂纹，随后在循环荷载作用下裂纹扩展，最终发生断裂. 近20年来，许多学者通过试验研究了钢结构超低周疲劳破坏的机理及疲劳寿命的预测方法. 如周晖等^[3]对梁柱节点的超低周疲劳性能进行实验研究. Ge等^[4-5]以无加劲肋的厚钢板桥墩为对象，研究钢桥墩的超低周疲劳破坏形态. Usami等^[6]根据金属阻尼器的超低周疲劳试验研究结果，认为结构的超低周疲劳性能低于母材. 廖燕华等^[7]根据钢材焊接接头的超低周疲劳试验结果，确认了焊接接头超低周疲劳寿命低于母材. 既有的研究结果表明，焊接部位是钢结构超低周疲劳破坏的易损位置，且受到焊接构造方式的影响.

为了指导钢结构超低周疲劳强度设计，一些学者在传统低周疲劳领域内的Coffin-Mason公式基础上提出适用于超低周疲劳的寿命预测公式. 如Tateishi等^[8]提出用分段表示的超低周疲劳寿命经验预测公式. Xue^[9]通过引入指数函数和附加的材料参数，提出兼顾低周和超低周疲劳寿命预测的统一表达式. 除此之外，也有学者从微观力学的角度研究结构的超低周疲劳特性，如Kanvinde等^[10]基于Anderson^[11]提出的延性破坏空穴扩张模型（VGM模型），建立反复荷载下材料疲劳启裂条件的循环空穴扩张模型（CVGM模型）；Tong等^[12]在Bonora^[13]研究的基础上，提出适用于超低周疲劳断裂预测的连续损伤力学模型. 在上述寿命预测公式中，局部塑性应变履历是验算结构超低周疲劳强度的主要参数. 为了更具体地探究钢结构超低周疲劳的影响因素，Tataishi等^[14]通过对T型焊接接头的试验和数值模拟，认为焊趾半径对塑性应变集中有明显的影响. Kato等^[15]针对厚钢板T型焊接接头的未熔透问题进行试验研究，认为当焊接接头的未熔透长度大于钢板厚度的15%时，未熔透长度对接头的超低周疲劳强度有不可忽略的影响.

上述研究现状表明，已有一些学者对焊接接头的超低周疲劳性能进行研究，但是局部应变计算方法繁杂、有限元模型单元数量庞大，相关研究比较欠缺，尚未取得全面的认识，所得结果不能用来指导焊接部位构造优化设计. 本文在Abaqus平台下开发基于Arlequin 算法的多尺度计算程序，用多尺度的结构计算方法实现了任意粗糙单元和精细单元过渡区间网格划分的目的. 通过一系列T型接头的数值分析结果，比较不同焊接构造及加载工况对疲劳寿命的影响，为T型接头焊接构造的优化提供依据.

1. 计算对象及计算方法

1.1. 计算对象

焊接接头在传递地震荷载时起到重要作用，是钢结构超低周疲劳破坏的易损位置. T型焊接接头是钢结构桥梁中常见的焊接形式，如钢桥墩底板与腹板、翼板与端板、梁柱节点等均采用这种形式的焊接. 为了方便计算和比较，本文参考文献[14]的计算模型，以图1（a）所示的简支结构中间焊接竖向腹板的T型接头为对象，计算焊缝构造对局部应变的影响.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

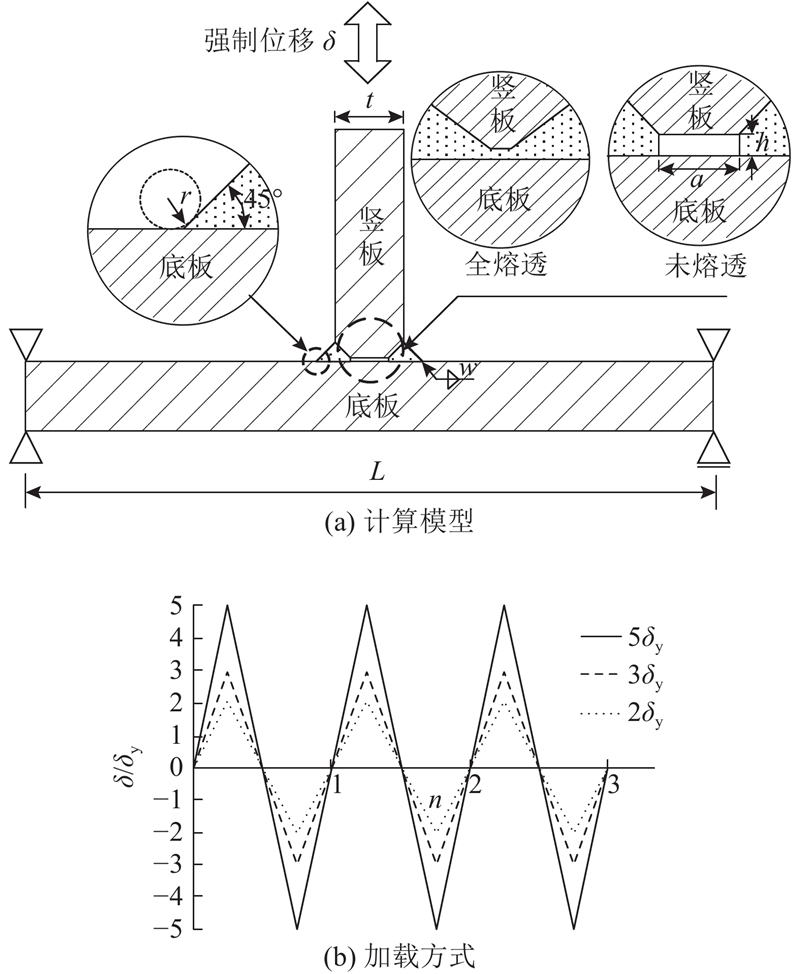
图 1 T型焊接接头计算模型以及加载方式

Fig.1 Analytical model and loading form of T-welded joint

该计算模型由长度为L的水平简支钢板和与之垂直的竖向钢板组成，竖向钢板的下端与水平钢板焊接，上端施加如图1（b）所示的强制循环变形δ，加载程序中的δ_y为简支钢板达到初始屈服时的位移. 图1（a）中，r为焊趾半径，焊脚长度为w，取w=10 mm. 图1（b）中，n为加载次数. 取钢板厚度t为12和36 mm 2种，对应的L分别取160和480 mm. 当t=12 mm时，采用全熔透双面剖口焊接；当t=36 mm时，采用未熔透的双面剖口焊接，未熔透位置的间隙为h，长度为a.

材料采用Q345qC钢，母材、焊接材料及热影响区的Chaboche混合强化模型参数如表1所示^[16]. 表中，σ_|0为塑性应变为0时的屈服应力，Q_∞为屈服强度的最大变化值，ε_f′为疲劳塑性系数，b为屈服面随塑性应变增加的变化率，C_kin，i为第i次的随动强化模量初始值，C_kin，i /γ_i为背应力的最大变化值，γ_i为背应力随塑性应变增加的变化率，c为疲劳塑性指数.

表 1 Q345qC钢材的Chaboche混合强化模型参数

Tab.1 Parameters of chaboche' strengthening model for Q345qC steel

材料	σ_\|0 / MPa	Q_∞/ MPa	b	C_kin，1/MPa	γ₁	C_kin，2 /MPa	γ₂	C_kin，3 /MPa	γ₃	ε_f′	c
母材	354.10	13.2	0.6	44373.7	523.8	9346.6	120.2	946.1	18.7	0.8219	−0.6550
热影响区	312.57	9.8	0.7	32242.4	199.2	3858.5	43.1	329.2	0.3	−	−
焊缝	428.45	17.4	0.4	12752.3	160.0	1111.2	160.0	630.5	26.0	0.6097	−0.6786

新窗口打开| 下载CSV

1.2. 计算方法

1.2.1. 结构多尺度算法

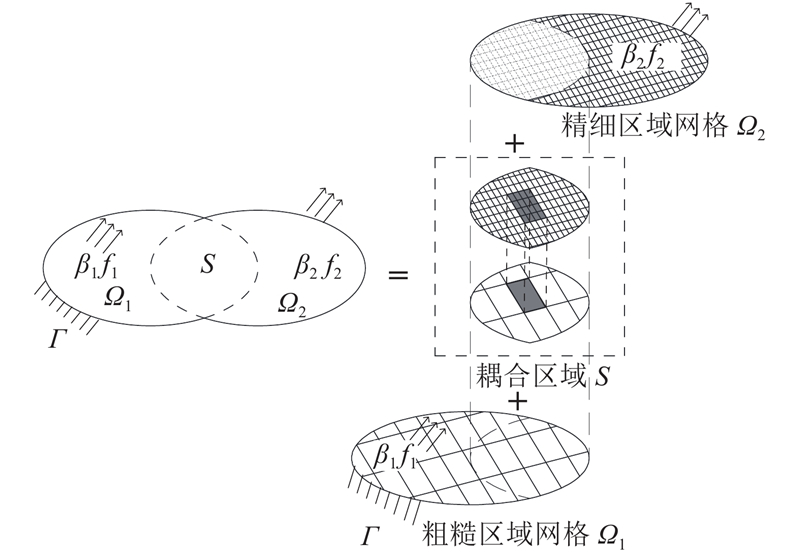
目前，对焊接部位局部应变的计算除了精细的数值模拟以外，没有其他通用性强的计算方法. 利用精细有限元计算接头塑性应力存在网格划分困难、计算量大的问题. 田村洋等^[17]尝试采用多重子结构法，计算焊接位置的局部塑性应力. 该方法通过边界条件建立粗糙模型和精细模型之间的对应关系，但两者之间的边界条件在弹塑性计算中不能精确模拟. 为了避免精细有限元模型带来的繁杂计算量，保证计算结果的可靠性，采用Ben^[18]提出的Arlequin算法，分析焊接接头的局部应变分布. 该算法可以实现不同类型网格之间的过渡，且网格划分的自由度大.

如图2所示，Arlequin算法的主要思想是将结构整体划分成Ω₁和Ω₂ 2个区域，2个区域之间存在重合区域S. 在Ω₁和Ω₂区域内，可以根据计算精度需求分别划分不同单元，2个区域的单元种类和网格密度可以完全不同. 在耦合区S，根据Ω₁区域和Ω₂区域的变形协调关系，建立同时过渡2种单元的耦合算子，实现多尺度的结构计算方法. 利用该算法，可以不考虑Ω₁和Ω₂之间的单元协调. 整个结构计算模型可以根据计算目的的需要，灵活变换不同的单元类型或者网格尺寸，例如在精度要求较高的区域采用精细网格划分，在其他区域采用粗糙网格划分；在关心的区域采用精细的实体单元、在不关心的区域采用粗糙的梁单元. Ben等^[18-21]利用该方法，达到简化结构分析的计算目的. 本文参考文献[19]的方法，在Abaqus平台上开发基于Arlequin算法的耦合单元，实现了在Abaqus平台上结构多尺度分析的简化.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 Arlequin算法的计算区域划分

Fig.2 Calculation zone of Arlequin algorithm

根据Arlequin算法可知，在区域Ω₁和Ω₂重合区域S内2种单元之间的耦合单元刚度方程为

(1) $ \left[ {\begin{array}{*{20}{c}} {{\alpha _1}{{{k}}_1}}&{\bf{0}}&{{{C}}_{\lambda 1}^{\rm{T}}}\\ {\bf{0}}&{{\alpha _2}{{{k}}_2}}&{ - {{C}}_{\lambda 2}^{\rm{T}}}\\ {{{{C}}_{\lambda 1}}}&{ - {{{C}}_{\lambda 2}}}&{\bf{0}} \end{array}} \right]\left[ { \begin{array}{l} {{{u}}_1}\\ {{{u}}_2}\\ {{\lambda }} \end{array} } \right] = \left[ { {\begin{array}{*{20}{c}} {{\beta _1}{{{f}}_1}}\\ {{\beta _2}{{{f}}_2}}\\ {\bf{0}} \end{array}} } \right]. $

式中：k₁为耦合区域S内按Ω₁划分的单元刚度矩阵；k₂为耦合区域S内按Ω₂划分的单元刚度矩阵；α_i和β_i分别为区域内分配给Ω_i区的刚度和荷载系数，

(2) ${\alpha _1} + {\alpha _2} = {\beta _1} + {\beta _2} = 1,$

其中，0≤α_i≤1.0，0≤β_i≤1.0.

当采用H¹耦合时，耦合算子C定义为

(3) ${{C}}\left( {{{\lambda }}{\rm{,}}\;{{u}}} \right) = \int_{{S_\lambda }} {\left( {{{\lambda }} \cdot {{u}} + {l^2}{{\varepsilon }}\left( {{\lambda }} \right){{:\varepsilon }}\left( {{u}} \right)} \right){\rm{d}}\varOmega }. $

式中：参数l为缩放参数，作用是使得前后2项量纲相同，当l=0时耦合为L²耦合.

1.2.2. 计算精度验证

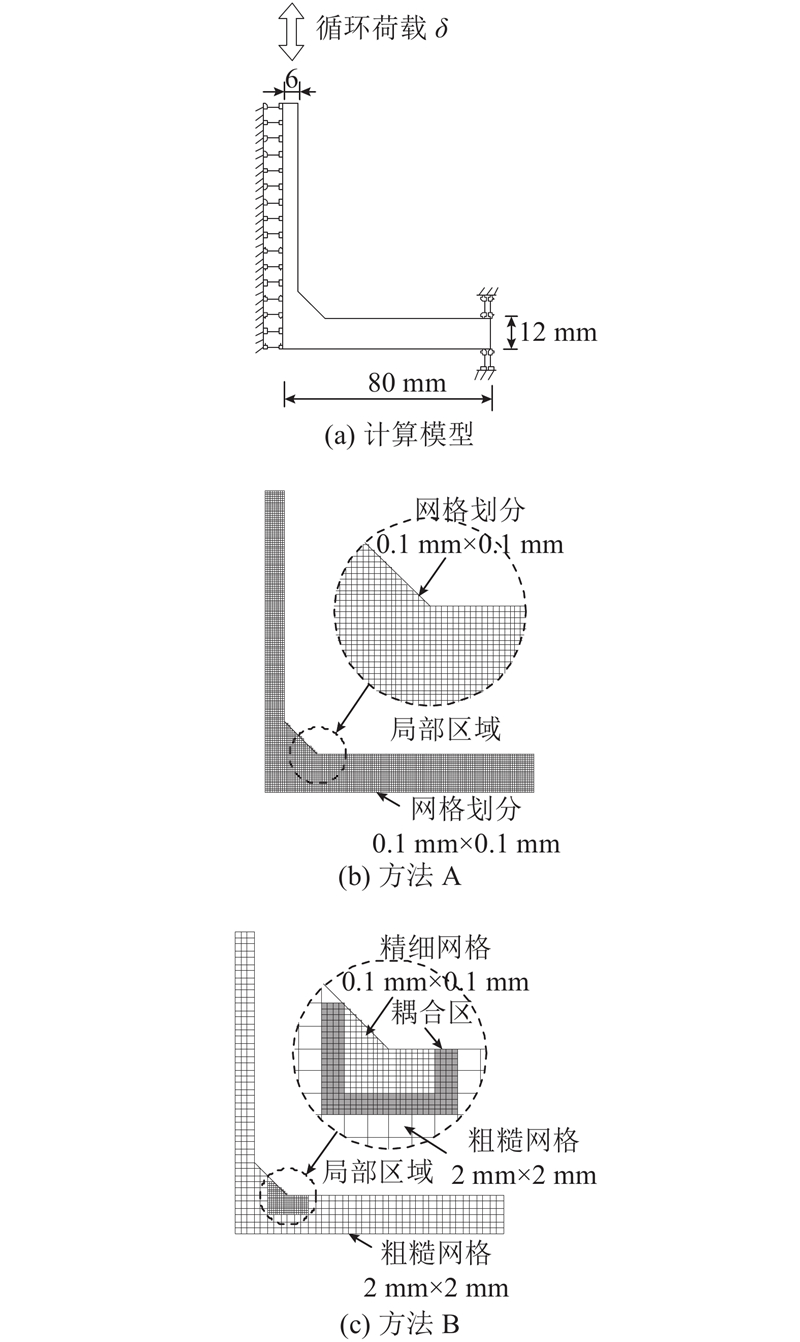
为了验证该方法的计算精度，取T型焊接结构为例进行分析. t=12 mm，w=10 mm， r=0，L=160 mm，加载模式为单调加载，最大强制位移为5δ_y. 考虑到计算模型具有对称性，取如图3（a）所示的半结构进行计算分析. 利用如图3（b）、（c）所示的2种有限元模型，开展算法精度的验证. 方法A为精细的有限元模型，网格尺寸为0.1 mm×0.1 mm，单元数量达到189 440. 方法B为应用了Arlequin算法的多尺度计算方法，在粗糙区域内网格尺寸为2 mm×2 mm，精细区域的网格尺寸为0.1 mm×0.1 mm，单元总数为13 996. 由于粗糙与精细网格之间的密度相差悬殊，如图3所示的网格形式仅为示意图. 在多尺度模型中，设宽为2 mm的范围为耦合区，建立耦合单元来进行2种密度单元之间的过渡.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 多尺度算法验证的有限元计算模型

Fig.3 Finite element models for structural multi-scale algorithm verification

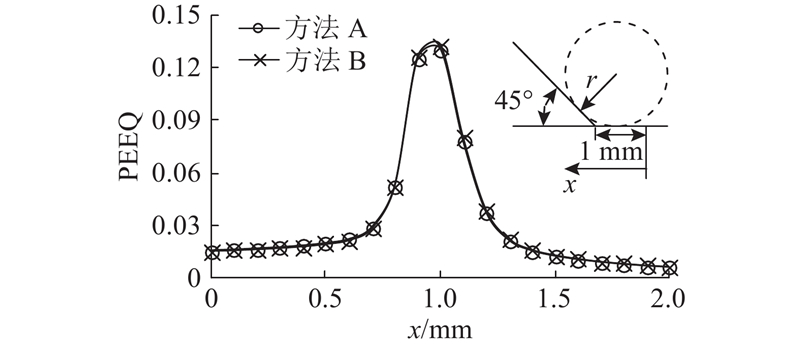
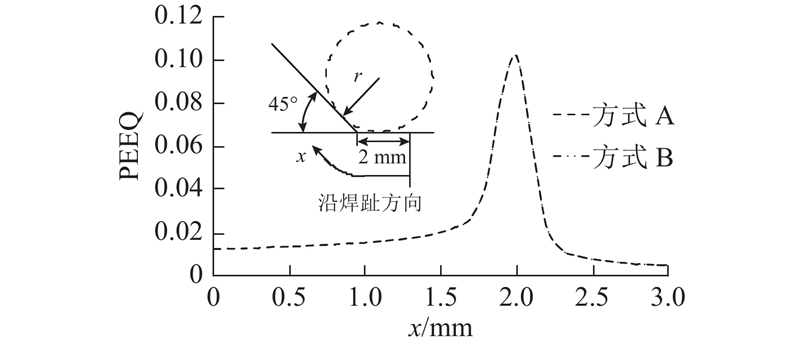
如图4所示为采用2种数值分析方法在焊趾两侧1 mm范围内的等效塑性应变PEEQ分布情况. 可以看出，2种算法的塑性应变履历相差非常小，表明采用了Arlequin法的多尺度结构计算方法能够以相对较小的计算量获得足够精确的数值解. 在不特别说明的情况下，后续所提到的数值模拟均为采用了Arlequin法的多尺度结构建模思路.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 多尺度算法验证结果

Fig.4 Results of structural multi-scale algorithm verification

2. 参数影响分析

为了能够直观地进行比较，以材料、加载制度及结构几何形态为研究参数，对T型焊接接头进行参数敏感性分析.

2.1. 材料参数对计算结果的影响

由于焊缝周围的材料力学性质受焊接施工的影响较大，根据以往学者的研究可知，焊接区域附近的材料可以分为焊接材料、热影响区和母材3种. 为了比较不同材料划分区域的影响，对T型焊接接头按图5采用2种材料划分方式。1）方式A：严格按母材、热影响区和焊缝的所在区域赋予对应的材料参数；2）方式B：仅在焊趾部位区分母材、热影响区和焊缝3个区域，赋予对应的材料参数，其他区域均按母材考虑，不细分材料的分布.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 材料分配方式

Fig.5 Material assignment methods of welded joint zone

计算采用如图3（c）所示的多尺度模型，强制变形采用最大为5δ_y的单调荷载. 如图6所示为利用2种模型得到的等效塑性应变对比结果. 可以发现，焊趾外的材料参数对焊趾塑性应变计算结果的影响较小，等效塑性应变的比值约为1.0. 为了方便起见，均采用方式B来赋予单元的材料参数.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 材料赋值对等效塑性应变的影响

Fig.6 Effect of material assignment methods on equivalent plastic strain at weld toe

2.2. 加载幅值对计算结果的影响

为了比较不同加载程度对塑性应变比值的影响，采用3种不同的等幅值循环加载模式，相应的加载幅值分别设为2δ_y、3δ_y和5δ_y. 如图7所示为焊趾附近的等效塑性应变计算结果. 可知，最大等效塑性应变发生的位置不受加载幅值的影响，但幅值随强制位移幅度基本上呈比例增加.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 强制位移幅度对等效塑性应变的影响

Fig.7 Effect of forced displacement amplitude on equivalent plastic strain at weld toe

2.3. 发生最大塑性应变位置

当钢板较厚时，采用全熔透焊接较困难，在实际施工过程中可能存留有一段未熔透长度. 为了比较未熔透区长度对焊趾处等效塑应变分布情况的影响，分别以焊趾与未熔透区端部为研究对象，研究等效塑应变最大值发生的地方. 通常未熔透端部的边界情况有如图8所示的2种理想化形式（在接头中的位置参照图1（a））：垂直边界和圆弧形边界. 有限元模型中，t取值为36 mm， L为480 mm， w为10 mm，a分别取值为0、8、16 mm，高度h取值为0、0.5、1、2 mm，r为0 mm.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 未熔透端部示意图

Fig.8 Schematic diagram of unwelded zone end

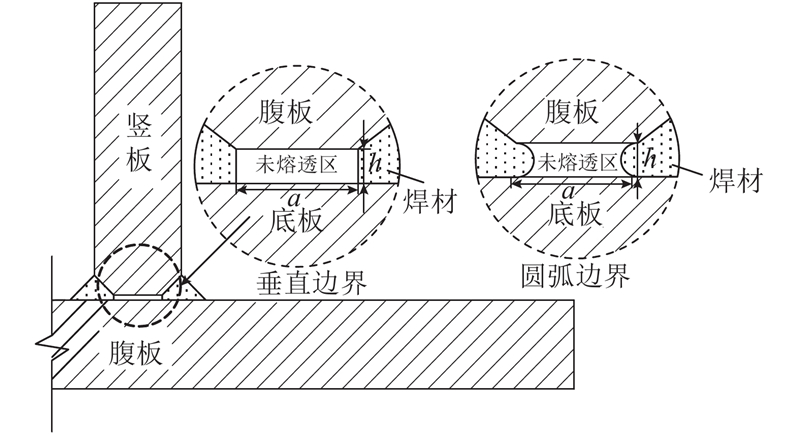
如表2所示为在不同未熔透长度下最大等效塑应变发生的地方的统计结果. 可以看出，无论是垂直边界还是圆弧边界，未熔透位置的局部塑性应变小于焊趾位置，接头的超低周疲劳性能由焊趾位置的塑性应变控制. 后面所讨论的塑性应变仅局限于焊趾位置处.

表 2 考虑未熔透影响的等效塑性应变

Tab.2 Equivalent plastic strain considering effect of unwelded zone on weld toe

编号	a /mm	h /mm	发生位置	PEEQ
1	0	0	焊趾	3.58
2	8.0	1.0	焊趾	3.57
2	8.0	1.0	垂直边界	0.10
3	16.0	1.0	焊趾	3.57
3	16.0	1.0	垂直边界	0.04
4	16.0	1.0	圆弧边界	0.11
4	16.0	2.0	焊趾	3.57

新窗口打开| 下载CSV

2.4. 焊趾半径的影响

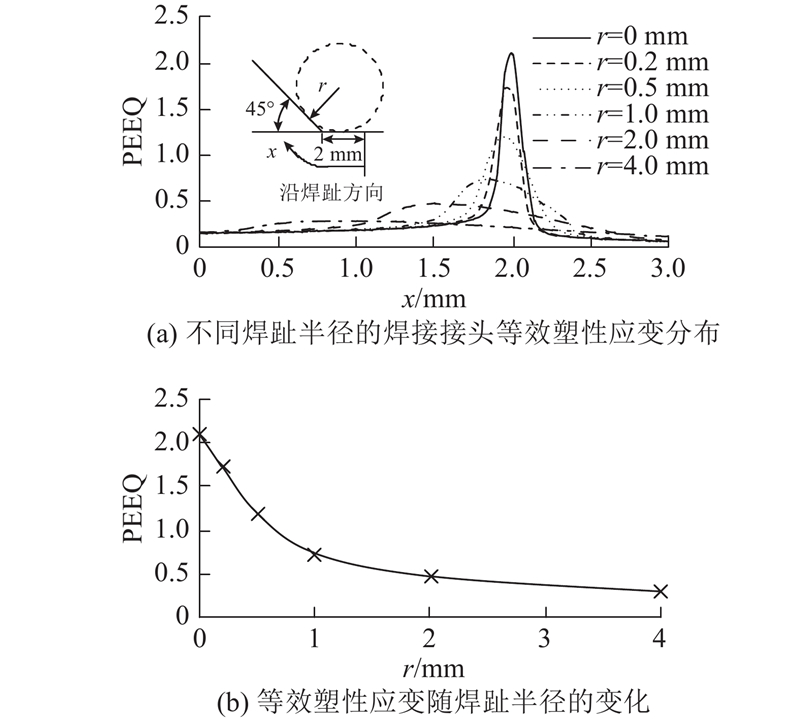
为了比较焊趾半径对局部塑性应变的影响，计算模型保持板厚为12 mm不变，分别取r为0、0.2、0.5、1、2、4 mm进行分析. 计算结果如图9所示. 可知，焊趾半径对焊趾处塑性应变集中程度有很大的影响，当焊趾半径为0~1.0 mm时，塑性应变有明显的减小；随着焊趾半径的增大，塑性应变的减小程度开始放缓.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 焊趾半径对最大等效塑性应变的影响

Fig.9 Effect of toe radius on maximum equivalent plastic strain

2.5. 焊趾平整的影响

由于焊接工艺的原因，通常焊缝表面会存在凸起或凹陷等不平整的情况. 为了分析焊趾处焊缝表面的不平整对焊趾位置等效塑性应变的影响，以板厚为12 mm、焊趾半径为4 mm的焊接接头为对象进行计算分析，比较在焊趾表面凹陷或凸起对焊趾处等效塑性应变的影响. 如图10所示为表面不平整的形式，分为下陷的凹坑和上鼓的凸面2种形式. 具体的焊趾不平整参数如表3所示. 表中，r₀为曲线半径，h₀为不平整高度。

表 3 焊趾不平整参数表

Tab.3 Unevenness parameter for welding toe

类型	r₀/mm	h₀/mm	发生位置
一个凹陷	0.2、0.5、1.0、2.0	0.5	焊趾中点
一个凸起	0.2、0.5、1.0、2.0	0.5	焊趾中点

新窗口打开| 下载CSV

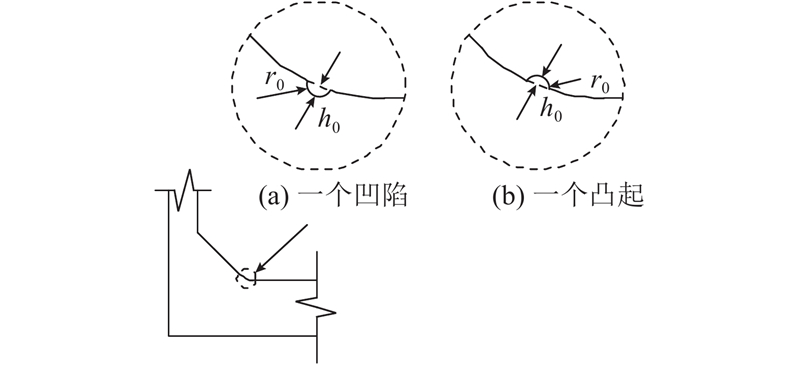
图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10 焊接表面不平整形式

Fig.10 Form of roughness welding surface

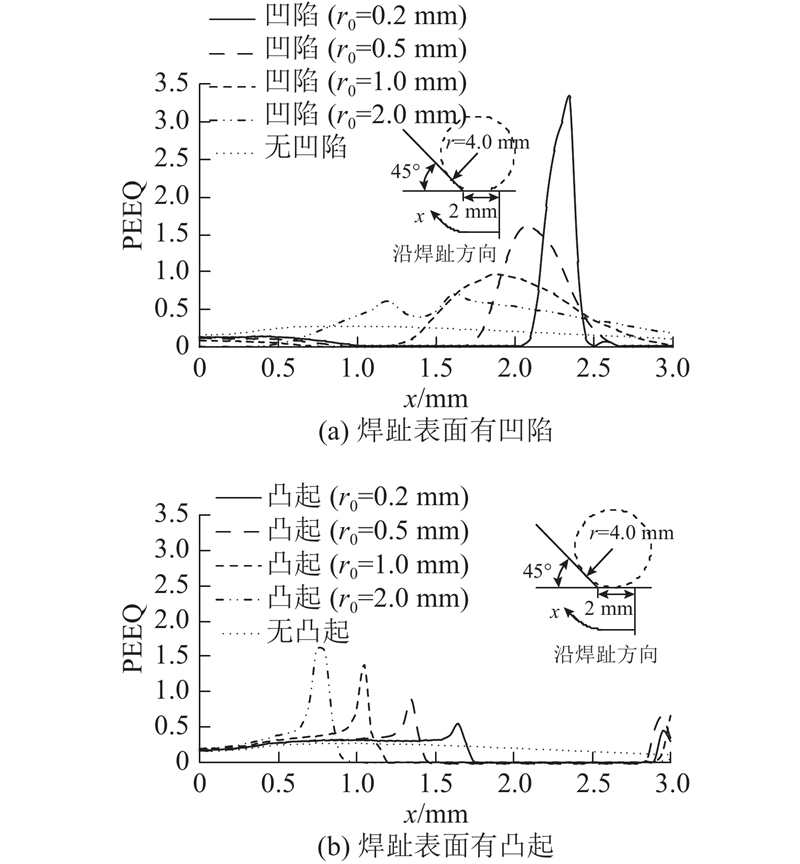
如图11所示为考虑焊趾表面凹陷或凸起时的等效塑性应变计算结果. 焊趾表面的凹陷会明显增大焊趾附近的最大等效塑性应变，凸起对焊趾局部塑性应变的影响相对较小，但在凸起开始和结束位置由于形成凹面会产生应变集中的现象. 当凹陷深度相同时，r₀越小，等效塑性应变越大，尖锐的凹坑是容易发生超低周疲劳的部位.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11 焊接表面不平整对等效塑性应变的影响

Fig.11 Effect of roughness on equivalent plastic strain at weld toe

3. T型接头超低周疲劳寿命分析

通过分析参数影响可知，焊趾半径及焊缝表面凹凸不平对T型接头的等效塑性应变有较大的影响. 为了比较这些参数对钢结构超低周疲劳寿命的影响，利用Coffin-Manson公式进行分析.

Coffin等^[22-23]根据钢结构试样在不同塑性应变幅下的疲劳试验结果，得到关于塑性应变幅Δε_p和疲劳寿命N_f（以疲劳破坏时所需要等幅加载的圈数表征）的经验曲线. 试验结果表明，这些试样的塑性应变幅对数值和低周疲劳启裂时的寿命对数值之间具有线性关系，即

(4) ${{\Delta {\varepsilon _{\rm{p}}}} / 2} = \varepsilon {'_{\rm{f}}}{\left( {2{N_{\rm{f}}}} \right)^c}.$

式中： $ \varepsilon {'_{\rm{f}}} $、c均为常数，根据试验点的回归获得. 根据光滑圆棒试样的循环荷载试验结果可知，焊接材料的 $ \varepsilon {'_{\rm{f}}} $=0.609 7，c=−0.678 6^[16]. 根据塑性应变结果，可以计算结构的超低周疲劳寿命.

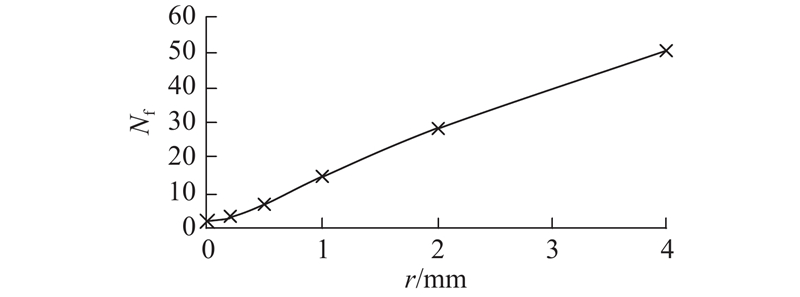
如图12所示为焊趾半径对超低周疲劳寿命的影响. 可以看出，焊趾半径的增加会大幅度增加T型接头的超低周疲劳寿命.

如表4所示为焊缝表面凹凸曲线半径对接头超低周疲劳寿命的影响. 通过对比可知，焊缝表面尖锐的凹陷对结构超低周疲劳强度的影响较凸起不利. 当凹陷深度相同时，焊趾半径越大，对应的结构超低周疲劳强度越大.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12 疲劳寿命-焊趾半径比较图

Fig.12 Comparison map of fatigue life-toe radius

表 4 焊缝表面凹凸曲线半径-疲劳寿命对照表

Tab.4 Comparison table of radius of concave convex curve of weld surface-fatigue life

曲线类型	N_f
曲线类型	r₀=0.2 mm	r₀=0.5 mm	r₀=1.0 mm	r₀=2.0 mm
凹陷	4.71	9.76	18.31	27.53
凸起	27.22	10.32	6.37	5.98

新窗口打开| 下载CSV

4. 结　论

（1）Arlequin法结合Abaqus平台，可以有效地进行结构多尺度的弹塑性分析.

（2）当钢板较厚时，按照规范（埋弧焊的推荐坡口）的坡口面可以保证带未熔透区构件与全熔透构件的超低周疲劳基本接近，在未熔透区首先发生超低周疲劳破坏的可能性较小.

（3）焊趾位置是塑性应变集中的位置，增大焊趾半径可以减少焊趾的局部塑性应变，改善焊接头的抗超低周疲劳性能；在焊趾半径增大到一定程度后，增大焊趾半径的效果不再明显.

（4）焊趾处焊接表面凹坑对焊趾的超低周疲劳性能有不利的影响，特别是尖锐的凹坑会显著降低焊趾的超低周疲劳寿命. 磨平焊趾表面可以改善接头的超低周疲劳性能.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

GATES W E, MORDEN M

Professional structural engineering experience related to welded steel moment frames following the Northridge earthquake

[J]. Structural Design of Tall and Special Buildings, 1996, 5 (1): 29- 44

DOI:10.1002/(SICI)1099-1794(199603)5:1<29::AID-TAL63>3.0.CO;2-V [本文引用: 1]

[2]

NAKASHIMA M, INOUE K, TADA M

Classification of damage to steel buildings observed in the 1995 Hyogoken-Nanbu earthquake

[J]. Engineering Structures, 1998, 20 (4/6): 271- 281