[1]
朱会杰, 王新晴, 芮挺, 等 基于平移不变CNN的机械故障诊断研究
[J]. 振动与冲击 , 2019 , 38 (5 ): 45 - 52
[本文引用: 1]
ZHU Hui-jie, WANG Xin-qing, RUI Ting, et al Machinery fault diagnosis based on shift invariant CNN
[J]. Journal of Vibration and Shock , 2019 , 38 (5 ): 45 - 52
[本文引用: 1]
[2]
杨宇, 罗鹏, 甘磊, 等. SADBN及其在滚动轴承故障分类识别中的应用[J]. 振动与冲击, 2019, 38(15): 11-16.
[本文引用: 1]
YANG Yu, LUO Peng, GAN Lei, et al. SADBN and its application in rolling bearing fault identification and classification [J]. Journal of Vibration and Shock , 2019, 38(15): 11-16.
[本文引用: 1]
[3]
JORDI B V, RUBEN P, JAVIER M R, et al Short-frequency Fourier transform for fault diagnosis of induction machines working in transient regime
[J]. IEEE Transactions on Instrumentation and Measurement , 2017 , 66 (3 ): 432 - 440
DOI:10.1109/TIM.2016.2647458
[本文引用: 1]
[4]
程卫东, 赵德尊 用于滚动轴承转频估计的EMD软阈值降噪算法
[J]. 浙江大学学报: 工学版 , 2016 , 50 (3 ): 428 - 435
[本文引用: 1]
CHENG Wei-dong, ZHAO De-zun EMD soft-thresholding denoising algorithm for rolling element bearing rotational frequency estimation
[J]. Journal of Zhejiang University: Engineering Science , 2016 , 50 (3 ): 428 - 435
[本文引用: 1]
[5]
SHUAI J, LEE S K Bearing fault detection utilizing group delay and the Hilbert-Huang transform
[J]. Journal of Mechanical Science and Technology , 2017 , 31 (3 ): 1089 - 1096
DOI:10.1007/s12206-017-0208-z
[本文引用: 1]
[6]
杨先勇, 周晓军, 张文斌, 等 基于形态小波和S变换的滚动轴承故障特征提取
[J]. 浙江大学学报: 工学版 , 2010 , 44 (11 ): 2088 - 2092
[本文引用: 1]
YANG Xian-yong, ZHOU Xiao-jun, ZHANG Wen-bin, et al Rolling bearing fault feature extraction based on morphological wavelet and S-transform
[J]. Journal of Zhejiang University: Engineering Science , 2010 , 44 (11 ): 2088 - 2092
[本文引用: 1]
[7]
周奇才, 沈鹤鸿, 赵炯, 等 基于改进堆叠式循环神经网络的轴承故障诊断
[J]. 同济大学学报: 自然科学版 , 2019 , 47 (10 ): 1500 - 1507
[本文引用: 1]
ZHOU Qi-cai, SHEN He-hong, ZHAO Jiong, et al Bearing fault diagnosis based on improved stacked recurrent neural network
[J]. Journal of Tongji University: Natural Science , 2019 , 47 (10 ): 1500 - 1507
[本文引用: 1]
[8]
ZHUANG Z, LV H, XU, et al A deep learning method for bearing fault diagnosis through stacked residual dilated convolutions
[J]. Applied Sciences , 2019 , 9 (9 ): 1823
DOI:10.3390/app9091823
[本文引用: 1]
[9]
田源. 基于深度学习的中文命名实体识别方法研究[D]. 长沙: 湖南大学, 2018: 42-56.
[本文引用: 1]
TIAN Yuan. The research of Chinese named entity recognition based on deep learning [D]. Changsha: Hunan University, 2018: 42-56.
[本文引用: 1]
[10]
LEI Y, JIA F, LIN J, et al An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data
[J]. IEEE Transactions on Industrial Electronics , 2016 , 63 (5 ): 3137 - 3147
DOI:10.1109/TIE.2016.2519325
[本文引用: 1]
[11]
于洋, 何明, 刘博, 等 基于TL-LSTM的轴承故障声发射信号识别研究
[J]. 仪器仪表学报 , 2019 , 40 (5 ): 51 - 59
[本文引用: 1]
YU Yang, HE Ming, LIU Bo, et al Research on acoustic emission signal recognition of bearing fault based on TL-LSTM
[J]. Chinese Journal of Scientific Instrument , 2019 , 40 (5 ): 51 - 59
[本文引用: 1]
[12]
NGIAM J, CHEN Z, BHASKAR S A, et al. Sparse filtering [C] // Proceedings of Advances in Neural Information Processing Systems . Cambridge: MIT Press, 2011: 1125-1133.
[本文引用: 1]
[13]
陈赟 基于稀疏滤波的信号识别
[J]. 电信快报 , 2015 , (8 ): 46 - 48
[本文引用: 1]
CHEN Yun signal recognition based on sparse filtering
[J]. Telecom Express , 2015 , (8 ): 46 - 48
[本文引用: 1]
[15]
ALEXIS B, PRASAD S, FRÉDÉRIC B, et al Well-posedness of the permutation problem in sparse filter estimation with ℓp minimization
[J]. Applied and Computational Harmonic Analysis , 2013 , 35 (3 ): 394 - 406
DOI:10.1016/j.acha.2012.11.001
[本文引用: 1]
[16]
何金洋 基于稀疏滤波和神经网络的人脸识别算法
[J]. 理论探讨 , 2016 , 7 (5 ): 28 - 31
[本文引用: 1]
HE Jin-yang The facial recognition algorithm based on sparse filtering-neural networks
[J]. Theoretical Investigation , 2016 , 7 (5 ): 28 - 31
[本文引用: 1]
[17]
李永国. 变量预测模型模式识别方法及其在滚动轴承故障诊断中的应用[D]. 长沙: 湖南大学, 2015: 6-12.
[本文引用: 1]
LI Yong-guo. Variable predictive model based class discriminate and its application in fault diagnosis of roller bearing [D]. Changsha: Hunan University, 2015: 6-12.
[本文引用: 1]
[18]
YANG H, LV J, GUO C Weighted composite quantile regression estimation and variable selection for varying coefficient models with heteroscedasticity
[J]. Journal of the Korean Statistical Society , 2015 , 44 (1 ): 77 - 94
DOI:10.1016/j.jkss.2014.05.005
[本文引用: 1]
[19]
HILL J B Robust generalized empirical likelihood for heavy tailed autoregressions with conditionally heteroscedastic errors
[J]. Journal of Multivariate Analysis , 2015 , 135 : 131 - 152
DOI:10.1016/j.jmva.2014.12.008
[本文引用: 1]
[21]
HALUNGA A, ORME C D, YAMAGATA T A heteroskedasticity robust Breusch-Pagan test for contemporaneous correlation in dynamic panel data models
[J]. Journal of Econometrics , 2017 , 198 (2 ): 209 - 230
DOI:10.1016/j.jeconom.2016.12.005
[本文引用: 1]
[22]
万书亭, 佟海侠, 董炳辉 基于最小二乘支持向量机的滚动轴承故障诊断
[J]. 振动. 测试与诊断 , 2010 , 30 (2 ): 149 - 152
[本文引用: 1]
WAN Shu-ting, TONG Hai-xia, DONG Bing-hui Bearing fault diagnosis using wavelet packet transform and least square support vector machines
[J]. Journal of Vibration, Measurement and Diagnosis , 2010 , 30 (2 ): 149 - 152
[本文引用: 1]
[23]
GE F, JU Y, QI Z, et al Parameter estimation of a Gaussian mixture model for wind power forecast error by Riemann L-BFGS optimization
[J]. IEEE Access , 2018 , (6 ): 38892 - 38899
[本文引用: 1]
[24]
李旭芳, 段春林, 张冬波, 等 遥测数据时间序列滑动窗口动态分割技术
[J]. 飞行器测控学报 , 2015 , 34 (4 ): 345 - 349
[本文引用: 1]
LI Xu-fang, DUAN Chun-lin, ZHANG Dong-bo, et al A dynamic slide windows segmentation technology for telemetry time series
[J]. Journal of Spacecraft TT and C Technology , 2015 , 34 (4 ): 345 - 349
[本文引用: 1]
[25]
YU F, KOLTUN V. Multi-scale context aggregation by dilated convolutions [C] // International Conference on Learning Representations . San Juan, Puerto Rico: ICLR, 2016.
[本文引用: 1]
[26]
LORENZO J, BARRA R, YAMAGISHI J, et al Improving Spanish speech synthesis intelligibility under noisy environments
[J]. Journal of the Acoustical Society of America , 2016 , 140 (4 ): 2961 - 2962
[本文引用: 1]
[27]
LONG J, SHELHAMER E, DARRELL T Fully convolutional networks for semantic segmentation
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 , 39 (4 ): 640 - 651
[本文引用: 1]
[28]
NAIM I, RILEY P, GILDEA D Feature-based decipherment for machine translation
[J]. Computational Linguistics , 2018 , 44 (2 ): 1 - 33
[本文引用: 1]
[29]
张利刚. 基于全空洞卷积神经网络的图像语义分割[D]. 长春: 东北师范大学, 2018: 9-15.
[本文引用: 1]
ZHANG Li-gang. Image semantic segmentation based on full cavitation convolutional neural network [D]. Changchun: Northeast Normal University, 2018: 9-15.
[本文引用: 1]
[30]
张新峰, 闫昆鹏, 赵珣 基于双向LSTM的手写文字识别技术研究
[J]. 南京师大学报 , 2019 , 42 (3 ): 58 - 64
[本文引用: 1]
ZHANG Xin-feng, YAN Kun-peng, ZHAO Xun Handwriting Chinese text recognition using BiLSTM network
[J]. Journal of Nanjing Normal University , 2019 , 42 (3 ): 58 - 64
[本文引用: 1]
[31]
YANG Y, FU P, HE Y Bearing fault automatic classification based on deep learning
[J]. IEEE Access , 2018 , (6 ): 71540 - 71554
[本文引用: 1]
[32]
乔美英, 刘宇翔, 兰建义 基于VMD和马氏距离SVM的滚动轴承故障诊断
[J]. 中山大学学报: 自然科学版 , 2019 , 58 (5 ): 8 - 16
[本文引用: 1]
QIAO Mei-ying, LIU Yu-xiang, LAN Jian-yi Fault diagnosis method of rolling bearings based on VMD and mahalanobis distance SVM
[J]. Journal of Sun Yat-sen University: Medical Sciences , 2019 , 58 (5 ): 8 - 16
[本文引用: 1]
[33]
LI X, TIAN J, XU M, et al. DBLSTM-based multi-scale fusion for dynamic emotion prediction in music [C] // 2016 IEEE International Conference on Multimedia and Expo . Seattle: IEEE, 2016: 1-6.
[本文引用: 1]
基于平移不变CNN的机械故障诊断研究
1
2019
... 滚动轴承在工业领域中有广泛的应用,轴承的稳定运行可以提高企业的工作效率[1 ] ,一旦轴承发生故障就会带来巨大的经济损失,严重时还会威胁到人身安全. ...
基于平移不变CNN的机械故障诊断研究
1
2019
... 滚动轴承在工业领域中有广泛的应用,轴承的稳定运行可以提高企业的工作效率[1 ] ,一旦轴承发生故障就会带来巨大的经济损失,严重时还会威胁到人身安全. ...
1
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
1
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
Short-frequency Fourier transform for fault diagnosis of induction machines working in transient regime
1
2017
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
用于滚动轴承转频估计的EMD软阈值降噪算法
1
2016
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
用于滚动轴承转频估计的EMD软阈值降噪算法
1
2016
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
Bearing fault detection utilizing group delay and the Hilbert-Huang transform
1
2017
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
基于形态小波和S变换的滚动轴承故障特征提取
1
2010
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
基于形态小波和S变换的滚动轴承故障特征提取
1
2010
... 在轴承故障诊断领域,传统的方法先对特征进行提取,然后通过各种分类器进行分类识别[2 ] . Burrie等[3 ] 提出基于短时傅里叶变换(short-time Fourier transform,STFT)的电机暂态故障诊断方法;程卫东等[4 ] 提出经验模态分解与小波软阈值相结合的降噪方法;Jin等[5 ] 提出结合群时延希尔伯特的轴承故障诊断方法;杨先勇等[6 ] 提出基于极大提升形态小波(max-lifting morphological wavelet,MLMW)分析和S变换的滚动轴承故障特征提取方法. 以上的方法,在特征处理的过程中都加入了人的主观因素,无法完全提取特征. ...
基于改进堆叠式循环神经网络的轴承故障诊断
1
2019
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
基于改进堆叠式循环神经网络的轴承故障诊断
1
2019
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
A deep learning method for bearing fault diagnosis through stacked residual dilated convolutions
1
2019
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
1
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
1
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data
1
2016
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
基于TL-LSTM的轴承故障声发射信号识别研究
1
2019
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
基于TL-LSTM的轴承故障声发射信号识别研究
1
2019
... 在故障诊断分类识别方面,深度学习将特征提取和故障诊断结合在一起. 周奇才等[7 ] 提出基于改进堆叠式循环神经网络的轴承故障诊断模型,通过门控单元解决梯度消失的问题;Zilong等[8 ] 提出由空洞卷积、门卷积和残差网络组合的网络模型,空洞卷积增大了局部感受野,增加了卷积核的接收域;田源[9 ] 提出基于迭代空洞卷积网络的命名实体模型,提高了网络训练精度;Yaguo等[10 ] 利用2层稀疏滤波网络提取特征,结合softmax进行分类,效果显著. 轴承信号是典型的时间序列数据,而长短时记忆网络(long short-term memory,LSTM)处理时间序列数据有独特的优势. 于洋等[11 ] 提出LSTM与迁移学习(transfer learning,TL)相结合的故障识别方法,可以有效地对多类故障识别. 这些方法的不足之处在于,深度学习的网络模型较复杂,在网络训练过程中会消耗大量的时间. ...
1
... 稀疏滤波是Ngiam[12 ] 提出的针对特征提取的无监督学习滤波器. 与传统的需要大量超参数调优的特征提取方法相比,稀疏滤波只需调整1个超参数[13 ] . 它先归一化特征矩阵的行,再归一化矩阵的列;将归一化后的特征矩阵元素相加得到目标函数;优化目标函数,得到最优特征矩阵. ...
基于稀疏滤波的信号识别
1
2015
... 稀疏滤波是Ngiam[12 ] 提出的针对特征提取的无监督学习滤波器. 与传统的需要大量超参数调优的特征提取方法相比,稀疏滤波只需调整1个超参数[13 ] . 它先归一化特征矩阵的行,再归一化矩阵的列;将归一化后的特征矩阵元素相加得到目标函数;优化目标函数,得到最优特征矩阵. ...
基于稀疏滤波的信号识别
1
2015
... 稀疏滤波是Ngiam[12 ] 提出的针对特征提取的无监督学习滤波器. 与传统的需要大量超参数调优的特征提取方法相比,稀疏滤波只需调整1个超参数[13 ] . 它先归一化特征矩阵的行,再归一化矩阵的列;将归一化后的特征矩阵元素相加得到目标函数;优化目标函数,得到最优特征矩阵. ...
Well-posedness of the permutation problem in sparse filter estimation with ?p minimization
1
2013
... 这样,所有的特征便落在二范数的单位球上[15 ] . ...
基于稀疏滤波和神经网络的人脸识别算法
1
2016
... 对轴承故障诊断而言,特征之间一般存在一定的内在关系[16 -17 ] ,比如具有同方差性. 由于轴承振动信号比较复杂,不同变量之间的方差往往不同,经常出现异方差性[18 -19 ] . 同时,随着时间的变化,方差也会有相应的变化,比如采集数据的传感器位置不同会影响方差的大小. ...
基于稀疏滤波和神经网络的人脸识别算法
1
2016
... 对轴承故障诊断而言,特征之间一般存在一定的内在关系[16 -17 ] ,比如具有同方差性. 由于轴承振动信号比较复杂,不同变量之间的方差往往不同,经常出现异方差性[18 -19 ] . 同时,随着时间的变化,方差也会有相应的变化,比如采集数据的传感器位置不同会影响方差的大小. ...
1
... 对轴承故障诊断而言,特征之间一般存在一定的内在关系[16 -17 ] ,比如具有同方差性. 由于轴承振动信号比较复杂,不同变量之间的方差往往不同,经常出现异方差性[18 -19 ] . 同时,随着时间的变化,方差也会有相应的变化,比如采集数据的传感器位置不同会影响方差的大小. ...
1
... 对轴承故障诊断而言,特征之间一般存在一定的内在关系[16 -17 ] ,比如具有同方差性. 由于轴承振动信号比较复杂,不同变量之间的方差往往不同,经常出现异方差性[18 -19 ] . 同时,随着时间的变化,方差也会有相应的变化,比如采集数据的传感器位置不同会影响方差的大小. ...
Weighted composite quantile regression estimation and variable selection for varying coefficient models with heteroscedasticity
1
2015
... 对轴承故障诊断而言,特征之间一般存在一定的内在关系[16 -17 ] ,比如具有同方差性. 由于轴承振动信号比较复杂,不同变量之间的方差往往不同,经常出现异方差性[18 -19 ] . 同时,随着时间的变化,方差也会有相应的变化,比如采集数据的传感器位置不同会影响方差的大小. ...
Robust generalized empirical likelihood for heavy tailed autoregressions with conditionally heteroscedastic errors
1
2015
... 对轴承故障诊断而言,特征之间一般存在一定的内在关系[16 -17 ] ,比如具有同方差性. 由于轴承振动信号比较复杂,不同变量之间的方差往往不同,经常出现异方差性[18 -19 ] . 同时,随着时间的变化,方差也会有相应的变化,比如采集数据的传感器位置不同会影响方差的大小. ...
靶场光学测量数据异方差性检验及修正
1
2008
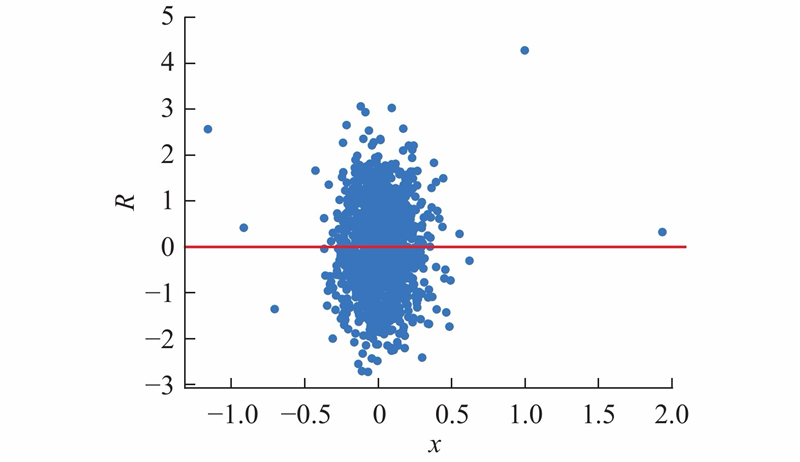
... 在对数据分析的过程中,常采用图形法[20 ] 和Breusch-Pagan法[21 ] 检测数据是否存在异方差. 其中图形法是根据数据标准化残差在水平参考线两侧分布的均匀程度来判断. Breusch-Pagan法是通过计算置信水平p 来判断,若p 小于设定的判别界限(p =0.05),则原始数据中存在异方差;反之,则不存在异方差. ...
靶场光学测量数据异方差性检验及修正
1
2008
... 在对数据分析的过程中,常采用图形法[20 ] 和Breusch-Pagan法[21 ] 检测数据是否存在异方差. 其中图形法是根据数据标准化残差在水平参考线两侧分布的均匀程度来判断. Breusch-Pagan法是通过计算置信水平p 来判断,若p 小于设定的判别界限(p =0.05),则原始数据中存在异方差;反之,则不存在异方差. ...
A heteroskedasticity robust Breusch-Pagan test for contemporaneous correlation in dynamic panel data models
1
2017
... 在对数据分析的过程中,常采用图形法[20 ] 和Breusch-Pagan法[21 ] 检测数据是否存在异方差. 其中图形法是根据数据标准化残差在水平参考线两侧分布的均匀程度来判断. Breusch-Pagan法是通过计算置信水平p 来判断,若p 小于设定的判别界限(p =0.05),则原始数据中存在异方差;反之,则不存在异方差. ...
基于最小二乘支持向量机的滚动轴承故障诊断
1
2010
... 消除异方差,常采用的是加权最小二乘法[22 ] . 对数变换也能消除异方差. 根据这一特点,对稀疏滤波的目标函数进行改进: ...
基于最小二乘支持向量机的滚动轴承故障诊断
1
2010
... 消除异方差,常采用的是加权最小二乘法[22 ] . 对数变换也能消除异方差. 根据这一特点,对稀疏滤波的目标函数进行改进: ...
Parameter estimation of a Gaussian mixture model for wind power forecast error by Riemann L-BFGS optimization
1
2018
... 当W X [23 ] 求出稀疏滤波的权值矩阵W m 次迭代的曲率信息来构造Hessian矩阵的近似矩阵. 具体计算公式如下: ...
遥测数据时间序列滑动窗口动态分割技术
1
2015
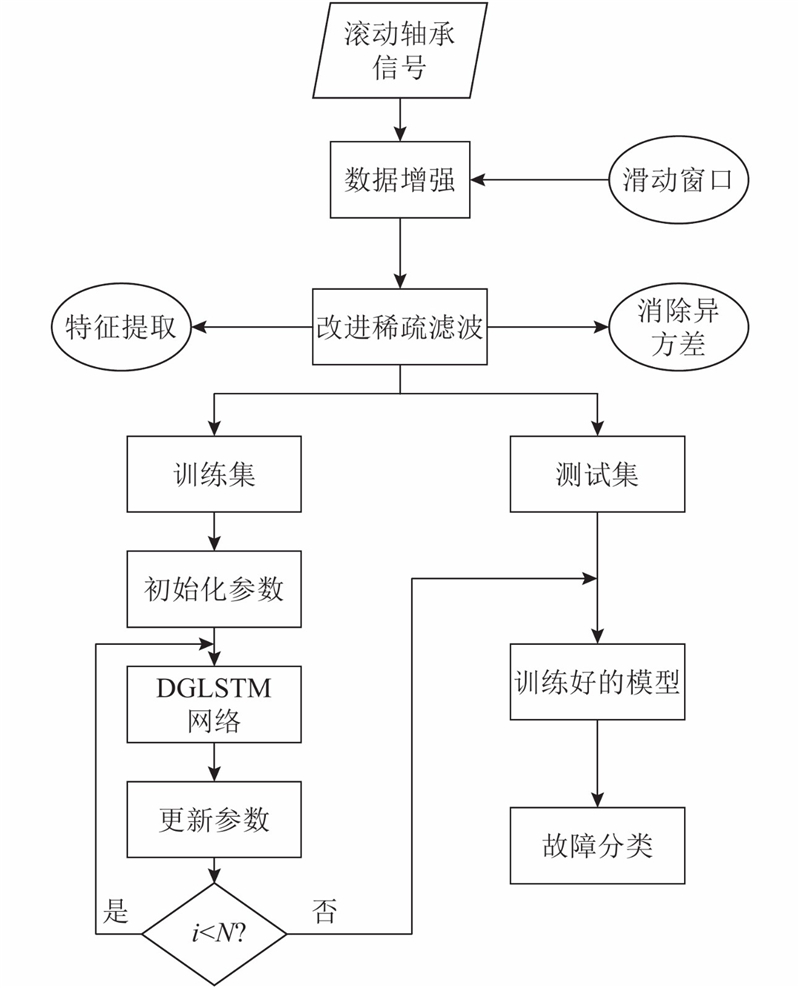
... 在进行网络训练之前,为了避免由于样本较少而出现过拟合现象,采用数据增强技术. 轴承数据是时间序列数据,采用滑动窗口的方式进行数据增强[24 ] . 图4 中,沿时间轴对时间序列进行重采样. ...
遥测数据时间序列滑动窗口动态分割技术
1
2015
... 在进行网络训练之前,为了避免由于样本较少而出现过拟合现象,采用数据增强技术. 轴承数据是时间序列数据,采用滑动窗口的方式进行数据增强[24 ] . 图4 中,沿时间轴对时间序列进行重采样. ...
1
... DGLSTM网络的主要部分是4层空洞门卷积层,它是由空洞卷积和门卷积组成. 其中,空洞卷积又称扩张卷积,由Yu等[25 ] 提出. 最初空洞卷积是被设计出来用在上下文分析的场景的,后来被广泛应用于语音合成[26 ] 、语义分割[27 ] 、机器翻译[28 ] 等领域. ...
Improving Spanish speech synthesis intelligibility under noisy environments
1
2016
... DGLSTM网络的主要部分是4层空洞门卷积层,它是由空洞卷积和门卷积组成. 其中,空洞卷积又称扩张卷积,由Yu等[25 ] 提出. 最初空洞卷积是被设计出来用在上下文分析的场景的,后来被广泛应用于语音合成[26 ] 、语义分割[27 ] 、机器翻译[28 ] 等领域. ...
Fully convolutional networks for semantic segmentation
1
2015
... DGLSTM网络的主要部分是4层空洞门卷积层,它是由空洞卷积和门卷积组成. 其中,空洞卷积又称扩张卷积,由Yu等[25 ] 提出. 最初空洞卷积是被设计出来用在上下文分析的场景的,后来被广泛应用于语音合成[26 ] 、语义分割[27 ] 、机器翻译[28 ] 等领域. ...
Feature-based decipherment for machine translation
1
2018
... DGLSTM网络的主要部分是4层空洞门卷积层,它是由空洞卷积和门卷积组成. 其中,空洞卷积又称扩张卷积,由Yu等[25 ] 提出. 最初空洞卷积是被设计出来用在上下文分析的场景的,后来被广泛应用于语音合成[26 ] 、语义分割[27 ] 、机器翻译[28 ] 等领域. ...
1
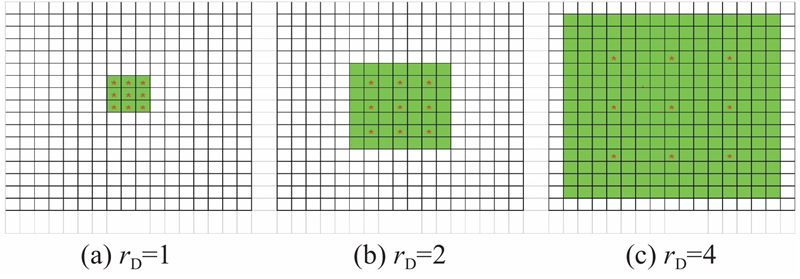
... 如图5(a) 所示为空洞率为1的3×3空洞卷积,此时的空洞卷积和普通的卷积操作一样;如图5(b) 所示为空洞率为2的3×3卷积,其中,只有9个红点的权重不为0,其余的均为0,此时卷积的感受野已经增大到7×7;同理,在图5(c) 中是空洞率为4的空洞卷积,感受野增大到了15×15. 对比传统呈线性增长的卷积操作,空洞卷积的感受野呈指数级增长[29 ] . ...
1
... 如图5(a) 所示为空洞率为1的3×3空洞卷积,此时的空洞卷积和普通的卷积操作一样;如图5(b) 所示为空洞率为2的3×3卷积,其中,只有9个红点的权重不为0,其余的均为0,此时卷积的感受野已经增大到7×7;同理,在图5(c) 中是空洞率为4的空洞卷积,感受野增大到了15×15. 对比传统呈线性增长的卷积操作,空洞卷积的感受野呈指数级增长[29 ] . ...
基于双向LSTM的手写文字识别技术研究
1
2019
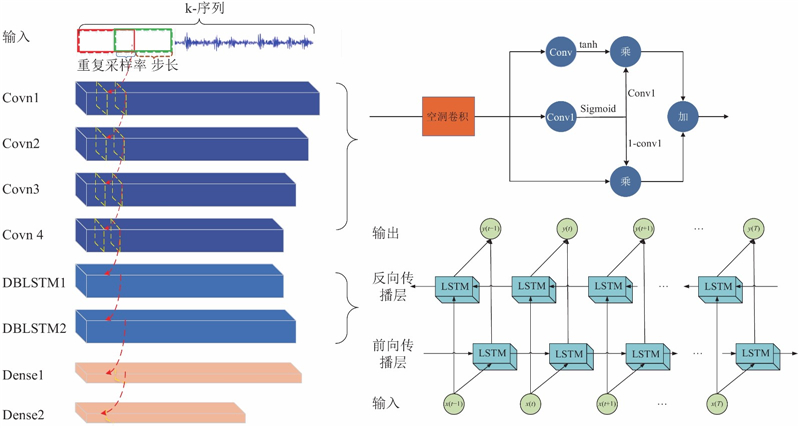
... 将经过空洞卷积层的数据传入双向LSTM网络中进行训练. 由于2个LSTM之间没有连接,双向LSTM网络可以看作2个单向LSTM网络构成[30 ] . 从图4 可以看出,在前向传播层中,所有的数据由t =1到t =T 完成前向传播;在反向传播层中,反向传播的神经元其实也在运行着前向传播的动作,只是由t =T到t =1进行传播. 数据传入全连接层进行分类,构成稀疏空洞门卷积网络(ISP-DGLSTM),整体算法流程图如图6 所示. ...
基于双向LSTM的手写文字识别技术研究
1
2019
... 将经过空洞卷积层的数据传入双向LSTM网络中进行训练. 由于2个LSTM之间没有连接,双向LSTM网络可以看作2个单向LSTM网络构成[30 ] . 从图4 可以看出,在前向传播层中,所有的数据由t =1到t =T 完成前向传播;在反向传播层中,反向传播的神经元其实也在运行着前向传播的动作,只是由t =T到t =1进行传播. 数据传入全连接层进行分类,构成稀疏空洞门卷积网络(ISP-DGLSTM),整体算法流程图如图6 所示. ...
Bearing fault automatic classification based on deep learning
1
2018
... 凯斯西储大学(Case Western Reserve University,CWRU)轴承数据常被用作轴承故障诊断的判别,CWRU实验台[31 ] 是由2HP电机、编码器、测功器组成,实验轴承为SKF6205型电机轴承. 如图7 所示,实验数据采集来自安装在电机驱动端和风扇端的加速度传感器,根据电动机转速不同分为0 HP、1 HP、2 HP、3 HP负载数据,采样频率为12 kHz,本文实验选择驱动端数据,如表1 所示. 表中,D 为直径,L D 为负载. 在实际实验时,轴承失效有3种可能的位置,分别为内环、外环和滚动单元. 为了验证本研究所提方法的可靠性,在驱动端的每个位置收集了3个故障的数据,分别为7、14和21 mm,每个故障类型采集400个样本,每1 200个信号组成一组样本. 试验数据包含10种信号,分别为正常信号和故障信号. ...
基于VMD和马氏距离SVM的滚动轴承故障诊断
1
2019
... 为了验证模型的性能,采用如图8 所示的动力传动系统诊断模拟器(driveline diagnostic simulator,DDS)实验台进行实验. DDS实验台是一个由变速驱动电机、编码器、扭转传感器、主齿轮箱、副平型齿轮箱、可编程磁闸和传感器组成的完整的动力系统装置[32 ] . 该实验台采集的滚动轴承的外环、内环故障以及滚动元件数据对研究齿轮箱的噪声特性和振动特性具有实际意义. ...
基于VMD和马氏距离SVM的滚动轴承故障诊断
1
2019
... 为了验证模型的性能,采用如图8 所示的动力传动系统诊断模拟器(driveline diagnostic simulator,DDS)实验台进行实验. DDS实验台是一个由变速驱动电机、编码器、扭转传感器、主齿轮箱、副平型齿轮箱、可编程磁闸和传感器组成的完整的动力系统装置[32 ] . 该实验台采集的滚动轴承的外环、内环故障以及滚动元件数据对研究齿轮箱的噪声特性和振动特性具有实际意义. ...
1
... 轴承振动信号是典型的时间序列数据,采用滑动窗口的方式在时间序列上进行重采样,以防止出现过拟合现象;由于轴承数据采集过程中存在大量噪声,采用改进稀疏滤波对特征进行提取,滤除数据中存在的异方差;将提取的特征输入空洞门卷积网络进行分类,并通过不同数据的实验对比验证所提方法的性能. 所提的网络模型在2层双向LSTM网络(DBLSTM)[33 ] 的基础上建立. ...