拓扑优化是一种在指定设计域内寻找最优材料分布的结构优化方法. 自Bendsoe和Kikuchi首次提出均匀化方法以来[1],拓扑优化,尤其是连续体拓扑优化发展十分迅速. 此后,又逐渐推出了变密度法[2-3]、水平集法[4-5]、独立连续映射方法[6-8]和渐进结构优化方法[9-10]等拓扑优化方法,并在结构概念设计阶段得到了广泛应用. 目前关于结构拓扑优化的研究大多注重于减小结构的柔度[11-13]. 但工程实践中更关注结构是否符合强度要求,即结构中的最大应力要低于材料的许用应力,以保证结构安全. 因此,近年来应力相关的拓扑优化问题备受关注. 应力优化问题主要有3大挑战[14]:应力的非线性行为、应力奇异、应力的局部性质.
应力奇异现象主要出现在采用变密度法的优化问题中. 优化时由于低密度单元具有与其密度不相符的高应力,使得优化算法不能有效更新设计变量. 采用应力插值模型[16-17]可以有效克服应力奇异现象. 离散拓扑优化方法,如水平集法和渐进结构优化方法,因为不存在中间密度单元,所以不会出现应力奇异现象,且拓扑优化结果边界清晰. 水平集法的缺点是较为依赖初始设计. Huang等[18-19]提出的双向渐进结构优化(bi-directional evolutionary structural optimization,BESO)方法采用启发式算法更新设计变量,避免使用数学规划方法求解优化问题,降低了计算代价,优化效率较高,因此BESO方法是一种极具潜力的拓扑优化方法.
应力的局部性质是指应力仅能表示单元自身的力学性能,不能反映结构的整体性能. 当采用传统方法进行应力优化时,需要构建与设计域中单元数目相当的约束,此举显著增加了计算时长,难以应用于实际问题. 目前主要使用应力全局化方法解决应力局部性质带来的计算量大的问题. 其中一种应力全局化方法采用凝聚函数逼近结构中的最大应力,建立应力的全局函数. 典型的凝聚函数有Kreisselmeier-Steihauser(K-S)函数和P范数. 王选等[20-21]采用K-S函数,Liu等[15, 22]采用P范数研究应力优化问题,优化效果显著. 另外一种应力全局化方法是隋允康等[23-24]提出的畸变比能法,该方法基于第四强度理论,将应力优化等效为畸变比能优化,并进一步转化为应变能优化. 畸变比能法极大提高了应力优化的计算效率,可应用于设计变量较多的应力优化问题. 但该方法得到的结果偏于保守,无法消除结构中的应力集中区域.
1. 应力拓扑优化模型
1.1. 畸变比能
根据第四强度理论:当结构内一点处的畸变比能(也称畸变能密度)达到了材料的极限值时,该点处的材料就发生塑性屈服. 单元i的畸变比能定义为
1.2. 畸变比能全局化策略
式中:sKS为畸变比能的全局函数,μ为常数,n为设计域中的单元个数. 当μ 趋于无穷大时,全局函数sKS退化为结构中的最大畸变比能,即sKS→max (si),i=1,2,···,n,sKS失去全局性.
1.3. 拓扑优化模型
本研究讨论的是提高结构强度的拓扑优化方法,为了保证结构的安全,须最小化结构中的最大畸变比能. 1.2节建立了畸变比能的全局函数,结合BESO方法,拓扑优化模型为
式中:V为当前结构的体积分数;V*为优化前设定的约束体积分数;vi为单元i在初始结构中的体积分数;xi为拓扑设计变量,代表单元i的状态. 当xi=1时,表示单元i为实单元;当xi=xmin时,表示单元i为空单元. 取xmin=0.001,以避免结构整体刚度矩阵奇异.
使用离散设计变量,目标函数连续性不足,无法推导单元灵敏度. 为了增加目标函数的连续性,并避免重新划分网格,采用文献[14]介绍的方法,对弹性模量和单元应力进行插值:
式中:Ei、E0分别为单元i和实体材料的弹性模量;σi为单元i的应力,对于平面应力单元,σi=[σx,σy,τxy]T,σx、σy、τxy分别为单元中心处沿x向和y向的正应力以及切应力;Di、D0分别为单元i和实体材料的本构矩阵;Bi为单元i的应变矩阵;ui为单元i所属节点的位移矢量;p、q为常数,本研究取p=3,q=0.5.
2. 单元灵敏度计算方法
2.1. 全局函数对设计变量的导数
2.2. 畸变比能对设计变量的导数
根据链式求导法则,单元i的畸变比能si对设计变量xj的导数可表示为
畸变比能对von Mises应力的导数根据式(1)可得
σvm, i可表示为
式中:V为转换矩阵. 对于平面应力单元,
因此,σvm, i对σi的导数为
由式(5)可知,σi对xj的导数为
结合式(5)、(9)、(11)、(12)可知,σvm, i对xj的导数为
线性结构静力平衡方程可表示为
式中:K为结构的整体刚度矩阵,U为结构中所有节点的位移矢量,F为外部施加的载荷矢量. 由于外力在优化过程中保持不变,式(14)两侧对设计变量xj求导数,可得
引入维度转换矩阵Ci,该矩阵可将结构整体位移矢量U转变为式(12)中的单元所属节点的位移矢量ui,即:
将式(15)和(16)代入式(13),有
将式(8)和(17)代入式(7),得
2.3. 伴随变量法
将式(18)代入式(6),畸变比能全局函数sKS对xj的导数为
为了方便求解式(19),引入伴随变量λ,使
则式(19)可简化为
整体刚度矩阵K是由所有单元刚度矩阵经维度转换,并按照直接刚度法原理组装而成,即有
单元j的刚度矩阵仅与本单元对应的设计变量xj有关,因此K对xj的导数为
式中:kj为单元j的刚度矩阵,kj,(0)是单元j为实单元时的刚度矩阵.
将式(23)代入式(21),可求出sKS对设计变量xj的导数为
按照BESO方法删除低灵敏度单元的设计变量更新策略,将式(24)添加负号以后,可得到单元j的灵敏度为
3. BESO方法
BESO方法是一种在优化过程中逐步增加和删除一部分单元使结构进化至最优材料布局的拓扑优化方法. 该方法采用的灵敏度过滤、修正方法和优化设计流程,可避免拓扑优化中常见的棋盘格现象和网格依赖性,并稳定优化设计过程[18].
3.1. 灵敏度过滤
应力优化时,由于应力的非线性行为,相邻单元的灵敏度数值可能相差较大. 直接使用式(25)计算得到的单元灵敏度更新设计变量,材料分布可能不连续,继而导致优化不收敛. 为了将单元灵敏度更加均匀地分布到临近单元上,引入一个无实际物理意义的概念—节点灵敏度,节点j的灵敏度定义为
式中:M为与节点j相连的单元个数. 为了进一步平滑灵敏度,以单元i的形心为圆心,将半径rmin的子空间内的所有节点灵敏度整合,作为单元i的灵敏度:
式中:l为子空间内的节点个数,ωij为节点j相对于单元i的权重,可表示为
式中:rij为单元i的形心与节点j之间的距离. 该灵敏度过滤方法使得空单元也具有一定的灵敏度,从而有可能恢复为实单元. 显然,位于高灵敏度区域的空单元恢复概率更大.
3.2. 迭代过程稳定策略
BESO方法采用离散设计变量,因此更新设计变量(即材料的重新分布)可能会使目标函数在迭代过程中出现振荡. 在处理应力优化问题时,这种现象更加明显. 为此,将当前迭代的灵敏度与前一次迭代的灵敏度取均值,作为当前迭代的最终灵敏度,以稳定优化过程,即
式中:αi, k和αi, k−1分别为单元i第k次迭代及第k−1次迭代的灵敏度.
3.3. 单元更新准则
第k次迭代在增加和删除单元之前,首先须确定第k+1次迭代的体积分数:
式中:RE为体积分数的进化率. 确定体积分数以后,将所有单元按灵敏度数值从大到小排列. 对于实单元,如果灵敏度αi≤αdel,k,则转为空单元;对于空单元,如果灵敏度αi≥αadd,k,则转为实单元. 单元增加阈值αadd,k和删除阈值αdel,k按照下列步骤确定.
1)取αN=αadd,k=αdel,k. αN为按从大到小次序排列的第N个单元的灵敏度,N=Vk+1×n.
2)计算增加单元比例RA根据初步确定的单元增加阈值αadd,k,记大于αadd,k的空单元个数为t,取RA=t/n. 若RA小于预先设定的最大单元增加比值RA,max,则跳过3),否则按照3)重新确定αadd,k.
3)计算αadd,k. 为了限制每次迭代增加单元的个数,每次迭代转为实单元的空单元个数T最多为T=RA,max×n. 将所有空单元的灵敏度从大到小排列,取前T个空单元转为实单元,即将这些空单元的设计变量由xmin更新为1. 在增加单元个数确定以后,由于下一次迭代的体积分数已经确定,需要删除的单元个数亦即确定. 按照单元灵敏度从小到大的顺序删除相应个数的实单元,即将这些实单元的设计变量由1更新为xmin.
设定最大单元增加比RA,max的意义在于稳定优化过程. 如果直接使用第1)步方法设定的增加阈值和删除阈值更新设计变量,该次迭代可能会增加较多的单元. 与此同时会删除较多的单元,以维持下一步的体积分数. 但材料分布可能因此出现剧烈变化,难以收敛至最优解.
3.4. BESO方法流程
BESO方法迭代步骤可归纳如下.
1)构建待优化结构的有限元模型,取设计域内所有单元对应的设计变量初始值为1;
2)指定优化设计参数,如进化率RE、灵敏度过滤半径rmin、最大单元增加比RA, max、参数μ、p和q等;
3)执行有限元分析;
4)按照式(25)计算初始单元灵敏度;
5)根据式(26)、(27)、(29)确定最终单元灵敏度;
6)使用3.3节介绍的方法更新设计变量;
7)根据设计变量更新有限元模型;
8)重复步骤3)~7),直至达到设定的收敛条件.
4. 数值算例
算例1
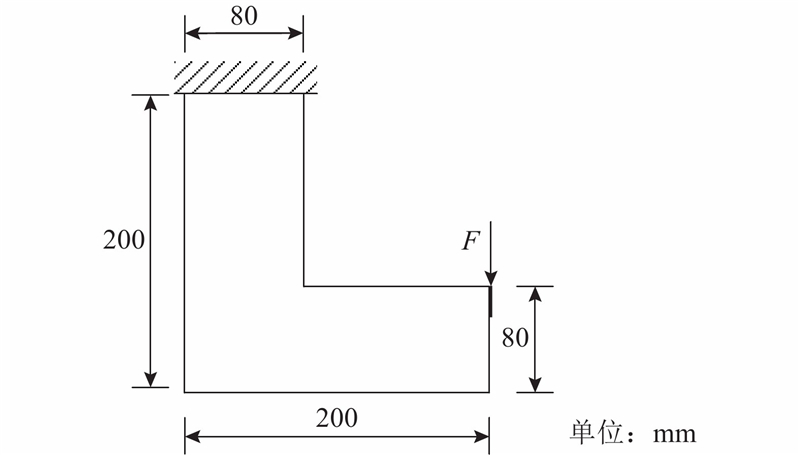
图 1
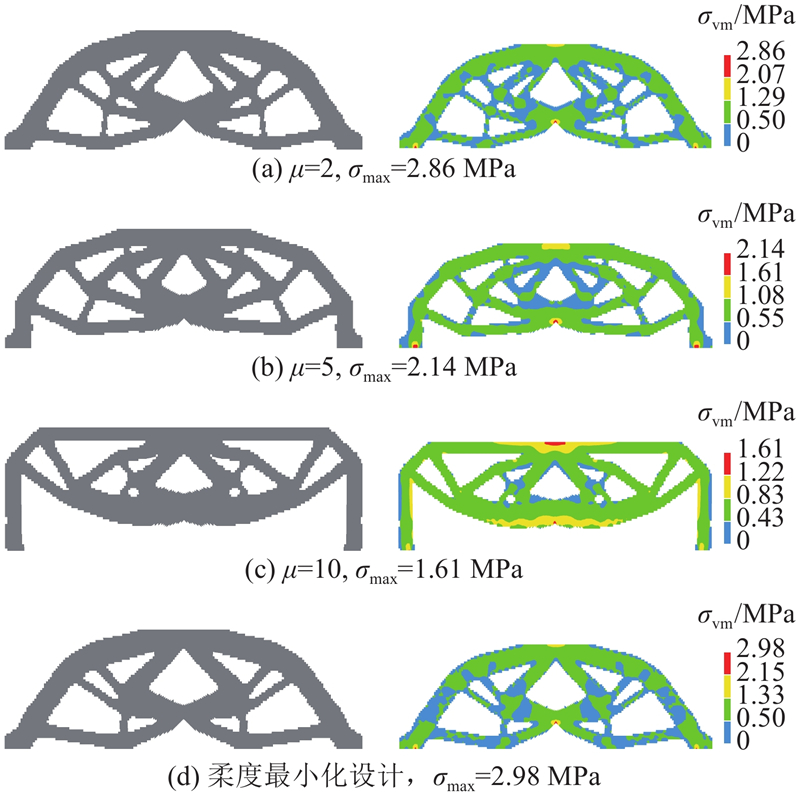
优化时,μ分别取2、5、10,得到的拓扑优化结果及相应的von Mises应力云图如图2(a)~(c)所示. 在3种情况下,最终结果的σmax分别为1.71、1.55和1.33 MPa. 相较于初始最大应力,分别下降了15.8%、23.7%和34.5%,优化效果显著. 图2(d)为柔度最小化设计的优化结果和von Mises应力云图,与μ=2得到的结果构型相近,应力集中效应未得到缓解. 由图2(a)~(c)可知,当μ 增大时,结构中的应力集中区域逐渐消失,结构中的应力分布更加均匀. 当μ=10时,结构中的大部分单元处于同一应力水平,优化效果最好. 继续增大μ,畸变比能全局函数的非线性程度增大,病态现象严重. 当μ >10时,材料分布开始出现不连续现象,优化过程不收敛. 这说明通过合理设置参数 μ,可以有效缓解结构中的应力集中效应,提高结构强度.
图 2
图 2 L型梁优化结果及von Mises应力云图
Fig.2 Optimal designs and von Mises stress contours of L-bracket
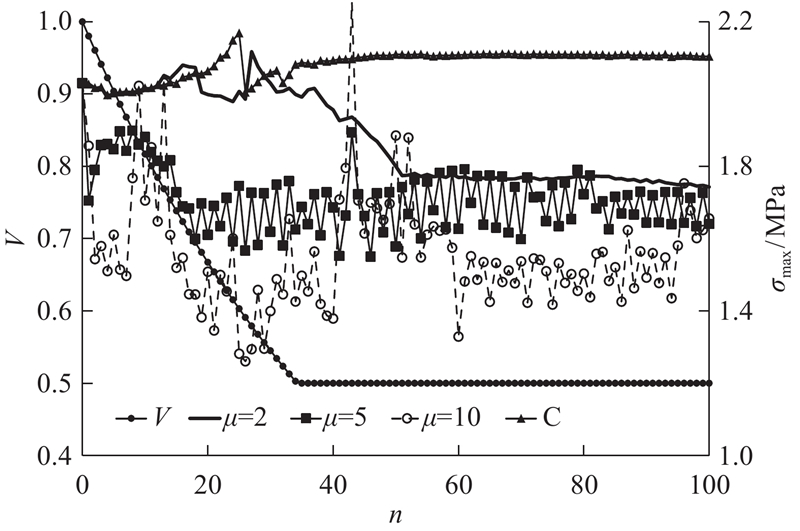
L型梁优化的体积分数及σmax迭代历史如图3所示。图中,C表示柔度最小化设计,n为迭代次数. 由图3可知,当μ=2时,在应力优化初始阶段,由于应力集中未被消除,σmax下降不明显. 第27次迭代后,随着应力集中部位逐渐被删除,σmax逐步下降,且下降过程平稳. 当μ =5、10时,由于L型梁的拐角在优化初始阶段即被删除,并代之以圆弧形结构,应力集中被消除,σmax显著下降. 当结构体积分数达到设定值时,尽管拓扑构型保持不变,但局部仍在增加和删除单元,而应力对拓扑变化较为敏感,因此σmax仍在一定范围内波动. 其中,由于目标函数的非线性程度增大,μ =10时的最大应力迭代历史较μ =5时的迭代历史波动明显. 因为柔度最小化设计无法消除应力集中的影响,所以当结构体积分数下降时,σmax还会略有上升.
图 3
图 3 L型梁体积分数及最大von Mises应力迭代历史
Fig.3 Evolution history of volume fraction and maximum von Mises stress of L-bracket
图 4
图 4 L型梁不同体积分数优化结果及最大von Mises应力
Fig.4 Optimal designs and maximal von Mises stress contours of L-bracket with different volume fractions
如图5所示为μ =10时L型梁的进化过程. 观察发现,在优化初始阶段,L型梁拐角处的单元即被移除,σmax从2.03 MPa下降至1.85 MPa. 随着材料的不断移除,σmax下降幅度逐渐减小. 在第60次迭代时,σmax下降至1.33 MPa,相比于柔度最小化设计的2.1 MPa,下降了36.7%.
图 5
算例2
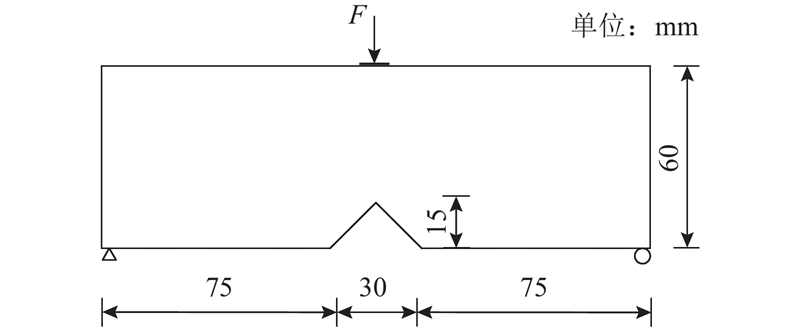
算例2为底端带有缺口的MBB梁,结构尺寸及边界条件如图6所示. 在该梁顶端中部施加一个F=10 N的垂向载荷,为了避免应力集中,该力均匀地分布在梁上端中部的11个节点上. 使用四节点矩形平面应力单元来离散设计域,单元尺寸为1 mm,灵敏度过滤半径rmin=3 mm,约束体积分数V*=0.5. 初始结构的最大von Mises应力为2.49 MPa,出现在梁底端的缺口处.
图 6
图 7
图 7 MBB梁优化结果及von Mises应力云图
Fig.7 Optimal designs and von Mises stress contours of MBB beam
图 8
算例3
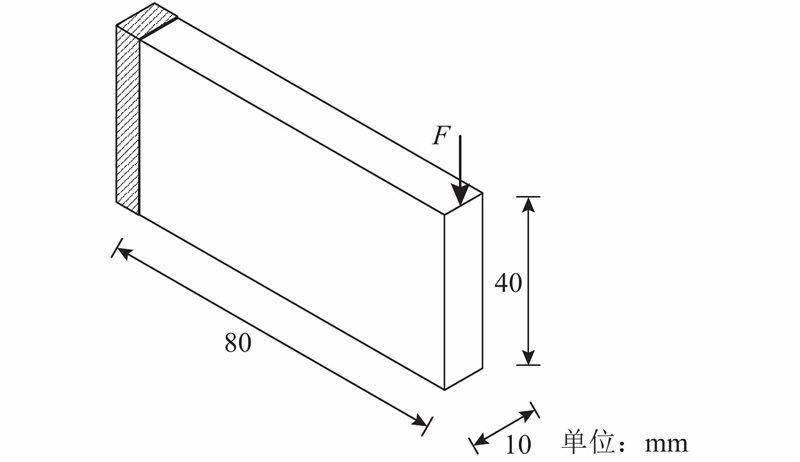
算例3为三维悬臂梁,其尺寸及边界条件如图9所示. 悬臂梁根部固定,在右侧上端施加一个F=25 N的垂向载荷. 为了避免应力集中,该力均匀地分布在悬臂梁右上角的25个节点上. 使用8节点六面体单元来离散设计域,单元尺寸为1 mm,灵敏度过滤半径rmin=3 mm,约束体积分数V*=0.3. 初始结构中σmax=2.53 MPa,出现在加载区域.
图 9
图 9 三维悬臂梁结构尺寸及边界条件示意图
Fig.9 Dimension and boundary conditions of 3D cantilever
图 10
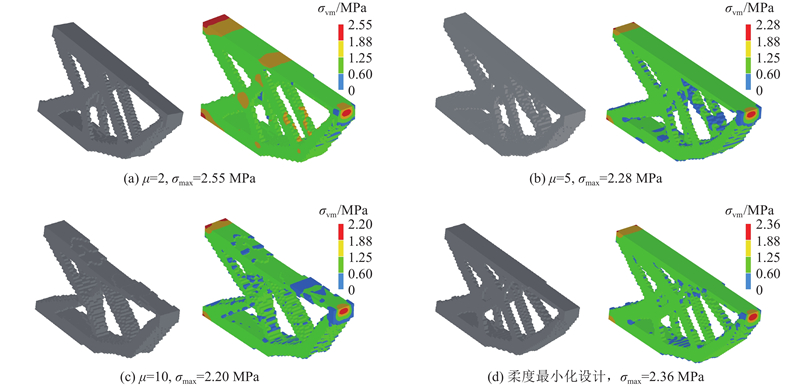
图 10 三维悬臂梁优化结果及von Mises应力云图
Fig.10 Optimal designs and von Mises stress contours of 3D cantilever
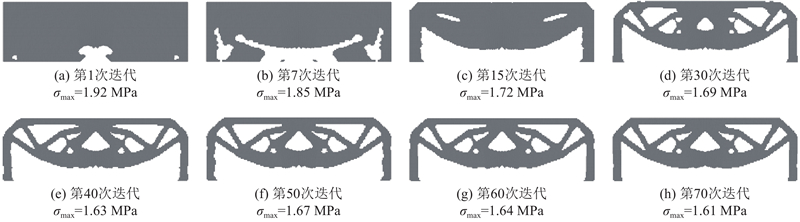
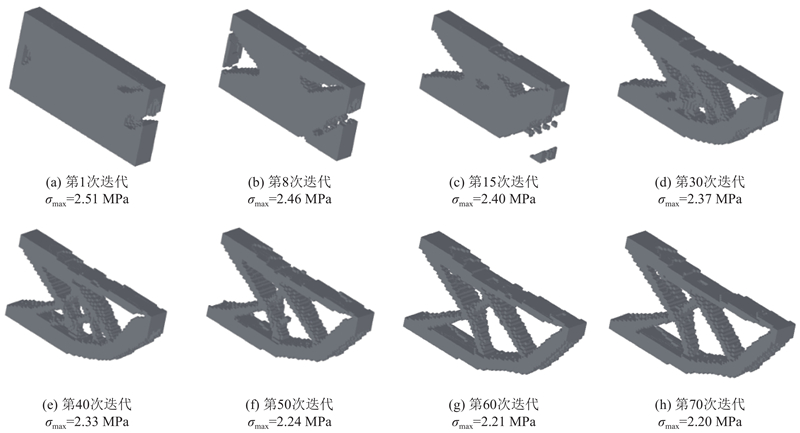
如图11所示为μ=10时三维悬臂梁的进化过程. 随着材料的不断移除,结构中的最大应力逐渐下降,在第50次迭代以后,结构中的最大应力无明显变化.
图 11
图 11 μ=10时三维悬臂梁的优化历程
Fig.11 Optimization process of 3D cantilever with μ of 10
5. 结 语
本研究提出的考虑体积约束的应力极小化渐进结构优化方法,设计域中没有中间密度单元,避免了应力奇异,并可以得到边界清晰的拓扑优化结果. 畸变比能全局化策略显著提升了应力优化问题的计算效率. BESO方法使用的灵敏度过滤和修正方法克服了应力的非线性行为,使优化过程更加稳定.
数值算例结果表明,使用不同的K-S凝聚函数参数μ 可以得到不同的优化结果. 当μ 值较小时,得到的优化结果与柔度最小化设计结果相似. 适当增大μ 值,结构中的最大应力逐渐减小,关键区域的应力集中效应得到缓解,结构中的应力分布更加均匀. 但当μ 取值过大时,畸变比能全局函数的非线性程度增大,并退化为结构中的最大畸变比能,全局函数失去了全局性. 材料分布因此变化剧烈,优化过程无法收敛. 研究表明,设定的约束体积分数不同,拓扑优化结果也不同,即优化结果依赖体积分数. 为克服体积分数的影响,下一步将研究以体积分数作为目标函数的应力约束优化问题.
所提出的方法可以解决二维和三维结构的应力拓扑优化问题,而且当单元数量较多时,仍能保持较高的计算效率,具有实际工程应用价值.
参考文献
Generating optimal topologies in structural design using a homogenization method
[J].DOI:10.1016/0045-7825(88)90086-2 [本文引用: 1]
飞轮壳结构刚度对机体NVH性能的影响
[J].
Influence of flywheel cover structural stiffness on engine body NVH performance
[J].
基于变密度法的周期性拓扑优化
[J].DOI:10.3901/JME.2013.13.132 [本文引用: 1]
Periodic topology optimization using variable density method
[J].DOI:10.3901/JME.2013.13.132 [本文引用: 1]
A level-set method for shape optimization
[J].DOI:10.1016/S1631-073X(02)02412-3 [本文引用: 1]
Stress-based shape and topology optimization with the level set method
[J].DOI:10.1016/j.cma.2017.09.001 [本文引用: 2]
基于ICM方法的刚架拓扑优化
[J].
Topological optimization of frame based on ICM method
[J].
结构拓扑优化ICM方法的改善
[J].
The improvement for the ICM method of structural topology optimization
[J].
A simple evolutionary procedure for structural optimization
[J].DOI:10.1016/0045-7949(93)90035-C [本文引用: 1]
3D and multiple load case bi-directional evolutionary structural optimization (BESO)
[J].DOI:10.1007/s001580050119 [本文引用: 1]
Minimum compliance topology optimization of shell-infill composites for additive manufacturing
[J].DOI:10.1016/j.cma.2017.08.018 [本文引用: 1]
Evolutionary topology optimization for structural compliance minimization considering design-dependent FSI loads
[J].DOI:10.1016/j.finel.2017.07.005
多相材料的连续体结构拓扑优化设计
[J].
Topology optimization of continuum structure with multiple materials
[J].
Stress-based topology optimization for continua
[J].DOI:10.1007/s00158-009-0440-y [本文引用: 7]
Stress optimization of smooth continuum structures based on the distortion strain energy density
[J].DOI:10.1016/j.cma.2018.08.031 [本文引用: 5]
ε-relaxed approach in structural topology optimization
[J].DOI:10.1007/BF01197454 [本文引用: 1]
On an alternative approach to stress constraints relaxation in topology optimization
[J].DOI:10.1007/s00158-007-0203-6 [本文引用: 1]
Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method
[J].DOI:10.1016/j.finel.2007.06.006 [本文引用: 4]
Bidirectional evolutionary method for stiffness optimization
[J].
基于改进的双向渐进结构优化法的应力约束拓扑优化
[J].
Stress-constrained topology optimization based on improved bi-directional evolutionary optimization method
[J].
An enhanced aggregation method for topology optimization with local stress constraints
[J].DOI:10.1016/j.cma.2012.10.019 [本文引用: 1]
Stress-based topology optimization using bi-directional evolutionary structural optimization method
[J].DOI:10.1016/j.cma.2018.01.035 [本文引用: 4]
结构拓扑优化ICM显式化与抛物型凝聚函数对于应力约束的集成化
[J].
The ICM explicitation approach to the structural topology optimization and the integrating approach to stress constraints based on the parabolic aggregation function
[J].
连续体结构拓扑优化应力约束凝聚化的ICM方法
[J].
Stress-constrained topology optimization based on improved bi-directional evolutionary optimization method
[J].
应力约束处理为应变能集成的连续体结构拓扑优化
[J].
ICM method of the topology optimization for continuum structures with stress constraints approached by the integration of strain energies
[J].
结构畸变比能处理的应力约束全局化的连续体结构拓扑优化
[J].
Continuum structural topology optimization with globalized stress constraint treated by structural distortional strain energy density
[J].