跳频(frequency hopping,FH)调制方式作为FH通信的重要参数,能够为敌我属性判别、定位干扰引导和情报信息提取等作战响应提供有力的保障. 现有的调制方式识别算法主要包括似然比判决和特征提取识别2类方法. 似然比判决方法的计算复杂度较高,模型失配问题严重,实际应用范围受限. 特征提取识别方法[1-4]主要利用瞬时波形、时频能量、星座图及高阶累积量等特征实现调制方式识别. Wang等[5]对接收的信号进行折叠预处理,利用改进的KS(Kolmogorov Smirnov,KS)分类器对调制方式进行识别;利用该算法降低了KS分类器的复杂度,所需信号的样本数量更少,识别速度更快. 赵雄文等[6]提取信号的高阶累积量和循环谱多维特征组成特征向量,利用智能决策方法进行分类识别;采用该算法能够实现9种数字调制方式的识别,识别率较高,抗噪性能较好. Xie等[7]将压缩感知理论运用到调制识别中,通过亚奈奎斯特速率采集信号,提取小波循环特征,同时采用分级特征缩减方法进一步降低数据维度;该算法的计算复杂度较低,识别调制样式种类较少. 上述方法均是通过提取人工设计的信号浅层特征实现调制方式识别,且特征设计依赖于研究人员的经验,提取难度大,适用的调制方式种类范围小,如何利用信号本身隐藏的深层特征,自动完成深层特征的提取和分类是目前研究的热点问题.
深度学习[8-12]通过训练和学习大量样本数据,形成多层深度神经网络,从而提取出样本深层隐藏特征,解决了人工设计特征难的问题,已在通信领域中得到应用. Li等[13]计算甚高频信号的循环频谱特征,利用卷积神经网络进行训练学习识别,识别率较高,所需样本数量较多,训练时间相对较长. 郭立民等[14]提出栈式稀疏自编码器的雷达信号调制方式识别算法,该算法对雷达信号进行时频变换,将时频矩阵作二值化处理和分割后作为自编码器的训练学习样本,但稀疏自编码器属于浅层学习网络,对训练样本的深层特征表示能力不足,在低信噪比下,分类识别能力下降. 上述方法只适用于定频信号,对于载频伪随机跳变的FH信号,识别效果下降明显. 本文提出基于组合时频变换和卷积神经网络(convolutional neural network,CNN)的FH信号调制方式识别算法. 该算法通过组合时频变换提取FH信号时频图,利用自适应维纳滤波算法滤除时频图的背景噪声,提高时频图的表征能力;利用连通域检测和双线插值算法,将时频图分割成适合CNN训练学习的维度. 为了提高CNN的分类识别性能,通过自适应矩估计[15](adaptive moment estimation,Adam)算法对CNN超参数进行优化.
1. 算法原理
假设采集
式中:
令FH信号的跳周期为
式中:
图 1
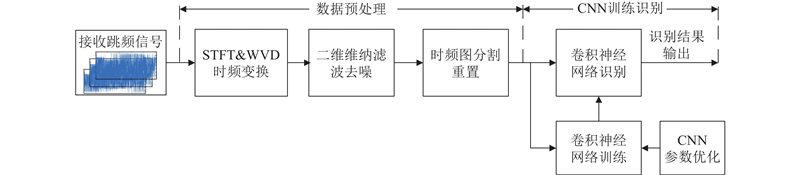
图 1 基于CNN的跳频调制方式识别流程
Fig.1 Identification process of FH modulation based on CNN
不同调制类型信号之间最重要的区别是相位函数形式,即瞬时频率函数的差异特性. 本文算法的核心思想是将FH调制方式识别问题转换为时频图特征识别问题. 从图1可知,该系统由数据预处理和CNN训练识别两部分组成,其中数据预处理主要是对时频图进行去噪提取和分割重置,CNN训练识别主要是对已重置时频图进行训练学习和分类识别.
1.1. FH信号时频图提取
目前,时频变换方法主要有短时傅里叶变换(short-time Fourier transform,STFT)、Wigner-Ville分布(Wigner-Ville distribution,WVD)、伪Wigner-Ville分布(pseudo Wigner-Ville distribution,PWVD)、平滑伪魏格纳分布(smoothed pseudo Wigner-Ville distribution,SPWVD)、Cohen分布(Choi-Williams distribution,CWD)和稀疏重构类算法. STFT无交叉项影响,时频分辨率低;WVD交叉项严重,时频分辨率高;PWVD和SPWVD通过增加窗函数,对交叉项有一定的抑制作用,但时频分辨率相比WVD下降明显. CWD的时频聚焦性和交叉项抑制相互制约. 稀疏重构类算法主要有近似0范数算法和稀疏贝叶斯(sparse Bayesian learning,SBL)算法[16]. 该类算法利用FH信号在时频域的稀疏性,通过构建频率域的超完备字典,求解欠定线性方程组的最优稀疏解,实现时频参数估计. 该类算法需要已知跳频频率集先验条件来构建频率字典,在求解最优解过程中计算复杂度较高. 利用STFT无交叉项和WVD时频分辨率高的特点,通过STFT&WVD组合时频方法完成采样数据的时频变换,具体的算法流程如下.
1)完成时域采样数据的STFT时频变换
2)对
3)根据式(3)对
式中:
4)STFT&WVD组合时频变化的结果
为了对比分析STFT&WVD方法提取FH信号的时频图效果,设置采样率为200 kHz,在信噪比为0 dB的条件下,采集长度为1 500个采样点的FH信号,噪声为高斯白噪声,跳周期为200个采样点,调制方式为QPSK,跳频率集设置为{10,45,20,30,15,40,50} kHz,CWD的参数
图 2
图 2 4种时频变换方法的FH信号时频图
Fig.2 Time-frequency diagrams of FH signals based on four time-frequency transform methods
1.2. 时频图去噪与分割
令图像
可以计算得到滤除白噪声之后的图像
式中:
为了降低计算复杂度并简化卷积神经网络分类器的复杂性,利用连通域检测方法提取每一跳的时频图,通过双线性插值算法调整每跳时频图的大小. 将图像
式中:
图 3
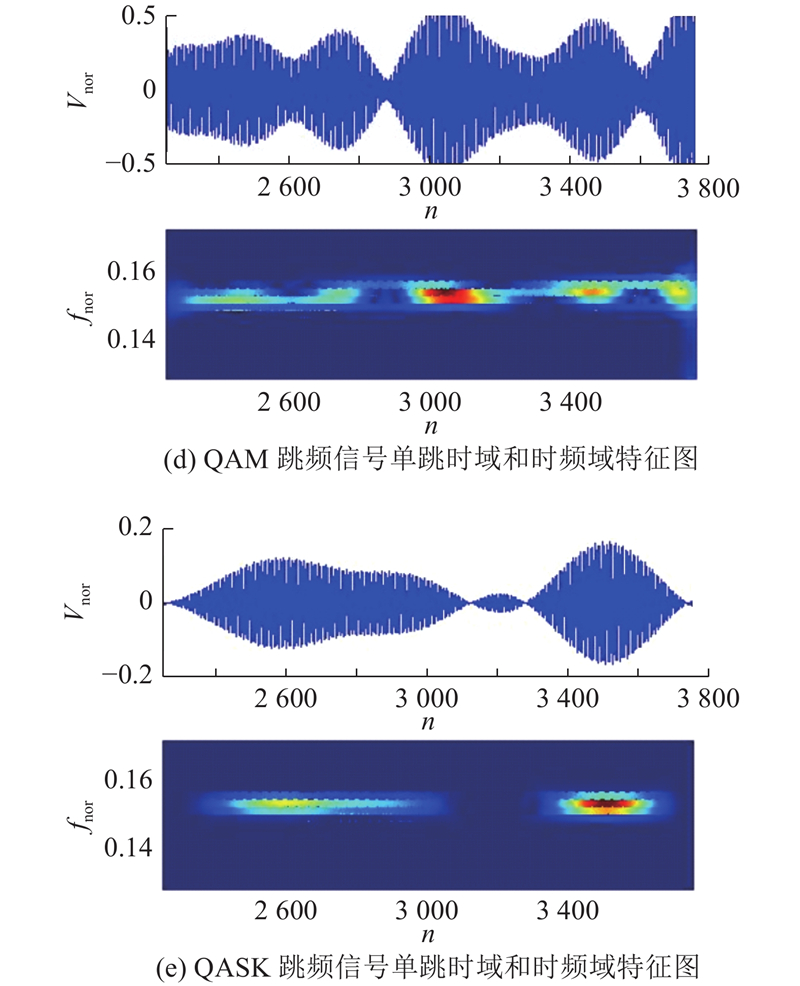
由图3可知,不同调制方式的跳频信号时频图能够有效地反映调制信号的波形特点和能量分布特征. 特别是对于时域波形特征明显的MSK和QASK调制方式,时频图特征更加显著. 在数据预处理阶段,提取每段时域样本数据的单跳时频图,按照采样时序组成训练测试集. 该集合既可以反映不同调制方式FH信号时域波形和时频能量分布特征,又可以减小FH信号载频变化对信号能量分布的影响,提高CNN提取特征的表征能力.
图 3
图 3 5种跳频调制信号单跳时域和时频域特征图
Fig.3 Single-hop time-frequency feature map of five frequency hopping signals
1.3. CNN设计与分类
图 4
假设卷积层
式中:
为了使深度神经网络具备分层的非线性映射学习能力,在卷积输出之后需要添加非线性激活函数,引入PReLU[20]函数作为激活函数,能够自适应地从训练样本中学习参数,收敛速度快,错误率低. PReLU函数的表达式为
式中:
为了降低数据维数,避免过拟合,需要池化层对卷积输出结果进行处理. 假设池化层大小为
式中:
式中:
为了得到最终的分类结果,需要在输出层增加Softmax分类器,分类结果
式中:
CNN网络模型根据应用环境、数据类型及数据分布的特点,具有不同的最优模型结构. 为了提高CNN的FH调制识别性能,需要对网络的层数、卷积核的高度和宽度、卷积核的数目等超参数进行优化. 采用交叉熵代价函数作为损失函数,如下.
式中:
在CNN训练阶段,利用Adam方法优化CNN超参数,提高训练收敛速度和识别率. Adam参数的更新方法如下.
式中:
1.4. 算法步骤
基于卷积神经网络的FH信号调制识别系统的具体步骤如下.
1)通过STFT&WVD方法获得FH信号时频图
2)利用自适应维纳滤波算法滤除时频图背景噪声,得到清晰时频图
3)通过连通域检测算法提取FH信号各跳时频图,利用双线性插值算法调整每跳时频图的大小为
4)利用步骤1)~3)获得的时频图数据样本,训练本文的CNN网络.
5)利用经步骤4)训练好的CNN网络,识别经过步骤1)~3)预处理的待测FH时频图样本,得到最终分类结果.
2. 实验仿真与分析
2.1. 实验环境与数据集
该实验的电脑配置如下:Intel酷睿i7 6700K CPU @4 GHz,32 GB内存,Windows 1064 bit系统,GPU为NVIDIA GTX1060. 开发环境如下:Python编译器Anaconda,加速库CUDA 10.0,TensorFlow 2.0和PyCharm编辑器.
该实验数据集的FH信号跳周期为200采样点,采样率为200 kHz,频率集为{10,45,20,30,5,15,25,35,50} kHz,调制方式有BPSK、QPSK、8PSK、SDPSK、QASK、16QAM、32QAM和GMSK共8种,初始相位设为0,巴克码长在{5,7,9,13}中随机取值,码周期为随机16~32采样点,加性噪声为高斯白噪声,均值为零. 为了方便、快速地训练CNN网络,利用本文预处理方法提取FH信号的单跳时频图并调整时频图大小. 每种调制信号在信噪比为−10~10 dB的条件下,每间隔1 dB采集FH信号并按观测时序提取单跳时频图400幅,大小均为
式中:
2.2. CNN网络层数分析
图 5
图 6
图 6 4种CNN结构的调制识别率和损失值的训练结果
Fig.6 Training results of modulation recognition rate and loss value of four CNN structures
表 1 不同样本集下的4种CNN调制识别训练结果
Tab.1
| CNN结构 | 训练集 | 验证集 | 测试集 | |||||
| Rpsr / % | Lloss | Rpsr / % | Lloss | Rpsr / % | Lloss | |||
| CNN_1 | 100 | 0.0076 | 80.05 | 0.0892 | 79.59 | 0.0928 | ||
| CNN_2 | 100 | 0.0045 | 81.92 | 0.0812 | 81.21 | 0.0873 | ||
| CNN_3 | 100 | 0.0027 | 85.06 | 0.0553 | 84.83 | 0.0576 | ||
| CNN_4 | 100 | 0.0032 | 84.69 | 0.0574 | 84.14 | 0.0603 | ||
由表1可知,CNN_3的识别率较高,说明具有3个池化层和2个全连接层的网络结构对时频图的识别效果更好.CNN_3最后提取的特征大小是
2.3. CNN卷积层分析
卷积层是CNN网络结构的核心层,用来提取图像边缘、纹理、线条及局部特征信息. 卷积核越大,感受野越大,提取的特征信息越全面,但参数越多,导致网络的识别效率降低. 为了选取合适的卷积核尺寸和参数,采用CNN_3结构,分析卷积核
表 2 6种参数组合的CNN调制识别训练结果
Tab.2
| | r | | | |
| | 2 | 2269.476 | 2.92 | 91.32 |
| | 2 | 1585.653 | 5.24 | 87.39 |
| | 2 | 357.248 | 8.23 | 83.46 |
| | 4 | 357.248 | 8.23 | 86.75 |
| | 6 | 357.248 | 8.23 | 90.14 |
| | 8 | 357.248 | 8.23 | 91.18 |
由表2可知,在相同的网络结构下,
图 7
图 7 基于CNN的跳频调制方式识别结构
Fig.7 Identification structure of FH modulation based on CNN
2.4. CNN过拟合分析
表 3 不同Dropout比例的CNN调制识别训练结果
Tab.3
| p/% | 训练集 | 验证集 | 测试集 | |||||
| Rpsr / % | Lloss | Rpsr / % | Lloss | Rpsr / % | Lloss | |||
| 0 | 100 | 0.006 2 | 91.88 | 0.085 3 | 90.05 | 0.087 4 | ||
| 10 | 100 | 0.013 7 | 87.92 | 0.184 7 | 87.42 | 0.188 5 | ||
| 20 | 100 | 0.006 9 | 89.24 | 0.093 8 | 88.21 | 0.100 4 | ||
| 30 | 100 | 0.007 5 | 88.13 | 0.096 6 | 87.98 | 0.099 5 | ||
| 40 | 99.93 | 0.062 1 | 90.75 | 0.088 2 | 90.62 | 0.110 6 | ||
| 50 | 100 | 0.003 8 | 92.81 | 0.087 1 | 92.63 | 0.095 4 | ||
| 60 | 100 | 0.004 3 | 89.46 | 0.109 2 | 88.34 | 0.101 3 | ||
| 70 | 99.96 | 0.076 7 | 88.25 | 0.114 7 | 87.83 | 0.132 8 | ||
| 80 | 100 | 0.006 6 | 91.33 | 0.087 1 | 91.35 | 0.099 6 | ||
| 90 | 100 | 0.009 2 | 89.75 | 0.093 6 | 89.43 | 0.101 2 | ||
由表3可知,当Dropout比例p为50% 时,CNN网络的识别率最高,其他比例均不同程度地降低,主要是由于Dropout比例为50%时随机生成的网络结构最多,降低了网络的预测风险,但是收敛速度略有下降. 综合考虑,本文CNN网络添加50% 的Dropout来减弱过拟合.
2.5. 算法性能分析
对比分析文献[17]、[21]和本文算法的调制识别性能.Zhang等[17]采用CWD方法获取时频图并进行二值化处理,提取二值化时频图的不变矩、伪Zernike矩、Renyi熵及主成分分析特征,采用Elman神经网络分类器对提取的多维特征集进行分类识别. Zhang等[21]采用CWD方法提取时频图,通过最近邻插值算法重置时频图,利用经典的LeNet-5神经网络进行训练、分类识别. 在实验中,每种调制信号在信噪比为−10~6 dB的条件下,每间隔2 dB采集300个样本,每个样本时长为1 024个采样点,8种调制FH信号共28 800个测试样本. 在每个信噪比条件下开展20次识别仿真实验,文献[17]、[21]和本文算法在不同信噪比条件下的平均识别率如图8所示. 图中,
图 8
由图8可知,3种算法的识别率随着信噪比增加均有所提高,当信噪比大于2 dB时,3种算法的识别率基本保持不变,且该算法的识别率相对较高. 当信噪比小于−4 dB时,3种算法的识别率下降较明显. 当信噪比为−4 dB时,该算法的平均识别率可以达到85%,高于其他2种算法,特别是对于时频特征明显的QPSK、8PSK、QASK和GMSK调制方式,该算法在信噪比为−6 dB时,识别率大于80%. 文献[17]算法的识别率均低于文献[21]算法和本文算法,说明人工提取的特征具有一定的局限性,不能反映各调制方式的深层特征信息. 当信噪比小于−6 dB时,文献[21]算法的识别率很低,对8种调制方式基本不能正确识别. 当信噪比较低时,该算法较文献[21]算法具有更高的识别率和抗噪性能. 主要原因是该算法通过STFT&WVD组合时频方法和自适应维纳滤波,去除大部分背景噪声,提高了低信噪比条件下的时频图分辨率. 该算法建立了比LeNet-5更合理的CNN网络结构和参数设置,使得本文CNN网络比LeNet-5更适合FH调制识别场景.
表 4 信噪比为−4 dB时8种FH信号调制方式的识别结果
Tab.4
| 输出 | Rpsr /% | |||||||
| 输入BPSK | 输入QPSK | 输入SDPSK | 输入8PSK | 输入QASK | 输入16QAM | 输入32QAM | 输入GMSK | |
| BPSK | 89.2 | 1.3 | 6.8 | 1.8 | 0 | 1.6 | 0 | 1.5 |
| QPSK | 2.1 | 94.2 | 1.3 | 3.1 | 0.5 | 0 | 1.8 | 1.3 |
| SDPSK | 8.1 | 1.4 | 91.1 | 1.7 | 0 | 0 | 0 | 2.1 |
| 8PSK | 0.6 | 2.3 | 0.8 | 92.8 | 0 | 0 | 0 | 0.5 |
| QASK | 0 | 0.8 | 0 | 0.6 | 94.6 | 2.5 | 1.4 | 0 |
| 16QAM | 0 | 0 | 0 | 0 | 3.2 | 91.7 | 4.7 | 0 |
| 32QAM | 0 | 0 | 0 | 0 | 1.7 | 4.2 | 92.1 | 0 |
| GMSK | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 94.6 |
3. 结 语
本文提出基于卷积神经网络的FH信号调制方式识别系统,通过训练学习FH信号时频图深层特征,将调制识别问题转化为图像识别问题,避免了人工设计特征提取难度大的问题. 该系统采用STFT&WVD方法将FH信号时频变换,利用自适应维纳滤波算法滤除噪声,提高系统的抗噪性能;通过设计的11层卷积神经网络;实现FH信号调制方式识别. 仿真实验表明,在较低的信噪比条件下,本文方法对BPSK、QPSK、SDPSK、8PSK、QASK、16QAM、32QAM和GMSK共8种FH信号调制方式具有较高的识别率,为后续FH信号基带数据解调和网台分选打下坚实基础. 如何在保证分类正确率的基础上,提高系统学习分类的时效性,进一步优化CNN网络结构参数是下一步的研究重点.
参考文献
Low complexity automatic modulation classification based on order-statistics
[J].DOI:10.1109/TWC.2016.2623716 [本文引用: 1]
Cyclostationarity-based robust algorithms for QAM signal identification
[J].DOI:10.1109/LCOMM.2011.112311.112006
Feature space analysis of modulation classification using very high-order statistics
[J].DOI:10.1109/LCOMM.2013.080613.130070
基于记忆因子的连续相位调制信号最大似然调制识别
[J].
Maximum likelihood modulation recognition for continuous phase modulation signals using memory factor
[J].
Novel fold-based kolmogorov-smirnov modulation classifier
[J].DOI:10.1109/LSP.2016.2572666 [本文引用: 1]
基于高阶累积量和循环谱的信号调制方式混合识别算法
[J].
Mixed recognition algorithm for signal modulation schemes by high-order cumulants and cyclic spectrum
[J].
Cyclic feature based modulation recognition using compressive sensing
[J].DOI:10.1109/LWC.2017.2697853 [本文引用: 1]
Towards convolutional neural networks on pulse repetition interval modulation recognition
[J].DOI:10.1109/LCOMM.2018.2864725
Radar signal intra-pulse modulation recognition based on convolutional neural network
[J].
Deep learning models for wireless signal classification with distributed low-cost spectrum sensors
[J].
K-sparse autoencoder based automatic modulation classification with low complexity
[J].DOI:10.1109/LCOMM.2017.2717821 [本文引用: 1]
Robust automated VHF modulation recognition based on deep convolutional neural networks
[J].DOI:10.1109/LCOMM.2018.2809732 [本文引用: 1]
基于栈式稀疏自编码器的低信噪比下低截获概率雷达信号调制类型识别
[J].
Low probability of intercept radar signal recognition based on stacked sparse auto-encoder
[J].
基于稀疏贝叶斯重构的多跳频信号参数估计
[J].
Parameter estimation of multi-hop frequency signals based on sparse Bayesian reconstruction
[J].
LPI radar waveform recognition based on time-frequency distribution
[J].DOI:10.3390/s16101682 [本文引用: 5]
Watermarking in the space/spatial-frequency domain using two-dimensional Radon-Wigner distribution
[J].DOI:10.1109/83.913599 [本文引用: 1]
Deep learning: methods and applications
[J].
Convolutional neural networks for automatic cognitive radio waveform recognition
[J].
Optimized CNN based image recognition through target region selection
[J].
Image recognition method of multi-cluster kiwifruit in field based on convolutional neural networks
[J].
Improving neural networks by preventing co-adaptation of feature detectors
[J].