随着道路和车辆的增加，交通事故越来越多，人们生命财产安全受到较大威胁. 据统计，全球每年交通事故导致大约120万人死亡、5 000万人受伤，交通事故已然成为全球“第一杀手”^[1]. 随着科技的发展，准确预测交通事故的发生已成为人们关注的焦点. 及时预测交通事故，可以显著降低财产损失，保障人类生命安全. 基于此，交通事故预测模型的构建受到越来越多学者的关注^[2]. 主要预测方法包括传统的预测方法和当前主流的深度学习方法. 传统的预测方法通过单个或者多个数据来预测交通事故，这些方式通常适用于交通事故数据具有明显趋势的情况，有差分整合移动平均自回归模型(autoregressive integrated moving average model，ARIMA)和灰度模型^[3-4]. 张艳艳等^[5]利用ARIAM建立水上交通事故预测模型；Becker等^[6-7]利用灰度模型建立交通事故预测模型. 随着数据科学的蓬勃发展，深度学习方法在解决分类和回归问题中得到广泛应用. 与浅层方法相比^[8]，深度学习方法在提取数据隐藏的自然结构和固有的抽象特征方面具有更好的性能. 因此，深度学习方法在交通事故预测领域具有广阔的应用前景. 近几年受深度学习的启发，采用深度学习方法如长短期记忆(long short-term memory，LSTM)网络和反向传播神经(back propagation，BP)网络来建立交通事故预测模型. Wang等^[9-14]利用神经网络建立交通事故预测模型. 陈海龙等^[15]利用BP网络构建预测模型对交通事故进行预测；Zhao等^[16-17]利用LSTM网络进行交通事故预测. BP网络和LSTM神经网络能够实现交通事故的预测，但交通事故的影响因素较多，具有较强的不确定性、非线性、动态性和时变特性^[18]，无论是传统的机器学习方法还是深度学习方法对于预测大规模、非线性动态时变性的数据都较困难.

本研究提出双尺度长短期记忆网络的交通事故量预测模型. 双尺度方程是有效的数据处理方式，LSTM网络是深度学习领域的主流神经网络. 利用LSTM网络的非线性处理能力可以获得较好的预测结果. 本研究的创新之处在于将双尺度方程和LSTM网络在交通事故预测中进行结合，提高预测性能. 研究详细框架如下：1)利用双尺度分解方程将原始交通事故时间序列分解成若干子层，目的是降低原始交通事故数据的非平稳性，为深度学习预测提供更多稳定的子层数据；2)利用LSTM网络完成对低频子层数据的预测；3)利用双尺度重构方程对LSTM网络预测结果进行重构得到最终预测值.

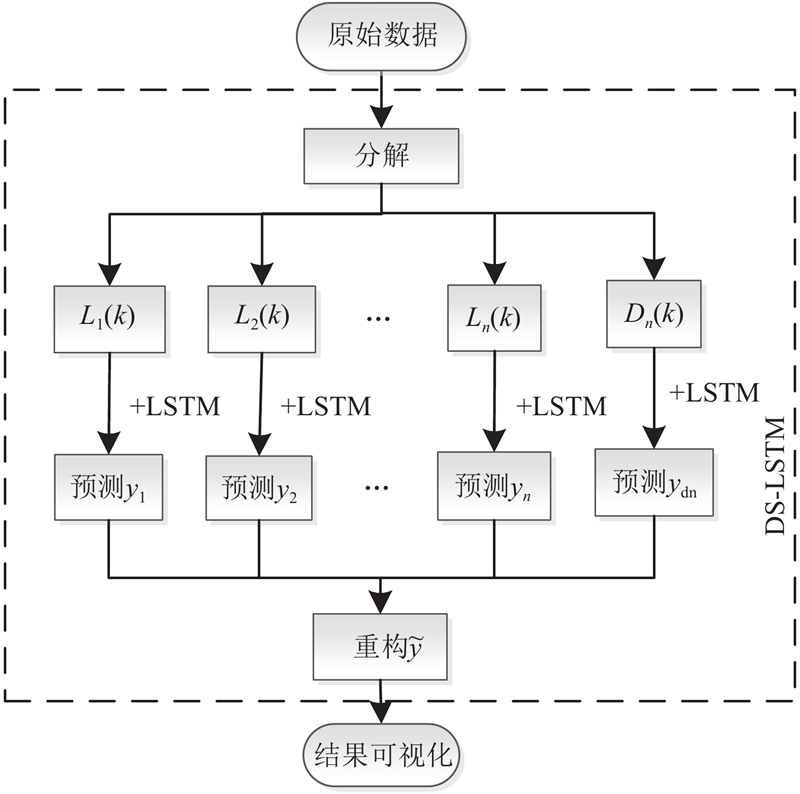
双尺度长短期记忆(dual scale-LSTM，DS-LSTM)网络的交通事故数量预测模型框架如图1所示. 图中， ${L_j}\left( k \right)$为原始数据分解得到的各低频子层数据， $j = 1,2, \cdots ,n$； ${D_n}\left( k \right)$为原始数据分解得到的高频数据； ${y_j}$为低频子层数据预测值； $\tilde y$为最终预测值；y_dn为最后一项的高频数据预测值. 整个过程的详细描述如下：1)利用双尺度分解方程分解原始交通事故时间序列数据到数个子层；2)利用长短期记忆网络预测低频子层数据；3)利用双尺度重构方程对步骤2)预测到的结果进行重构，输出最终值.

双尺度方程是有效的数据处理方式，可以对原始数据进行分解和重构处理。该方式对处理非平稳和类别复杂的数据有较好的效果，使非平稳数据经过处理后趋于近似平稳，并降低数据的复杂性^[19-21]. 具体计算如下：

(1) $\varphi \left( t \right) = \sum\nolimits_{n = - p}^q {h\left( n \right)} \varphi \left( {2t - n} \right),$

(2) $\psi \left( t \right) = \sum\nolimits_{n = 1 - q}^{1 + p} {g\left( n \right)\psi \left( {2t - n} \right)} .$

式中： $\varphi \left( t \right)$为父小波； $\psi \left( t \right)$为母小波； $h\left( n \right)$、 $g\left( n \right)$为滤波系数， $g\left( n \right) = {\left( { - 1} \right)^n}h\left( {1 - n} \right)$； $p$、 $q \geqslant 0$， $p + q$为奇数，令 $p + q + 1{\rm{ = }}2M$， $M$为正整数.

当 $n \in \left[ {0,p + q} \right]$时，式(1)、（2）分别变为

(3) $\varphi \left( t \right) = \sum\nolimits_{n = 0}^{p + q} {h\left( {n - p} \right)} \varphi \left( {2t - n + p} \right),$

(4) $\psi \left( t \right) = \sum\nolimits_{n = 0}^{p + q} {g\left( {n + 1 - q} \right)} \psi \left( {2t - n - 1 + q} \right).$

设 $a\left( n \right) \!=\! \sqrt 2 h\left( {n \!-\! p} \right),$ $n \!=\! 0,1, \cdots ,p \!+\! q,$ $b\left( n \right) = {\left( { - 1} \right)^{n - q + 1}}\times a\left( {2M - 1 - n} \right)$，则有 $h\left( n \right) = \sqrt 2 a\left( {n + p} \right) ,$ $n = - p, - p - 1, \cdots ,q .\,$ 将其分别代入式(3)、(4)，有

(5) $\begin{split} \varphi \left( t \right) =& \sqrt 2 \sum\nolimits_{n = 0}^{p + q} {a\left( n \right)} \varphi \left( {2t - n + p} \right) = \\ & \sqrt 2 \sum\nolimits_{n = 0}^{2M - 1} {a\left( n \right)} \varphi \left( {2t - n + p} \right) \end{split} ,$

(6) $\begin{split} \psi \left( t \right) =& \sum\nolimits_{n = 0}^{p + q} {\sqrt 2 b\left( n \right)\psi \left( {2t - n - 1 + q} \right)} = \\ & \sum\nolimits_{n = 0}^{2M - 1} {\sqrt 2 b\left( n \right)\psi \left( {2t - n - 1 + q} \right)}. \end{split} $

设 $t{\rm{ = }}{{\rm{2}}^{ - j}}t - k$， $\;\;t{\rm{ = }}t - k$，两边同乘 ${2^{{{ - j} / 2}}}$后分别代入式(5)、(6)，得到

(7) $\begin{split} {2^{{{ - j} / 2}}}\varphi \left( {{{\rm{2}}^{ - j}}t - k} \right) =& {2^{{{\left( { - j + 1} \right)} / 2}}}\sum\nolimits_{n = 0}^{2M - 1} {a\left( n \right)}\times\\& \varphi \left( {{2^{ - j + 1}}t - 2k - n + p} \right), \end{split} $

(8) $\begin{split} {2^{{{ - j} / 2}}}\psi \left( {t{\rm{ - }}k} \right) =& {2^{{{\left( { - j{\rm{ + 1}}} \right)} / 2}}}\sum\nolimits_{n = 0}^{2M - 1} {b\left( n \right)}\times\\& \psi \left( {2t - 2k - n - 1 + q} \right) . \end{split} $

假设给定离散信号 ${c^0}\left( k \right)$， $k = 0,1,2, \cdots ,{2^n}$. 根据分解思想，由式(7)、(8)推导得出：

(9) $\begin{split} {c_j(k)} =& \left\langle {f\left( t \right),{\varphi _{j,k}}\left( t \right)} \right\rangle = \int\limits_{\bf R} {f\left( t \right)} {\left( {{2^{{{ - j} / 2}}}\varphi \left( {{2^{ - j}}t - k} \right)} \right)^{1/2}} {\rm d}t = \\ & \sum\nolimits_{n = 0}^{2M \!-\! 1} {{a_n}\!{{\int\limits_{\bf R}\! {f\left( t \right)\left( {{2^{{{\left( {\! -\! j\! +\! 1} \right)} / 2}}}\!\varphi \left( {{2^{\! -\! j\! + \!1}}t\! -\! 2k \!-\! n\! +\! p} \right)} \right)} }^{1/2}}{\rm d}t}\! = \\ & \sum\nolimits_{n = 0}^{2M - 1} {{a_n}\left\langle {f\left( t \right),{\varphi _{j - 1,2k + n - p}}\left( t \right)} \right\rangle }=\\&\sum\nolimits_{n = 0}^{2M - 1} {{a_n}{c_{j - 1}}}({2k + n - p}) .\\[-13pt] \end{split} $

式中：f(t)为原始数据函数，c_j(k)为原始数据上的分解函数，φ_j,k(t)为分解函数的父波，a_n为得到的分解序列的权值参数.

定义函数 ${L_j}\left( k \right)$、 ${D_j}\left( k \right)$：

(10) ${L_j}\left( k \right) = {c_j}\left( k \right) = \sum\nolimits_{n = 0}^{2M - 1} {a\left( n \right){c_{j - 1}}\left( {2k + n - p} \right)} ,$

(11) ${D_j}\left( k \right) = {d_j}\left( k \right) = \sum\nolimits_{n = 0}^{2M - 1} {b\left( n \right){c_{j - 1}}\left( {2k + n + 1 - p} \right)} .$

式中： ${L_j}\left( k \right)$、 ${D_j}\left( k \right)$为原数据分解的序列， $j = 1,2, \cdots ,n $， $ k = 0,1,2 \cdots ,{2^{n - j}}$.

根据重构原理，由式(5)、(8)推导出重构方程：

(12) $\begin{split} f\left( t \right) =& \sum\nolimits_{k = 0}^{{2^{n - j}}} {{c_j}\left( k \right){2^{{{\left( {n - j} \right)} / 2}}}\varphi \left( {{2^{n - j}}t - k} \right)} +\\ & \sum\nolimits_{k = 0}^{{2^{n - j}}} {{d_j}\left( k \right){2^{{{\left( {n - j} \right)} / 2}}}\psi \left( {{2^{n - j}}t - k} \right)} . \end{split} $

设下列形式的信号 $f\left( t \right)$展开式：

(13) $\begin{split} f\left( t \right) =& \sum\nolimits_{k = 0}^{{2^{n - j}}} {{c_j}\left( k \right)} {2^{{{\left( {n - j} \right)} / 2}}}\sum\nolimits_{m = 0}^{2M - 1} {a\left( m \right)}\times\\&\varphi \left( {{2^{n - j + 1}}t - 2k - m + p} \right) + \\ & \sum\nolimits_{k = 0}^{{2^{n - j}}} {{d_j}\left( k \right)} {2^{{{\left( {n - j} \right)} / 2}}}\sum\nolimits_{m = 0}^{2M - 1} {b\left( m \right)}\times\\&\psi \left( {{2^{n - j + 1}}t - 2k - m + p - 1} \right) = {f_1}\left( t \right) + {f_2}\left( t \right) . \end{split} $

对上式两边同乘 ${2^{{{\left( {n - j + 1} \right)} / 2}}}\varphi \left( {{2^{n - j + 1}}t - 2n} \right)$，在 $\left( {{\rm{ - }}\infty ,\infty } \right)$上利用正交性积分. 在 ${f_1}\left( t \right)$中，仅当 $2k + m - p = 2n$，即 $m = 2n - 2k + p$时，对应项不为零，设 $m=2i + 1 \left( {i = 0,1, \cdots ,M - 1} \right)$，则 $k = n - i + {{\left( {p - 1} \right)} / 2}$；在 ${f_2}\left( t \right)$中，仅当 $2k + m - q + 1 = 2n$，即 $m = 2n + q - 1 - 2k$ 时，对应项不为零，设 $m=2i + 1\left( i = 0,1, \cdots , M - 1 \right)$，则 $k = n - i + {q / 2} - 1$. 综上可得

(14) $\begin{split} {c_{j - 1}}\left( {2n} \right) =& \sum\nolimits_{n = 0}^{M - 1} {a\left( {2k} \right)} {c_j}\left( {n - k + {{\left( {p - 1} \right)} / 2}} \right)+ \\ & \sum\nolimits_{n = 0}^{M - 1} {b\left( {2k} \right){d_j}\left( {n - k + {q / 2} - 1} \right)} . \end{split} $

同理可得

(15) $\begin{split} {c_{j - 1}}\left( {2n + 1} \right) =& \sum\nolimits_{n = 0}^{M - 1} {a\left( {2k + 1} \right){c_j}\left( {n - k + {{\left( {p + 1} \right)} / 2}} \right)} + \\ & \sum\nolimits_{n = 0}^{M - 1} {b\left( {2k + 1} \right){d_j}\left( {n - k + {q / 2}} \right)}. \\[-15pt] \end{split} $

最终预测值和权重分别为

(16) $\tilde y = \sum\nolimits_{i = 1}^n {{w_i}{{f}} {{\left( t \right)}_i}} + {w_{\rm dn}}{{f}} {\left( t \right)_{\rm dn}},$

(17) ${w_i} = \sum\nolimits_{i = 1}^{n + 1} {{{\left( {{{{{f}} {{\left( t \right)}_i}} \bigg/ {\sum\limits_{j = 1}^{n + 1} {{{f}} {{\left( t \right)}_j}} }}} \right)}_i}}. $

式中：下标 $i$表示低频子层、 ${{\rm dn}}$表示高频子层； ${w_i}$、 ${w_{\rm dn}}$为各子层预测值权重， $f{\left( t \right)_i}$、 $f{\left( t \right)_j}$为各子层预测结果， ${w_{n + 1}}$、 $f{\left( t \right)_{n + 1}}$为 ${w_{\rm dn}}$、 $f{\left( t \right)_{\rm dn}}$.

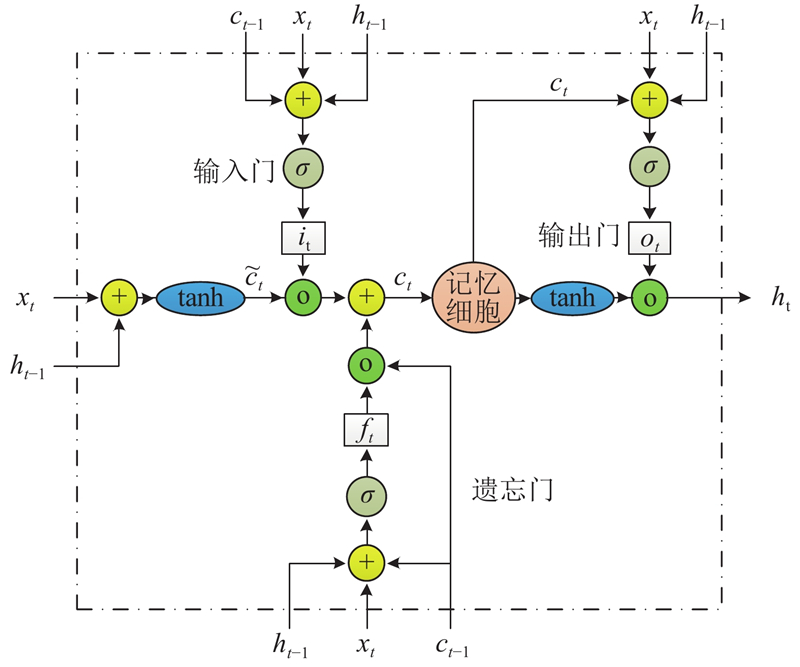
LSTM由循环神经网络(recurrent neural network, RNN)优化演变而来，原始RNN的隐藏层只有一个状态，对于短期输入较敏感，若对RNN增加一个状态，使其对长期输入也敏感，则能使得RNN具有长期记忆功能. LSTM主要由输入门、遗忘门、输出门组成，结构如图2所示：

一个记忆块在 $t$时刻的计算过程^[22]如下：

(18) ${\tilde c_t} = \tanh \;\left( {{w_{{\rm{cx}}}}{x_t} + {w_{{\rm{ch}}}}{h_{t - 1}} + {b_{\rm{c}}}} \right),$

(19) ${i_t} = \sigma \left( {{w_{{\rm{ix}}}}{x_t} + {w_{{\rm{ih}}}}{h_{t - 1}} + {w_{{\rm{ic}}}}{c_{t - 1}} + {b_{\rm{i}}}} \right),$

(20) ${f_t} = \sigma \left( {{w_{{\rm{fx}}}}{x_t} + {w_{{\rm{fh}}}}{h_{t - 1}} + {w_{{\rm{fc}}}}{c_{t - 1}} + {b_{\rm{f}}}} \right),$

(21) ${o_t} = \sigma \left( {{w_{{\rm{ox}}}}{x_t} + {w_{{\rm{oh}}}}{h_{t - 1}} + {w_{{\rm{oc}}}}{c_t} + {b_{\rm{o}}}} \right),$

(22) ${c_t} = {c_{t - 1}} \circ {f_t} + {i_t} \circ {\tilde c_t},$

(23) ${h_t} = {o_t} \circ \tanh \;{{c_t}} .$

式中： ${\tilde c_t}$为t时刻记忆细胞的更新状态； ${i_t}$、 ${f_t}$、 ${o_t}$、 ${c_t}$、 ${h_t}$分别为输入门、遗忘门、输出门、记忆细胞以及隐藏层在 $t$时刻的状态； ${x_t}$为 $t$时刻的输入； ${h_{t - 1}}$、 ${c_{t - 1}}$分别为隐藏层及记忆细胞在 $t - 1$时刻的输出； ${w_{{\rm{cx}}}}$、 ${w_{{\rm{ch}}}}$分别为记忆细胞与输入 ${x_t}$和隐藏层的权值； ${w_{{\rm{ix}}}}$、 ${w_{{\rm{ih}}}}$、 ${w_{{\rm{ic}}}}$分别为输入门与 ${x_t}$、隐藏层、记忆细胞的权值； ${w_{{\rm{fx}}}}$、 ${w_{{\rm{fh}}}}$、 ${w_{{\rm{fc}}}}$分别为遗忘门与 ${x_t}$、隐藏层、记忆细胞的权值； ${w_{{\rm{ox}}}}$、 ${w_{{\rm{oh}}}}$、 ${w_{{\rm{oc}}}}$分别为输出门与 ${x_t}$、隐藏层、记忆细胞的权值； ${b_{\rm{c}}}$、 ${b_{\rm{i}}}$、 ${b_{\rm{f}}}$、 ${b_{\rm{o}}}$为偏置项； $\sigma \left( \cdot \right)$、 $\tanh \;\left( \cdot \right)$为激活函数；“ $ \circ $”为哈达玛积，即逐点乘.

通过式(9)~(11)将原始数据分解成 ${L_j}\left( k \right)$、 ${D_j}\left( k \right)$这2个序列，将分解后的序列输入LSTM预测模型. 原始数据经过预处理后n层分解为 ${c^0}\left( k \right){\rm{ = }}{L_1}\left( k \right) + {L_2}\left( k \right) + \cdots + {L_n}\left( k \right) + {D_n}\left( k \right).$通过式(12)~(17)得到预测模型的预测值 ${y_1},{y_2},{y_3}, \cdots ,{y_n},{y_{\rm dn}}$，然后利用重构获得最终预测值 $\tilde y$.

在衡量模型性能时使用4个标准：平均绝对误差(mean absolute error，MAE)、均方误差(mean squared error，MSE)、均方根误差 (root mean squard error，RMSE)和准确度(accuracy，ACC)来评估预测模型^[23-24]. 相关定义如下：

(24) ${\rm{MAE}} = \frac{1}{N}\sum\limits_t {\left| {\tilde y\left( t \right) - y\left( t \right)} \right|} ,$

(25) ${\rm{MSE}} = \sqrt {{{\left( {\tilde y\left( t \right) - y\left( t \right)} \right)}^2}}, $

(26) ${\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {y\left( t \right) - \tilde y\left( t \right)} \right)}^2}} } ,$

(27) ${\rm{ACC}} = 1 - {{{ {\sum\limits_{t = 0}^N {\bigg| {\tilde y\left( t \right) - y\left( t \right)} \bigg|} } } \Bigg/ {\sum\limits_{t = 0}^N {y\left( t \right)} }}}.$

式中： $y(t)$为 $t$时刻交通事故数的实测值， $\tilde y(t)$为预测值， $N$为样本个数.

采用Kaggle比赛公开的2011~2015年利兹和UK地区的交通事故数据. 使用2011~2014年数据集训练预测模型，2015年数据集测试预测模型. 2个数据集的数据量和数据复杂度不同，利兹数据集训练数据有10万条，测试数据有4000条；UK数据集训练数据有50万条，测试数据有1万条. 本研究主要使用2个数据集中的事故发生时天气状态、事故发生的道路表面状态和事故发生量等数据项.

实验是在Windows10的Python3.6.6、TensorFlow1.12.0和Keras2.2.4下进行的. 分别将利兹和UK的2011~2014年的天气状况、路面状态和事故量作为训练输入；2015年的天气状况和路面状态作为预测模型输入，模型输出为事故量. 每个实验包含4个交通事故预测模型：LSTM模型^[25]、GRU模型^[26]、SAEs模型^[27]和本研究所提出的DS-LSTM模型.

为了测试DS-LSTM的有效性，须确定该模型的参数—训练次数(epochs). 由于数据的差异性，在达到较好的训练结果时模型参数有一定的差异.

如表1所示，随着epochs的增加，混合模型准确度有所提高，但当达到一定值之后，准确度会下降. 在使用利兹数据集时，当epochs=900时DS-LSTM模型的预测准确度较高；在使用UK数据集时，当epochs=700时DS-LSTM模型预测准确度最高.

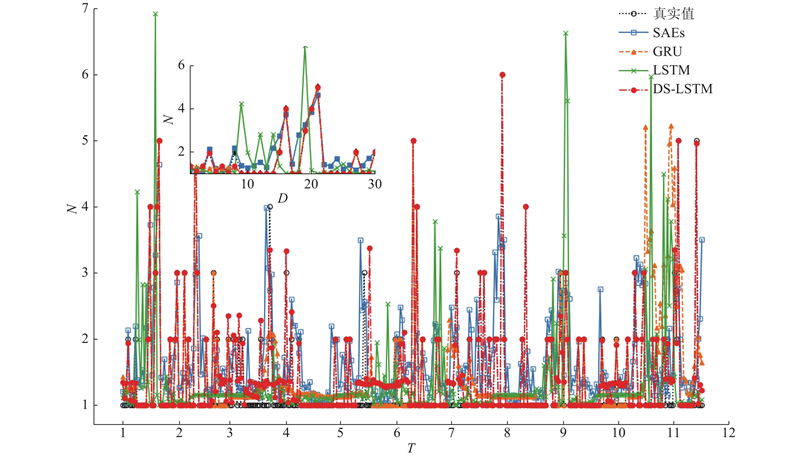
当epochs=900时，4种交通事故预测模型结果如图3所示. 图中，N为事故量，T为时间月份，左上角小图为1月1日—1月30日的事故发生量的局部放大结果，D为时间日期. 可以看出，DS-LSTM模型预测结果相较于(LSTM、GRU、SAEs)模型更加接近真实值.

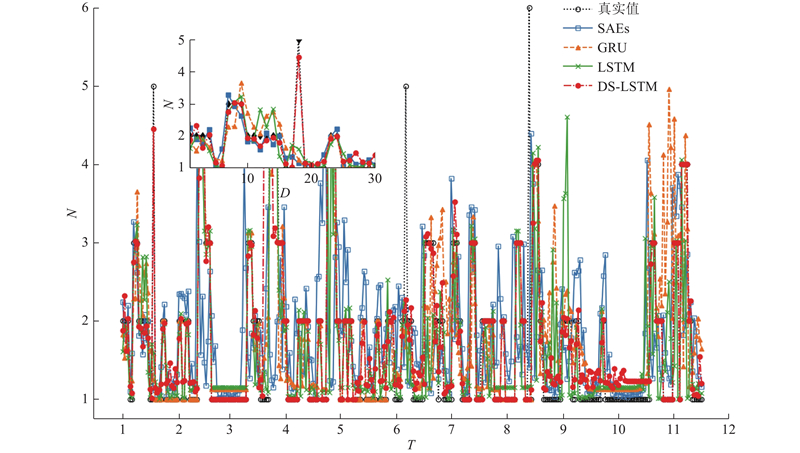
当epochs=700时，4种交通事故的预测模型结果如图4所示. 图中，左上角小图为1月1日—1月30日事故发生量的局部放大结果. 可以看出，DS-LSTM模型的预测结果相较于其他3个模型(LSTM、GRU、SAEs)更加接近真实值.

由于2个数据集在离散程度和数据特征上有所不同，利用同种参数进行实验得到结果，如图3、 4所示. 可以看出，混合模型较于单个神经网络的预测准确度有显著提高. 比如，当从利兹数据集更换为UK数据集时，对图3、4进行分析，发现在单个神经网络情况下(如LSTM)，预测结果出现较大偏差；利用式(9)~(11)处理得到的数据，数据趋于近似平稳，利用式(12)~(17)重构预测值，预测准确度有显著提高.

当根据常用的模型评价标准，达到最优预测模型时，各模型的性能指标如表2所示. 由表1、2可以看出，同一个数据集DS-LSTM的预测模型精度要高于LSTM、GRU和SAEs模型. 例如，当利兹数据集的epochs=900时，预测模型DS-LSTM性能指标相较于LSTM：MAE降低0.1061、MSE降低0.3771、RMSE降低0.3105，可以看出DS-LSTM的预测性能较好，在相同参数下准确度为83.2079%，相较于LSTM提高约6%、相较于GRU提高约38%、相较于SAEs提高约30%；当UK数据集的epochs=700时，预测模型DS-LSTM性能指标相较于LSTM：MAE降低0.3235、MSE降低0.5306、RMSE降低0.4925，可以看出DS-LSTM的预测性能较好，在相同参数下准确度为88.187 0%，相较于LSTM提高约28%，相较于GRU提高约38%，相较于SAEs提高约33%.

通过以上实验结果得出，在不同epochs情况和不同数据集下，本研究所提出的混合模型DS-LSTM的预测性能相对于其他模型有显著提高，由此证明该模型的有效性和鲁棒性.

提出新的交通事故量预测模型. 这种预测模型对于道路交通事故有较好的预测效果，利用4种预测模型对2个数据集进行测试. 实验结果表明混合模型DS-LSTM相比LSTM、GRU和SAEs等预测模型，准确率有显著提高.

后续将进一步研究交通数据集的特征提取和处理方法. 比如有效提取事故数据集中影响交通事故的天气、路面状况信息，并利用其他深度学习优化方法提高交通事故预测的准确率；降低本研究提出的混合模型训练时间，提高模型性能.