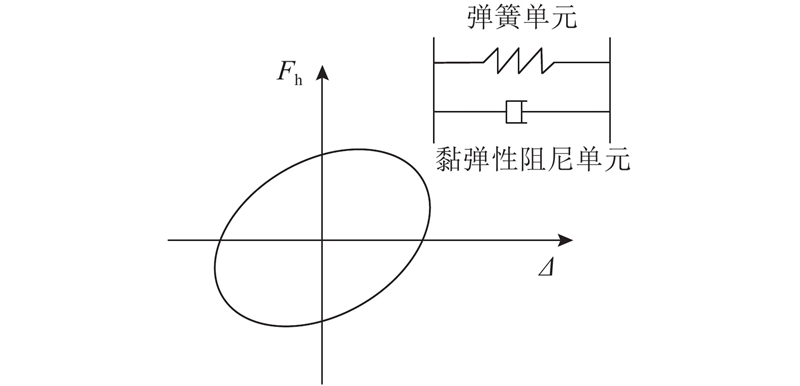
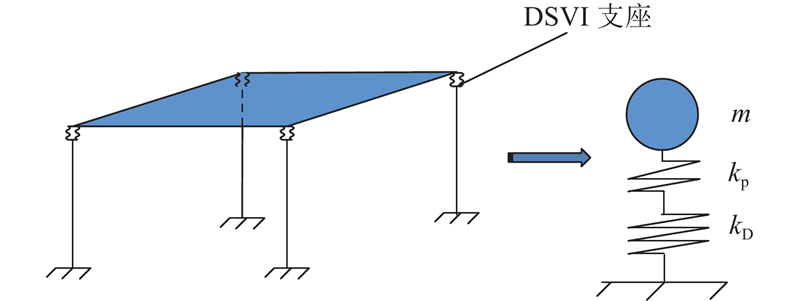
图 1
为了研究碟簧竖向隔震单自由度(disc spring vertical isolation-single degree of freedom,DSVI-SDOF)体系的地震响应,本文首先基于碟簧竖向隔震支座的受力特点,提出非对称恢复力模型(简称“非对称模型”);然后,建立DSVI-SDOF体系的时程分析程序;在此基础上对典型DSVI-SDOF体系进行非线性动力时程分析,研究非对称模型对其位移、速度、加速度等地震响应分析结果的影响.
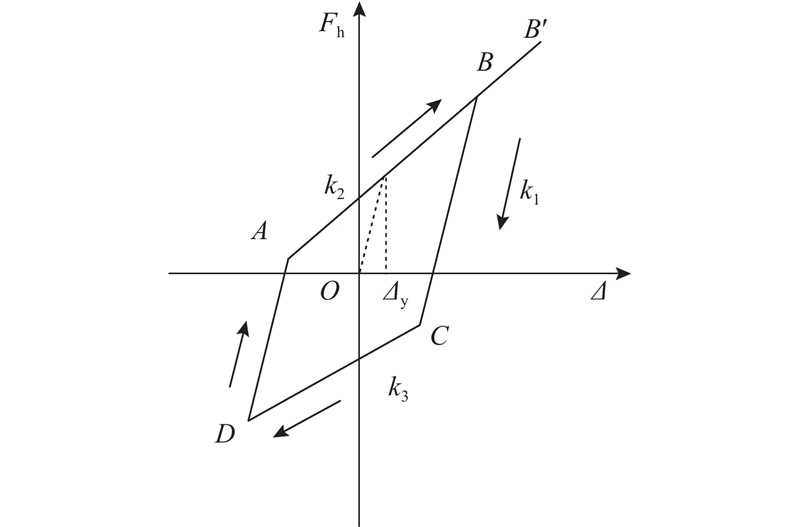
1. 非对称模型
图 2
图 3
图 4
图 5
式中:μ为碟簧材料的泊松比,E为碟簧材料的弹性模量,D、d、 t、h0分别为碟簧的外径、内径、厚度及行程.
在加载工况下,考虑摩擦力影响的单片碟簧荷载为
式中:
DSVI支座强化刚度k2的表达式为
式中:md为DSVI支座中碟簧组的对合数,fj为单片碟簧在荷载Fsj作用下的位移,可通过联立式(1)和(2)计算得到.
在卸载工况下,考虑摩擦力影响的单片碟簧荷载为
DSVI支座卸载刚度k3的表达式为
式中:fx为单片碟簧在荷载Fsx作用下的位移,可通过联立式(1)和(2)计算得到.
DSVI支座加载刚度k1的表达式为
DSVI支座的屈服位移
2. DSVI-SDOF体系的动力分析
DSVI-SDOF体系的动力微分方程为
式中:
其中,
3. 试验验证
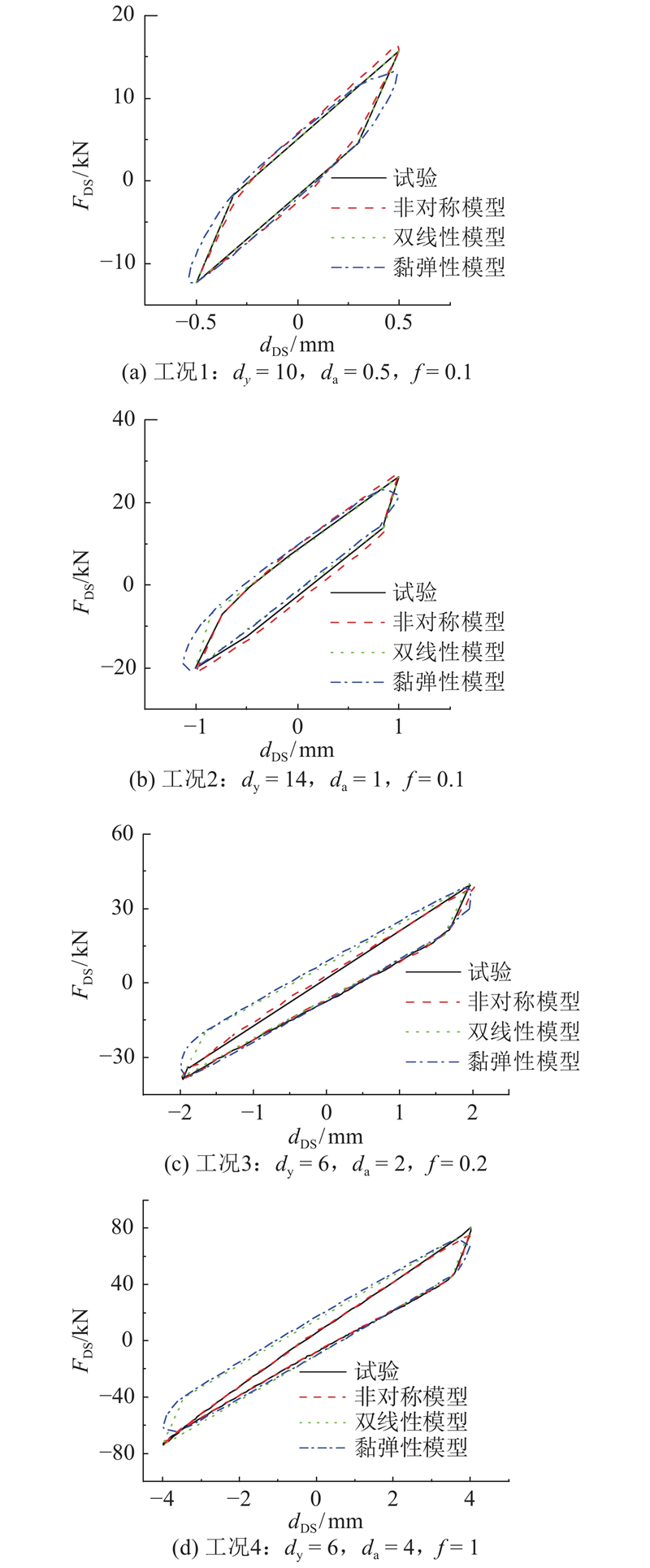
利用Matlab软件建立基于非对称模型的DSVI-SDOF体系的非线性动力时程分析程序,并选用文献[18]中DSVI支座的试验结果对非对称模型的有效性进行验证. DSVI支座采用直径为200 mm的碟簧(内径为102 mm,总高度为15 mm,厚度为8 mm)制成. 每个叠合组由5片碳簧组成,4个叠合组对合组合形成DSVI支座. 碟簧锥面间摩擦系数
图 6
图 6 荷载作用下模拟值和试验值的比较
Fig.6 Comparison of experimental and simulation results under loadings
1)在动荷载作用下,基于非对称模型的DSVI支座荷载-位移滞回曲线的模拟值与试验值吻合较好,两者具有相似的特征和相近的数值,验证了本文建立的非对称模型的准确性.
2)当动荷载幅值较小时,非对称模型、双线性模型、黏弹性模型均能较好地模拟DSVI支座的力学行为. 当动荷载幅值较大时,双线性模型和黏弹性模型难以表征DSVI支座的力学行为,非对称模型的模拟结果优于双线性模型和黏弹性模型的模拟结果,究其原因,是由于双线性模型和黏弹性模型为对称性模型,无法表征DSVI支座的非对称性特征.
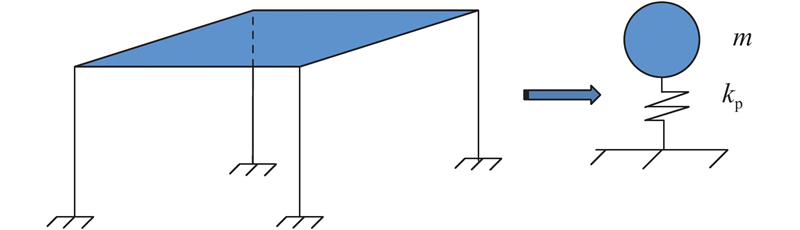
4. 模型分析
图 7
图 8
DSVI支座选用直径为400 mm的碟簧(内径为202 mm,总高度为29.5 mm,厚度为21 mm)制成. 每个叠合组由4片碟簧组成,8个叠合组对合组合形成DSVI支座. DSVI支座的刚度如下:加载刚度kD1 = 72 kN/mm,强化刚度kD2 = 40.35 kN/mm,卸载刚度kD3 = 32.49 kN/mm.
建立非隔震框架结构的等效单自由度(SDOF)体系. 不考虑梁柱刚度对SDOF体系竖向振动的影响,模型D的竖向刚度
建立DSVI隔震框架结构的等效DSVI-SDOF体系. 4个DSVI支座并联形成DSVI-SDOF体系的隔震支座,将其简化成一个DSVI-S支座. DSVI-SDOF体系的竖向刚度
DSVI-SDOF体系的质点重量均为4 536 kN. DSVI-SDOF体系中DSVI-S支座的刚度取值如下.
1)非对称模型:加载刚度k1=155.9 kN/mm,强化刚度k2=109.4 kN/mm,卸载刚度k3=94.0 kN/mm. 屈服位移
2)双线性模型:初始刚度ks1 = 155.9 kN/mm,屈服后刚度ks2 = 109.4 kN/mm. 屈服位移
3)黏弹性模型:等效竖向刚度
5. 地震隔震分析
图 9
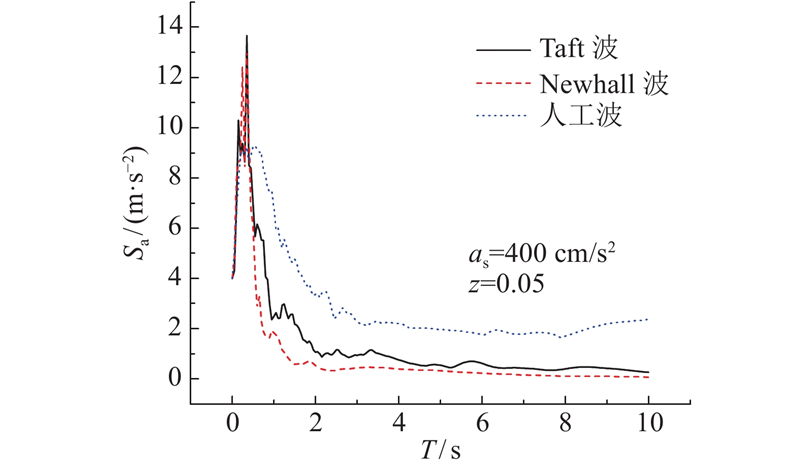
利用Matlab软件分别建立基于非对称模型、双线性模型及黏弹性模型的DSVI-SDOF体系非线性动力时程分析程序. 非隔震框架结构及隔震框架结构的竖向等效黏滞阻尼比均取为0.05,数值积分方法采用Wilson-θ法. 利用上述程序对第4章所建立的4个分析模型进行非线性动力时程分析,研究DSVI-SDOF体系的地震响应特征. 在地震响应分析过程中,地震动的峰值加速度分别取70、200、400、510和620 cm/s2.
5.1. 峰值位移响应
对称性模型地震响应计算的相对误差计算式为
式中:Eo为非对称模型所计算的地震响应(如:位移、加速度、力、能量等),Ebe为对称性模型(双线性模型及黏弹性模型)所计算的地震响应.
隔震结构地震响应隔震率的计算式为
式中:Ef为非隔震结构模型所计算的地震响应(如位移、加速度等),Ei为隔震结构模型所计算的地震响应. 隔震结构的地震响应隔震率主要与隔震支座的等效刚度和等效阻尼比有关。
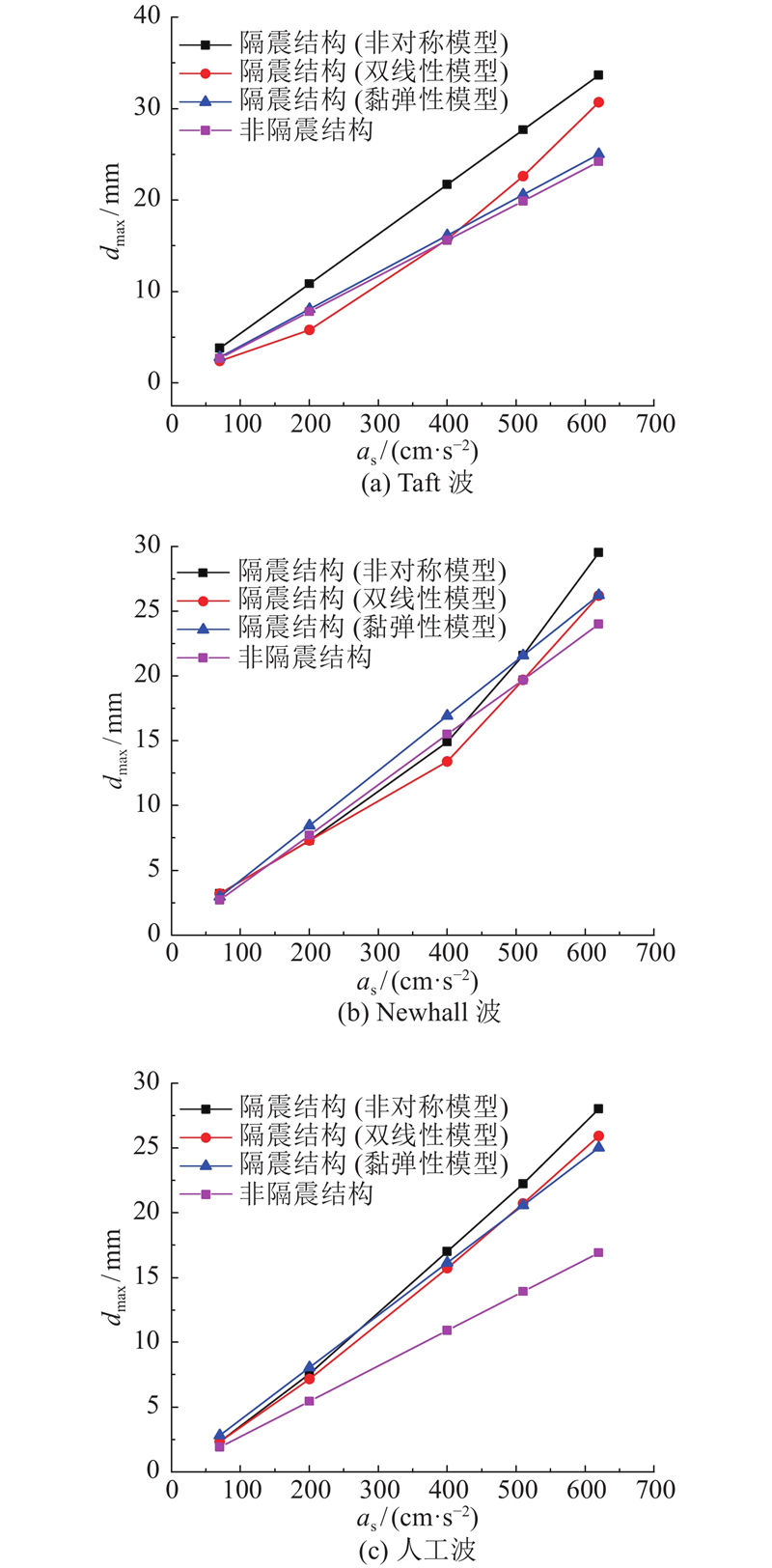
图 10
图 10 碟簧竖向隔震单自由度(DSVI-SDOF)体系峰值位移对比
Fig.10 Comparison of maximum displacements of disc spring vertical isolation-single degree of freedom (DSVI-SDOF) system
图 11
图 11 DSVI-SDOF体系峰值位移的相对误差
Fig.11 Relative errors of maximum displacements of DSVI-SDOF system
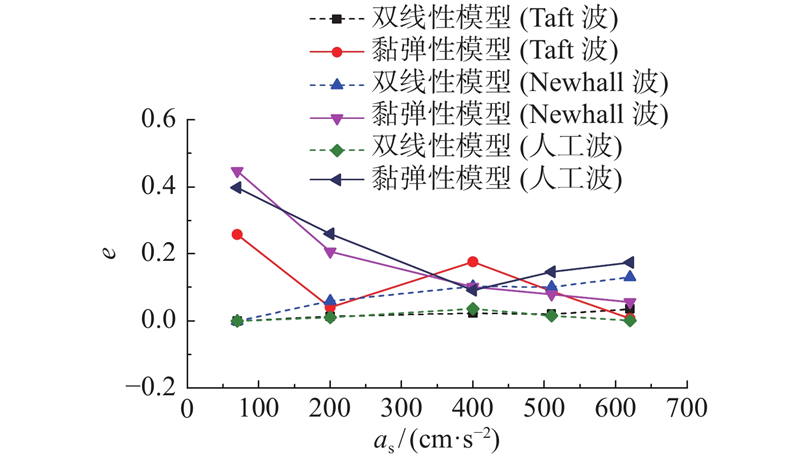
1)在不同地震动作用下,采用双线性模型计算得到的DSVI-SDOF体系峰值位移的分析结果均小于采用非对称模型计算得到的分析结果,采用双线性模型的计算结果的相对误差为8%~13%. 究其原因,是由于双线性模型的卸载刚度大于非对称模型的卸载刚度,从而减小了相同地震力作用下DSVI-SDOF体系峰值位移的分析结果.
2)采用黏弹性模型计算得到的DSVI-SDOF体系的峰值位移的分析结果与采用非对称模型计算得到的分析结果相对误差在18%~90%,其计算精度远低于采用双线性模型的计算结果. 当地震动峰值加速度较小时,采用黏弹性模型计算得到的DSVI-SDOF体系的峰值位移的分析结果与采用非对称模型计算得到的分析结果相对误差较大,随着地震动峰值加速度的增加,两者之间的相对误差逐渐减小. 因为随着地震动峰值加速度的增加,DSVI-S支座的位移逐渐增加,其附加等效黏滞阻尼比逐渐减小[15]. 在本文黏弹性模型中,附加阻尼比取为DSVI-S支座位移最大时的阻尼比,其取值与地震动峰值加速度较大工况下DSVI-S支座的实际附加黏滞阻尼比相接近.
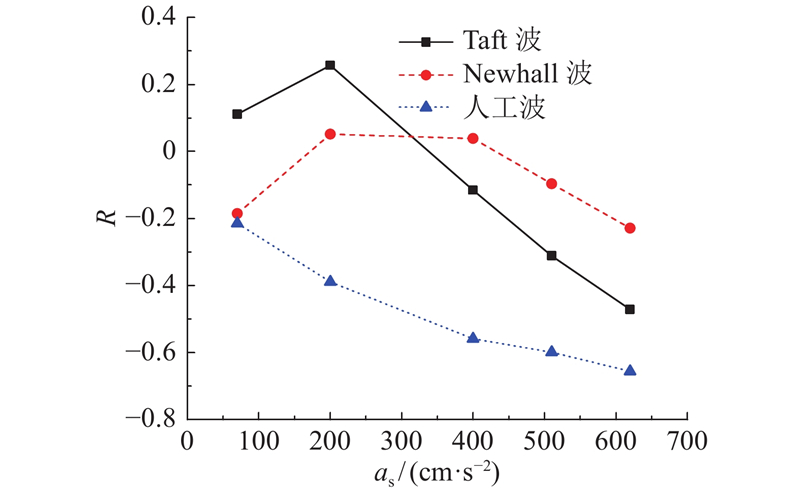
如图12所示为DSVI-SDOF体系峰值位移的隔震率. 可知,在大部分荷载工况下,DSVI-SDOF体系峰值位移的隔震率为负值,表明DSVI-S支座放大了DSVI-SDOF体系的峰值位移响应.
图 12
图 12 DSVI-SDOF体系峰值位移的隔震率
Fig.12 Isolation ratios of maximum displacements of DSVI-SDOF system
1)当地震动峰值加速度为70 cm/s2时,DSVI-SDOF体系峰值位移的放大效应较小,原因为非对称模型的初始加载刚度较大.
2)随着地震动峰值加速度的增加,DSVI-SDOF体系峰值位移隔震率绝对值逐渐增加,当地震动峰值加速度为620 cm/s2时,隔震率绝对值高达60%. 随着地震动峰值加速度的增加,DSVI-SDOF体系峰值位移的隔震率绝对值逐渐增大. 这是因为非对称模型的非对称性逐渐增强,其竖向等效刚度逐渐变小,耗能能力逐渐减弱.
5.2. 峰值加速度响应
图 13
图 13 DSVI-SDOF体系峰值加速度对比
Fig.13 Comparison of maximum accelerations of DSVI-SDOF system
图 14
图 14 DSVI-SDOF体系峰值加速度的相对误差
Fig.14 Relative errors of maximum accelerations of DSVI-SDOF system
1)采用双线性模型计算得到的DSVI-SDOF体系峰值加速度分析结果与采用非对称模型计算得到的分析结果相差不多,两者的相对误差在2%~13%.
2)采用黏弹性模型计算得到的DSVI-SDOF体系峰值加速度与采用非对称模型计算得到的峰值加速度的相对误差较为离散,在30%~100%. 不同地震动作用下DSVI-SDOF体系的加速度分析结果较为离散,这主要与地震动的频谱特性及结构的动力特性有关.
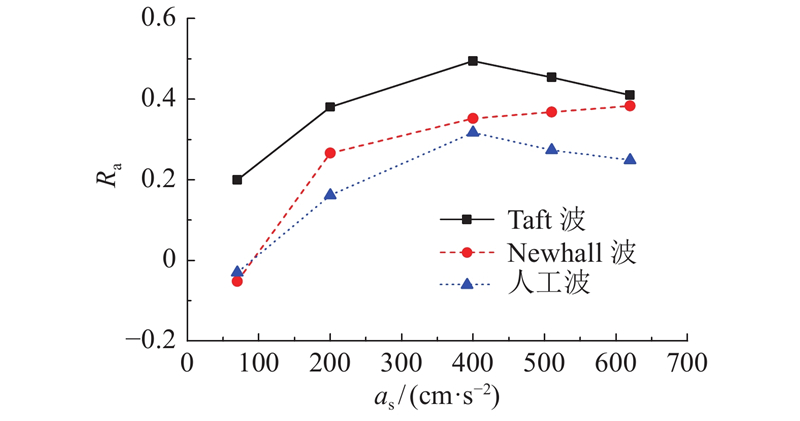
如图15所示为DSVI-SDOF体系峰值加速度的隔震率Ra. 可知,DSVI-S支座有效隔离了竖向加速度的传递.
图 15
图 15 DSVI-SDOF体系峰值加速度的隔震率
Fig.15 Isolation ratios of maximum accelerations of DSVI-SDOF system
1)当地震动峰值加速度为70 cm/s2时,DSVI-SDOF体系的峰值加速度的隔震率较小,原因为非对称模型的初始加载刚度较大.
2)随着地震动峰值加速度的增加,DSVI-SDOF体系的峰值加速度隔震率逐渐增加,当地震动峰值加速度为400 cm/s2时,峰值加速度的隔震率在20%~50%. 究其原因,是由于在此阶段,对DSVI-SDOF体系峰值加速度隔震率起控制作用的DSVI-S支座竖向等效刚度逐渐减小.
3)当地震动峰值加速度为620 cm/s2时,峰值加速度的隔震率有所降低. 究其原因,是由于在此阶段,对DSVI-SDOF体系峰值加速度隔震效果起控制作用的DSVI-S支座的耗能能力逐渐减弱.
5.3. 峰值力响应
图 16
图 17
图 17 DSVI-SDOF体系峰值力的相对误差
Fig.17 Relative errors of maximum forces of DSVI-SDOF system
1)在不同地震动作用下,采用双线性模型计算得到的DSVI-SDOF体系的峰值力与采用非对称模型计算得到的峰值力的相对误差在5%~9%. 究其原因,是由于非对称模型的卸载刚度小于双线性模型的卸载刚度.
2)在不同地震动作用下,采用黏弹性模型计算得到的DSVI-SDOF体系的峰值力与采用非对称模型计算得到的峰值力的相对误差较为离散,在0~60%. 不同地震动作用下DSVI-SDOF体系的加速度分析结果较为离散,这主要跟地震动的频谱特性及结构的动力特性有关.
如图18所示为DSVI-SDOF体系峰值力的隔震率RF. 由图可知,DSVI-S支座有效隔离了竖向地震力的传递.
图 18
图 18 DSVI-SDOF体系峰值力的隔震率
Fig.18 Isolation ratios of maximum forces of DSVI-SDOF system
1)在地震动峰值加速度为70 cm/s2时,DSVI-SDOF体系的峰值力的隔震,原因为非对称模型的初始加载刚度较大.
2)随着地震动峰值加速度的增加,DSVI-SDOF体系的地震力的隔震率逐渐增加,当地震动峰值加速度为400 cm/s2时,峰值地震力的隔震率在20%~50%. 究其原因,是由于随着地震动峰值加速度的增加,DSVI-S支座的位移逐渐增加,其竖向等效刚度逐渐减小,但其耗能能力变化较小. 在此阶段,DSVI-S支座竖向等效刚度的减小对DSVI-SDOF体系峰值力的隔震起控制作用.
3)当地震动峰值加速度为620 cm/s2时,DSVI-SDOF体系的峰值地震力的隔震率有所减小. 这是因为随着地震动峰值加速度的增加,DSVI-S支座的位移逐渐增加,非对称模型的非对称性逐渐增强,其耗能能力逐渐减弱,但其等效竖向刚度变化较小. 在此阶段,DSVI-S支座耗能能力的减弱对DSVI-SDOF体系峰值力的隔震效果起控制作用.
4)DSVI-SDOF体系的峰值力的隔震效果较为有限,建议增加附加阻尼装置,以增加DSVI-SDOF体系的耗能能力,从而提高其峰值力隔震效果.
5.4. DSVI-S支座的力-位移滞回曲线
如图19所示为不同地震动作用下DSVI-S支座的力-位移滞回曲线. 图中,dD-S和FD-S分别为DSVI-S支座的位移和受力.
图 19
图 19 碟簧竖向隔震简化(DSVI-S)支座力-位移滞回曲线对比
Fig.19 Comparison of force-displacement hysteretic curves of disc spring vertical isolation simplified(DSVI-S)bearing
1)在不同地震动作用下,采用非对称模型计算得到的DSVI-S支座的力-位移滞回曲线分析结果为梯形,该梯形具有典型的非对称性;采用双线性模型计算得到的DSVI-S支座的力-位移滞回曲线分析结果为平行四边形;采用黏弹性模型计算得到的DSVI-S支座的力-位移滞回曲线分析结果为一条直线.
2)非对称模型能够准确描述DSVI-S支座的力学行为,从而能够较为准确地模拟DSVI-SDOF体系的地震响应.
3)在不同地震动作用下,采用双线性模型计算得到的DSVI-S支座的力-位移滞回曲线的分析结果与非对称模型分析结果在位移为负值时相差较大,在位移为正值时相差较小. 究其原因,是由于非对称模型考虑了卸载刚度的减小,而双线性模型并没有考虑该因素.
5.5. 能量响应
图 20
图 21
图 21 DSVI-S支座消耗能量的相对误差
Fig.21 Relative errors of dissipated energy of DSVI-S bearing
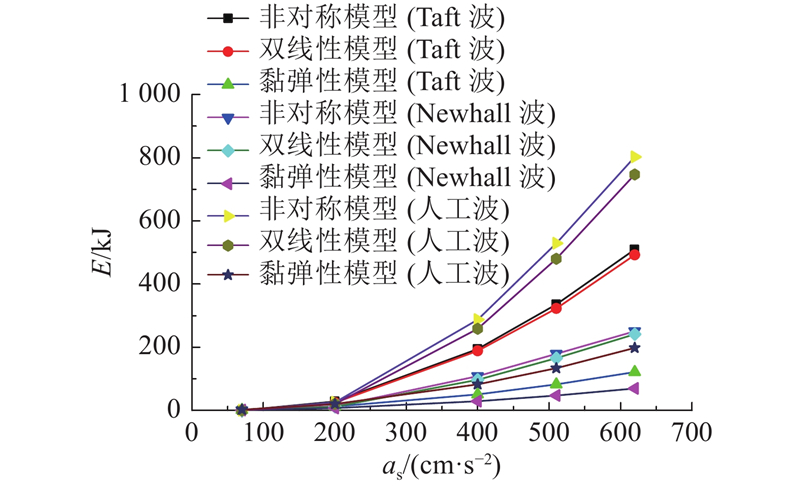
1)不同地震动作用下,采用非对称模型计算得到的DSVI-S支座的滞回耗能均大于采用双线性模型的计算结果,采用双线性模型计算得到的DSVI-S支座的滞回耗能的相对误差在5%~18%. 这是因为在不同地震动作用下,采用非对称模型计算得到的DSVI-S支座力和位移的分析结果均大于采用双线性模型的分析结果,从而导致采用非对称模型计算得到的DSVI-S支座的力-位移滞回曲线面积大于采用双线性模型的计算结果,进而导致采用非对称模型的DSVI-S支座的滞回耗能计算值大于采用双线性模型的滞回耗能计算值.
2)采用黏弹性模型计算得到的DSVI-S支座的滞回耗能仅占采用非对称模型计算值的25%左右. 究其原因,正如第5章所述,是由于在黏弹性计算模型中,附加等效黏滞阻尼比的取值偏小. 在黏弹性模型中,附加等效黏滞阻尼比的取值对结构地震响应的影响较大. 此外,随着预压位移的增加,DSVI-S支座的等效黏滞阻尼比逐渐减小. 因此,采用单一的附加等效黏滞阻尼比难以准确计算DSVI-S隔震结构在不同峰值加速度地震动作用下的准确地震响应.
5.6. 典型的时程曲线
如图22分别为DSVI-SDOF体系的力时程对比(as = 510 cm/s2). 图中,tD为时间,FD为DSVI-SDOF体系的受力. 由图可知,不同的DSVI支座恢复力模型对DSVI-SDOF体系地震响应的计算结果有着显著的影响,其具体影响结果已在第5.1~5.5节进行分析,此处不再赘述.
图 22
图 22 DSVI-SDOF体系力时程的对比
Fig.22 Comparison of force time histories of DSVI-SDOF system
6. 结 论
(1)非对称模型能够准确描述DSVI支座的非对称力学行为,能够较为准确地模拟DSVI-SDOF体系的地震响应.
(2)采用双线性模型计算得到的DSVI-SDOF体系的位移、加速度地震响应的相对误差小于20%;采用黏弹性模型计算得到的DSVI-SDOF体系的位移、加速度地震响应的相对误差在0~100%.
(3)随着地震动峰值加速度的增加,DSVI-SDOF体系的峰值加速度、峰值地震力的隔震率先增大后减小. 当地震动峰值加速度为400 cm/s2时,DSVI-SDOF体系的隔震效果达到最优,峰值加速度和峰值地震力的隔震率均在20%~50%.
DSVI-SDOF体系的峰值加速度及峰值力的隔震效果较为有限,建议增加附加阻尼装置以增加DSVI-SDOF体系的耗能能力,从而提高DSVI-SDOF体系的隔震效果.
参考文献
Energy-based method for nonlinear characteristics analysis of Belleville springs
[J].
碟形弹簧竖向减震装置的性能试验研究
[J].
Mechanical performance of a vertical seismic isolation system employing a dish spring
[J].
基于某博物馆的新型三维隔振装置作用性能研究
[J].
Application performance study of new three-dimensional vibration isolation device based on one museum structure
[J].
强震区多跨长联连续梁桥减隔震设计
[J].
Seismic mitigation and isolation design for multi-span and long-unit continuous girder bridge inmeizoseismal area
[J].
设置碟形弹簧的框架-摇摆墙结构抗震性能试验研究
[J].
Experimental investigation on seismic performance of frame-rocking wall structures using disc springs
[J].
碟形弹簧竖向隔震结构振动台试验及数值模拟研究
[J].DOI:10.3321/j.issn:1000-6869.2008.06.014 [本文引用: 2]
Shaking table test and numerical analysis of vertical-isolated building model with combined disk spring bearing
[J].DOI:10.3321/j.issn:1000-6869.2008.06.014 [本文引用: 2]
新型三维多功能隔振支座设计及其隔振分析
[J].
Design of novel three dimension multifunctional isolation bearing and its isolation behavior analysis
[J].
Cyclic behavior and failure mechanism of self-centering energy dissipation braces with pre-pressed combination disc springs
[J].DOI:10.1002/eqe.2844 [本文引用: 1]
Development and experimental verification of a pre-pressed spring self-centering energy dissipation brace
[J].DOI:10.1016/j.engstruct.2016.08.043 [本文引用: 1]
Combined vibration isolator of disc springs for closed high-speed precision press: design and experiments
[J].DOI:10.1139/tcsme-2014-0031 [本文引用: 1]
Mechanical properties of disc-spring vibration isolators based on boundary friction
[J].
Analyses of static and dynamic behavior of coned disk springs: effects of friction boundaries
[J].
On the influence of friction in the calculation of conical disk springs
[J].
Investigation of hybrid and different cross-section composite disc springs using finite element method
[J].
碟形弹簧力学性能研究
[J].
Mechanical properties of disc springs
[J].
碟形弹簧复合隔震支座力学性能试验与数值模拟研究
[J].
Experiment and numerical simulation on mechanical performance of disc spring compound isolation bearings
[J].
Mechanical model parameters for viscoelastic dampers
[J].DOI:10.1061/(ASCE)0733-9399(2009)135:6(581) [本文引用: 1]