索杆张力结构^[1-2]是结构效率极高的一类新型空间结构，具有重量轻、跨度大的优点. 典型体系包括张拉整体、索穹顶与索桁架等^[3]. 此类结构虽然仅由拉索和压杆等简单受力构件组成，但刚度构成机理非常复杂. 结构刚度同时来源于预应力贡献的几何刚度和材料贡献的线弹性刚度^[4]. 由于受到建造误差、环境腐蚀、支座刚度退化等因素的影响，实际结构可能存在不容忽视的预应力偏差^[5]和构件损伤，因此监测结构刚度的变化非常重要.

动力测试法^[6-7]是进行结构刚度监测的主流方法. 一般情况下，索杆张力结构具有密集的模态，比如某100 m跨Geiger索穹顶前30阶模态全部分布在1~5 Hz的窄带内^[8]. 由于密集模态识别困难^[9]，动力测试法在索杆张力结构中的应用极少. 注意到静力响应直接与结构刚度相关，且测试精度相对较高，因此采用静力测试法^[10]来监测索杆张力结构的刚度变化具有较大潜力. 郭彦林等^[11-12]提出了一种仅根据少数静力位移测量值来识别车幅式张拉屋盖结构索力的方法，并对其索力的识别误差展开了系统分析.

实际上，在损伤识别^[13]和模型修正^[14]等刚度监测后续工作中，常常需要利用实际结构在全自由度空间上的完整静力位移. 在现场测试中，由于光线遮挡、测试通道、工程造价等因素的影响，位移测点的数量往往有限. 将少数测点的实测位移有效扩展为全自由度上的完整位移非常重要.

动力测试法中有关振型扩展的研究非常多^[15]，但静力测试法中有关静力位移扩展的研究很少. 针对静力位移扩展，目前有报道的主要有2种方法. 第一种是文献[16]方法. 该方法将静力平衡方程按照测点自由度和非测点自由度进行分块，并基于测点响应直接求出完整位移. 该方法需要将所有的荷载作用点选作测点，并且依赖理想结构的刚度信息. 第二种是插值法^[17]. 该方法利用线性或样条曲线进行插值以实现静力位移扩展. 对于几何拓扑复杂的索杆张力结构，插值法并不适用.

本研究提出一种新的静力位移扩展方法来快速测量索杆张力结构的静力位移场. 首先，将贡献模态组合成Fisher信息阵，并基于Fisher信息阵行列式最大化原则提出相应的迭代策略来优选测点位置，以得到贡献模态组合系数的无偏估计. 其次，针对结构模态之间可能存在弱相关性的问题，提出一种提取严格正交基的主成分分析方法，以论证结构模态被选作自由度空间基向量的合理性. 最后，以某200 m跨环形张力罩棚结构^[18]为例，针对所提方法阐述其使用流程，考察其扩展精度，并讨论其优缺点.

文献[19]推导得出了索杆张力结构基于模态展开的静力位移统一表达公式，现简述如下.

在荷载p作用下，理想结构的静力位移 ${{d}}$可以近似表达为

(1) ${{d}} = \sum\nolimits_{s \in {{{E}}_{\rm{p}}}}^{} {{\alpha _s}} {{{\theta }}_s}.$

式中： ${{{\theta }}_s}$为理想结构第s阶振型； ${\alpha _s}$为对应于 ${{{\theta }}_s}$的组合系数，也被称作 ${{{\theta }}_s}$方向的广义位移；E_p为贡献模态集合. ${\alpha _s}$的表达式和E_p的具体筛选方法详见文献[19].

在相同荷载p作用下，实际结构的静力位移 ${\tilde{ d}}$总是可以近似表达为

(2) ${\tilde{ d}} = \sum\nolimits_{s \in {{{E}}_{\rm{p}}}}^{} {\left( {{{\bar \alpha }_s}} \right)} {{{\theta }}_s}.$

式中： ${\bar \alpha _s}$为对应于 ${{{\theta }}_s}$的组合系数.

根据式（1）、（2），由于在相同荷载p作用下，理想结构和实际结构的静力位移总是可以近似表达为少数贡献模态的线性组合，位移的变化主要体现在贡献模态组合系数的变化上. 若能基于少数测点的实测位移无偏估计真实的 ${\bar \alpha _s}$，则根据式（2）可以直接实现实际结构静力位移的扩展.

采用矩阵和向量的形式来重新表达式（2）：

(3) ${\tilde{ d}} = {{\bar \theta }}_{\rm{c}}^{}{{\bar \alpha }}.$

式中： ${{{\bar \theta }}_{\rm{c}}}$是由集合 ${{{E}}_{\rm{p}}}$中各贡献模态组成的振型矩阵； ${{\bar \alpha }}$是对应于 ${{{\bar \theta }}_{\rm{c}}}$中各贡献模态的组合系数. 求解式（3）得到 ${{\bar \alpha }}$的估计值为

(4) ${{\bar \alpha }} = {\left( {{{\bar \theta }}_{\rm{c}}^{\rm{T}}{{\bar \theta }}_{\rm{c}}^{}} \right)^{ - 1}}{{\bar \theta }}_{\rm{c}}^{\rm{T}}{\tilde{ d}}.$

可以认为由式（4）得到的 ${{\bar \alpha }}$是真实值. 但实际结构的静力测试均包含测量噪声，因此实测静力位移为

(5) ${\hat{ d}} = {{\bar \theta }}_{\rm{c}}^{}{{\bar \alpha }} + {{N}}.$

式中： ${{N}}$为零均值高斯分布平稳白噪声，其方差为 $\psi _0^2$. 进而由式（4）得到组合系数实测值为

(6) ${\hat{ \alpha }} = {\left( {{{\bar \theta }}_{\rm{c}}^{\rm{T}}{{\bar \theta }}_{\rm{c}}^{}} \right)^{ - 1}}{{\bar \theta }}_{\rm{c}}^{\rm{T}}{\hat{ d}}.$

由式（5）对测量噪声的假定，贡献模态组合系数实测值 ${\hat{ \alpha }}$与真实值 ${{\bar \alpha }}$之间的误差可以采用方差的形式 $E\left( {\left( {{{\bar \alpha }}{\rm{ - }}{\hat{ \alpha }}} \right){{\left( {{{\bar \alpha }}{\rm{ - }}{\hat{ \alpha }}} \right)}^{\rm{T}}}} \right)$来衡量，并满足下式^[20]：

(7) $E\left( {\left( {{{\bar \alpha }}{\rm{ - }}{\hat{ \alpha }}} \right){{\left( {{{\bar \alpha }}{\rm{ - }}{\hat{ \alpha }}} \right)}^{\rm{T}}}} \right) \geqslant {\left( {\psi _0^2\;{{\varLambda }}} \right)^{ - 1}}.$

式中： ${{\varLambda }}$为Fisher信息矩阵（fisher information matrix, FIM）， ${{\varLambda }} = {{\bar \theta }}_{\rm{c}}^{\rm{T}}{{\bar \theta }}_{\rm{c}}^{}$.

为了尽量减小实测值 ${\hat{ \alpha }}$与真实值 ${{\bar \alpha }}$之间的误差，实现贡献模态组合系数的无偏估计，应当优选测点位置来保证FIM行列式最大. 将 ${{{\bar \theta }}_{\rm{c}}}$的某一行（对应某个自由度，或称测点）删除后，FIM的行列式^[20]变为

(8) $\det \left( {{{\varLambda }}'} \right) = \det \left\{ {{{\varLambda }}\left[ {1 - {{\left( {{{\bar \theta }}_{\rm{c}}^{}} \right)}_q}{{{\varLambda }}^{ - 1}}\left( {{{\bar \theta }}_{\rm{c}}^{}} \right)_q^{\rm{T}}} \right]} \right\}.$

式中： ${\left( {{{\bar \theta }}_{\rm{c}}^{}} \right)_q}$为 ${{\bar \theta }}_{\rm{c}}^{}$的第q行， ${{\varLambda }}'$为删除某个自由度之后的FIM.

由式（8）可知，自由度q对FIM的贡献为

(9) ${S_q} = {\left( {{{\bar \theta }}_{\rm{c}}^{}} \right)_q}{{{\varLambda }}^{ - 1}}\left( {{{\bar \theta }}_{\rm{c}}^{}} \right)_q^{\rm{T}}.$

根据式（9），计算所有自由度对FIM的贡献度，排序后将贡献度最小的自由度删除，再重新计算所保留自由度的FIM和其贡献度，并不断迭代，直到FIM保留的自由度数量等于预设的测点数量为止. 在确定好测点后，根据式（6）得到实测值 ${\hat{ \alpha }}$的无偏估计值，进而得到由少数测点位移扩展而来的完整静力位移 ${\hat{ d}} = {{\bar \theta }}_{\rm{c}}^{}{\hat{ \alpha }}$. 为了避免出现不定解，测点数量应当不小于 ${{\bar \theta }}_{\rm{c}}^{}$中贡献模态的数量.

引入2种指标来衡量静力位移的扩展效果. 第一种是模态保证准则（modal assurance criterion，MAC）指标^[21]. 该指标一般用于模态振型的相关性检验，可以用来衡量实际的完整位移 ${\tilde{ d}}$和扩展后的完整位移 ${\hat{ d}}$之间的相关程度，即

(10) ${\rm{MAC}}\left( {{\tilde{ d}},{\hat{ d}}} \right) = \frac{{{{\left( {{{{\tilde{ d}}}^{\rm{T}}}{\hat{ d}}} \right)}^2}}}{{\left( {{{{\tilde{ d}}}^{\rm{T}}}{\tilde{ d}}} \right)\left( {{{{\hat{ d}}}^{\rm{T}}}{\hat{ d}}} \right)}}.$

显然，MAC指标的值介于0~1. 当MAC=0时， ${\tilde{ d}}$和 ${\hat{ d}}$毫无相关性；而当MAC=1时， ${\tilde{ d}}$和 ${\hat{ d}}$完全相关. 从某种意义上讲，MAC值越大，静力位移的扩展精度越高.

另外一种是误差范数（mean value of error-norm，MVE）指标，其值取为静力位移扩展绝对误差的欧几里得距离平均值，即

(11) ${\rm{MVE}}\left( {{\hat{ d}},{\tilde{ d}}} \right) = \frac{1}{n}\sqrt {{{\left( {{\hat{ d}} - {\tilde{ d}}} \right)}^{\rm{T}}}\left( {{\hat{ d}} - {\tilde{ d}}} \right)} .$

MVE值越小，静力位移的扩展精度越高. 当MVE=0时， ${\tilde{ d}}$和 ${\hat{ d}}$完全相同.

文献[19]在推导静力位移的统一表达公式时假设 ${{{\theta }}_j}\left( {j = 1,2, \cdots ,{\rm{ }}n} \right)$构成了一组n维空间基向量. 实际上，早在1969年，Fox等^[22]在推导经典的振型一阶灵敏度时也应用了该假设. 但不难发现， ${{{\theta }}_j}\left( {j = 1,2, \cdots ,{\rm{ }}n} \right)$只对质量矩阵正交，并不一定两两正交，即 ${{{\theta }}_j}$之间可能存在一定的线性相关性. 可见，该假设不够严谨. 为了验证采用 ${{{\theta }}_j}$作n维空间基向量的合理性，引入主成分分析（principal component analysis，PCA）^[23]方法来提取满足两两正交要求的新的基向量. PCA是一种降维统计方法，借助于一个正交变换，将相关的原随机向量转化成不相关的新随机向量. 具体而言，将各阶模态（振型）视作“随机向量”，其构成的振型矩阵记为X（n×n），则协方差矩阵R=XX ^T. R的SVD分解结果为

(12) ${\rm{SVD}}({{{R}}}) = {{US}}{{{U}}^{\rm{T}}}.$

式中： ${{U}} = \left[ {{u_1},{u_2}, \cdots ,{u_n}} \right]$为由特征向量组成的酉矩阵； ${{{u}}_i}$为第i个特征向量； ${{S}} = {\rm{diag}}\left( {{S_1},{S_2}, \cdots ,{S_n}} \right)$为对角矩阵； ${S_i}$为特征值，且 ${S_1} \geqslant {S_2} \geqslant \cdots \geqslant {S_n} \geqslant 0$ $\left( {i = 1,2, \cdots ,n} \right)$.

假设共有l阶特征值大于0，则前l阶特征向量组成一组新的正交基. 若l=n，则 ${{{\theta }}_j}\left( {j = 1,2, \cdots ,{\rm{ }}n} \right)$可以转换成一组新的n维空间基向量 ${{{u}}_s}\left( {s = 1,2, \cdots ,{\rm{ }}n} \right)$（称为主成分正交基），结构模态的线性表达经过转换可以等效为主成分正交基的线性表达；若l<n，则 ${{{\theta }}_j}$不能完全包含n维空间的信息，结构模态的线性表达也就无法等效为主成分正交基的线性表达.

为了进一步验证PCA法的有效性，将由m阶贡献模态 ${{{\bar \theta }}_{\rm{c}}}$组成的振型矩阵进行主成分分析，并将得到的主成分正交基 ${{{\bar u}}_{\rm{c}}}$代替式（3）~（9）中的 ${{{\bar \theta }}_{\rm{c}}}$，进行测点位置优化和静力位移扩展.

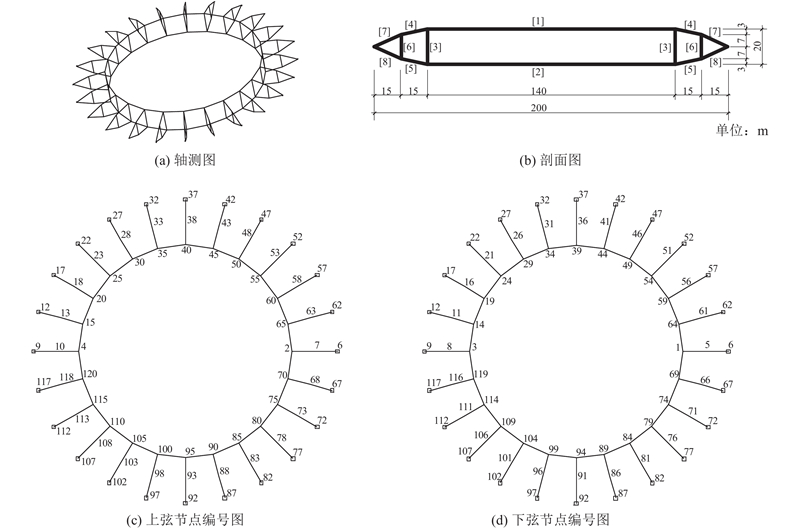
如图1（a）所示为某200 m跨轴对称环形张力罩棚结构. 该结构共有120个节点（外围24个节点固定于周边刚性环梁上）和192根构件. 定义不考虑预应力、自重及外荷载作用时的状态为结构的零状态，其自平衡构型如图1（b）所示（[]内数字为构件组号）. 如图1（c）和（d）所示分别为上、下弦节点的编号. 假设索、杆的质量密度均为7 850 kg/m³，而弹性模量分别为1.7×10¹¹和2.06×10¹¹ N/m². 根据结构的对称性和构件所在位置设定构件类型，并将所有构件划分为8组. 构件组号与构件位置的对应关系如图1（b）所示. 构件组号与构件类型、构件编号的对应关系如表1所示. 表1同时给出了截面面积A_k、平衡态下的构件轴力t_k以及构件长度误差e_uk等结构参数. 其中，k为构件编号.

为使算例参数尽可能贴近工程实际，表1给出的构件轴力和截面面积应当满足结构设计的强度条件和刚度条件. 在施加预应力后，结构由零状态变为平衡态，此时拉索应力取值在450~500 MPa，为常用拉索设计强度的30%左右；压杆（假设可以保证整体稳定性）应力在165~195 MPa，介于Q345钢设计强度的50%~60%. 考虑作用于上弦屋面的满跨均布和半跨均布2种设计工况（均为竖向均布荷载0.5 kN/m²）. 在2种设计工况作用下（同时考虑结构自重），结构最大位移为232 mm，小于限值240 mm（等于罩棚悬挑长度的1/125）.

为简化计算，结构自重仅考虑构件重量. 以在平衡态施加结构自重后得到的平衡构型作为后期加载的基准构型. 该基准构型下的结构可称为理想结构. 在实际的静力测试中，往下弦节点施加铅锤荷载最为方便，因此考虑2种荷载工况：工况1，在所有下弦节点各施加10 kN铅锤荷载（即满跨加载，共48个加载点）；工况2，在同一侧下弦节点各施加10 kN铅锤荷载（即半跨加载，共24个加载点）.

将相同荷载作用下理想结构和实际结构的贡献模态进行对比，以验证用少数贡献模态线性表达静力位移的准确性. 具体步骤如下：1）对理想结构进行模态分析得到各阶理想模态；2）生成包含随机结构参数偏差的实际结构；3）计算理想结构和实际结构的静力位移，并比较各阶理想模态的贡献变化.

根据国家相关规范^[24-26]的规定，假设构件长度误差限值e_uk如表1所示，支座的竖向位置偏差限值 $\Delta {z_{\rm{u}}}$= $ \pm {H_1}/3\;000$且 $\left| {\Delta {z_{\rm{u}}}} \right| \leqslant 30$ mm，径向水平位置偏差限值 $\Delta {r_{\rm{u}}}$= $ \pm {H_1}/{\rm{1}}\;000$且 $\left| {\Delta {r_{\rm{u}}}} \right| \leqslant 10$ mm，其中， H₁表示支座所在支承柱的离地高度，假设等于30 m. 同时，假定各构件长度误差和支座位置偏差均为独立变量，并按零均值高斯分布. 根据“ $3\sigma $原则”^[3]，构件k的长度误差标准值可取为 $\left| {{e_{{\rm{u}}k}}} \right|/3$，而支座i的竖向与径向水平位置偏差标准值可分别取为 $\Delta {z_{{\rm{u}}i}}/3$和 $\Delta {r_{{\rm{u}}i}}/3$. 此外，采用折减构件弹性模量的方法^[27]来模拟构件损伤. 选取第25、89、127和163号构件作为损伤构件，分别折减其弹性模量的20%、15%、25%和20%，再生成一组随机构件长度误差和支座位置偏差；将其同时引入理想结构有限元模型，得到包含随机结构参数偏差的某实际结构.

根据文献[19]分别计算工况1、2荷载作用下各阶理想模态对理想结构和实际结构的广义位移 ${\alpha _j}$. 对于工况1，提取对理想结构静力位移贡献最大的前5阶理想模态，并列于表2. 其中，γ_j为模态j的相对贡献大小. 不妨设定截断阈值 ${\gamma _{\rm{u}}}$=0.01（详文献[19]， ${\gamma _{\rm{u}}}$的取值会影响贡献模态截断带来的误差）. 由表2可知，理想结构和实际结构的静力位移均可用前3阶理想模态近似线性表达，工况1的贡献模态可取 ${{{E}}_{{\rm{p}}1}}$={9，98，148}，共3阶. 对于工况2，提取对理想结构位移贡献最大的前18阶理想模态，如表3所示. 由表3可知，理想结构和实际结构的静力位移均可近似用前17阶理想模态线性表达，工况2的贡献模态可取 ${{{E}}_{{\rm{p}}2}}$={2，3，7，8，9，12，13，15，39，40，42，43，48，49，50，56，98}，共17阶. 可见，不同的荷载工况作用在同一结构上会激发不同的模态，所需的贡献模态数量也有较大差别. 需要指出的是，贡献模态的数量由截断阈值 ${\gamma _{\rm{u}}}$决定. 当 ${\gamma _{\rm{u}}}$增大时，贡献模态数量相应减少而模态截断误差相应增大；反之，贡献模态数量相应增加而模态截断误差相应减小. 在实际应用中，可以通过试算来平衡贡献模态数量和位移扩展精度的关系，从而确定截断阈值.

为了进一步考察所选取贡献模态适应结构参数变化的能力，采用蒙特卡洛法进行统计分析，同时考虑构件长度误差、支座位置偏差和构件损伤这3种随机参数. 对于构件长度误差和支座位置偏差，假设其限值与分布模式和前述一致. 对于构件损伤，记其限值为 ${\delta _{\rm{u}}}$. 在0~50%范围内考虑6种不同的 ${\delta _{\rm{u}}}$取值，如表4所示. 假设构件损伤在区间[0，δ_u]内均匀分布. 针对每种构件损伤限值，均随机生成500个样本，并分别计算工况1、2荷载作用下各阶理想模态对各样本的广义位移 ${\alpha _j}$和相对系数 ${\gamma _j}$. 根据 ${\gamma _{\rm{u}}}$=0.01这一阈值条件提取各个样本下的贡献模态，贡献模态变化概率与构件损伤限值的关系如表4所示. 其中，P_f1、P_f2分别为工况1、2的贡献模态保持不变的概率，P_s1、P_s2则分别为贡献模态发生变化的概率. 由表4可知，随着构件损伤限值的增加，工况1贡献模态保持不变的概率逐渐降低，而工况2的贡献模态一直保持不变. 经分析，工况1贡献模态的变化全部由第153阶模态引起. 蒙特卡洛分析表明： ${\gamma _{153}}$有时会大于 ${\gamma _{\rm{u}}}$，即工况1下的贡献模态集合 ${{{E}}_{{\rm{p}}1}}$偶尔由{9，98，148}变化为{9，98，148，153}. 但是， ${\gamma _{153}}$出现的最大值为0.011 5，仅比 ${\gamma _{\rm{u}}}$略大. 可见，即使第153阶理想模态未被保留在 ${{{E}}_{{\rm{p}}1}}$中，也不会对模态截断精度产生太大的影响. 因此可以判断，基于理想结构选取的贡献模态即使在结构损伤程度（或非线性程度）很大的情况下也能够很好地适应实际结构随机参数的变化，贡献模态的这种稳定性有利于保证静力位移的扩展精度.

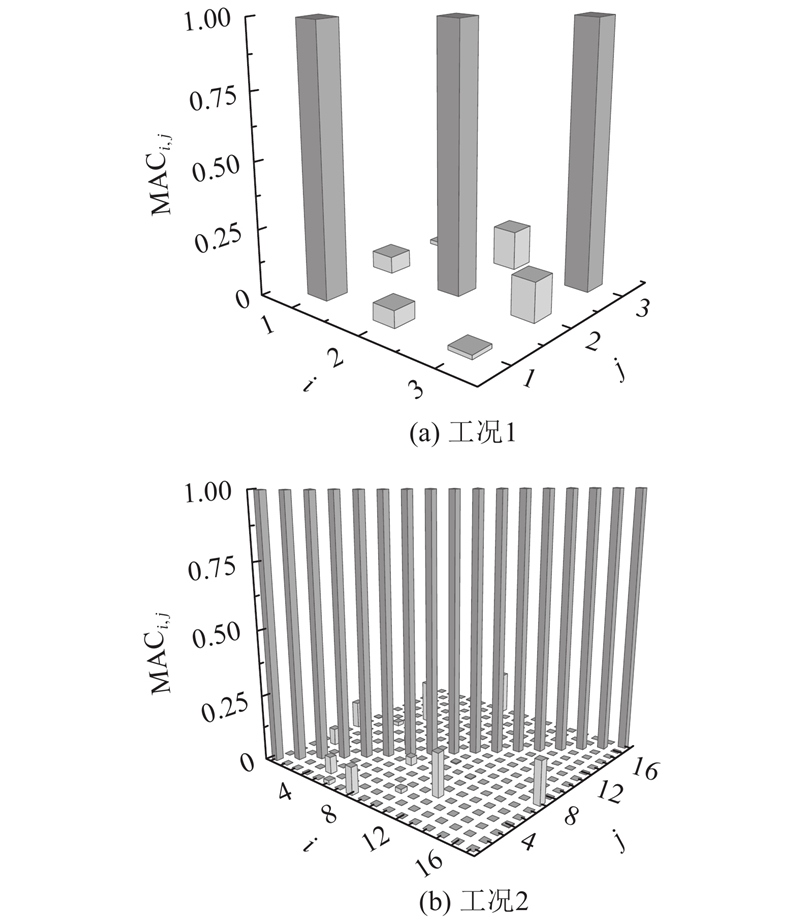
由于各阶模态仅关于质量矩阵正交，考虑到质量矩阵一般情况下都不是单位矩阵，各阶模态之间可能存在相关性. 将模态（振型）分别代替式（10）中的位移，计算出任意2阶模态之间的MAC值，以衡量其线性相关程度. 以工况1中的3阶贡献模态和工况2中的17阶贡献模态为例，计算贡献模态之间的MAC值并绘制三维柱状图，分别如图2（a）和（b）所示. 由图2可知，少数模态之间的MAC值并不为0，如图2（a）中的MAC_2,3=0.151（下标2、3分别对应第98、148号模态）和图2（b）中的MAC_7,17=0.165（下标7、17分别对应第13、98号模态）. 可见，各阶模态并不严格满足正交性要求. 从表面上看，直接以理想模态作为自由度空间的基向量并不合理.

采用PCA法来考察采用理想模态线性表达静力位移的合理性. 按式（12）对所有理想模态组成的振型矩阵X进行SVD分解，并将特征值对最大值归一化，且由大到小排序，可得第288阶特征值为0.247（总自由度数n =288）. 可见，尽管各阶理想模态之间并非严格正交，由于其包含着n个n×1维严格正交基向量的信息，静力位移可以等效表达成n个严格正交基向量的线性组合. 可见，采用理想模态代替严格正交基向量来线性表达静力位移是合理的.

进一步对贡献模态进行主成分分析. 按式（12）对工况1中由3阶贡献模态组成的振型矩阵X₁进行主成分分析. 将归一化特征值进行排序，前4阶特征值分别为1、0.298、0.245和0. 可见，经主成分分析后，工况1的3阶贡献模态可以转换成3阶主成分正交基. 同样对工况2中由17阶贡献模态组成的振型矩阵X₂进行主成分分析. 将归一化特征值进行排序，第17阶特征值为0.139，而第18阶特征值为0. 可见，经主成分分析后，工况2的17阶贡献模态同样可以转换成17阶主成分正交基. 工况1和工况2的贡献模态数量都分别等于相应主成分正交基（为严格正交基）的数量. 值得注意的是，若将主成分正交基代替贡献模态进行后续测点位置优化和静力位移扩展，其计算结果与采用贡献模态时完全一致（第5.4和5.5节不再重复给出相关数据）. 这种贡献模态与主成分正交基的等效性再次证明将理想模态作为“基向量”是有效的.

基于贡献模态集合E_p1和E_p2，采用第3章所述的迭代策略分别对工况1、2的测点位置进行优化. 一般情况下，测点数量取为贡献模态数量加1即可（满足测点数量不小于贡献模态数量的要求）. 相应地，工况1需要4个测点，最优位置为{1x，1z，38z，39y}；ix、iy、iz分别表示节点i的x、y、z方向. 工况2需要18个测点，最优位置为{5y，10z，18z，24z，28z，38z，48z，54z，58z，68z，74z，78z，88z，94z，98z，108z，118z，119z}.

由于文献[16]方法的测点需要与加载点相同，工况1、2分别需要48、24个测点，其位置与相应的加载点相同. 为了考察测点数量对所提方法静力位移扩展结果的影响，对工况1、2均增加测点数量至24. 此时2种工况的最优测点位置分别为{1x，1z，2x，3x，3z，4x，7z，10z，23z，34z，38z，39y，39z，40z，53z，64z，69z，78z，93z，94y，94z，95z，108z，119z}和{1z，5y，7z，10z，18z，24z，28z，38z，44z，48z，54z，58z，63z，68z，74z，78z，84z，88z，94z，98z，104z，108z，118z，119z}.

为了考虑测量误差的影响，假设实测位移的噪声添加方式为

(13) ${{\tilde{ d}}_k} = {\tilde{ d}}_k^*\left( {1 + \varepsilon \cdot {\varPsi }} \right).$

式中： ${{\tilde{ d}}_k}$、 ${\tilde{ d}}_k^*$分别为实际结构位移在第k个自由度上的含噪、无噪位移值， $\varepsilon $为噪声水平， ${{\varPsi }}$为满足标准正态分布的随机数.

在0~8%变化噪声水平（如表5、6所示），考察噪声水平对所提方法扩展效果的影响. 以第5.2节生成的实际结构为例，对每种工况和每种噪声水平，均随机生成5 000个带噪声的实测位移样本. 根据式（10）、（11）分别计算各样本对应的静力位移扩展评价指标，并统计出MAC指标的最小值MAC_min和MVE指标的最大值MVE_max. 对于同一种工况和相同噪声水平，MAC_min越大，MVE_max越小，则静力位移扩展的效果越好.

由表5可知，对于工况1，当测点数量从4个增加到24个时，所提方法的扩展效果有较大改善；所提方法（4个测点）比文献[16]方法（48个测点）扩展效果要差一些；而所提方法（24个测点）在较高噪声（2%以上）时比文献[16]方法表现更佳，具有更强的抗噪能力，但在较低噪声时，表现更差一些. 由表6可知，对于工况2，所提方法采用24个测点时的扩展效果比采用18个测点时更好；当均采用24个测点时，所提方法比文献[16]方法的扩展效果稍差一些. 可见，荷载工况和测点数量会影响静力位移的扩展结果.

总体而言，所提方法的扩展效果较好. 工况1中，在测点比加载点少50%的情况下，所提方法也能获得和文献[16]方法相当的扩展效果，表明该方法对某些荷载工况（贡献模态数远小于加载点数）是非常有效的，且能大幅减少测点数量. 在实际应用中，可以主动选择贡献模态数量较少的荷载工况进行加载，有利于提升静力测试的效率.

本研究以环形张力罩棚结构为例，提出了一种新的静力位移扩展方法来快速测量索杆张力结构的静力位移场，为此类结构的静力测试提供了一种新的选择，主要结论如下.

1）存在随机结构参数偏差的实际结构静力位移可以近似表示为少数理想模态（即贡献模态）的线性组合. 算例结果表明，不同荷载工况所需要的贡献模态数量可能差别较大，但贡献模态均能适应结构参数的较大变化并保持良好的稳定性.

2）所提迭代策略可以优化测点位置，同时实现贡献模态组合系数的无偏估计，从而保证静力位移的扩展精度. 算例结果表明，荷载工况和测点数量均对扩展效果有较大影响.

3）主成分分析结果表明，结构模态包含着自由度空间完整的严格正交基向量信息. 尽管各阶模态之间存在一定相关性，采用结构模态代替严格正交基来线性表达静力位移是有效的.

4）文献[16]方法要求测点与加载点相同，当加载点很少时，文献[16]方法更具优势；而所提方法要求测点数不少于贡献模态数，当加载点很多但贡献模态较少时，所提方法的测试效率更高.