压电材料既能作为作动器又能作为传感器,可以直接贴附在结构表面,且具有频带宽、功耗低、附加质量轻等特点,目前被广泛应用于薄壁结构的主动振动控制[16-20]. 在压电材料的极化方向上施加过大的负电压会导致材料去极化;对压电材料施加过大的正向电压也会使材料发生击穿,导致短路,因此在实际工程中压电作动器的控制电压总是存在着幅值限制. 目前Ying等[21]已对压电结构非线性随机振动进行了bang-bang电压控制的研究,但是bang-bang控制器所产生的控制电压连续性较差,容易引起结构抖振;bang-bang控制器的输出力都为正负极限值,使得电压的控制效率较低,因此须对已有的bang-bang电压控制律进行改进.Ying等[22-23]提出非线性随机最优力有界控制策略,但是压电主动振动控制是通过逆压电效应来产生力,因此须进一步将有界控制力转化为有界电压才能符合实际压电作动器的控制要求.
本研究利用压电作动器对轴向受压梁的非线性随机振动进行最优电压有界控制. 推导表面贴附压电作动片轴向受压梁的非线性随机振动机电耦合动力学方程;根据动力学方程特性,利用随机平均法和动态规划方程导出非线性随机最优电压有界控制律. 对轴向受压简支梁的非线性随机振动进行电压有界最优控制,并与bang-bang电压控制律比较控制效果和效率.
1. 贴附压电作动器的轴向受压梁非线性随机动力学模型
如图1所示为表面贴附压电作动片的轴向受压梁. 图中,L为矩形截面梁长度,b为宽度,h为厚度,Fa为端部所受轴向压力的幅值;为了实现对称弯曲控制,在梁的上、下表面对称贴有厚度为hp,宽度与梁截面相同的压电作动片;x-y-z为整体坐标系,1-2-3为压电材料坐标系,x1*、x2*为压电片在梁长度方向上的边界坐标,并假设上、下压电片都沿3方向极化.
图 1
图 1 表面贴附压电作动片的轴向受压梁
Fig.1 Axial compressed beam with surface attached piezoelectric actuation patches
设u(x,t)、w(x,t)分别为梁中性面上点在纵坐标x和横坐标z上的位移量. 轴向受压梁的等效横向刚度减小,在不大的外界激励下也会产生大幅振动,因此须引入von Kármán几何非线性项,梁中任意一点的应变可以表示为
可以得到梁的变形能:
式中:E为梁材料的弹性模量,dV为梁的体积微元.
本研究主要针对细长梁结构,因此仅考虑压电作动片沿纵向的电致应变,忽略其宽度和厚度方向的应变,将文献[20]中的压电本构关系简化为
式中:T为压电作动片中的应力,Ep为压电材料的弹性模量;
式中:V1、V2分别为上、下压电作动片的体积.
将式(1)代入式(2)、(4),并将梁的变形能和压电作动片的机电势能相加,可以得到总势能:
式(5)中存在轴向受压梁的轴向变形u关于x坐标的一阶导∂u/∂x,使得直接求解较困难. 根据文献[1]可知∂u/∂x可以用横向位移w关于x坐标的一阶导∂w/∂x来表示,即
式中:Fa为小于一阶屈曲力的轴向压力. 式(6)可以用于两端固定、两端简支以及一端固定另一端简支的梁边界情况[1].
假设压电作动片的长度和截面拉伸模量相比于主结构的相应参数都较小,忽略压电片对梁整体轴向变形的影响. 将式(6)直接代入式(5),得到总势能:
由于后文将采用Lagrange方程得到动力学方程,式(7)中的最后一行常数项可以删去.
系统的总动能为梁和压电作动片动能之和:
式中:ρ、ρp分别为梁和压电片的材料密度.
根据Galerkin法,设横向振动位移为
式中:η为振幅系数,W为振型函数.
将式(9)代入式(7)、(8),可以得到离散形式的动能和势能. 将势能、动能代入保守系统Lagrange方程:
从而得到Duffing振子形式的动力学方程:
式中:Fc(t)为压电作动片控制力,系数m、k、q表达式为
由式(12)可知,仅刚度系数k与轴向压力Fa相关, Fa越大,k越小,其他系数与Fa无关. k的减小将导致固有频率减小且稳态振幅增大,使梁结构出现低频大幅振动.
Fc(t)的表达式为
式中,Aa为单位电压产生的控制力.
对系统施加高斯白噪声
假设
式中:2D为激励强度,δ(τ)为Dirac函数.
2. 随机平均法
令振幅系数η=Q,导数
式中:H为Hamilton能量.
假设式(16)中
由于上述Hamilton系统可积且非共振,相应的平均
式中:B(t)为单位纳维过程,
其中,Ql为广义坐标Q的积分限,Ql(H)、G(H, Ql)和T(H, Ql)的表达式分别为
3. 随机最优电压有界控制及响应
3.1. 随机最优电压有界控制
对于半无限长时间区间上的有界遍历控制,性能指标为
式中:
其中,g(H)通常为H的多项式,须事先设定;R为模态控制力的权值.
利用动态规划原理可以导出动态规划方程:
式中:λ为最优控制成本,为常数,λ=J(Fc*),Fc*为最优控制力;U为所有可行控制力的域;V=V(H, t)为值函数.
考虑到压电作动片的控制力与控制电压的关系(式(13)),可以通过对动态规划方程(式(23))右侧求导得到使控制成本函数λ最小的
该非线性随机最优电压有界控制律包括非线性随机无界最优控制电压(式(24)上式)和bang-bang控制电压(式(24)下式),因此其连续性较bang-bang控制要好.
将该控制律代入动态规划方程(式(23)),可以得到最终的动态规划方程:
式中:λ=g(0)+D∂V/∂H|H=0,Qcr为当控制电压达到边界时广义坐标Q可以达到的最大值:
最优控制律中的∂V/∂H可以通过数值方法求解完全平均动态规划方程(式(25))得到.
3.2. 随机最优电压有界控制响应
受本研究中平均漂移系数和平均扩散系数的形式(式(19)第1、2式)所限,无法通过FPK方程得到Hamilton能量H概率分布的解析表达式,因而只能采用数值方法得到H和控制电压
式中:E[·]为期望,下标u、c分别表示无控和有控情况.
4. 数值计算分析
4.1. 计算条件
以贴有压电作动片的轴向受压简支梁为例,对其进行非线性随机最优电压有界控制,模型参数如表1所示.
表 1 梁及压电作动器的模型参数
Tab.1
| 参数部件 | L/m | b/m | h/mm | ρ/(g∙cm−3) | E/GPa | d31/(pC∙N−1) |
| 梁 | 1.00 | 0.01 | 4.0 | 2.7 | 70 | − |
| 压电作动器 | 0.02 | 0.01 | 0.5 | 7.8 | 61 | −300 |
简支梁的一阶横向振型函数为
假设轴向力分别为0 N、Fa=0.8Fcr=0.8EIπ2/L2≈29.5 N,并引入外部谐激励 0.1cos (ωt),再将上述条件代入式(11),可以分别得到无轴向力和受轴向力情况的非线性动力学方程:
图 2
图 2 轴向受压梁的非线性幅频响应
Fig.2 Nonlinear amplitude frequency response of axial compressed beam
4.2. 非线性随机最优电压有界控制律与bang-bang电压控制律对比
将振型函数(式(28))代入式(12)第1式和式(13),可以得到简支梁上压电作动器的一阶控制力:
对于简支梁的第1阶模态控制,可以根据经验将压电作动器布置在模态峰值处,即选择x1*=0.49,x2*=0.51. 将此布置参数连同表1中的模型参数代入一阶模态控制力公式(式(30))得到模态控制力系数Aa/m=−2.845e−3N/(kg·V).
假设模态阻尼比ξ1=0.005,g(H)=0,R1=1. 由于无法得到动态规划方程(式(25))中∂V/∂H的解析表达式,采用龙格库塔法. 根据式(26)可知,为了使Qcr不出现复数且初始控制信号不至于过大,假设初始条件为
求解步长h=H0/2. 并且计算响应也采用龙格库塔法,假设初值[Q,P]T=[0, 0]T,根据前面得到的频响结果取采样频率为150 Hz,仿真时长为40 s.
图 3
图 3 2种电压控制律下的受压简支梁位移响应与控制电压样本
Fig.3 Displacement response sample and control voltage sample of compressed simply supported beam under two control laws
在不同激励强度D以及不同压电作动器电压限幅
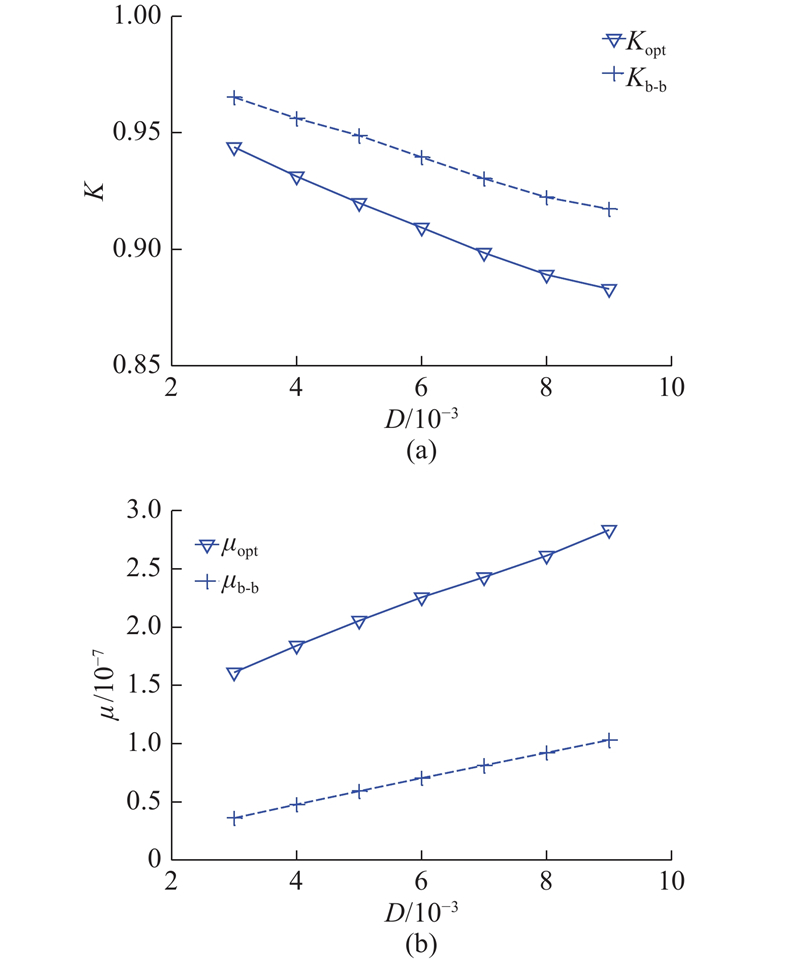
取一组激励强度D=3×10−3、4×10−3、5×10−3、6×10−3、7×10−3、8×10−3、9×10−3,电压限幅为±400 V,可以得到本研究导出电压控制律与bang-bang电压控制律下轴向受压简支梁控制效果K和电压控制效率μ随激励强度D的变化,分别如图4(a)、(b)所示.图中,下标opt、b-b分别表示本研究导出的非线性随机电压有界控制和bang-bang控制.再取一组压电作动器电压限幅值
图 4
图 4 2种电压控制律下的控制效果和电压控制效率随激励强度的变化
Fig.4 Variation of control effectiveness and voltage control efficiency with function of excitation intensity under two control laws
图 5
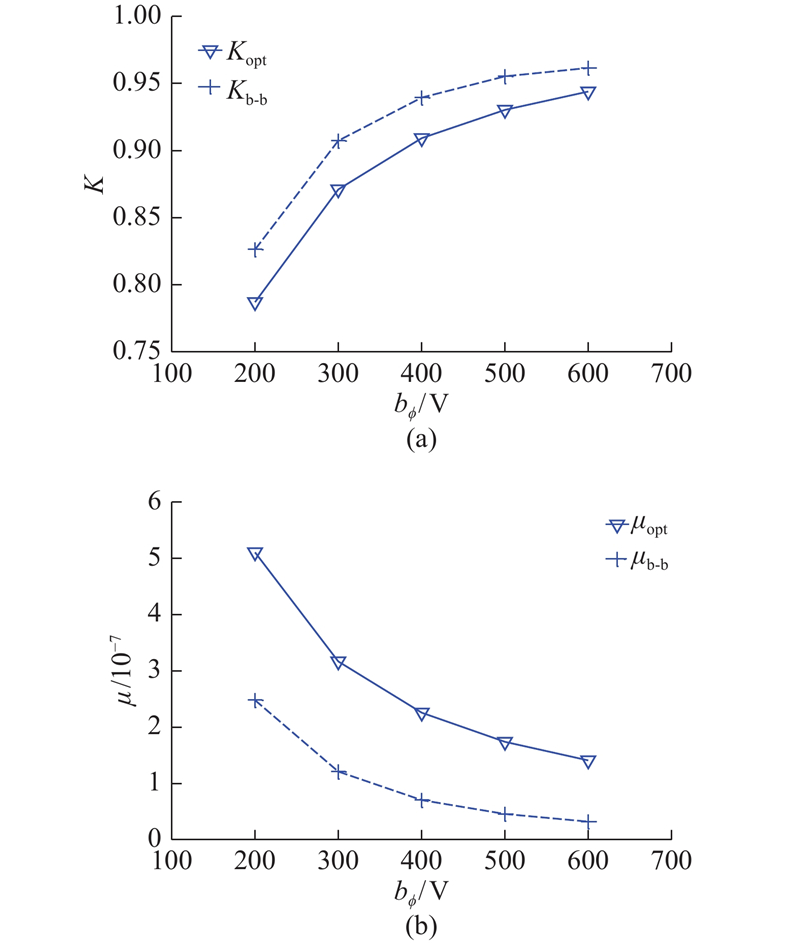
图 5 2种电压控制律下控制效果和电压控制效率随电压限幅的变化
Fig.5 Variation of control effectiveness and voltage control efficiency with function of voltage bound under two control laws
此外还可以发现,随着激励强度D增大,控制效果K单调减小,电压控制效率μ单调增大;随着电压限幅
5. 结 论
(1)本研究基于几何非线性理论和压电本构关系,推导表面贴附压电作动片的轴向受压梁的机电耦合能量表达式,并基于Galerkin法和Lagrange方程建立非线性随机振动主动控制动力学模型.
(2)基于随机平均法和动态规划原理,导出改进型的非线性随机振动最优电压有界控制律,该控制律包括无界的非线性随机最优控制电压以及bang-bang控制电压.
(3)利用本研究导出的电压有界控制律对轴向受压简支梁的强非线性随机振动实现有效的抑制. 仿真结果表明,与bang-bang电压控制律相比,非线性随机最优电压有界控制律的控制效果略有降低,但电压控制效率大幅提高,且控制电压的连续性较好. 为轴向受压细长结构的几何非线性随机振动控制提供一定参考.
(4)本研究导出的随机最优电压有界控制律只能针对单模态振动或解耦后的多阶模态,然而任意位置贴附的压电作动器会对多阶模态都有作用,导致模态耦合,因此未来须进一步开展针对耦合模态力的多阶随机最优电压有界控制律研究.
参考文献
Postbuckling and free vibrations of composite beams
[J].DOI:10.1016/j.compstruct.2008.06.006 [本文引用: 3]
双环可展桁架结构动力学分析与试验研究
[J].
Dynamic analysis and test research of double-ring deployable truss structure
[J].
弹性基础上压杆的横向非线性自由振动与屈曲
[J].DOI:10.6052/1000-0879-13-409 [本文引用: 1]
The transverse nonlinear free vibration and the buckling of compressive bar on an elastic foundation
[J].DOI:10.6052/1000-0879-13-409 [本文引用: 1]
温室风振分析中的压杆弯曲振动动态刚度阵模型
[J].
Dynamic stiffness matrix models for the flexural vibration of compression bar in greenhouse wind vibration analysis
[J].
Dynamic performance of post-buckled precompressed piezoelectric actuator elements
[J].DOI:10.1142/S0219455412500423 [本文引用: 1]
Dynamic elastic-axis shifting: an important enhancement of piezoelectric postbuckled precompressed actuators
[J].
Electromechanical modeling and nonlinear analysis of axially loaded energy harvesters
[J].DOI:10.1115/1.4002786 [本文引用: 1]
Vibration suppression in a simple tension-aligned array structure
[J].DOI:10.2514/1.J052127 [本文引用: 1]
Enhanced structural behavior of flexible laminated composite beams
[J].DOI:10.1016/j.compstruct.2007.05.007 [本文引用: 1]
Piezoelectric control of columns prone to instabilities and nonlinear modal interaction
[J].DOI:10.1088/0964-1726/17/3/035001 [本文引用: 1]
Nonlinear vibration control of a piezoelectric beam with a fuzzy logic controller
[J].
Nonlinear structural vibration suppression using dynamic neural network observer and adaptive fuzzy sliding mode control
[J].DOI:10.1177/1077546309103284 [本文引用: 1]
Stochastic averaging of quasi-integrable Hamiltonian systems
[J].DOI:10.1115/1.2789009 [本文引用: 1]
An optimal nonlinear feedback control strategy for randomly excited structural systems
[J].
Integrated design optimization of structure and vibration control with piezoelectric curved shell actuators
[J].DOI:10.1177/1045389X16641203 [本文引用: 1]
Numerical and experimental investigation of active vibration control in a cylindrical shell partially covered by a laminated PVDF actuator
[J].DOI:10.1088/0964-1726/17/3/035024
Experiments on active precision isolation with a smart conical adapter
[J].
Multi-parameter optimization of piezoelectric actuators for multi-mode active vibration control of cylindrical shells
[J].DOI:10.1016/j.jsv.2018.04.021 [本文引用: 1]
Optimal bounded control for nonlinear stochastic smart structure systems based on extended Kalman filter
[J].
A stochastically averaged optimal control strategy for quasi-Hamiltonian systems with actuator saturation
[J].DOI:10.1016/j.automatica.2006.04.023 [本文引用: 1]
Stochastic optimal control of quasi integrable Hamiltonian systems subject to actuator saturation
[J].DOI:10.1177/1077546307086893 [本文引用: 1]