本文基于欧拉曲梁理论,采用状态空间法,得到了弹性地基上连续曲梁的首末端状态变量间的矩阵传递关系. 根据梁弹簧模型对接头力学行为的线性化假定,得到了接头处状态变量的矩阵传递关系. 通过推导,最终将问题归结为求解关于初始截面内力和变形的6个线性代数方程. 本文的解析解具有形式简洁,计算效率高,便于编程求解的优点,并且可适用于任意的荷载和接头分布形式.
1. 问题描述
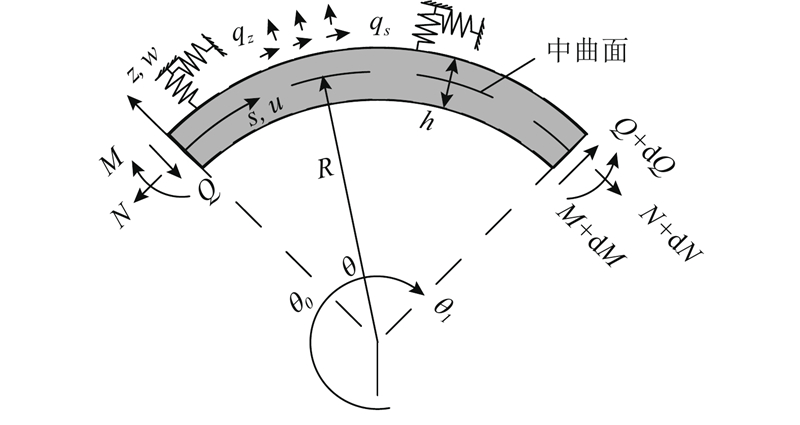
图 1
2. 盾构隧道衬砌环解析模型
2.1. 弹性地基上的曲梁模型
图 2
图 2 弹性地基上单个连续曲梁段模型
Fig.2 Model diagram of single continuous curved beam resting on elastic foundation
根据欧拉曲梁理论[16]可知,截面上的轴力和弯矩为
式中:A和I分别为截面的面积和抗弯惯性矩. 截面的转角φ定义为
弹性地基上曲梁的平衡方程为
式中:Q为剪力,
把式(1)~(4)整理成矩阵形式,无量纲化可得
式中:
其中
无量纲位移、内力和坐标为
根据矩阵理论可知,式(5)的解为
式中:
传递矩阵
图 B.1
在式(11)中取θ=θ1,得到单个曲梁段两端状态向量
若只有一段管片,则式(15)中两端状态向量共12个未知数,方程数为6,需要补充两端各6个边界条件进行求解.
2.2. 接头模型
由于管片间接头的存在,衬砌的整体刚度将受到削弱. 采用集中弹簧,模拟接头的抗弯、抗剪和抗压特性. 当需要考虑接头在受到不同方向内力时的刚度差异时,可以针对不同的接头受力方向采用不同的弹簧刚度,具体可以通过多次试算实现. 假定分析对象为介于第j个曲梁段和第j+1个曲梁段间的第j个接头,根据弹簧的变形关系及内力的连续性,有
式中:
式中:
其中
若弹簧的刚度无穷大,则表示管片之间的连接是完美的,等同于连续管片截面. 由式(18)可知,此时矩阵
2.3. 弹性地基上的盾构隧道衬砌环曲梁模型
如果衬砌由n个接头和n段管片组成管片环,如图3所示,结合2.1和2.2节建立的2个状态变量传递关系,从第n段管片末端截面依次传递到第1个管片起始端,可以得到第n个接头两侧截面状态向量间的传递关系如下:
图 3
式中:
第1段的起始端和第n段的末端通过第n个接头相连,于是有
把式(25)代入式(20),可得只关于第1段管片的起始端截面处状态向量的代数方程:
式中:
式(26)由6个关于第1段管片起始端截面6个物理量的代数方程组成,求解后可得第1段管片始端截面处的3个内力及对应的3个位移,然后可由式(12)求得第1段管片内任意截面处的内力和位移. 结合式(17),求得第2段管片的起始端截面的状态向量,重复以上过程,可以确定所有管片分段内任意截面处的内力和位移.
3. 数值算例
3.1. 本文解析结果的验证
对文献[10]的上海地铁工程实际案例进行模拟. 为了对比验证,采用统一的模型参数,分别利用Abaqus和本文的解析解进行分析. 衬砌由6块均等的管片组成,接头的具体位置为30°、90°、150°、210°、270°和330°(角度由衬砌底部开始沿顺时针方向计算). 管片的弹性模量为35 GPa,截面高度为0.3 m,
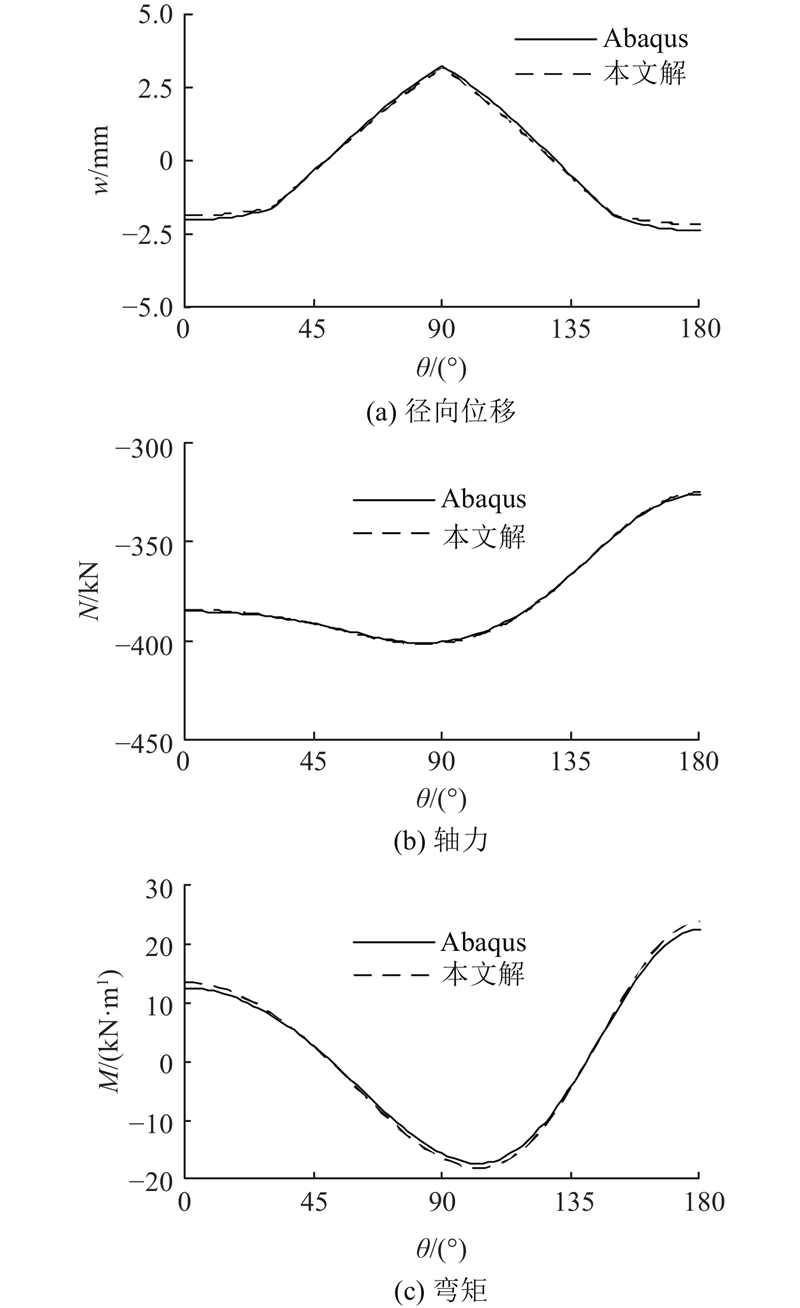
衬砌外径为2.5 m,衬砌纵向取1.0 m计算. 在数值计算时,采用欧拉伯努利梁单元B23模拟管片,沿衬砌全圆周设置径向和环向接地弹簧单元(connect points to ground). 土弹簧的径向抗力系数kz=5 000 kPa/m,环向抗力系数ku取径向抗力系数的1/3[11]. 管片间接头的行为分别由径向、轴向和转动方向的点对点弹簧单元模拟(connect two points),纵向每延米的接头弹簧转动刚度参考文献[10]的取值范围,取5 400 kN·m/(rad·m). 考虑到实际工程中其他2个方向的刚度较大,分别取纵向每延米的接头弹簧剪切刚度和轴向刚度为kw=107 kN/m2和ku=1010 kN/m2. 衬砌受到的荷载如附录B中图B.1所示,各项荷载的幅值分别为q1=165.8 kPa,q2=187.9 kPa,q3=116.1 kPa,q4=60.2 kPa和q5=7.5 kPa. 图4(a)~(c)分别给出本文解析解与Abaqus数值计算径向位移、弯矩和轴力计算结果的对比. 可以看出,两者结果非常接近,验证了本文解析解的正确性.
图 4
图 4 本文解析解与Abaqus数值解计算结果对比
Fig.4 Comparison between present analytical results and numerical results of Abaqus
图 5
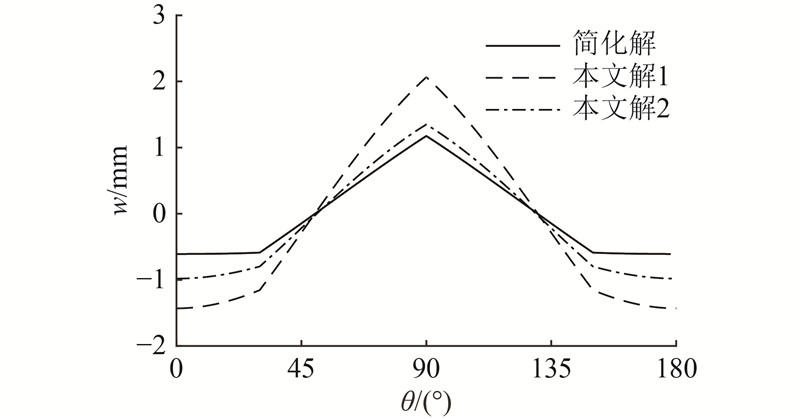
3.2. 接头弹簧刚度的影响
考察接头弹簧刚度对计算结果的影响,为了便于分析,忽略了接头弹簧刚度在不同方向弯矩作用下的刚度变化. 在下面的分析中,接头的位置分别为42°、107°、172°、188°、253°和318°,假定管片的截面几何尺寸h和材料参数E以及衬砌的半径R与算例中一致,保持不变. 根据式(29)[11]可知,
图6(a)~(d)给出在
图 6
图 6 不同接头转动弹簧刚度下,无量纲衬砌内力和收敛位移最大值随无量纲土弹簧径向抗力系数的变化曲线
Fig.6 Curves of normalized maximum internal forces and convergences varying with normalized soil reaction coefficient under different normalized rotational joint stiffness
图 7
图 7 不同接头剪切弹簧刚度下,无量纲衬砌内力和收敛位移最大值随无量纲土弹簧径向抗力系数的变化曲线
Fig.7 Curves of normalized maximum internal forces and convergences varying with normalized soil reaction coefficient under different normalized shear joint stiffness
图8(a)~(d)给出在
图 8
图 8 不同接头轴向弹簧刚度下,无量纲化衬砌内力和收敛位移最大值随土弹簧径向抗力系数的变化曲线
Fig.8 Curves of normalized maximum internal forces and convergences varying with normalized soil reaction coefficient under different normalized axial joint stiffness
1)当接头轴向刚度无穷大时,此时衬砌轴向刚度无削弱,内缩趋势微小,衬砌的水平变形由横扩趋势主导,衬砌水平收敛位移随
2)当无量纲接头轴向刚度大于1.2×10−2时,由于接头轴向刚度的削弱加剧了衬砌的内缩趋势,但横扩趋势占主导地位. 当
3)当无量纲化接头轴向刚度介于1.2×10−2和4.8×10−3时,接头轴向刚度的进一步削弱加剧了衬砌的内缩趋势,内缩趋势开始发挥主要作用. 当
4)当无量纲化接头轴向刚度小于4.8×10−3时,接头轴向刚度的削弱过多,导致内缩趋势对衬砌变形起控制作用,此时衬砌的水平变形始终为内缩,且随着
4. 结 论
(1)在盾构隧道应用的典型地层范围内,相比其他2个方向的接头刚度,接头剪切刚度对衬砌内力和位移的影响可以忽略. 接头转动刚度对衬砌弯矩的影响显著,接头轴向刚度对衬砌的轴力影响显著.
(2)衬砌的变形形态由衬砌整体受压内缩趋势以及竖向和水平向荷载差异导致的竖缩横扩趋势共同决定. 当竖缩横扩趋势起主导作用时,衬砌表现为传统的“横鸭蛋型”变形形态;反之,衬砌表现为整体内缩变形形态.
(3)接头轴向刚度的削弱,将导致内缩作用的加剧,存在临界接头轴向刚度,在该刚度下衬砌在较小的土弹簧径向抗力系数下,已表现为整体内缩变形形态.
(4)土弹簧的存在对以上2种趋势的发展起限制作用,随着土弹簧抗力系数的增大,这种限制作用愈加明显,且对竖缩横扩趋势发展的限制作用更显著,这会导致衬砌由原来的“横鸭蛋型”变形形态发展为整体内缩变形形态.
附录A
矩阵
矩阵
附录B
将式(A.1)代入式(14),可以得到荷载积分向量
式中:
图B.1给出常用的衬砌受到的地层荷载分布形式[10]. 图中,荷载方向沿垂直和水平方向. 为了计算
表 B.1 各荷载相关积分
Tab.B.1
| | 关于双曲余弦函数的积分系数 | 关于双曲正弦函数的积分系数 |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | |
参考文献
2D numerical investigation of segmental tunnel lining behavior
[J].DOI:10.1016/j.tust.2013.03.008 [本文引用: 1]
盾构隧道管片施工期上浮特性
[J].
Characteristics of upward moving for lining during shield tunneling construction
[J].
地面堆载下盾构隧道管片与环缝接头的性状分析
[J].
Shield tunnel segment and circumferential joint performance under surface surcharge
[J].
Simplified analysis for tunnel supports
[J].
盾构隧道衬砌结构受力分析的梁-弹簧系统模型
[J].
Study on two beam-spring models for the numerical analysis of segments in shield tunnel
[J].
Structural design of linings for bored tunnels in soft ground
[J].
An analytical solution for jointed tunnel linings in elastic soil or rock
[J].DOI:10.1139/T08-075
The influence of interfacial joints on the structural behavior of segmental tunnel rings subjected to ground pressure
[J].DOI:10.1016/j.tust.2018.08.025
An analytical solution for a jointed shield-driven tunnel lining
[J].
A new numerical approach to the hyperstatic reaction method for segmental tunnel linings
[J].DOI:10.1002/nag.2277 [本文引用: 5]
基于L-S理论的压电球壳广义热冲击分析
[J].
Generalized thermal shock analysis of piezoelectric spherical shell based on L-S theory
[J].
State space formulation for composite beams with partial interaction
[J].
Levy solution for bending analysis of functionally graded sandwich plates based on variable plate theory
[J].DOI:10.1016/j.compstruct.2017.06.048 [本文引用: 1]
Theories and analyses of thin and moderately thick laminated composite curved beams
[J].DOI:10.1016/0020-7683(93)90152-W [本文引用: 2]
Guidelines for the design of shield tunnel lining
[J].DOI:10.1016/S0886-7798(00)00058-4 [本文引用: 1]