SMA结构的动力学建模和分析是相当复杂的,因为动力学中存在滞回现象,且在应力场和热场之间存在非线性耦合[4-6]. 对SMA建模的难点在于SMA独特的形状记忆效应和由相变引起的结构非线性. 将SMA冷却至较低温度,然后使之产生永久变形,当再次加热时,SMA可以在高温下恢复初始形状. SMA的这种恢复原始形状的独特性质被称为形状记忆效应(SME). 在许多情况下,SMA只能恢复在高温下的起始形状,当再次冷却时,它将忘记在较低温度下的起始形状,故SME被称为单程形状记忆效应(OWSME). 合适的热处理手段可以使SMA具有双程形状记忆效应. 通过实验证明,如果在预处理时对SMA多次进行冷却-变形-加热循环,且每次在低温下对SMA进行相同的变形,那么SMA在冷却后,即使没有施加外部负载,也可以恢复SMA预处理时低温下的起始形状. 宏观上表现为SMA可以学习变形的方式,SMA这种能够恢复在高温及低温下的初始形状的独特性能被称为双程形状记忆效应(TWSME). 在训练SMA使之获得形状记忆效应的过程中,需要合理调整训练温度、时间及施加的负载等参数,训练完成后,要以合适的加工方式将SMA材料加工为目标结构,获得较好的形状记忆效果和使用寿命[7-8].
现在,人们已经认识到SMA的特性是受到外部负载时会发生可逆相变与马氏体变体重构. 这为建立用于描述SMA材料动力学特性的热-力学数学模型提供了基础,这些模型基于物理观察验证,可以为实际工程应用提供有效的理论模型. 本文基于热弹性相变的Landau理论,提出宏观微分模型. 利用非线性常微分方程描述OWSME,用不同相变的加权组合描述TWSME.
1. 马氏体相变
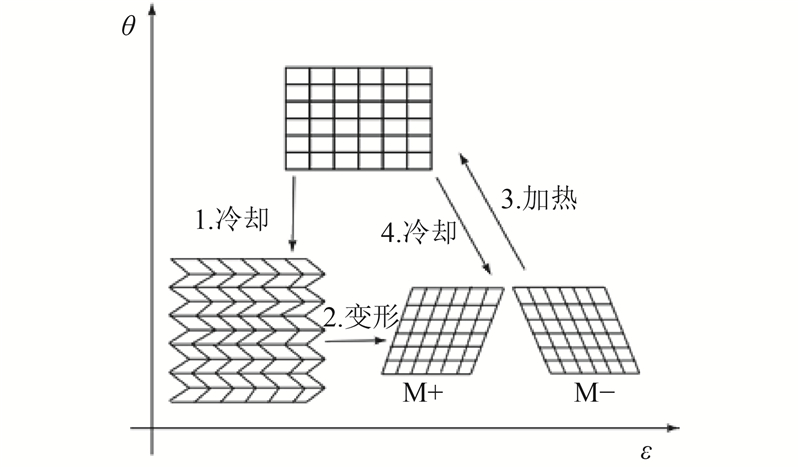
通过实验证明,SMA的OWSME和TWSME都是由马氏体相变和马氏体重定向引起的. 可知,建立SMA的动力学模型的最有效方法是使用数学的方法来描述相变. 如图1所示,SMA的一维结构中,在相变过程中涉及到2个马氏体变体相和1个奥氏体相. 相变可以由过热(A
图 1
图 1 马氏体相变与马氏体变体重构引起的形状记忆效应示意图
Fig.1 Diagrammatic sketch of shape memory effect caused by martensitic transformation and martensitic transformation reconstruction
为了方便建立模型,可以将SME通过如下方式和相变相关联. 在相变时,每个相都有一个特定的特征应变. 在高温时,只有奥氏体是稳定的,特征应变为零. 当材料冷却到较低温度时,奥氏体将变得不稳定,而此时马氏体是能够稳定存在的. 如果在冷却过程中没有施加外部负载,则2种马氏体变体具有相同的机会出现,即A
当对SMA进行多次循环热处理,且在每次循环中对其以相同方式施加同样的应力时,SMA记忆合金会以一种自适应的方式调整M+和M−,不用形成孪晶结构. 在该情况下,当SMA在没有外力负载的情况下冷却时,材料可以自发地形变到特定形状,因此SMA可以恢复低温下的形状. 通过加热或冷却来恢复SMA在高温和低温下的形状,即为TWSME.
SMA的其他独特性质同样可以归因于马氏体相变的宏观表现,例如超弹性效应是由外应力作用下奥氏体和马氏体之间的可逆相变引起的. 由于本文模型的建立是基于相变的唯象描述,模型可以很好地刻画SMA所有的这些特性.
2. 已有SMA模型及现状
现有的SMA模型可以分为微观模型和宏观模型. 在微观力学中,Falk[11]基于多井自由能密度创建一维的唯象非等温模型,将自由能以应变和温度的幂级数的形式表示,使得代表稳定性的能量最小值取决于温度项. 在Landau和Landau-Ginzburg理论被应用于相关问题以后,更多模型被提出,其中有一些考虑多轴加载情况的模型已被广泛使用. 微观力学模型主要关注相变动力学和界面/惯习面运动现象,常常涉及很多难以通过实验识别的参数.
近年来,考虑SMA材料在力热耦合条件下响应的模型不断发展. Wael等[15]提出宏观模型,只通过使用马氏体体积分数和应变张量这2个状态参数,描述了SMA材料的自适应性、马氏体取向重构、超弹性和单程形状记忆效应. Sedlak等[16]基于热力学不可逆过程提出多晶SMA材料的热力耦合模型,该模型可以模拟相变过程中的马氏体相、奥氏体相、作为中间相的R相以及马氏体取向重构. 该模型基于相变和取向重构,提出新颖的耗散函数,考虑在奥氏体和R相之间相变时材料的响应及材料的各向异性. Yu等[17-18]分别提出基于晶体塑性的本构模型和唯象模型模拟超弹性NiTi SMA的循环特性,该模型涉及到2个产热方式:非弹性变形的机械耗散和相变潜热. Xi等[19]根据Ginzburg-Landau的理论和热力学,提出可模拟具有超弹性的单晶NiTi形状记忆合金(SMA)循环相变的三维相场模型. 该模型考虑单晶模型下马氏体相变的形核过程及马氏体变体的生长,发现伴随着循环加载,残余马氏体的不断累积而产生材料内部缺陷,最终会影响可逆马氏体相变的发生. Yao等[20]提出不同加载速率下SMA响应的三维热力耦合模型,考虑了2个非弹性项:马氏体相变及相变诱发的塑性,利用有限元法将该模型从单晶尺度推广至多晶.
3. 单程形状记忆效应
图 2
图 2 马氏体相变及其自由能函数
Fig.2 Martensitic transformation with concerning Landau free energy
式中:ρ为SMA的密度,σ为应力,h为体力. 利用上述模型能够模拟相变中的非线性波传播,模型的具体实施还需要考虑边界条件.
当没有外加负载时,式(3)中
4. 双程形状记忆效应
当对SMA多次进行冷却-变形-加热循环,且每次在低温下对SMA进行相同的变形时,SMA将具有TWSME. TWSME的机理是在无外加负载的情况下冷却时,SMA在A
式中:β为正取向马氏体(M+)的体积分数;ε+、ε−为M+和M−所对应的特征应变,相应的值可以用式(4)计算得出.β仅与外加负载有关,若β为0.5,则整体应变为零.
该模型的关键在于预处理训练之后,β为一个不等于0.5的常数并被材料所记忆,当SMA在没有外部负载的情况下冷却时可以自动恢复到起始的马氏体状态. 由于M+和M−的特征应变是取决于材料的常数,在较低温度下材料的总应变将取决于材料及材料的温度. 上述机制阐述了TWSME.
对于动态建模,与M+相关的应变变化的控制方程为
式中:fv为保证马氏体相变得到M+变体所施加的驱动力,即保证相变过程中仅发生A
图 3
图 3 不同变体偏向下的马氏体相变
Fig.3 Martensite transformation with different variant deviation
式(7)与式(6)的fv相等,但符号相反,相应的示意图为图3(b).
fv很小,只要足够引起相变过程的变体倾向性即可. 人为引入驱动力fv的理由如下:为了单方面模拟A
fv的引入是为了描述形状记忆合金在训练过程中对相变过程的影响,从而将单程记忆效应和双程记忆效应统一进一个相同模型.
5. 数值实验结果
5.1. 热滞回环
第1个数值实验是为了验证M
图 4
图 4 不同变体倾向的马氏体相变
Fig.4 Martensite transformation with different variant deviation
在第2个数值试验中,SMA结构的初始温度设为300 K,初始应变设为零. SMA结构首先以400个偶数步长冷却至200 K. 在该实验中,式(6)、(7)中引入的驱动力fv=1.0×105 kg/(s2·m2). 在冷却过程中,将发生A
在上述模拟中,马氏体变体是施加驱动力所偏向的变体. 若改变驱动力的符号,则产生的马氏体变体将改变.
5.2. 应力滞回环
图 5
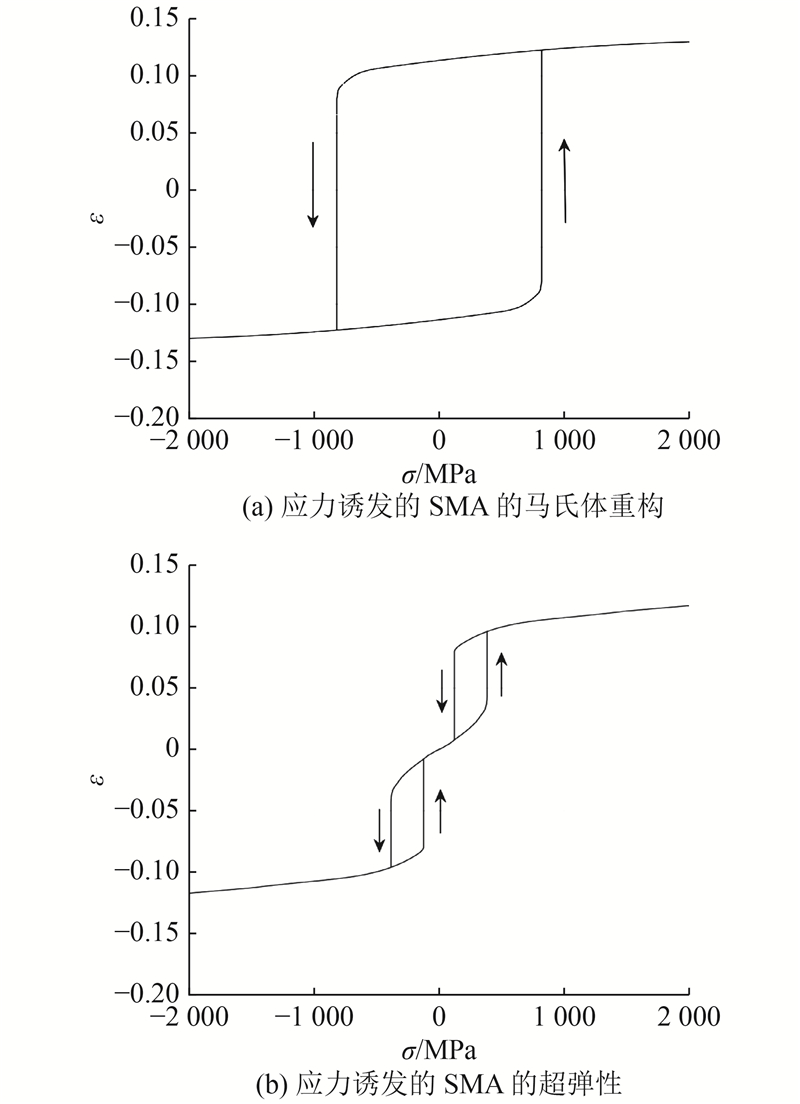
图 5 外力诱发SMA相变所产生的滞回环曲线
Fig.5 Hysteretic loop curve of SMA phase transition induced by external force
第2个数值实验是为了验证提出的模型能够捕获SMA的超弹性效应. 设定温度为255 K,此时奥氏体全局稳定,马氏体亚稳定即局部稳定. 施加的载荷是相同的正弦函数. 模拟结果如图5(b)所示. 可以看出在循环加载下存在2个滞回环曲线,2个滞回环分别对应奥氏体与2种不同马氏体变体之间的相变过程. 由于奥氏体在给定温度下是全局稳定的,当没有施加载荷时,应变将始终为零. 在给定温度下,马氏体是亚稳定的,当施加的载荷足够大时,会发生A
5.3. 双程形状记忆效应
数值实验是为了验证提出模型对于TWSME的刻画能力. 若SMA具有TWSME,则SMA在低温下的形状可以恢复,且低温形状取决于训练过程中所施加的外力负载. 考虑一维SMA结构,TWSME可以通过结构的宏观上的整体应变来表征. 设定SMA的初始温度为200 K,初始应变为0.03. 正取向马氏体M+体积分数β=0.625,该体积分数在预处理的训练后将成为SMA的一个材料常数. 通过对M+使用式(6),对M−使用式(7),计算A
图 6
图 6 与SMA双程形状记忆效应有关的热滞回环
Fig.6 Thermal hysteresis loops related to SMA two-way shape memory effect
从上述数值实验中可知,SMA材料的不同特性,包括OWSME和TWSME、超弹性效应,都可以通过提出的微分模型成功捕获. 基于唯象相变理论,提出的模型以非线性常微分方程表示. 提出的模型便于动态分析和控制.
6. 结 语
本文构建宏观微分模型,用于描述一维SMA结构中的双程形状记忆效应. 该模型基于SMA中热弹性相变的唯象理论,控制方程采用非线性常微分方程. 开展与热和力负载下的相变过程的数值模拟,得到相应的热滞回环曲线和应力滞回环曲线,双程形状记忆效应和超弹性均被成功模拟. 提出的模型便于动态分析和控制. 当使用合适的分段样条曲线替换该模型中的自由能函数时,该模型可以在实验数据上达到更好的拟合效果.
参考文献
A unified framework for modeling hysteresis in ferroic materials
[J].DOI:10.1016/j.jmps.2005.08.006 [本文引用: 1]
Impact induced phase transformation in shape memory alloys
[J].DOI:10.1016/S0022-5096(99)00044-7
Coupled thermomechanical dynamics of phase transitions in shape memory alloys and related hysteresis phenomena
[J].DOI:10.1016/S0093-6413(02)00216-1 [本文引用: 1]
Two-way shape memory effect induced by high-temperature isothermal training in [001]-oriented heterophase single crystals of Ni49Fe18Ga27Co6 alloy
[J].DOI:10.1007/s11182-018-1560-x [本文引用: 1]
A review on machining of NiTi shape memory alloys: the process and post process perspective
[J].
A review on shape memory metallic alloys and their critical stress for twinning
[J].DOI:10.1016/j.intermet.2018.11.005 [本文引用: 1]
Analysis of austenite-martensite phase boundary and twinned microstructure in shape memory alloys: the role of twinning disconnections
[J].DOI:10.1016/j.actamat.2018.11.003 [本文引用: 1]
Model free energy, mechanics, and thermomechanics of shape memory alloy
[J].DOI:10.1016/0001-6160(80)90030-9 [本文引用: 2]
Thermomechanic of transformation pseudoelasticity and shape memory effect in alloy
[J].DOI:10.1016/0749-6419(86)90016-1 [本文引用: 1]
One-dimensional thermo-mechanical constitutive relations for shape memory material
[J].
Finite element analysis of the behavior of shape memory alloy and their application
[J].
A three-dimensional model of the thermomechanical behavior of shape memory alloys
[J].DOI:10.1016/j.jmps.2007.03.012 [本文引用: 1]
Thermomechanical model for NiTi-based shape memory alloys including R-phase and material anisotropy under multi-axial loadings
[J].DOI:10.1016/j.ijplas.2012.06.008 [本文引用: 1]
study on the rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy based on a new crystal plasticity constitutive model
[J].DOI:10.1016/j.ijsolstr.2014.09.006 [本文引用: 1]
Rate dependent cyclic deformation of super-elastic NiTi shape memory alloy: thermo-mechanical coupled and physical mechanism-based constitutive model
[J].DOI:10.1016/j.ijplas.2015.05.011 [本文引用: 1]
Phase field modeling for cyclic phase transition of NiTi shape memory alloy single crystal with super-elasticity
[J].DOI:10.1016/j.commatsci.2017.11.017 [本文引用: 1]
Micromechanical modeling on thermomechanical coupling of cyclically deformed superelastic NiTi shape memory alloy
[J].DOI:10.1016/j.ijplas.2018.04.003 [本文引用: 1]
Driven domain walls in shape memory alloys
[J].DOI:10.1088/0022-3719/20/17/005 [本文引用: 2]
Thermo-mechanical wave propagation in shape memory alloy rod with phase transformations
[J].DOI:10.1080/15376490701673227 [本文引用: 2]
Numerical model for vibration damping resulting from the first order phase transformations
[J].DOI:10.1016/j.apm.2006.08.019 [本文引用: 3]
Convergent numerical approximations of the thermomechanical phase transitions in shape memory alloys
[J].
Rate dependence of hysteresis in one-dimensional phase transitions
[J].DOI:10.1016/S0927-0256(00)00103-8 [本文引用: 2]
Stress wave and phase transformation propagation at the atomistic scale in NiTi shape memory alloys subjected to shock loadings
[J].DOI:10.1007/s40830-018-0189-5 [本文引用: 1]
Nonlinear dynamics of shape memory alloy oscillators in tuning structural vibration frequencies
[J].DOI:10.1016/j.mechatronics.2012.09.004 [本文引用: 1]