相关研究表明,由钢筋锈蚀所引起的开裂、保护层脱落、钢筋截面积损失以及黏结力下降对衬砌的承载能力有极大的影响[14]. 在材料层次,Saetta等[15-16]结合理论与模拟,预测钢筋混凝土由于碳化侵蚀发生钢筋锈蚀的初始时间;Almusallam[17]采用试验方法研究钢筋锈蚀程度对其力学性能的影响;Coronelli[18]通过试验对钢筋锈蚀程度对其与混泥土的黏结力的影响进行深入研究. 这些针对钢筋混凝土在材料层次劣化的研究为后续构件层次劣化模型的构建提供了基础. 许多学者针对钢筋截面损失、保护层开裂、黏结力下降对钢筋混凝土梁承载能力的影响进行了深入研究. 然而,由于运营环境不同,利用此类模型描述隧道衬砌的劣化仍存在困难. 除此之外,影响隧道衬砌长期性能劣化的因素还包括植根材料本身性能参数的不确定性、人为施工造成构件尺寸的不确定性以及环境变量随机作用的不确定性等. 大量的工程实践证明这些不确定性会对构件承载能力造成影响[19-26],不过目前鲜有针对考虑不确定性的隧道衬砌承载能力的计算模型的研究.
本研究结合有限元衬砌外部荷载计算、时变承载能力概率模型建立以及蒙特卡洛模拟(Monte-Carlo simulation,MCS)方法结果所服从的分布分析构建隧道衬砌可靠度劣化模型的分析框架. 1)通过研究得到时变不确定性的衬砌抗弯承载力模型. 相关试验表明纵向钢筋截面积的减少以及钢筋混凝土之间黏结力的下降是造成衬砌性能劣化的主要原因[15-16, 18, 27-30]. 基于此,建立同时考虑钢筋截面面积减少以及黏结力下降引起的变形不协调的衬砌混凝土双筋截面模型,考虑受压区混凝土达到强度极限建立衬砌时变抗弯承载力计算模型. 2)通过对时变抗弯承载力模型中参变量的分析,结合统计学原理建立考虑参变量不确定性的抗弯承载能力时变概率模型. 3)采用MCS方法验证提出的概率模型的准确性以及计算效率. 通过分析MCS方法结果,对承载力模型输出结果所服从的分布进行研究. 4)通过有限元软件计算衬砌所受荷载,结合得到的时变承载力概率模型构建可靠度分析功能函数,采用结构安全联合委员会推荐(joint committee,JC)方法对衬砌服役期的可靠率与失效概率进行详细研究. 得到衬砌可靠度劣化的规律,以期为隧道维护策略的制定以及衬砌设计提供理论支持.
1. 衬砌时变抗弯承载能力计算
1.1. 时变抗弯承载能力计算过程
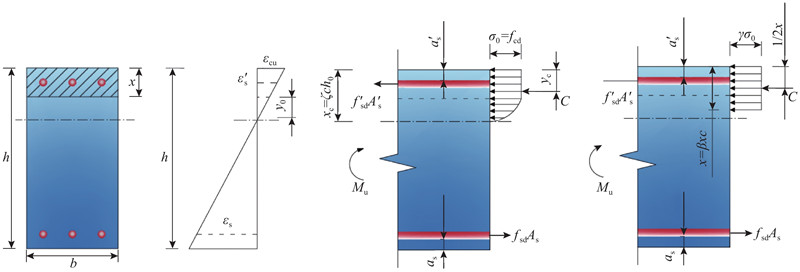
大量研究给出了经典的单筋截面梁承载能力的计算方法,本研究在此基础之上建立适用于隧道衬砌的双筋截面模型,并通过钢筋锈蚀率反映模型的时变特性.
试验表明钢筋截面减小以及钢筋混凝土黏结退化是钢筋混凝土结构抗弯承载能力减弱的主要因素[14]. 钢筋截面减小程度以及钢筋-混凝土黏结力下降导致的变形不协调程度均可以用钢筋锈蚀率(锈蚀部分质量占总质量的比重)来表示. 假设钢筋发生均匀锈蚀,锈蚀率的表达式为
式中:η(t)为t时刻钢筋的锈蚀率;db为钢筋直径;de为锈蚀深度. de的表达式[14]为
其中,J为腐蚀电流密度,t为时间.
考虑到锈蚀引起的钢筋截面减小,受拉区锈蚀钢筋的拉力表达式为
式中:As为受拉区钢筋总截面积,Es 为钢筋弹性模量,σs为钢筋应力,εs为受拉钢筋应变,ηt(t)为t时刻受拉区钢筋的截面锈蚀率.
受压区钢筋的合力表达式为
式中:
在锈蚀钢筋混凝土构件中,由于钢筋和混凝土会发生相对滑移,钢筋和混凝土之间不能满足变形协调几何关系. 由文献[31]的试验结果可以发现,截面上的混凝土平均应变仍然符合平截面假定. 因此,截面曲率
式中:εcu为混凝土的极限压应变,xc为中性轴高度,
图 1
式中:x为受压区高度,σ为等效矩形的应力,σ0为受压区应力极值.
将
锈蚀钢筋混凝土的钢筋和混凝土在同一点处的不协调程度表达式[31]为
式中:εc为混凝土应变.
徐善华[31]通过试验得到
将式(8)代入式(7),可以得到
由图1(b)可知
式中:εcs为锈蚀钢筋的应变,h0为截面有效高度,a1为受拉区钢筋中心距保护层外缘距离.
假设在衬砌破坏时受压区混凝土达到极限应变εcu. 由
式中:fcd为混凝土抗压强度;C为混凝土所受压力合力;
将式(6)、(11)代入式(12),可以得到
式中:
考虑到受拉区钢筋黏结力退化,在衬砌破坏时无法确定其是否已到达抗拉强度极限,受拉区钢筋合力点处的弯矩表达式为
1.2. 准确性验证
图 2
表 1 模型参数及试验与理论结果对比
Tab.1
| 编号 | fcd/MPa | fsd/MPa | η/% | Pm/kN | Ps/kN | |||
| Φ12 | Φ18 | 上缘 | 下缘 | |||||
| 1 | 34.55 | 359.6 | 366.7 | 1.14 | 4.10 | 172 | 168.7 | |
| 2 | 34.55 | 359.6 | 366.7 | 1.07 | 12.90 | 139 | 102.9 | |
| 3 | 34.55 | 359.6 | 366.7 | 0.85 | 6.10 | 144 | 149.3 | |
2. 考虑不确定性的抗弯承载能力概率模型
参数的不确定性对模型输出结果有较大的影响. 由式(13)、(14)可以看出,衬砌抗弯承载能力与混凝土抗压强度、钢筋锈蚀率等参数相关.
抗弯承载能力的计算模型可以简写为
式中:Jc为受压区钢筋腐蚀电流密度;Jt为受拉区钢筋腐蚀电流密度,h为截面高度.
考虑到衬砌一般为对称配筋,式(16)可以简化为
根据统计学原理,抗弯承载力概率模型的均值可以表示为
方差可以表示为
3. 可靠度指标计算
在得到隧道的初始计算参数以及地层等模型之后,衬砌所受的荷载可以通过有限元(finite element method, FEM)软件计算. 在得到衬砌承载弯矩后,结构可靠度指标计算的功能函数可以表达为
式中:Mu的均值和方差可分别由式(18)、(19)求出,M为外部荷载作用下的承受弯矩.
可靠度指标表达式为
式中:
定义变量Xi的灵敏度系数为
极限状态面上点的坐标未知,假设各参变量均值点为初始验算点
当存在非正态变量时,须对其进行当量正态化后再带入迭代计算. 设非正态变量X={X1,X2,
式中:Φ为标准正态分布的累积分布函数,φ为标准正态分布的概率密度函数。
当量正态化变量的均值与标准差表达式分别为
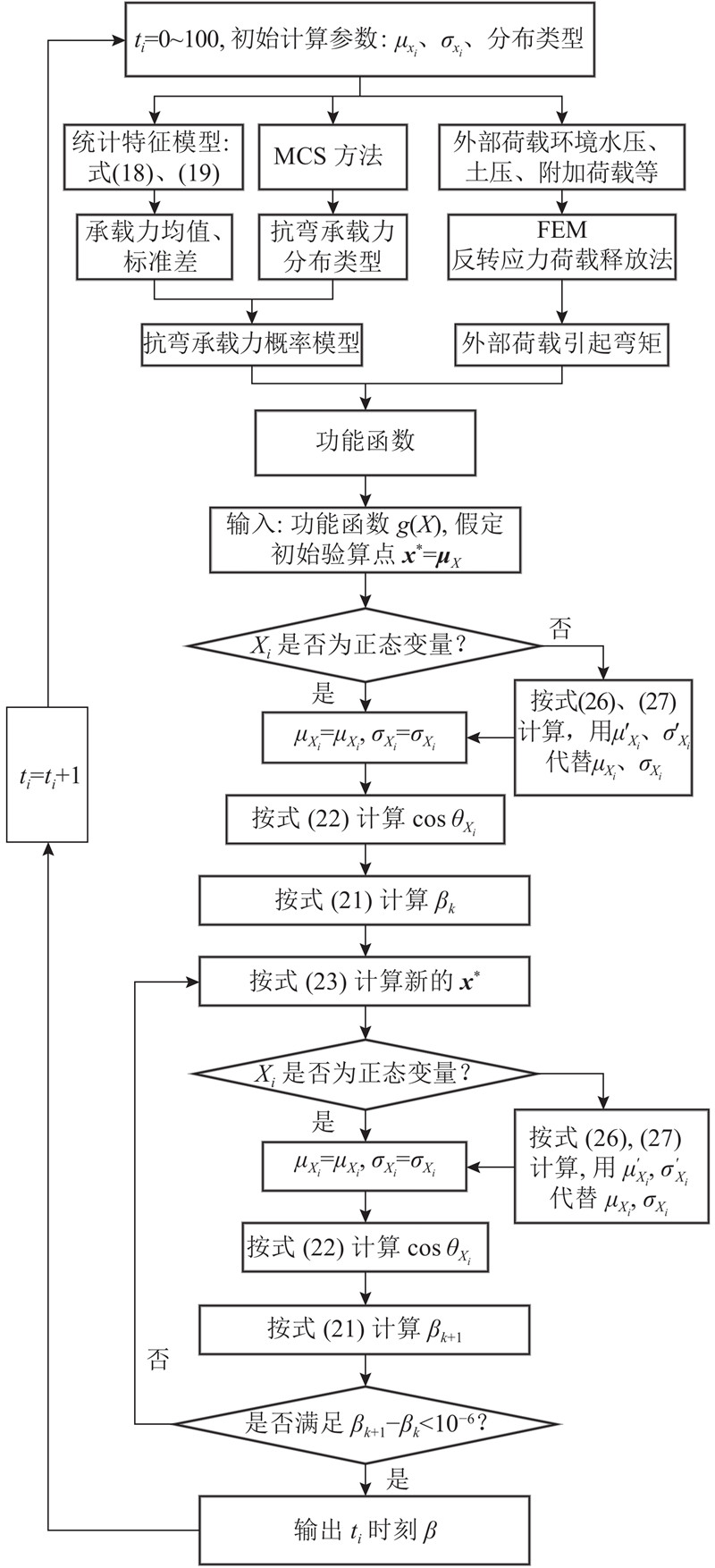
衬砌劣化可靠度计算的具体计算框架如图3所示. 以功能函数的求解为节点,整个计算的流程可以分为两部分. 在节点之前为功能函数的求解过程,主要包括3个步骤:1)抗弯承载能力时变概率模型的求解,通过式(18)、(19)求解得到任意时刻衬砌抗弯承载力的均值与方差;2)利用MCS 方法获取抗弯承载能力分布;3)利用有限元软件获取衬砌荷载模型. 通过第1)、2)步的求解可以获得可靠度计算的抗力模型,结合第3)步获取的荷载模型可以得到可靠度计算的功能函数,从而进行节点后的JC法可靠度迭代计算过程. 对不同时间节点的可靠度进行循环计算,可以得到隧道衬砌寿命周期内的可靠度劣化情况. 须指出的是,在由迭代过程求解出可靠度指标βk后,在按式(23)求解新的验算点
图 3
图 3 衬砌劣化可靠度计算流程
Fig.3 Flow chart of lining degradation reliability calculation
4. 算例与讨论
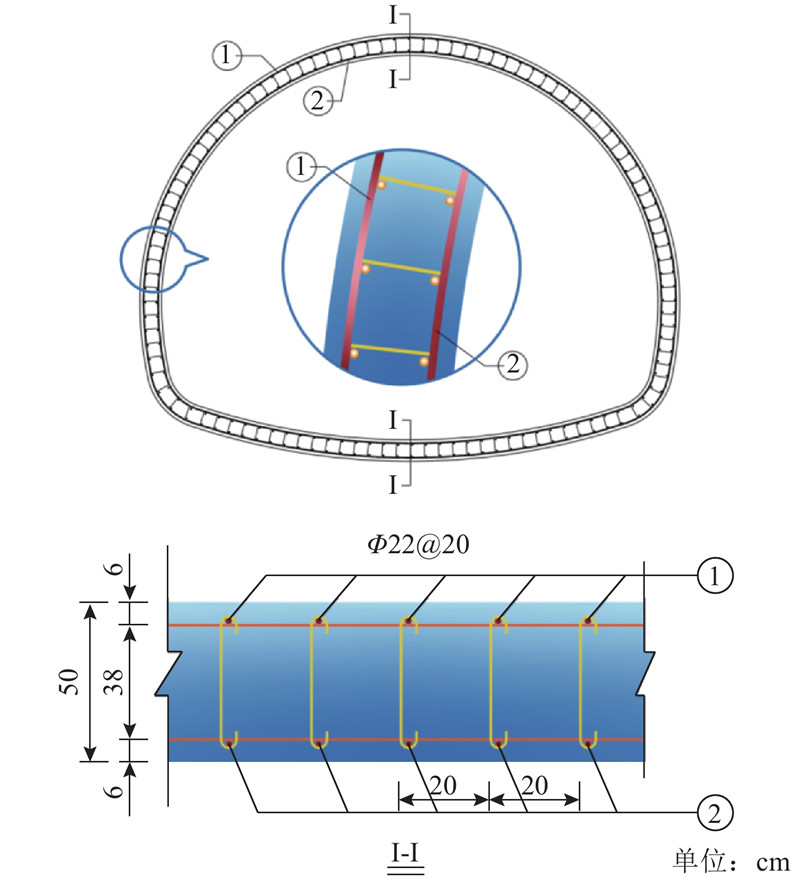
基本参数的概率统计特征是衬砌抗弯承载力时变概率特征分析的基础. 结构安全联合委员会(joint committee on structural safety,JCSS)给出了大量钢筋、混凝土等基本参数的概率统计特征值,其余参数的统计特征可通过长期收集或参考其他文献得到. 在本研究中,为了验证所述方法的应用及准确性,钢筋、混凝土以及截面几何参数的变异系数均取JCSS推荐值. 考虑到隧道内侧为大气环境,假定内侧的腐蚀电流密度为0. 以某深埋公路隧道为例,隧道的衬砌配筋如图4所示.
图 4
表 2 抗弯承载能力劣化计算参数
Tab.2
| 参数 | 分布类型 | 均值 | 变异系数 | 备注 |
| fcd/MPa | 对数正态 | 18.4 | 0.12 | JCSS(2012) |
| As/mm2 | 对数正态 | 1 900 | 0.05 | JCSS(2012) |
| Es/MPa | 正态 | 200 | 0.15 | JCSS(2012) |
| a′s/mm | 正态 | 65 | 0.10 | JCSS(2012) |
| h/mm | 正态 | 500 | 0.05 | JCSS(2012) |
| d/mm | 正态 | 22 | 0.05 | JCSS(2012) |
| Jin/(μA·cm−2) | 正态 | 0 | 0.10 | 假定 |
| Jout/(μA·cm−2) | 正态 | 0.5 | 0.10 | 文献[4] |
4.1. 理论方法准确性验证
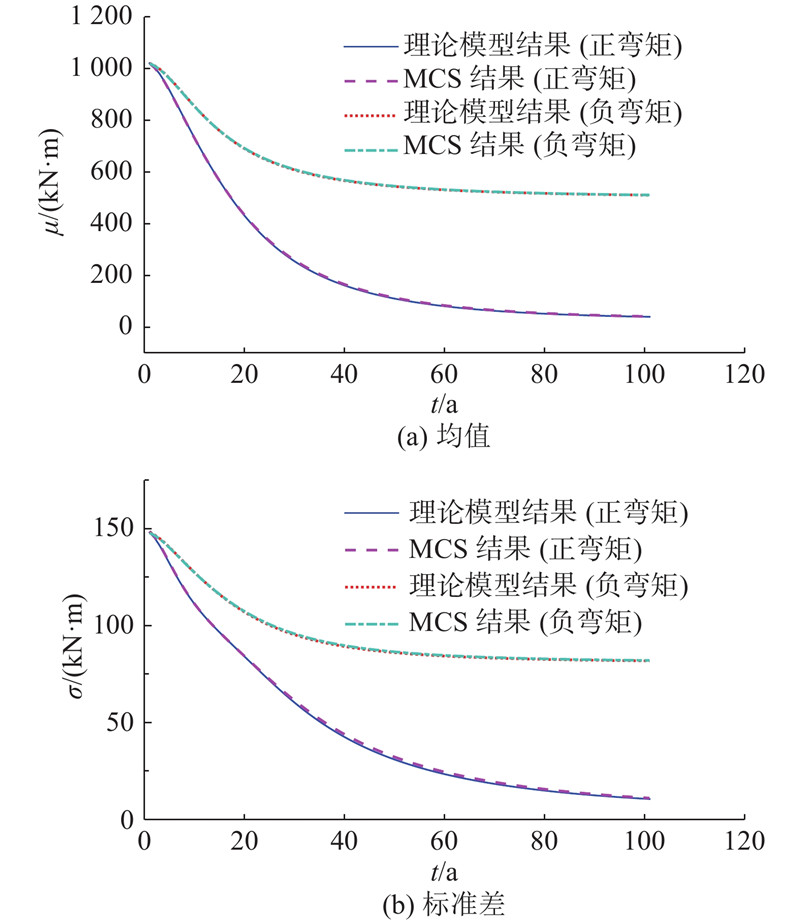
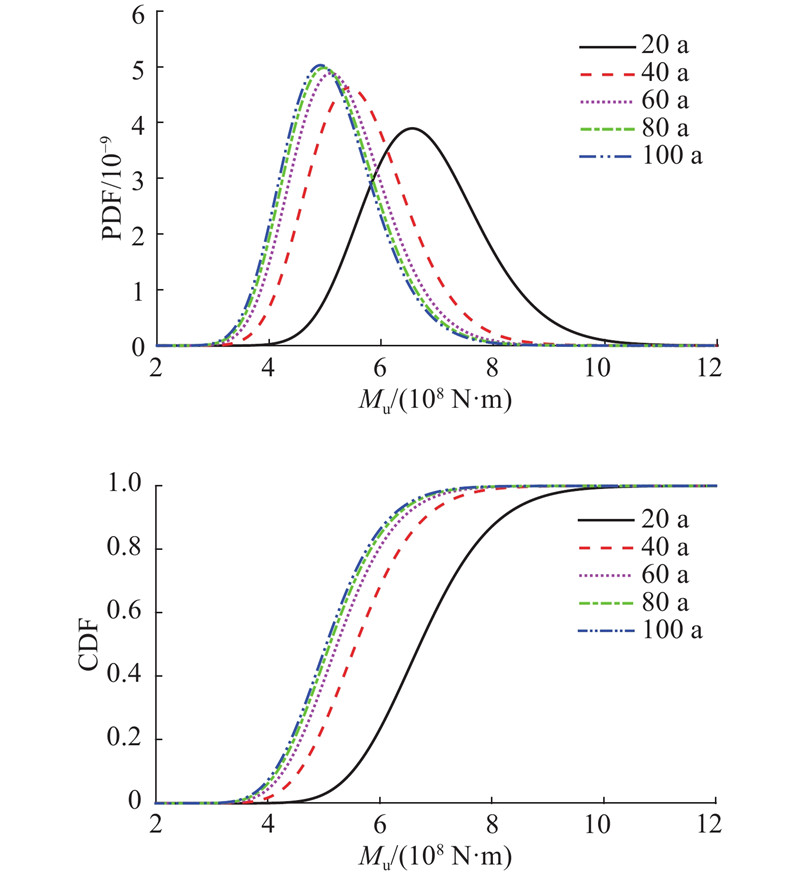
如图5所示为第2章建立的理论模型与1 000 000次MCS的衬砌抗弯承载力计算结果的对比. 图中,μ、σ分别为均值、标准差. 可以看出,理论模型结果与MCS方法的计算结果较一致,均值计算的最大误差为3.5%,标准差计算的最大误差为5.0%. 电脑配置为CPU CORE i5,Memory 16 GB;理论计算时长为115 s. MCS时长为9 400 s. 在理论计算过程中,内存占用为0.48 GB,MCS方法的内存占用为2.84 GB.
图 5
4.2. 衬砌劣化抗弯承载能力概率特征
图 6
图 6 抗弯承载能力频数直方图与概率曲线(正弯矩)
Fig.6 Frequency histogram and probability curve of flexural capacity (positive moment)
图 7
图 7 抗弯承载能力频数直方图与概率曲线(负弯矩)
Fig.7 Frequency histogram and probability curve of flexural capacity (negative moment)
图 8
图 8 抗弯承载能力统计特征(正弯矩)
Fig.8 Flexural capacity statistical characteristics (positive moment)
图 9
图 9 抗弯承载能力统计参数特征(负弯矩)
Fig.9 Flexural capacity statistical characteristics (negative moment)
4.3. 可靠度计算
图 10
图 11
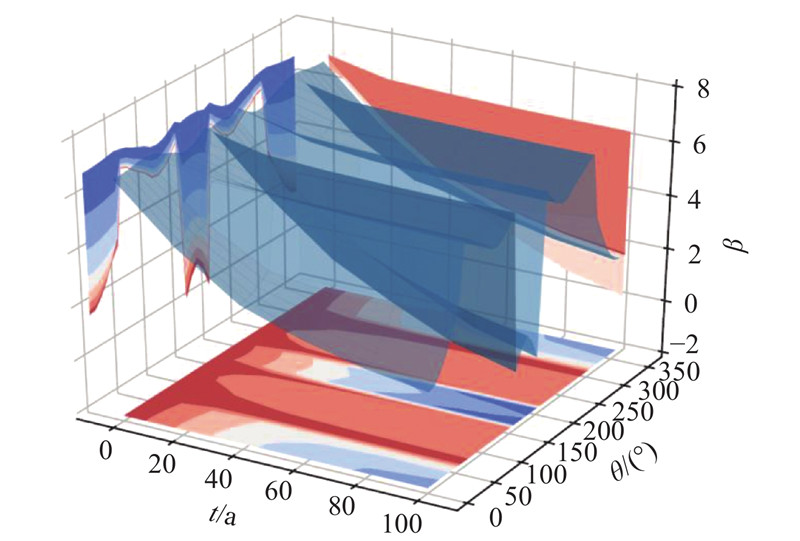
图 11 抗弯承载能力可靠度与时间以及角度三维曲面
Fig.11 Three-dimension surface of lining reliability index of flexural capacity with time and angle
由图10可以看出,衬砌自拱顶至拱肩范围内承受正弯矩,拱肩至拱脚范围内承受负弯矩,仰拱范围内承受正弯矩. 拱顶与仰拱的正弯矩较大,分别为23.5、42.7 kN·m. 最大负弯矩出现在拱脚处,为88.8 kN·m. 由图11中可靠度曲面在θ-o-β平面的投影可以看出,正弯矩作用区域与负弯矩作用区域的可靠指标有较大差异,负弯矩区域可靠度高于正弯矩区域. 负弯矩作用区域可靠指标最小值远高于3.7(《建筑可靠度统一标准》[34]中一级结构构件的目标可靠度指标参考值为3.7). 由三维曲面在t-o-β平面的投影可以看出,随着时间的变化衬砌的抗弯承载可靠度指标变化较大,在前20 a可靠度指标降低较为迅速,之后降低较为缓慢.
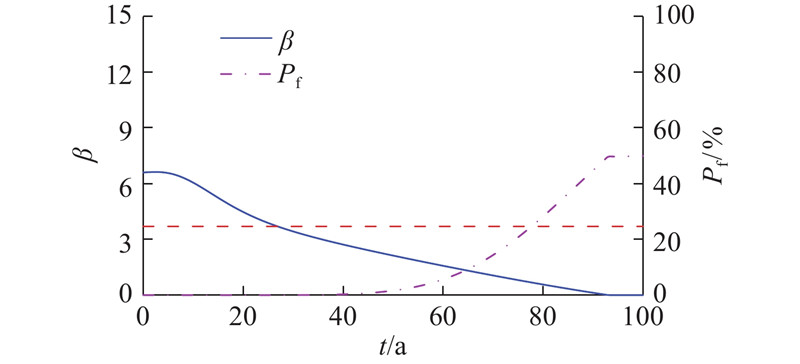
考虑最不利状况,拱顶向下160°处的可靠度指标与对应的失效概率随时间的变化关系如图12所示. 图中,Pf为失效概率可以看出,在衬砌钢筋发生锈蚀后不到30 a的时间内,其可靠度指标已不足3.7,对应失效概率已高于0.01%,由此可见,推后钢筋开始锈蚀的时间对保障隧道在服役期内满足目标可靠度具有重要意义.
图 12
图 12 160°处可靠度指标与失效概率
Fig.12 Reliability index and failure probability at 160 degree
5. 结 论
(1)随着时间的增长,抗弯承载力的均值和标准差均减小;
(2)当初始计算变量同时存在正态分布变量与对数正态分布变量时,抗弯承载力计算结果更服从对数正态分布;
(3)衬砌截面不同位置处的可靠度指标不同,在研究中应当注意最危险截面.
(4)研究考虑了隧道受地下水中氯离子侵蚀的抗弯承载特征. 其他腐蚀因素对衬砌可靠性影响也可以通过本研究框架实现.
(5)对弯矩正负不同区段须区别考虑拉压钢筋对应的锈蚀率.
(6)衬砌腐蚀电流密度与隧道环境温度、湿度等因素相关,接下来拟就这些因素展开研究.
参考文献
Northern line tunnel reconstruction at old street
[J].DOI:10.1680/tran.2002.153.1.1 [本文引用: 1]
Application of fiber-reinforced shotcrete in repair of tunnel linings in Hong Kong
[J].
Risk-cost optimised maintenance strategy for tunnel structures
[J].DOI:10.1016/j.tust.2017.06.008 [本文引用: 2]
An experimental study on durability of shield segments under load and chloride environment coupling effect
[J].DOI:10.1016/j.tust.2014.01.004
腐蚀离子环境中盾构隧道衬砌结构侵蚀劣化机理
[J].DOI:10.3969/j.issn.1001-7372.2017.08.014 [本文引用: 1]
Erosion degradation mechanism of shiled tunnel lining structure in corrosive ion environment
[J].DOI:10.3969/j.issn.1001-7372.2017.08.014 [本文引用: 1]
Mechanical performance of reinforced concrete and steel fiber-reinforced concrete precast tunnel lining segments: a case study
[J].
Mechanical behavior of quasi-rectangular segmental tunnel linings: first results from full-scale ring tests
[J].DOI:10.1016/j.tust.2017.09.019 [本文引用: 1]
The ultimate bearing capacity of rectangular tunnel lining assembled by composite segments: an experimental investigation
[J].
Ultimate load-carrying capacity of the longitudinal joints in segmental tunnel linings
[J].
内张钢圈加固盾构隧道结构承载能力的试验研究:整环加固法
[J].
Experimental study of ultimate bearing capacity of shiled tunnel reforced by full-ring steel plate
[J].
Behaviour of tunnel lining strengthened by textile-reinforced concrete
[J].DOI:10.1080/15732479.2015.1076009 [本文引用: 1]
盾构隧道钢纤维混凝土管片接头极限承载力试验
[J].DOI:10.3969/j.issn.1001-7372.2017.08.015 [本文引用: 1]
Experimental investigation on ultimate bearing capacity of steel fiber reinforced concrete segment joints in shield tunnels
[J].DOI:10.3969/j.issn.1001-7372.2017.08.015 [本文引用: 1]
Engineering failure analysis of corroded RC beams in flexure and shear
[J].DOI:10.1016/j.engfailanal.2017.12.015 [本文引用: 3]
Experimental investigation and numerical modeling of carbonation process in reinforced concrete structures part I: theoretical formulation
[J].DOI:10.1016/j.cemconres.2003.09.009 [本文引用: 2]
Experimental investigation and numerical modeling of carbonation process in reinforced concrete structures part II. practical applications
[J].
Effect of degree of corrosion on the properties of reinforcing steel bars
[J].DOI:10.1016/S0950-0618(01)00009-5 [本文引用: 1]
Corrosion cracking and bond strength modeling for corroded bars in reinforced concrete
[J].
Dynamic response analysis of stochastic truss structures under non-stationary random excitation using the random factor method
[J].DOI:10.1016/j.cma.2007.02.005 [本文引用: 1]
Probabilistic interval analysis for structures with uncertainty
[J].DOI:10.1016/j.strusafe.2010.01.002
Robust stability analysis of structures with uncertain parameters using mathematical programming approach
[J].DOI:10.1002/nme.4758
Time-variant random interval response of concrete-filled steel tubular composite curved structures
[J].DOI:10.1016/j.compositesb.2016.03.029
Uncertainty analysis of creep and shrinkage effects in long-span continuous rigid frame of sutong bridge
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000147
Probabilistic degradation modelling of circular tunnels assembled from segmental linings
[J].
基于Spreadsheet法的盾构衬砌截面可靠度分析
[J].
Reliability analysis of shield lining sections using Spreadsheet method
[J].
盾构隧道衬砌截面的承载能力功能函数
[J].DOI:10.3969/j.issn.1006-2106.2009.05.015 [本文引用: 1]
Functions for the bearing capacity of lining cross-section of shield tunnel
[J].DOI:10.3969/j.issn.1006-2106.2009.05.015 [本文引用: 1]
Influence of corrosion and cracking on bond behavior and strength of reinforced-concrete members
[J].
Structural assessment of corroded reinforced concrete beams: Modeling guidelines
[J].DOI:10.1061/(ASCE)0733-9445(2004)130:8(1214)
Severely corroded RC with cover cracking
[J].DOI:10.1061/(ASCE)ST.1943-541X.0000633
Effect of reinforcing steel area loss on flexural behavior of reinforced-concrete beams
[J].
锈蚀钢筋混凝土双筋矩形梁抗弯承载力分析
[J].
Analysis of the flexual bearing capacity of corroded reinforced concrete beams with double reinforced rectangular section
[J].