基于数据驱动的建模方法较适用且高效. 典型数据驱动方法的建模手段是首先获得具备空间特征的基函数. 如基于Karhunen-Loève(KL)变换[11]和基于奇异值分解(singular value decomposition, SVD)[12]的建模方法,经时空分离后获得空间基函数的主成分模型,然后采用神经网络[13]、支持向量机[14]以及模糊方法[15]、Wiener模型[16]等建立时序模型. Zhang等[17]基于主成分分析方法(principal component analysis, PCA)、混合自回归外生(autoregressive exogenous, ARX)和径向基函数(radial basis function, RBF)神经网络模型建立分布参数系统模型,取得了一定的效果. 这些方法实质上是线性降阶手段,并没有考虑系统的强非线性特性,因此只适用于线性或弱非线性系统. 近年来,非线性PCA方法[18]和时空支持向量机[19-21]被用于建立非线性的分布参数系统,取得了一定的效果. 对于强非线性的分布参数系统,基于局部线性嵌入(locally linear embedding, LLE)[22-24]算法的建模方法以数据局部线性关系来表征高维数据的非线性特性,因此具有更好的建模效果. 但是该方法不适用于局部非线性流形结构的系统,而且低维空间的非局部流形结构与局部流形结构可能重叠在一起,导致数据发生混乱,以至于无法完整保留数据的本质特征.
本研究提出基于低维约束嵌入的分布参数系统建模方法. 与传统建模方法不同,本研究通过非线性映射数据的方法,将数据的非线性关系问题转化为线性求解问题,采用流形学习方法,在保持数据局部流形结构的同时,约束数据非局部流形结构在低维嵌入的位置,避免数据产生混乱现象,从而完整地保留数据的本质特征,获得代表空间特征的基函数. 采用最小二乘支持向量机(least squares support vector machine, LS-SVM)建立系统的时序模型,通过时空整合重构完整的预测模型. 最后,通过对加热炉的热过程进行建模以验证所提出建模方法的有效性.
1. 问题描述
典型的分布参数系统可由以下偏微分方程描述:
复杂的边界条件以及初始条件分别为
式中:
根据式(1)~(3),分布参数系统的建模面临以下挑战:1)系统的输出状态具有时空耦合特性和无限维特性;2)非线性特性不仅存在于空间特征上,还存在于时间尺度方向上;3)系统状态受复杂边界条件、初始条件的影响;4)在系统中存在不可预知的因素.
根据时空分离理论,基于数据驱动的分布参数系统建模一般可以将输出分解为一系列无穷多个正交向量
在实际工业过程中,不可能设置无穷多个传感器,因此通常用一个有限维的主成分模型替代原来的系统:
目前存在的数据建模方法,如KL变换、SVD方法、LLE算法等在处理强非线性问题上均有不足. 基于KL变换和SVD方法的分布参数系统的建模过程本质上是线性处理方法,只适用于线性或弱非线性系统;基于LLE算法的建模缺乏对局部数据的非线性联系以及非局部结构的约束限制的考虑. 针对以上问题,提出新的建模方法,对于分布参数系统的模型预测控制,具有重大意义.
2. 建模策略
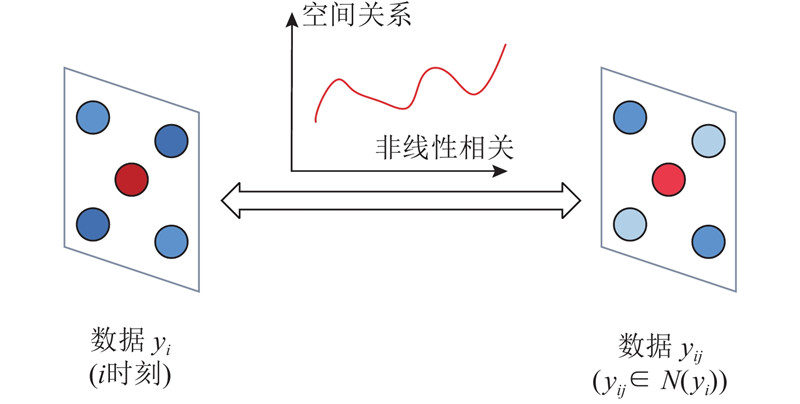
由于复杂的能量交换问题,如热辐射、化学反应过程等,分布参数系统具有强非线性特性,具体表现为每一时刻的数据与其邻域数据之间存在非线性联系,如图1所示. 图中,N
图 1
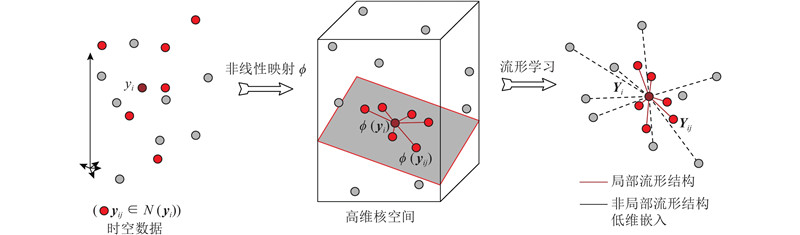
传统的流形学习方法LLE算法只考虑数据的局部流形结构,未对数据的非局部结构进行约束,导致数据的非局部结构与局部结构在低维空间里的位置可能产生重叠. 为了克服这种现象,所提出的低维约束嵌入方法,在从高维核空间保留其局部流形结构到低维嵌入空间的同时,约束其非局部流形结构,以区分数据点的局部流形结构与非局部流形结构. 通过离散数据点的非局部流形结构,分离不同数据点的局部流形结构,避免在不同数据点间的局部流形结构可能发生的重叠现象,使数据的本质更全面地保留在低维空间中,如图2所示.
图 2
图 2 低维约束嵌入建模策略的空间基函数学习过程
Fig.2 Learning process for spatial basis functions of low-dimensional constrained embedding modeling strategy
在确定空间基函数之后,须确定低阶的时序模型. 分布参数系统的强非线性不仅体现在空间特征上,还体现在时间尺度上,所以要求时间系数的模型具有良好的非线性逼近能力. LS-SVM能逼近任意非线性系统,将非线性问题转化为线性问题,对于建立非线性的时间模型具有独特优势.
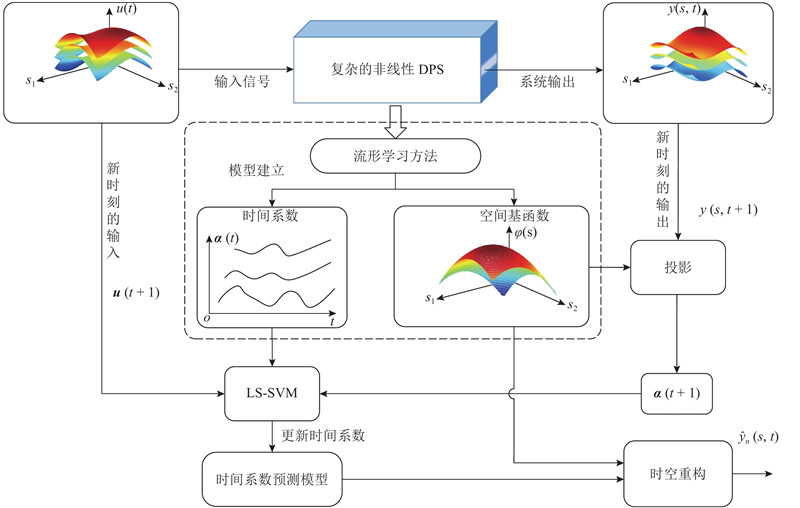
基于时空模型的分解整合过程,提出基于低维约束嵌入的时空建模方法,总建模框架如图3所示,关键点如下:1)通过非线性投影函数,在高维空间内根据局部流形结构约束以及非局部流形结构约束,获取数据的低维嵌入,通过数据组合得到能代表分布参数系统强非线性的空间基函数
图 3
图 3 低维约束嵌入方法的时空建模框架
Fig.3 Spatiotemporal modeling framework of low-dimensional constrained embedding method
基于数据驱动的低维约束嵌入建模方法,既保持了数据局部流形结构的非线性联系,还约束了低维空间下的局部流形结构与非局部流形结构,因此该方法能保留数据的全局流形结构,有效地建立强非线性的分布参数系统模型.
2.1. 空间特征学习
将原始的时空数据通过非线性映射函数
式中:
通过KNN方法计算
式中:
式中:
设拉格朗日乘子为
式中,
可解出:
映射前后的高维
可以进行如下化简:
式中:
式(14)的优化方程保证了从高维核空间到低维嵌入转化时的数据局部流形结构. 基于非局部流形结构的约束,通过最大化数据与其非局部结构之间的距离来实现,建立以下约束方程:
定义
式(16)可以改写为:
定义
化简式(16),可以得到:
基于目标优化方程式(15)、(20),构建局部以及非局部约束的总优化方程:
进行求导可得:
令其导数为零:
考虑了分布参数系统数据结构中局部与非局部关系的优化目标(式(22)),可以转化为求解式(24)的广义特征值特征向量问题,即低维输出
维度n可通过以下公式确定:
式中:
通过低维嵌入与时空数据的线性重构,可以得到空间基函数:
式中:
2.2. 时序模型建立
在获取空间基函数之后,时间系数模型
式中:
采取LS-SVM训练数据
式中:
其中,C为惩罚因子,e为建模误差.
根据分布参数系统性质,LS-SVM的模型输出
式中:
建立拉格朗日方程:
式中:
其中,核函数矩阵表达式为
通过求解式(32),求出
通过整合空间基函数(式(26))和时间系数模型(式(34)),得到最终的可以代表强非线性分布参数系统的时空预测模型:
3. 实验验证
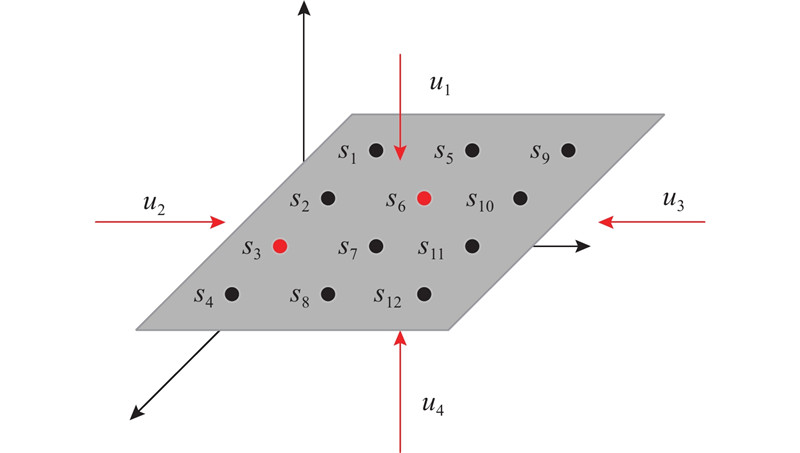
图 4
图 5
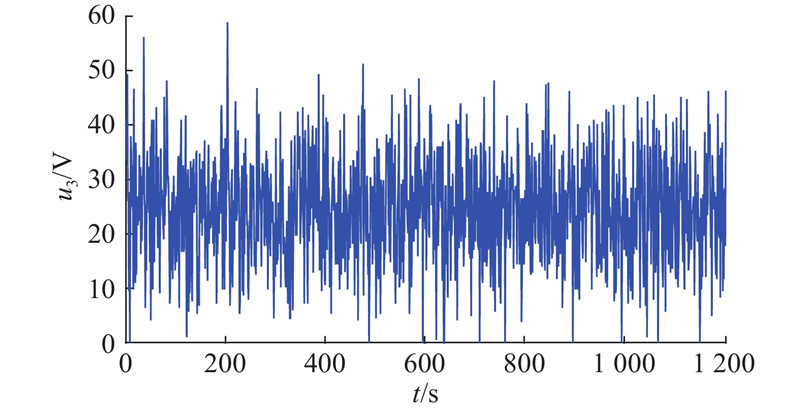
以随机信号作为系统输入,采样间隔为30 s,共采集来自12个传感器的1 204组实验数据. 如图6所示为控制信号
图 6
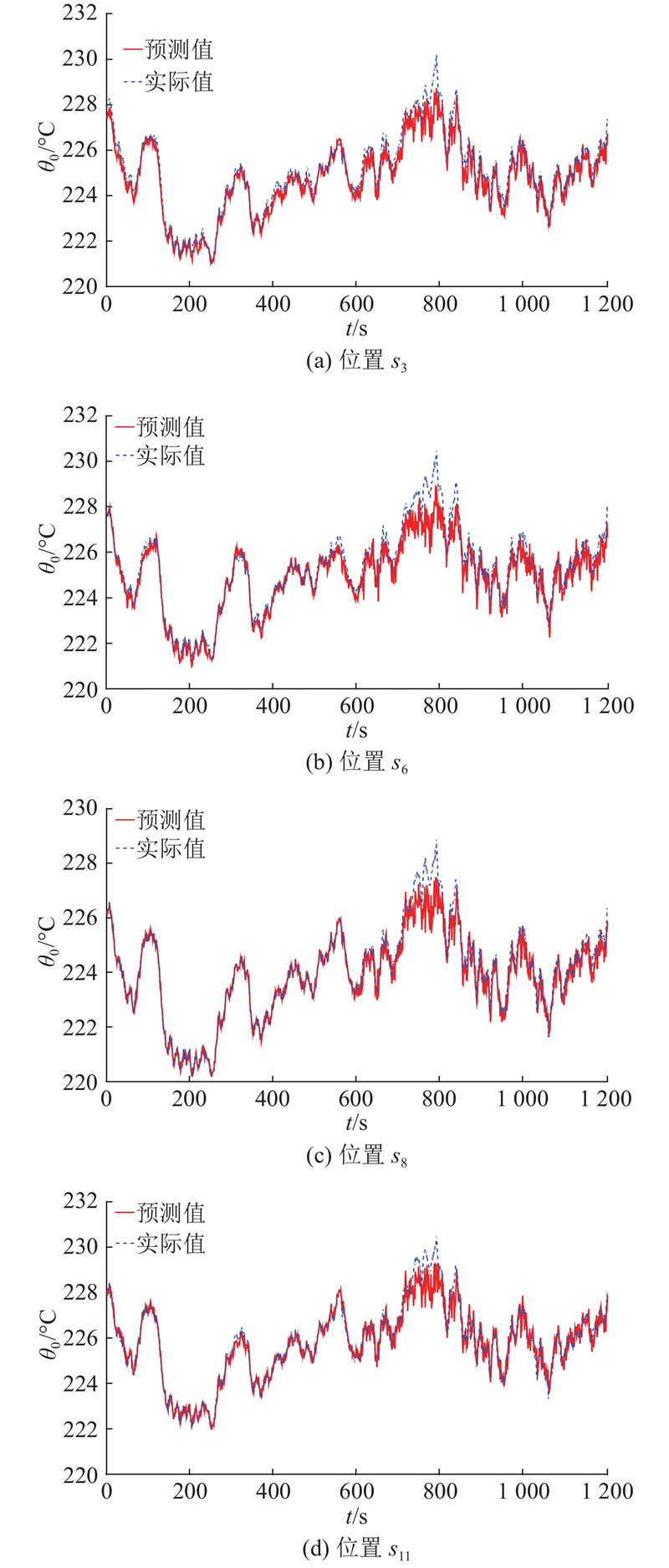
图 7
图 7 不同位置处模型预测值与真实值的温度对比
Fig.7 Temperature contrast between model predictive value and real value in different positions
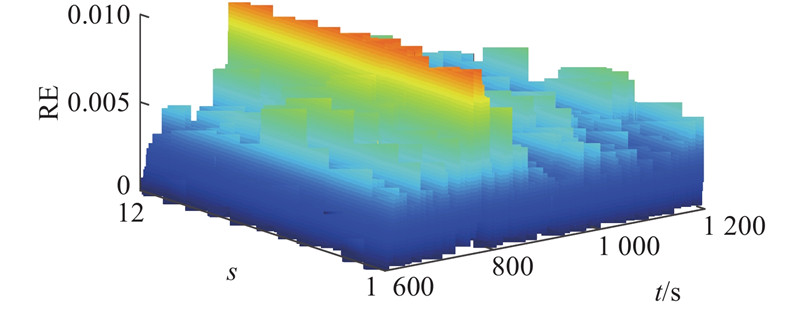
图 8
图 8 模型预测与真实值的相对误差
Fig.8 Relative error between model predictive and real values
为了更好地验证模型性能,采取基于KL变换和LLE算法的建模方法作为对比. 对于以上的建模方法,在获取空间基函数后,也采用LS-SVM进行时序动态建模,以均方根误差(root mean square error,RMSE)作为模型性能指标:
式中:N、L分别为矩阵
表 1 3种方法下模型的均方根误差
Tab.1
| 建模方法 | 建模误差 | 测试误差 |
| KL | 1.177 7 | 1.267 5 |
| LLE | 0.276 1 | 0.736 1 |
| 本研究方法 | 0.114 2 | 0.584 0 |
表 2 3种方法下未训练点的均方根误差
Tab.2
| 建模方法 | RMSE | |
| s3 | s6 | |
| KL | 2.361 4 | 0.744 6 |
| LLE | 0.631 9 | 0.643 7 |
| 本研究方法 | 0.457 1 | 0.562 8 |
4. 结 语
基于分布参数系统数据局部与非局部的优化问题,提出基于低维约束嵌入的建模方法. 考虑到空间特征的非线性,利用非线性映射和流形学习方法,保持空间特征的局部非线性与全局非线性联系;基于对数据非局部结构的优化,通过最大化样本与其非局部结构的距离,约束其在低维空间的位置,避免不同数据局部流形结构之间发生混乱现象,获得更切合于分布参数系统的空间基函数;采用LS-SVM建立时序方向上的非线性动态行为,通过时空整合完成强非线性分布参数系统的建模.
针对空间特征的非线性问题,传统建模方法存在一定的局限性. 低维约束嵌入方法除了考虑上述的因素,还优化数据非局部结构,相较于传统建模方法,从理论上具有更强的建模能力. 实验结果表明,所提出的方法能有效建立强非线性分布参数系统的模型,具备较好的模型预测性能. 与基于KL变换和LLE算法的建模方法相比,所提出的建模方法精度更高、预测更准确. 所提出的方法认为采集到的所有数据均有效,并未考虑到噪声的处理,但实际上,分布参数系统中噪声是普遍存在的. 因此,分布参数系统中噪声的预处理,是未来重要的研究方向之一.
参考文献
Data-driven quality monitoring techniques for distributed parameter systems with application to hot-rolled strip laminar cooling process
[J].DOI:10.1109/ACCESS.2018.2812919 [本文引用: 1]
Distributed parameter system identification using finite element differential neural networks
[J].DOI:10.1016/j.asoc.2016.01.004 [本文引用: 1]
Thermal modeling and validation of temperature distributions in aprismatic lithium-ion battery at different discharge rates and varying boundary conditions
[J].DOI:10.1016/j.applthermaleng.2015.11.019 [本文引用: 1]
Exponential pointwise stabilization of semi-linear parabolic distributed parameter systems via the Takagi-Sugeno fuzzy PDE model
[J].
Feedback optimal control of distributed parameter systems by using finite-dimensional approximation schemes
[J].DOI:10.1109/TNNLS.2012.2192748 [本文引用: 1]
Spectral-approximation-based intelligent modeling for distributed thermal processes
[J].DOI:10.1109/TCST.2005.847329 [本文引用: 1]
Green's-function approach to linear response in solids
[J].DOI:10.1103/PhysRevLett.58.1861 [本文引用: 1]
Data-driven H∞ infinity control for nonlinear distributed parameter systems
[J].DOI:10.1109/TNNLS.2015.2461023 [本文引用: 1]
Improved empirical eigenfunctions based model reduction for nonlinear distributed parameter systems
[J].DOI:10.1021/ie301179e [本文引用: 1]
The use of the Karhunen-Loève decomposition for the modeling of distributed parameter systems
[J].DOI:10.1016/0009-2509(95)00230-8 [本文引用: 1]
Identification and control of distributed parameter systems by means of the singular value decomposition
[J].DOI:10.1016/0009-2509(95)00017-Y [本文引用: 1]
Neural network based boundary control of a vibrating string system with input deadzone
[J].DOI:10.1016/j.neucom.2017.09.050 [本文引用: 1]
支持向量机的时间序列回归与预测
[J].DOI:10.3969/j.issn.1004-731X.2006.07.014 [本文引用: 1]
Time series regression and prediction of support vector machine
[J].DOI:10.3969/j.issn.1004-731X.2006.07.014 [本文引用: 1]
Mixed H2/H∞ fuzzy proportional-spatial integral control design for a class of nonlinear distributed parameter systems
[J].DOI:10.1016/j.fss.2016.01.004 [本文引用: 1]
A Karhunen-Loève decomposition based Wiener modeling approach for nonlinear distributed parameter processes
[J].DOI:10.1021/ie0710869 [本文引用: 1]
Decoupled ARX and RBF neural network modeling using PCA and GA optimization for nonlinear distributed parameter systems
[J].DOI:10.1109/TNNLS.2016.2631481 [本文引用: 1]
Nonlinear dimension reduction based neural modeling for distributed parameter processes
[J].DOI:10.1016/j.ces.2009.06.053 [本文引用: 1]
Robust spatiotemporal LS-SVM modeling for nonlinear distributed parameter system with disturbance
[J].
A novel spatiotemporal LS-SVM method for complex distributed parameter systems with applications to curing thermal process
[J].
Online spatiotemporal LS-SVM modeling approach for time-vary distributed parameter processes
[J].DOI:10.1021/acs.iecr.7b00984 [本文引用: 1]
Nonlinear dimensionality reduction by locally linear embedding
[J].
Nonlocal structure constrained neighborhood preserving embedding model and its application for fault detection
[J].
Local properties embedding based nonlinear spatiotemporal modeling for Lithiumion battery thermal process
[J].DOI:10.1109/TIE.2018.2818645 [本文引用: 1]