由于自然风的脉动分量,大跨空间结构在风荷载作用下构件所受的应力会不断变化,从而造成疲劳破坏. 现行规范对结构的疲劳损伤考虑不全面,有必要研究大跨空间结构在风荷载下的疲劳性能,分析并确定最容易发生疲劳破坏的热点区域.
常用的疲劳寿命计算方法有时域法,以Matsuiski等[1]提出的雨流法应用最广. 雨流法的计算结果精确,但计算量大,因此许多学者提出了频域内疲劳损伤计算方法. Huang等[2-4]提出多种等效应力法计算公式;Crandall等[5-6]分别研究窄带过程和宽带过程的疲劳损伤计算方法. 王之宏等[7-9]分别通过等效应力法、雨流法和等效窄带法对桅杆结构进行风振疲劳分析,王世村等[10-11]改进了等效窄带法并对输电塔结构风振疲劳进行计算. Holmes[12]提出考虑风速风向分布的高耸结构疲劳寿命年限估算的简化计算方法. Repetto等[13-16]等结合风速风向的分布,估算了高耸结构疲劳寿命. Gu等[17-18]分别对杨浦大桥和青马大桥的风振疲劳损伤进行评估. 王钦华等[19]分析风速风向联合分布函数对结构风振疲劳的影响. 张春涛等[20]建立风向风速联合分布模型,提出输电塔的风致疲劳计算方法. 楼文娟等[21]构建风速风向联合分布模型,验证了模型的有效性.
本文基于某煤棚网架表面多点同步风洞测压试验结果,开展结构有限元风振时程分析,得到大跨干煤棚结构的风致动力响应;结合Miner疲劳线性累积损伤理论,采用雨流法、等效应力法、等效窄带法和等效宽带法共4种方法,计算煤棚网架结构构件的风振疲劳损伤值,比较各方法的计算结果;结合煤棚所在地的风速气象资料,建立风速风向联合概率密度函数,计算大跨干煤棚在考虑实际风速风向分布影响下的年均疲劳损伤,根据高强螺栓应力经验公式估算干煤棚网架螺栓球节点的风振疲劳损伤.
1. 疲劳分析方法
1.1. 疲劳模型
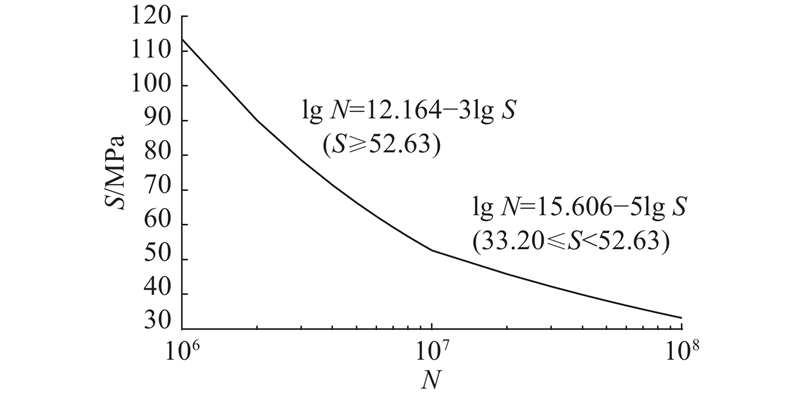
图 1
图 1 挪威规范中适用空间网壳结构形式的S-N曲线
Fig.1 S-N curve for long-span lattice structure in Det Noeske Veritas Recommended Practice
式中:N为发生疲劳破坏的应力循环次数,m和K为材料疲劳参数.
由于构件所受的应力不是恒定不变的,不能简单地利用式(1)计算疲劳损伤. 为了进行变幅疲劳计算,需要引入疲劳累计损伤理论. 所用的疲劳损伤理论为Miner线性损伤法则[26],公式如下:
式中:D为累积损伤值,Ni为第i个应力幅对应的发生疲劳破坏的应力循环次数,ni为第i个应力幅出现的次数.
虽然Miner法则忽略了应力顺序的影响,但它对疲劳寿命的影响不大. 此外,由于疲劳损伤受平均应力的影响较大,可以用Goodman法则来计算等效应力幅,即
式中:Sm为平均应力,St为材料的抗拉强度,Sa0、Sa为零平均应力及非零平均应力的应力幅.
1.2. 雨流法
雨流计数法又可以称为“塔顶法”[1],在结构疲劳寿命计算中运用非常广泛. 它可以对封闭的应力-应变迟滞回曲线进行逐个计数,从而得到应力循环幅值分布.
由于应力时程数据较复杂,手动计算极耗时,参照董乐义等[27]提出的四点判断法,编写了二阶段雨流法计算程序. 在统计所有应力幅后,利用Goodman法则修正平均应力的影响;将修正后的应力幅代入S-N曲线,可得各个应力幅对应的疲劳损伤;将各应力幅的疲劳损伤线性叠加,可得该段应力时程所产生的疲劳损伤.
1.3. 频域法
由于雨流法时域方法的计算量巨大,且有一定局限性,国内外学者提出多种频域内疲劳损伤的计算方法,如等效应力法、等效窄带法、等效宽带法等.
1.3.1. 等效应力法
对于随机应力过程,可以定义等效应力幅Sh[4]为
式中:p(S)为应力幅分布的概率密度函数,m为材料疲劳参数.
根据式(4),Chaudhury等[3]提出半经验计算公式:
式中:
利用式(5)计算得到等效应力后,经Goodman法则修正,再代入S-N曲线,可得该等效应力对应的疲劳损伤.
1.3.2. 等效窄带法
对于窄带高斯随机过程,T时间段内的累积疲劳损伤[5]可以表示为
式中:m和K为材料疲劳参数;
其中M2为应力谱2阶矩,M0为应力谱0阶矩.
式(9)是疲劳损伤计算中的一个常用公式,但有它自身的局限性,式(9)一般适用于钢结构在弹性阶段内的高周疲劳寿命[5].
Wirsching[6]的研究指出,宽带应力过程的累积疲劳损伤可以用窄带过程的累积疲劳损伤乘以一个等效系数
Wirsching通过大量计算,利用最小二乘法,统计给出a、b的计算式如下:
式中:m为材料疲劳参数.
1.3.3. 等效宽带法
Petrucci等[28]提出适用于宽带应力过程的频域疲劳寿命计算公式:
式中:Dr为疲劳损伤度,当Dr=1时结构发生疲劳破坏;m、K为材料疲劳参数;M2和M4为应力谱2阶矩和4阶矩;
2. 风洞试验及结构风振时程分析
2.1. 风洞试验
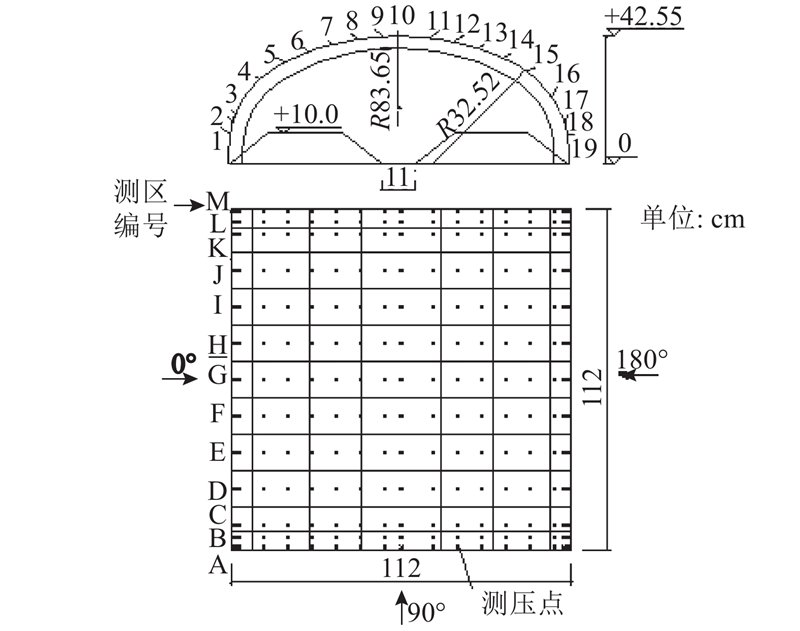
以位于浙江温州苍南地区的某干煤棚为例,该干煤棚风洞试验在浙江大学ZD-1边界层风洞中开展. 采用工程塑料制作干煤棚刚性模型,如图2所示. 模型缩尺比为1∶100,模型总高度约为0.43 m,纵向长1.12 m,跨度方向长1.12 m. 风洞试验风场类型A类,风剖指数为0.12. 模型表面布置了247对同步测量的内、外压测点,测点布置如图3所示. 风洞试验风向角为0°~360°,间隔为10°,共36个风向角,脉动风压测量采样频率为625 Hz,取30 s采样时长,风洞测试风速约为13 m/s. 该干煤棚位于我国东南沿海台风高发区,根据相关资料100年一遇的基本风压取为1.32 kPa,在原型高度43 m处100 年重现期10 min平均设计风速为54.75 m/s. 可以确定该次风洞试验的风速缩尺比为1∶4.17,时间缩尺比为1∶24. 对应原型的采样时间间隔为0.038 4 s,脉动风压数据时长取600 s. 风洞内模拟风场的平均风速、湍流度剖面及脉动风速功率谱如图4所示.
图 2
图 3
图 4
2.2. 干煤棚结构风振分析
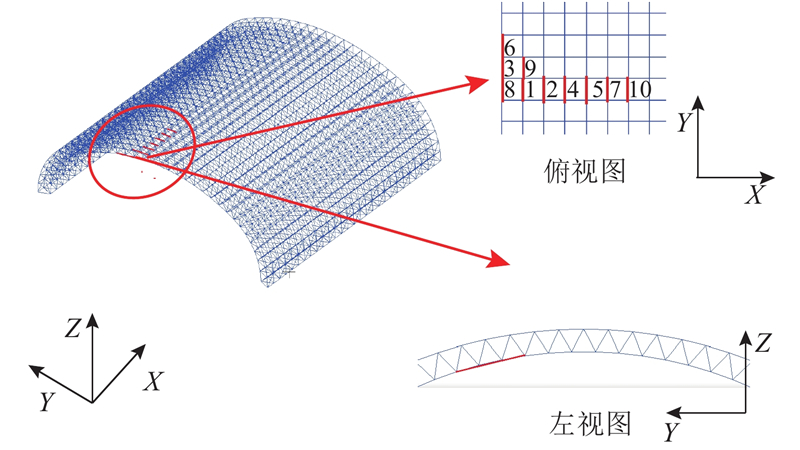
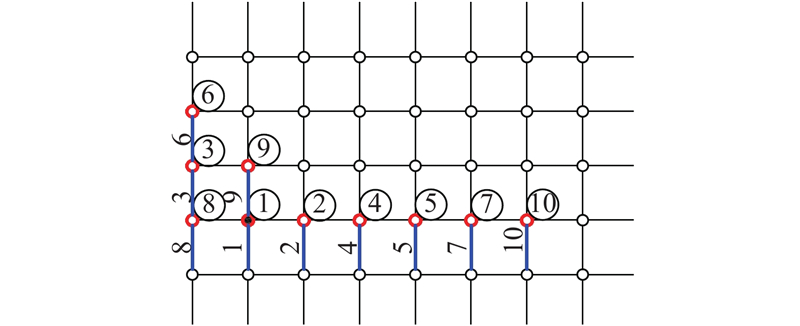
建立苍南干煤棚网架的有限元模型,如图5所示,网架上、下弦杆和腹杆均选用圆形薄壁钢管. 弦杆截面尺寸在跨中位置选用ϕ140×4、ϕ159×6,在越接近两侧的位置选用较大的截面ϕ180×8、ϕ219×10;腹杆的截面尺寸主要为ϕ88.5×4和ϕ114×4. 材料均为Q235钢,弹性模量为206 GPa,密度为7 850 kg/m3,采用桁架单元模拟弦杆及腹杆.
图 5
图 5 干煤棚网架有限元模型及60°风向角下关键杆件位置图
Fig.5 FEM model and positions of key members under 60°wind
随机风荷载作用下的大跨干煤棚结构动力响应可以通过求解多自由度体系动力微分方程来获得:
式中:
式中:
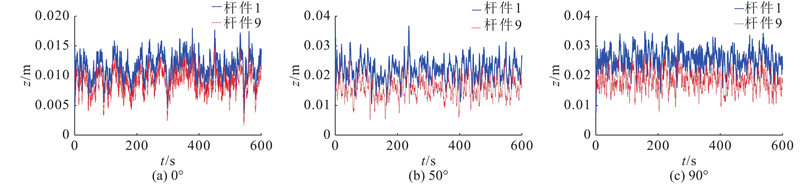
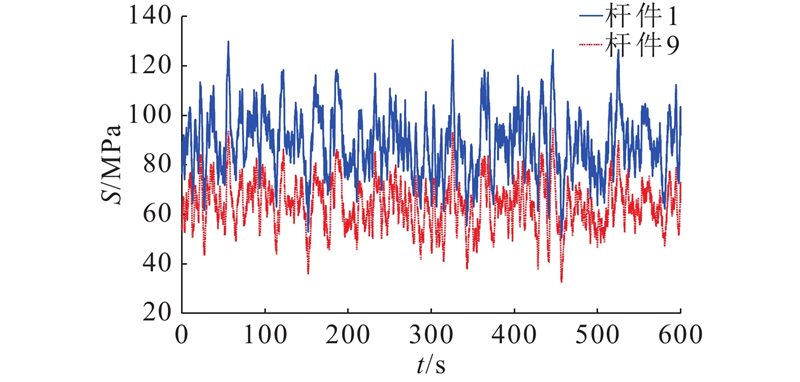
利用刚性模型测压试验获得的多点同步风压时程数据,在有限元模型中施加多点同步风力时程,开展时域内风振分析,得到干煤棚结构上各节点的位移、加速度响应. 以干煤棚端跨跨中附近位置杆件1和杆件9为例(见图5),图6、7给出2根杆件在0°、50°和90° 3个风向角下的Y方向(跨向)和Z方向(竖向)的位移时程结果,由于3个风向角下X向位移均很小,未列出X向位移时程. 从图6可以看出,杆件1上节点在0°、50°和90° 3个风向角下的Y向平均位移分别为0.4、37.8及1.2 mm,脉动位移分别为1.9、4.3及4.0 mm,可见50°风向下干煤棚Y向位移显著大于0°和90° 2个风向下的位移;杆件1上节点在3个风向角下的Z向平均位移分别为11.4、21.7及25.4 mm,脉动位移分别为2.0、3.6及3.4 mm,50°风向和90°风向下干煤棚的竖向振动较明显. 综上所述,0°风向下的干煤棚端跨位移均较小;90°风向下干煤棚端跨在竖向振动较显著;50°等斜风向角下干煤棚在跨向和竖向的风致位移均较大,有较显著的风振效应.
图 6
图 6 杆件1和杆件9上节点Y向位移时程图
Fig.6 Displacement time history results of member 1 and member 9 at Y direction
图 7
图 7 杆件1和杆件9上节点Z向位移时程图
Fig.7 Displacement time history results of member 1 and member 9 at Z direction
3. 疲劳损伤的计算结果
3.1. 雨流法
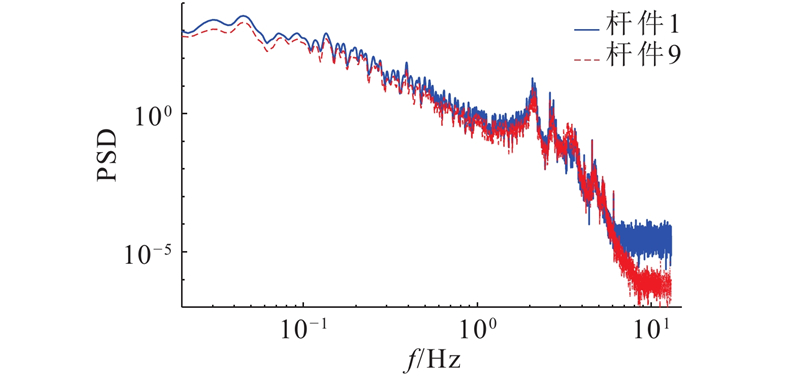
在风荷载作用下,大跨干煤棚中各个构件的受力形式和大小区别较大,风振疲劳一般出现在交替拉应力较大的杆件中. 在50°风向角下,干煤棚端跨杆件受到较大的交替拉应力. 为了对比起见,选取端跨杆件1和杆件9(见图5)作为关键杆件,通过时域内风振计算可以获得应力时程数据,根据疲劳理论可以进一步计算累积疲劳损伤. 杆件1和杆件9的应力时程图与功率谱分别如图8、9所示,计算得到功率谱的带宽参数分别为
图 8
图 9
图 9 关键杆件1和杆件9的应力功率谱图
Fig.9 Power spectral density of stress for two key members
图 10
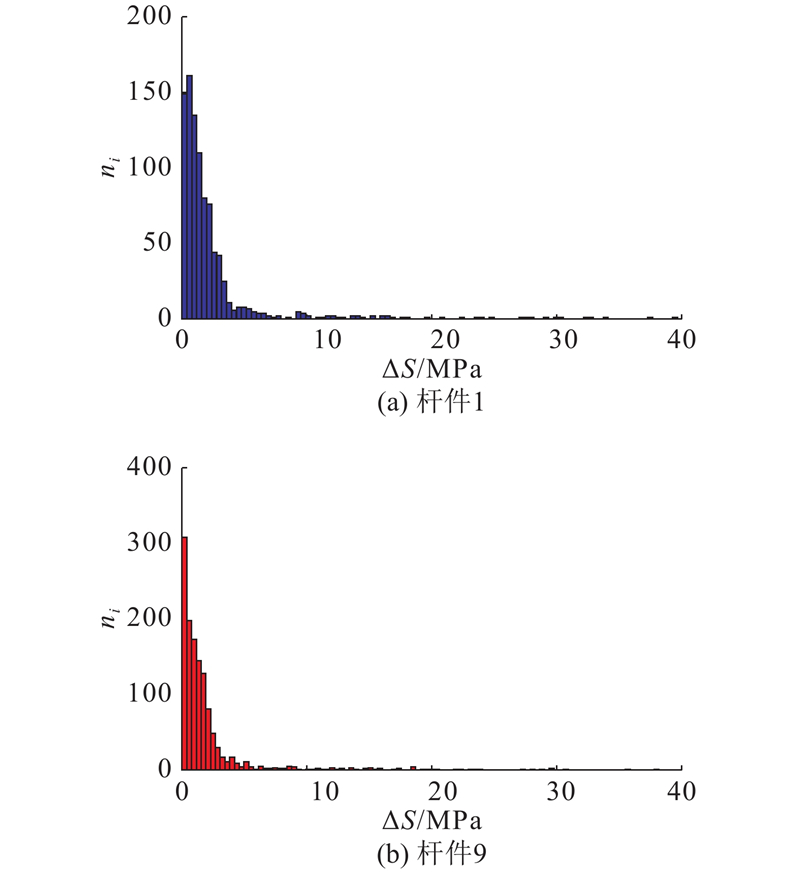
图 10 关键杆件应力幅值分布图
Fig.10 Probability distribution of stress amplitudes for two key members
同理可以计算各风向角下干煤棚各杆件的应力幅值,选取应力幅最大的10根杆件,依据Miner疲劳线性累积损伤理论,按照式(2)计算得到各杆件在600 s强风振下的累积疲劳损伤值,结果如表1所示. 表中,θs为风洞试验模拟得到的风向角.
表 1 各风向角下应力幅最大的10根杆件疲劳损伤
Tab.1
| 10−8 | ||||||||||
| θs/(°) | 杆件1 | 杆件2 | 杆件3 | 杆件4 | 杆件5 | 杆件6 | 杆件7 | 杆件8 | 杆件9 | 杆件10 |
| 0 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| 10 | 0.72 | 0.57 | 0.56 | 0.42 | 0.23 | 0.19 | 0.16 | 0.13 | 0.07 | 0.03 |
| 20 | 6.54 | 5.72 | 5.04 | 4.77 | 4.13 | 2.63 | 1.60 | 1.45 | 1.17 | 0.89 |
| 30 | 12.48 | 11.45 | 10.09 | 9.30 | 9.05 | 6.30 | 5.11 | 3.31 | 3.07 | 2.72 |
| 40 | 27.28 | 25.82 | 24.02 | 21.73 | 21.60 | 15.95 | 14.74 | 13.56 | 12.51 | 11.06 |
| 50 | 30.44 | 29.19 | 17.23 | 15.05 | 12.66 | 8.61 | 6.50 | 6.46 | 5.14 | 4.36 |
| 60 | 45.67 | 39.23 | 33.83 | 33.06 | 27.57 | 18.70 | 15.57 | 15.40 | 14.84 | 11.26 |
| 70 | 12.52 | 10.77 | 10.29 | 8.72 | 7.43 | 5.16 | 4.75 | 4.00 | 2.58 | 1.99 |
| 80 | 1.49 | 1.09 | 1.02 | 0.71 | 0.52 | 0.29 | 0.21 | 0.15 | 0.13 | 0.13 |
| 90 | 0.75 | 0.52 | 0.51 | 0.29 | 0.22 | 0.22 | 0.17 | 0.14 | 0.03 | 0.03 |
| 120 | 22.07 | 18.28 | 16.02 | 14.24 | 13.10 | 8.72 | 6.84 | 6.72 | 6.58 | 4.23 |
| 140 | 33.97 | 31.06 | 27.23 | 24.94 | 23.04 | 17.66 | 14.08 | 13.50 | 8.52 | 8.51 |
| 180 | 0.07 | 0.07 | 0.06 | 0.05 | 0.05 | 0.04 | 0.02 | 0.02 | 0.02 | 0.01 |
| 200 | 8.65 | 7.30 | 6.28 | 5.65 | 5.24 | 3.47 | 2.45 | 2.27 | 2.19 | 1.05 |
| 220 | 43.79 | 41.30 | 37.49 | 33.55 | 30.77 | 23.89 | 19.67 | 17.51 | 14.17 | 14.09 |
| 270 | 0.51 | 0.36 | 0.27 | 0.22 | 0.22 | 0.17 | 0.15 | 0.13 | 0.12 | 0.11 |
| 310 | 23.75 | 21.13 | 18.57 | 16.81 | 16.01 | 11.27 | 9.66 | 8.92 | 8.00 | 5.36 |
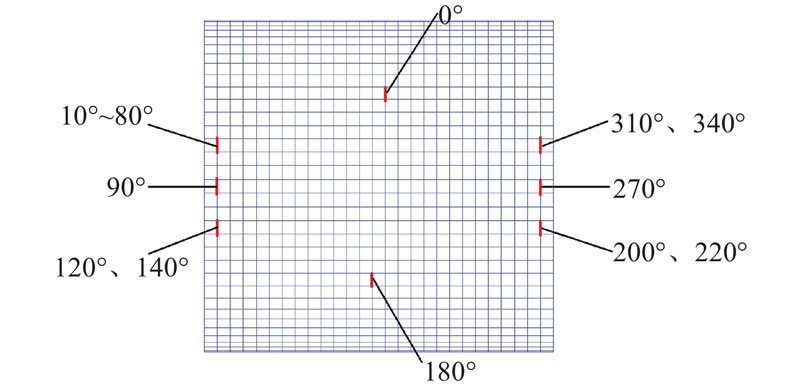
从表1可以看出,各风向角下煤棚各杆件的疲劳损伤值数量级大多为10−9~10−7,最大的疲劳损伤值为4.57×10−7. 根据计算结果可以发现,不同风向角对疲劳损伤的影响很大:由于0°、90°风向角下的构件受力普遍较小,产生的疲劳损伤小,基本不会发生疲劳破坏;根据2.2节的风振分析结果可知,干煤棚在40°、50°和60°等斜风向角下,具有更显著的风振效应,即动力放大作用,关键杆件的风致应力水平更高,疲劳损伤更大. 各风向角下疲劳损伤最大的杆件如图11所示,所有杆件都为下弦杆. 从图11可以看出,斜风向角下,跨中靠近来流方向的第2根下弦杆最容易发生破坏,0°和180°风向角下,迎风面中部1/4跨处下弦杆最容易发生破坏.
图 11
图 11 各风向角下疲劳损伤最大杆件位置示意图(下弦)
Fig.11 Locations of members of maximum fatigue damage at different wind angles (lower chords)
3.2. 频域法
对于引起疲劳损伤较大的50°风向角工况,开展相应的频域内疲劳损伤计算. 表2给出50°风向角下3种频域计算方法与雨流法的疲劳损伤计算结果对比. 表中,D为累计疲劳损伤,w为频域法计算结果与雨流法计算结果的相对误差. 其中等效应力法采用式(5),即Chaudhury&Dover公式计算. 从表2可知,3种频域法的结果除个别数据外,均比雨流法大,计算结果偏于安全;在计算精度方面,等效宽带法与雨流法相比,除杆件8的误差达到40%外,其余杆件的相对误差约为20%,较精确,杆件7的误差最小,仅1.87%;等效窄带法的相对误差约为30%,略差于等效宽带法;等效应力法的相对误差最大,最大偏差超过50%. 由于该干煤棚结构的典型风致应力谱(见图9)具有较大的带宽参数,说明对应的风致应力时程为一宽带随机过程样本,频域法中的等效宽带法总体上更适合该类结构的风致疲劳快速评估.
表 2 50°风向角下10根关键杆件疲劳损伤计算结果对比
Tab.2
| 杆件序号 | D/10−8 | w/% | ||||||
| 雨流法 | 等效应力法 | 等效窄带法 | 等效宽带法 | 等效应力法 | 等效窄带法 | 等效宽带法 | ||
| 1 | 30.44 | 46.55 | 38.91 | 32.65 | 52.92 | 27.83 | 7.26 | |
| 2 | 29.19 | 42.12 | 35.79 | 32.89 | 44.30 | 22.62 | 12.70 | |
| 3 | 17.23 | 23.39 | 21.06 | 20.74 | 35.75 | 22.20 | 20.37 | |
| 4 | 15.05 | 22.25 | 18.02 | 13.19 | 47.89 | 19.76 | −12.37 | |
| 5 | 12.66 | 15.87 | 15.32 | 15.97 | 25.33 | 21.01 | 26.10 | |
| 6 | 8.61 | 9.94 | 11.05 | 11.05 | 15.45 | 28.34 | 28.34 | |
| 7 | 6.50 | 9.82 | 9.08 | 6.63 | 51.05 | 39.66 | 1.87 | |
| 8 | 6.46 | 6.87 | 8.34 | 9.06 | 6.38 | 29.12 | 40.17 | |
| 9 | 5.14 | 6.41 | 6.80 | 5.59 | 24.72 | 32.31 | 8.79 | |
| 10 | 4.36 | 5.17 | 5.60 | 5.23 | 18.57 | 28.31 | 19.98 | |
3.3. 考虑风速风向联合分布的疲劳损伤
风的作用可以来自任何方向,且每个方向上风的强度和出现的频率不同,因此结构的疲劳寿命估算需要考虑风速风向的分布规律. 如图12所示为已建成苍南干煤棚的周边地貌图. 该干煤棚位于我国东南沿海温州地区,常常会受各类强风的作用,包括台风的袭击,因此对于干煤棚风致疲劳损伤的分析特别需要考虑当地风速风向分布特性的影响.
图 12
图 13
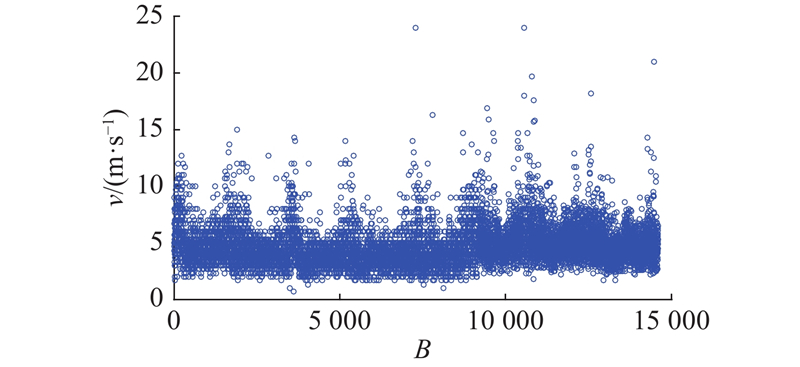
图 13 1977—2016年日最大风速序列
Fig.13 Data sequence of daily maximum wind from 1977 to 2016
图 14
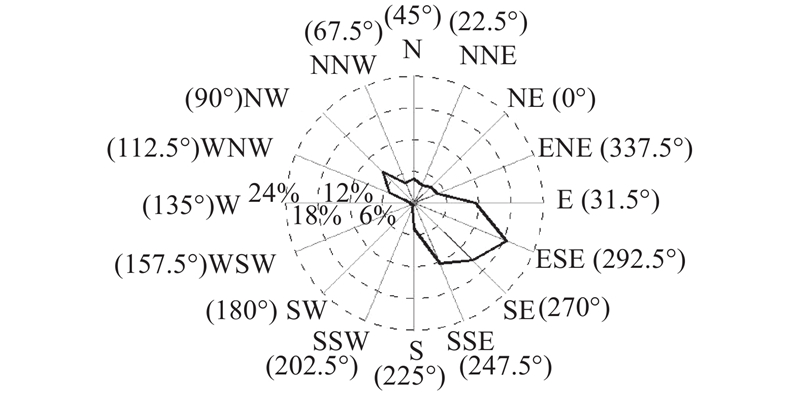
图 14 1977—2016年日最大风速对应风向玫瑰图
Fig.14 Wind directional rose of daily maximum wind from 1977 to 2016
日最大风速可以近似地假设服从双参数Weibull分布,概率密度函数为
式中:vq为q级风下的风速;A为尺度参数;λ为形状参数,可以通过对日最大风速进行最大似然法拟合得到. 基于所选取的日最大风速样本,可得λ=2.814,A=5.120. 对于风向角的概率分布,可以在离散的风向频度函数基础上近似建立风向角的连续性概率密度函数模型,结合风速条件概率密度模型,构建风向风速的离散-连续混合联合分布模型. 风向概率密度函数可以近似采用如下3参数Weibull分布来模拟:
式中:风向角
图 15
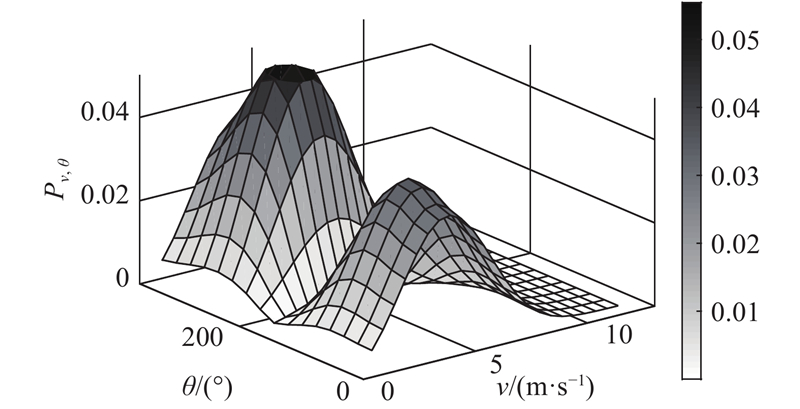
图 15 风速风向联合概率密度函数
Fig.15 Joint probability density function of wind speed and wind direction
综合考虑全年风向风速的分布特性,通过雨流法计算构件风致疲劳损伤. 将风速分为Q级(增量为1 m/s),构件在给定风向θj(j=1,2,···,W)、第q级平均风速vq作用下第r个应力幅所产生的疲劳损伤为Dqr,则在共W个风向、Q级平均风速作用下产生R个应力幅的累积疲劳损伤为
式中:Pθj为风向θj年均出现概率,P(vq)为vq风速年均出现概率. 为了考察平均风速为vq时导致的风振疲劳效应,可以定义如下风速比:
式中:U100为当地10 m高度处100年一遇的设计风速,取U100=45.96 m/s. 考虑速压比关系和线弹性结构,第q级平均风速vq作用下构件第r个应力幅约为
式中:Sr为计算得到的百年一遇设计风速条件下的结构风振响应第r个应力幅. 同理,第q级平均风速vq对应的时间步长变为设计风速下的1/kq倍. 利用S-N曲线即式(1),计算第q级平均风速vq作用下构件第r个应力幅Sqr对应的疲劳损伤:
表 3 60°风向角下关键杆件截面尺寸、时均应力值及疲劳损伤
Tab.3
| 杆件 | D×t/(mm×mm) | S/mm2 | | D/10−6 |
| 1 | 159×8 | 1 947 | 88.8 | 6.05 |
| 2 | 159×8 | 1 947 | 87.8 | 5.87 |
| 3 | 180×10 | 2 748 | 86.0 | 5.49 |
| 4 | 159×8 | 1 947 | 85.0 | 5.31 |
| 5 | 159×8 | 1 947 | 80.2 | 4.42 |
| 6 | 219×10 | 3 360 | 75.3 | 3.66 |
| 7 | 159×6 | 1 470 | 71.9 | 3.18 |
| 8 | 159×8 | 1 947 | 69.9 | 2.93 |
| 9 | 180×8 | 2 211 | 63.8 | 2.24 |
| 10 | 159×6 | 1 470 | 63.5 | 2.19 |
3.4. 球节点疲劳损伤预测
对于空间网架结构而言,杆件与球节点连接处往往会由于应力集中而更容易发生破坏. 苍南干煤棚网架结构节点形式全部采用螺栓球节点,节点构造详见图16,对螺栓球节点的风致疲劳损伤进行估算.
图 16
图 17
式中:d为螺栓直径. 对于M36高强螺栓,Kt=4.8,由于螺杆与桁架杆的面积不同,螺杆应力为桁架杆的1.68倍.
对于螺栓球节点,应力幅
利用式(25),通过雨流计数法得到各个应力循环幅值. 考虑风速风向的联合分布,计算得到螺栓球节点的年均累积疲劳损伤和疲劳寿命,结果如表4所示. 可以看出,10个关键螺栓球节点的疲劳累积损伤均较大,在设计中应予以重视,防止局部球节点的疲劳破坏. 其中螺栓球①的损伤最大,即3.17×10−2,折算为疲劳寿命
表 4 关键螺栓球节点年累积疲劳损伤和疲劳寿命
Tab.4
| 螺栓球编号 | D/10−2 | T/a |
| ① | 3.17 | 31.55 |
| ② | 3.08 | 32.47 |
| ③ | 2.88 | 34.72 |
| ④ | 2.78 | 35.97 |
| ⑤ | 2.32 | 43.10 |
| ⑥ | 1.92 | 52.08 |
| ⑦ | 1.67 | 59.88 |
| ⑧ | 1.54 | 64.94 |
| ⑨ | 1.17 | 85.47 |
| ⑩ | 1.15 | 86.96 |
4. 结 论
(1)雨流法的计算精度最高,但计算效率不高;频域疲劳损伤计算方法中,等效宽带法与雨流法的相对误差约为20%、较精确,这主要是因为该大跨干煤棚结构的风致应力时程基本为一宽带谱过程,等效窄带法次之,等效应力法的误差最大.
(2)相比于0°和90°风向角,干煤棚结构在40°、50°和60°等斜风向作用下更容易引发疲劳损伤.
(3)考虑风速风向联合分布的疲劳计算结果表明,网架杆件的风振疲劳损伤普遍较小,螺栓球节点的疲劳损伤更显著. 关键螺栓球节点的年均累积疲劳损伤最大值为3.17×10−2,折合疲劳寿命为31.55 a.
参考文献
Fatigue of metals subjected to varying stress
[J].
A reliability analysis of fatigue crack growth under random loading
[J].DOI:10.1111/ffe.1989.12.issue-3 [本文引用: 1]
Fatigue analysis of offshore platforms subject to sea wave loading
[J].DOI:10.1016/0142-1123(85)90003-9 [本文引用: 1]
An analytical solution for fast fatigue assessment under wide-band random loading
[J].DOI:10.1016/0142-1123(91)90596-Q [本文引用: 2]
Fatigue under wide band random stresses
[J].
桅杆结构的风振疲劳分析
[J].DOI:10.3969/j.issn.1001-3598.1994.03.002 [本文引用: 1]
Analysis of wind-induced fatigue in guyed steel masts
[J].DOI:10.3969/j.issn.1001-3598.1994.03.002 [本文引用: 1]
基于频域的桅杆结构风振疲劳分析
[J].DOI:10.3969/j.issn.1001-3598.1999.04.011
The study of guyed mast fatigue based on stress spectrum under wind vibration
[J].DOI:10.3969/j.issn.1001-3598.1999.04.011
格构式桅杆顺风向风振疲劳可靠性分析
[J].DOI:10.3969/j.issn.1001-3598.2004.02.013 [本文引用: 1]
Analysis of fatigue reliability of the lattice guyed-mast along wind vibration
[J].DOI:10.3969/j.issn.1001-3598.2004.02.013 [本文引用: 1]
自立式单杆输电塔顺风向风振疲劳分析
[J].
Analysis on alongwind fatigue of free standing single rod transmission tower
[J].
Fatigue life under along-wind loading: closed-form solution
[J].DOI:10.1016/S0141-0296(01)00073-6 [本文引用: 1]
Directional wind-induced fatigue of slender vertical structure
[J].DOI:10.1061/(ASCE)0733-9445(2004)130:7(1032) [本文引用: 1]
Bimodal alongwind fatigue of structures
[J].DOI:10.1061/(ASCE)0733-9445(2006)132:6(899)
Closed form solution of the alongwind-induced fatigue damage to structures
[J].DOI:10.1016/j.engstruct.2009.05.016
Long term simulation of wind-induced fatigue loadings
[J].
Fatigue life estimation of steel girder of Yangpu cable -stayed bridge due to buffeting
[J].DOI:10.1016/S0167-6105(98)00209-8 [本文引用: 1]
Buffeting-induced fatigue damage assessment of a long suspension bridge
[J].DOI:10.1016/j.ijfatigue.2008.03.031 [本文引用: 1]
风速风向联合分布对结构风致疲劳寿命可靠性的影响
[J].DOI:10.3969/j.issn.1000-3835.2009.12.040 [本文引用: 1]
Influence of joint distribution of wind speed and wind direction on wind induced fatigue life reliability
[J].DOI:10.3969/j.issn.1000-3835.2009.12.040 [本文引用: 1]
考虑风向风速联合分布的输电塔线体系风振疲劳研究
[J].
Study on wind-induced fatigue of transmission tower-line coupled system considering the joint distribution of wind speed and wind direction
[J].
极值风速风向的联合概率密度函数
[J].
Joint probability density function of extreme wind speed and direction
[J].
Non-Gaussian time-dependent statistics of wind pressure processes on a roof structure
[J].DOI:10.12989/was.2016.23.4.275 [本文引用: 1]
开孔大跨屋盖结构的内部风效应研究
[J].
Internal wind effect for long-span roof structure with openings
[J].
大跨开孔结构屋盖风致响应分析的多模态精细时程积分法
[J].
Analysis on wind-induced dynamic response for long-span roof of opening structure by multi-modal precise time-integration method
[J].
Cumulative damage in fatigue
[J].
雨流计数法及其在程序中的具体实现
[J].DOI:10.3969/j.issn.1674-5795.2004.03.014 [本文引用: 1]
Rain flow count method and its realization in programming
[J].DOI:10.3969/j.issn.1674-5795.2004.03.014 [本文引用: 1]
Fatigue life prediction under wide band random loading
[J].DOI:10.1111/ffe.2004.27.issue-12 [本文引用: 2]