在桩头竖向力、水平力、弯矩的耦合作用下,桩侧土对桩的侧向作用、竖向作用以及桩端土对桩端的竖向作用可分别用p-y、t-z、Q-z弹簧模型描述[5]. Wei等[6]研究p-y弹簧对循环荷载下导管架基础海上风机动力响应的影响,并与无桩-土相互作用的工况进行对比. Abhinav等[7-8]研究在随机风、浪荷载条件下,导管架基础海上风机在无桩-土相互作用、弹性桩-土相互作用[5]2种工况下的频率、极限承载力以及动力响应差异. 上述研究均表明,不考虑桩-土相互作用会导致导管架基础的位移响应被低估. 目前对于循环荷载下导管架基础海上风机动力响应的研究较少,尤其是对考虑桩-土相互作用循环弱化效应的动力响应缺乏认识.
本研究针对导管架基础海上风机,开展极端循环荷载下整体结构的动力响应的计算与分析,在数值计算中分别采用美国石油学会(American petroleum institute,API)规范系列模型(p-y、t-z、Q-z)[5]、可考虑桩-土界面竖向强度和刚度循环弱化效应的弹塑性t-z模型以及桩-土侧向弹塑性p-y模型. 评估各部分弹簧对泥面处抗倾覆弯矩的贡献以及t-z、p-y弹簧的循环弱化效应对导管架基础顶点处转角、位移动力响应的影响.
1. 导管架基础海上风机结构组成
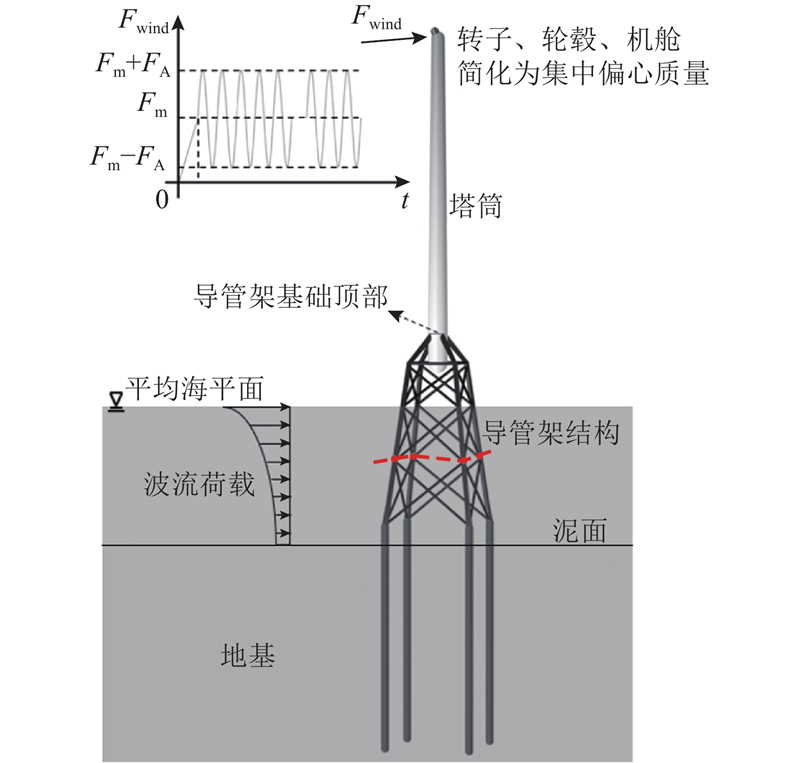
图 1
图 1 导管架基础海上风机模型示意图
Fig.1 Schematic diagram of model for jacket supported offshore wind turbine
2. 桩-土相互作用API规范模型
API 规范中推荐的p-y、t-z、Q-z弹性模型[5]被广泛应用于海洋工程桩基设计. 该方法较全面地考虑了土体非线性、土层变化、土体种类等影响. 其中,砂土中桩的p-y曲线表达式为
式中:A为循环荷载效应系数,在循环荷载下A=0.9;p为泥面以下深度X m处作用于桩上的水平土抗力;K为土抗力初始模量;y为深度X m处桩的侧向位移;pu为单位桩长的极限水平抗力. 相关参数确定方法请参考API规范[5].
砂土中桩的t-z曲线表达式为
式中:τmax为桩-土界面极限剪切强度,K0为地基侧压力系数,σz为有效上覆土压力,δ为桩-土界面摩擦角. 桩-土界面竖向抗力τ的发挥与桩-土相对位移z有关,API规范[5]中给出了τ/τmax与z的关系曲线.
砂土中桩的Q-z曲线表达式为
式中:q为桩端单位面积极限承载力,
3. 循环弱化p-y模型
表 1 弹塑性p-y模型参数
Tab.1
| 模型参数 | 数值 |
| 内摩擦角φ/(°) | 39 |
| 地基弹性模量ηh/(N·m−3) | 3.4×107 |
| p-y曲线形状参数hs | 0.1 |
| 刚度衰减参数αd | 0.001 |
| 有效重度γ'/(KN·m−3) | 10.4 |
4. 循环弱化t-z模型
4.1. 循环弱化t-z模型的建立
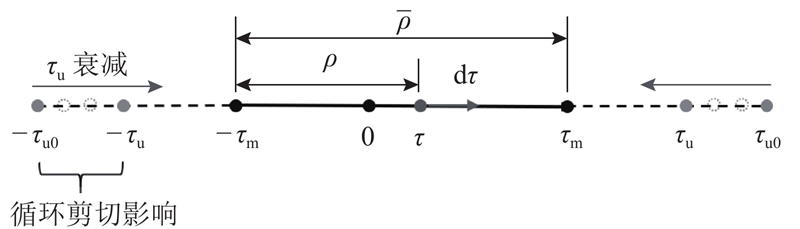
图 2
图 2 考虑循环弱化的弹塑性t-z模型
Fig.2 Elastoplastic t-z model considering cyclic degradation
式中:Kep为弹塑性抗力系数;Ke为弹性抗力系数;Kp为塑性抗力系数;h为t-z曲线形状参数;τm为强度边界范围内的历史最大界面剪应力;
4.2. t-z模型参数标定
1)界面初始极限强度. τu0可从界面剪切试验中直接获得,若无相关试验数据,可由式(9)计算得出:
2)弹性抗力系数. Ke描述t-z弹簧的弹性行为,表达式为
3)曲线形状参数. 曲线形状参数h控制t-z曲线的形状,调整h可使模拟曲线与试验曲线保持基本一致.
4)循环界面残余强度. 在界面循环剪切试验中,界面强度呈现先快速下降后近似线性下降的规律. 在经历足够的循环剪切次数之后,界面强度趋于稳定,可将其视为循环界面剪切残余强度.
5)卸载刚度修正系数. 在界面剪切试验中发现,t-z曲线的初始卸载刚度明显大于初始加载刚度,故须对卸载刚度进行修正. 卸载刚度修正系数B为初始卸载刚度Kun与初始加载刚度Ke之比:
6)界面强度衰减参数. 参数a、b用于描述法向应力衰减,表达式分别为
式中:σn(0)为界面初始法向应力,Δσ(I)、Δσ(II) 分别为I、II阶段(快速衰减阶段、线性稳定衰减阶段)衰减的法向应力,ηa、ηb为调整系数.
表 2 标定后的弹塑性t-z模型参数
Tab.2
| 模型参数 | 数值 | 模型参数 | 数值 | |
| δ/(°) | 21.5 | B | 2.5 | |
| z50/mm | 0.5 | a | 0.04 | |
| h | 4.0 | b | 0.5 | |
| τr/τu0 | 0.317 |
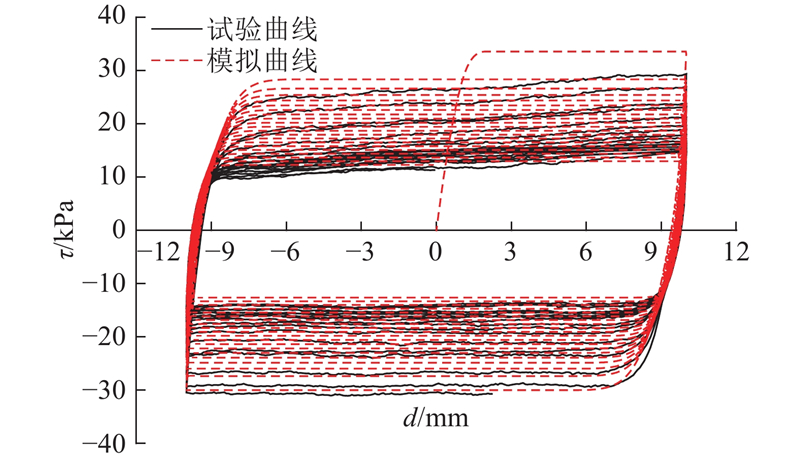
图 3
图 3 t-z模型模拟结果与等常刚度界面剪切试验结果的对比
Fig.3 Comparison of simulation results of t-z model and interface shear test results under constant normal stiffness
5. 数值模型与计算结果
对比分析各部分弹簧对泥面处抗倾覆弯矩的贡献并评估不同p-y、t-z模型对导管架基础海上风机动力响应的影响. 设计算例如表3所示,其中工况1中的3种弹簧模型均采用API规范[5]中的弹性模型,工况2中仅有t-z模型为弹塑性模型,工况3中仅有p-y模型为弹塑性模型,工况4中t-z、p-y模型均为具有循环弱化效应的弹塑性模型. 3种API规范[5]模型的参数取值如表4所示. 循环弱化p-y、t-z模型的参数取标定后参数. 利用有限元软件COMSOL 对导管架基础海上风机进行整体建模,结合MATLAB进行二次开发将上述循环弱化p-y、t-z模型写入有限元模型中,对导管架基础海上风机进行极端循环荷载下的动力时程计算与分析.
表 3 不同桩-土相互作用计算工况
Tab.3
| 计算工况 | p-y模型 | t-z模型 | Q-z模型 |
| 1 | API | API | API |
| 2 | API | 弹塑性 | API |
| 3 | 弹塑性 | API | API |
| 4 | 弹塑性 | 弹塑性 | API |
表 4 API规范的p-y、t-z、Q-z模型参数
Tab.4
| 模型 | φ/(°) | δ/(°) | Nq | A | γ'/(KN·m−3) |
| p-y模型 | 39 | − | − | 0.9 | 10 |
| t-z模型 | − | 21.5 | − | − | 10 |
| Q-z模型 | − | − | 20 | − | 10 |
5.1. 导管架支撑结构与荷载
表 5 导管架基础海上风机主要参数
Tab.5
| 几何参数 | 数值 |
| 转子、轮毂、机舱集中质量/t | 466.8 |
| 塔筒长度/m | 73.0 |
| 塔筒底部直径/m | 5.5 |
| 导管架部分高度/m | 44.6 |
| 导管架顶部根开/m | 12.0 |
| 导管架底部根开/m | 22.0 |
| 桩长/m | 50.0 |
| 桩径/m | 2.0 |
| 桩壁厚/mm | 30.0 |
考虑海上风机处于台风极端荷载工况下的停机状态. Abhinav等[8]针对平均风速为50 m/s和脉动风湍流强度为10%的条件,联合TurbSim和FAST软件计算100个湍流风速时程下风机塔筒顶部等效风荷载,在考虑安全系数后,风对塔筒顶部的作用力Fmax=1.125 MN,本研究选用该值作为等效风荷载. 作用在塔筒顶部的等效循环集中力表达式为
式中:T为波浪周期;tc为计算时间;Fm为定常风荷载,FA为脉动风荷载,本研究中取Fm=FA=0.5Fmax=0.562 5 MN.
对于波流荷载,利用海工软件SACS进行计算,采用流函数理论并考虑海流作用的影响. 五十年一遇的1%波高H1%=10.76 m,对应T=10.10 s,为了保证计算精度,波浪流函数取9阶. 波浪对导管架结构的拖曳力系数CD=1.2,惯性力系数CM=2.0[24],海流速度为2.15 m/s. 为了方便在有限元模型中施加波流力,采用泥面弯矩等效原则,将作用在导管架结构上的波流力等效为4个集中力,分别施加在导管架结构的4根斜主导管上,加载高度如图1中虚线所示.
沿导管架对角线方向施加风、浪荷载以体现最不利工况,设定波流荷载为不变荷载,风荷载为可变循环荷载. 在数值计算中,为了防止突加荷载对风机动力响应的影响,将不变荷载在5 s之内由0线性增大到设定值,之后再施加循环荷载.
5.2. 泥面处抗倾覆弯矩组成分析
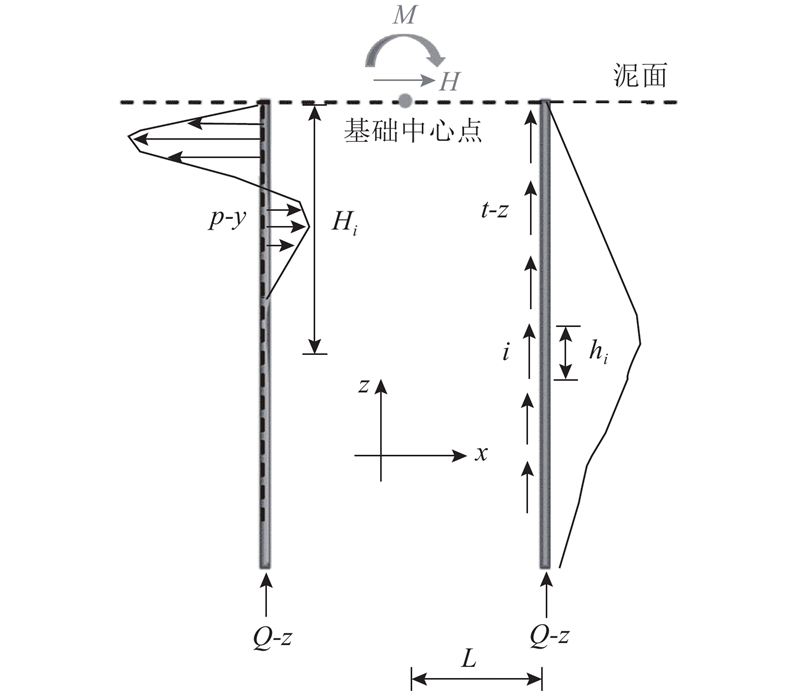
对导管架基础海上风机而言,上部风机承受的风荷载、导管架部分承受的波流荷载可等效为作用在泥面位置基础中心点处的集中水平力H和倾覆弯矩M,如图4所示. 水平抗力由p-y弹簧提供,泥面处抗倾覆弯矩由p-y、t-z、Q-z弹簧共同提供,表达式分别为
图 4
图 4 导管架基础泥面处弯矩计算示意图
Fig.4 Schematic diagram of moment caculatuion of jacket foundation at mudline
式中:Mpy为p-y弹簧力对泥面处的抗倾覆弯矩,Mtz为t-z弹簧力对基础中心点的抗倾覆弯矩,MQz为Q-z弹簧力对基础中心点的抗倾覆弯矩,j为桩编号,N为每根桩划分的段数,Pi为第i桩段单位长度的水平力,hi为第i桩段的长度,Hi为第i桩段中心点到泥面的竖向距离,τi为第i桩段桩侧单位面积的竖向力,Lj为第j根桩中心点到基础中心点的水平距离,Qj为第j根桩的桩端力.
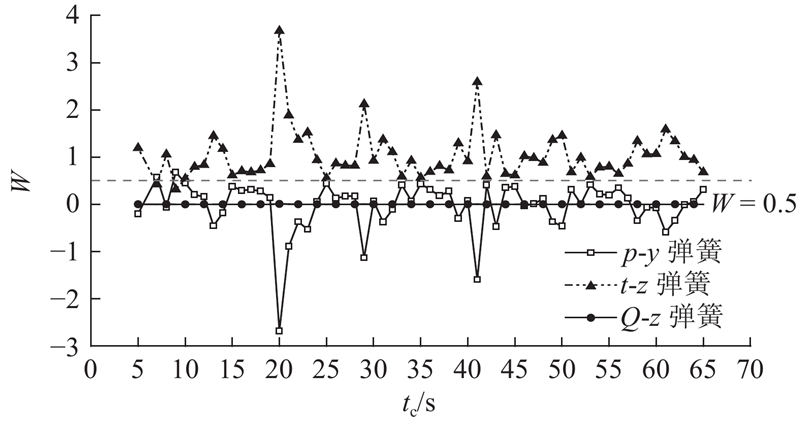
针对工况1,分析各部分弹簧力(p-y、t-z、Q-z)对导管架基础泥面处抗倾覆弯矩贡献的时程响应. 如图5所示为在静荷载施加结束5 s之后的计算结果. 图中,W为各部分弹簧对泥面处抗倾覆弯矩贡献占比. 可以看出,t-z、p-y弹簧的贡献占比波动较大,且t-z弹簧的贡献明显大于p-y弹簧,两者基本关于0.5贡献占比参考线上下对称. 在风机受循环荷载的过程中,p-y弹簧力在泥面位置形成的弯矩可能为负,说明此时浅部土体的水平抗力形成的负弯矩大而深部土体的水平抗力形成的正弯矩小,p-y弹簧对风机的抗倾覆发挥负面作用. Q-z弹簧贡献占比小于0.01,可以忽略不计. 因此,在3种弹簧模型中,t-z弹簧对导管架基础抗倾覆性能发挥着最重要的作用,应在工程设计中予以重点关注.
图 5
图 5 各部分弹簧对泥面处抗倾覆弯矩贡献时程图
Fig.5 Time history of contribution of different springs to anti-overturning moment at mudline
5.3. 基础顶点处动力响应分析
海上风机基础顶点处的转角是风机能否正常运行的重要评价指标. 根据挪威船级社海上风机设计规范[9],25 a服役期内基础顶点处的累积转角须小于0.25°. 本研究重点关注不同桩-土相互作用对导管架基础顶点处的转角、位移动力响应的影响.
5.3.1. 导管架基础顶点处的转角响应
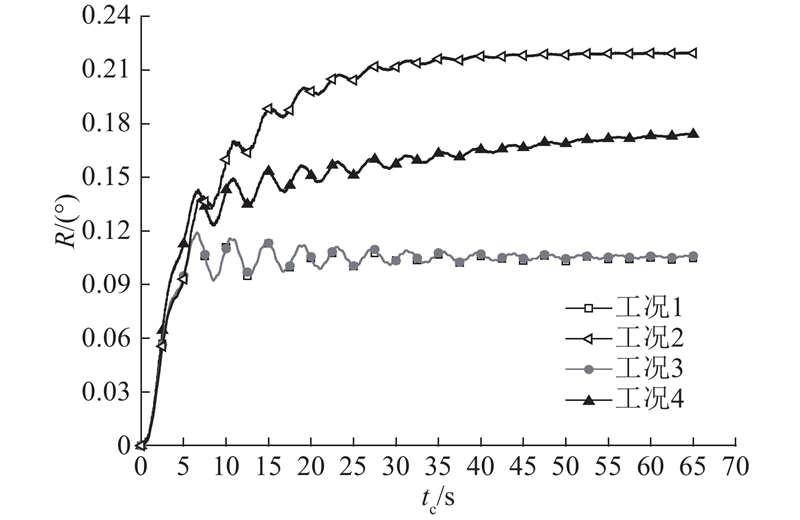
如图6所示为导管架基础顶点处的转角响应时程图. 图中,R为基础顶点处转角. 在循环荷载作用下,1)工况1转角响应最小且最快达到稳定,工况2转角响应最大且稳定较慢,说明弹塑性t-z弹簧的循环弱化对基础顶点处转角响应的影响显著,使转角增大109.4%;2)工况3转角响应与工况1基本一致,说明弹塑性p-y弹簧的循环弱化对基础顶点处转角响应的影响不明显,使转角增大1.2%;3)工况4转角响应介于工况1、2之间,t-z、p-y弹簧的循环弱化耦合作用使该点处的转角增大66.1%,说明相比于仅考虑t-z弹簧的循环弱化,同时考虑t-z、p-y弹簧的循环弱化可使基础顶点处的转角响应有所减小. 这是由于桩基的水平抗力由p-y弹簧提供,工况4中弹塑性p-y弹簧随荷载循环不断弱化,导管架结构平动量明显大于工况2. 工况2中导管架结构转动更加明显,工况4中导管架结构平动更加明显,受力模式的不同导致工况2转角响应大于工况4.
图 6
图 6 导管架基础顶点处转角响应时程图
Fig.6 Time history chart of rotation response at top of jacket foundation top
5.3.2. 导管架基础顶点处的位移响应
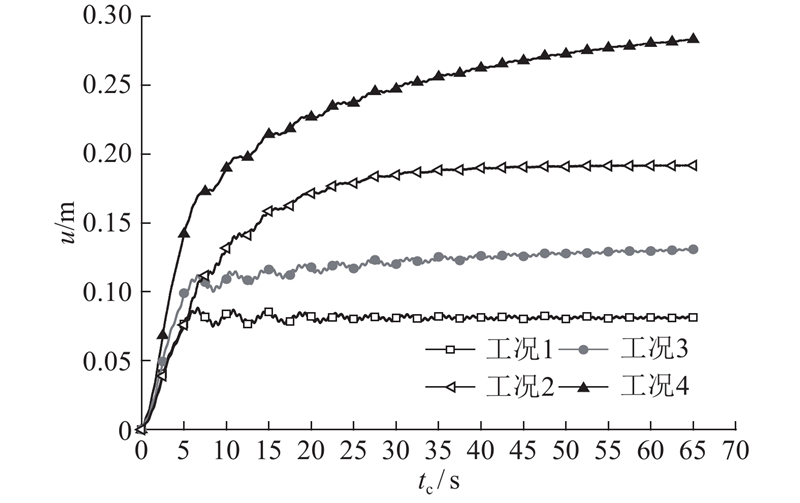
如图7所示为导管架基础顶点处水平位移响应时程图. 图中,u为基础顶点处水平位移. 可以看出:1)工况1中水平位移响应幅值最小且最快达到稳定;2)工况2中弹塑性t-z弹簧的循环弱化导致该点处水平位移增大135.4%;3)工况3中弹塑性p-y弹簧循环弱化导致该点处水平位移增大 60.7%;4)工况4中弹塑性p-y、t-z弹簧的循环弱化耦合作用使得该点处水平位移增加更加明显,为247.8%. 如图8所示为导管架基础顶点处竖向位移响应时程图. 图中,w为基础顶点处竖向位移. 在循环荷载作用下,1)工况1竖向位移响应最小且最快达到稳定;2)工况2中该点竖向位移响应有较明显的增加,t-z弹簧的循环弱化导致该点竖向位移增大8.9%;3)工况3中竖向位移响应与工况1基本一致,说明p-y弹簧的循环弱化对基础顶点处竖向位移响应的影响不明显;4)工况4 中竖向位移响应最大且无稳定趋势,说明t-z、p-y 弹簧的循环弱化耦合作用会大大增加基础顶点处的竖向位移响应,使得该点处竖向位移增大158.1%.
图 8
图 8 导管架基础顶点处竖向位移响应时程图
Fig.8 Time history chart of vertical displacement response at top of jacket foundation
图 7
图 7 导管架基础顶点处水平位移响应时程图
Fig.7 Time history chart of horizontal displacement response at top of jacket foundation
6. 结 论
(1)导管架基础海上风机在承受极端循环荷载的过程中,t-z弹簧对泥面处抗倾覆弯矩的贡献最大,p-y弹簧对泥面处抗倾覆弯矩的贡献可能为负,其主要作用为抵抗水平力,Q-z弹簧对泥面处抗倾覆弯矩的贡献较小,可忽略不计.
(2)相比于API规范桩-土相互作用弹性模型,考虑桩-土竖向相互作用的循环弱化效应,即考虑t-z弹簧的循环弱化效应会大大增加基础顶点处的转角响应.
(3)若同时考虑桩-土竖向、侧向作用的循环弱化,即t-z、p-y弹簧循环弱化的耦合作用,导管架基础的平动更为明显,基础顶点处的位移响应明显增大,但转角响应相比于仅考虑t-z弹簧循环弱化的情况有所减小. 因此,在导管架基础海上风机设计中,须充分考虑桩-土作用的循环弱化效应.
参考文献
海上风电坐稳世界第三"十三五"目标有望完成
[J].
The goal of stabilizing offshore wind power in the 13th Five-Year Plan is expected to be fulfilled
[J].
Stochastic response of jacket supported offshore wind turbines for varying soil parameters
[J].DOI:10.1016/j.renene.2016.09.019 [本文引用: 1]
台风对我国海上风电开发的影响
[J].DOI:10.3969/j.issn.1672-9064.2013.03.001 [本文引用: 1]
The influence of typhoon on offshore wind power development in China
[J].DOI:10.3969/j.issn.1672-9064.2013.03.001 [本文引用: 1]
Soil-structure interaction on the response of jacket-type offshore wind turbine
[J].DOI:10.1007/s40684-015-0018-7 [本文引用: 1]
Nonlinear dynamical behavior of jacket supported offshore wind turbines in loose sand
[J].DOI:10.1016/j.marstruc.2017.10.002 [本文引用: 1]
Coupled hydrodynamic and geotechnical analysis of jacket offshore wind turbine
[J].DOI:10.1016/j.soildyn.2015.03.002 [本文引用: 2]
软黏土中水平受荷桩的静力和循环p–y曲线
[J].
Static and cyclic p-y curves for laterally loaded piles in soft clay
[J].
砂土中大直径单桩水平受荷离心模型试验
[J].
Centrifuge modelling of a large-diameter single pile under lateral loads in sand
[J].
循环荷载下饱和粉土地基单桩水平承载特性试验研究
[J].
Model tests on lateral bearing capacity of single piles under cyclic loads in saturated silt
[J].
Behavior of monopile foundations under cyclic lateral load
[J].DOI:10.1016/j.compgeo.2008.12.003 [本文引用: 1]
刚度衰减模型在大直径桩累积侧向位移分析中的应用
[J].
Application of degradation model in analysis of cumulative lateral displacement of monopile foundation
[J].
弹塑性p–y模型及非线性地基梁的增量有限元法
[J].
Elastoplastic p-y model and incremental finite element method for nonlinear foundation beams
[J].
考虑泊松效应影响的弹塑性荷载传递模型
[J].
Elastoplastic load transfer model considering Poisson effect
[J].
A multidirectional p–y model for lateral sand-pile interactions
[J].DOI:10.1016/j.sandf.2013.02.002
Bounding surface plasticity. I: mathematical foundation and hypoplasticity
[J].DOI:10.1061/(ASCE)0733-9399(1986)112:9(966)
A sand model with state-dependent dilatancy
[J].DOI:10.1680/geot.2002.52.3.173 [本文引用: 1]
Estimation of pile friction degradation from shear box tests
[J].DOI:10.1520/GTJ10253J [本文引用: 1]
Pile skin friction in sands from constant normal stiffness tests
[J].DOI:10.1520/GTJ11004J [本文引用: 1]