碰撞检测是机器人、电脑游戏和虚拟现实等领域的经典问题,其目的是确定不同物体在运动过程中是否存在碰撞及碰撞发生的时间和位置,传统的碰撞检测算法多是针对这些领域提出. 当大量颗粒碰撞团聚时,已有的团聚体会因新颗粒或颗粒簇的加入而不断发生形状变化. 对可变形物体的碰撞检测主要有如下几种传统算法:层次包围盒法、空间分割法和图像空间法. 常用的包围盒类型有:轴对齐包围盒(axis-aligned bounding box, AABB)、有向包围盒(oriented bounding box, OBB)和固定方向凸包(fixed direction hull, FDH)[3-4]. 然而,团聚体的逐渐长大和不停旋转迫使上述包围盒不断更新且成本较高,这极大地降低了碰撞检测的执行效率. 空间分割法的数据存储量大且灵活性差[5-6],而图像空间法无法提供准确的碰撞信息[7-8],因此,很难将空间分割法和图像空间法用于大量颗粒团聚过程中的精细碰撞检测.
针对目前传统算法存在执行效率低和准确性差等问题,本文结合颗粒团聚过程的自身特点,提出一种基于“包围球-最大检测区域”预处理的两步式碰撞检测算法,并将其与传统算法对比,验证其高效性和准确性.
1. 碰撞检测预处理
1.1. 包围球
相较于其他类型的包围盒,包围球(bounding sphere,BS)的结构更加简单,更新成本更低且无需因团聚体的旋转而不停更新. 本文中,单一颗粒的包围球就是其本身,无需构建;团聚体的包围球被设定为一个恰好完全包含团聚体的球且包围球的球心与团聚体的质心重合,如图1所示. 一般地,团聚体中所有颗粒的密度可认为相同,则其包围球的球心坐标C和半径R可表示为
图 1
式中:(xi,yi,zi)和ri分别为团聚体中第i个颗粒的球心坐标和半径,li为团聚体中第i个颗粒球心到团聚体质心的距离,Np为团聚体中颗粒的数量.
1.2. 最大检测区域
图 2
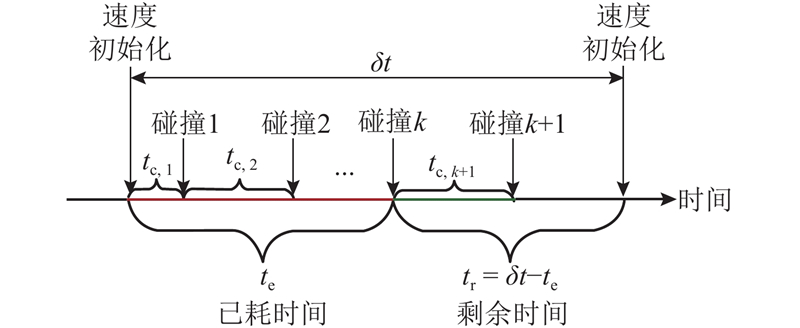
式中:tc, j(2 ≤ j ≤ k)为已发生的碰撞j与已发生的碰撞j –1间的时间间隔,tc, 1为已发生的碰撞1与模拟时间步长开端间的时间间隔. 因此,下一个将要发生的碰撞k + 1与已发生的碰撞k间的时间间隔不会超过该模拟时间步长的剩余时间tr,且tr可表示为
换言之,在下一个碰撞或新的模拟时间步长到来之前,单一颗粒或团聚体沿X、Y、Z三轴方向的最大位移分别为
式中:L0, x、L0, y和L0, z分别为单一颗粒或团聚体沿X、Y、Z三轴的位移,vt, x、vt, y和vt, z分别为单一颗粒或团聚体平移速度沿X、Y、Z三轴的分量. 假设vt, x、vt, y和vt, z分别沿X、Y、Z三轴的正方向,在下一个碰撞k + 1或新的模拟时间步长到来之前,每个单一颗粒或团聚体与其他单一颗粒或团聚体的碰撞必然发生在如下最大碰撞区域(maximum collision region,MCR)内:
式中:(x0,y0,z0)为单一颗粒或团聚体在碰撞k发生时其包围球的球心坐标.
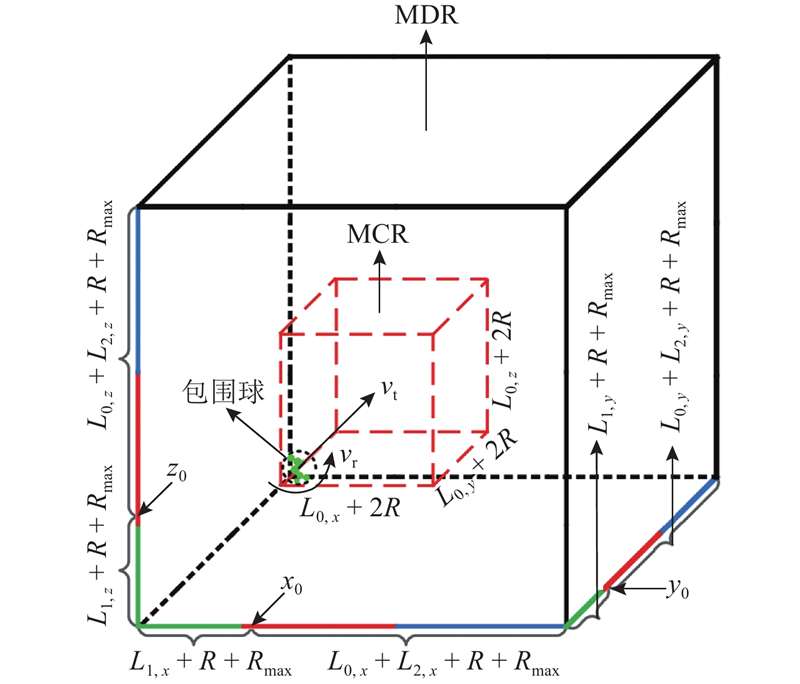
当单一颗粒或团聚体的MCR确定后,其最大检测区域(maximum detection region,MDR)随之也可确定. 在下一个碰撞k + 1或新的模拟时间步长到来之前,仅MDR内的其他单一颗粒或团聚体可能与目标对象发生碰撞. 单一颗粒或团聚体(即目标对象)的MDR可表示为
式中:Rmax为下一个碰撞k + 1或新的模拟时间步长到来之前所有包围球半径的最大值,L1,x + Rmax、L1,y + Rmax和L1,z + Rmax分别为MCR和MDR对应的左、前和下壁面间的距离,L2,x + Rmax、L2、y + Rmax和L2,z + Rmax分别为MCR和MDR对应的右、后和上壁面间的距离. L1, x、L1, y、L1, z、L2, x、L2, y和L2, z可根据下列式子得出:
式中:vt, x, pmax、vt, y, pmax和vt, z, pmax分别为所有单一颗粒和团聚体平移速度沿X、Y、Z三轴正方向分量的最大值,vt, x, nmax、vt, y, nmax和vt, z, nmax分别为所有单一颗粒和团聚体平移速度沿X、Y、Z三轴负方向分量的最大值. 为直观理解MCR和MDR的构造及其关系,图3给出了其示意图. 需要指出的是,式(5)和(6)仅是在目标对象vt, x、vt, y和vt, z的方向沿X、Y、Z三轴正方向的情况下得出的,其他7种情况下的MCR和MDR表达式可类比得出,不再赘述. MDR的引入可有效避免目标对象与整个模拟区域内其他所有单一颗粒或团聚体间的暴力碰撞检测,仅考虑与其MDR内的其他单一颗粒或团聚体间的碰撞检测即可,从而大大节省碰撞检测的执行时间.
图 3
2. 碰撞检测主过程
2.1. 粗略筛选
图 4
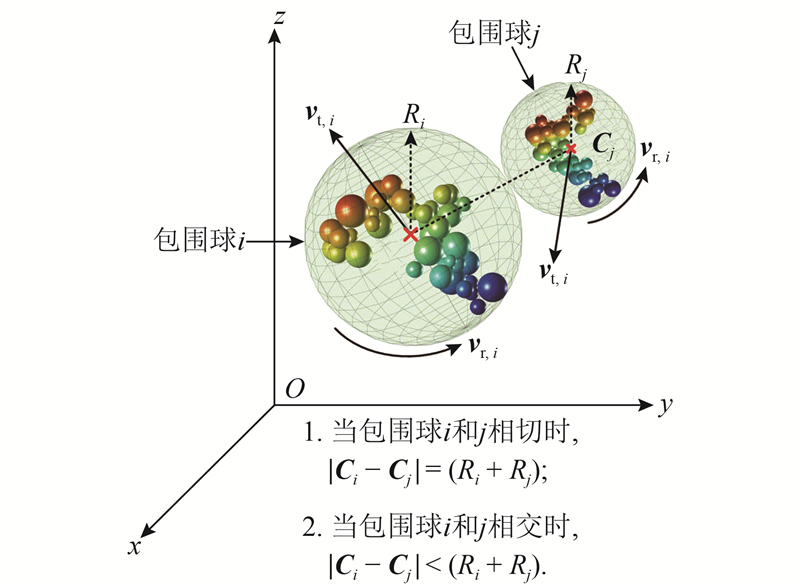
图 4 发生碰撞的两包围球的几何关系
Fig.4 Geometrical relation of two bounding spheres colliding with each other
式中:t为发生碰撞的时间且t从最近已发生的碰撞k开始算起,vt, i, 0和vt, j, 0分别为包围球i和j在t = 0时的平移速度,Ci, 0和Cj, 0分别为包围球i和j在t = 0时的球心坐标,Ri, 0和Rj, 0分别为包围球i和j在t = 0时的半径. 上述方程是否有解,可通过下列判别式的符号来确定:
当D < 0时,式(8)无解,即两包围球不会发生碰撞;当 D ≥ 0时,式(8)有解:
当D ≥ 0时,t2 ≥ t1. 需要注意的是,碰撞检测是对时间域(0, tr]内未来事件的预测,因此0<t≤tr. 也就是说,即便式(8)有解,两包围球也不一定会发生碰撞. 例如,当0 > t2 ≥ t1时,两包围球已飞离彼此,只是在其平移运动反方向的延长线上发生了碰撞;当tr ≥ t2 ≥ 0 ≥ t1或t2 > tr > 0 ≥ t1时,两包围球在t = 0时已处于相切或相交状态,并将在t = t2时分离或在t = tr时速度初始化,进入下一个模拟时间步长;当t2 ≥t1 > tr时,两包围球在t = tr时速度初始化,进入下一个模拟时间步长. 因此,仅当tr ≥ t2 ≥ t1 > 0或 t2 > tr ≥ t1 > 0时,两包围球将在 t = t1时发生碰撞,假设两包围球碰撞后仍按原平移方向继续运动,那么两者将在t = t2时分离或在t = tr时速度初始化,进入下一个模拟时间步长.
2.2. 精细确定
粗略筛选通过求解关于时间的一元二次方程将不可能发生的碰撞筛选掉. 然而,对将要发生碰撞的两包围球而言,当包围的目标对象至少有1个是团聚体时,团聚体的不停旋转可能导致两目标对象在时间域[T1,T2]仍不会碰撞,其中时间域表示如下:
为提高碰撞检测的准确性,离散碰撞检测法所选用的采样时间间隔Δt应尽量小,但过小的Δt又将大大增加碰撞检测所需的执行时间. 为此,本文选用一种自适应的、先疏后密的时间间隔策略,首层碰撞检测的时间间隔Δt1表示如下:
式中:rmin为两目标对象中最小颗粒的半径. 那么,首层的离散采样时间点可如下表示:
考虑到两目标对象仅能在其包围球相交区域内发生碰撞,相交区域外的碰撞检测可忽略. 精细确定阶段的详细实现步骤如下:
2)如果T1 = T2,则两目标对象的包围球发生相切碰撞,只需检测当t = T1时两目标对象是否均存在颗粒表面与两包围球的碰撞点相切的情况,若存在,则两目标对象发生碰撞;如果T1 < T2,则采用图5中的颗粒碰撞检测策略对两包围球相交区域内两目标对象间的每对颗粒进行碰撞检测,若在所有采样时间点上均未发现碰撞,则两目标对象最终不发生碰撞,若在某个采样时间点上发现两目标物体间存在颗粒相切或相交的情况,则停止对剩下采样时间点的碰撞检测并进入下一步;
图 5
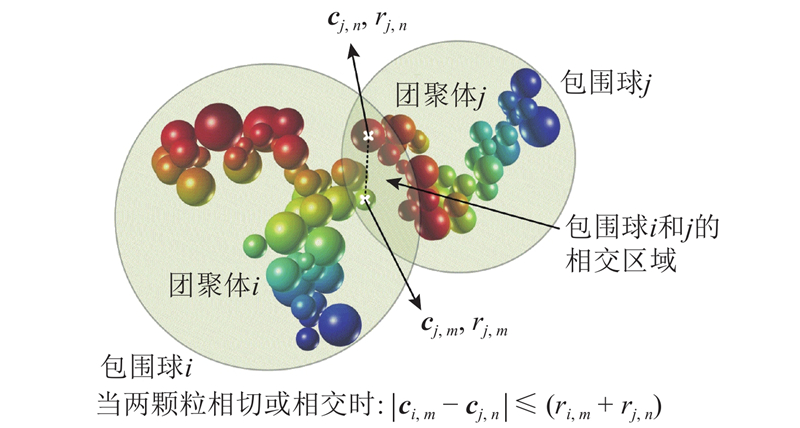
图 5 包围球相交区域内颗粒间的碰撞检测
Fig.5 Collision detection between particles in intersection of two bounding spheres
3)计算每对发生接触颗粒的球心间距与其半径之和的比值:
式中:ci, m和cj, n分别为团聚体i中第m个颗粒和团聚体j中第n个颗粒的球心坐标,ri, m和rj, n分别为团聚体i中第m个颗粒和团聚体j中第n个颗粒的半径. 考虑到现实的团聚体中存在颗粒表层重叠的现象[17]且检测出两颗粒恰好碰撞(ε = 1)极其耗时,将0.95 ≤ ε ≤ 1的两颗粒视为发生了有效碰撞,而ε< 0.95意味着两颗粒重叠过多,碰撞发生的时间点应回退. 如果每对发生接触的颗粒的ε均落在[0.95,1],则两目标对象被视为发生了碰撞,且碰撞点发生在ε最接近0.95的颗粒对之间. 如果存在某对颗粒的ε < 0.95的情况,则进入下一步;
4)在此层碰撞检测中,选用更小的时间间隔Δti (仅是上一层时间间隔Δti −1的1/10),从上一层的采样时间点回退,重复步骤2)~ 4),直到每对发生接触的颗粒的ε均落在[0.95,1]为止,最终找出两目标对象发生碰撞的准确时间和位置.
3. 实现结果分析
为验证上述优化算法的高效性和准确性,本文采用表1中的传统算法1和2[16]作为对比,算法3为本文所提出的算法. 团聚体同时具有的平移和旋转运动导致其组成颗粒的运动轨迹复杂,无法直接通过求解关于时间的一元二次方程来实施连续精细的碰撞检测. 因此,算法1和2在碰撞检测的全过程中均采用基于时间域的离散碰撞检测法,且其时间域均被设定为(0,tr]. 具体来讲,算法1的离散碰撞检测过程和第2.2节中的方法一样,需对两目标对象间每对颗粒进行精细碰撞检测;在算法2的离散碰撞检测过程中,首先判断两目标对象的AABB包围盒是否发生碰撞,如果2个包围盒发生碰撞,再对两目标对象间每对颗粒进行精细碰撞检测. 另外,算法1和2同样将0.95 ≤ ε ≤ 1的碰撞视为有效碰撞;将首层碰撞检测的采样时间间隔Δt1设定为式(12)的计算值,且下一层碰撞检测的采样时间间隔为上一层的1/10. 由于大量颗粒团聚过程中的碰撞检测涉及众多向量和矩阵运算,表1中的3种算法均采用Matlab语言编写并通过一台配有Intel Core i7-4.2 GHz处理器和DDR4-32 Gb内存的计算机完成执行任务.
表 1 两种传统算法和新算法的技术对比
Tab.1
| 序号 | 预处理 | 主过程 |
| 算法 1 | 无 | DCD (△t自适应且可变) |
| 算法 2 | AABB | DCD (△t自适应且可变) |
| 算法 3 | BS+MDR | CCD+DCD (△t自适应且可变) |
图 6
图 6 层流乙烯扩散火焰中轴线处碳黑基础颗粒团聚过程
Fig.6 Primary soot particle aggregation along centerline of laminar ethylene diffusion flame
图 7
图 7 火焰中轴线处碳黑基础颗粒碰撞团聚过程的
Fig.7 Typical TEM images of primary soot particle aggregation along flame centerline and corresponding simulation images
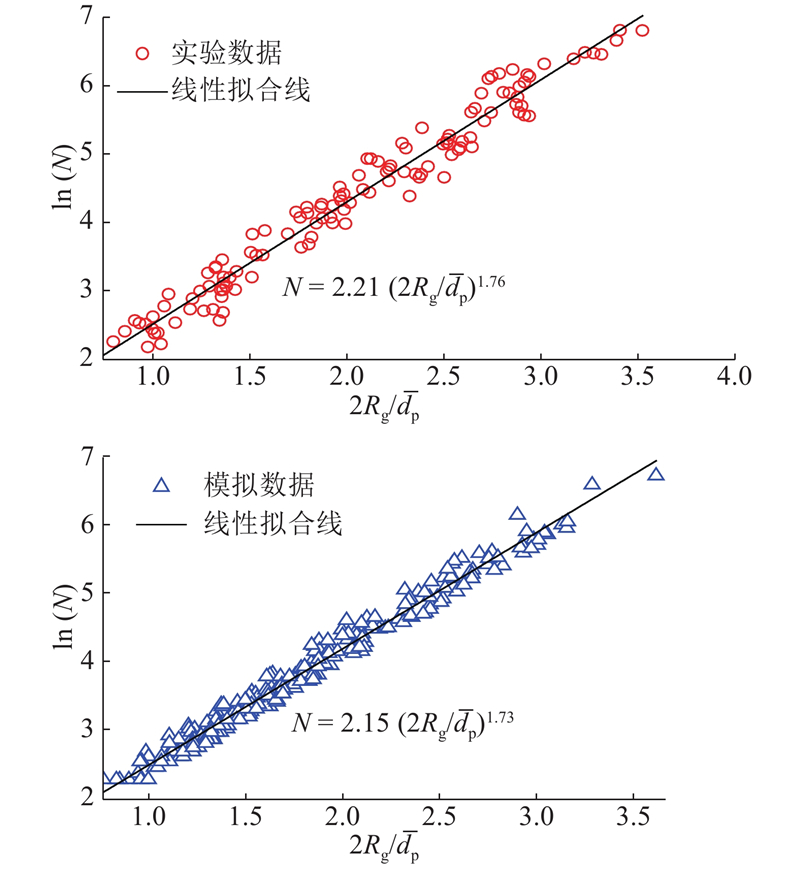
在碳黑基础颗粒团聚过程的模拟中,为避免碳黑基础颗粒的空间位置和运动速度不同而导致碰撞事件(由参与碰撞的双方及其速度和位置共同决定)不同,下一轮碰撞检测开始时,所有碳黑基础颗粒的空间位置和运动速度均以上一轮算法3的碰撞检测结果作为初始条件. 在不考虑3种算法所需的执行时间且均能满足第2章提出的碰撞检测准确度的前提下,模拟结果显示上述3种算法均能准确地从众多可能发生的所有碰撞中检测出第一个将要发生的碰撞. 从图7中可以看出,模拟所得的碳黑颗粒云团的外貌形态和在对应火焰高度上实验捕捉到的基本一致,完整地呈现了原本单一离散分布的碳黑基础颗粒经碰撞后逐渐形成尺寸越来越大的碳黑团聚体的过程. 图8给出了模拟生成的碳黑团聚体与实验观测到的碳黑团聚体的形态结构直观对比,可以看出,模拟生成的碳黑团聚体与具有相近N、Df和kf的真实碳黑团聚体在形态结构上非常相似,且模拟的碳黑团聚体中没有出现碳黑基础颗粒过度重合(ε < 0.95)和相离( ε > 1)的情况. 图9给出了火焰中碳黑团聚体分形参数的实验确定值和相应的模拟值. 其中,Rg和
图 9
图 9 碳黑团聚体分形参数的实验确定值和模拟值
Fig.9 Experimental determination values and simulation values for fractal properties of soot aggregates
图 8
图 8 模拟碳黑团聚体与实验捕捉到的真实碳黑团聚体的形态结构比较
Fig.8 Morphological comparison of simulated soot aggregates with real ones captured experimentally
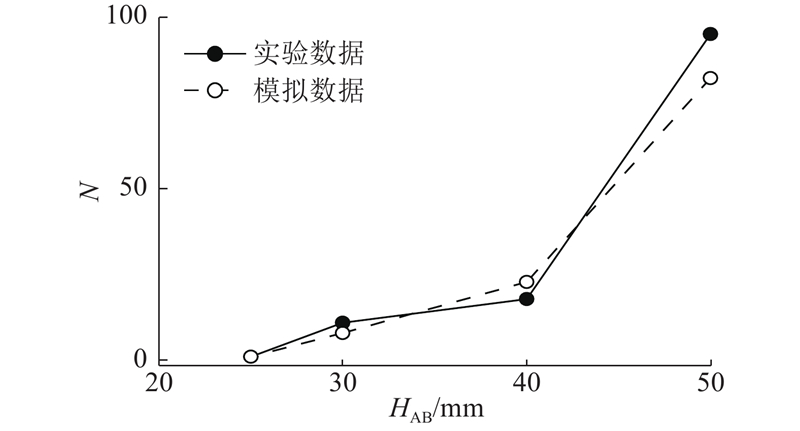
图 10
图 10 不同火焰高度上碳黑团聚体中基础颗粒平均数的模拟值和实验确定值对比
Fig.10 Comparison of simulation values for mean primary particle number per simulated soot aggregate with experimental determination values at different flame heights
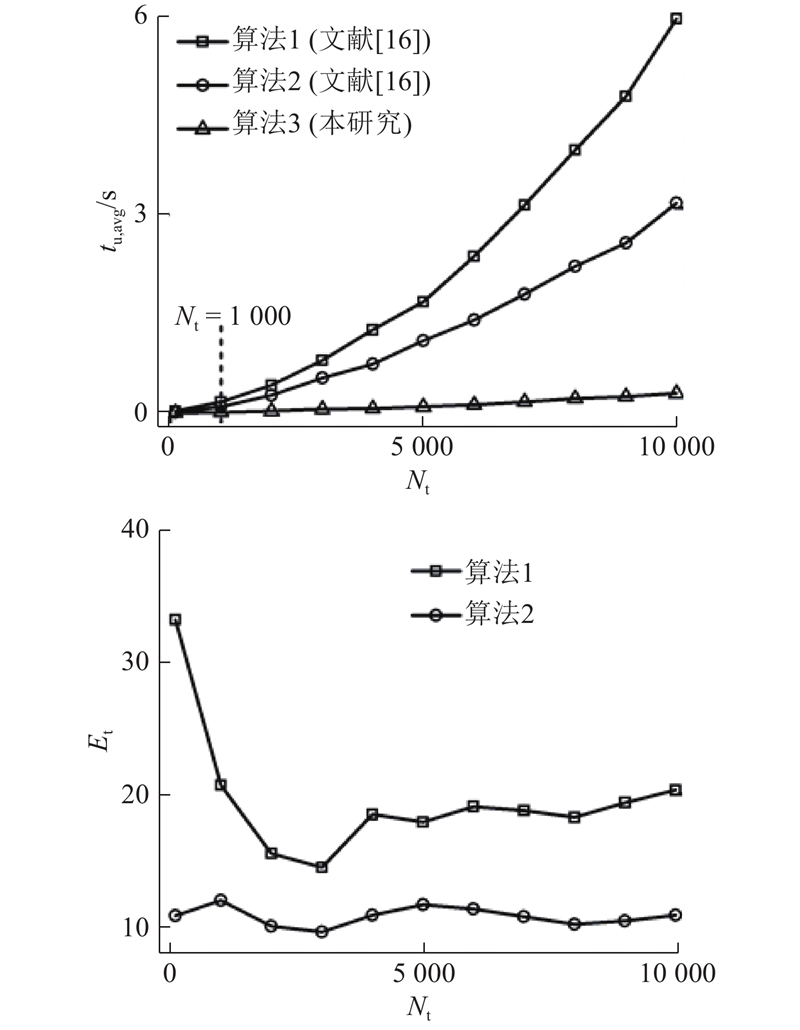
为了准确对比3种算法的执行效率,需要使用3种算法对相同的碰撞事件分别作出检测,以便获得其各自所需的执行时间. 图11给出了11种Nt条件下3种算法在每一轮碰撞检测中从众多将要发生的碰撞中准确检测出首个碰撞所需的平均执行时间:
图 11
图 11 3种算法碰撞检测执行时间和效率的对比
Fig.11 Comparison of average execution time and execution efficiency of collision detection using three algorithms
式中:tu, i为第i轮碰撞检测中准确检测出首个碰撞所需的执行时间,Nu为所要执行的碰撞检测的总轮数且被设定为2 000. 从图11中可以看出,当Nt < 1 000时,3种算法的 tu, avg都较小(< 160 ms),且绝对差不大;当Nt > 1 000时,算法1和2的 tu, avg随Nt增长迅速,而算法3的tu, avg随Nt则增长相对缓慢,结果算法3的tu, avg远小于算法1和2的tu, avg. 算法3执行时间的大幅度降低主要得益于“包围球-最大检测区域”和粗略筛选的引入,这些处理方法显著缩减了所要检测的碰撞双方的数量和精细确定阶段离散碰撞检测的次数. 另外,算法3相对于算法1和2的执行效率的提升倍数Et可用如下公式表示:
式中:tu,avg,3为算法3的平均执行时间。图11给出了11种Nt条件下算法3相对于算法1和2的执行效率的提升倍数Et,可以看出,算法3相对于算法1可将执行效率提升15~30倍,相对于算法2可将执行效率提升 10左右。
当算法1和2的执行时间与算法3所需的执行时间一致时,采用算法1和2模拟得到的碳黑团聚体,如图12所示. 从图中可以看出,当执行时间一样时,算法1和2将没有足够的执行时间来避免碳黑基础颗粒间过度重叠的问题(即没时间回退),导致达不到指定的碰撞检测精度. 另外,算法1和2也可能没有足够的执行时间检测到原本将要发生的碰撞. 因此,当执行时间过少时,采用算法1和2生成的碳黑团聚体将和采用算法3生成的碳黑团聚体差别越来越大,最终模拟结束后很难找到符合要求的碳黑团聚体.
图 12
图 12 当算法1或2与算法3所需的执行时间一致时采用算法1和2模拟得到的团聚体
Fig.12 Simulated soot aggregtes using algorithms 1 or 2 when execution times are equal to those of algorithm 3
综上所述,在满足相同碰撞检测准确性的前提下,算法3执行效率更高,更适用于大量颗粒团聚过程中的碰撞检测.
4. 结 语
结合布朗颗粒团聚过程中其平移速度和旋转速度每隔一段极短时间就需要重新初始化的自身特点,本文提出了一种基于“包围球-最大检测区域”预处理的“粗略筛选-精细确定”两步式碰撞检测算法. 模拟测试结果表明:在保证相同的碰撞检测准确性的前提下,当参与团聚的总颗粒数Nt < 1 000时,该优化算法和传统碰撞检测算法在每一轮碰撞检测中从众多将要发生的碰撞中准确检测出首个碰撞所需的平均执行时间 tu, avg的绝对差值不大,皆少于160 ms;当Nt > 1 000时,传统碰撞检测算法的 tu, avg随Nt呈指数级增长,而该优化算法随Nt的增长却较为平缓,结果该优化算法的tu, avg远小于传统算法的tu, avg,且其可将碰撞检测的执行效率提升10~30倍. 所提出的更加高效的碰撞检测算法将有助于大规模颗粒团聚过程模拟的快速实现.
参考文献
Cluster-cluster aggregation simulation in a concentrated suspension
[J].DOI:10.1016/j.jcis.2011.07.024 [本文引用: 3]
Brownian dynamics simulation of soot primary particle aggregation in laminar ethylene diffusion flames
[J].DOI:10.1016/j.physa.2018.09.119 [本文引用: 7]
可变形物体间的精确碰撞检测方法研究
[J].DOI:10.3778/j.issn.1002-8331.2009.01.054 [本文引用: 1]
Research on precise collision detection between deformable objects
[J].DOI:10.3778/j.issn.1002-8331.2009.01.054 [本文引用: 1]
结合轴对齐包围盒和空间划分的碰撞检测算法
[J].
Collision detection algorithm based on AABB bounding box and space division
[J].
基于空间分割与椭球包围盒的碰撞检测算法
[J].DOI:10.3778/j.issn.1002-8331.1405-0105 [本文引用: 1]
Collision detection algorithm based on ellipsoid bounding box and spatial decomposition
[J].DOI:10.3778/j.issn.1002-8331.1405-0105 [本文引用: 1]
USSCD: 一个基于均匀空间分割的快速碰撞检测算法
[J].
USSCD: a fast collision detection algorithm based on uniform spatial subdivision
[J].
基于图像的快速碰撞检测算法
[J].
A fast collision detection algorithm in image space
[J].
一种基于图像空间的碰撞检测算法
[J].
Collision detection algorithm based on image space
[J].
Brownian dynamics simulation of hard-sphere colloidal dispersions
[J].
Rheology and dynamics of colloidal dispersions
[J].DOI:10.1103/PhysRevLett.82.1792
Brownian dynamics, molecular dynamics, and Monte Carlo modeling of colloidal systems
[J].DOI:10.1016/j.cis.2004.10.001 [本文引用: 1]
Brownian dynamics simulation of the aggregation of submicron particles in static gas
[J].DOI:10.1016/j.compchemeng.2013.03.028 [本文引用: 3]
Impact of morphology on the radiative properties of fractal soot aggregates
[J].DOI:10.1016/j.jqsrt.2016.09.005 [本文引用: 1]
A feasible and accurate method for calculating the radiative properties of soot particle ensembles in flames
[J].DOI:10.1016/j.jqsrt.2018.11.023 [本文引用: 1]