随着市场竞争的日益激烈,环境保护意识的逐渐增强,如何更好地利用资源与能源以达到最优操作的目标,已经成为过程工业研究的重要内容. 传统的过程设计方法不能兼顾过程优化与运行控制的集成问题,造成过程设计与运行中各个环节相互脱节、衔接不够,成为制约过程工业发展的瓶颈问题.
过程工业中的实时优化(real time optimization,RTO)是指结合工艺知识和现场操作数据,通过快速、高效的优化计算,对操作运行中的生产装置参数进行调整,增强其对环境变化、市场变化的适应能力,保持生产装置始终处于高效、低耗、安全的最优工作状态[1]. 过程装置一旦投入运行,将始终被一系列影响因素所干扰. 影响因素可以分为外部不确定性和内部不确定性2种[2]:外部不确定性包括原料变化、公用资源的供应约束、市场需求变化和气候变化等;内部不确定性包括过程设备特性漂移以及来自过程中其他单元的影响等. 实时优化的目的是在满足所有约束条件的前提下,不断调整最佳工作点,以克服外部和内部不确定性因素,从而保证过程始终能够达到最佳经济效益[3]. 现有的工业生产系统大多能保持平稳的运行状态. 因此,在过程工业领域,进行稳态实时优化是合理的简化,避免动态建模和求解的困难. 本研究所提出的优化方法也属于稳态实时优化方法.
复杂工业过程的实时优化问题常采用递阶控制方法. 这种方法既包含优化层,又包含控制层,其核心思想是每个决策单元同时响应子过程优化,所有的优化层通过相互迭代达到最优解. 但是在实际应用中,迭代的发生使工业过程不能达到最优解,同时还可能违反某些约束. Brdys等[4]提出,从实际过程中提取变量的稳态信息,反馈至上一层的决策单元中,并利用它修正最优解,使其接近真实最优解. 另外,递阶控制方法的求解精度依赖于初始点的选取,Roberts[5]提出将系统优化与参数估计2个问题分开处理,使用修正乘子交替处理系统优化与参数估计2个问题,直至收敛到最优解. 这一方法称为系统优化与参数估计集成方法(integrated system optimization and parameter estimation,ISOPE). Tatjewski等[6-7]通过对迭代优化算法中设定点控制问题的研究进一步改进ISOPE方法. 传统的实时优化问题是根据过程的数学模型,在相应的约束条件下,优化所提出的目标函数. 近年来,随着生产规模越来越大,生产过程越来越复杂,传统基于模型的实时优化方法由于很难获得精确可靠的过程模型而变得具有局限性[8]. 测量值优化概念的引入,极大克服了传统优化方法的弊端,提高了预期的性能指标[9-10]. 最优性必要条件跟踪法[11]和自优化控制法[12]就属于这类优化策略. Araújo等[13]给出测量值优化策略更精确的定义,并将其成功应用于田纳西-伊斯曼挑战问题[14]. Halvorsen等[15]指出最优操作点附近的二阶近似值可以被用于寻找测量值的组合方式. 最优输出灵敏度矩阵也可以被用于寻找测量值的组合[16]. Srinivasan等[17-18]完成了其他相关优化策略的研究,并且考虑了不确定性因素的影响. 上述测量值组合的计算都是基于离线方法得到的,不需要使用显式的过程模型[19].
本研究针对工业过程的最优操作问题,提出基于梯度信息的实时优化与控制集成策略,通过对被控变量的合理选取,将控制层与优化层联系起来,形成优化控制集成的级联结构;给出求解被控变量的解析方法,提高计算效率,使优化效果具有全局性;利用算例验证所提方法的优越性.
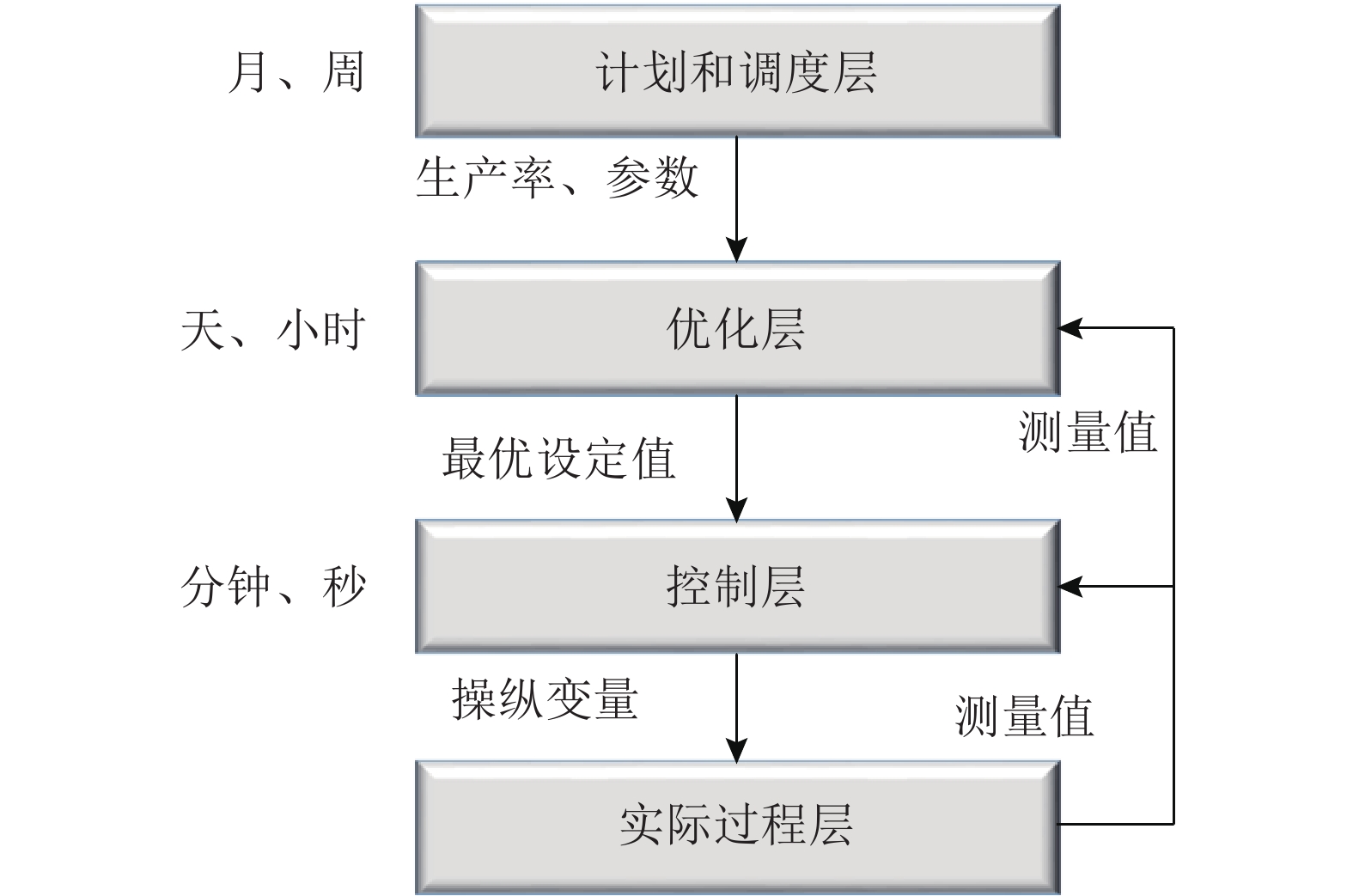
1. 过程系统的层次模型
图 1
近年来,随着优化技术的发展,在线优化技术被越来越多地用于寻找最优设定值. 不过,在线优化技术包括稳态检测、数据估计和数据调和等复杂的前序步骤,同时在线优化问题本身也是大规模的非线性优化问题. 鉴于以上原因,本研究提出基于梯度信息的稳态实时优化方法,这种方法不需要使用显式的过程模型,而是通过收集测量值,计算过程的梯度信息. 梯度信息可以被用来更新最优设定值,一旦设定值更新完成,将被传递到控制层作为目标去实现,设定值的更新大约需要几分钟至几小时. 优化层以下是控制层,控制层可以产生操纵变量直接作用于实际过程装置. 控制层包含2个部分,分别为多变量协调控制和基础回路调节. 多变量协调控制主要用于实现实时优化给出的最优设定值,其运行周期为秒或分钟. 目前过程工业主流的多变量协调控制算法是模型预测控制(model predictive control,MPC). MPC控制在处理各类操作变量和输出变量约束方面,有显著优势[22-23]. 基础回路调节主要用于消除快速干扰,实现单回路或串级回路的基本平稳运行,其运行周期一般等于集散控制系统的采样周期. 基础回路调节的主流控制算法是比例积分微分控制(proportion integral derivative, PID). 为了集成实时优化与控制,被控变量的选取尤为重要. 被控变量选取方法的主要思想为,在最优设定值更新期间,使所选被控变量对扰动信息不敏感. 在设定值更新期间只需要将被控变量调节到期望的设定值,就可以达到满意的控制效果. 所提出的实时优化与控制集成的级联结构如图2所示.
图 2
图 2 实时优化与控制集成的级联结构
Fig.2 Cascade structure of real time optimization and control integration
2. 基于梯度信息的稳态实时优化方法
2.1. 方法概述
考虑如下带有约束的稳态实时优化问题:
式中:
式中:w 为除去控制积极约束消耗的自由度后,剩余自由度对应的过程设定值向量.
式(2)中的等式约束(包括模型方程和积极约束)隐式地包含在目标函数
式中:
设新的迭代点为
式中:
假设海森矩阵
上述方法可以在一步迭代之后达到一阶最优性必要条件. G 、 H都与梯度信息有关,因此将此方法命名为基于梯度信息的稳态实时优化方法. 在通常情况下,由于可行性问题,需要在增量
为了计算增量
2.2. 利用最小二乘思想求解梯度向量
提出利用最小二乘思想求解梯度向量
设
则在设定点
令
设
则有
又因
根据矩阵
根据最小二乘的思想,求解线性矩阵方程组式(13)的解,即求解如下最小二乘问题:
式中:
最小二乘问题式(14)的最优解
3. 非线性过程被控变量的选取方法
真实的工业过程具有不同程度的非线性,如果将已有的线性优化控制方法应用于非线性过程,控制效果只能在标称工作点附近得到保证,具有较大的局限性. 考虑如下过程的最优化操作问题:
式中:
定义损失函数表达式为
式中:
将式(18)相对于
式中:
关于被控变量选取的推论如下:任意被控变量
上述推论的证明如下:
在不引起歧义的前提下,为了表述方便,后文直接用
针对连续的扰动空间
将式(23)写成矩阵的表达形式,并定义
式中:
由于矩阵
式(26)的最优解不一定存在,需要对决策变量
其最优解
综上所述,非线性过程被控变量的选取步骤如下. 1)将连续的扰动空间
4. 实时优化与控制集成策略
综合第2、3节的内容可以得到非线性过程实时优化与控制集成策略,具体表述如下:
在每一采样时刻
1)根据最小二乘思想,计算梯度向量
2)根据BFGS方法,计算海森矩阵的逆矩阵
3)更新设定点
4)通过第3节方法选取非线性过程的被控变量,即
5)通过相应的控制算法,将选取的被控变量
6)更新操纵变量
5. 实例研究
5.1. 数值算例
考虑如下单目标、单变量数值优化问题:
y 的表达式为
其标称工作点为
对
由
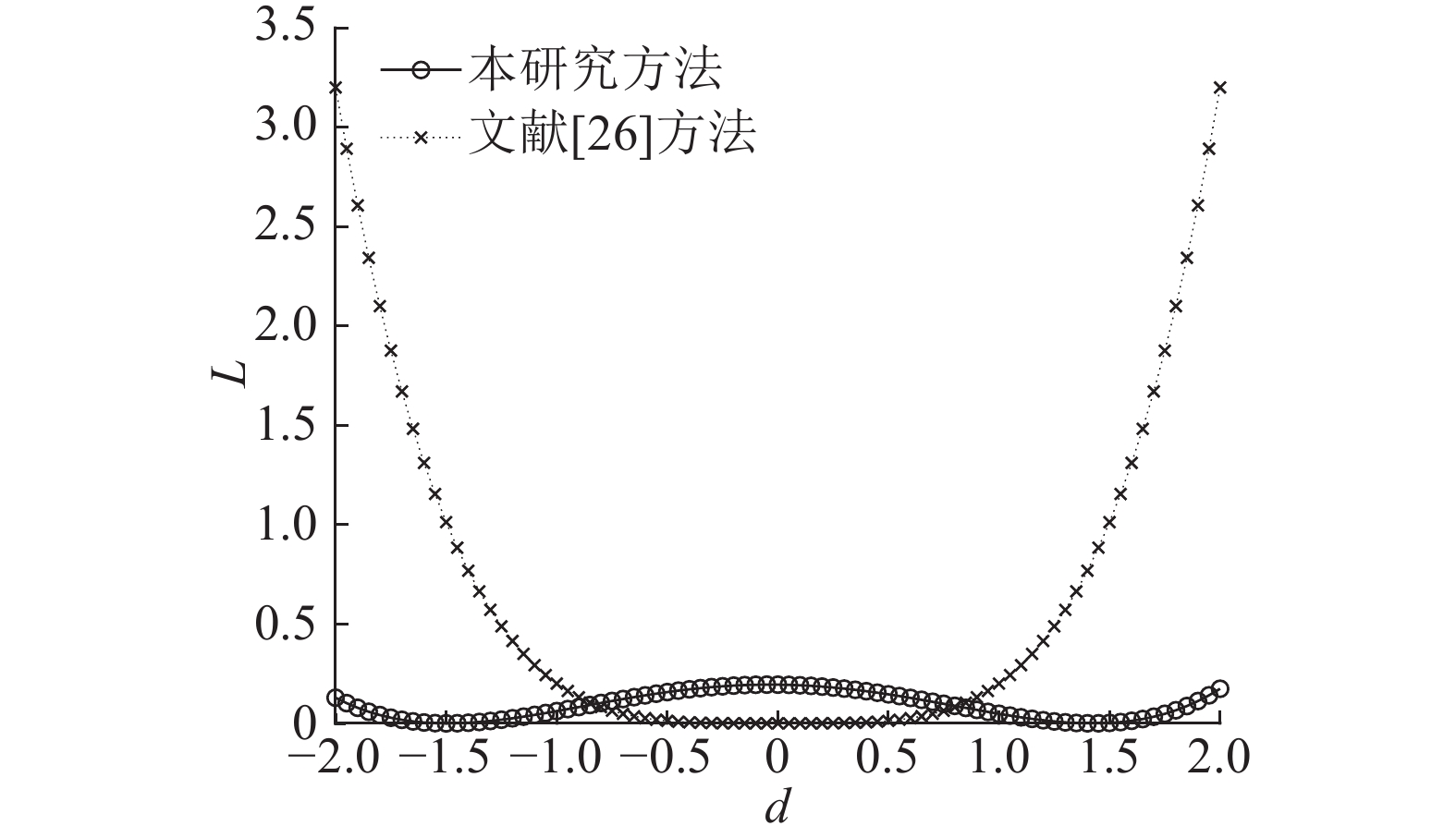
为了对比效果,使用文献[26]提出的基于零空间方法所选择的被控变量:
在扰动空间
图 3
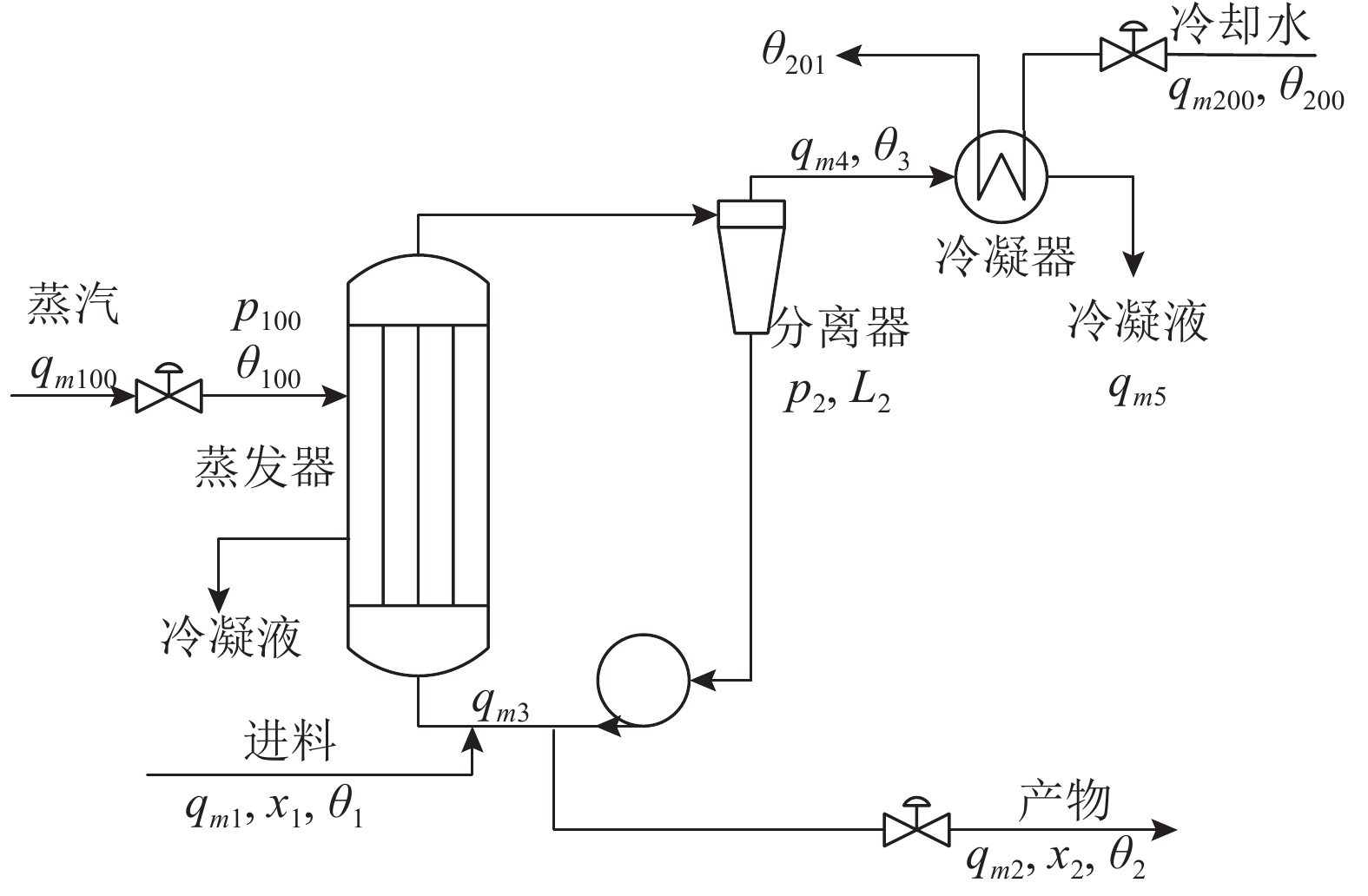
5.2. 蒸发过程
图 4
表 1 蒸发过程中变量的物理含义和标称值
Tab.1
| 变量名称 | 物理含义 | 标称值 | 单位 |
| qm1 | 进料质量流量 | 9.469 | kg/min |
| qm2 | 产物质量流量 | 1.334 | kg/min |
| qm3 | 循环质量流量 | 24.721 | kg/min |
| qm4 | 气相质量流量 | 8.135 | kg/min |
| qm5 | 冷凝液质量流量 | 8.135 | kg/min |
| x1 | 进料摩尔分数 | 5.0% | − |
| x2 | 产物摩尔分数 | 35.0% | − |
| 进料温度 | 40.000 | °C | |
| 产物温度 | 88.400 | °C | |
| 气相温度 | 81.066 | °C | |
| L2 | 分离器液位 | 1.000 | m |
| p2 | 操作压力 | 51.412 | kPa |
| qm100 | 蒸汽质量流量 | 9.434 | kg/min |
| 蒸汽温度 | 151.520 | °C | |
| p100 | 蒸汽压力 | 400.000 | kPa |
| Q100 | 热负荷 | 345.292 | kW |
| qm200 | 冷却水质量流量 | 217.738 | kg/min |
| 冷却水入口温度 | 25.000 | °C | |
| 冷却水出口温度 | 45.550 | °C | |
| Q200 | 冷却器热负荷 | 313.210 | kW |
该蒸发过程的
扰动变量
该过程的目标函数为最小化操作成本
该过程与产品质量、安全性、操作限制相关的约束条件如下:
式(38)中有2个约束在整个扰动空间中都是积极约束,即
表 2 本研究方法与文献[26]方法的计算效果对比
Tab.2
| 测量子集 | 本研究方法 | 文献[26]方法 | |||||
| Lav | Lmax | t/s | Lav | Lmax | t/s | ||
| y1 | 4.33 | 34.28 | 0.185 | 9.92 | 56.72 | 0.412 | |
| y2 | 0.37 | 5.08 | 0.354 | 0.53 | 7.86 | 1.271 | |
| y3 | 0.28 | 3.93 | 0.783 | 0.46 | 6.24 | 3.464 | |
| y4 | 0.42 | 6.65 | 1.371 | 0.61 | 9.93 | 7.323 | |
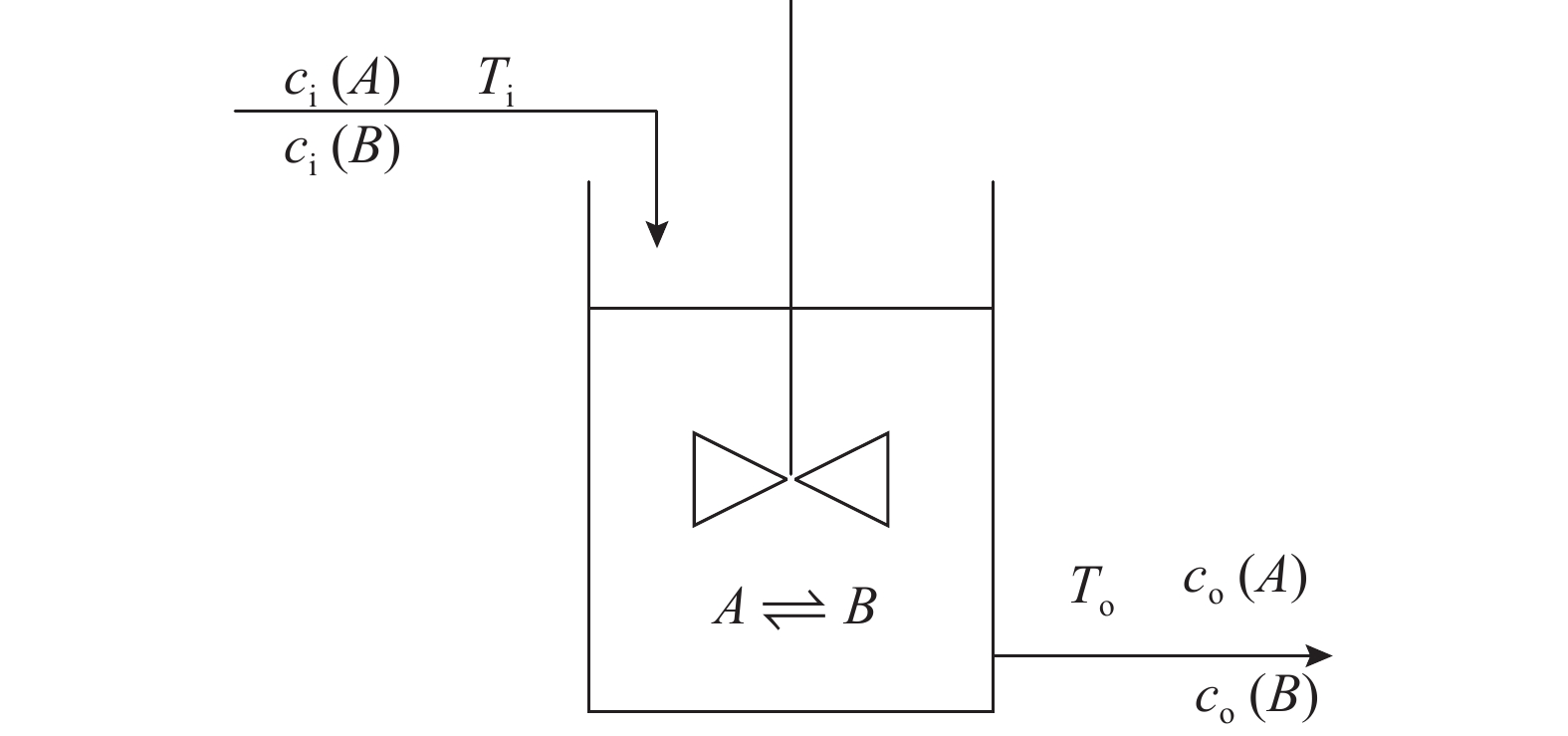
5.3. CSTR放热反应过程
连续搅拌釜式反应器(continuous stirred tank reactor,CSTR)包含可逆放热反应过程
图 5
图 5 连续搅拌釜式反应器反应原理图
Fig.5 Reaction schematic diagram of continuous stirred tank reactor
根据质量守恒定律和能量守恒定律,可以得到系统的微分方程描述形式:
式中:
该放热反应过程的
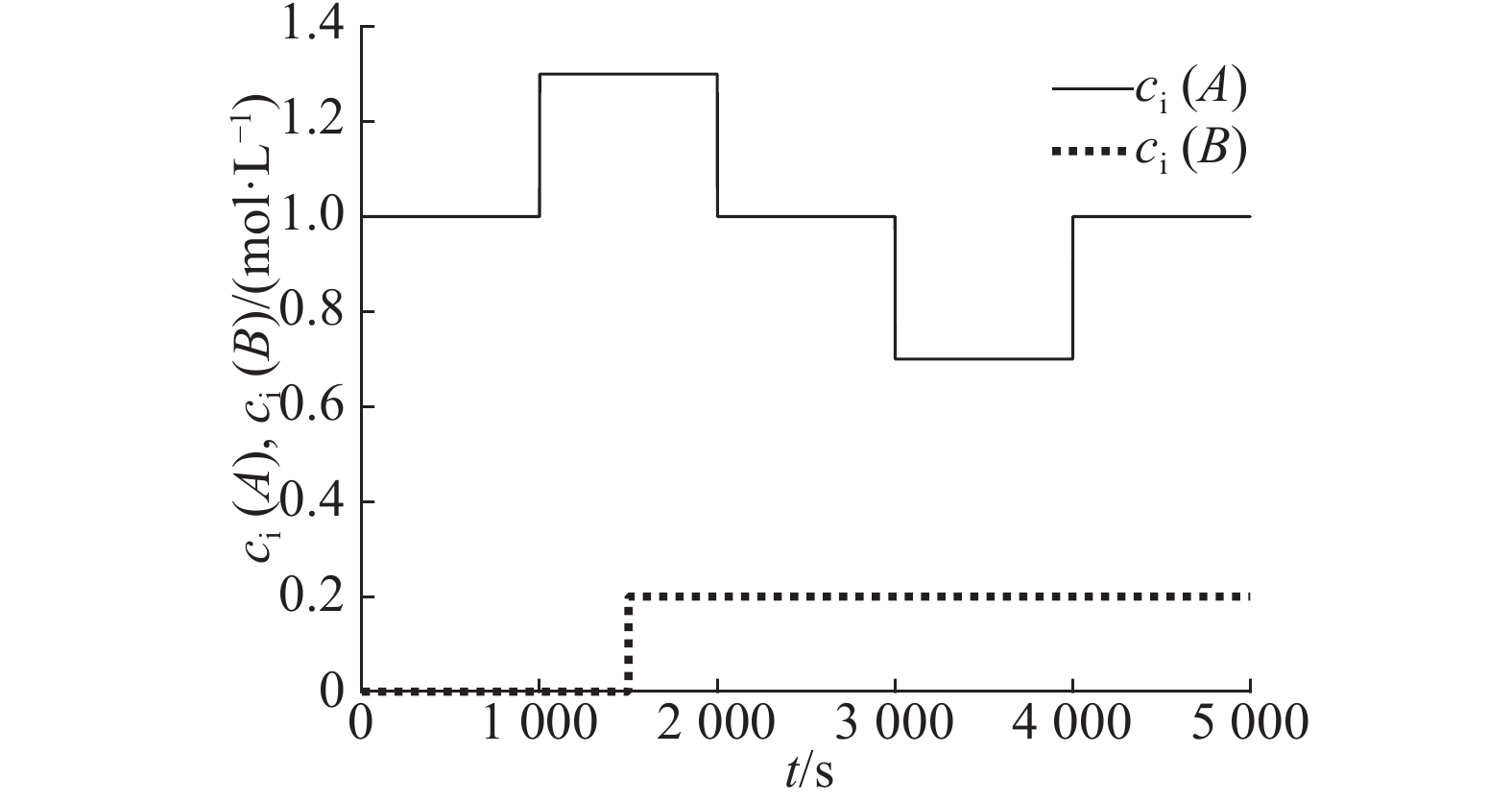
扰动变量
目标函数定义如下:
表 3 CSTR模型中变量的标称值
Tab.3
| 变量名称 | 标称值 | 单位 |
| co(A) | 0.498 | mol/L |
| co(B) | 0.502 | mol/L |
| To | 426.803 | K |
| ci(A) | 1 | mol/L |
| ci(B) | 0 | mol/L |
| Ti | 424.292 | K |
| τ | 60 | s |
图 6
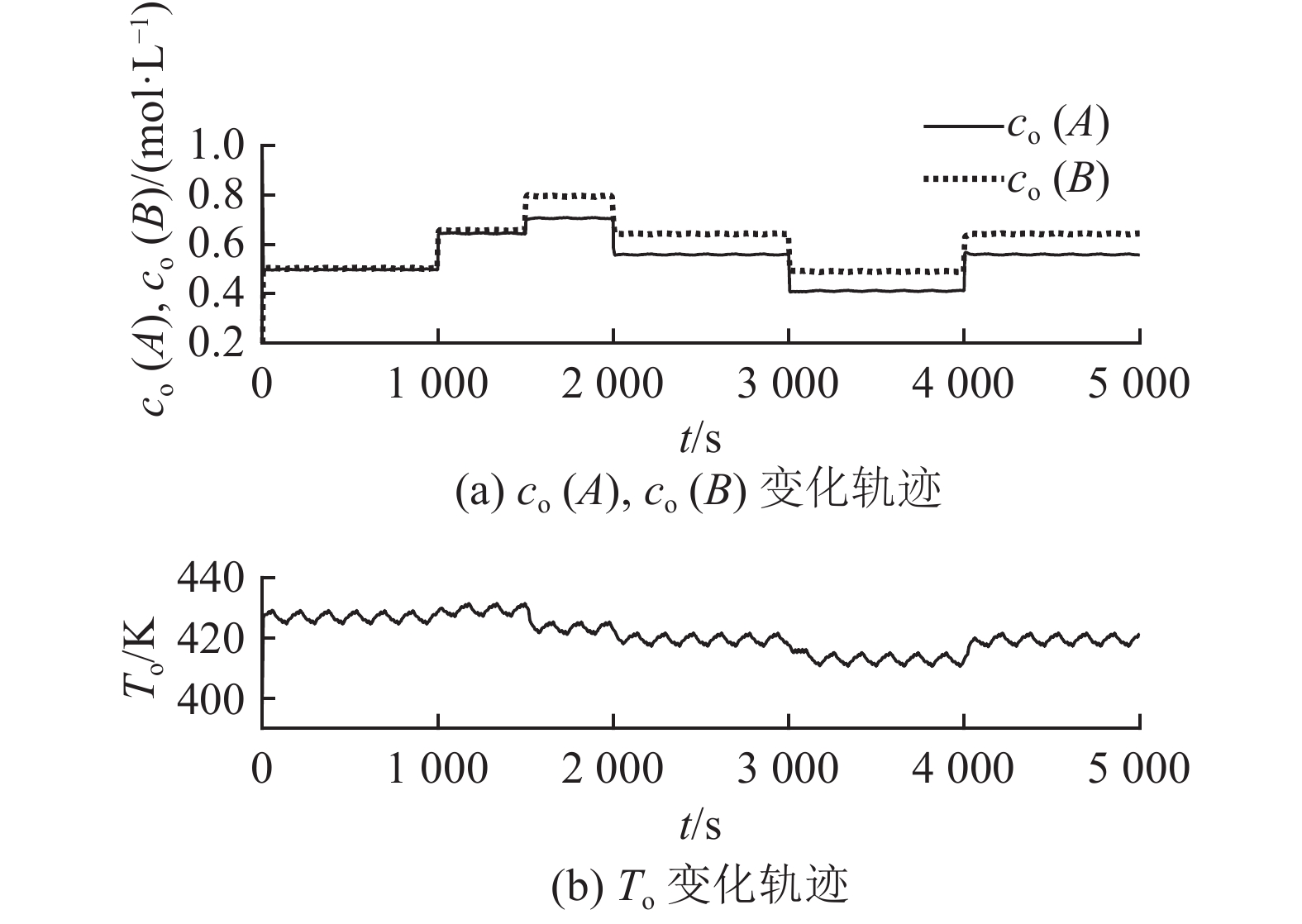
为了对比控制效果,选择文献[28]提出的最优条件跟踪法. 文献[28]提出的方法得到的测量变量
图 7
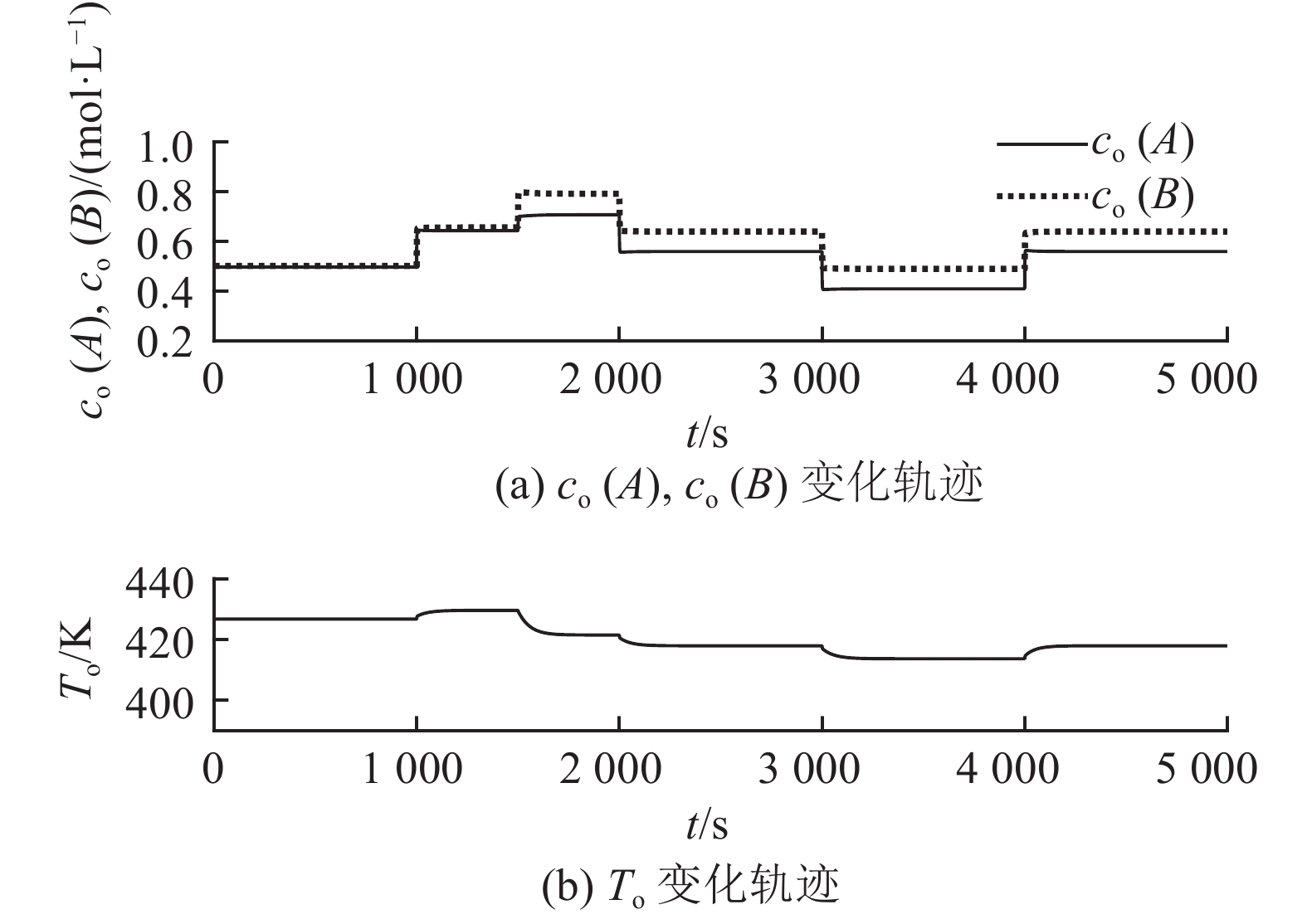
图 8
图 8 本研究方法得到的测量变量的变化轨迹
Fig.8 Trajectories of variables measured through proposed method
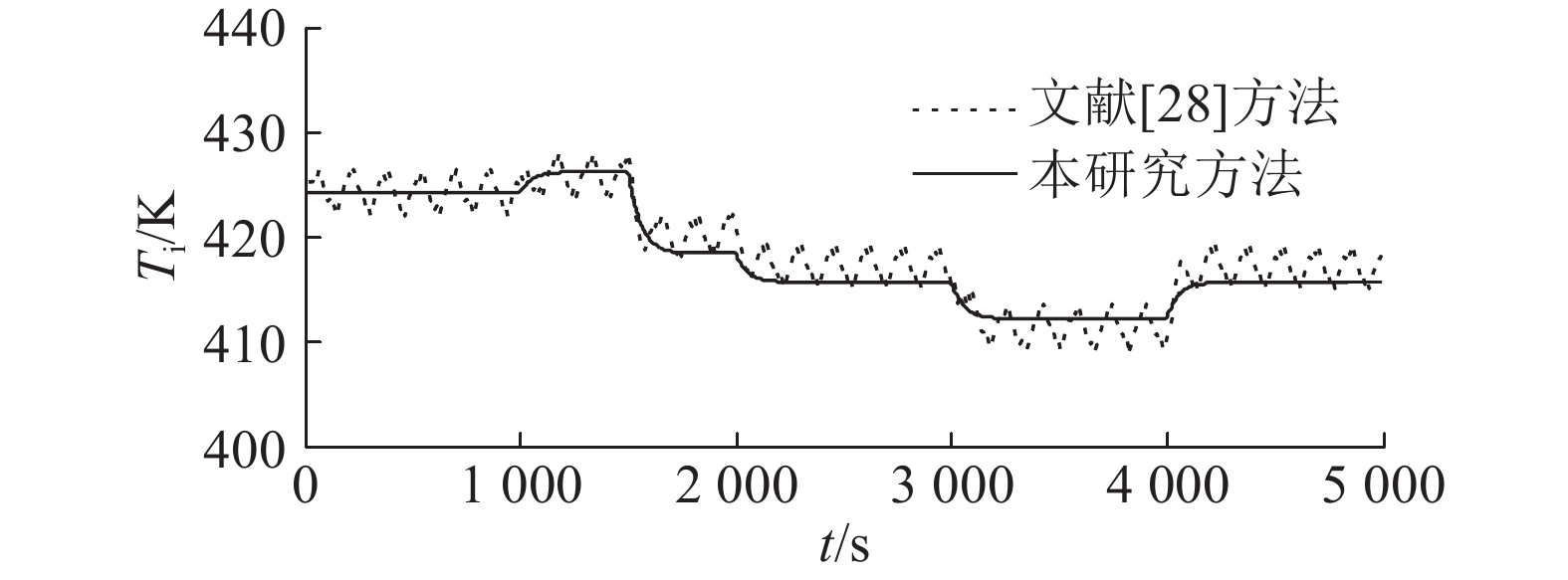
图 9
图 10
6. 结 论
(1)提出实时优化与控制集成的级联结构,对于优化层采用基于梯度信息的稳态实时优化方法,控制层中的多变量协调控制采用MPC控制算法,基础回路调节采用PID控制算法,通过对被控变量的合理选择,将优化层与控制层联系起来.
(2)提出基于梯度信息的稳态实时优化方法,通过对过程测量值的在线采集,估计过程的梯度信息,进而更新设定值. 由于不需要使用显式的过程模型,可以有效抑制模型失配对优化目标的影响.
(3)提出利用最小二乘思想求解梯度向量的方法,降低了计算成本,可以应用于大规模工业过程的稳态实时优化.
(4)提出非线性过程被控变量的选取方法,利用非线性模型计算平均损失,优化效果具有全局性. 为了快速求解非线性规划问题,对某些条件进行合理假设,从而获得次优解. 同时给出求解次优解被控变量的解析方法,由于只需要对构造出的矩阵进行特征值分解,不需要计算一阶或二阶灵敏度矩阵,提高了计算效率.
通过对数值算例、蒸发过程和放热反应过程的研究,验证了本研究提出的方法的有效性. 下一步研究的重点是考虑更加真实的过程对象,例如包含随机噪声的过程系统,或者过程的约束条件存在病态的情况. 另外,如何选择测量变量子集也是值得研究的方向.
参考文献
Enterprise-wide modeling and optimization: an overview of emerging research challenges and opportunities
[J].
Real time optimization as a tool for increasing petroleum refineries profits
[J].
Real-time optimization under parametric uncertainty: a probability constrained approach
[J].
An algorithm for steady-state system optimization and parameter estimation
[J].DOI:10.1080/00207727908941614 [本文引用: 1]
Iterative optimizing set-point control: the basic principle redesigned
[J].
Iterative set-point optimization of batch chromatography
[J].DOI:10.1016/j.compchemeng.2005.02.035 [本文引用: 1]
On the various local solutions to a two-input dynamic optimization problem
[J].DOI:10.1016/j.compchemeng.2016.09.003 [本文引用: 1]
Plantwide control: the search for the self-optimizing control structure
[J].DOI:10.1016/S0959-1524(00)00023-8 [本文引用: 1]
A necessary condition of optimality for uncertain optimal control problem
[J].DOI:10.1007/s10700-012-9147-4 [本文引用: 1]
Self-optimizing control of a two-stage refrigeration cycle
[J].DOI:10.1016/j.ifacol.2016.07.295 [本文引用: 1]
Application of plantwide control to the HDA process: I. steady-state optimization and self-optimizing control
[J].DOI:10.1016/j.conengprac.2006.10.014 [本文引用: 1]
Selection of controlled variables and robust setpoints
[J].
Optimal selection of controlled variables
[J].DOI:10.1021/ie020833t [本文引用: 1]
Global self-optimizing control for uncertain constrained process systems
[J].DOI:10.1016/j.ifacol.2017.08.691 [本文引用: 1]
Run-to-run optimization via control of generalized constraints
[J].DOI:10.1016/S0967-0661(01)00051-X [本文引用: 1]
Dynamic optimization of batch processes: II. role of measurements in handling uncertainty
[J].DOI:10.1016/S0098-1354(02)00117-5 [本文引用: 1]
Optimal measurement combinations as controlled variables
[J].DOI:10.1016/j.jprocont.2008.01.002 [本文引用: 1]
Cyber-physical modeling and cyber-contingency assessment of hierarchical control systems
[J].
Control structure design for complete chemical plants
[J].
RTO: an overview and assessment of current practice
[J].DOI:10.1016/j.jprocont.2011.03.009 [本文引用: 1]
Null space method for selecting optimal measurement combinations as controlled variables
[J].DOI:10.1021/ie060285+ [本文引用: 10]
Local self-optimizing control with average loss minimization
[J].DOI:10.1021/ie070897+ [本文引用: 1]
Use of measurements for enforcing the necessary conditions of optimality in the presence of constraints and uncertainty
[J].DOI:10.1016/j.jprocont.2004.11.006 [本文引用: 7]