房屋结构的地震易损性分析是采用概率统计方法预测结构在不同强度的地震作用下,达到或超过各级性能损伤水平的概率. 分析时,首先确定系统的随机变量并建立易损性分析样本,再输入不同的地震波进行动力响应分析,计算不同地震条件下结构破损状态的概率分布[1]. 目前,采用易损性分析方法评估地震引起的损伤,已被广泛地应用于各种房屋结构类型的抗震能力评估中. 地震易损性曲线是易损性的图形化表示.
结构工程地震灾变与岩土体特性密不可分,根据相关调查资料[2]可知,地震波通过岩土体传播和频谱放大,对上部结构的破坏更严重. 地基土体动力特性直接决定了结构基础的破坏形式,特别是当上部结构与地基刚度相差较大时,地基对结构动力响应的影响更突出[3]. 人们对地震波传播过程中地基的放大效应已有充分的认识,并进一步认识到局部地形作为不均匀散射体,会使地震波发生复杂的散射、波形转换及相干作用,使地震波产生局部放大或缩幅效应,从而对地震波特性产生关键性影响[4]. Tafazzoli等[5]对含矩形软弱土区域的地基进行动力分析发现,当矩形区域的宽度与深度之比小于4时,局部地形对地震波的放大作用十分显著. 金峰等[6]对含半椭圆形软弱土区域的地基动力分析发现,沉积层表面各点的响应显著放大. 尤红兵等[7]利用间接边界元方法,在频域内求解层状场地中任意形状沉积河谷对平面SH波的散射效应时发现,沉积河谷的散射效应使得地表位移幅值显著增大.
在新一代《中国地震波参数区划图(GB 18306—2015)》中,浙江省全面消除了非设防区. 杭嘉湖地区经济发达、人口密集、灾害波及效应大,该区域大部分地区从6度设防调整至7度设防[12],这意味着对区域内结构抗震性能要求的提高[13]. 杭嘉湖平原为典型的冲积平原,河流、河谷众多,所形成的河流淤积土具有强度低、土颗粒均匀、孔隙率高和地下水位高等特点;再加上杭嘉湖地区的城镇化程度高,回填池塘、河道并在回填后的地基上构筑房屋的情况非常普遍,导致典型的局部河谷、盆地特征. 基于杭嘉湖地区的典型地层、地质特点,研究地基软、硬土分布不均匀造成的局部河谷地形对结构动力响应和易损性的影响,对评估杭嘉湖地区房屋结构的抗震性能具有重要意义.
本文结合杭嘉湖地区的地质条件、结构特点以及抗震设防现状,选取18条地震波输入,对比不考虑地基、均质地基和河谷地基条件下典型民用住宅结构的动力响应. 考察房屋结构位于河谷不同位置处的响应差异,基于动力时程分析结果和概率统计方法,提出适用于杭嘉湖地区多层框架结构的地震易损性曲线. 以上工作为杭嘉湖地区典型的多层框架结构抗震性能的评估和抗震加固、维修决策提供了参考依据.
1. 分析模型
1.1. 结构模型
杭嘉湖地区历来经济发达,一方面近年来兴建了大量的高层、超高层公建、民建结构,另一方面存在大量老旧小区. 这些民用住宅以砖混结构与框架结构为主,楼层一般为5~7层,地基处理简单,抗震性能较差.
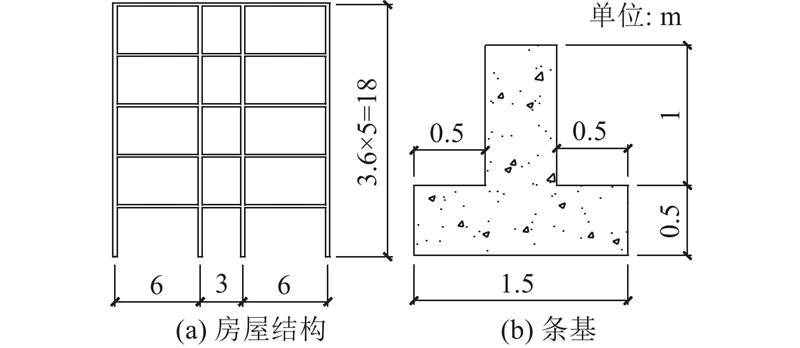
将这类典型民用住宅简化为5层3跨框架结构(下文中简称房屋结构),建立对应的二维模型,层高3.6 m,总高18 m. 梁的截面尺寸为200 mm×400 mm,C30混凝土、HRB335钢筋. 柱的截面尺寸为600 mm×600 mm,所用材料与梁一致. 基础形式为条形基础,埋深为1.5 m,C30混凝土,具体尺寸如图1所示. 楼面和屋面荷载取7 kN/m2.
图 1
结构的梁、柱构件均采用Timoshenko梁单元,混凝土和钢筋材料分别采用编辑材料属性和修改关键字的方式进行设置. 其中混凝土采用ABAQUS自带的混凝土损伤塑性(concrete damage plasticity)模型,该模型考虑损伤效应,能够较好地模拟地震作用下的混凝土力学行为[14]. 基本参数的取值[15]如下:混凝土弹性模量Ee取为2.2×104 MPa,泊松比μ取为0.2,混凝土单轴受压峰值应力fc,r和应变εc,r分别取为3.0 MPa和1.36×10−4,混凝土单轴受拉峰值应力ft,r和应变εt,r分别取为39.6 MPa和3.15×10−3. 为了考虑钢筋混凝土受拉硬化效应和箍筋的约束作用,根据高向玲等[15]提出的方法对混凝土的应力-应变关系进行修正. 钢筋通过编辑*rebar关键字在梁单元中实现插入,用来模拟钢筋混凝土构件中的纵筋,截面刚度直接根据钢筋纤维和混凝土纤维的单轴应力-应变关系,依据平截面假定积分得到[16]. 条基采用四节点缩减积分平面应变单元,混凝土材料的设置方式和材料参数与房屋结构构件一致. 考虑到实际施工中,柱-条基之间的连接方式多与柱-承台之间相同[17],因此参考庄海洋等[18]《土-桩-隔震结构动力相互作用》第8章中结构与承台的绑定连接方法,定义房屋结构与条基之间的连接.
为了使二维模型真实地反映三维结构的动力响应,对房屋结构的材料属性沿进深方向进行等效处理,即把相关参数除以布置间距换算成每延米的对应量,需要等效的参数包括弹性模量、单轴应力-应变曲线中的应力以及材料密度.
1.2. 地基模型
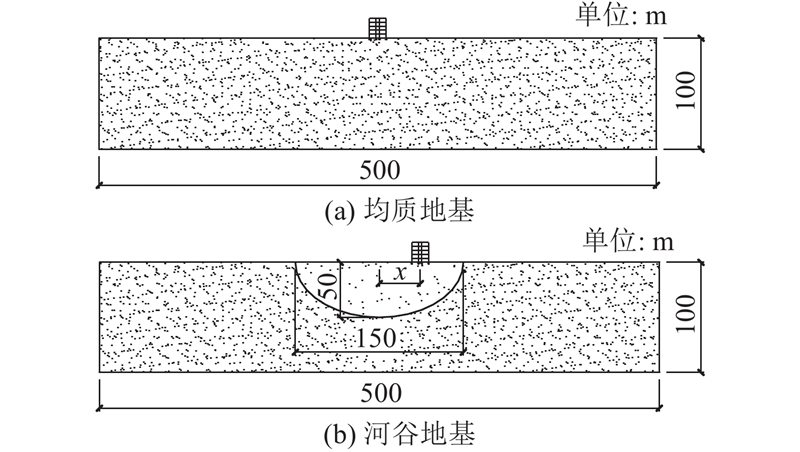
为了研究地基特性对房屋结构动力响应及易损性的影响,分析2种不同的地基:均质地基和河谷地基,同时与不考虑土-结动力相互作用的房屋结构动力响应进行比较. 不考虑地基的模型只建立房屋结构,约束柱底非激振方向上的自由度.
在均质地基中,将地基简化为单一均质粉质黏土,地基厚100 m,宽500 m,如图2(a)所示;考虑沉积河谷沿河流方向延伸,顺流向接近均质地基,因此取垂直流向的横剖面研究局部河谷地形的影响. 将河谷地基中的软土淤积区域简化为半椭圆型,顶面最宽处为150 m,深度为50 m,如图2(b)所示. 淤积软土周边为粉质黏土. 地基土体选用Mohr-Coulomb弹塑性模型,采用杭嘉湖地区常见的土层参数,参数取值来自文献[19]及其他工程资料,如表1所示. 地基土体采用四节点缩减积分平面应变单元,为了避免缩减积分导致的“沙漏效应”,在网格模块中勾选Enhance命令来解决沙漏问题. 为了研究房屋结构处于河谷不同位置处的动力响应特征,在河谷地基模型中分别考虑结构在河谷中心、河谷边沿以及处于两者之间的3种情况. 为了表述方便,将结构轴心离河谷中心的距离定义为x,用x=0、60和30 m分别表示以上3种情况.
表 1 地基土体参数
Tab.1
| 土层 | ρ/(kg·m−3) | E/MPa | μ | c/kPa | φ/(°) |
| 淤泥质土 | 1 820 | 149 | 0.49 | 5 | 20 |
| 粉质黏土 | 2 000 | 329 | 0.49 | 8 | 25 |
图 2
条基与地基土体的接触采用《ABAQUS在岩土工程中的应用》[20]第5章介绍的接触面对法. 选择刚度较大的条基表面作为接触面对的主控面,接触面之间的法向行为定义为“硬接触”,限制基础与地基土体在接触面上的法向行为,避免相互穿透,两者接触时才能产生法向接触应力,分离时应力为0;切向行为采用“罚函数”中的库仑摩擦模型,极限切应力可以表示为
式中:μ为条基和地基土体间的摩擦系数,p为接触面的法向应力,φ为对应土层的内摩擦角.
由于瑞利阻尼为正交阻尼,可以解耦复杂的动力方程,且具有形式简单、数学处理方便等优点,因此采用瑞利阻尼模拟地基和结构的阻尼. 阻尼矩阵
式中:α为质量比例阻尼,β为刚度比例阻尼.
α和β的计算方法较多,选用Hudson等[21]提出的QUAD4法进行计算:
1.3. 地震波输入和边界条件
分析时,仅考虑垂直入射SV波的作用. 不考虑土-结动力相互作用时,将地表的地震波记录以加速度的形式直接施加在房屋结构柱底端,来实现外部激励. 考虑土-结动力相互作用时,多通过等效线性化法[26]或时域非线性逐步积分法[27]等,将地表地震波记录反演至基岩(模型底部)处作为激励输入,保证地震波传播到地表时与实测记录相当. 本文利用等效线性地震场地响应分析软件EERA的反演功能,将均质地基地表地震波反演至地基底部,再将得到的加速度时程积分为速度时程,根据式(6)将速度转化为结点力施加在地基的底部边界上[28],作为激励输入. 在分析局部河谷地形的影响时,地震波输入与均质地基相同,考察相同输入下局部地形对地震波的放大作用. 利用等效线性化方法实现地震波反演的优势是计算原理和迭代思路简单,土体动力参数容易获取,地震分析计算量少,已被证明在数值模拟中结果合理[27].
式中:uz为地基底部边界上节点的切向运动位移,ρ为质量密度,cs为S波的波速.
图 3
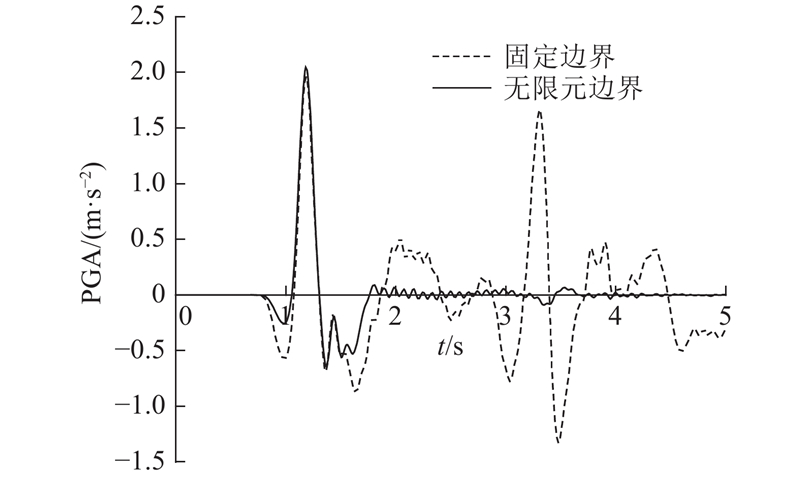
图 3 地表中心点加速度时程曲线
Fig.3 Acceleration time history curve of surface center point
当地震波首次传播至地表时,两条曲线几乎重叠,加速度信号经自由表面反射形成峰值为2 m/s2的半正弦波. 之后,2条曲线的差异较大,在固定边界下,由于能量无法透射,地震波在计算区域内来回振荡,地表多次接收到加速度信号,产生多个峰值,从而引起较大误差;在无限元边界下,地震波反射至底部边界后能够很好地被吸收,地表不再接收到地震波信号,加速度趋近于0. 可见,无限元边界吸收能量的效果较好,应用无限元边界分析土-结动力相互作用问题是可靠的.
1.4. 地震波选取
表 2 实际地震记录
Tab.2
| 地震名称 | 年份 | Ms | R/km |
| EL Centro | 1979 | 6.6 | 2.5 |
| Chichi | 1999 | 7.6 | 7.3 |
| Taft | 1952 | 7.4 | 41.0 |
| Kobe | 1995 | 6.9 | 15.5 |
| Loma Prieta1 | 1989 | 6.9 | 70.4 |
| Loma Prieta2 | 1989 | 6.9 | 28.6 |
| Loma Prieta3 | 1989 | 6.9 | 35.5 |
| Northridge1 | 1994 | 6.7 | 7.1 |
| Northridge2 | 1994 | 6.7 | 6.2 |
| Whittier Narrows | 1987 | 5.3 | 4.4 |
| Coalinga | 1983 | 6.0 | 10.0 |
| Kocaeli | 1999 | 7.4 | 67.5 |
| Mammoth Lake | 1980 | 4.9 | 7.5 |
| San Fernando | 1971 | 6.6 | 12.0 |
| Coyote | 1979 | 5.7 | 12.6 |
| Nahanni | 1985 | 6.8 | 6.0 |
| Duzce | 1999 | 7.2 | 8.2 |
| Cape Mendocino | 1992 | 7.1 | 9.5 |
图 4
2. 动力响应
2.1. 结构自振周期
不考虑地基和均质地基的一阶自振周期分别为0.88和1.78 s,河谷地形3处的自振周期均为1.79 s. 可以看出,不考虑地基模型的房屋结构一阶自振周期约为其他模型的一半,均质地基模型与河谷地基模型之间的差异很小. 这是由于考虑地基后,整个模型质量大大增加,导致自振周期大幅上升,该现象在考虑土-结动力相互作用的动力分析中普遍存在[34]. 此外,局部河谷地形对模型自振周期的影响不明显;房屋结构在河谷地基中的所处位置对模型的自振周期没有影响.
2.2. 局部河谷地形下地基的放大效应
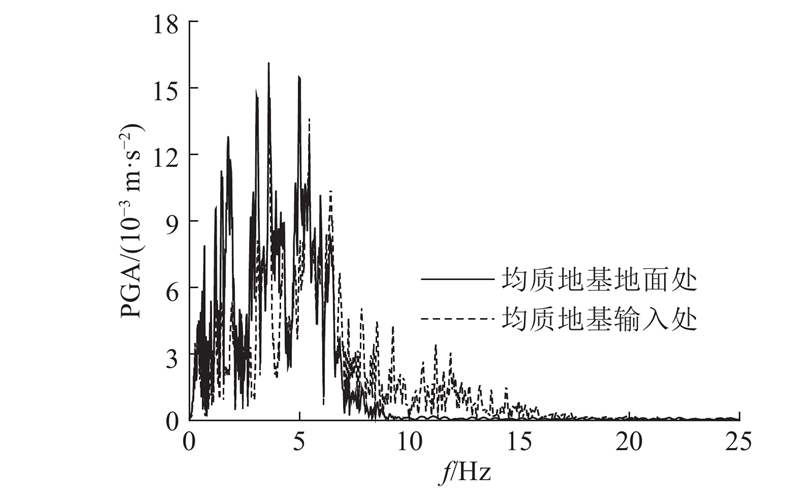
地震波的反演分析表明,均质地基对地震波具有滤波与放大作用. 以Northridge1波为例,图5给出均质地基模型地面处和反演分析得到的基底处的加速度曲线. 当地表加速度峰值为1.0 m/s2时,反演得到基底加速度峰值为0.7 m/s2,放大系数为1.4. 在不同的地震波输入下,均质地基模型的加速度放大系数略有不同,变化范围为1.07~1.51. 如图6所示为图5中加速度时程对应的傅里叶谱. 地基对加速度的不同频率成分作用不同,如图6所示,Northridge1波频谱变化特征为低频加震和高频减震,其中频率为0.3~5.0 Hz的低频分量加震现象比较明显,频率>7.5 Hz的高频分量减震现象比较明显. 此外,不同地震波的频谱在均质地基的作用下表现出类似的变化规律,但加震和减震的频率范围不同.
图 5
图 5 均质地基模型地面、基底处的加速度时程曲线
Fig.5 Acceleration time history curve of homogeneous foundation model at ground and base
图 6
图 6 均质地基模型地面、基底的加速度傅里叶谱
Fig.6 Acceleration fourier spectrum of homogeneous foundation model at ground and base
在Northridge1波的输入下,均质地基模型柱底加速度峰值为1.0 m/s2,河谷地基模型x=0、30、60 m处加速度峰值分别为12.9、12.5、10.3 m/s2,可见河谷地基结构柱底处的加速度峰值整体上高于均质地基,且不同位置的地震放大效果不同.
图 7
图 7 均质地基、河谷地基模型柱底加速度反应谱比
Fig.7 Acceleration response spectral ratio of homogeneous foundation and valley foundation model at bottom of column
在不同的地震波输入下,均呈现出地震波附加放大的聚焦效应,但聚焦点的位置因地震波的主频不同而变化,这一现象与Semblat等[38]的研究成果一致. 针对本文研究的工况,各地震波的聚焦点多出现在河谷中心处,少数出现在河谷边沿处.
2.3. 结构变形
以Northridge1波输入为例,说明局部河谷地形对房屋结构变形的影响. 计算表明,房屋结构各层的最大侧向位移发生在结构端点处,因此将结构各层左侧端点作为参考点进行分析. 图8(a)给出不考虑地基、均质地基和河谷地基模型的结构侧向最大位移包络线. 图中,L为层数,0层指柱底位置. 从图8可以看出,侧向位移有一个共同特征,即1层处楼房侧移最大、2~5层依次减小. 由于没有约束各模型柱底水平方向的自由度,允许柱底发生侧向位移,导致0层的侧向最大位移受到较大影响. 为了消除这一影响,给出如图8(b)所示的层间最大位移包络线. 层间最大位移是地震作用过程中相邻两参考点发生的最大相对位移. 与不考虑地基模型相比,考虑土-结动力相互作用后,层间最大位移发生位置从4层变为1层,这一结构变形规律与汶川地震灾害调查中的框架结构破坏现象一致[39];层间最大位移从2.53 mm变为3.33 mm(均质地基),放大了1.3倍,河谷地基模型中层间最大位移增大更明显,x=0、30、60 m处的层间最大位移分别为不考虑地基模型的1.8、1.5、1.4倍,可见局部河谷地形对结构变形具有明显的放大作用,且房屋结构离河谷中心越近,结构变形越大. 在其他地震波的作用下,呈现出类似的特征,表现为:在河谷地基中,房屋结构距聚焦点越近,结构变形越大.
图 8
3. 房屋结构的地震易损性
3.1. 地震易损性分析方法
杭嘉湖地区的设防烈度为6、7度,根据建筑抗震设计规范[40]中所规定的抗震设防烈度和设计基本地震加速度峰值(PGA)取值的对应关系,同时考虑到易损性曲线的完整性,将所选18条地震波的PGA分别调整为0.5、1、2、3和4 m/s2;根据1.3节方法,将调幅后的地震波分别输入到各组模型中,则每组模型地震易损性分析的样本容量均为90个.
将5组模型共450个样本进行时程分析,得到各组模型在不同地震峰值、不同地震波输入下的层间最大位移角,李刚[42]认为在相同的PGA下层间最大位移角服从对数正态分布:
式中:
结构的破坏概率函数,即在某一特定的PGA下层间最大位移角超过某一性能水平限值的概率
式中:
通过以上计算,可得各模型在不同PGA下的超越概率,将其描绘在以PGA为横坐标、超越概率为纵坐标的坐标系中,并依次连接,绘得对应的地震易损性曲线.
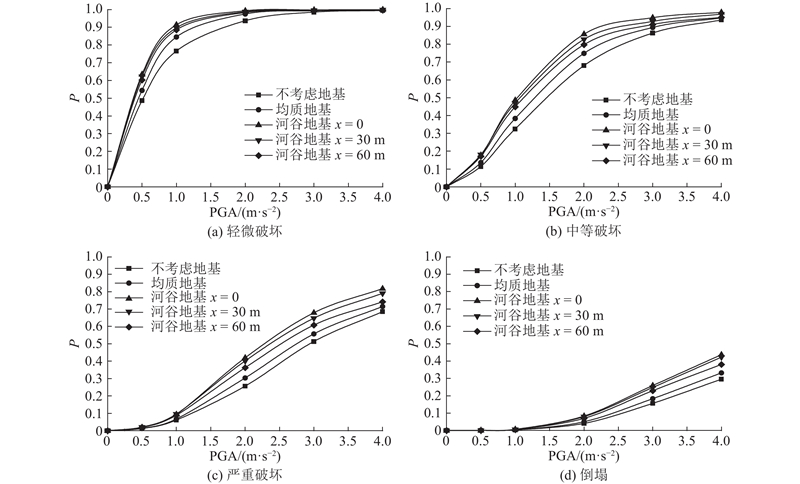
3.2. 考虑河谷地形影响的地震易损性曲线
图 9
图 9 考虑局部河谷地形的结构地震易损性曲线
Fig.9 Seismic fragility curves considering local valley terrain
从图9(a)可知,在轻微破坏性能水平下,5组模型的易损性曲线随PGA变化的趋势基本一致,均表现为在PGA较小时超越概率增长较迅速,在PGA=1 m/s2处易损性曲线出现拐点,随后超越概率增长变缓并逐渐趋近于1. 不考虑地基模型的超越概率整体上小于其他2种模型,说明不考虑土-结动力相互作用,会低估轻微破坏性能水平下的超越概率. 河谷地基的超越概率整体上大于均质地基,可见位于河谷地基上的房屋结构更易发生破坏,河谷地基x=0、30、60 m处的易损性相差不大.
图9(b)~(d)所示的3组曲线具有类似的特征:在中等破坏、严重破坏和倒塌性能水平下,超越概率在PGA较小时随着PGA的增加缓慢增长,当曲线出现第1个拐点(对应3种性能水平拐点位置分别为:PGA=0.5、1、2 m/s2处)后超越概率增长加快,以中等破坏性能水平为例,曲线在PGA=2 m/s2处出现第2个拐点,随后超越概率增长变慢并逐渐趋近于1. 对于严重破坏和倒塌性能水平,本文虽然未绘出完整的易损性曲线,但可以推测随着PGA的增大,超越概率的变化趋势与中等破坏性能水平类似. 除此之外,还能从图9(b)~(d)中得到与图9(a)类似的结论:在考虑土-结动力相互作用和局部河谷地形的影响后,房屋结构在相应性能水平下的超越概率有一定程度的增大. 房屋结构在性能水平较低的中等破坏、严重破坏和倒塌状态下,河谷地基不同位置处易损性的差异较轻微破坏明显增大.
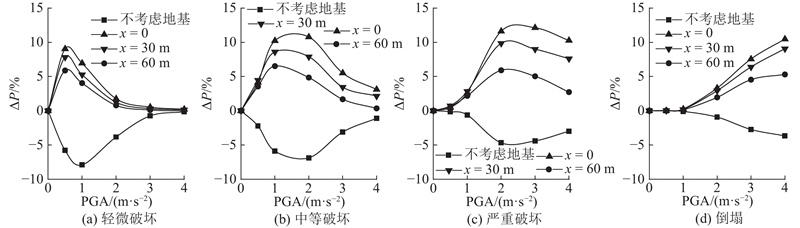
为了定量分析土-结动力相互作用与局部河谷地形对结构易损性的影响,不考虑土-结相互作用、河谷地基x=0、30、60 m处结构的超越概率分别与位于均质地基上结构的超越概率作差比较,得到相应的超越概率增加量ΔP,如图10所示. 可以看出,在各性能水平下,不考虑地基影响时,超越概率减小,降幅最大为−7.9%,发生在轻微破坏性能水平下. 河谷地基3处超越概率均增大,最大增幅为12.1%,发生在严重破坏性能水平下的x=0处. 在相同的性能水平下,3条增幅曲线的变化趋势一致. 小震时,三者重合,表明位于河谷地基不同位置处的增加量一致,当PGA增大时,不同位置处的增加量不同,以轻微破坏性能水平为例,位于x=0、30、60 m处的超越概率最大可以增加9.0%、7.8%、5.9%,即结构离河谷中心越近,越容易破坏. 在其他性能水平下超越概率增加量表现出类似的规律. 这是由于在所研究的工况中,大多数地震波的聚焦点出现在河谷中心处,位于河谷中心附近的结构将承受更大的地震波作用,导致在相同条件下结构距河谷中心越近、损伤程度越高,发生破坏的概率越大. 在土-结动力相互作用与局部河谷地形的影响下,结构在不同性能水平下超越概率增加量峰值所对应的PGA从小到大分别为: 轻微损伤、中等损伤、严重损伤、倒塌.
图 10
图 10 河谷地形影响的超越概率增加量
Fig.10 Exceedance probability increase of local valley terrain
4. 结 语
杭嘉湖地区为冲积平原区,土体强度较低,地基具有较典型的局部河谷、盆地特征. 本文结合杭嘉湖地区的地形特点、地基条件及抗震设防区划要求,建立考虑土-结动力相互作用的框架结构数值模型,在所选取的18条地震波作用下,对比不考虑地基、均质地基、河谷地基条件下房屋结构的动力响应和地震易损性,分析结构位于河谷地基不同位置处的响应差异.
不考虑土-结动力的相互作用,多会低估房屋结构的结构变形,对应的易损性性能水平超越概率偏低,最大偏差为7.9%,结果偏于危险. 局部河谷地形独特的聚焦效应会增大房屋结构的结构变形,加剧房屋结构震害. 河谷地基中不同位置处房屋结构的结构变形明显不同. 本文所研究的工况下,房屋结构距河谷中心越近,结构变形越大、相应性能水平的超越概率的增量越大,最大增量为12.1%. 对位于河谷地基上的房屋结构进行易损性分析时,应根据相应地质勘探资料计算地震波聚焦点范围,考虑结构与聚焦点的相对位置对房屋结构易损性的影响.
参考文献
汶川大地震震害特点与成因分析
[J].
Characteristics and mechanism analysis of the Great Wen Chuan Earthquake
[J].
上部结构与地基相对刚度比对土-结构体系基频影响试验研究
[J].
Experimental investigation on the effect of the relative stiffness ratio between superstructure and ground soil on the fundamental frequency of soil-structure system
[J].
Seismic site effects observed on sediments and basaltic lavas outcropping in a test site of Catania, Italy
[J].
半椭圆形河谷上沉积层地震响应研究
[J].
Seismic response of sedimentary layers in semi-oval valley
[J].
层状场地中任意形状沉积河谷对平面SH波的散射
[J].
Scattering of planar SH waves by arbitrary shaped sediments in a layered field
[J].
基于性能的方钢管混凝土框架结构地震易损性分析
[J].
Performance-based seismic fragility analysis of CFST frame structures
[J].
Seismic fragilities for non-ductile reinforced concrete frames: role of aleatoric and epistemic uncertainties
[J].
Fragility analysis of steel moment frames with various seismic connections subjected to sudden loss of a column
[J].
新版《中国地震波参数区划图》简介及对浙江省的影响
[J].
Influence of the brief introduction of the new edition of《Zoning Map of the Seismic Parameters of China》
[J].
不同抗震设防RC框架结构抗倒塌能力的研究
[J].
Study on the collapse-resistant capacity of RC frames with different seismic fortification levels
[J].
基于ABAQUS梁单元的钢筋混凝土框架结构数值模拟
[J].
Numerical simulation of a RC frame based on abaqus beam elements
[J].
土-桩-框架结构非线性相互作用的精细数值模型及其验证
[J].
The fine numerical model of soil-pile-frame structure nonlinear interaction and its verification
[J].
嵌固部位柱钢筋的施工工艺
[J].
Construction process of reinforced steel bar embedded in site
[J].
嘉兴市软弱地基工程特性及桩基持力层评价
[J].
Evaluation on features of soft foundation engineering andbearing layer of pile in Jiaxing city
[J].
Numerical analysis of ground surface vibration induced by underground train movement
[J].
结构地震反应时程分析中的阻尼问题评述
[J].
Comments on damping in structural seismic response time analysis
[J].
瑞利阻尼系数确定方法对高土石坝地震反应的影响研究
[J].
Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response
[J].
改进的瑞利阻尼系数计算方法在岸桥结构地震反应分析中的应用
[J].
Application of improved Rayleigh damping coefficient calculation method in seismic response analysis of shore bridge structure
[J].
汶川MS8. 0地震河谷地形对汉源县城高烈度异常的影响
[J].
Effects of river valley topography on anomalously high intensity in the Hanyuan town during the Wenchuan
[J].
波动方程的逆散射与迭代线性化反演
[J].
Inverse scattering of wave equations and iterative linearization inversion
[J].
ABAQUS动力无限元人工边界研究
[J].
Study of ABAQUS dynamic infinite element artificial boundary
[J].
基于无限元和波场分离法的地震响应数值分析
[J].
Numerical analysis of seismic response based on infinite element and wave field separation method
[J].
On near-fault ground motion characteristics through multi-scale method
[J].
Quantification of building seismic performance factors
[J].
苏浙沪及邻区深部构造及其与地震活动性的关系
[J].
Deep structures and their relation to earthquake activity in Suzhizi and neighboring areas
[J].
考虑桩-土-结构相互作用下斜拉桥桥塔地震反应模拟
[J].
Seismic response simulation of cable-stayed bridge tower considering pile-soil-structure interaction
[J].
Empirical model for basin effects accounts for basin depth and source location
[J].
场地盆地效应的振动台试验
[J].
Shaking table test of site basin effect
[J].
圆弧状沉积盆地与软土单覆盖层出平面地表运动对比
[J].
Comparison of out-of-plane surface ground motion between a circular-arc alluvial valley and a single overburden soft layer
[J].
汶川8. 0级地震中各类建筑结构地震易损性统计分析
[J].
Statistical analysis of the seismic fragility of various types of building structures in WenchuanM8. 0 earthquake
[J].