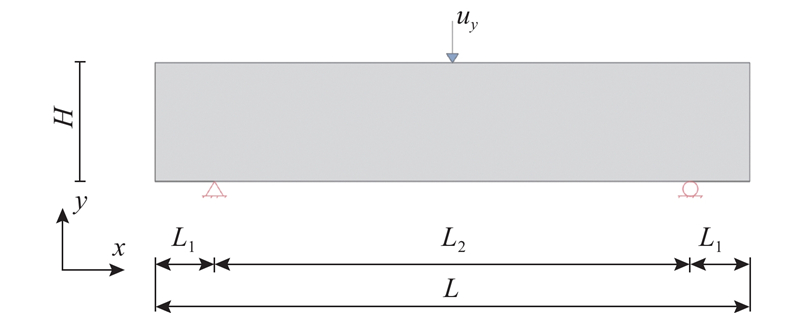
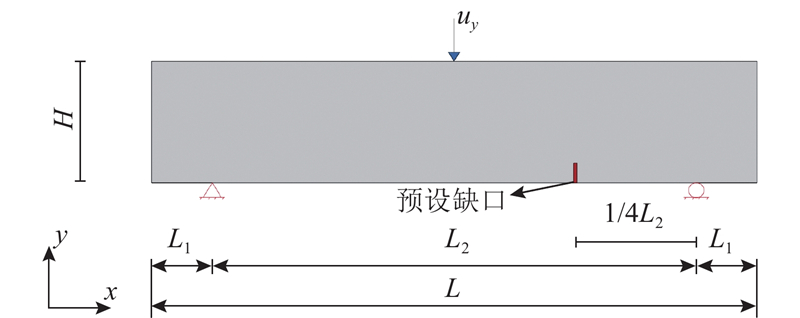
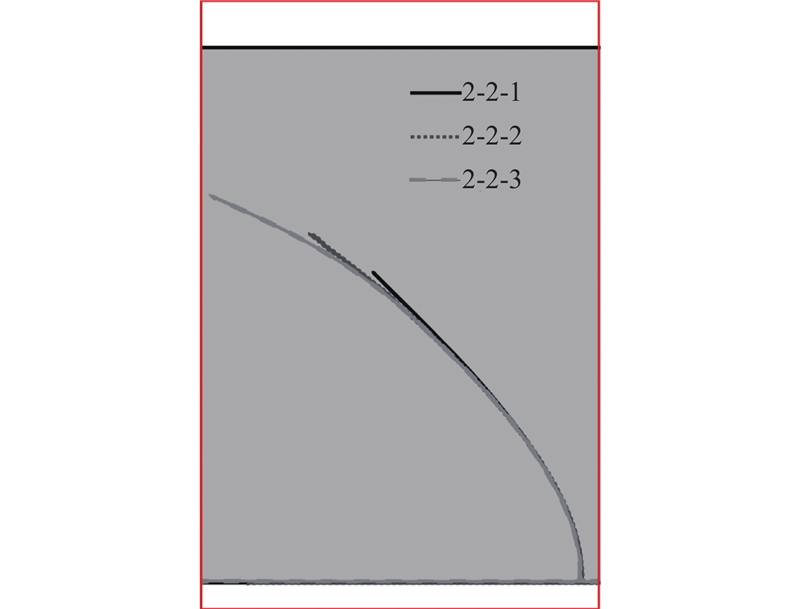
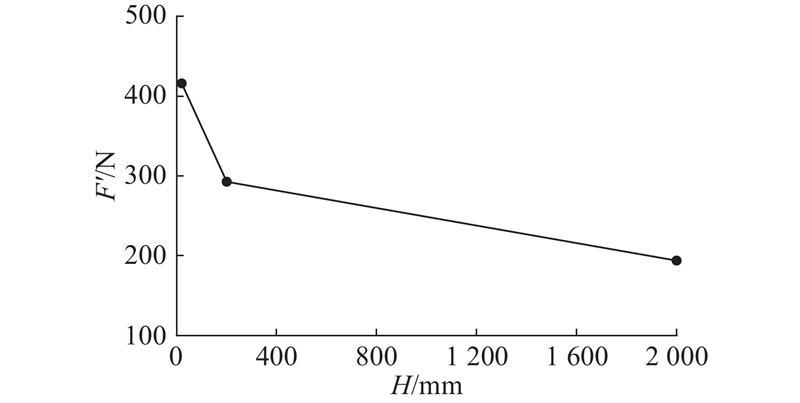
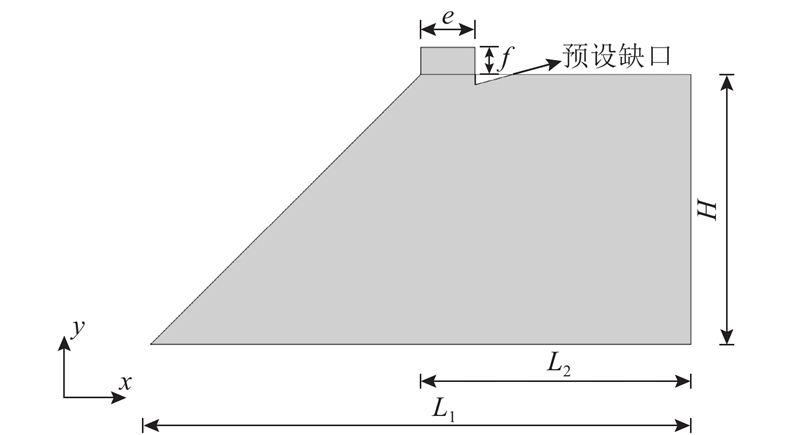
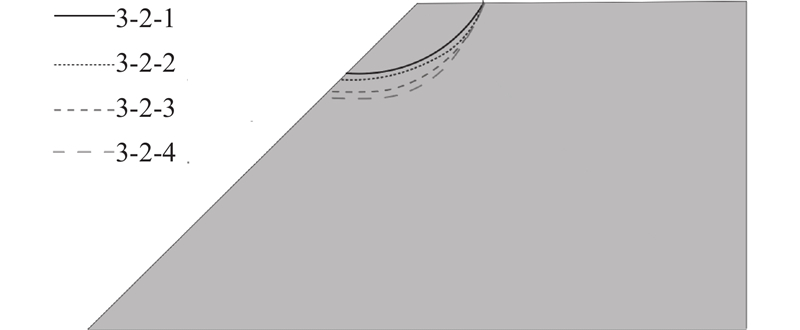
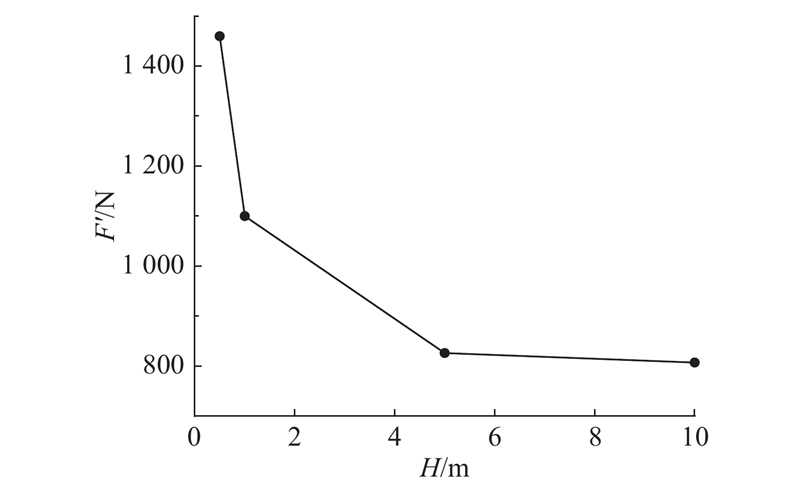
如图11 所示为缺口三点弯梁模型,其中L 1 =1/10 L ,在梁中截面向右1/4 L 2 处预设长度为a 的缺口,网格密度为1000 ×200,保持不同尺寸模型网格数量不变. 荷载施加步骤与2.1节相同. 土体材料为理想弹性体,弹性模量为145 MPa,泊松比为0.35. 黏聚区域模型参数c = 192.9 kPa、G c = 208 N/m、$ {\delta }_{\text{n}}{}_{\text{c}}=0.7\,\,\,\text{mm} $ $ {\delta }_{\text{n}}{}_{\text{r}}=2.16\,\,\,\text{mm} $ . 缺口三点弯梁模型工况设置如表3 所示.
[1]
KRAMER S L Performance-based design methodologies for geotechnical earthquake engineering
[J]. Bulletin of Earthquake Engineering , 2014 , 12 (3 ): 1049 - 1070
DOI:10.1007/s10518-013-9484-x
[本文引用: 1]
[3]
蒋明镜 现代土力学研究的新视野: 宏微观土力学
[J]. 岩土工程学报 , 2019 , 41 (2 ): 195 - 254
[本文引用: 1]
JIANG Mingjing New paradigm for modern soil mechanics: geomechanics from micro to macro
[J]. Chinese Journal of Geotechnical Engineering , 2019 , 41 (2 ): 195 - 254
[本文引用: 1]
[4]
凌道盛, 李奖, 王文军, 等 人工制备土的结构性及其对应变局部化的影响
[J]. 浙江大学学报: 工学版 , 2019 , 53 (9 ): 1689 - 1696
DOI:10.3785/j.issn.1008-973X.2019.09.007
[本文引用: 1]
LING Daosheng, LI Jiang, WANG Wenjun, et al Structure of artificial soils and its influence on strain localization
[J]. Journal of Zhejiang University: Engineering Science , 2019 , 53 (9 ): 1689 - 1696
DOI:10.3785/j.issn.1008-973X.2019.09.007
[本文引用: 1]
[5]
ROSCOE K H The influence of strains in soil mechanics
[J]. Géotechnique , 1970 , 20 (2 ): 129 - 170
[本文引用: 1]
[6]
RATTEZ H, SHI Y, SAC-MORANE A, et al Effect of grain size distribution on the shear band thickness evolution in sand
[J]. Géotechnique , 2022 , 72 (4 ): 350 - 363
DOI:10.1680/jgeot.20.p.120
[本文引用: 1]
[7]
WANG Z Y, WANG P, YIN Z Y, et al Micromechanical investigation of the particle size effect on the shear strength of uncrushable granular materials
[J]. Acta Geotechnica , 2022 , 17 (10 ): 4277 - 4296
DOI:10.1007/s11440-022-01501-z
[本文引用: 1]
[8]
BUI T Q, HU X A review of phase-field models, fundamentals and their applications to composite laminates
[J]. Engineering Fracture Mechanics , 2021 , 248 : 107705
DOI:10.1016/j.engfracmech.2021.107705
[本文引用: 1]
[9]
WANG L, SU H, ZHOU K A phase-field model for mixed-mode cohesive fracture in fiber-reinforced composites
[J]. Computer Methods in Applied Mechanics and Engineering , 2024 , 421 : 116753
DOI:10.1016/j.cma.2024.116753
[本文引用: 1]
[10]
周鑫, 于佳佳, 吴文杰, 等 基于非局部理论的Hoek-Brown软化塑性模型
[J]. 防灾减灾工程学报 , 2025 , 45 (1 ): 13 - 20
DOI:10.13409/j.cnki.jdpme.20241104002
[本文引用: 1]
ZHOU Xin, YU Jiajia, WU Wenjie, et al Hoek-brown softening plasticity model based on nonlocal theory
[J]. Journal of Disaster Prevention and Mitigation Engineering , 2025 , 45 (1 ): 13 - 20
DOI:10.13409/j.cnki.jdpme.20241104002
[本文引用: 1]
[11]
姚仰平, 武孝天, 崔文杰 基于岩土材料临界状态理论的有限元非局部软化算法: 以CSUH模型为例
[J]. 岩石力学与工程学报 , 2023 , 42 (7 ): 1759 - 1766
DOI:10.13722/j.cnki.jrme.2022.1124
[本文引用: 1]
YAO Yangping, WU Xiaotian, CUI Wenjie A finite element nonlocal strain-softening algorithm based on the critical state theory for geomaterials: a case study with csuh model
[J]. Chinese Journal of Rock Mechanics and Engineering , 2023 , 42 (7 ): 1759 - 1766
DOI:10.13722/j.cnki.jrme.2022.1124
[本文引用: 1]
[12]
CASTELLI M, ALLODI A, SCAVIA C A numerical method for the study of shear band propagation in soft rocks
[J]. International Journal for Numerical and Analytical Methods in Geomechanics , 2009 , 33 (13 ): 1561 - 1587
DOI:10.1002/nag.778
[本文引用: 1]
[13]
PALMER A C, RICE J R The growth of slip surfaces in the progressive failure of over-consolidated clay
[J]. Proceedings of the Royal Series A , 1973 , 332 : 527 - 548
DOI:10.1098/rspa.1973.0040
[14]
喻葭临. 土中剪切带扩展机理研究和扩展过程模拟 [D]. 北京: 清华大学, 2009: 1–142.
[本文引用: 1]
YU Jialin. Mechanism investigation and numerical simulation of evolution of shear band in soil [D]. Beijing: Tsinghua University, 2009: 1–142.
[本文引用: 1]
[15]
程靳, 赵树山. 断裂力学 [M]. 北京: 科学出版社, 2006: 9–24.
[本文引用: 1]
[16]
FLÁDR J, BÍLÝ P Specimen size effect on compressive and flexural strength of high-strength fibre-reinforced concrete containing coarse aggregate
[J]. Composites Part B: Engineering , 2018 , 138 : 77 - 86
DOI:10.1016/j.compositesb.2017.11.032
[本文引用: 1]
[17]
VU C C, WEISS J, PLÉ O, et al The potential impact of size effects on compressive strength for the estimation of the Young’s modulus of concrete
[J]. Materials and Structures , 2021 , 54 (5 ): 196
DOI:10.1617/s11527-021-01795-7
[本文引用: 1]
[18]
BAREITHER C A, BENSON C H, EDIL T B Comparison of shear strength of sand backfills measured in small-scale and large-scale direct shear tests
[J]. Canadian Geotechnical Journal , 2008 , 45 (9 ): 1224 - 1236
DOI:10.1139/T08-058
[本文引用: 1]
[19]
WU P K, MATSUSHIMA K, TATSUOKA F Effects of specimen size and some other factors on the strength and deformation of granular soil in direct shear tests
[J]. Geotechnical Testing Journal , 2008 , 31 (1 ): 45 - 64
DOI:10.1520/GTJ100773
[本文引用: 1]
[20]
CANTOR D, OVALLE C Sample size effects on the critical state shear strength of granular materials with varied gradation and the role of column-like local structures
[J]. Géotechnique , 2025 , 75 (1 ): 29 - 40
DOI:10.1680/jgeot.23.00032
[本文引用: 1]
[21]
NING F, LIU J, ZOU D, et al Super-large-scale triaxial tests to study the effects of particle size on the monotonic stress–strain response of rockfill materials
[J]. Acta Geotechnica , 2025 , 20 (4 ): 1847 - 1858
DOI:10.1007/s11440-024-02471-0
[本文引用: 1]
[22]
ZERAATI-SHAMSABADI M, SADREKARIMI A A DEM study on the effects of specimen and particle sizes on direct simple shear tests
[J]. Granular Matter , 2025 , 27 (2 ): 36
DOI:10.1007/s10035-025-01513-y
[23]
JIN J, JIN Q, LI M, et al Analysis of large-scale in situ shear tests of sandy gravel with cobbles
[J]. International Journal of Civil Engineering , 2024 , 22 (11 ): 2031 - 2040
DOI:10.1007/s40999-024-00969-y
[24]
蒋明杰, 吉恩跃, 王天成, 等 粗粒土抗剪强度的缩尺效应规律试验研究
[J]. 岩土工程学报 , 2023 , 45 (4 ): 855 - 861
[本文引用: 1]
JIANG Mingjie, JI Enyue, WANG Tiancheng, et al Experimental study on laws of scale effects of shear strength of coarse-grained soils
[J]. Chinese Journal of Geotechnical Engineering , 2023 , 45 (4 ): 855 - 861
[本文引用: 1]
[25]
TIJSSENS M G A, VAN DER GIESSEN E, SLUYS L J Modeling of crazing using a cohesive surface methodology
[J]. Mechanics of Materials , 2000 , 32 (1 ): 19 - 35
DOI:10.1016/S0167-6636(99)00044-7
[本文引用: 1]
[26]
凌道盛, 涂福彬, 卜令方 基于黏聚区域模型的边坡渐进破坏过程强化有限元分析
[J]. 岩土工程学报 , 2012 , 34 (8 ): 1387 - 1393
[本文引用: 2]
LING Daosheng, TU Fubin, BU Lingfang Enhanced finite element analysis of progressive failure of slopes based on cohesive zone model
[J]. Chinese Journal of Geotechnical Engineering , 2012 , 34 (8 ): 1387 - 1393
[本文引用: 2]
[27]
石天翔, 张昕, 王洋洋, 等 基于强度理论的内聚力模型的有限元实现及应用
[J]. 浙江大学学报: 工学版 , 2023 , 57 (3 ): 573 - 582
DOI:10.3785/j.issn.1008-973X.2023.03.015
[本文引用: 1]
SHI Tianxiang, ZHANG Xin, WANG Yangyang, et al Finite element implementation and application of strength theory based cohesive zone model
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (3 ): 573 - 582
DOI:10.3785/j.issn.1008-973X.2023.03.015
[本文引用: 1]
[29]
HU C, WANG L, LING D, et al Experimental and numerical investigation on the tensile fracture of compacted clay
[J]. Computer Modeling in Engineering and Sciences , 2020 , 123 (1 ): 283 - 307
DOI:10.32604/cmes.2020.07842
[本文引用: 1]
[30]
凌道盛, 徐泽龙, 蔡武军, 等 压实黏土梁弯曲开裂性状试验研究
[J]. 岩土工程学报 , 2015 , 37 (7 ): 1165 - 1172
[本文引用: 1]
LING Daosheng, XU Zelong, CAI Wujun, et al Experimental study on characteristics of bending cracks of compacted soil beams
[J]. Chinese Journal of Geotechnical Engineering , 2015 , 37 (7 ): 1165 - 1172
[本文引用: 1]
[32]
HU C, YANG Q, LING D, et al Numerical simulations of arbitrary evolving cracks in geotechnical structures using the nonlinear augmented finite element method (N-AFEM)
[J]. Mechanics of Materials , 2021 , 156 : 103814
DOI:10.1016/j.mechmat.2021.103814
[本文引用: 2]
[33]
凌道盛, 韩超, 陈云敏, 等 土结接触面黏聚区域模型及渐进累积破坏分析
[J]. 岩土工程学报 , 2011 , 33 (9 ): 1405 - 1411
[本文引用: 1]
LING Daosheng, HAN Chao, CHEN Yunmin, et al Interfacial cohesive zone model and progressive failure of soil-structure interface
[J]. Chinese Journal of Geotechnical Engineering , 2011 , 33 (9 ): 1405 - 1411
[本文引用: 1]
Performance-based design methodologies for geotechnical earthquake engineering
1
2014
... 岩土工程领域的设计已经由基于变形和强度设计转变为基于性能设计[1 ] ,极端荷载作用下岩土体破坏过程成为基于性能的岩土工程设计的关键. 超重力试验具有缩尺和缩时效应,能够提升常重力大时空尺寸的工程问题研究效率. 基于连续介质假定和相似律的超重力模型试验,通常采用同质材料制备以保证模型应力应变关系相同[2 ] ,适用于变形问题,对具有应变局部化的破坏问题是否适用值得深入研究. ...
土体的本构模型和超重力物理模拟
1
2020
... 岩土工程领域的设计已经由基于变形和强度设计转变为基于性能设计[1 ] ,极端荷载作用下岩土体破坏过程成为基于性能的岩土工程设计的关键. 超重力试验具有缩尺和缩时效应,能够提升常重力大时空尺寸的工程问题研究效率. 基于连续介质假定和相似律的超重力模型试验,通常采用同质材料制备以保证模型应力应变关系相同[2 ] ,适用于变形问题,对具有应变局部化的破坏问题是否适用值得深入研究. ...
土体的本构模型和超重力物理模拟
1
2020
... 岩土工程领域的设计已经由基于变形和强度设计转变为基于性能设计[1 ] ,极端荷载作用下岩土体破坏过程成为基于性能的岩土工程设计的关键. 超重力试验具有缩尺和缩时效应,能够提升常重力大时空尺寸的工程问题研究效率. 基于连续介质假定和相似律的超重力模型试验,通常采用同质材料制备以保证模型应力应变关系相同[2 ] ,适用于变形问题,对具有应变局部化的破坏问题是否适用值得深入研究. ...
现代土力学研究的新视野: 宏微观土力学
1
2019
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
现代土力学研究的新视野: 宏微观土力学
1
2019
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
人工制备土的结构性及其对应变局部化的影响
1
2019
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
人工制备土的结构性及其对应变局部化的影响
1
2019
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
The influence of strains in soil mechanics
1
1970
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Effect of grain size distribution on the shear band thickness evolution in sand
1
2022
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Micromechanical investigation of the particle size effect on the shear strength of uncrushable granular materials
1
2022
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
A review of phase-field models, fundamentals and their applications to composite laminates
1
2021
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
A phase-field model for mixed-mode cohesive fracture in fiber-reinforced composites
1
2024
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
基于非局部理论的Hoek-Brown软化塑性模型
1
2025
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
基于非局部理论的Hoek-Brown软化塑性模型
1
2025
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
基于岩土材料临界状态理论的有限元非局部软化算法: 以CSUH模型为例
1
2023
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
基于岩土材料临界状态理论的有限元非局部软化算法: 以CSUH模型为例
1
2023
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
A numerical method for the study of shear band propagation in soft rocks
1
2009
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
The growth of slip surfaces in the progressive failure of over-consolidated clay
0
1973
1
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
1
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
1
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Specimen size effect on compressive and flexural strength of high-strength fibre-reinforced concrete containing coarse aggregate
1
2018
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
The potential impact of size effects on compressive strength for the estimation of the Young’s modulus of concrete
1
2021
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Comparison of shear strength of sand backfills measured in small-scale and large-scale direct shear tests
1
2008
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Effects of specimen size and some other factors on the strength and deformation of granular soil in direct shear tests
1
2008
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Sample size effects on the critical state shear strength of granular materials with varied gradation and the role of column-like local structures
1
2025
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Super-large-scale triaxial tests to study the effects of particle size on the monotonic stress–strain response of rockfill materials
1
2025
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
A DEM study on the effects of specimen and particle sizes on direct simple shear tests
0
2025
Analysis of large-scale in situ shear tests of sandy gravel with cobbles
0
2024
粗粒土抗剪强度的缩尺效应规律试验研究
1
2023
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
粗粒土抗剪强度的缩尺效应规律试验研究
1
2023
... 应变局部化是岩土体破坏的主要模式,其特征为岩土体变形集中于厚度很小的狭长带状应变局部化区域,常表现为滑移面、剪切带或变形带的形成[3 -4 ] . Roscoe[5 ] 利用X射线技术测量双轴压缩式样的应变局部化区域厚度,发现该厚度约为20倍土体平均粒径. 随后其他学者开展类似研究,发现虽然应变局部化区域厚度因土体类型差异而不同,但均与土体平均粒径相关[6 -7 ] . 诸多学者开展大量研究,通过显式或隐式地引入反映应变局部化区域非均匀变形的材料内尺度参数,建立能够表征应变局部化区域的各类材料模型,如相场模型[8 -9 ] 、非局部模型[10 -11 ] 和黏聚区域模型[12 -14 ] 等. 为了描述材料的断裂特性,如断裂韧性和临界能量释放率的断裂力学参数被引入断裂力学[15 ] . 材料内尺度参数和断裂力学参数均由材料本身决定,通常仅与材料颗粒粒径相关,与材料构成的结构体形状、大小无关. 诸多学者研究表明,无论是准脆性材料(如岩石、混凝土),还是颗粒材料(如砂土),其强度均存在尺寸效应. Fládr等[16 ] 使用6种强度的混凝土材料对4种尺寸的立方体试件进行抗压试验,发现试验尺寸越小,强度越高,且强度越高的混凝土材料其抗压强度受试样尺寸的影响越小. Vu等[17 ] 使用3种混凝土和4种不同尺寸的527个圆柱形混凝土试件进行非破坏性试验和破坏性试验,发现弹性模量受试样尺寸影响较小,抗压强度与试样尺寸存在显著相关性. 对于颗粒材料,Bareither等[18 ] 对30种不同含砾量天然砂充填体的小尺寸和大尺寸直剪试验结果表明,对于同一充填体,小尺寸模型峰值摩擦角大于大尺寸模型. Wu等[19 ] 进行等比例不同尺寸的砂土直剪试验,发现剪切峰值强度随模型长度与土体平均粒径之比增大而减小,残余强度指标不受影响. Cantor等[20 ] 开展不同粒径组合在不同试验尺寸中的离散元试验,研究样品尺寸对抗剪强度的影响,认为剪切箱高度与样品最大颗粒粒径之比大于15时结果较为可靠. 类似的试验研究和数值模拟均发现:试样尺寸与材料颗粒粒径之比增大,试样强度降低[21 -24 ] . ...
Modeling of crazing using a cohesive surface methodology
1
2000
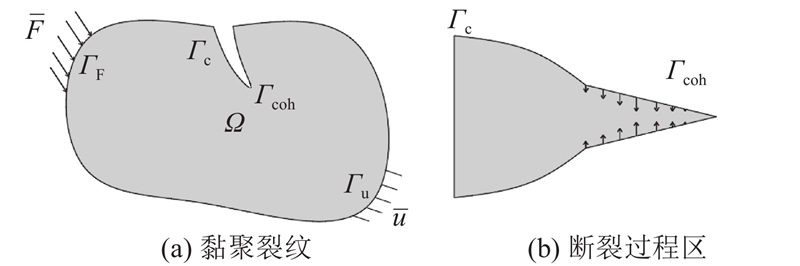
... 黏聚区域模型通过引入如图1 所示的黏聚区域$\varOmega $ $ \varGamma_{\text{coh}} $ [25 ] ,$ \varGamma_{\text{c}} $ [26 ] . ...
基于黏聚区域模型的边坡渐进破坏过程强化有限元分析
2
2012
... 黏聚区域模型通过引入如图1 所示的黏聚区域$\varOmega $ $ \varGamma_{\text{coh}} $ [25 ] ,$ \varGamma_{\text{c}} $ [26 ] . ...
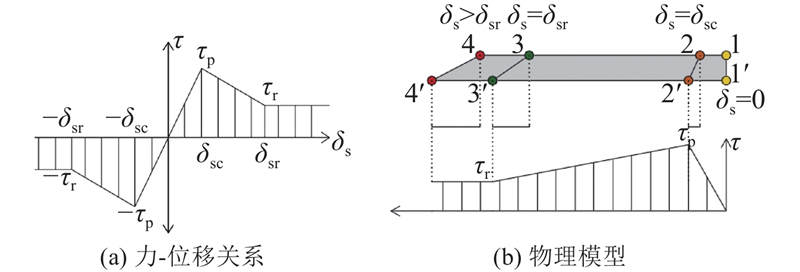
... 摩擦型黏聚区域模型[26 ] (frictional cohesive zone model,FCZM)表达式为 ...
基于黏聚区域模型的边坡渐进破坏过程强化有限元分析
2
2012
... 黏聚区域模型通过引入如图1 所示的黏聚区域$\varOmega $ $ \varGamma_{\text{coh}} $ [25 ] ,$ \varGamma_{\text{c}} $ [26 ] . ...
... 摩擦型黏聚区域模型[26 ] (frictional cohesive zone model,FCZM)表达式为 ...
基于强度理论的内聚力模型的有限元实现及应用
1
2023
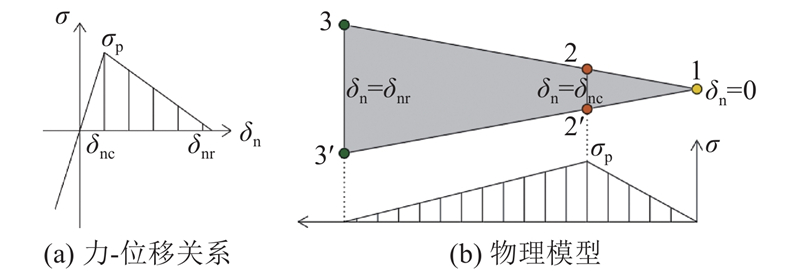
... 如图2 所示为拉伸破坏模式断裂过程区力-位移关系与物理模型,拉应力$ \sigma $ c 提供,分为3个阶段. 1)强化阶段:黏聚力随法向相对分离位移$ {\delta }_{\text{n}} $ $ {\delta }_{\text{nc}} $ $ {\sigma }_{\text{p}} $ . 2)损伤阶段[27 ] :黏聚力随$ {\delta }_{\text{n}} $ $ {\delta }_{\text{n}} $ $ {\delta }_{\text{nr}} $ 图2 中点2与2′、点3与3′分别代表在初始状态下重合的点. 点1处$ {\delta }_{{\mathrm{n}}}\text{=}0 $ $ {\delta }_{\text{n}}\text{=}{\delta }_{\text{nc}} $ $ {\delta }_{\text{n}}\text{=}{\delta }_{\text{nr}} $
基于强度理论的内聚力模型的有限元实现及应用
1
2023
... 如图2 所示为拉伸破坏模式断裂过程区力-位移关系与物理模型,拉应力$ \sigma $ c 提供,分为3个阶段. 1)强化阶段:黏聚力随法向相对分离位移$ {\delta }_{\text{n}} $ $ {\delta }_{\text{nc}} $ $ {\sigma }_{\text{p}} $ . 2)损伤阶段[27 ] :黏聚力随$ {\delta }_{\text{n}} $ $ {\delta }_{\text{n}} $ $ {\delta }_{\text{nr}} $ 图2 中点2与2′、点3与3′分别代表在初始状态下重合的点. 点1处$ {\delta }_{{\mathrm{n}}}\text{=}0 $ $ {\delta }_{\text{n}}\text{=}{\delta }_{\text{nc}} $ $ {\delta }_{\text{n}}\text{=}{\delta }_{\text{nr}} $
Cohesive crack analysis of size effect
1
2009
... 拉伸破坏过程的软化行为主要来自金属、混凝土和复合材料的黏聚力失效. 断裂过程区长度与材料属性相关. 在断裂力学中,假设基于材料的断裂过程区具有均匀的应力和能量耗散形式. 该假设定义了准脆性材料拉伸破坏的断裂过程区长度[28 ] , ...
Experimental and numerical investigation on the tensile fracture of compacted clay
1
2020
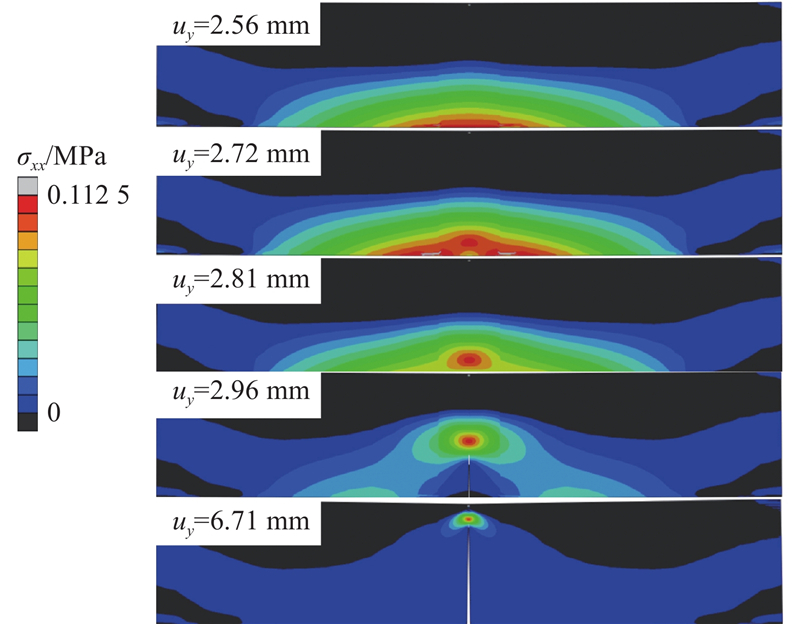
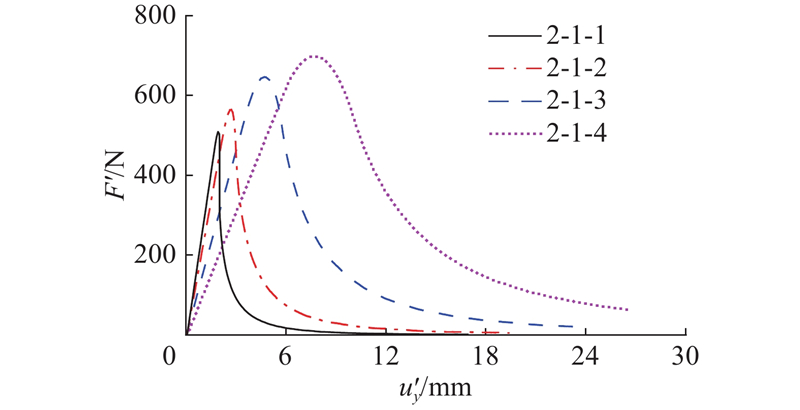
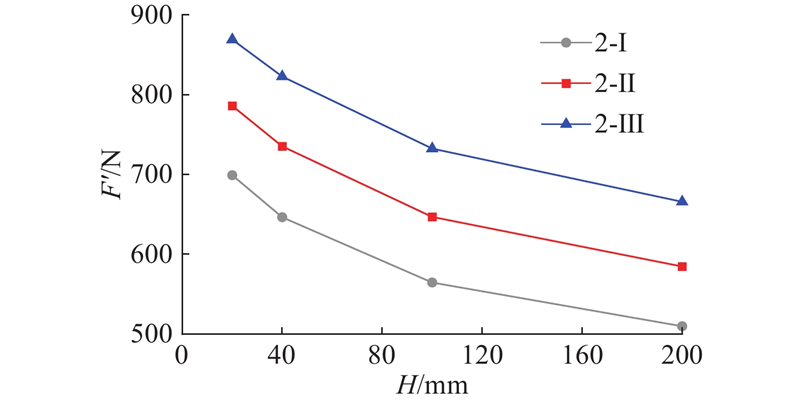
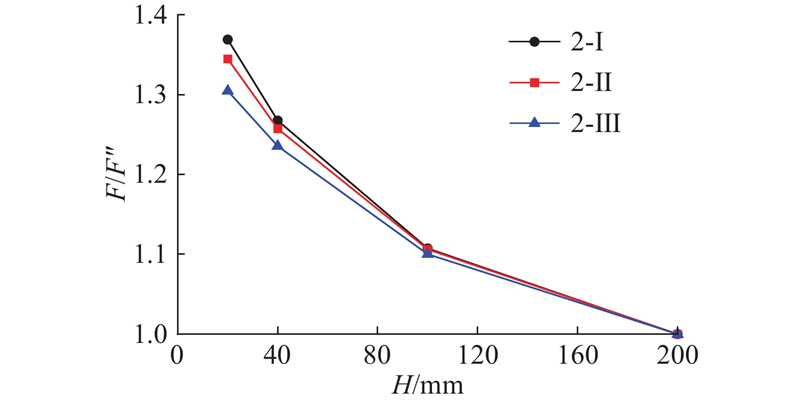
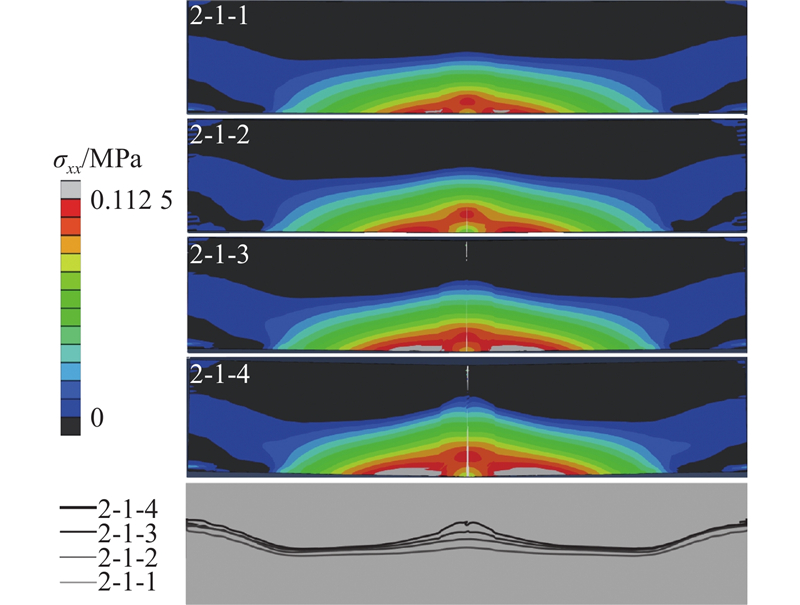
... 设计如图5 所示的二维平面应变三点弯梁模型,其中L 、H 分别为模型的长和高,支座到梁外侧的距离L 1 =1/10L . 在完成网格敏感性分析后,选取网格密度为500×100(网格密度选取均经过分析),保持不同尺寸模型网格数量不变. 土体参数及黏聚区域模型参数取值参考文献[29 ]、[30 ];土体材料为理想弹性体,弹性模量为90 MPa,泊松比为0.35. 为了研究材料韧性对尺寸效应的影响,另取材料2-Ⅱ、2-Ⅲ. 材料2-Ⅱ、2-Ⅲ 相对于2-Ⅰ 改变了$ {\delta }_{\text{nc}} $ $ {\delta }_{\text{nr}} $ G c 数值越大,代表材料韧性越强[31 ] . 黏聚区域模型参数设置如表1 所示,其中$ {\sigma }_{\text{p}} $ 表2 所示各工况,相似比n 为原型长度与模型长度的比值. 为了保证不同尺寸模型的应力状态相同,先对整个模型施加重力荷载并进行自重平衡计算,对模型施加n g 重力荷载(1g = 9.81 m/s2 );随后进行位移清零,在梁中截面上部的刚性块中心施加竖直向下的位移荷载u y 0.1125 MPa,如图6 所示. 三点弯梁中截面下端最先达到抗拉强度,形成断裂过程区,随着位移荷载不断施加,下端发生开裂,拉应力逐渐减小,断裂过程区向上方扩展,最终至梁中上侧. 当加载位移u y
压实黏土梁弯曲开裂性状试验研究
1
2015
... 设计如图5 所示的二维平面应变三点弯梁模型,其中L 、H 分别为模型的长和高,支座到梁外侧的距离L 1 =1/10L . 在完成网格敏感性分析后,选取网格密度为500×100(网格密度选取均经过分析),保持不同尺寸模型网格数量不变. 土体参数及黏聚区域模型参数取值参考文献[29 ]、[30 ];土体材料为理想弹性体,弹性模量为90 MPa,泊松比为0.35. 为了研究材料韧性对尺寸效应的影响,另取材料2-Ⅱ、2-Ⅲ. 材料2-Ⅱ、2-Ⅲ 相对于2-Ⅰ 改变了$ {\delta }_{\text{nc}} $ $ {\delta }_{\text{nr}} $ G c 数值越大,代表材料韧性越强[31 ] . 黏聚区域模型参数设置如表1 所示,其中$ {\sigma }_{\text{p}} $ 表2 所示各工况,相似比n 为原型长度与模型长度的比值. 为了保证不同尺寸模型的应力状态相同,先对整个模型施加重力荷载并进行自重平衡计算,对模型施加n g 重力荷载(1g = 9.81 m/s2 );随后进行位移清零,在梁中截面上部的刚性块中心施加竖直向下的位移荷载u y 0.1125 MPa,如图6 所示. 三点弯梁中截面下端最先达到抗拉强度,形成断裂过程区,随着位移荷载不断施加,下端发生开裂,拉应力逐渐减小,断裂过程区向上方扩展,最终至梁中上侧. 当加载位移u y
压实黏土梁弯曲开裂性状试验研究
1
2015
... 设计如图5 所示的二维平面应变三点弯梁模型,其中L 、H 分别为模型的长和高,支座到梁外侧的距离L 1 =1/10L . 在完成网格敏感性分析后,选取网格密度为500×100(网格密度选取均经过分析),保持不同尺寸模型网格数量不变. 土体参数及黏聚区域模型参数取值参考文献[29 ]、[30 ];土体材料为理想弹性体,弹性模量为90 MPa,泊松比为0.35. 为了研究材料韧性对尺寸效应的影响,另取材料2-Ⅱ、2-Ⅲ. 材料2-Ⅱ、2-Ⅲ 相对于2-Ⅰ 改变了$ {\delta }_{\text{nc}} $ $ {\delta }_{\text{nr}} $ G c 数值越大,代表材料韧性越强[31 ] . 黏聚区域模型参数设置如表1 所示,其中$ {\sigma }_{\text{p}} $ 表2 所示各工况,相似比n 为原型长度与模型长度的比值. 为了保证不同尺寸模型的应力状态相同,先对整个模型施加重力荷载并进行自重平衡计算,对模型施加n g 重力荷载(1g = 9.81 m/s2 );随后进行位移清零,在梁中截面上部的刚性块中心施加竖直向下的位移荷载u y 0.1125 MPa,如图6 所示. 三点弯梁中截面下端最先达到抗拉强度,形成断裂过程区,随着位移荷载不断施加,下端发生开裂,拉应力逐渐减小,断裂过程区向上方扩展,最终至梁中上侧. 当加载位移u y
基于强度尺寸效应的准脆性材料脆性指标研究
1
2006
... 设计如图5 所示的二维平面应变三点弯梁模型,其中L 、H 分别为模型的长和高,支座到梁外侧的距离L 1 =1/10L . 在完成网格敏感性分析后,选取网格密度为500×100(网格密度选取均经过分析),保持不同尺寸模型网格数量不变. 土体参数及黏聚区域模型参数取值参考文献[29 ]、[30 ];土体材料为理想弹性体,弹性模量为90 MPa,泊松比为0.35. 为了研究材料韧性对尺寸效应的影响,另取材料2-Ⅱ、2-Ⅲ. 材料2-Ⅱ、2-Ⅲ 相对于2-Ⅰ 改变了$ {\delta }_{\text{nc}} $ $ {\delta }_{\text{nr}} $ G c 数值越大,代表材料韧性越强[31 ] . 黏聚区域模型参数设置如表1 所示,其中$ {\sigma }_{\text{p}} $ 表2 所示各工况,相似比n 为原型长度与模型长度的比值. 为了保证不同尺寸模型的应力状态相同,先对整个模型施加重力荷载并进行自重平衡计算,对模型施加n g 重力荷载(1g = 9.81 m/s2 );随后进行位移清零,在梁中截面上部的刚性块中心施加竖直向下的位移荷载u y 0.1125 MPa,如图6 所示. 三点弯梁中截面下端最先达到抗拉强度,形成断裂过程区,随着位移荷载不断施加,下端发生开裂,拉应力逐渐减小,断裂过程区向上方扩展,最终至梁中上侧. 当加载位移u y
基于强度尺寸效应的准脆性材料脆性指标研究
1
2006
... 设计如图5 所示的二维平面应变三点弯梁模型,其中L 、H 分别为模型的长和高,支座到梁外侧的距离L 1 =1/10L . 在完成网格敏感性分析后,选取网格密度为500×100(网格密度选取均经过分析),保持不同尺寸模型网格数量不变. 土体参数及黏聚区域模型参数取值参考文献[29 ]、[30 ];土体材料为理想弹性体,弹性模量为90 MPa,泊松比为0.35. 为了研究材料韧性对尺寸效应的影响,另取材料2-Ⅱ、2-Ⅲ. 材料2-Ⅱ、2-Ⅲ 相对于2-Ⅰ 改变了$ {\delta }_{\text{nc}} $ $ {\delta }_{\text{nr}} $ G c 数值越大,代表材料韧性越强[31 ] . 黏聚区域模型参数设置如表1 所示,其中$ {\sigma }_{\text{p}} $ 表2 所示各工况,相似比n 为原型长度与模型长度的比值. 为了保证不同尺寸模型的应力状态相同,先对整个模型施加重力荷载并进行自重平衡计算,对模型施加n g 重力荷载(1g = 9.81 m/s2 );随后进行位移清零,在梁中截面上部的刚性块中心施加竖直向下的位移荷载u y 0.1125 MPa,如图6 所示. 三点弯梁中截面下端最先达到抗拉强度,形成断裂过程区,随着位移荷载不断施加,下端发生开裂,拉应力逐渐减小,断裂过程区向上方扩展,最终至梁中上侧. 当加载位移u y
Numerical simulations of arbitrary evolving cracks in geotechnical structures using the nonlinear augmented finite element method (N-AFEM)
2
2021
... 按照相似准则设计不同尺寸大小的直剪模型和边坡模型,分析尺寸效应对以剪切破坏模式为主的模型试验的影响. 通过直剪试验研究分析效应对模型承载力的影响,通过边坡模型试验分析尺寸效应对裂纹扩展路径的影响. XFEM程序在有限元软件Abaqus中可以直接使用,界面简洁、建模方便,直剪试验采用XFEM进行模拟. 针对耦合型破坏模式,Hu等[32 ] 在AFEM程序中嵌入耦合型的黏聚区域模型和双曲线型的莫尔-库伦准则,对模拟压剪破坏问题具有独特优势,边坡试验通过AFEM程序进行模拟. ...
... 如图21 所示为边坡模型. 在土坡上方刚性块中心点对边坡进行位移加载,位移荷载为u y g ,仅考虑尺寸对边坡滑裂带路径的影响. 土体参数及黏聚区域模型参数选取参考文献[32 ],土体材料为理想弹性体,弹性模量为10 MPa,泊松比为0.4,c =34 kPa,$ {\delta }_{\text{sc}} $ $ {\varphi }_{\text{p}} $ r c =0.5,工况设置如表6 所示. ...
土结接触面黏聚区域模型及渐进累积破坏分析
1
2011
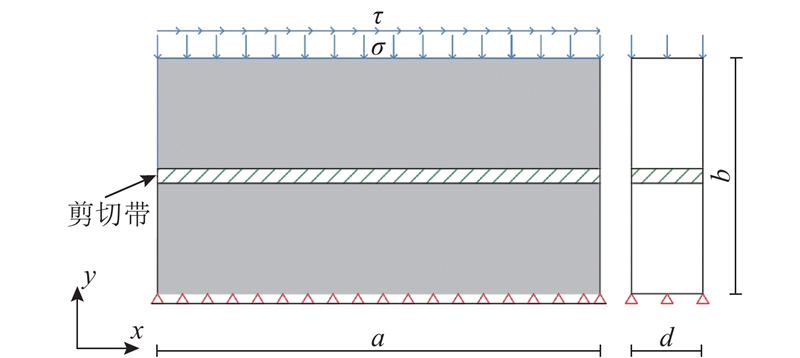
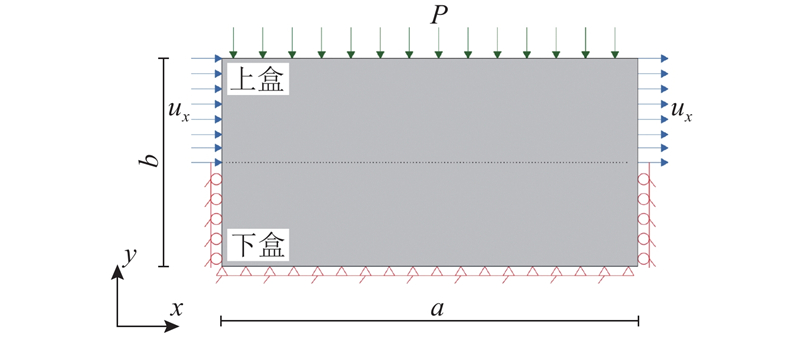
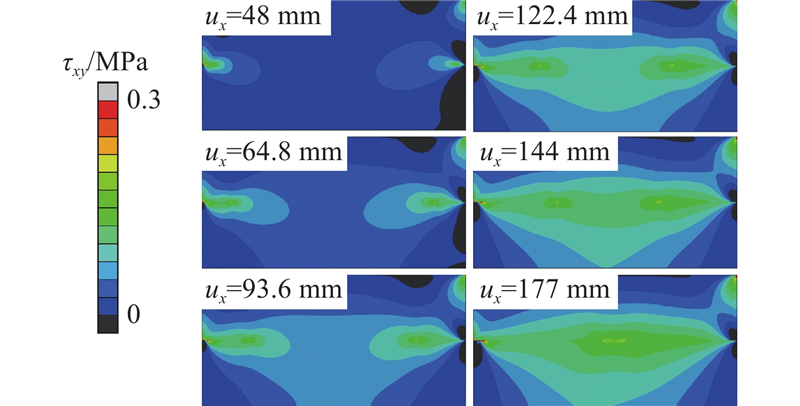
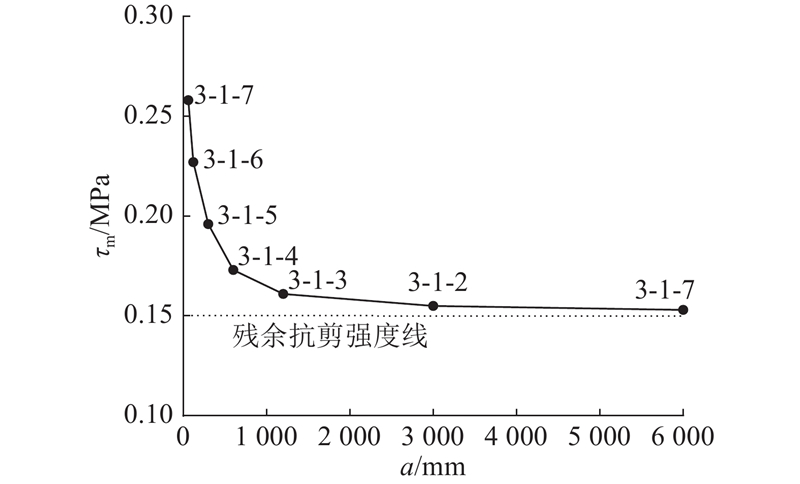
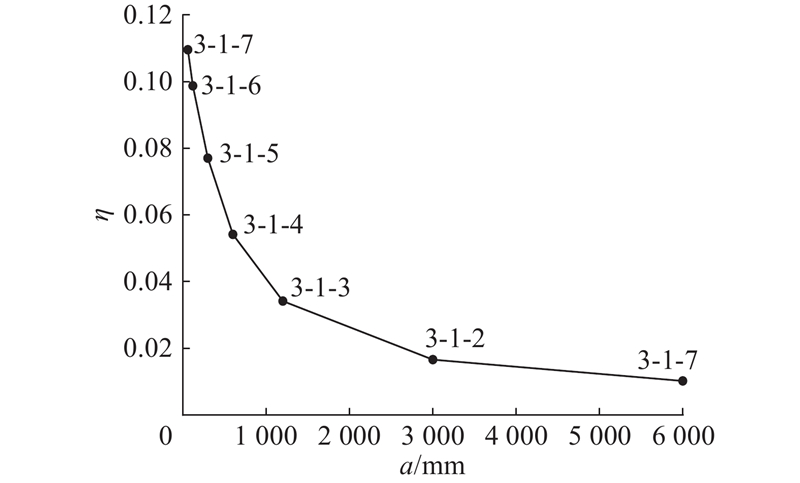
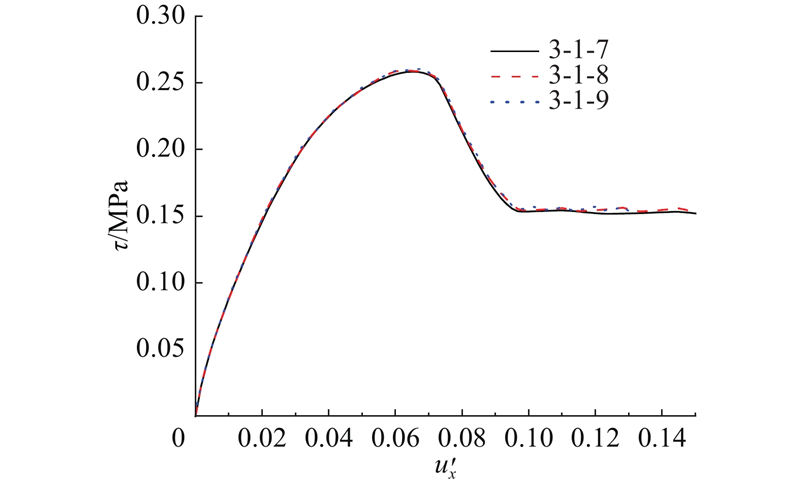
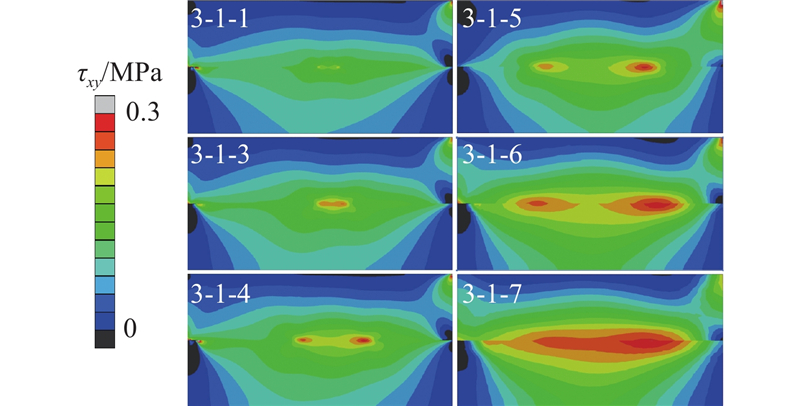
... 选用工况3-1-7到3-1-9进行异质材料的缩尺直剪模型试验,异质材料的黏聚区域模型参数$ {\delta }_{\text{nc}} $ $ {\delta }_{\text{nr}} $ G c 同样符合相似准则. 如图19 所示为此3组试验的平均剪应力τ -加载位移归一值$u_x^{\prime} $ $u_x^{\prime} $ u x a 的比值. 此组试验力-位移曲线完全重合,未发生尺寸效应. 由此可以证明,尺寸效应由材料的特征长度不随缩尺发生变化引起. 由直剪模型破坏过程可知,加载过程中剪切面上的应力分布不均匀,上、下盒界面及其附近区域的应力明显高于其他区域. 剪切开始时,左右两侧先出现断裂过程区,随着位移荷载施加,左右两侧进入残余阶段,断裂过程区向中部移动. 左右2个部分断裂过程区在剪切面中部汇合时,直剪模型达到结构承载力. 如图20 所示为各工况达到峰值平均剪应力时的剪应力云图,可以观察到小尺寸模型剪切面上的平均剪应力水平远高于大尺寸模型. 在破坏过程中,断裂过程区尖端黏聚力为零,末端达到残余应力,尖端至末端之间剪应力先升高再降低,且应力水平高于其他区域. 当模型剪切面长度L 远大于断裂过程区长度l 时,破坏过程呈现渐进破坏的特征,此现象与凌道盛等[33 ] 进行的试验结果一致. 断裂过程区长度与材料属性相关,不随缩尺发生变化,根据节点应力分析,剪切破坏断裂过程区长度同样为$ l={G}_{\text{c}}E/{\sigma }^{2} $ . 模型尺寸减小,潜在剪切面长度L 随之减小,而断裂过程区长度不变,断裂过程区占潜在剪切面的比值l /L 增大,剪切面上峰值平均剪应力增大,结构相对承载力增大. ...
土结接触面黏聚区域模型及渐进累积破坏分析
1
2011
... 选用工况3-1-7到3-1-9进行异质材料的缩尺直剪模型试验,异质材料的黏聚区域模型参数$ {\delta }_{\text{nc}} $ $ {\delta }_{\text{nr}} $ G c 同样符合相似准则. 如图19 所示为此3组试验的平均剪应力τ -加载位移归一值$u_x^{\prime} $ $u_x^{\prime} $ u x a 的比值. 此组试验力-位移曲线完全重合,未发生尺寸效应. 由此可以证明,尺寸效应由材料的特征长度不随缩尺发生变化引起. 由直剪模型破坏过程可知,加载过程中剪切面上的应力分布不均匀,上、下盒界面及其附近区域的应力明显高于其他区域. 剪切开始时,左右两侧先出现断裂过程区,随着位移荷载施加,左右两侧进入残余阶段,断裂过程区向中部移动. 左右2个部分断裂过程区在剪切面中部汇合时,直剪模型达到结构承载力. 如图20 所示为各工况达到峰值平均剪应力时的剪应力云图,可以观察到小尺寸模型剪切面上的平均剪应力水平远高于大尺寸模型. 在破坏过程中,断裂过程区尖端黏聚力为零,末端达到残余应力,尖端至末端之间剪应力先升高再降低,且应力水平高于其他区域. 当模型剪切面长度L 远大于断裂过程区长度l 时,破坏过程呈现渐进破坏的特征,此现象与凌道盛等[33 ] 进行的试验结果一致. 断裂过程区长度与材料属性相关,不随缩尺发生变化,根据节点应力分析,剪切破坏断裂过程区长度同样为$ l={G}_{\text{c}}E/{\sigma }^{2} $ . 模型尺寸减小,潜在剪切面长度L 随之减小,而断裂过程区长度不变,断裂过程区占潜在剪切面的比值l /L 增大,剪切面上峰值平均剪应力增大,结构相对承载力增大. ...