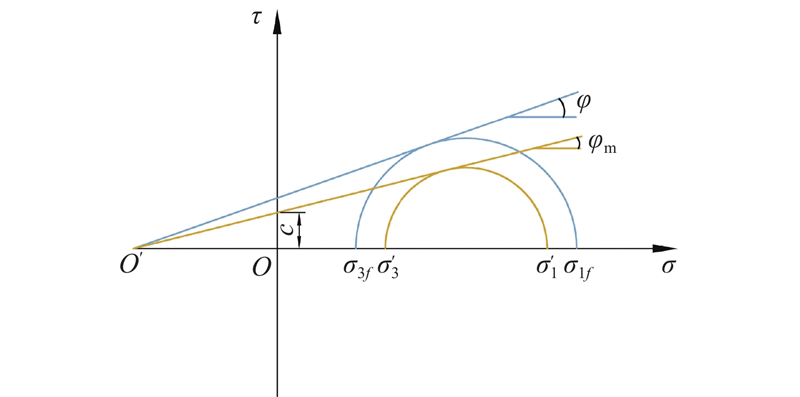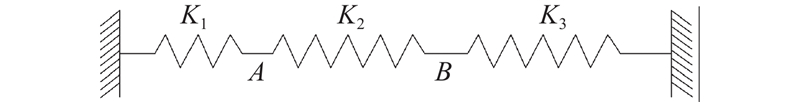许多学者针对冻土边坡框架结构和锚杆2个主要结构的内力和变形开展了大量研究. 在框架结构内力及变形方面,言志信等[3]将横梁、立柱和挡土板构成空间框架,强调横梁和立柱的计算单元,指出梁、柱不仅承担坡体传递给梁截面上的均布荷载,还承担挡土板传递来的三角形(或梯形)土压力荷载,通过二者的叠加计算横梁和立柱内力. 肖世国等[4]考虑框架梁和坡体之间的相互作用,采用Winkler地基模型计算框架梁设计内力. 侯小强等[5]对整个框架结构进行计算单元划分,提出符合实际工程需要的预应力框架锚杆设计方法. Ye等[6]通过建立弹性框架梁模型,推导出锚定框架结构中梁和柱的变形和内力计算公式. Liu[7]引用Winkler地基计算模型,推导出框架结构底柱受泥土约束的等效高度计算公式. 上述计算模型均未考虑框架梁之间的土拱效应,仅从内力和变形方面满足力学性能,没有解决土拱挤碎的工程问题.
锚杆锚固段与岩土界面的相互作用是确保框锚稳定支挡的关键. 针对锚固段与岩土界面相互作用的研究不少,其中黄明华等[8]从锚杆荷载位移关系出发,建立双指数曲线剪切滑移模型,利用室内模型试验验证模型的合理性. 周炳生等[9]从锚固体界面剪切位移分布曲线出发,推导全长黏结式锚杆锚固段剪应力分布规律. 张耀升等[10]假定锚杆弹性段剪应力沿锚固深度呈现四分之一椭圆弧,推导出注浆锚杆临界锚固长度并结合室内模型试验验证公式的正确性. 李伟等[11]基于冻融循环的三轴剪切实验提出在冻融循环条件下框架锚杆锚固段的轴力和剪应力的解析解. Li等[12]依据岩土体峰值剪切强度和残余剪切强度特征,提出锚固体剪应力均匀分布模式,分析锚固段剪应力的动力学演变过程. Fan等[13]通过设计高、中、低3种强度的拉拔试验,建立拉力型锚杆有效长度和极限承载力的计算方法. Ren等[14]基于锚固段剪切滑移模型,构建适合黏土地层的剪应力分布高斯函数模型. Yuan等[15]通过拉拔试验和微观结构表征研究冻融循环下锚杆的锚固力、锚杆与水泥砂浆黏结强度的变化规律. 高欣亚等[16]开展冬季桩锚结构室外试验,分析土体冻胀对锚杆内力及桩身内力的影响. 上述计算模型均未考虑坡面冻融循环引发锚杆轴力变化影响以及冻融作用下锚杆与岩土界面力学关系,没有解决框架土拱胀缩变形产生锚杆拉力失效的工程问题.
本研究从冻融演化角度出发,分别建立框架梁土拱、锚固段注浆体与地层界面之间的计算模型,形成冻融演化过程框架-土体-锚杆尺度协同效应的计算方法. 旨在揭示冻融过程影响下框架内力、锚杆内力及其尺度效应之间的关系,为冻土地区框架锚杆边坡加固设计提供理论依据和技术支持.
1. 冻融循环作用下框架锚杆工作原理及基本假定
1.1. 工作原理
框架锚杆通过锚固段提供的拉拔力传递至框架,使框架与坡面产生相互作用力;该作用力沿框架梁的水平方向和竖直方向形成土拱效应,反作用于坡体以确保边坡稳定. 冬季降温导致坡面岩土体体积膨胀,产生冻胀作用使框架锚杆轴力显著增加. 尤其坡面岩土体积冻胀迫使锚杆张拉力增加,注浆体与地层之间不同区间的界面强度发生变化,锚固段的有效长度受到影响. 为了研究冻融循环作用下框架锚杆工作原理,本研究1)建立满足冻融过程下框架纵横梁产生的水平土拱和竖向土拱计算模型;2)根据冻融过程框架土拱效应的变化对锚杆锚固力的影响,建立锚固段注浆体与岩土界面的计算模型,揭示冻融演化过程中框架和锚固段几何尺度的影响关系.
1.2. 基本假定
季节性冻土区边坡经历四季冻融演化过程:冬季水分迁移导致冰透镜体发育形成冻胀现象,引发坡体朝临空方向产生位移;春季融化期坡体出现部分回缩,冰-水相变作用形成框架内土拱空间效应重构机制,影响锚杆支护力学效应. 为了探究冻融过程框架与坡面、锚固段注浆体与地层界面之间的相互作用演化机制,从冻融过程分别建立土拱和锚杆2种计算模型,基本假定如下. 1)主要研究冻融过程框架-土-锚杆协同效应机制,不考虑周期性多次冻融循环引发的框架-土-锚杆之间协同变化影响. 2)假定土体呈均质,忽略坡体土拱内土体的自重影响,建立土拱计算模型. 3)在框架锚杆支护边坡过程中,水平方向产生的土拱所受的土压力按照均布荷载考虑[17],竖直方向产生的土拱所受的土压力按照梯形分布的荷载考虑. 4)为了防止土拱挤碎破坏,以框架梁产生的土拱土压力小于容许土压力和容许抗剪强度为原则,形成的土拱满足莫尔-库伦破坏准则. 5)框架锚杆在冻胀力的作用下始终保持静力平衡.
2. 冻融作用下框架土拱计算模型
2.1. 框架土拱模型分布
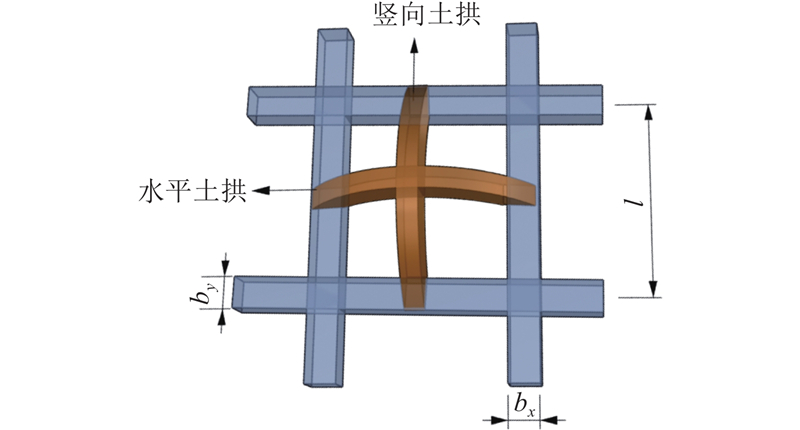
在框架锚杆支护边坡过程中,框架梁沿水平方向和竖直方向呈正交布置,形成多个四边形框架结构. 在土拱效应模型中,相邻纵向框架梁之间产生水平土拱效应,相邻横向框架梁之间产生竖向土拱效应,如图1所示.
图 1
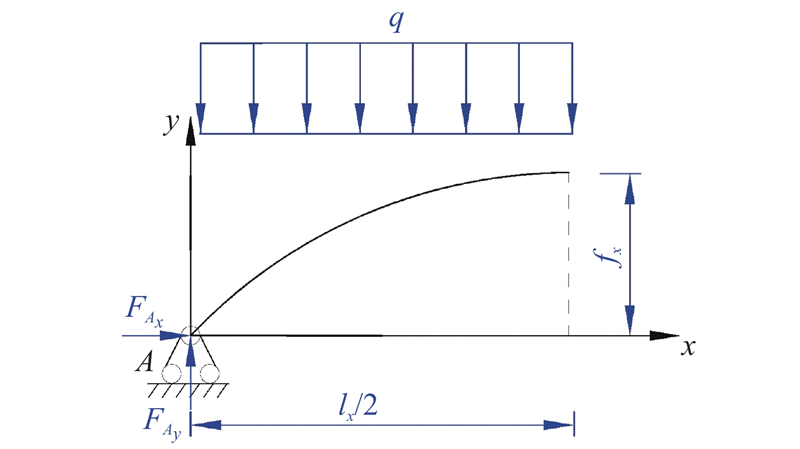
2.2. 水平方向土拱计算模型
图 2
图 2 水平土拱下框架受力分析
Fig.2 Mechanical analysis of frame under horizontal soil arching
根据文献[18],水平方向上的拱轴线的拱高为
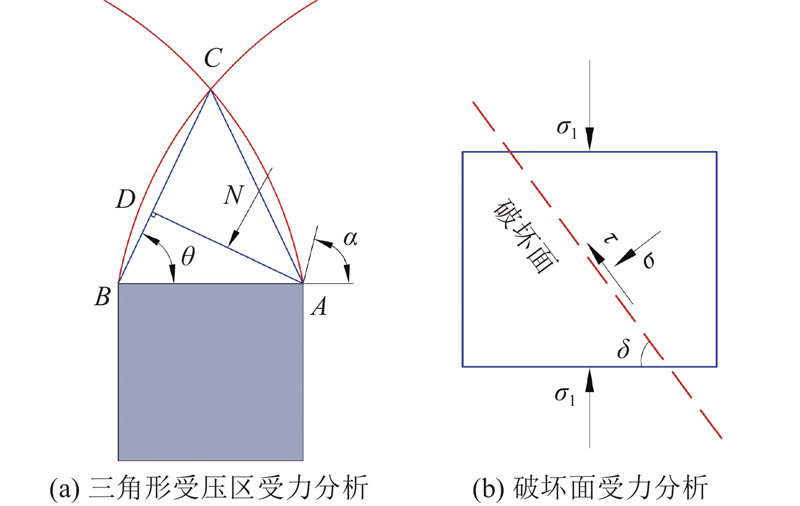
图 3
图 3 三角形受压区及破坏面受力分析
Fig.3 Mechanical analysis of triangular compression zone and failure surface
求得拱脚处存在最大压应力:
2.3. 竖直方向土拱计算模型
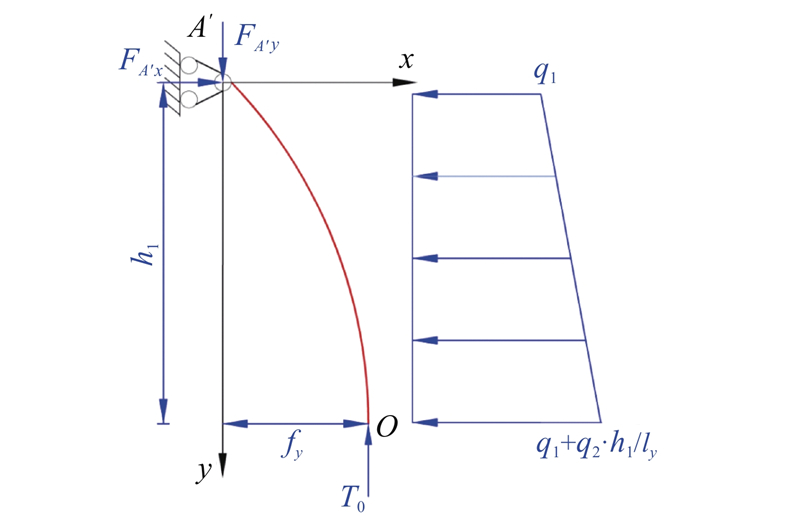
由于边坡坡顶至坡脚的水平力沿竖向逐渐增加,作用在上下相邻水平横向框架梁上产生的拱脚压应力大小不相同. 如图4所示,设框架梁上所受滑坡推力呈梯形分布,
图 4
依据荷载的分布情况考虑结构的稳定性,梯形荷载施加给土拱的力和拱脚处所受水平方向的反作用力应大小相等,可以得到
令
基于拱轴线上只存在水平方向的轴力假定,得到
由
分析式(8)、(10)可知,竖向土拱的拱轴线及拱顶位置随荷载不同而发生的移动,当
2.4. 冻融演化过程中土拱计算模型修正
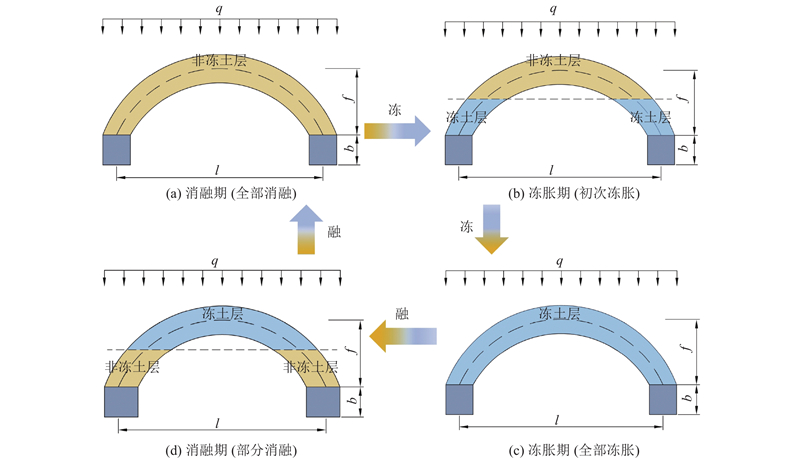
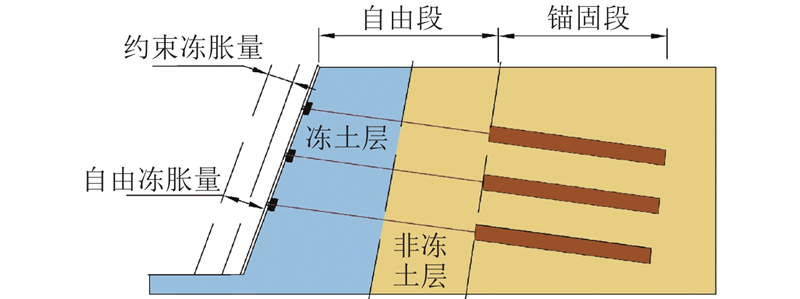
季节性冻土地区最大冻深通常大于1 m[20],造成支护结构出现较为严重的冻胀,因此构建的土拱计算模型按照最大冻胀深度大于土拱矢高来考虑较为客观. 在冻融演过程中,坡面反应最为明显,冬季低温时期冻胀过程由坡面向坡内发展,春季升温时期,坡面由表及里融化,这2个过程恰好相反. 如图5所示,冻胀至消融环过程存在4种土拱工况: 1)在夏季消融施工期,土拱作用区完全处于消融状态:2)刚进入冬季,土拱拱脚部分率先冻胀,拱顶部分为非冻土区;3)进入深冬时期,土拱整体为冻胀状态;4)刚进入春融时期,坡体表面处于消融状态,拱脚部分处于消融状态,拱顶部分处于冻胀状态. 冻融2种工况下坡面岩土强度相差较大,须分析冻土层和非冻土层最不利破坏截面抗剪强度和抗压强度的影响,通过冻融演化过程明确土拱计算模型关键控制参数.
图 5
冻融演化过程中框架间会产生4种土拱效应工况,要保证土拱的稳定性,冻土层和非冻土层之间的临界土体须满足土体的抗剪强度要求. 当临界土体处于极限平衡状态时,
图 6
式中:
当
3. 锚固段注浆体与岩土界面计算模型
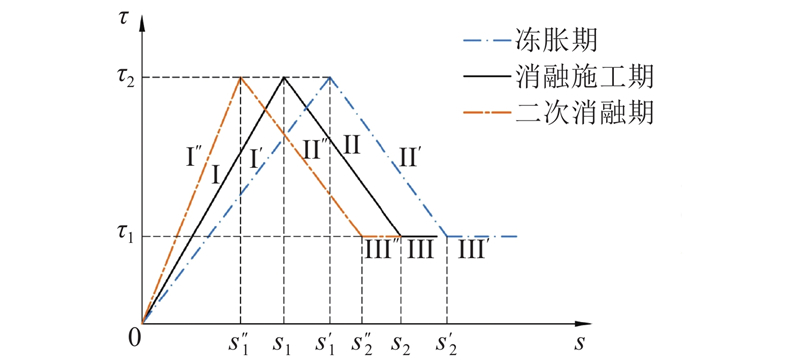
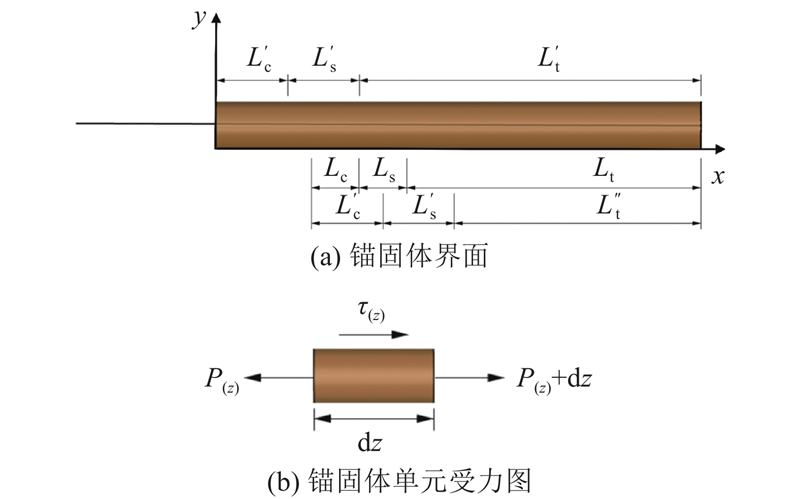
受冻融的影响,框架土拱效应及锚杆锚固力发生变化. 根据土拱效应的变化过程,确定合理的锚固段注浆体与岩土界面的有效长度是保证锚杆支护体系足够安全性的关键. 锚固段注浆体与岩土界面存在3个阶段的应力应变,对应3个长度:锚固段中残余段、弹塑性段和弹性段. 在冻融演化过程中,由于锚固段轴力的不断变化,导致锚固段的3个阶段长度发生变化. 考虑冻融作用下锚固段长度的演化过程,在消融期施工时锚杆锚固力应满足坡体正常的稳定要求,此期间的应力包括残余阶段应力
图 7
图 7 锚固体界面的界面切应力与剪切位移本构模型
Fig.7 Structural modelling of interfacial shear stresses and shear displacements at anchorage interface
式中:s为锚杆-岩体界面之间的相对剪切位移;
图 8
在冻融演化过程中,锚固段轴力不断变化导致锚固段的3个阶段长度发生变化. 在消融施工期,锚固段轴力应满足坡体稳定性要求,此时锚固段注浆体与岩土体界面以弹性阶段、弹塑性阶段为主,令
弹塑性阶段剪切位移
在冻胀期,水平冻胀力的存在导致锚固段轴力增加,剪切位移也随之增大;当界面土体的剪应力衰减到
当z=Lc+Ls时,
由于
结合式(15)和式(19),求得弹性段长度
弹塑性阶段
当z=Lc时,
依据残余区锚杆轴力随着滑移长度变化关系式[23]对残余长度内切应力积分,求得残余长度
4. 冻胀量计算
冻胀力动态变化过程对框架-土体-锚杆协调变形有直接影响. 因温度梯度和水分迁移,冻胀期边坡自由冻胀变形量达到峰值;框架锚杆对边坡的支护作用使得土体产生最大的约束冻胀变形,产生框架-土体-锚杆最强的相互作用力. 为此计算土体自由冻胀量h[26],由框架锚杆变形量求得约束冻胀量,叠加这2种冻胀变形即可求得土体冻胀量.
图 9
图 10
图 10 弹簧代替框架锚杆计算示意图
Fig.10 Schematic calculation of spring instead of frame anchors
框架锚杆所受的冻胀力[28]表示为
式中:
5. 算例分析
5.1. 工程概况
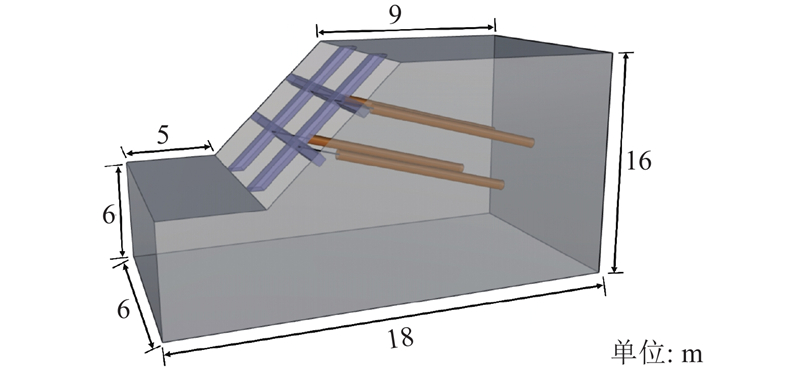
如图11所示,西北地区某边坡支护工程边坡高度为18 m,土体冻结温度为−1 ℃,冬半年平均地表温度为−17 ℃. 初步拟定框架锚杆支护边坡所用混凝土标号为C30,锚杆杆体采用HRB400钢筋,取锚杆间距为2 m,混凝土的弹性模量为3.0×104 MPa,锚杆弹性模量为3.5×105 MPa,锚杆注浆体弹性模量为3.0×104 MPa,锚杆孔径为150 mm,锚杆长度为10 m. 框架横梁宽度设计宽度为550 mm,立柱设计宽度为500 mm,横梁和立柱之间的间距为2 m. 该边坡岩土体以粉质黏土
图 11
表 1 边坡土质参数
Tab.1
| 工况 | ||||
| 消融施工期 | 18.2 | 22 | 23.2 | 19 |
| 冻胀期 | 18.8 | 48 | 23.6 | 60 |
| 二次消融期 | 18.1 | 20 | 22.8 | 22 |
5.2. 框架尺度计算
图 12
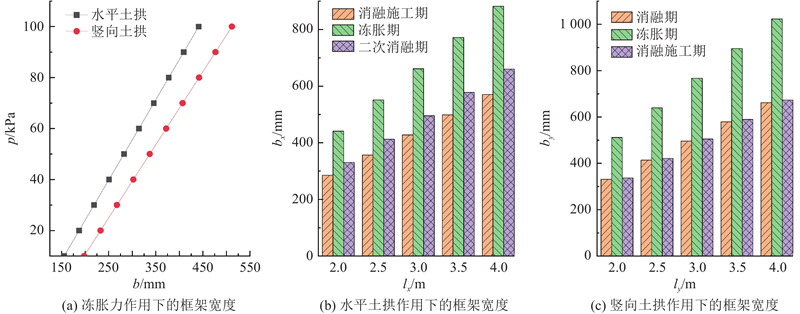
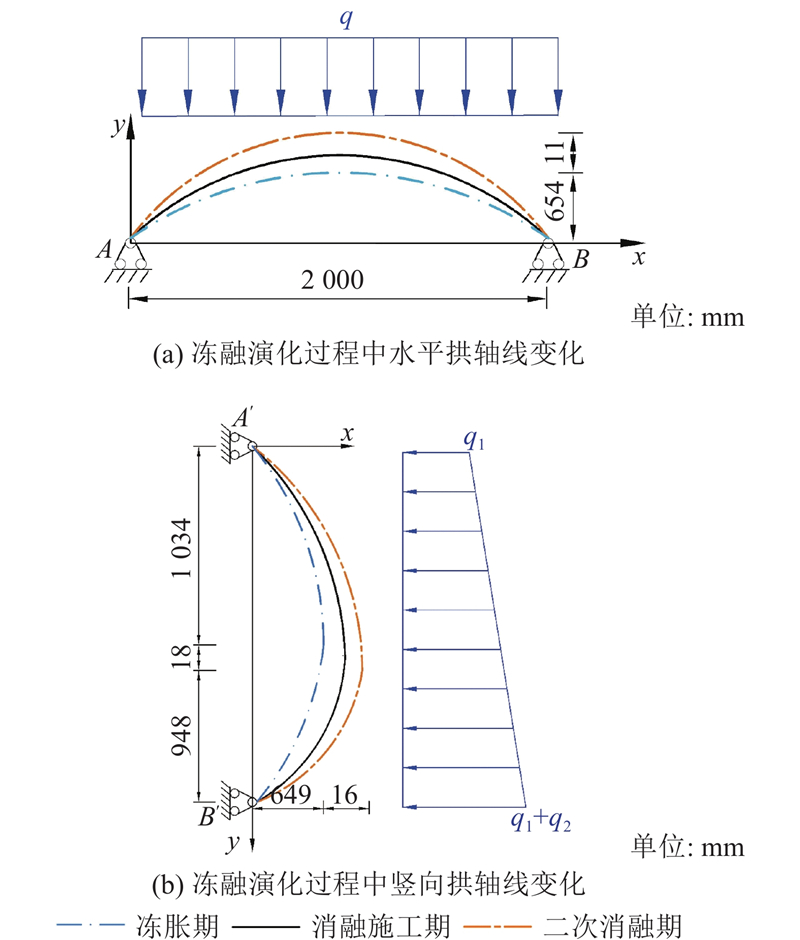
利用式(5)和式(11)分别计算冻胀力p与横梁by、立柱bx的几何尺度关系,如图13所示. 为了揭示土拱效应与框架几何尺度变化关系,选取p=100 kPa计算分析消融施工期—冻胀期—二次消融期3阶段演化过程中框架几何尺度变化关系. 由图14(a)可知,当立柱间距为2 m时,消融施工期水平拱轴线矢高为660 mm;进入冬季后,土体力学参数有所提高,导致冻胀期水平拱轴线拱顶向坡面回缩6 mm,二次消融期水平拱轴线拱顶向坡内扩展5 mm. 由图14(b)可知,当横梁间距为2 m时,消融施工期竖向拱轴线矢高为654 mm,冻胀期竖向拱轴线拱顶坡面回缩5 mm,二次消融期竖向拱轴线拱顶向坡内扩展11 mm. 由此可知,在冻融演化过程中拱轴线变化幅度较小,可不考虑对土拱效应的影响. 由图13(a)可知,随着冻胀力增大,土拱效应越明显,框架宽度随之增加. 由图13(b)、(c)可知,随着框架梁之间的距离增大,土拱效应越明显,框架宽度增加,其中水平土拱作用下框架宽度二次消融期大于消融施工期,冻胀期比其他工况大1.3~1.5倍. 竖向土拱作用下框架宽度二次消融期和消融施工期几乎相等,冻胀期比其他工况大1.5倍. 在工程设计中,框架横梁宽度为550 mm、立柱宽度为500 mm,本次计算方法得出横梁计算宽度为511 mm,立柱计算宽度为440 mm,设计尺寸和计算尺寸相对误差各占7%和12%,设计尺度略有保守.
图 13
图 14
图 14 冻融演化过程中拱轴线的变化
Fig.14 Change in arch axis under freeze-thaw evolution process
5.3. 锚杆尺度计算
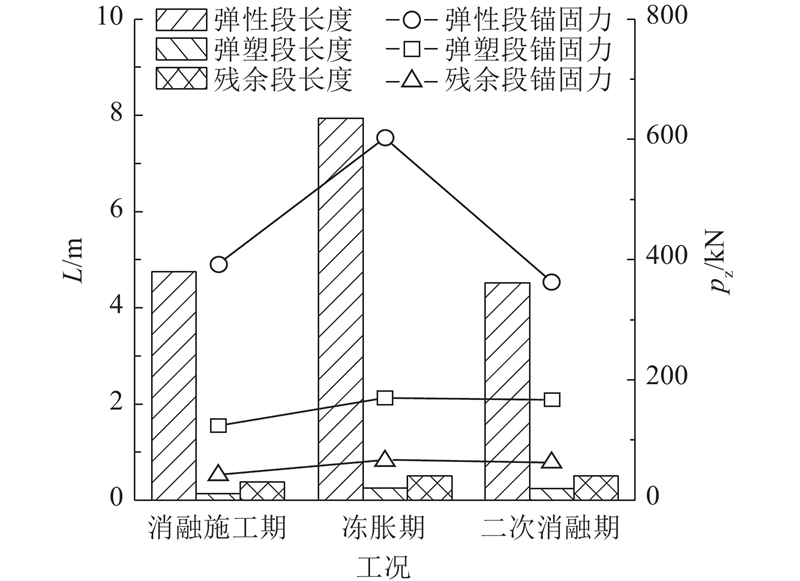
在冻融演化过程中,锚杆锚固力发生变化的关键影响因素是最不利荷载作用下的锚固段有效长度. 如图15所示,依据冻融过程锚固段实测荷载-位移的关系式[30],计算消融施工期、冻胀期、二次消融期冻融演化过程中锚固段弹性阶段、弹塑性阶段及残余阶段的长度L及锚固力pz. 按照消融施工期—冻胀期—二次消融期3阶段循环进行分析,其中消融施工期锚固段弹塑性阶段和残余阶段长度较小,锚固段长度最长,表明以弹性阶段承担锚固力为主;冻胀期弹性阶段、弹塑性阶段及残余阶段相对消融施工期均有所增加,弹性段增长最为明显;二次消融期相对冻胀期弹性阶段长度缩短明显且小于消融施工期,弹塑性阶段及残余阶段间具有不可逆性,因此锚固段长度和冻胀期保持一致. 由于弹性段承担了绝大部分锚固力,从消融施工期、冻胀期、二次消融期分析弹性段长度变化,冻胀期弹性段长度远大于消融施工期,为1.6~1.7倍,为二次消融期的2.0~2.2倍.
图 15
图 15 不同工况下锚杆锚固段长度理论计算值
Fig.15 Theoretically calculated value of anchorage length under different working conditions
5.4. 验证分析
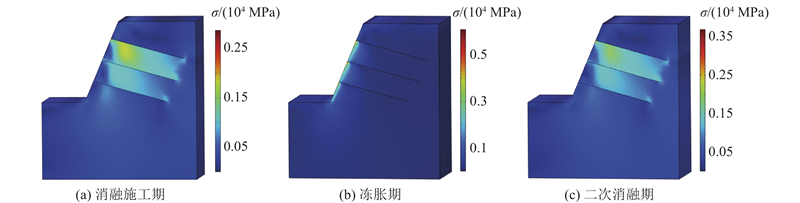
为了验证计算方法的合理性,通过数值模拟和现场监测相结合的方式,对冻融演化过程消融期、冻胀期和二次消融期数据进行对比分析. 如图16所示为冻融过程框架锚杆边坡支护应力云图. 数值模拟分析表明,冻胀期锚杆轴力高于消融施工期约1.38倍,高于二次消融期约1.27倍. 为了防止冻胀期锚杆轴力增加过大,导致锚固段失效锚杆拔出造成安全隐患,依据最不利工况设计原则,建议以冻胀期工况作为框架锚杆设计基准较为合理.
图 16
图 16 冻融过程中框架锚杆边坡支护应力云图
Fig.16 Stress nephogram of slope retaining with frame anchors during freeze-thaw cycles
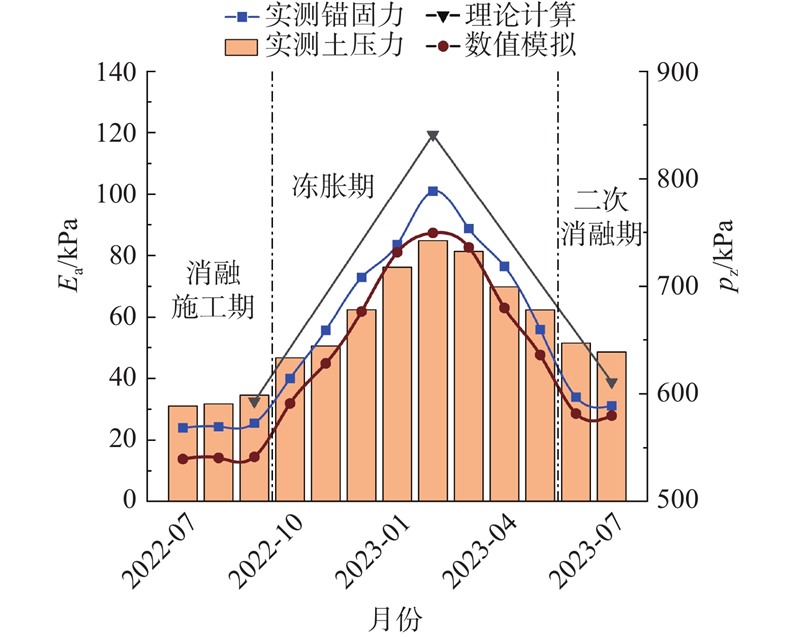
冻融演化过程中现场实测土压力Ea和锚固力pz如图17所示. 分析冻融演化过程中消融期—冻胀期—二次消融期锚杆轴力动态变化可知,理论计算结果总体上略高于实测值,数值模拟略低于实测值. 由误差分析可知,以现场监测数值为基准,理论值和现场监测相对误差为0.60%、数值模拟和现场监测误差为0.52%,属于正常工程可控范围,且变化趋势基本一致,表明该理论计算方法合理可行.
图 17
图 17 关键参数月份现场监测与理论推导数据对比
Fig.17 Comparison between field-monitored and theoretically derived data for key parameters
6. 结 语
本研究基于冻融演化过程,考虑框架与坡面、锚固段注浆体与岩土界面之间的相互作用,建立框架作用下土拱、锚杆注浆体与地层之间的计算模型,并结合具体算例,揭示冻融演化过程中框架间土拱、锚杆内力及其尺度效应之间的关系,主要结论如下. 1)依据框架梁与坡面作用产生土压力力学模型,满足土体莫尔-库伦强度准则,按照合理拱轴线基本假定原则,分别建立框架作用下的水平土拱和竖向土拱几何尺度计算模型,明确冻融演化过程土拱计算模型的关键控制参数. 2)从工程施工与运营角度出发,清晰描述消融施工期、冻胀期和二次消融期的演化过程,构建冻融作用下锚固体界面的切应力与剪切位移本构模型,建立残余段、弹塑段与弹性段长度的计算模型,通过现场监测数据和数值模拟验证理论计算方法的合理性. 3)随着坡面冻胀力的增加,框架几何宽度显著增加. 在水平土拱作用下,框架宽度在二次消融期大于消融施工期,冻胀期宽度是其他工况的1.3~1.5倍;在竖向土拱作用下,二次消融期与消融施工期的框架宽度几乎相等,冻胀期宽度是其他工况的1.5倍. 4)随冻胀力增加锚杆的内力增加,锚杆锚固段长度增加明显,其中弹性阶段、弹塑性阶段及残余阶段相对消融施工期均有所增加,弹性段增长最为明显,确定以冻胀期为最不利工况的框架锚杆尺度设计基准. 本文探究冻融演化过程中冻融对框架-锚-土相互作用机制,关于冻融循环的影响有待今后深入分析.
参考文献
多年冻土区L型挡墙水平冻胀效应计算方法与分析
[J].
Calculation method and analysis of horizontal frost heave effect of L-shaped retaining wall in permafrost regions
[J].
考虑冻土与结构相互作用的梯形渠道冻胀破坏弹性地基梁模型
[J].
Elastic foundation beam model of frost heave damage of trapezoidal canal considering interaction between frozen soil and lining stucture
[J].
青藏高原多年冻土特征、变化及影响
[J].DOI:10.1360/TB-2019-0191 [本文引用: 1]
Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau
[J].DOI:10.1360/TB-2019-0191 [本文引用: 1]
冻融循环导致洛川黄土边坡剥落病害产生机制的试验研究
[J].
Test research on mechanism of freezing and thawing cycle resulting in loess slope spalling hazards in Luochuan
[J].
黄土边坡框架锚杆结构的加固研究
[J].
Study on grillage supporting structure with anchor bars on loess slope reinforcement
[J].
软岩高边坡多级框架锚杆设计计算方法
[J].
Design method for multi-frame beams with anchor bolts used to stabilize high soft-rock slope
[J].
框架预应力锚杆高边坡加固机理及优化设计研究
[J].
The reinforcement mechanism of high slope and optimization design research using the frame supporting structure with prestressed anchor
[J].
Analysis of deformation and stress characteristics of anchored-frame structures for slope stabilization
[J].DOI:10.1155/2020/8870802 [本文引用: 1]
Internal force analysis of frame structure considering the soil constraint
[J].DOI:10.4028/www.scientific.net/AMM.777.38 [本文引用: 1]
拉力型锚杆锚固段拉拔受力的非线性全历程分析
[J].
Nonlinear full-range analysis of load transfer in fixed segment of tensile anchors
[J].
全长黏结式锚杆锚固段荷载传递特性研究
[J].
Study on load transfer characteristics of wholly grouted bolt
[J].
注浆锚杆界面应力分析及临界锚固长度计算
[J].
Analysis of interface stress of grouting rockbolt and calculation of critical anchorage length
[J].
季冻黄土地区框锚边坡预应力锚杆内力计算方法
[J].
Calculation and analysis of internal forces of prestressed anchor on frame anchors supporting slope in the seasonal freeze-thaw loess area
[J].
Distribution pattern of anchorage stress and water sensitivity analysis of red clay
[J].
Calculation method of the effective anchorage length of anchorage structures based on analysis of the ultimate bearing capacity
[J].DOI:10.1007/s10706-021-01751-w [本文引用: 1]
Study on effective anchorage length of anchor cable based on Gauss’s function
[J].DOI:10.1088/1755-1315/94/1/012203 [本文引用: 1]
Experimental and numerical investigation on the deterioration mechanism for grouted rock bolts subjected to freeze–thaw cycles
[J].DOI:10.1007/s10064-021-02279-2 [本文引用: 1]
土体冻胀对桩锚支护结构影响试验研究
[J].
Experimental study on the effect of soil frost heave on pile-anchor supporting structure
[J].
考虑土拱效应预应力锚拉桩土压力研究
[J].
Study of earth pressure of prestressed anchor pile considering soil arching
[J].
中国西部土壤冻融起止期和冻结深度及其与气温关系的时空分布特征分析
[J].
The spatio-temporal distribution of the start-end date and freezing depth and their relationships with air temperature over the western China
[J].
滑面极径-应力-强度耦合关联下非线性破坏特征边坡稳定性极限平衡分析方法
[J].
Limit equilibrium method for analyzing slope stability with nonlinear failure characteristics considering the coupling relationship of polar diameter, stress, and strength of the slip surface
[J].
框架锚杆锚固寒区边坡的多场耦合分析
[J].
Analysis on coupling model of permafrost slope reinforced by frame structure with anchors
[J].
锚杆岩体界面载荷传递规律及锚固长度设计
[J].
Load transfer law and anchorage length design at interface between rock bolts and rock mass
[J].
Laboratory evaluation of cement-based grouts and grouted rock anchors
[J].