[1]
LUO H, ZHANG J, LIU X, et al Large-scale 3D reconstruction from multi-view imagery: a comprehensive review
[J]. Remote Sensing , 2024 , 16 (5 ): 773
DOI:10.3390/rs16050773
[本文引用: 1]
[2]
于海洋, 封顺天, 崔立鹏 面向城市数字孪生的多尺度三维建模方法研究
[J]. 电子技术应用 , 2022 , 48 (7 ): 78 - 80
[本文引用: 1]
YU Haiyang, FENG Shuntian, CUI Lipeng Research on multi-scale 3D modeling method for urban digital twin
[J]. Application of Electronic Technique , 2022 , 48 (7 ): 78 - 80
[本文引用: 1]
[4]
RABBANI T, VAN DEN HEUVEL F A, VOSSELMANN G Segmentation of point clouds using smoothness constraint
[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences , 2006 , 36 (5 ): 248 - 253
[本文引用: 1]
[5]
QI C R, YI L, SU H, et al. PointNet++: deep hierarchical feature learning on point sets in a metric space [EB/OL]. (2017−06−07)[2024−03−14]. https://arxiv.org/pdf/1706.02413.
[本文引用: 1]
[6]
WANG R, HUANG S, YANG H. Building3D: an urban-scale dataset and benchmarks for learning roof structures from point clouds [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Paris: IEEE, 2024: 20019–20029.
[本文引用: 1]
[7]
YANG G, XUE F, ZHANG Q, et al. UrbanBIS: a large-scale benchmark for fine-grained urban building instance segmentation [C]// Proceedings of the ACM SIGGRAPH 2023 Conference Proceedings . Los Angeles: ACM, 2023: 1–11.
[本文引用: 1]
[8]
PETERS R, DUKAI B, VITALIS S, et al Automated 3D reconstruction of LoD2 and LoD1 models for all 10 million buildings of the Netherlands
[J]. Photogrammetric Engineering and Remote Sensing , 2022 , 88 (3 ): 165 - 170
DOI:10.14358/PERS.21-00032R2
[本文引用: 1]
[9]
NAN L, WONKA P. PolyFit: polygonal surface reconstruction from point clouds [C]// Proceedings of the IEEE International Conference on Computer Vision . Venice: IEEE, 2017: 2372–2380.
[本文引用: 3]
[11]
HUANG J, STOTER J, PETERS R, et al City3D: large-scale building reconstruction from airborne LiDAR point clouds
[J]. Remote Sensing , 2022 , 14 (9 ): 2254
DOI:10.3390/rs14092254
[本文引用: 3]
[12]
BAUCHET J P, LAFARGE F City reconstruction from airborne lidar: a computational geometry approach
[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences , 2019 , 4 : 19 - 26
[本文引用: 1]
[13]
CHEN Z, SHI Y, XIONG Z, et al. Polyhedron-based graph neural network for compact building model reconstruction [C]// Proceedings of 2023 IEEE International Geoscience and Remote Sensing Symposium . Pasadena: IEEE, 2023: 923–926.
[本文引用: 1]
[14]
CHEN Z, SHI Y, NAN L, et al PolyGNN: polyhedron-based graph neural network for 3D building reconstruction from point clouds
[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2024 , 218 : 693 - 706
DOI:10.1016/j.isprsjprs.2024.09.031
[本文引用: 3]
[15]
HE X, LV C, HUANG P, et al. WindPoly: polygonal mesh reconstruction via winding numbers [C]// Computer Vision – ECCV 2024 . [S.l.]: Springer, 2024: 294–311.
[本文引用: 1]
[16]
HUANG S, WANG R, GUO B, et al. PBWR: parametric-building-wireframe reconstruction from aerial LiDAR point clouds [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2024: 27778–27787.
[本文引用: 1]
[17]
LI L, SONG N, SUN F, et al Point2Roof: end-to-end 3D building roof modeling from airborne LiDAR point clouds
[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2022 , 193 : 17 - 28
DOI:10.1016/j.isprsjprs.2022.08.027
[本文引用: 1]
[18]
JAVEED M A, GHAFFAR M A, ASHRAF M A, et al Lane line detection and object scene segmentation using otsu thresholding and the fast Hough transform for intelligent vehicles in complex road conditions
[J]. Electronics , 2023 , 12 (5 ): 1079
DOI:10.3390/electronics12051079
[本文引用: 1]
[19]
SYED M H, KUMAR S. Road lane line detection based on ROI using Hough transform algorithm [C]// Proceedings of Third International Conference on Computing, Communications, and Cyber-Security . Singapore: Springer, 2023: 567–580.
[20]
MATARNEH S, ELGHAISH F, AL-GHRAIBAH A, et al An automatic image processing based on Hough transform algorithm for pavement crack detection and classification
[J]. Smart and Sustainable Built Environment , 2025 , 14 (1 ): 1 - 22
DOI:10.1108/SASBE-01-2023-0004
[本文引用: 1]
[21]
QI C R, LITANY O, HE K, et al. Deep Hough voting for 3D object detection in point clouds [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2019: 9276–9285.
[本文引用: 1]
[22]
ZHANG J Q, DUAN H B, CHEN J L, et al HoughLaneNet: lane detection with deep Hough transform and dynamic convolution
[J]. Computers and Graphics , 2023 , 116 : 82 - 92
[本文引用: 1]
[23]
ZHAO H, JIANG L, JIA J, et al. Point transformer [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2022: 16239–16248.
[本文引用: 1]
[24]
LI J, ZHOU J, XIONG Y, et al. An adjustable farthest point sampling method for approximately-sorted point cloud data [C]// Proceedings of the IEEE Workshop on Signal Processing Systems . Rennes: IEEE, 2022: 1–6.
[本文引用: 1]
[25]
HU J, SHEN L, SUN G. Squeeze-and-excitation networks [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 7132–7141.
[本文引用: 1]
[26]
Republic of Estonia Land and Spatial Development Board. Building 3D model data [EB/OL]. [2024−04−15]. https://geoportaal.maaamet.ee/eng/Download-3D-data-p837.html.
[本文引用: 1]
[27]
DONG L, XIAO Y, LI Y, et al A collision detection algorithm based on sphere and EBB mixed hierarchical bounding boxes
[J]. IEEE Access , 2024 , 12 : 62719 - 62729
[本文引用: 1]
[28]
WU M, SUN M, ZHANG F, et al A fault detection method of electric vehicle battery through Hausdorff distance and modified Z -score for real-world data
[J]. Journal of Energy Storage , 2023 , 60 : 106561
[本文引用: 1]
[29]
LIN F, YUE Y, ZHANG Z, et al. InfoCD: a contrastive chamfer distance loss for point cloud completion [C]// Proceedings of the 37th Conference on Neural Information Processing Systems . New Orleans: [s.n.], 2023: 1–14.
[本文引用: 1]
Large-scale 3D reconstruction from multi-view imagery: a comprehensive review
1
2024
... 三维建筑是实景三维城市场景中的重要组成部分. 借助无人机搭载的高分辨率相机或激光雷达传感器,利用三维重建技术能够高效地获得大规模的三维建筑模型,模型的表达模式通常为三维点云或三角网格[1 ] . 三维建筑模型往往存在顶点数量多、噪声大、结构缺失等缺陷,给建筑模型的存储、传输、可视化与编辑等带来巨大挑战,也阻碍了模型在地理信息、智慧城市、低空经济等领域的应用[2 ] . ...
面向城市数字孪生的多尺度三维建模方法研究
1
2022
... 三维建筑是实景三维城市场景中的重要组成部分. 借助无人机搭载的高分辨率相机或激光雷达传感器,利用三维重建技术能够高效地获得大规模的三维建筑模型,模型的表达模式通常为三维点云或三角网格[1 ] . 三维建筑模型往往存在顶点数量多、噪声大、结构缺失等缺陷,给建筑模型的存储、传输、可视化与编辑等带来巨大挑战,也阻碍了模型在地理信息、智慧城市、低空经济等领域的应用[2 ] . ...
面向城市数字孪生的多尺度三维建模方法研究
1
2022
... 三维建筑是实景三维城市场景中的重要组成部分. 借助无人机搭载的高分辨率相机或激光雷达传感器,利用三维重建技术能够高效地获得大规模的三维建筑模型,模型的表达模式通常为三维点云或三角网格[1 ] . 三维建筑模型往往存在顶点数量多、噪声大、结构缺失等缺陷,给建筑模型的存储、传输、可视化与编辑等带来巨大挑战,也阻碍了模型在地理信息、智慧城市、低空经济等领域的应用[2 ] . ...
Efficient RANSAC for point-cloud shape detection
1
2007
... 将三维建筑点云重建为稀疏而精确的多边形网格模型能够有效解决上述问题. 多边形网格模型能够紧凑表达物体的表面特征,减少数据存储量,间接提高数据处理和传输的效率. 由于点云数据本身具有无序性和缺乏内在结构的特点,直接从点云中重建结构化、层次化的多边形网格模型难度大,本研究以三维建筑点云为对象,将其重建为轻量级的多边形网格模型. 现有的三维建筑表面重建方法分为2个大类. 1)依据建筑的平面信息重建出网格模型,侧重于利用建筑物的平面布局特征,依赖于建筑平面检测的准确性. 现有的建筑点云平面检测方法主要有RANSAC[3 ] 以及区域增长法[4 ] . RANSAC针对不同的建筑点云手动调节参数,迭代计算的开销较大. 区域增长法依赖于种子点的选择,不合适的种子点可能导致不完整或者错误的区域扩展;该方法对噪声和离群点也比较敏感,容易陷入局部最优解,导致一些重要表面特征丢失. 2)通过识别建筑的边缘或顶点来实现模型的简化,侧重于捕捉建筑物的轮廓和结构特征,但是从建筑点云中直接预测边缘和顶点比较困难. ...
Segmentation of point clouds using smoothness constraint
1
2006
... 将三维建筑点云重建为稀疏而精确的多边形网格模型能够有效解决上述问题. 多边形网格模型能够紧凑表达物体的表面特征,减少数据存储量,间接提高数据处理和传输的效率. 由于点云数据本身具有无序性和缺乏内在结构的特点,直接从点云中重建结构化、层次化的多边形网格模型难度大,本研究以三维建筑点云为对象,将其重建为轻量级的多边形网格模型. 现有的三维建筑表面重建方法分为2个大类. 1)依据建筑的平面信息重建出网格模型,侧重于利用建筑物的平面布局特征,依赖于建筑平面检测的准确性. 现有的建筑点云平面检测方法主要有RANSAC[3 ] 以及区域增长法[4 ] . RANSAC针对不同的建筑点云手动调节参数,迭代计算的开销较大. 区域增长法依赖于种子点的选择,不合适的种子点可能导致不完整或者错误的区域扩展;该方法对噪声和离群点也比较敏感,容易陷入局部最优解,导致一些重要表面特征丢失. 2)通过识别建筑的边缘或顶点来实现模型的简化,侧重于捕捉建筑物的轮廓和结构特征,但是从建筑点云中直接预测边缘和顶点比较困难. ...
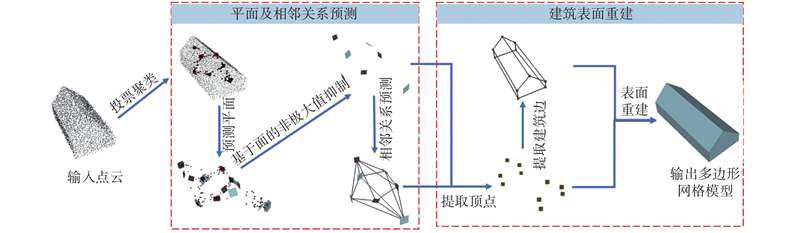
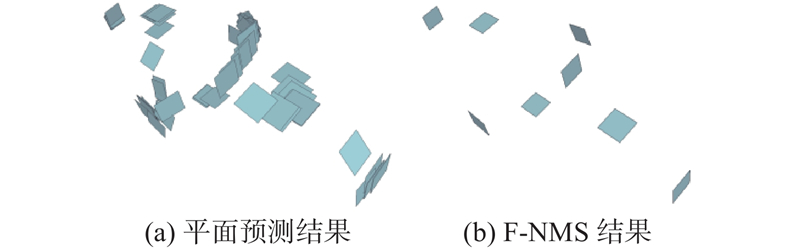
1
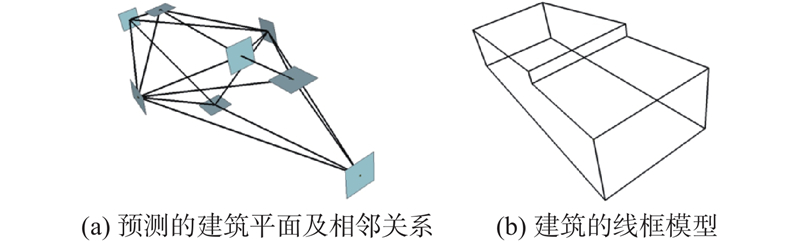
... 针对平面预测困难的问题,本研究借鉴深度霍夫投票的3D目标检测算法的思路,通过数据驱动构建建筑点云中的平面预测深度学习模型. 先由PointNet++[5 ] 网络输出投票点及投票点的特征;再通过投票网络使投票点偏移到平面中心点位置附近;之后进行投票点聚类,使用聚类结果预测建筑平面的参数. 其中平面的预测参数是面的中心点、法线以及置信度. 在本研究中,建筑平面(面)指的是每个平面点云的最小包围框;为了有效去除初始预测平面中存在的众多冗余面,提出基于平面的非极大值抑制算法(face-based non-maximal suppression algorithm,F-NMS);在网络模型中设计针对建筑平面的相邻关系预测模块,自动构建建筑平面的拓扑关系图;设计建筑轻量级重建的模块,在平面及其相邻关系的基础上进一步提取建筑多边形平面的顶点和边缘,构建准确和紧致的多边形网格模型. 现有的建筑点云数据集主要有Building3D[6 ] 、UrbanBIS[7 ] ,这些数据集都没有平面预测所需的标签,为此本研究设计算法,自动将LoD2[8 ] 的建筑三角网格数据转换为带建筑平面标签的建筑点云数据. ...
1
... 针对平面预测困难的问题,本研究借鉴深度霍夫投票的3D目标检测算法的思路,通过数据驱动构建建筑点云中的平面预测深度学习模型. 先由PointNet++[5 ] 网络输出投票点及投票点的特征;再通过投票网络使投票点偏移到平面中心点位置附近;之后进行投票点聚类,使用聚类结果预测建筑平面的参数. 其中平面的预测参数是面的中心点、法线以及置信度. 在本研究中,建筑平面(面)指的是每个平面点云的最小包围框;为了有效去除初始预测平面中存在的众多冗余面,提出基于平面的非极大值抑制算法(face-based non-maximal suppression algorithm,F-NMS);在网络模型中设计针对建筑平面的相邻关系预测模块,自动构建建筑平面的拓扑关系图;设计建筑轻量级重建的模块,在平面及其相邻关系的基础上进一步提取建筑多边形平面的顶点和边缘,构建准确和紧致的多边形网格模型. 现有的建筑点云数据集主要有Building3D[6 ] 、UrbanBIS[7 ] ,这些数据集都没有平面预测所需的标签,为此本研究设计算法,自动将LoD2[8 ] 的建筑三角网格数据转换为带建筑平面标签的建筑点云数据. ...
1
... 针对平面预测困难的问题,本研究借鉴深度霍夫投票的3D目标检测算法的思路,通过数据驱动构建建筑点云中的平面预测深度学习模型. 先由PointNet++[5 ] 网络输出投票点及投票点的特征;再通过投票网络使投票点偏移到平面中心点位置附近;之后进行投票点聚类,使用聚类结果预测建筑平面的参数. 其中平面的预测参数是面的中心点、法线以及置信度. 在本研究中,建筑平面(面)指的是每个平面点云的最小包围框;为了有效去除初始预测平面中存在的众多冗余面,提出基于平面的非极大值抑制算法(face-based non-maximal suppression algorithm,F-NMS);在网络模型中设计针对建筑平面的相邻关系预测模块,自动构建建筑平面的拓扑关系图;设计建筑轻量级重建的模块,在平面及其相邻关系的基础上进一步提取建筑多边形平面的顶点和边缘,构建准确和紧致的多边形网格模型. 现有的建筑点云数据集主要有Building3D[6 ] 、UrbanBIS[7 ] ,这些数据集都没有平面预测所需的标签,为此本研究设计算法,自动将LoD2[8 ] 的建筑三角网格数据转换为带建筑平面标签的建筑点云数据. ...
Automated 3D reconstruction of LoD2 and LoD1 models for all 10 million buildings of the Netherlands
1
2022
... 针对平面预测困难的问题,本研究借鉴深度霍夫投票的3D目标检测算法的思路,通过数据驱动构建建筑点云中的平面预测深度学习模型. 先由PointNet++[5 ] 网络输出投票点及投票点的特征;再通过投票网络使投票点偏移到平面中心点位置附近;之后进行投票点聚类,使用聚类结果预测建筑平面的参数. 其中平面的预测参数是面的中心点、法线以及置信度. 在本研究中,建筑平面(面)指的是每个平面点云的最小包围框;为了有效去除初始预测平面中存在的众多冗余面,提出基于平面的非极大值抑制算法(face-based non-maximal suppression algorithm,F-NMS);在网络模型中设计针对建筑平面的相邻关系预测模块,自动构建建筑平面的拓扑关系图;设计建筑轻量级重建的模块,在平面及其相邻关系的基础上进一步提取建筑多边形平面的顶点和边缘,构建准确和紧致的多边形网格模型. 现有的建筑点云数据集主要有Building3D[6 ] 、UrbanBIS[7 ] ,这些数据集都没有平面预测所需的标签,为此本研究设计算法,自动将LoD2[8 ] 的建筑三角网格数据转换为带建筑平面标签的建筑点云数据. ...
3
... 依据建筑平面信息构建建筑简化模型的常规步骤:1)通过传统算法(如RANSAC、区域增长法)检测得到建筑平面,2)根据平面将模型切割成小块的平面或多边体,3)从这些切割形体中选出合适的子集来构建简化的建筑模型. Nan等[9 ] 提出PolyFit系统,通过改进的RANSAC提取平面,让提取的平面进行相互切割,形成多个小块的平面,再将问题转化为二值标记问题,从切割出来的大量小块平面中选出合适的候选平面集合,然后将候选平面集合拟合成简化结果. Bouzas等[10 ] 通过识别建筑平面之间的相邻关系重建出简化模型. Huang等[11 ] 使用建筑高程图提取建筑轮廓并生成垂直平面,再结合传统算法(如RANSAC)提取的平面重建出简化模型. Bauchet等[12 ] 提出利用机载LiDAR扫描数据将城市环境中的建筑物重建为简洁多边形网格的方法,使用平面将空间分割成多个多面体,随后基于投票方案和能量函数对多面体进行标注的方法得到建筑物的内外表面,从而得到建筑物的多边形网格. Chen等[13 ] 使用深度神经网络学习隐式场来选出合适的多面体子集,进而重建出简化模型. Chen等[14 ] 引入图神经网络来选择多面体子集,重建出建筑的简化模型. He等[15 ] 提出WindPoly,通过多边形平面检测、自适应分区和环绕数优化,实现无需法向量、高效且几何一致的低多边形网格重建. 上述方法易受噪声干扰,且须手动调节参数,本研究通过深度霍夫投票来预测建筑平面,无需手动调节参数. ...
... Building simplified performance comparison and evaluation form (
σ =0.02)
Tab.4 方法 $ {N}_{\mathrm{p}} $ $ {N}_{\mathrm{f}} $ S /MBHD/m CD/m $ {r}_{{\mathrm{e}}} $ 原始 2048000 — 112 — — — 本研究 4998 3434 0.349 0.30 0.15 4.6 PolyFit[9 ] 14708 3782 0.939 0.30 0.14 3.8 City3D[11 ] 22522 6520 1.560 0.93 0.59 36.4 PolyGNN[14 ] 18224 4440 0.643 0.33 0.15 2.6
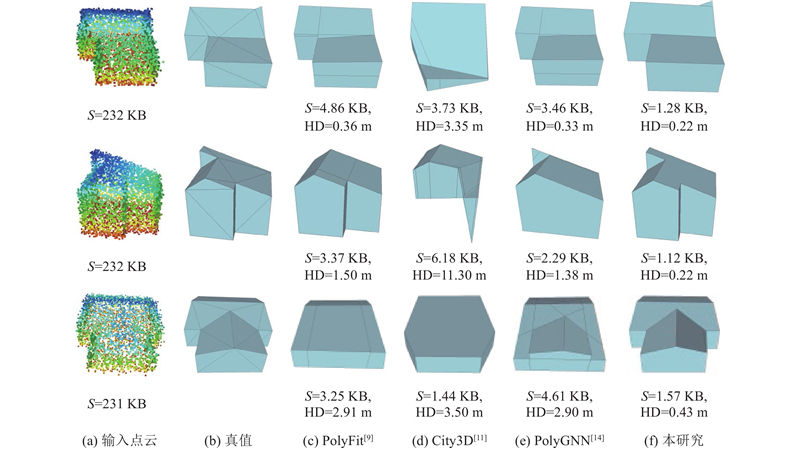
如图8 所示为不同方法生成的建筑模型可视化效果对比. 可以看出,对比其他方法,所提方法重建的建筑多边形网格模型所需面片数量最少且与真值的建筑点云高度相符. City3D须调整到合适的参数才能获得比较好的结果,本研究使用City3D默认的参数进行重建. PolyFit和PolyGNN在某些数据上的HD略小于所提方法的模型,但在表达模型所需的面片数量上,所提方法远远小于PolyFit和PolyGNN. 原因是本研究所提方法表达1个平面只需要1个多边形网格,而PolyFit和PolyGNN需要多个多边形网格. ...
... Quantitative evaluation results of building simplified noise resistance
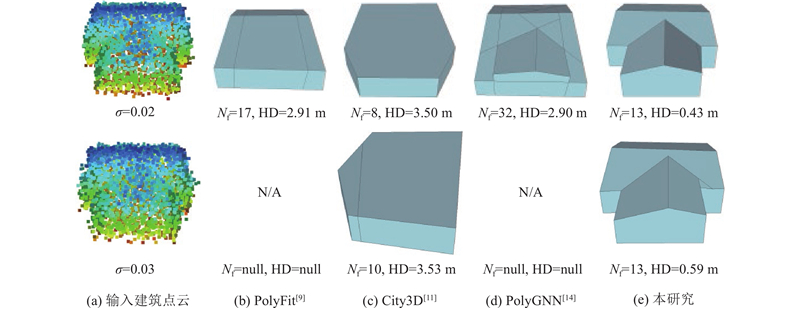
Tab.5 方法 基于学习 CD↓/m HD↓/m $ {r}_{{\mathrm{e}}} $ σ =0.02σ =0.03σ =0.02σ =0.03σ =0.02σ =0.03PolyFit[9 ] × 0.14 0.19 0.30 0.42 3.8 17.0 City3D[11 ] × 0.59 0.75 0.93 1.10 36.4 35.2 PolyGNN[14 ] √ 0.15 0.24 0.33 0.50 2.6 15.2 本研究 √ 0.15 0.17 0.30 0.36 4.6 4.2
6. 结 语 本研究提出基于深度学习的建筑点云轻量级表面重建方法. 为了检测出建筑点云中的平面,使用基于深度霍夫投票的方法,将点云聚类到所在平面的中心点附近,提高了建筑平面预测的准确性. 本研究提出基于面的非极大值抑制算法有效去除了预测面中的冗余面;在相邻关系预测模块中,提出配对面注意力模块;设计能够利用预测面以及面相邻关系构建多边形网格模型的方法,实现了建筑点云的有效简化. 所提表面重建方法在保证建筑点云结构完整性的同时,极大降低了存储需求,提高了数据传输和处理效率;在三维城市建模、智慧城市和地理信息系统等领域具有广泛的应用价值. 所提表面重建方法主要针对以平面结构为主的建筑点云,对于包含曲面结构(如圆柱体、圆锥体、球体等)的建筑适用性较弱. 在未来的研究中,1)计划结合基于隐式表示的深度学习方法(如NeRF、SDF)进行曲面建筑的重建能力改进;2)借鉴稳健的低多边形网格表示方法,将建筑点云三角网格化后转化为低多边形网格. ...
Structure-aware building mesh polygonization
1
2020
... 依据建筑平面信息构建建筑简化模型的常规步骤:1)通过传统算法(如RANSAC、区域增长法)检测得到建筑平面,2)根据平面将模型切割成小块的平面或多边体,3)从这些切割形体中选出合适的子集来构建简化的建筑模型. Nan等[9 ] 提出PolyFit系统,通过改进的RANSAC提取平面,让提取的平面进行相互切割,形成多个小块的平面,再将问题转化为二值标记问题,从切割出来的大量小块平面中选出合适的候选平面集合,然后将候选平面集合拟合成简化结果. Bouzas等[10 ] 通过识别建筑平面之间的相邻关系重建出简化模型. Huang等[11 ] 使用建筑高程图提取建筑轮廓并生成垂直平面,再结合传统算法(如RANSAC)提取的平面重建出简化模型. Bauchet等[12 ] 提出利用机载LiDAR扫描数据将城市环境中的建筑物重建为简洁多边形网格的方法,使用平面将空间分割成多个多面体,随后基于投票方案和能量函数对多面体进行标注的方法得到建筑物的内外表面,从而得到建筑物的多边形网格. Chen等[13 ] 使用深度神经网络学习隐式场来选出合适的多面体子集,进而重建出简化模型. Chen等[14 ] 引入图神经网络来选择多面体子集,重建出建筑的简化模型. He等[15 ] 提出WindPoly,通过多边形平面检测、自适应分区和环绕数优化,实现无需法向量、高效且几何一致的低多边形网格重建. 上述方法易受噪声干扰,且须手动调节参数,本研究通过深度霍夫投票来预测建筑平面,无需手动调节参数. ...
City3D: large-scale building reconstruction from airborne LiDAR point clouds
3
2022
... 依据建筑平面信息构建建筑简化模型的常规步骤:1)通过传统算法(如RANSAC、区域增长法)检测得到建筑平面,2)根据平面将模型切割成小块的平面或多边体,3)从这些切割形体中选出合适的子集来构建简化的建筑模型. Nan等[9 ] 提出PolyFit系统,通过改进的RANSAC提取平面,让提取的平面进行相互切割,形成多个小块的平面,再将问题转化为二值标记问题,从切割出来的大量小块平面中选出合适的候选平面集合,然后将候选平面集合拟合成简化结果. Bouzas等[10 ] 通过识别建筑平面之间的相邻关系重建出简化模型. Huang等[11 ] 使用建筑高程图提取建筑轮廓并生成垂直平面,再结合传统算法(如RANSAC)提取的平面重建出简化模型. Bauchet等[12 ] 提出利用机载LiDAR扫描数据将城市环境中的建筑物重建为简洁多边形网格的方法,使用平面将空间分割成多个多面体,随后基于投票方案和能量函数对多面体进行标注的方法得到建筑物的内外表面,从而得到建筑物的多边形网格. Chen等[13 ] 使用深度神经网络学习隐式场来选出合适的多面体子集,进而重建出简化模型. Chen等[14 ] 引入图神经网络来选择多面体子集,重建出建筑的简化模型. He等[15 ] 提出WindPoly,通过多边形平面检测、自适应分区和环绕数优化,实现无需法向量、高效且几何一致的低多边形网格重建. 上述方法易受噪声干扰,且须手动调节参数,本研究通过深度霍夫投票来预测建筑平面,无需手动调节参数. ...
... Building simplified performance comparison and evaluation form (
σ =0.02)
Tab.4 方法 $ {N}_{\mathrm{p}} $ $ {N}_{\mathrm{f}} $ S /MBHD/m CD/m $ {r}_{{\mathrm{e}}} $ 原始 2048000 — 112 — — — 本研究 4998 3434 0.349 0.30 0.15 4.6 PolyFit[9 ] 14708 3782 0.939 0.30 0.14 3.8 City3D[11 ] 22522 6520 1.560 0.93 0.59 36.4 PolyGNN[14 ] 18224 4440 0.643 0.33 0.15 2.6
如图8 所示为不同方法生成的建筑模型可视化效果对比. 可以看出,对比其他方法,所提方法重建的建筑多边形网格模型所需面片数量最少且与真值的建筑点云高度相符. City3D须调整到合适的参数才能获得比较好的结果,本研究使用City3D默认的参数进行重建. PolyFit和PolyGNN在某些数据上的HD略小于所提方法的模型,但在表达模型所需的面片数量上,所提方法远远小于PolyFit和PolyGNN. 原因是本研究所提方法表达1个平面只需要1个多边形网格,而PolyFit和PolyGNN需要多个多边形网格. ...
... Quantitative evaluation results of building simplified noise resistance
Tab.5 方法 基于学习 CD↓/m HD↓/m $ {r}_{{\mathrm{e}}} $ σ =0.02σ =0.03σ =0.02σ =0.03σ =0.02σ =0.03PolyFit[9 ] × 0.14 0.19 0.30 0.42 3.8 17.0 City3D[11 ] × 0.59 0.75 0.93 1.10 36.4 35.2 PolyGNN[14 ] √ 0.15 0.24 0.33 0.50 2.6 15.2 本研究 √ 0.15 0.17 0.30 0.36 4.6 4.2
6. 结 语 本研究提出基于深度学习的建筑点云轻量级表面重建方法. 为了检测出建筑点云中的平面,使用基于深度霍夫投票的方法,将点云聚类到所在平面的中心点附近,提高了建筑平面预测的准确性. 本研究提出基于面的非极大值抑制算法有效去除了预测面中的冗余面;在相邻关系预测模块中,提出配对面注意力模块;设计能够利用预测面以及面相邻关系构建多边形网格模型的方法,实现了建筑点云的有效简化. 所提表面重建方法在保证建筑点云结构完整性的同时,极大降低了存储需求,提高了数据传输和处理效率;在三维城市建模、智慧城市和地理信息系统等领域具有广泛的应用价值. 所提表面重建方法主要针对以平面结构为主的建筑点云,对于包含曲面结构(如圆柱体、圆锥体、球体等)的建筑适用性较弱. 在未来的研究中,1)计划结合基于隐式表示的深度学习方法(如NeRF、SDF)进行曲面建筑的重建能力改进;2)借鉴稳健的低多边形网格表示方法,将建筑点云三角网格化后转化为低多边形网格. ...
City reconstruction from airborne lidar: a computational geometry approach
1
2019
... 依据建筑平面信息构建建筑简化模型的常规步骤:1)通过传统算法(如RANSAC、区域增长法)检测得到建筑平面,2)根据平面将模型切割成小块的平面或多边体,3)从这些切割形体中选出合适的子集来构建简化的建筑模型. Nan等[9 ] 提出PolyFit系统,通过改进的RANSAC提取平面,让提取的平面进行相互切割,形成多个小块的平面,再将问题转化为二值标记问题,从切割出来的大量小块平面中选出合适的候选平面集合,然后将候选平面集合拟合成简化结果. Bouzas等[10 ] 通过识别建筑平面之间的相邻关系重建出简化模型. Huang等[11 ] 使用建筑高程图提取建筑轮廓并生成垂直平面,再结合传统算法(如RANSAC)提取的平面重建出简化模型. Bauchet等[12 ] 提出利用机载LiDAR扫描数据将城市环境中的建筑物重建为简洁多边形网格的方法,使用平面将空间分割成多个多面体,随后基于投票方案和能量函数对多面体进行标注的方法得到建筑物的内外表面,从而得到建筑物的多边形网格. Chen等[13 ] 使用深度神经网络学习隐式场来选出合适的多面体子集,进而重建出简化模型. Chen等[14 ] 引入图神经网络来选择多面体子集,重建出建筑的简化模型. He等[15 ] 提出WindPoly,通过多边形平面检测、自适应分区和环绕数优化,实现无需法向量、高效且几何一致的低多边形网格重建. 上述方法易受噪声干扰,且须手动调节参数,本研究通过深度霍夫投票来预测建筑平面,无需手动调节参数. ...
1
... 依据建筑平面信息构建建筑简化模型的常规步骤:1)通过传统算法(如RANSAC、区域增长法)检测得到建筑平面,2)根据平面将模型切割成小块的平面或多边体,3)从这些切割形体中选出合适的子集来构建简化的建筑模型. Nan等[9 ] 提出PolyFit系统,通过改进的RANSAC提取平面,让提取的平面进行相互切割,形成多个小块的平面,再将问题转化为二值标记问题,从切割出来的大量小块平面中选出合适的候选平面集合,然后将候选平面集合拟合成简化结果. Bouzas等[10 ] 通过识别建筑平面之间的相邻关系重建出简化模型. Huang等[11 ] 使用建筑高程图提取建筑轮廓并生成垂直平面,再结合传统算法(如RANSAC)提取的平面重建出简化模型. Bauchet等[12 ] 提出利用机载LiDAR扫描数据将城市环境中的建筑物重建为简洁多边形网格的方法,使用平面将空间分割成多个多面体,随后基于投票方案和能量函数对多面体进行标注的方法得到建筑物的内外表面,从而得到建筑物的多边形网格. Chen等[13 ] 使用深度神经网络学习隐式场来选出合适的多面体子集,进而重建出简化模型. Chen等[14 ] 引入图神经网络来选择多面体子集,重建出建筑的简化模型. He等[15 ] 提出WindPoly,通过多边形平面检测、自适应分区和环绕数优化,实现无需法向量、高效且几何一致的低多边形网格重建. 上述方法易受噪声干扰,且须手动调节参数,本研究通过深度霍夫投票来预测建筑平面,无需手动调节参数. ...
PolyGNN: polyhedron-based graph neural network for 3D building reconstruction from point clouds
3
2024
... 依据建筑平面信息构建建筑简化模型的常规步骤:1)通过传统算法(如RANSAC、区域增长法)检测得到建筑平面,2)根据平面将模型切割成小块的平面或多边体,3)从这些切割形体中选出合适的子集来构建简化的建筑模型. Nan等[9 ] 提出PolyFit系统,通过改进的RANSAC提取平面,让提取的平面进行相互切割,形成多个小块的平面,再将问题转化为二值标记问题,从切割出来的大量小块平面中选出合适的候选平面集合,然后将候选平面集合拟合成简化结果. Bouzas等[10 ] 通过识别建筑平面之间的相邻关系重建出简化模型. Huang等[11 ] 使用建筑高程图提取建筑轮廓并生成垂直平面,再结合传统算法(如RANSAC)提取的平面重建出简化模型. Bauchet等[12 ] 提出利用机载LiDAR扫描数据将城市环境中的建筑物重建为简洁多边形网格的方法,使用平面将空间分割成多个多面体,随后基于投票方案和能量函数对多面体进行标注的方法得到建筑物的内外表面,从而得到建筑物的多边形网格. Chen等[13 ] 使用深度神经网络学习隐式场来选出合适的多面体子集,进而重建出简化模型. Chen等[14 ] 引入图神经网络来选择多面体子集,重建出建筑的简化模型. He等[15 ] 提出WindPoly,通过多边形平面检测、自适应分区和环绕数优化,实现无需法向量、高效且几何一致的低多边形网格重建. 上述方法易受噪声干扰,且须手动调节参数,本研究通过深度霍夫投票来预测建筑平面,无需手动调节参数. ...
... Building simplified performance comparison and evaluation form (
σ =0.02)
Tab.4 方法 $ {N}_{\mathrm{p}} $ $ {N}_{\mathrm{f}} $ S /MBHD/m CD/m $ {r}_{{\mathrm{e}}} $ 原始 2048000 — 112 — — — 本研究 4998 3434 0.349 0.30 0.15 4.6 PolyFit[9 ] 14708 3782 0.939 0.30 0.14 3.8 City3D[11 ] 22522 6520 1.560 0.93 0.59 36.4 PolyGNN[14 ] 18224 4440 0.643 0.33 0.15 2.6
如图8 所示为不同方法生成的建筑模型可视化效果对比. 可以看出,对比其他方法,所提方法重建的建筑多边形网格模型所需面片数量最少且与真值的建筑点云高度相符. City3D须调整到合适的参数才能获得比较好的结果,本研究使用City3D默认的参数进行重建. PolyFit和PolyGNN在某些数据上的HD略小于所提方法的模型,但在表达模型所需的面片数量上,所提方法远远小于PolyFit和PolyGNN. 原因是本研究所提方法表达1个平面只需要1个多边形网格,而PolyFit和PolyGNN需要多个多边形网格. ...
... Quantitative evaluation results of building simplified noise resistance
Tab.5 方法 基于学习 CD↓/m HD↓/m $ {r}_{{\mathrm{e}}} $ σ =0.02σ =0.03σ =0.02σ =0.03σ =0.02σ =0.03PolyFit[9 ] × 0.14 0.19 0.30 0.42 3.8 17.0 City3D[11 ] × 0.59 0.75 0.93 1.10 36.4 35.2 PolyGNN[14 ] √ 0.15 0.24 0.33 0.50 2.6 15.2 本研究 √ 0.15 0.17 0.30 0.36 4.6 4.2
6. 结 语 本研究提出基于深度学习的建筑点云轻量级表面重建方法. 为了检测出建筑点云中的平面,使用基于深度霍夫投票的方法,将点云聚类到所在平面的中心点附近,提高了建筑平面预测的准确性. 本研究提出基于面的非极大值抑制算法有效去除了预测面中的冗余面;在相邻关系预测模块中,提出配对面注意力模块;设计能够利用预测面以及面相邻关系构建多边形网格模型的方法,实现了建筑点云的有效简化. 所提表面重建方法在保证建筑点云结构完整性的同时,极大降低了存储需求,提高了数据传输和处理效率;在三维城市建模、智慧城市和地理信息系统等领域具有广泛的应用价值. 所提表面重建方法主要针对以平面结构为主的建筑点云,对于包含曲面结构(如圆柱体、圆锥体、球体等)的建筑适用性较弱. 在未来的研究中,1)计划结合基于隐式表示的深度学习方法(如NeRF、SDF)进行曲面建筑的重建能力改进;2)借鉴稳健的低多边形网格表示方法,将建筑点云三角网格化后转化为低多边形网格. ...
1
... 依据建筑平面信息构建建筑简化模型的常规步骤:1)通过传统算法(如RANSAC、区域增长法)检测得到建筑平面,2)根据平面将模型切割成小块的平面或多边体,3)从这些切割形体中选出合适的子集来构建简化的建筑模型. Nan等[9 ] 提出PolyFit系统,通过改进的RANSAC提取平面,让提取的平面进行相互切割,形成多个小块的平面,再将问题转化为二值标记问题,从切割出来的大量小块平面中选出合适的候选平面集合,然后将候选平面集合拟合成简化结果. Bouzas等[10 ] 通过识别建筑平面之间的相邻关系重建出简化模型. Huang等[11 ] 使用建筑高程图提取建筑轮廓并生成垂直平面,再结合传统算法(如RANSAC)提取的平面重建出简化模型. Bauchet等[12 ] 提出利用机载LiDAR扫描数据将城市环境中的建筑物重建为简洁多边形网格的方法,使用平面将空间分割成多个多面体,随后基于投票方案和能量函数对多面体进行标注的方法得到建筑物的内外表面,从而得到建筑物的多边形网格. Chen等[13 ] 使用深度神经网络学习隐式场来选出合适的多面体子集,进而重建出简化模型. Chen等[14 ] 引入图神经网络来选择多面体子集,重建出建筑的简化模型. He等[15 ] 提出WindPoly,通过多边形平面检测、自适应分区和环绕数优化,实现无需法向量、高效且几何一致的低多边形网格重建. 上述方法易受噪声干扰,且须手动调节参数,本研究通过深度霍夫投票来预测建筑平面,无需手动调节参数. ...
1
... 相对于平面检测,使用传统方法进行建筑的顶点和边缘检测更易受到噪声干扰,深度学习检测因此备受青睐. 如PBWR系统[16 ] ,为端到端的建筑屋顶线框预测深度神经网络模型,它先初始化一定数量的线条,随后让网络使用这些线条去拟合点云模型,最终得到建筑屋顶的线框模型. Point2Roof[17 ] 由深度学习方法从建筑屋顶点云数据中预测建筑角点,再预测角点之间的连接关系,最终得到屋顶的线框模型. 上述方法仅对建筑屋顶进行线框模型重建,面对复杂屋顶时重建结果与真实情况偏差较大,且难以直接应用于整个建筑,特别是在建筑底部存在着部分缺失的情况下. 本研究不直接预测顶点或边缘,而是先预测平面及其相邻关系,再通过平面的求交来获得建筑顶点和边缘,以构建出更准确的建筑多边形模型. ...
Point2Roof: end-to-end 3D building roof modeling from airborne LiDAR point clouds
1
2022
... 相对于平面检测,使用传统方法进行建筑的顶点和边缘检测更易受到噪声干扰,深度学习检测因此备受青睐. 如PBWR系统[16 ] ,为端到端的建筑屋顶线框预测深度神经网络模型,它先初始化一定数量的线条,随后让网络使用这些线条去拟合点云模型,最终得到建筑屋顶的线框模型. Point2Roof[17 ] 由深度学习方法从建筑屋顶点云数据中预测建筑角点,再预测角点之间的连接关系,最终得到屋顶的线框模型. 上述方法仅对建筑屋顶进行线框模型重建,面对复杂屋顶时重建结果与真实情况偏差较大,且难以直接应用于整个建筑,特别是在建筑底部存在着部分缺失的情况下. 本研究不直接预测顶点或边缘,而是先预测平面及其相邻关系,再通过平面的求交来获得建筑顶点和边缘,以构建出更准确的建筑多边形模型. ...
Lane line detection and object scene segmentation using otsu thresholding and the fast Hough transform for intelligent vehicles in complex road conditions
1
2023
... 霍夫投票是计算机视觉领域中经典的形状检测算法. 算法原理是将每个像素点在参数空间中投影,然后在参数空间中寻找出现次数超过阈值的点,这些点对应的参数即为所要检测的几何形状参数[18 -20 ] . Qi等[21 ] 借鉴广义霍夫投票过程,提出用于三维目标检测的深度学习方法,赋予点云深度网络投票机制,通过投票生成靠近对象中心的新点,解决点云稀疏导致难以聚合对象中心附近场景上下文的问题. 网络端到端可优化,相比经典霍夫投票多个独立模块难以联合优化的情况[22 ] ,具有明显优势. 本研究借鉴深度霍夫投票思想,提出针对建筑平面检测的深度霍夫投票网络,解决现有建筑平面检测方法中参数须指定和鲁棒性不足的问题. ...
An automatic image processing based on Hough transform algorithm for pavement crack detection and classification
1
2025
... 霍夫投票是计算机视觉领域中经典的形状检测算法. 算法原理是将每个像素点在参数空间中投影,然后在参数空间中寻找出现次数超过阈值的点,这些点对应的参数即为所要检测的几何形状参数[18 -20 ] . Qi等[21 ] 借鉴广义霍夫投票过程,提出用于三维目标检测的深度学习方法,赋予点云深度网络投票机制,通过投票生成靠近对象中心的新点,解决点云稀疏导致难以聚合对象中心附近场景上下文的问题. 网络端到端可优化,相比经典霍夫投票多个独立模块难以联合优化的情况[22 ] ,具有明显优势. 本研究借鉴深度霍夫投票思想,提出针对建筑平面检测的深度霍夫投票网络,解决现有建筑平面检测方法中参数须指定和鲁棒性不足的问题. ...
1
... 霍夫投票是计算机视觉领域中经典的形状检测算法. 算法原理是将每个像素点在参数空间中投影,然后在参数空间中寻找出现次数超过阈值的点,这些点对应的参数即为所要检测的几何形状参数[18 -20 ] . Qi等[21 ] 借鉴广义霍夫投票过程,提出用于三维目标检测的深度学习方法,赋予点云深度网络投票机制,通过投票生成靠近对象中心的新点,解决点云稀疏导致难以聚合对象中心附近场景上下文的问题. 网络端到端可优化,相比经典霍夫投票多个独立模块难以联合优化的情况[22 ] ,具有明显优势. 本研究借鉴深度霍夫投票思想,提出针对建筑平面检测的深度霍夫投票网络,解决现有建筑平面检测方法中参数须指定和鲁棒性不足的问题. ...
HoughLaneNet: lane detection with deep Hough transform and dynamic convolution
1
2023
... 霍夫投票是计算机视觉领域中经典的形状检测算法. 算法原理是将每个像素点在参数空间中投影,然后在参数空间中寻找出现次数超过阈值的点,这些点对应的参数即为所要检测的几何形状参数[18 -20 ] . Qi等[21 ] 借鉴广义霍夫投票过程,提出用于三维目标检测的深度学习方法,赋予点云深度网络投票机制,通过投票生成靠近对象中心的新点,解决点云稀疏导致难以聚合对象中心附近场景上下文的问题. 网络端到端可优化,相比经典霍夫投票多个独立模块难以联合优化的情况[22 ] ,具有明显优势. 本研究借鉴深度霍夫投票思想,提出针对建筑平面检测的深度霍夫投票网络,解决现有建筑平面检测方法中参数须指定和鲁棒性不足的问题. ...
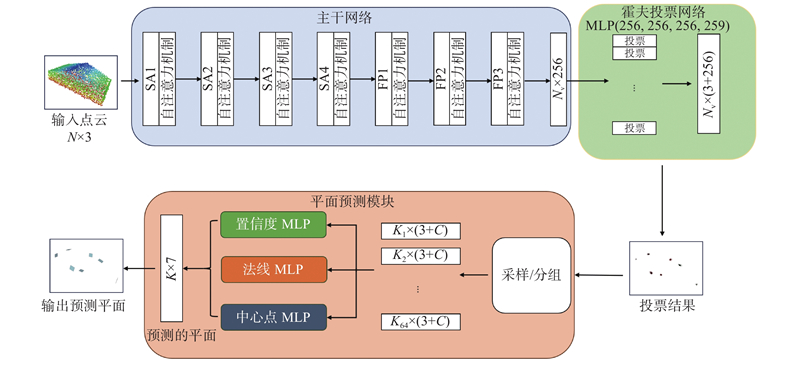
1
... 将三维目标检测中基于深度霍夫投票的方法用于建筑点云平面的检测中,让投票点自行偏移至所属平面的中心点附近,实现点云的聚类,根据聚类的结果预测出建筑平面. 平面预测模块的网络结构如图2 所示,其中N 为输入点云数目,SA1~SA4为自注意力模块,FP1~FP3为前向传播模块,C 为投票点特征维度. 主干网络基于PointNet++网络模型设计,结合基于向量的自注意力模块[23 ] 辅助PointNet++更好地捕捉点云全局的上下文关系. 设主干网络输出的投票点集$ P=\{{\boldsymbol{p}}_{1},{\boldsymbol{p}}_{2}, \cdots ,{\boldsymbol{p}}_{N_{\mathrm{v}}}\} $ $ N_{\mathrm{v}} $ $ {\boldsymbol{p}}_{i}\in {\mathbf{R}}^{D} $
1
... 聚合建筑点云平面特征的步骤如下. 1)使用最远点采样[24 ] 在投票点中采样64个中心点,记为$ {K}_{i},i=1,2,\cdots ,64 $ . 2)对$ {K}_{i} $ $ K\times 16\times \left(3+{C}\right) $ . 3)使用MLP以及最大池化的方法聚合投票点的特征,得到建筑点云平面特征$ K\times {C}_{\mathrm{f}} $ $ {C}_{\mathrm{f}} $
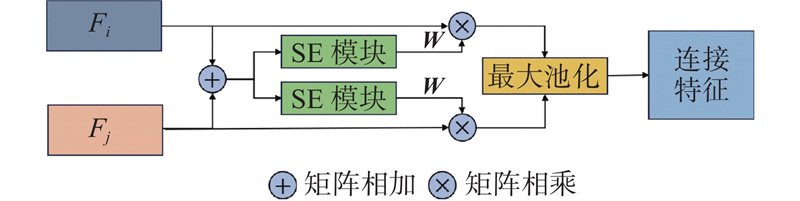
1
... 受到Hu等[25 ] 提出的通道注意力机制——压缩-激励(squeeze-and-excitation,SE)模块启发,本研究设计配对面注意力模块(paired face attention module,PFA)来辅助融合2个建筑点云平面的特征,通过动态权重机制增强关键特征,抑制无关信息的干扰. 传统特征拼接方法仅能实现特征的简单组合,无法区分不同通道特征的重要性(如位置坐标、法线向量、置信度等). PFA能够显著提升模型对复杂拓扑结构的表达能力,它不采用固定融合策略,会针对每对平面特征自适应生成权重矩阵. 在生成的权重矩阵中关键特征的权重较大,不相关特征会被分配较小的权重,使得模型更加关注关键特征并且抑制不相关特征. ...
1
... 数据集源于爱沙尼亚3D空间数据站的LoD2+级建筑三角网格数据[26 ] . 为了生成带多种标签的建筑点云数据,设计数据处理原型系统,对原始数据进行如下4个步骤的自动化处理. 1)点云采样:对原始数据进行归一化处理,对每个三角网格执行基于重心坐标的点云采样操作,将所有三角网格的采样结果合并,得到整个建筑的采样点云;2)点云聚类:根据三角面片的法线以及三角面片之间的垂直距离粗略筛选出在同一建筑平面上的三角面片. 通过对比三角面片之间是否存在共点进一步筛选出属于同一建筑平面的三角面片. 该三角面片对应的采样点云即为属于同一平面上的点云;3)相邻关系计算:若2个建筑平面相邻,则对应的2个三角面片集合中必定存在共点,通过判断2个建筑平面对应的三角面片集合是否存在共点得到相邻关系;4)最小包围框计算:提取建筑平面对应的三角面片集合中的所有边并去除重复的边,得到该建筑平面的外边;对外边使用轴对齐包围盒(axis aligned bounding box,AABB)算法[27 ] 生成建筑平面的最小包围框. ...
A collision detection algorithm based on sphere and EBB mixed hierarchical bounding boxes
1
2024
... 数据集源于爱沙尼亚3D空间数据站的LoD2+级建筑三角网格数据[26 ] . 为了生成带多种标签的建筑点云数据,设计数据处理原型系统,对原始数据进行如下4个步骤的自动化处理. 1)点云采样:对原始数据进行归一化处理,对每个三角网格执行基于重心坐标的点云采样操作,将所有三角网格的采样结果合并,得到整个建筑的采样点云;2)点云聚类:根据三角面片的法线以及三角面片之间的垂直距离粗略筛选出在同一建筑平面上的三角面片. 通过对比三角面片之间是否存在共点进一步筛选出属于同一建筑平面的三角面片. 该三角面片对应的采样点云即为属于同一平面上的点云;3)相邻关系计算:若2个建筑平面相邻,则对应的2个三角面片集合中必定存在共点,通过判断2个建筑平面对应的三角面片集合是否存在共点得到相邻关系;4)最小包围框计算:提取建筑平面对应的三角面片集合中的所有边并去除重复的边,得到该建筑平面的外边;对外边使用轴对齐包围盒(axis aligned bounding box,AABB)算法[27 ] 生成建筑平面的最小包围框. ...
A fault detection method of electric vehicle battery through Hausdorff distance and modified Z -score for real-world data
1
2023
... 1)豪斯多夫距离[28 ] (Hausdorff distance,HD),通过计算生成的多边形网格模型和原始网格之间的豪斯多夫距离来评估模型性能,计算式为 ...
1
... 2)倒角距离(chamfer distance,CD)[29 ] ,通过计算集合$ P $ $ G $