可调速型磁力耦合器的结构优化及其退磁故障的有效诊断对提高工业生产安全性尤为重要. 常用的故障诊断方法包括专家系统、模糊数学和多种机器学习算法. 常见的数据预处理方法包括奇异值分解[7],小波变换[8],傅里叶变换[9]等. 加入分类器也可实现故障诊断,如随机森林[10],多层感知机[11],支持向量机[12],K近邻算法[13],贝叶斯算法[14]等机器学习算法[15]. 上述机器学习方法依赖数据处理和专家经验调参,普适性不强[16]. 随着计算能力的提升,深度学习方法逐渐被运用到故障诊断中. Alsumaidaee等[17]提出神经网络算法,通过卷积神经网络对输入进行特征提取,特征传入长短期记忆模块,最后通过全连接层实现故障分类;该算法能够有效模拟时间序列数据并提取有意义的特征完成分类任务. 韩康等[18]提出基于空洞卷积和增强型多尺度自适应特征融合模型,有效过滤噪声信号,增强网络判别特征学习的能力. 邱建琪等[19]采用2个带有残差模块的卷积神经网络,对输入的电流信号与振动信号并行提取隐藏特征,并设计中间特征融合模块有效融合电流和振动的各层隐藏特征. 传统的卷积神经网络训练时间长、参数多,易引起过拟合,训练样本过小会使网络效果变差,局限性较多. 以上深度学习方法的应用对象大部分为轴承或永磁电机,对磁力耦合器进行退磁故障诊断分析的较少.
本研究提出可控混合式磁力耦合器,构建可控混合式磁力耦合器退磁故障诊断模型(Gramian angular summation field and SE-residual neural network,GANN). 引入注意力机制提升训练数据细节的提取和处理,使网络模型满足小样本情况的故障诊断;使用格拉姆角和场(Gramian angular summation field, GASF)进行数据预处理,将一维数据映射为二维图像,有效解决数据深层状态特征提取不全面的问题;将注意力机制与深度残差网络(ResNet)结合,对二维图像数据进行自适应学习,实现可控混合式磁力耦合器退磁故障的有效诊断.
1. 可控混合式磁力耦合器
1.1. 可控混合式磁力耦合器结构
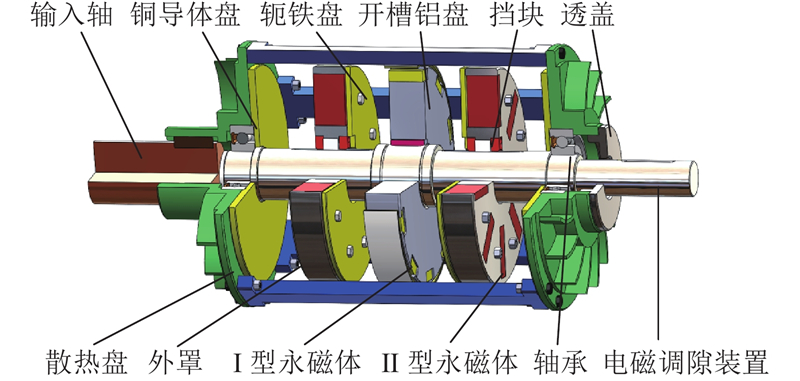
如图1所示,可控混合式磁力耦合器主要由输入轴、铜导体盘、轭铁盘、永磁体、开槽铝盘、以及电磁调隙装置等部分组成,整体结构可分为2个部分:动力传输机构和电磁调隙机构. 动力传输机构的工作原理:动力通过输入轴输入,带动外箱体轭铁盘旋转,铜导体盘伴随外箱体旋转切割磁感应线产生涡流,涡流产生的感应磁场与原磁场相互作用产生力矩带动输出轴旋转,驱动负载做功. 轴向移动调隙功能主要通过电磁调隙装置来实现. 绕组、硅钢片、开槽圆环以及键等零件共同组成轴向移动部件,对导线通电,使轴向移动部件在永磁体产生的磁场中受洛伦兹力作用而沿轴向运动,改变电流的方向,实现往复运动,精准调节铜导体盘与永磁体之间的气隙.
图 1
图 1 可控混合式磁力耦合器结构模型
Fig.1 Structural model of controllable hybrid magnetic coupler
1.2. 退磁故障仿真分析
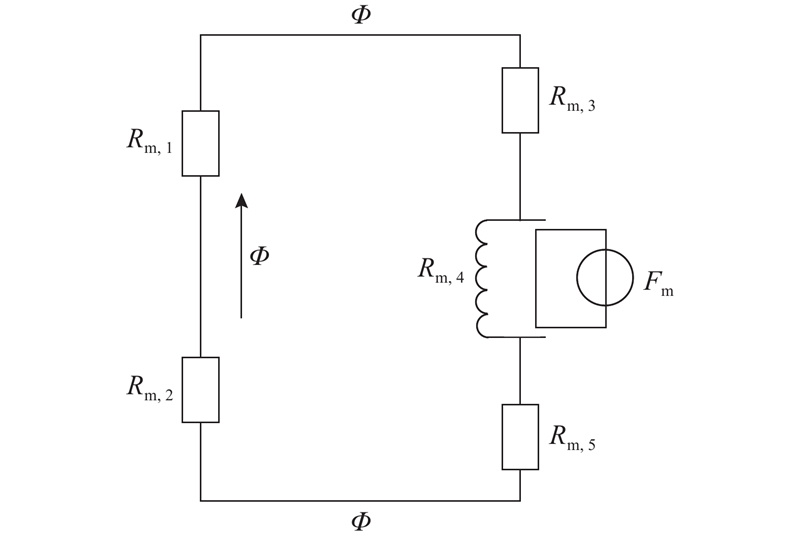
为了研究永磁体性能退化对系统运行状态的影响,以磁力耦合器为对象,建立永磁体主磁通的等效磁路模型,如图2所示. 根据图中磁路结构,磁动势
图 2
图 2 可控混合式磁力耦合器主磁通等效磁路图
Fig.2 Equivalent magnetic circuit diagram of main magnetic flux for controllable hybrid magnetic coupler
根据法拉第电磁感应定律,在导体盘中将感应出电动势:
式中:
式中:
式(4)为导体盘温度场分布的热传导方程,其中
通过Ansys Electronic建立可控混合式磁力耦合器的磁场、电场有限元仿真模型,根据设计的基础模型,建立等比例8极的可控混合式磁力耦合器模型,模型参数如表1所示. 对于所研究的均匀退磁情况,在Ansys Electronic中通过设置永磁体材料的剩磁
表 1 可控混合式磁力耦合器模型参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 气隙长度/m | 0.007 | 永磁体厚度/m | 0.003 | |
| 铜盘半径/m | 0.030 | 永磁体宽度/m | 0.008 | |
| 铜盘厚度/m | 0.005 | 永磁体长度/m | 0.010 |
图 3
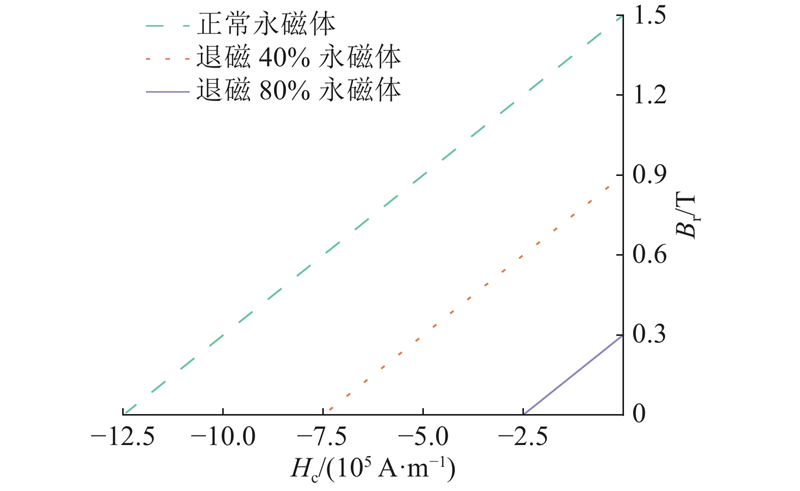
图 3 烧结钕铁硼N35磁体在不同退磁程度下的磁性曲线
Fig.3 Magnetic curves of sintered Nd-Fe-B (grade N35) under various demagnetization levels
图 4
图 4 不同退磁程度下的永磁体磁密分布、磁场强度示意图
Fig.4 Schematic diagram of magnetic density distribution and magnetic field strength of permanent magnets under various demagnetization levels
2. 数据集制作
2.1. 格拉姆角和场
格拉姆角场是将一维数据序列转换为二维图像的方法,通过计算数据点之间的夹角余弦值来实现. 这种方法有助于捕捉时间序列数据中的动态和周期性特征,常用于数据可视化、分类、聚类以及时间序列数据的分析和处理. 对于长度为
式中:
4)利用极坐标变换后的数据序列点的相角和或相角差算得格拉姆角场,计算式为
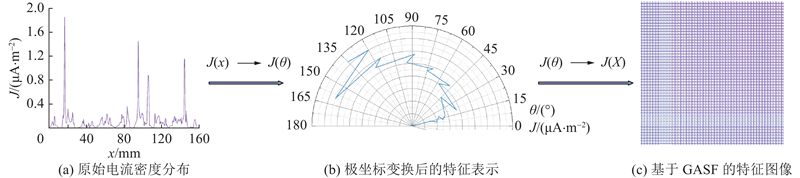
格拉姆角和场编码流程如图5所示.
图 5
2.2. 数据集制作
对Ansys Electronic中建立的可控混合式磁力耦合器模型进行仿真分析,在0.2 s内对距离铜导体盘5 mm的不同位置采集160 000个电流密度数据,通过GASF每次取256个数据点进行数据升维. 3种退磁情况下获得的数据通过升维后各得到625个样本,将得到的样本以4∶1的比例构建训练集与测试集,如表2所示.
表 2 电流密度数据集内容
Tab.2
| 退磁类型 | 标签 | 样本数量 | |
| 训练集 | 测试集 | ||
| 正常 | Co | 500 | 125 |
| 40%退磁 | Re40 | 500 | 125 |
| 80%退磁 | Re80 | 500 | 125 |
3. 退磁故障诊断模型
3.1. 注意力机制
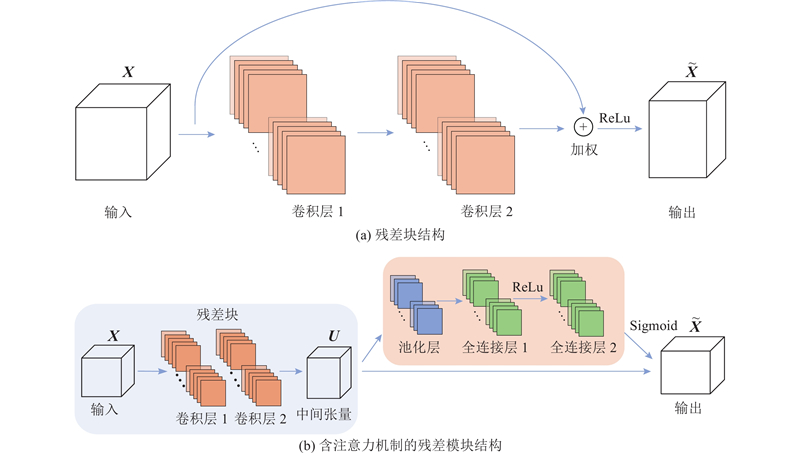
为了合理分配每个通道的权重,使网络能够自适应地学习每个通道的重要性,提高模型的表达能力和性能,对网络残差结构进行改进,引入压缩-激励模块(squeeze and excitation, SE)[21]. SE能够自适应地学习每个通道的重要性,增强有效特征,提高网络对重要特征的关注,解决特征融合过程中信息丢失、过拟合的问题,有助于模型更好地利用全局信息,提升模型的表达能力和泛化能力. 残差块是残差网络特有的结构,它的存在解决了深度网络模型的退化问题,避免梯度消失,提高了网络的效率和性能. 如图6所示,残差块由2个3×3的卷积以及激活函数ReLu组成. 将SE与残差块相结合,形成含有注意力机制的残差模块(squeeze residual, SR). 加入SE后的残差网络虽增加了少许计算量,但模型的准确性和鲁棒性得到大幅提升.
图 6
图 6 不同残差模块的结构示意图
Fig.6 Schematic diagrams of different residual-block architectures
3.2. 模型结构
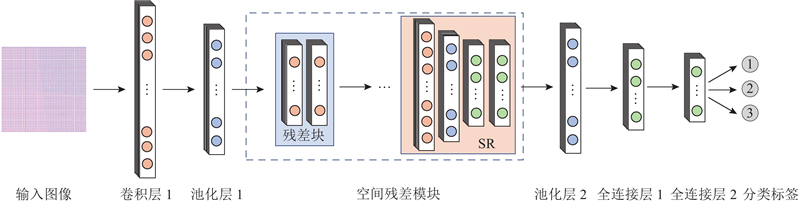
如图7所示为基于注意力机制的改进残差网络结构(SE-residual neural network, SNN),在ResNet34的基础上加入注意力机制构建而成. 将原本网络结构中的4个残差块替换成残差块、SR交替的结构,称为空间残差模块(SResidual). 将GASF与SNN结合,构建退磁故障诊断模型GANN. 当残差网络较深时,靠近输入层易出现梯度消失或者梯度爆炸的情况,导致网络难以训练,模型难以优化. 将残差块和SR交替设计,使梯度回传到较浅的层,有效缓解梯度的消失和爆炸,提高网络对输入图像细节信息的捕捉能力和处理能力.
图 7
图 7 基于注意力机制的改进残差网络结构示意图
Fig.7 Schematic diagram of improved residual network architecture based on attention mechanism
4. 实验过程
4.1. 实验设计
表 3 退磁故障诊断模型参数
Tab.3
| 层级 | 卷积核大小 | 步长 | 输入通道 | 输出通道 | 激活函数 |
| 卷积层1 | 7 | 2 | 3 | 64 | ReLu |
| 池化层1 | 3 | 2 | — | — | — |
| SResidual×8 | — | — | — | — | — |
| 池化层2 | 7 | 1 | — | — | — |
| 全连接层1 | — | — | 512 | — | |
| 全连接层2 | — | — | 512 | 3 | — |
表 4 空间残差模块参数
Tab.4
| 层级 | 卷积核大小 | 步长 | 输入通道 | 输出通道 | 激活函数 |
| 卷积层1 | 3 | 1 | 256 | 256 | ReLu |
| 卷积层2 | 3 | 1 | 256 | 256 | ReLu |
| 卷积层3 | 3 | 1 | 512 | 512 | ReLu |
| 卷积层4 | 3 | 1 | 512 | 512 | ReLu |
| 池化层 | 7 | 1 | — | — | — |
| 全连接层1 | — | — | 512 | 32 | — |
| 全连接层2 | — | — | 32 | 512 | Sigmoid |
图 8
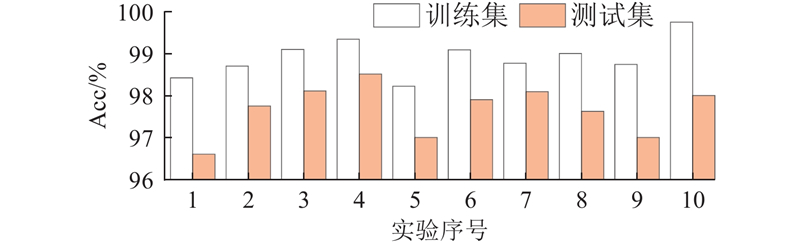
图 8 退磁故障诊断模型10次实验的准确率
Fig.8 Accuracy of ten experiments for demagnetization fault diagnosis model
表 5 退磁故障诊断模型故障诊断结果
Tab.5
| 故障标签 | P | R | F1 |
| 01 | 97.72 | 95.23 | 95.32 |
| 02 | 96.01 | 95.01 | 96.95 |
| 03 | 98.11 | 96.89 | 97.50 |
4.2. 消融实验
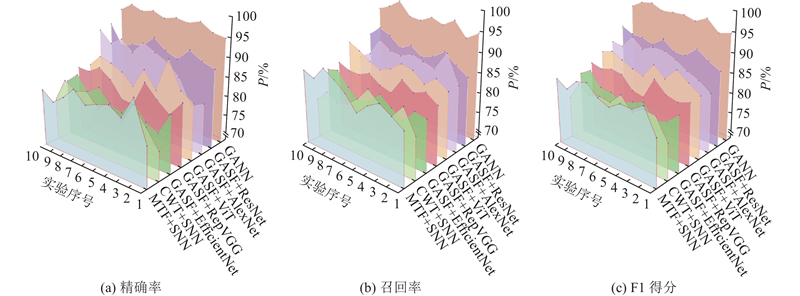
为了进一步验证GASF对数据处理的影响,进行模块消融实验,在相同网络结构与训练参数条件下,对比3种时频特征表示方法,包括GASF、马尔可夫转移场(Markov transition field,MTF)以及连续小波变换(continuous wavelet transform,CWT). 其中,MTF 通过描述时间序列状态转移概率构建二维特征图像,CWT 通过多尺度时频分析提取信号的局部特征信息,结果如表6所示. 其中MTF+SNN的准确率为86.33%,CWT+SNN的准确率为82.06%,均低于GANN的准确率. 在相同数据集、相同训练配置下比较不同模型在可控混合式磁力耦合器退磁故障诊断任务中的识别性能,包括 EfficientNet、RepVGG、Vision Transformer(ViT)和 AlexNet. EfficientNet 通过复合缩放策略在网络深度、宽度与分辨率之间实现平衡,兼顾模型精度与计算效率;RepVGG采用重参数化思想,在保持推理阶段结构简洁的同时提升特征提取能力;ViT 基于自注意力机制建模全局特征依赖关系,具有较强的全局建模能力;AlexNet 作为经典卷积神经网络,结构简单,常用于深度模型性能对比与基线验证. 其中GASF+EfficientNet、GASF+RepVGG、GASF+ViT、GASF+AlexNet的准确率分别为82.63%、82.94%、87.01%、88.30%. 消融实验的F1 值、精确率和召回率如图9所示. 在相同 SNN 网络结构下,不同特征构建方法对模型性能具有显著影响. 相比 MTF 和 CWT,基于 GASF 的特征表示在 P、R以及F1等指标上均取得更优结果,说明 GASF 能够更有效地表征退磁故障的时序相关性与特征差异性. 进一步地,将 GASF 与 SNN 结合构建的 GANN 在多组实验中表现出更高的稳定性和鲁棒性,验证了所提模型结构设计的合理性与有效性.
表 6 退磁故障诊断模型的模块消融实验结果
Tab.6
| 模型 | Acc | P | R | F1 |
| MTF+SNN | 86.33 | 83.69 | 85.14 | 84.37 |
| CWT+SNN | 82.06 | 81.64 | 85.52 | 81.54 |
| GASF+EfficientNet | 82.63 | 81.77 | 81.84 | 81.79 |
| GASF+RepVGG | 82.94 | 83.76 | 84.25 | 83.99 |
| GASF+ViT | 87.01 | 85.89 | 86.64 | 86.23 |
| GASF+AlexNet | 88.30 | 88.50 | 87.89 | 88.11 |
| GASF+ResNet | 92.63 | 90. 55 | 88.94 | 89.72 |
| GASF+ResNet_layer1 | 91.28 | 90.27 | 89.52 | 89.89 |
| GASF+ResNet_layer4 | 93.71 | 93.09 | 91.33 | 92.20 |
| GANN | 97.67 | 97.28 | 95.71 | 96.59 |
图 9
图 9 退磁故障诊断模型的模块性能参数对比
Fig.9 Performance-parameter comparison across modules of demagnetization fault diagnosis model
为了深入探究注意力机制在不同网络层级中的作用效果,对ResNet34结构进行局部添加SE的消融实验. 分别在浅层(layer1)、深层(layer4)添加SE,并与原始未加入注意力机制的ResNet34进行性能对比. 不加SE模块的模型准确率为92.63%;在浅层添加SE时,模型准确率为91.28%,较原始ResNet34略有下降;在深层添加SE时,准确率提升至93.71%. 该结果表明,SE在深层特征提取阶段具有更明显的增强作用,可能是退磁故障特征更多体现在高层抽象语义中,在浅层引入SE机制扰乱了底层纹理特征的学习,导致性能轻微下降.
4.3. 实验验证
搭建如图10所示的实验台进行可控混合式磁力耦合器传动特性实验. 三相异步电机采用380 V三相低速电动机,通过变频器控制电动机,实验台额定功率为55 kW,建议转速范围为0~1 500 r/min. 可控混合式磁力耦合器采用高剩磁、高矫顽力的铷铁硼永磁材料,维持稳定的磁场输出. 测量回路配置NCTES3000转矩转速测量仪(测试精度:0.2%,量程:500 N·m),输出轴连接输出负载,通过可调节电阻箱模拟不同大小的负载转矩. 采用MCC1608G 数据采集卡(量程为±10 V模拟输出),CT5201恒流适配源,霍尔传感器(灵敏度为30 V/T)配合LabVIEW软件编写的数据采集程序,对电流数据进行同步采集、存储与实时显示.
图 10
图 10 可控混合式磁力耦合器实验台
Fig.10 Experimental platform for controllable hybrid magnetic coupler
为了验证GANN模型在可控混合式磁力耦合器均匀退磁故障诊断中的有效性,制备3组永磁体样本,通过高温退磁法处理永磁体,利用磁通计(精度±0.5%)测量剩磁强度,确保退磁均匀性,永磁体退磁数据如表7所示. 采用霍尔效应传感器(分辨率0.1 A)采集磁力耦合器运行时的电流数据,采样频率10 kHz. 固定传感器于不同空间位置(中心、边缘),每组实验重复3次以消除随机误差. 实测电流信号特征如表8所示,退磁程度越高,电流幅值降低,谐波占比显著增加. 将获取的电流数据通过GASF变换后输入训练好的SNN中,重点分析SNN在真实数据上的分类准确率、误分类情况和泛化误差. 实验结果表明,SNN的退磁故障识别平均准确率达96.5%,验证了GANN在实际应用中的可行性.
表 7 永磁体剩磁强度实测数据
Tab.7
| 退磁类型 | Br/T | 均匀性误差/% | |
| 正常 | 1.48~1.52 | 1.50 | ±1.3 |
| 退磁40% | 0.88~0.92 | 0.90 | ±2.2 |
| 退磁80% | 0.29~0.31 | 0.30 | ±3.3 |
表 8 磁力耦合器电流信号特征分析
Tab.8
| 退磁类型 | I/A | 谐波占比/% | 高频噪声能量占比/% |
| 正常 | 4.8~10.2 | <5 | <3 |
| 退磁40% | 2.9~6.1 | 10~15 | 8~12 |
| 退磁80% | 0.8~3.2 | 20~30 | 15~25 |
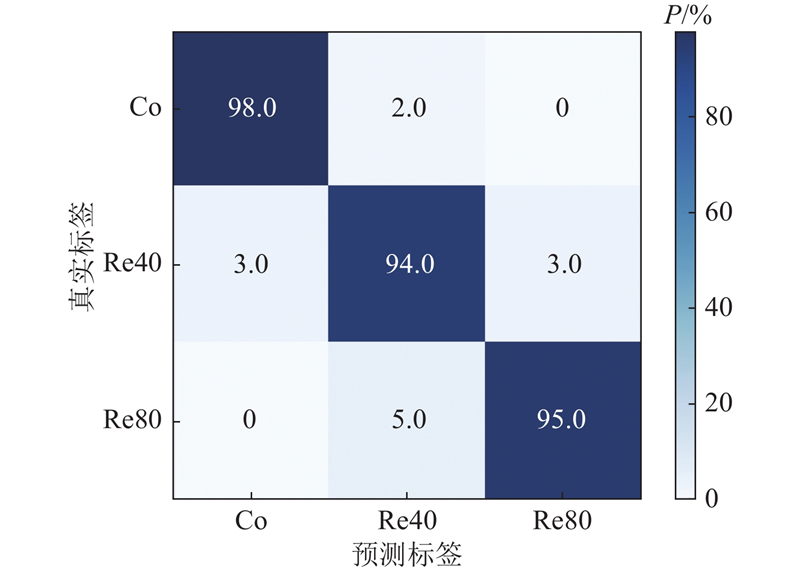
GANN在真实数据上的分类结果如图11所示,正常状态识别准确率最高(98%),退磁80%样本因噪声干扰存在5%误判. 进一步分析模型误分类情况,发现模型主要在特定类别(如高转速低负载状态)下出现分类错误. 通过观察误分类样本的特征分布发现,这些样本的涡流信号存在较高的噪声干扰,或其特征与相邻类别较为接近,导致模型区分度下降. 这表明,模型在某些复杂工况下的识别能力仍有提升空间,可通过优化特征提取或增强数据集来改进分类效果. 泛化误差分析表明,模型在训练数据和真实实验数据上的差异较小,说明其具有良好的泛化能力. 在极端工况(如高频扰动或非稳定磁场)下,分类精度有所下降,可能与训练数据的覆盖范围有限有关.
图 11
图 11 退磁故障诊断模型在真实数据上的分类结果
Fig.11 Classification results of demagnetization fault diagnosis model on real data
5. 结 语
本研究提出融合注意力机制的改进残差网络,残差块和含有注意力机制的残差块交替设计,有效缓解梯度消失和爆炸,增强网络对输入图像细节信息的捕捉能力和处理能力. 经验证,所提退磁故障诊断模型对可控混合式磁力耦合器均匀退磁故障诊断平均准确率为96.5%. 本研究训练数据主要来源于仿真与实验平台,模型在真实工业工况下的适应性尚需进一步验证;模型在复杂工况或多工况下的稳定性及准确性有待进一步提升和改进. 后续研究计划在实际工业环境中采集更多样本,探索轻量化模型在边缘计算设备上的部署与优化,提高模型的实用性和泛化性.
参考文献
基于自适应经验傅里叶分解的机械故障诊断方法
[J].
Adaptive empirical Fourier decomposition based mechanical fault diagnosis method
[J].
改进随机森林算法在电机轴承故障诊断中的应用
[J].
Applications of the improved random forest algorithm in fault diagnosis of motor bearings
[J].
高性能永磁同步平面电机及其关键技术发展综述
[J].
Development of the high-performance synchronous permanent magnet planar motor and its key technologies
[J].
磁场同步跟随式电磁悬浮微驱动器的理论分析与建模
[J].
Analysis and modeling of an electromagnetic levitation micro-actuator
[J].
基于PSO-LSSVM的永磁同步直线电机局部退磁故障识别
[J].
Local demagnetization fault recognition of permanent magnet synchronous linear motor based on PSO-LSSVM
[J].
3-D analysis for the torque of permanent magnet coupler
[J].
Designing high-accuracy permanent magnets for low-power magnetic resonance imaging
[J].DOI:10.1109/tmag.2018.2795592 [本文引用: 1]
永磁涡流耦合传动特性研究
[J].
Research on characteristics of permanent magnet eddy-current coupling drive
[J].
基于小波—奇异值分解差分谱的弱故障特征提取方法
[J].
Extraction method of faint fault feature based on wavelet-SVD difference spectrum
[J].
基于局部均值分解和K近邻算法的滚动轴承故障诊断方法
[J].
Fault diagnosis method based on LMD and KNN algorithms for rolling bearing
[J].
基于概率神经网络算法的永磁同步直线电机局部退磁故障诊断研究
[J].
Partial demagnetization fault diagnosis research of permanent magnet synchronous motors based on the PNN algorithm
[J].
Bearing intelligent fault diagnosis method based on continuous wavelet convolutional neural network
[J].
基于线性判别分析和分步机器学习的变压器故障诊断
[J].
Transformer fault diagnosis based on linear discriminant analysis and step-by-step machine learning
[J].
Small sample fault diagnosis method for wind turbine gearbox based on optimized generative adversarial networks
[J].
Fault detection for medium voltage switchgear using a deep learning hybrid 1D-CNN-LSTM model
[J].
基于空洞卷积和增强型多尺度特征自适应融合的滚动轴承故障诊断
[J].
Rolling bearing fault diagnosis based on dilated convolution and enhanced multi-scale feature adaptive fusion
[J].
基于残差卷积网络的多传感器融合永磁同步电机故障诊断
[J].
Fault diagnosis of multi-sensor fusion permanent magnet synchronous motor based on residual convolutional neural network
[J].