[1]
ZAVVAR E, ROSA-SANTOS P, GHAFOORI E, et al Analysis of tubular joints in marine structures: a comprehensive review
[J]. Marine Structures , 2025 , 99 : 103702
DOI:10.1016/j.marstruc.2024.103702
[本文引用: 1]
[2]
中国船级社. 海洋工程结构物疲劳强度评估技术指南 2022 [EB/OL]. (2022−05−11) [2024−05−18]. https://www.ccs.org.cn/ccswz/specialDetail?id=202205110218529632.
[本文引用: 5]
[3]
American Bureau of Shipping. Guide for fatigue assessment of offshore structures [S]. Houston: American Bureau of Shipping, 2020.
[4]
Det Norske Veritas. Fatigue design of offshore steel structures: DNV-RP-C203 [S]. Oslo: Det Norske Veritas, 2024.
[本文引用: 2]
[5]
American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms: working stress design: RP2A-WSD [S]. Washington DC: American Petroleum Institute, 2010.
[6]
International Standardization Organization. Petroleum and natural gas industries - fixed steel offshore structures: ISO 19902-2022 (E) [S]. Genova: International Standardization Organization, 2022.
[本文引用: 2]
[7]
International Standardization Organization. Fatigue — design procedure for welded hollow-section joints — recommendations: ISO 14347-2008 [S]. Genova: International Standardization Organization, 2008.
[8]
ZHAO X, HERION S, PACKER J, et al. Design guide for circular and rectangular hollow section welded joints under fatigue loading: CIDECT design guide No. 8 [M]. Cologne: TÜV-Verlag, 2001.
[本文引用: 3]
[9]
Lloyd’s Register of Shipping. Stress concentration factors for simple tubular joints: assessment of existing and development of new parametric formulae: OTH 354 [R]. Nottingham: Health and Safety Executive , 1997.
[本文引用: 6]
[10]
甘进, 乐京霞, 吴卫国, 等 海洋平台KK型管节点的疲劳性能试验研究
[J]. 武汉理工大学学报: 交通科学与工程版 , 2011 , 35 (5 ): 980 - 983
DOI:10.3963/j.issn.1006-2823.2011.05.026
GAN Jin, LE Jingxia, WU Weiguo, et al Experimental study on fatigue properties of tubular KK-joints of offshore platform
[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering , 2011 , 35 (5 ): 980 - 983
DOI:10.3963/j.issn.1006-2823.2011.05.026
[11]
张哲文. 不锈钢T型相贯节点疲劳性能研究 [D]. 合肥: 合肥工业大学, 2021: 1–89.
[本文引用: 1]
ZHANG Zhewen. Research on fatiguebehaviour of stainless steel welded tubular T-joints [D]. Hefei: Hefei University of Technology, 2021: 1–89.
[本文引用: 1]
[12]
LOZANO-MINGUEZ E, BRENNAN F P, KOLIOS Α J Reanalysis of offshore T-joint fatigue life predictions based on a complete weld profile model
[J]. Renewable Energy , 2014 , 71 : 486 - 494
DOI:10.1016/j.renene.2014.05.064
[本文引用: 3]
[13]
HECTORS K, DE WAELE W Influence of weld geometry on stress concentration factor distributions in tubular joints
[J]. Journal of Constructional Steel Research , 2021 , 176 : 106376
DOI:10.1016/j.jcsr.2020.106376
[本文引用: 3]
[15]
American Welding Society. Structural welding Code-steel: ANSI/AWS D1.1M-2015 [S]. Miami: American Welding Society, 2015.
[本文引用: 1]
[16]
BAO S, LI X, WANG B Study on hot spot stress of three-planar tubular Y-joints under combined axial loads
[J]. Thin-Walled Structures , 2019 , 140 : 478 - 494
DOI:10.1016/j.tws.2019.03.025
[本文引用: 3]
[17]
袁智深, 姚尧, 卢微然, 等 平面外弯矩作用下T形圆管节点热点应力分布
[J]. 湖南大学学报: 自然科学版 , 2022 , 49 (5 ): 151 - 159
DOI:10.16339/j.cnki.hdxbzkb.2022059
[本文引用: 2]
YUAN Zhishen, YAO Yao, LU Weiran, et al Hot spot stress distribution of CHS T-joints under out-of-plane bending
[J]. Journal of Hunan University: Natural Sciences , 2022 , 49 (5 ): 151 - 159
DOI:10.16339/j.cnki.hdxbzkb.2022059
[本文引用: 2]
[18]
AHMADI H, ZAVVAR E The effect of multi-planarity on the SCFs in offshore tubular KT-joints subjected to in-plane and out-of-plane bending loads
[J]. Thin-Walled Structures , 2016 , 106 : 148 - 165
DOI:10.1016/j.tws.2016.04.020
[本文引用: 3]
[19]
奚丽生, 方培君, 黄越, 等 海洋平台T型管节点相贯焊缝外形尺寸研究
[J]. 海洋工程 , 1990 , 8 (2 ): 27 - 34
DOI:10.16483/j.issn.1005-9865.1990.02.004
[本文引用: 1]
XI Lisheng, FANG Peijun, HUANG Yue, et al A study of weld profiles of tubular T joints for offshore platforms
[J]. The Ocean Engineering , 1990 , 8 (2 ): 27 - 34
DOI:10.16483/j.issn.1005-9865.1990.02.004
[本文引用: 1]
[20]
陈惠南, 赵怀普, 武国庆 T型管节点钢模型轴载下的热点应力测量和疲劳裂纹萌生寿命监测
[J]. 机械强度 , 1988 , 10 (2 ): 52 - 61
[本文引用: 2]
CHEN Huinan, ZHAO Huaipu, WU Guoqing The hot spot stresses measurment and initial fatigue crack life detection of steel welded tubular T joints under axial loading
[J]. Journal of Mechanical Strength , 1988 , 10 (2 ): 52 - 61
[本文引用: 2]
[21]
兰德省, 易伟同, 祝磊, 等 基于三维扫描模型的兵马俑足踝有限元分析
[J]. 文物保护与考古科学 , 2021 , 33 (3 ): 19 - 26
DOI:10.16334/j.cnki.cn31-1652/k.20200801852
[本文引用: 1]
LAN Desheng, YI Weitong, ZHU Lei, et al FEM simulation on the ankles of Terra-cotta Warriors based on 3D scanning models
[J]. Sciences of Conservation and Archaeology , 2021 , 33 (3 ): 19 - 26
DOI:10.16334/j.cnki.cn31-1652/k.20200801852
[本文引用: 1]
[22]
KOLIOS A, WANG L, MEHMANPARAST A, et al Determination of stress concentration factors in offshore wind welded structures through a hybrid experimental and numerical approach
[J]. Ocean Engineering , 2019 , 178 : 38 - 47
DOI:10.1016/j.oceaneng.2019.02.073
[本文引用: 1]
[23]
杨犇, 章子华, 周春恒, 等 基于三维扫描的带肋钢筋-混凝土界面黏结失效精细有限元分析
[J]. 工程力学 , 2024 , 41 (Suppl.1 ): 215 - 221
DOI:10.6052/j.issn.1000-4750.2023.05.S024
[本文引用: 1]
YANG Ben, ZHANG Zihua, ZHOU Chunheng, et al Refined finite element analysis of interfacial bonding failure between ribbed steel rebar and concrete upon 3D scanning
[J]. Engineering Mechanics , 2024 , 41 (Suppl.1 ): 215 - 221
DOI:10.6052/j.issn.1000-4750.2023.05.S024
[本文引用: 1]
[24]
Det Norske Veritas. Design of offshore wind turbine structures: DNV-OS-J101 [S]. Oslo: Det Norske Veritas, 2011.
[本文引用: 2]
[25]
鲍石榴. 海上风机三桩基础结构三平面Y型焊接钢管节点热点应力研究 [D]. 大连: 大连理工大学, 2020: 1–201.
[本文引用: 1]
BAO Shiliu. Study on hot spot stress for welded steel three-planar tubular Y-joints of offshore wind turbine tripod substructure [D]. Dalian: Dalian University of Technology, 2020: 1–201.
[本文引用: 1]
[26]
LEE Y, PAN J, HATHAWAY R B, 等. 疲劳试验测试分析理论与实践 [M]. 张然治, 译. 北京: 国防工业出版社, 2011: 5–7.
[本文引用: 1]
[27]
陆国庆. T型管节点疲劳热点应力集中系数的分析方法研究 [D]. 重庆: 重庆交通大学, 2024: 1–89.
[本文引用: 1]
LU Guoqing. Analysis method of fatigue hot spot stress concentration factor of tubular T-joints [D]. Chongqing: Chongqing Jiaotong University, 2024: 1–89.
[本文引用: 1]
[28]
THIBAUX P, COOREMAN S. Computation of stress concentration factors for tubular joints [C]// Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering . Nantes: AMSE, 2013: 9–14.
[本文引用: 1]
[29]
EFTHYMIOU M. Development of SCF formulae and generalized influence functions for use in fatigue analysis [C]// Proceedings of Offshore Tubular Joints Conference, Recent Developments in Tubular Joint Technology . Surrey: UEG Offshore Research, 1988: 1–33.
[本文引用: 1]
[30]
祝磊, 叶桢翔, 赵岩 焊缝建模对T型圆钢管节点轴压承载力计算的影响
[J]. 建筑结构 , 2013 , 43 (Suppl.2 ): 498 - 501
[本文引用: 1]
ZHU Lei, YE Zhenxiang, ZHAO Yan Effect of weld modeling on computation of axial compressive strength of circular steel tubular T-joints
[J]. Building Structure , 2013 , 43 (Suppl.2 ): 498 - 501
[本文引用: 1]
[31]
贾俊平, 何晓群, 金勇进. 统计学 [M]. 8版. 北京: 中国人民大学出版社, 2021: 273–274.
[本文引用: 1]
Analysis of tubular joints in marine structures: a comprehensive review
1
2025
... 圆形截面(circular hollow section, CHS)焊接管节点广泛存在于各类海洋工程结构中. 由于长期遭受风、浪、流等复杂交变载荷作用,焊趾部位易发生疲劳破坏,严重影响结构安全[1 ] . 在管节点疲劳寿命评估的热点应力法(hot spot stress, HSS)中,无量纲化的应力集中系数(stress concentration factor, SCF)是关键参数[2 -6 ] . ...
5
... 圆形截面(circular hollow section, CHS)焊接管节点广泛存在于各类海洋工程结构中. 由于长期遭受风、浪、流等复杂交变载荷作用,焊趾部位易发生疲劳破坏,严重影响结构安全[1 ] . 在管节点疲劳寿命评估的热点应力法(hot spot stress, HSS)中,无量纲化的应力集中系数(stress concentration factor, SCF)是关键参数[2 -6 ] . ...
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... [2 ,6 ,9 -11 ];FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
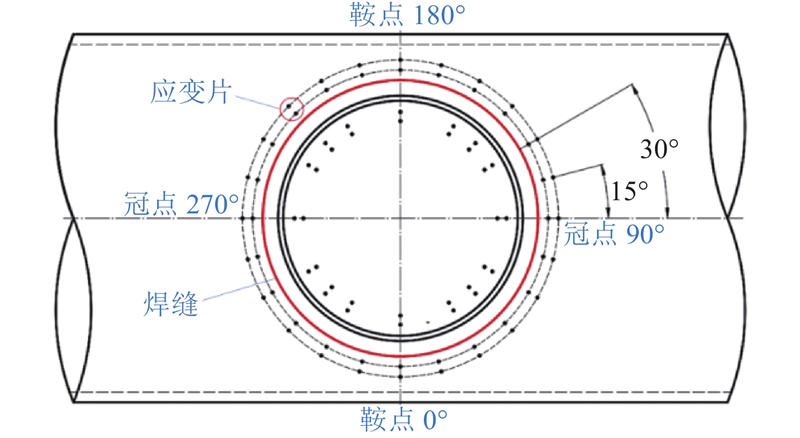
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
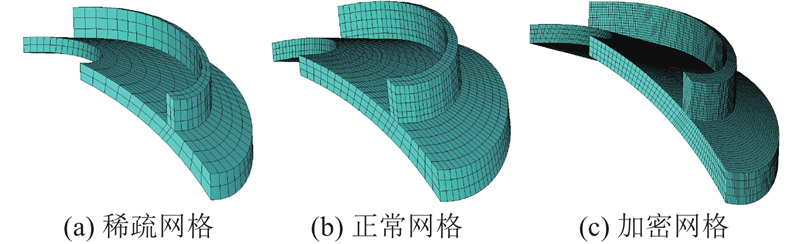
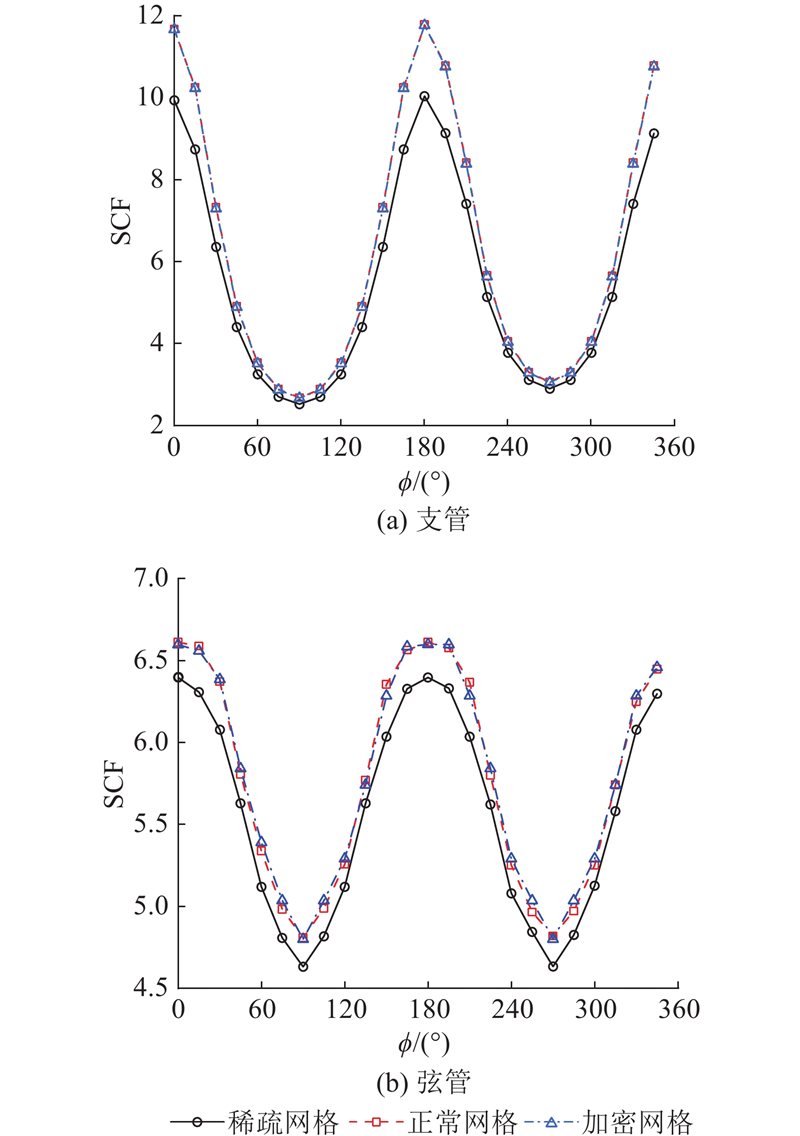
... 根据不同尺寸网格计算的支管与弦管焊趾处SCF如图16 所示. 可以看出,除稀疏网格外,正常网格与加密网格求得的SCF无明显差异,本研究使用正常网格计算SCF. 正常网格尺寸与文献[17 ]中使用的网格尺寸相当,明显小于文献[2 ]推荐的网格尺寸,但大于文献[14 ]、[28 ]使用的网格尺寸. ...
2
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
... ,4 ,8 ,24 ],弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
2
... 圆形截面(circular hollow section, CHS)焊接管节点广泛存在于各类海洋工程结构中. 由于长期遭受风、浪、流等复杂交变载荷作用,焊趾部位易发生疲劳破坏,严重影响结构安全[1 ] . 在管节点疲劳寿命评估的热点应力法(hot spot stress, HSS)中,无量纲化的应力集中系数(stress concentration factor, SCF)是关键参数[2 -6 ] . ...
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
3
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
... 试验在重庆交通大学山区桥梁及隧道工程国家重点实验室进行. 试验装置由加载架、作动器、试件和约束底座组成,如图8 所示. 在试验时,T形管节点弦管两端用销钉连接在支座上,为铰接(pinned chord ends)形式[8 -9 ] ,支管端部和作动器相连. 管节点安装如图9 所示. 试验采用的作动器为英国SERVOTEST公司的电液伺服作动器,最大载荷为500 kN,最高速度为0.36 m/s,行程为250 mm. 试件安装好后,轴向拉伸荷载分为多组进行逐级递增(0~150 kN)和递减(150~0 kN)施加,以消除试件焊接及安装过程中造成的残余应力[25 ] . 采用力控模式,对试件进行逐级加载和卸载,加载和卸载速度均为100 kN/min,加载梯级为每级20 kN. 使用扬州晶明测试技术有限公司生产的JM3811静态应变仪采集应变数据(采样频率为10 Hz,温漂不大于1.5 με/h). 当外载荷分别为200、220、240、260、280 kN时,保持载荷恒定2 min,采集各测点的应变数据,每次采集的时间长约为40 s. 采集每个测点位置的三向应变数据. 根据文献[9 ]、[26 ]中的公式计算每个测点位置的最大主应力. 疲劳热点应力计算式为 ...
6
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... ,9 -11 ];FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... [9 ,12 -14 ]. 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... 试验在重庆交通大学山区桥梁及隧道工程国家重点实验室进行. 试验装置由加载架、作动器、试件和约束底座组成,如图8 所示. 在试验时,T形管节点弦管两端用销钉连接在支座上,为铰接(pinned chord ends)形式[8 -9 ] ,支管端部和作动器相连. 管节点安装如图9 所示. 试验采用的作动器为英国SERVOTEST公司的电液伺服作动器,最大载荷为500 kN,最高速度为0.36 m/s,行程为250 mm. 试件安装好后,轴向拉伸荷载分为多组进行逐级递增(0~150 kN)和递减(150~0 kN)施加,以消除试件焊接及安装过程中造成的残余应力[25 ] . 采用力控模式,对试件进行逐级加载和卸载,加载和卸载速度均为100 kN/min,加载梯级为每级20 kN. 使用扬州晶明测试技术有限公司生产的JM3811静态应变仪采集应变数据(采样频率为10 Hz,温漂不大于1.5 με/h). 当外载荷分别为200、220、240、260、280 kN时,保持载荷恒定2 min,采集各测点的应变数据,每次采集的时间长约为40 s. 采集每个测点位置的三向应变数据. 根据文献[9 ]、[26 ]中的公式计算每个测点位置的最大主应力. 疲劳热点应力计算式为 ...
... . 采用力控模式,对试件进行逐级加载和卸载,加载和卸载速度均为100 kN/min,加载梯级为每级20 kN. 使用扬州晶明测试技术有限公司生产的JM3811静态应变仪采集应变数据(采样频率为10 Hz,温漂不大于1.5 με/h). 当外载荷分别为200、220、240、260、280 kN时,保持载荷恒定2 min,采集各测点的应变数据,每次采集的时间长约为40 s. 采集每个测点位置的三向应变数据. 根据文献[9 ]、[26 ]中的公式计算每个测点位置的最大主应力. 疲劳热点应力计算式为 ...
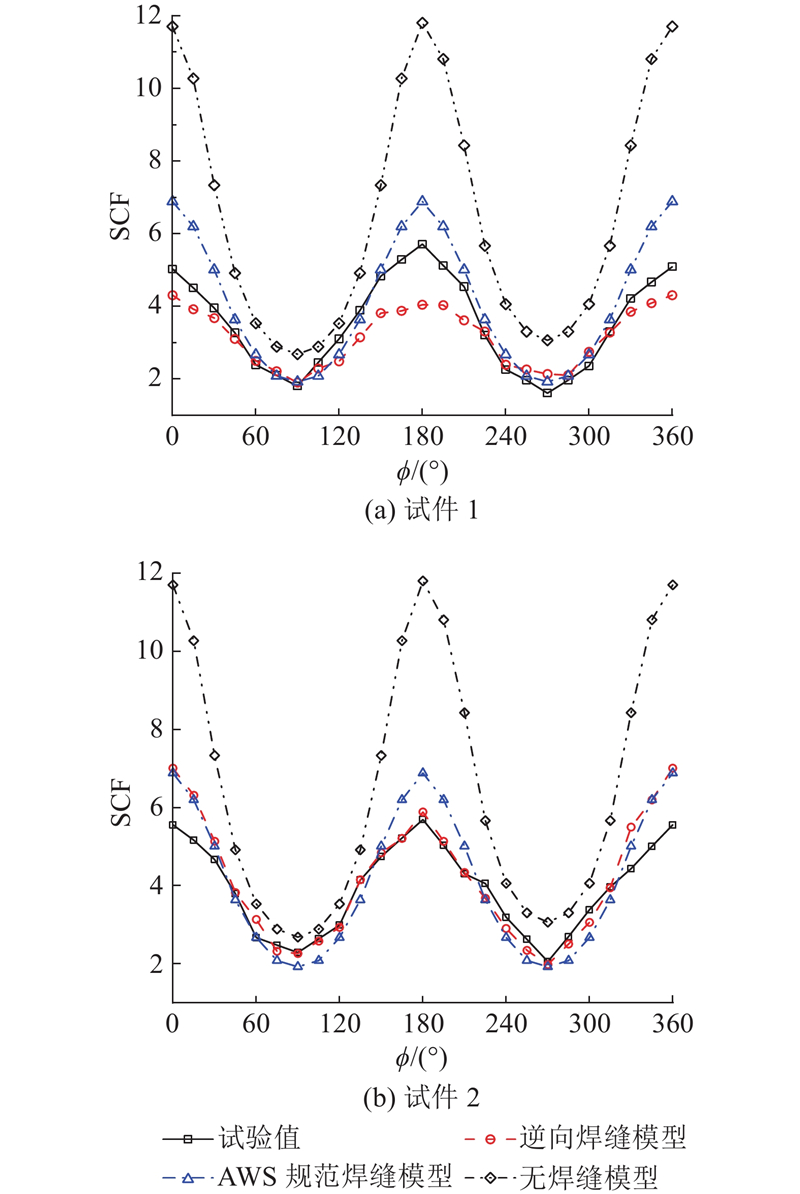
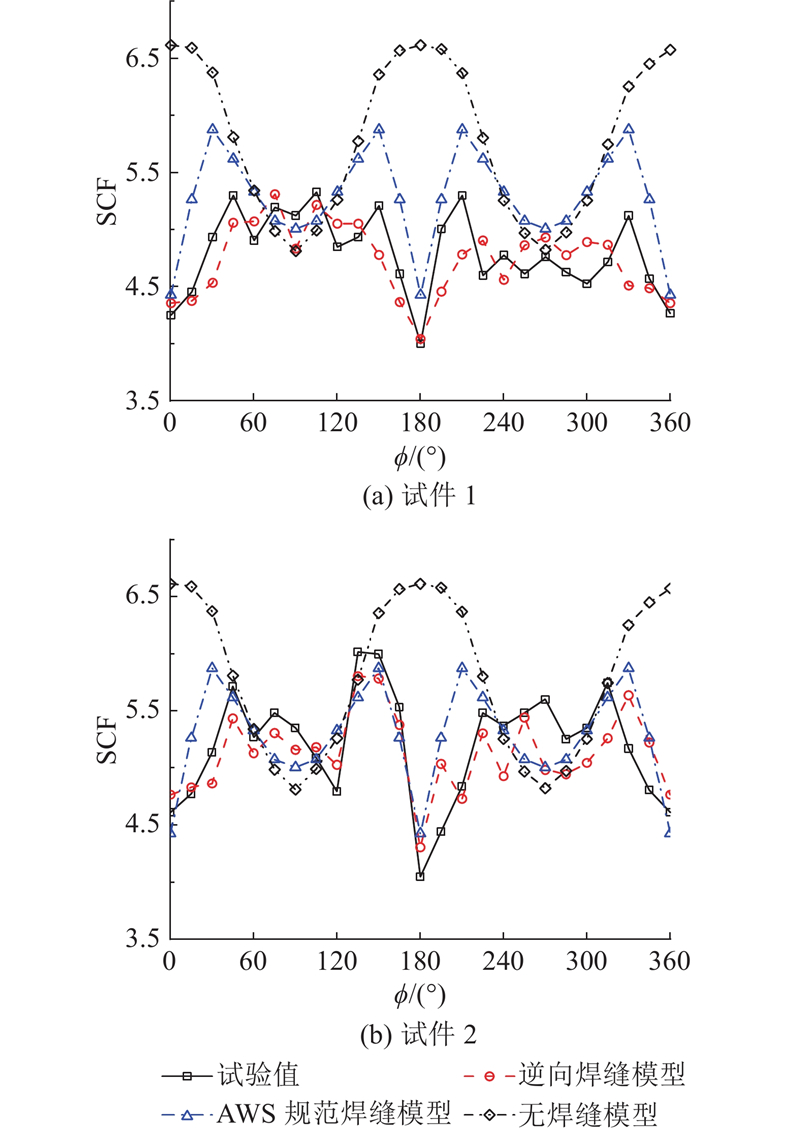
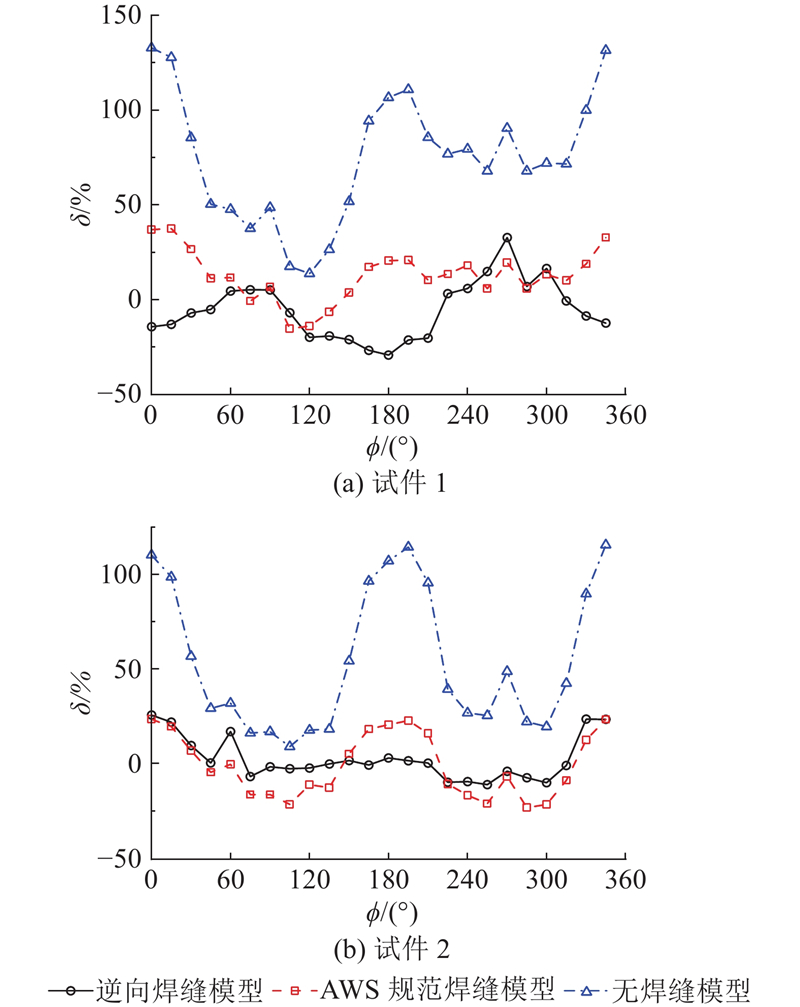
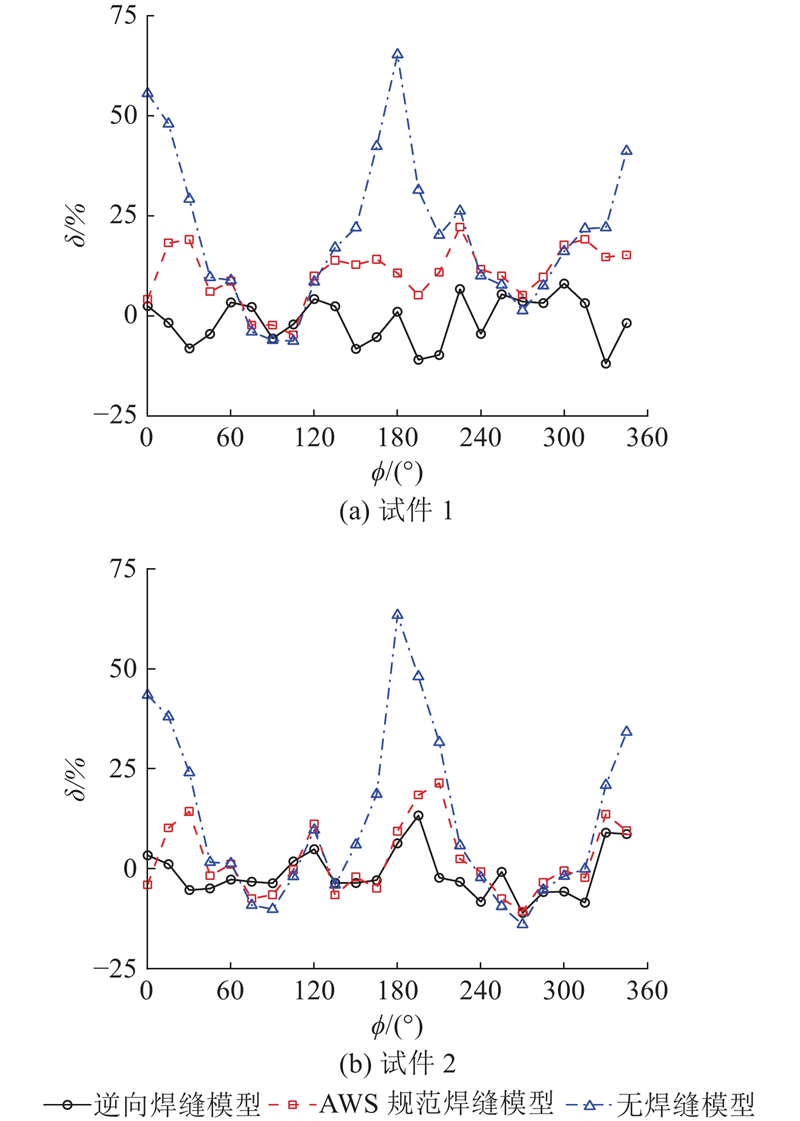
... 将3种有限元计算结果与试验数据进行对比分析. 对于支管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图17 所示. 可以看出,3种有限元模型的计算结果变化规律与试验数据相符;无焊缝模型的计算结果明显大于试验数据,这与文献[9 ]、[12 ]~[14 ]的结论一致,主要原因是焊缝能够在一定程度上增加管节点的刚度[29 -30 ] ,导致SCF减小;AWS规范焊缝模型、逆向焊缝模型的计算结果与试验数据接近. 对于弦管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图18 所示. 可以看出,AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据相符,无焊缝模型的计算结果与试验数据的变化规律不同;AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据接近. ...
海洋平台KK型管节点的疲劳性能试验研究
0
2011
海洋平台KK型管节点的疲劳性能试验研究
0
2011
1
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
1
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
Reanalysis of offshore T-joint fatigue life predictions based on a complete weld profile model
3
2014
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... [12 -14 ,16 -18 ]. ...
... 将3种有限元计算结果与试验数据进行对比分析. 对于支管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图17 所示. 可以看出,3种有限元模型的计算结果变化规律与试验数据相符;无焊缝模型的计算结果明显大于试验数据,这与文献[9 ]、[12 ]~[14 ]的结论一致,主要原因是焊缝能够在一定程度上增加管节点的刚度[29 -30 ] ,导致SCF减小;AWS规范焊缝模型、逆向焊缝模型的计算结果与试验数据接近. 对于弦管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图18 所示. 可以看出,AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据相符,无焊缝模型的计算结果与试验数据的变化规律不同;AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据接近. ...
Influence of weld geometry on stress concentration factor distributions in tubular joints
3
2021
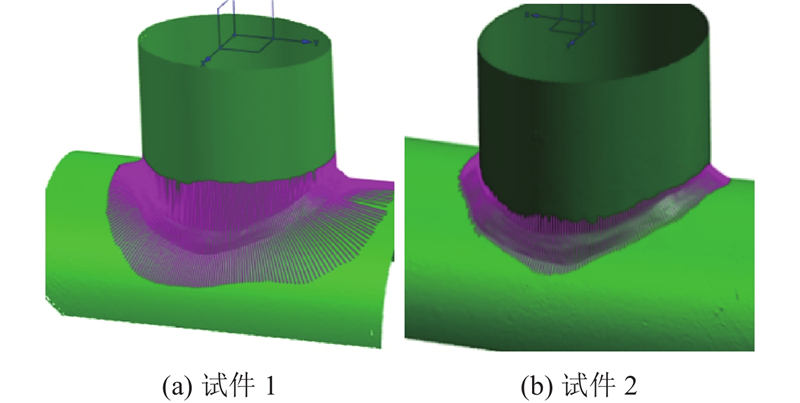
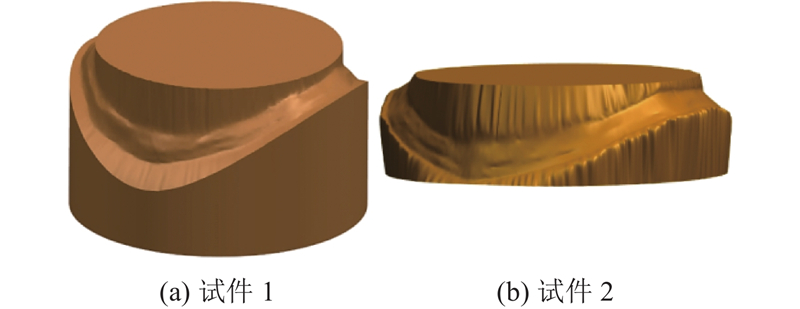
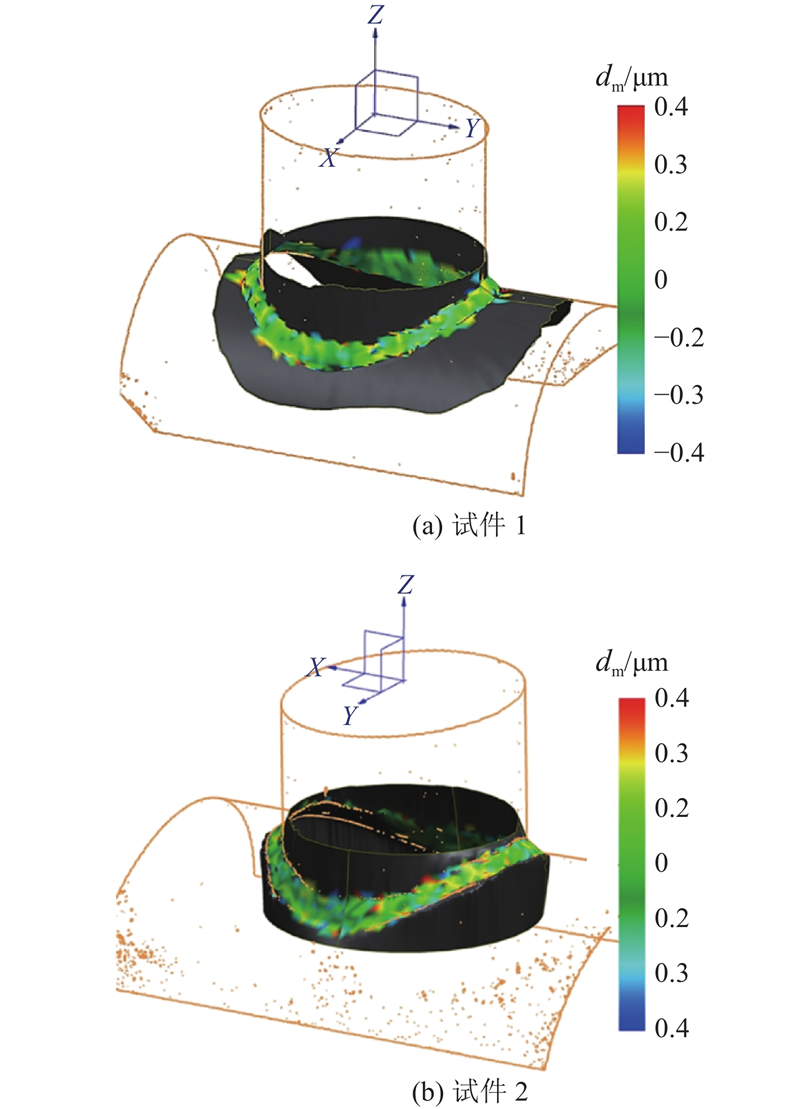
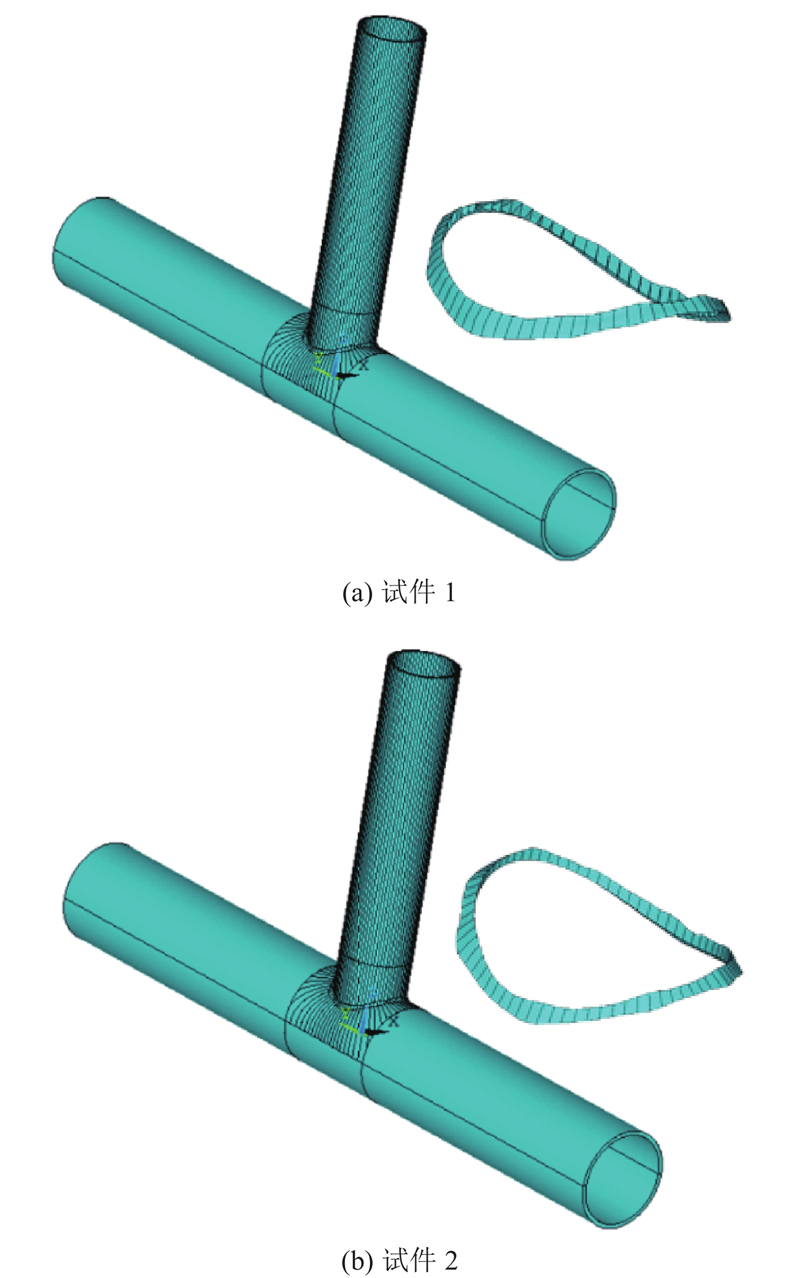
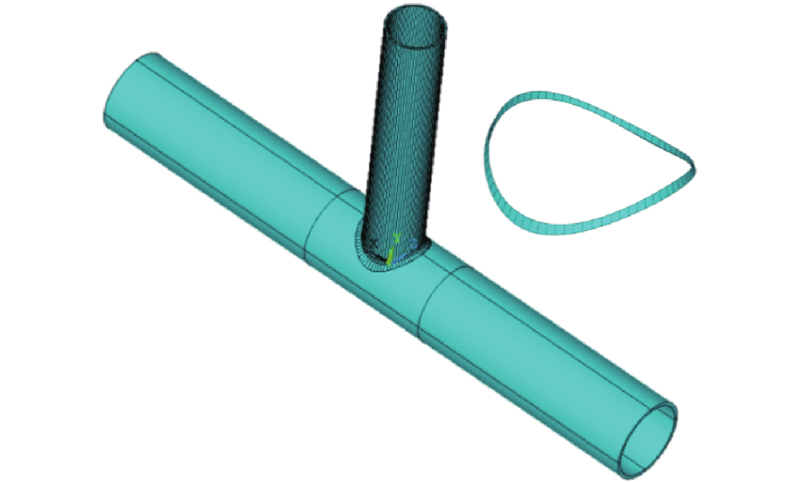
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
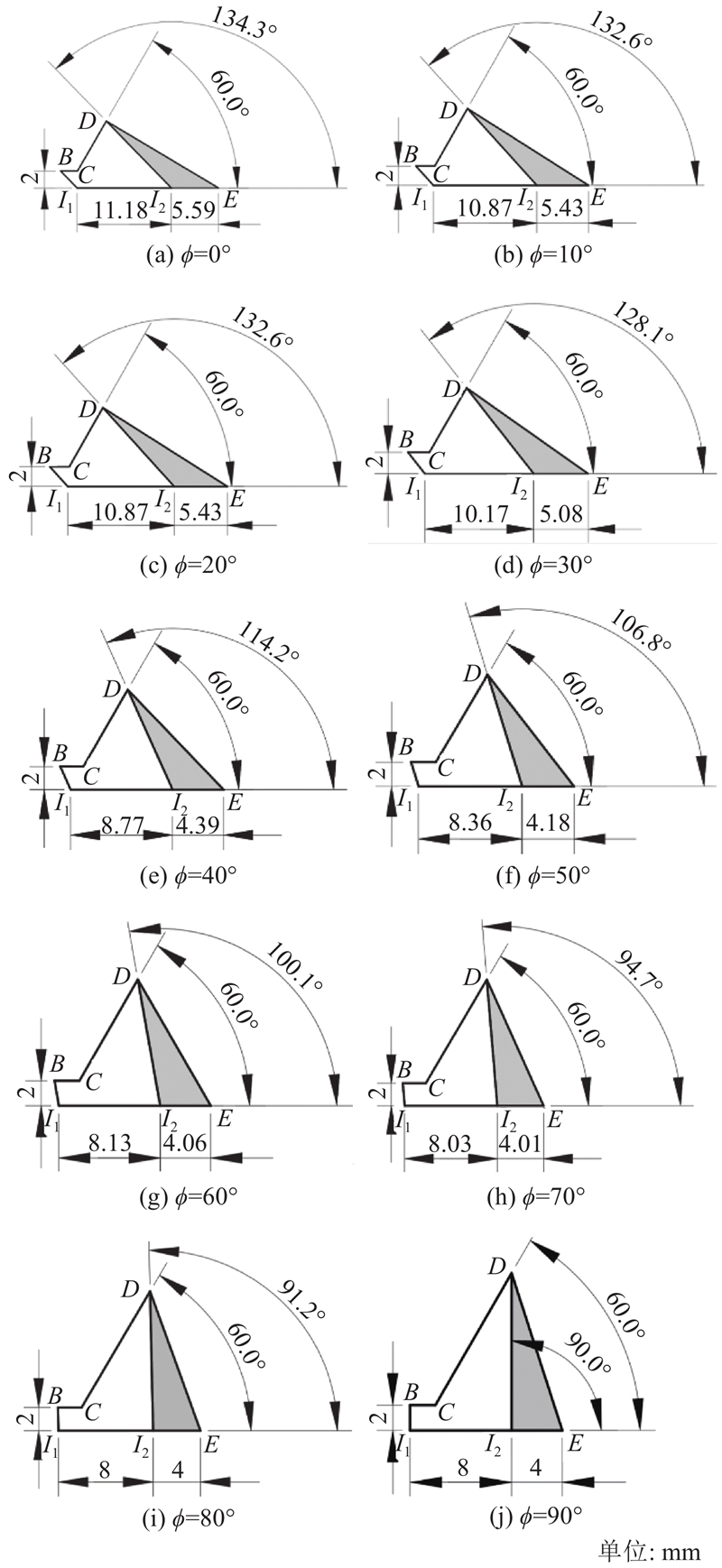
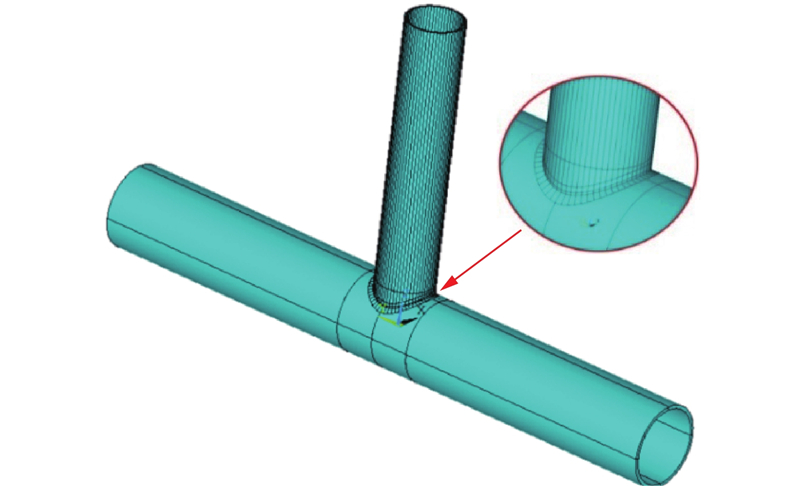
... 按照AWS规范中T/Y形管节点全焊透焊缝(complete joint penetration, CJP)的建议,根据表1 中的试件尺寸,参考文献[13 ]、[27 ]在ANSYS软件中建立满足AWS规范要求的T形管节点模型. 测点布置角ϕ 对应的焊缝截面形状以及相关尺寸如图11 所示,其中I 1 、I 2 分别为支管内、外表面与弦管外面的交点;D 、E 分别为支管、弦管上的焊趾;B 、C 、D 连成的折线为支管所开坡口. 参照逆向建模焊缝模型,对AWS规范焊模型进行分割,分割后的模型如图12 所示. ...
... 本研究建立的3种有限元模型,除了相贯线部位焊缝处有差异外,其余部分均相同. 在有限元分析过程中,这3个模型使用完全相同的单元类型、材料参数、边界约束条件以及外加载荷. 三维20节点实体单元是管节点SCF分析的常用单元[13 -14 ,16 -18 ] ,本研究采用Solid 95单元进行模型分析. 进行线弹性有限元分析时,材料参数只有弹性模量E 和泊松比ν ,参数取值和试验材料完全一致. 边界条件和试验测试完全相同,即弦管两端为铰接. 在ANSYS软件中使用耦合自由度的方法,将弦管两端面上的节点和圆心处的节点通过刚性连接耦合,耦合后的结果如图14 所示,通过约束圆心处节点的5个自由度(3个平动UX 、UY 、UZ 和2个转动ROTY 、ROTZ )以实现铰接. 在有限元模型的支管端面上施加1.0 Pa的面压力,即有限元模型中支管上的名义应力为1.0 Pa. 根据式(1),算出的$ {\sigma }_{\text{HSS}} $
K节点应力集中系数的试验和数值研究方法
7
2006
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... -14 ,16 -18 ]. ...
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
... 本研究建立的3种有限元模型,除了相贯线部位焊缝处有差异外,其余部分均相同. 在有限元分析过程中,这3个模型使用完全相同的单元类型、材料参数、边界约束条件以及外加载荷. 三维20节点实体单元是管节点SCF分析的常用单元[13 -14 ,16 -18 ] ,本研究采用Solid 95单元进行模型分析. 进行线弹性有限元分析时,材料参数只有弹性模量E 和泊松比ν ,参数取值和试验材料完全一致. 边界条件和试验测试完全相同,即弦管两端为铰接. 在ANSYS软件中使用耦合自由度的方法,将弦管两端面上的节点和圆心处的节点通过刚性连接耦合,耦合后的结果如图14 所示,通过约束圆心处节点的5个自由度(3个平动UX 、UY 、UZ 和2个转动ROTY 、ROTZ )以实现铰接. 在有限元模型的支管端面上施加1.0 Pa的面压力,即有限元模型中支管上的名义应力为1.0 Pa. 根据式(1),算出的$ {\sigma }_{\text{HSS}} $
... 根据不同尺寸网格计算的支管与弦管焊趾处SCF如图16 所示. 可以看出,除稀疏网格外,正常网格与加密网格求得的SCF无明显差异,本研究使用正常网格计算SCF. 正常网格尺寸与文献[17 ]中使用的网格尺寸相当,明显小于文献[2 ]推荐的网格尺寸,但大于文献[14 ]、[28 ]使用的网格尺寸. ...
... 将3种有限元计算结果与试验数据进行对比分析. 对于支管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图17 所示. 可以看出,3种有限元模型的计算结果变化规律与试验数据相符;无焊缝模型的计算结果明显大于试验数据,这与文献[9 ]、[12 ]~[14 ]的结论一致,主要原因是焊缝能够在一定程度上增加管节点的刚度[29 -30 ] ,导致SCF减小;AWS规范焊缝模型、逆向焊缝模型的计算结果与试验数据接近. 对于弦管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图18 所示. 可以看出,AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据相符,无焊缝模型的计算结果与试验数据的变化规律不同;AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据接近. ...
K节点应力集中系数的试验和数值研究方法
7
2006
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... -14 ,16 -18 ]. ...
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
... 本研究建立的3种有限元模型,除了相贯线部位焊缝处有差异外,其余部分均相同. 在有限元分析过程中,这3个模型使用完全相同的单元类型、材料参数、边界约束条件以及外加载荷. 三维20节点实体单元是管节点SCF分析的常用单元[13 -14 ,16 -18 ] ,本研究采用Solid 95单元进行模型分析. 进行线弹性有限元分析时,材料参数只有弹性模量E 和泊松比ν ,参数取值和试验材料完全一致. 边界条件和试验测试完全相同,即弦管两端为铰接. 在ANSYS软件中使用耦合自由度的方法,将弦管两端面上的节点和圆心处的节点通过刚性连接耦合,耦合后的结果如图14 所示,通过约束圆心处节点的5个自由度(3个平动UX 、UY 、UZ 和2个转动ROTY 、ROTZ )以实现铰接. 在有限元模型的支管端面上施加1.0 Pa的面压力,即有限元模型中支管上的名义应力为1.0 Pa. 根据式(1),算出的$ {\sigma }_{\text{HSS}} $
... 根据不同尺寸网格计算的支管与弦管焊趾处SCF如图16 所示. 可以看出,除稀疏网格外,正常网格与加密网格求得的SCF无明显差异,本研究使用正常网格计算SCF. 正常网格尺寸与文献[17 ]中使用的网格尺寸相当,明显小于文献[2 ]推荐的网格尺寸,但大于文献[14 ]、[28 ]使用的网格尺寸. ...
... 将3种有限元计算结果与试验数据进行对比分析. 对于支管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图17 所示. 可以看出,3种有限元模型的计算结果变化规律与试验数据相符;无焊缝模型的计算结果明显大于试验数据,这与文献[9 ]、[12 ]~[14 ]的结论一致,主要原因是焊缝能够在一定程度上增加管节点的刚度[29 -30 ] ,导致SCF减小;AWS规范焊缝模型、逆向焊缝模型的计算结果与试验数据接近. 对于弦管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图18 所示. 可以看出,AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据相符,无焊缝模型的计算结果与试验数据的变化规律不同;AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据接近. ...
1
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
Study on hot spot stress of three-planar tubular Y-joints under combined axial loads
3
2019
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
... 本研究建立的3种有限元模型,除了相贯线部位焊缝处有差异外,其余部分均相同. 在有限元分析过程中,这3个模型使用完全相同的单元类型、材料参数、边界约束条件以及外加载荷. 三维20节点实体单元是管节点SCF分析的常用单元[13 -14 ,16 -18 ] ,本研究采用Solid 95单元进行模型分析. 进行线弹性有限元分析时,材料参数只有弹性模量E 和泊松比ν ,参数取值和试验材料完全一致. 边界条件和试验测试完全相同,即弦管两端为铰接. 在ANSYS软件中使用耦合自由度的方法,将弦管两端面上的节点和圆心处的节点通过刚性连接耦合,耦合后的结果如图14 所示,通过约束圆心处节点的5个自由度(3个平动UX 、UY 、UZ 和2个转动ROTY 、ROTZ )以实现铰接. 在有限元模型的支管端面上施加1.0 Pa的面压力,即有限元模型中支管上的名义应力为1.0 Pa. 根据式(1),算出的$ {\sigma }_{\text{HSS}} $
平面外弯矩作用下T形圆管节点热点应力分布
2
2022
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
... 根据不同尺寸网格计算的支管与弦管焊趾处SCF如图16 所示. 可以看出,除稀疏网格外,正常网格与加密网格求得的SCF无明显差异,本研究使用正常网格计算SCF. 正常网格尺寸与文献[17 ]中使用的网格尺寸相当,明显小于文献[2 ]推荐的网格尺寸,但大于文献[14 ]、[28 ]使用的网格尺寸. ...
平面外弯矩作用下T形圆管节点热点应力分布
2
2022
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
... 根据不同尺寸网格计算的支管与弦管焊趾处SCF如图16 所示. 可以看出,除稀疏网格外,正常网格与加密网格求得的SCF无明显差异,本研究使用正常网格计算SCF. 正常网格尺寸与文献[17 ]中使用的网格尺寸相当,明显小于文献[2 ]推荐的网格尺寸,但大于文献[14 ]、[28 ]使用的网格尺寸. ...
The effect of multi-planarity on the SCFs in offshore tubular KT-joints subjected to in-plane and out-of-plane bending loads
3
2016
... SCF的计算主要采用参数化公式(如Efthymiou公式[2 -8 ] 和Lloyd’s Register公式[9 ] )和有限元法(finite element method, FEM). 参数化公式计算效率高,适用于T/Y/X/K形简单管节点,但无法处理复杂管节点[2 ,6 ,9 -11 ] ;FEM适用范围广,但若忽略焊缝影响,往往会得出偏保守的计算结果[9 ,12 -14 ] . 因此,精确模拟焊缝对SCF的计算至关重要. 焊缝的尺寸和形状随二面角变化[15 ] ,传统壳单元难以模拟,通常采用三维实体单元建模,并依据美国焊接学会(American Welding Society, AWS)规范或实测数据确定焊缝尺寸[12 -14 ,16 -18 ] . ...
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
... 本研究建立的3种有限元模型,除了相贯线部位焊缝处有差异外,其余部分均相同. 在有限元分析过程中,这3个模型使用完全相同的单元类型、材料参数、边界约束条件以及外加载荷. 三维20节点实体单元是管节点SCF分析的常用单元[13 -14 ,16 -18 ] ,本研究采用Solid 95单元进行模型分析. 进行线弹性有限元分析时,材料参数只有弹性模量E 和泊松比ν ,参数取值和试验材料完全一致. 边界条件和试验测试完全相同,即弦管两端为铰接. 在ANSYS软件中使用耦合自由度的方法,将弦管两端面上的节点和圆心处的节点通过刚性连接耦合,耦合后的结果如图14 所示,通过约束圆心处节点的5个自由度(3个平动UX 、UY 、UZ 和2个转动ROTY 、ROTZ )以实现铰接. 在有限元模型的支管端面上施加1.0 Pa的面压力,即有限元模型中支管上的名义应力为1.0 Pa. 根据式(1),算出的$ {\sigma }_{\text{HSS}} $
海洋平台T型管节点相贯焊缝外形尺寸研究
1
1990
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
海洋平台T型管节点相贯焊缝外形尺寸研究
1
1990
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
T型管节点钢模型轴载下的热点应力测量和疲劳裂纹萌生寿命监测
2
1988
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
T型管节点钢模型轴载下的热点应力测量和疲劳裂纹萌生寿命监测
2
1988
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
基于三维扫描模型的兵马俑足踝有限元分析
1
2021
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
基于三维扫描模型的兵马俑足踝有限元分析
1
2021
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
Determination of stress concentration factors in offshore wind welded structures through a hybrid experimental and numerical approach
1
2019
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
基于三维扫描的带肋钢筋-混凝土界面黏结失效精细有限元分析
1
2024
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
基于三维扫描的带肋钢筋-混凝土界面黏结失效精细有限元分析
1
2024
... 即使考虑焊缝尺寸,FEM结果仍与试验数据存在偏差[13 -14 ,16 -18 ] ,主要原因是焊缝形状的影响未被充分表征[19 -20 ] . 3D激光扫描技术(laser scanning technology, LST)能够精确地获取复杂曲面信息,已成功应用于文物的应力分析[21 ] 、平板焊缝SCF的计算[22 ] 以及钢筋-混凝土结构的建模[23 ] ,但尚未见其用于焊接管节点SCF的研究. 本研究提出3D LST与FEM结合的SCF精确计算方法. 以T形管节点为研究对象,利用3D LST逆向建模技术建立高精度焊缝模型,结合轴向拉伸试验数据,对比分析逆向焊缝模型、AWS规范焊缝模型及无焊缝模型的SCF计算结果,验证焊缝对SCF的影响以及各模型的准确性. ...
2
... 式中:$ F $ [4 ,20 ] ,本研究采用通用的两点线性插值方法进行推算. 插值点到焊趾的距离按照规范计算[2 ,4 ,8 ,24 ] ,弦管和支管上的插值点位置如图6 所示. 插值点的布置要求[14 ,17 ,24 ] 还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
... ,24 ]还须满足:1) 在支管上,插值点位置平行于支管轴线;2) 在弦管上,插值点所在位置垂直于焊缝. 按照插值点示意图的要求布置测点如图7 所示. 为了测试SCF分布,测点从鞍点开始按照逆时针方向布置. 对于弦管侧的焊趾,测点间隔为15°;对于支管侧的焊趾,测点间隔为30°,并在45°,135°,225°,315°处增加测点. 每个测点处布置1个三向应变片(型号为BX120-1CA,敏感珊尺寸为1 mm×1 mm). ...
1
... 试验在重庆交通大学山区桥梁及隧道工程国家重点实验室进行. 试验装置由加载架、作动器、试件和约束底座组成,如图8 所示. 在试验时,T形管节点弦管两端用销钉连接在支座上,为铰接(pinned chord ends)形式[8 -9 ] ,支管端部和作动器相连. 管节点安装如图9 所示. 试验采用的作动器为英国SERVOTEST公司的电液伺服作动器,最大载荷为500 kN,最高速度为0.36 m/s,行程为250 mm. 试件安装好后,轴向拉伸荷载分为多组进行逐级递增(0~150 kN)和递减(150~0 kN)施加,以消除试件焊接及安装过程中造成的残余应力[25 ] . 采用力控模式,对试件进行逐级加载和卸载,加载和卸载速度均为100 kN/min,加载梯级为每级20 kN. 使用扬州晶明测试技术有限公司生产的JM3811静态应变仪采集应变数据(采样频率为10 Hz,温漂不大于1.5 με/h). 当外载荷分别为200、220、240、260、280 kN时,保持载荷恒定2 min,采集各测点的应变数据,每次采集的时间长约为40 s. 采集每个测点位置的三向应变数据. 根据文献[9 ]、[26 ]中的公式计算每个测点位置的最大主应力. 疲劳热点应力计算式为 ...
1
... 试验在重庆交通大学山区桥梁及隧道工程国家重点实验室进行. 试验装置由加载架、作动器、试件和约束底座组成,如图8 所示. 在试验时,T形管节点弦管两端用销钉连接在支座上,为铰接(pinned chord ends)形式[8 -9 ] ,支管端部和作动器相连. 管节点安装如图9 所示. 试验采用的作动器为英国SERVOTEST公司的电液伺服作动器,最大载荷为500 kN,最高速度为0.36 m/s,行程为250 mm. 试件安装好后,轴向拉伸荷载分为多组进行逐级递增(0~150 kN)和递减(150~0 kN)施加,以消除试件焊接及安装过程中造成的残余应力[25 ] . 采用力控模式,对试件进行逐级加载和卸载,加载和卸载速度均为100 kN/min,加载梯级为每级20 kN. 使用扬州晶明测试技术有限公司生产的JM3811静态应变仪采集应变数据(采样频率为10 Hz,温漂不大于1.5 με/h). 当外载荷分别为200、220、240、260、280 kN时,保持载荷恒定2 min,采集各测点的应变数据,每次采集的时间长约为40 s. 采集每个测点位置的三向应变数据. 根据文献[9 ]、[26 ]中的公式计算每个测点位置的最大主应力. 疲劳热点应力计算式为 ...
1
... 试验在重庆交通大学山区桥梁及隧道工程国家重点实验室进行. 试验装置由加载架、作动器、试件和约束底座组成,如图8 所示. 在试验时,T形管节点弦管两端用销钉连接在支座上,为铰接(pinned chord ends)形式[8 -9 ] ,支管端部和作动器相连. 管节点安装如图9 所示. 试验采用的作动器为英国SERVOTEST公司的电液伺服作动器,最大载荷为500 kN,最高速度为0.36 m/s,行程为250 mm. 试件安装好后,轴向拉伸荷载分为多组进行逐级递增(0~150 kN)和递减(150~0 kN)施加,以消除试件焊接及安装过程中造成的残余应力[25 ] . 采用力控模式,对试件进行逐级加载和卸载,加载和卸载速度均为100 kN/min,加载梯级为每级20 kN. 使用扬州晶明测试技术有限公司生产的JM3811静态应变仪采集应变数据(采样频率为10 Hz,温漂不大于1.5 με/h). 当外载荷分别为200、220、240、260、280 kN时,保持载荷恒定2 min,采集各测点的应变数据,每次采集的时间长约为40 s. 采集每个测点位置的三向应变数据. 根据文献[9 ]、[26 ]中的公式计算每个测点位置的最大主应力. 疲劳热点应力计算式为 ...
1
... 按照AWS规范中T/Y形管节点全焊透焊缝(complete joint penetration, CJP)的建议,根据表1 中的试件尺寸,参考文献[13 ]、[27 ]在ANSYS软件中建立满足AWS规范要求的T形管节点模型. 测点布置角ϕ 对应的焊缝截面形状以及相关尺寸如图11 所示,其中I 1 、I 2 分别为支管内、外表面与弦管外面的交点;D 、E 分别为支管、弦管上的焊趾;B 、C 、D 连成的折线为支管所开坡口. 参照逆向建模焊缝模型,对AWS规范焊模型进行分割,分割后的模型如图12 所示. ...
1
... 按照AWS规范中T/Y形管节点全焊透焊缝(complete joint penetration, CJP)的建议,根据表1 中的试件尺寸,参考文献[13 ]、[27 ]在ANSYS软件中建立满足AWS规范要求的T形管节点模型. 测点布置角ϕ 对应的焊缝截面形状以及相关尺寸如图11 所示,其中I 1 、I 2 分别为支管内、外表面与弦管外面的交点;D 、E 分别为支管、弦管上的焊趾;B 、C 、D 连成的折线为支管所开坡口. 参照逆向建模焊缝模型,对AWS规范焊模型进行分割,分割后的模型如图12 所示. ...
1
... 根据不同尺寸网格计算的支管与弦管焊趾处SCF如图16 所示. 可以看出,除稀疏网格外,正常网格与加密网格求得的SCF无明显差异,本研究使用正常网格计算SCF. 正常网格尺寸与文献[17 ]中使用的网格尺寸相当,明显小于文献[2 ]推荐的网格尺寸,但大于文献[14 ]、[28 ]使用的网格尺寸. ...
1
... 将3种有限元计算结果与试验数据进行对比分析. 对于支管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图17 所示. 可以看出,3种有限元模型的计算结果变化规律与试验数据相符;无焊缝模型的计算结果明显大于试验数据,这与文献[9 ]、[12 ]~[14 ]的结论一致,主要原因是焊缝能够在一定程度上增加管节点的刚度[29 -30 ] ,导致SCF减小;AWS规范焊缝模型、逆向焊缝模型的计算结果与试验数据接近. 对于弦管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图18 所示. 可以看出,AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据相符,无焊缝模型的计算结果与试验数据的变化规律不同;AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据接近. ...
焊缝建模对T型圆钢管节点轴压承载力计算的影响
1
2013
... 将3种有限元计算结果与试验数据进行对比分析. 对于支管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图17 所示. 可以看出,3种有限元模型的计算结果变化规律与试验数据相符;无焊缝模型的计算结果明显大于试验数据,这与文献[9 ]、[12 ]~[14 ]的结论一致,主要原因是焊缝能够在一定程度上增加管节点的刚度[29 -30 ] ,导致SCF减小;AWS规范焊缝模型、逆向焊缝模型的计算结果与试验数据接近. 对于弦管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图18 所示. 可以看出,AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据相符,无焊缝模型的计算结果与试验数据的变化规律不同;AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据接近. ...
焊缝建模对T型圆钢管节点轴压承载力计算的影响
1
2013
... 将3种有限元计算结果与试验数据进行对比分析. 对于支管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图17 所示. 可以看出,3种有限元模型的计算结果变化规律与试验数据相符;无焊缝模型的计算结果明显大于试验数据,这与文献[9 ]、[12 ]~[14 ]的结论一致,主要原因是焊缝能够在一定程度上增加管节点的刚度[29 -30 ] ,导致SCF减小;AWS规范焊缝模型、逆向焊缝模型的计算结果与试验数据接近. 对于弦管焊趾部位,3种有限元模型计算的SCF与试验数据的比较如图18 所示. 可以看出,AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据相符,无焊缝模型的计算结果与试验数据的变化规律不同;AWS规范焊缝模型、逆向焊缝模型的计算结果变化规律与试验数据接近. ...
1
... 在统计学中常用的衡量预测模型与试验数据整体差异的指标主要有[31 ] 均方根误差RMSE和平均绝对百分比误差MAPE,表达式分别为 ...