风资源评估是风电场建设的关键环节,通过精确的风资源评估可以判断目标区域是否具备风电开发潜力,并为风电场的宏观选址与微观选址提供科学依据. 随着风电的快速发展,许多待建基地缺乏具有代表性且完整测风周期的观测数据,严重影响了风电场风资源评估的准确性.
数值模拟方法在风资源评估中的应用日益广泛,尤其是数值天气预报模式已被证明是高效的风资源评估工具. 天气研究与预报(weather research and forecasting, WRF)模式被视为评估风电场风资源的理想选择. Dayal等[1]利用24个气象站的数据,证实了WRF模式评估风资源的准确性. 在大规模风能资源评估[2]、陆上风电场风能规划[3]、海上风电场风能规划[4-5]等方面,WRF模式均取得了令人满意的效果,有效再现了风资源的分布特征. 作为中尺度模式,WRF模式相较于传统的计算流体力学(computational fluid dynamics, CFD)模型更适合大规模风电场的模拟需求. WRF模式能够为CFD模型提供初始和边界条件[6],提高CFD模拟的准确性. 在数值模拟的过程中,大气稳定度是影响入流边界风廓线、温度廓线的关键参数. 一方面,大气稳定度会对风资源的空间分布产生作用. 在夜间低湍流、稳定的大气条件下,风资源的空间变化幅度可能是在白天高湍流、不稳定条件下的2倍[7]. 大气稳定度还会影响风能资源进而影响电力输出,在中性状态下电力输出的增幅可达9%[8],在风电场布局时考虑局部大气稳定度分布可以实现更高的功率输出[9]. 在风资源和发电量评估中引入大气稳定度效应,与传统方法相比,评估的不确定性显著降低[10]. 另一方面,大气稳定度制约着风电场的整体性能. 大气稳定度不仅对风力机的选型至关重要,还会改变风电场的尾流效应[11],进而影响风电场的运行效率和发电性能[12]. 大气稳定度是调控风力机尾流演变的关键环境因子. 在不稳定条件下,风力机尾流恢复速度加快,尾流蜿蜒增强[13];在稳定条件下,尾流延伸距离显著增长,甚至会超过50 km[14]. 大气稳定度还关系着风电场中风力机的性能表现,如主风向下后排风力机在白天不稳定条件下表现不佳,在夜间稳定条件下表现优异[15]. 在山地条件下,大气稳定度和地形特性会对风力机的功率输出产生较大影响[16].
现有研究多聚焦于单一方面(如尾流)与大气稳定度的关联,缺乏对多参数(如空气密度、湍流强度)耦合作用的系统性分析,大气稳定度对风资源评估中各种风参数的影响尚未完全明晰. 针对陆上风电基地大气稳定度与风参数关联性的问题,本研究以具有代表性的内蒙古自治区阿拉善盟的2处待建设风电基地为对象,开展数值天气预报模拟,系统分析大气稳定度对风速、空气密度、垂直风速、湍流强度等风特征参数的影响,揭示大气稳定度在风电场运行中的作用机理.
1. 研究区域与数据来源
1.1. 风电基地信息
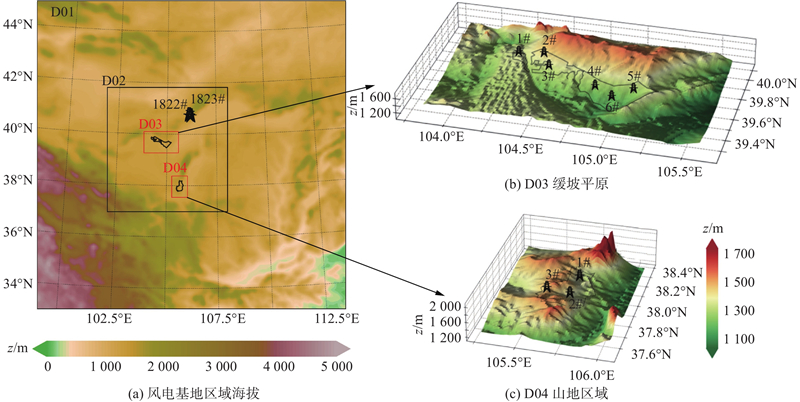
待建设风电基地位于内蒙古自治区西部的阿拉善盟左旗,如图1所示. 阿拉善盟左旗属于典型的沙戈荒区域,海拔1 100~1 700 m,为温带大陆性气候,但处于季风区与非季风区的分界线,受冬季季风的影响较大,主导风向为西北偏西风. 2个待建设风电基地的预计装机总容量为4 000 MW,其中西北方向的风电基地是典型的缓坡平原地形(网格编号为D03),东南方向的风电基地是典型的山地地形(网格编号为D04). 这2种地形不仅是沙戈荒风电基地的主要地形类型,也是更广泛的陆上风电大基地中常见的地貌特征. 在待建设风电基地的东北方向约110 km处有2座测风塔. 测风塔与风电基地相距较远,仅提供有限的测风数据,仍需中尺度“虚拟测风数据”为风资源精细化评估提供数据支撑.
图 1
图 1 风电基地区域海拔,天气研究与预报模式的三层嵌套网格
Fig.1 Elevation of wind farm clusters, and three nested grids of weather research and forecasting model
1.2. 测风数据
共有2座编号分别为1822#、1823#的测风塔用于数值风资源模拟验证. 测风塔的风速仪安装高度分别为10、30、70和90 m,风向标安装高度分别为10、50和90 m. 风速仪和风向标采集水平风速和风向的周期均为10 min,持续进行1个完整年(2017年7月至2018年7月)的风数据采集.
2. 中尺度模式及配置
2.1. 中尺度数值模式
WRF模式是高分辨率、可扩展的中尺度数值气象模式,广泛应用于天气预报、气候研究和风能资源评估等领域,其计算方法、灵活的程序结构和高度可定制的物理过程参数化为气象模拟和研究提供了强大的支持. WRF模式的数值计算采用完全可压缩、非静力平衡的动力框架. 控制方程以具有守恒性的变量的通量形式表示,确保模拟结果的物理一致性. 垂直坐标采用地形跟随的质量σ坐标或σ-p混合坐标系统,能够更好地适应复杂地形,提高大气边界层的模拟精度. 水平网格采用Arakawa C网格,温度、湿度、气压等变量定义在网格中央,风速分量定义在网格边界1/2处,这种网格布局有助于减少数值误差,提高计算精度. WRF模式采用2阶或3阶Runge-Kutta显式时间差分方案进行时间积分,通过多个物理过程的参数化方案(如辐射、对流、湍流扩散等)进一步提高模拟的准确性.
WRF模式的程序结构具有高度模块化和分层设计的特点,主要分为以下3个层次. 1)驱动层(WPS):负责模式初始化、输入/输出操作以及计算区域的嵌套与分解. 2)中间层(real.exe):作用是连接驱动层与模式层,完成数据预处理和区域设置任务. 3)模式层(wrf.exe):包含执行数值计算的核心部分,包括预报方程的求解和物理过程的处理. 在模式层中,动力框架和物理过程是独立模块,允许用户根据具体需求进行调整和优化,使模型的灵活性提升.
2.2. 配置方案及虚拟测风点
采用WRF V4.4对研究区域进行为期1年(2017年7月至2018年7月)的模拟,模拟区域采用3层嵌套网格,分辨率依次为9、3、1 km,其中最内层1 km的 2个网格编号为D03、D04,分别对应2处风电基地. D01~D04嵌套网格对应的网格数分别为150×150、175×181、151×94、70×94. 垂直方向采用65层网格. 模拟采用FNL(final operational global analysis)再分析资料与ASTER(advanced spaceborne thermal emission and reflection radiometer)高精度地形. WRF模式的物理参数化方案组合:MYNN2行星边界层方案,MYNN地表参数化方案,RRTM长波辐射方案,Duhia短波辐射方案,WSM6微物理过程方案,Noah陆面过程方案,Kain-Fritsch积云参数化方案. MYNN2是唯一可用于风电场参数化的行星边界层方案;由于后续研究加入风力机,将MYNN2作为行星边界层方案. 2处风电基地涉及2种典型地形,为此共设立9个虚拟测风点来检查大气稳定度的分布情况.
3. 关键风参数与大气稳定度
3.1. 关键风参数
3.1.1. 风速
风速是风资源评估中的核心参数,直接影响风电机组的输出功率. 风速的垂直剖面变化与大气稳定度、地面摩擦力以及大气湍流等因素密切相关. 一般来说,在稳定的大气状态下,低层大气中的风速较低;在不稳定状态下,风速可能会出现较大的波动. 准确的风速测量与分析对于评估风能潜力、选择合适的风电机组以及优化风电场布局至关重要.
3.1.2. 空气密度
空气密度也是影响风力发电效率的关键因素. 空气密度与气温、气压和湿度密切相关,一般随着海拔增加而减少. 当空气密度较大时,单位风速所携带的动能较多,增加了风力发电的潜力. 研究中须考虑空气密度的变化,特别是在不同气候和地形条件下空气密度变化对风资源评估的影响.
3.1.3. 垂直风速
垂直风速是指空气沿垂直方向的运动速度,在风电领域中通常与湍流的形成及大气稳定度变化密切相关. 垂直风速影响着风的垂直扩散过程及空气层结的稳定性. 在不同的大气状态下,垂直风速存在差异,进而影响空气的上升或下沉运动. 研究垂直风速对于理解大气层结的演变以及风力资源的垂直分布具有重要意义.
3.1.4. 湍流强度
湍流强度是衡量流体不规则运动强度的指标,通常表示为风速的标准差与平均风速之比. 湍流会导致风速波动,对风电机组的运行和风能捕获效率产生影响. 高湍流强度通常会导致风电机组在较短时间内经历大幅度的风速变化,这可能对机组的稳定性和性能产生不利影响. 研究湍流强度对于理解大气边界层的能量传输特性及评估风能资源在不同大气条件下的可利用性具有重要意义.
3.2. 大气稳定度
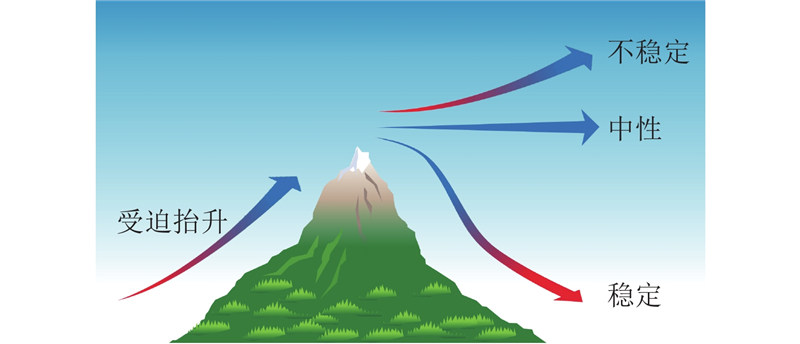
大气稳定度是大气的热力学特性,不同大气稳定度下空气会呈现不同的垂直运动趋势,如图2所示. 在稳定的大气状态下,气团由于地形受迫上升,其绝热膨胀后的温度会比高海拔的环境空气温度低,密度会大于环境空气,气团会返回原来的位置. 在不稳定的大气状态下,气团受迫上升后温度比周围空气更高,气团会持续上升. 中性大气状态则处在两者之间,气团上升后与周围空气温度一致,气团维持在上升后的高度. 不稳定的大气会增强气团的垂直运动趋势,稳定的大气会抑制气团的垂直运动趋势. 为了定量表示大气稳定度,许多学者采用理查森数、莫宁-奥布霍夫长度[17-18]来度量大气稳定度. 为了评估不同大气稳定度对风参数的影响,本研究采取莫宁-奥布霍夫长度来区分大气稳定度,根据Stull[19]定义的莫宁-奥布霍夫计算公式进一步推导得到
图 2
图 2 不同大气稳定度下空气的垂直运动趋势
Fig.2 Vertical air movement trends under different atmospheric stability conditions
式中:L为测风塔位置的莫宁-奥布霍夫长度;
4. 结果与讨论
4.1. 模型验证与大气稳定度分布
采用评估指标:均方根偏差RMSE、相关系数R和一致度IA,对模拟结果的准确性进行验证. RMSE用于评估模型的预测准确性,R用于评估预测值和观测值的趋势匹配程度,IA用于评估模型预测值是否与观测值分布一致. 如表1所示为2个测风塔90 m高度位置的全年日均模拟风速准确性指标评估结果. 可以看出,模拟风速与实测结果显示出良好的一致性. 以1822#测风塔的观测数据为基准,模拟风速的全年相关系数为0.86,一致度为0.92,表明模拟风速在趋势和分布方面与实测风速高度吻合,能够作为后续分析的可靠数据基础.
表 1 测风塔处全年风速模拟的准确性指标
Tab.1
| 测风塔 | RMSE/(m∙s−1) | R | IA |
| 1822# | 1.37 | 0.86 | 0.92 |
| 1823# | 1.46 | 0.84 | 0.91 |
统计9个虚拟测风点全年逐小时大气稳定情况,如图3所示. 大气稳定度的分布与地形之间具有较强的相关关系. 在D04虚拟测风塔代表的山地地形上,大气稳定度中性状态居多,特别是D04 3#虚拟测风塔,中性大气状态占比为34%,是D03中性大气状态平均占比的2.6倍;在D03虚拟测风塔代表的缓坡平原地形上,强稳定和强不稳定状态占比明显高于中性大气状态占比,强稳定大气状态占比在45%左右. 进一步分析山地区域中性大气状态占比高于缓坡平原的原因,山地区域的复杂地形会抑制稳定与不稳定大气状态的形成. 在夜间,陆地的大气边界层通常趋向稳定状态,此时,D04山地区域的复杂地形会显著增强近地面机械湍流,当气流经过山体时,地形的强迫作用会引发绕流、抬升及局地风加速现象[21],这些动力扰动会持续破坏大气层结的稳定性,使得大气状态趋向于中性;D03缓坡平原地表摩擦作用较弱,易在夜间形成稳定的大气边界层[19]. 在日间,由于太阳辐射的加热作用,陆地的大气边界层趋向不稳定状态,D04山地区域由于坡向和海拔高度差异,地表加热效应不均匀[22]. 具体来说,山地的高海拔地表吸热能力强于周围空气,导致高海拔空气受到额外的地表加热,抑制了太阳辐射引起的典型的下热上冷的自然空气温度梯度,进而抑制了不稳定大气状态的形成,使得大气状态更趋向中性.
图 3
图 3 虚拟测风塔的大气稳定度分布
Fig.3 Atmospheric stability distribution at virtual meteorological towers
在复杂地形的风力机选址实践中,一般优先选择高海拔区域(如山脊)布机,原因是山脊区域通常具有更好的风资源情况[23]. 大气稳定度在山地和缓坡平原区域的差异明显,山地大气趋于中性,缓坡平原反之.
4.2. 大气稳定度与风速
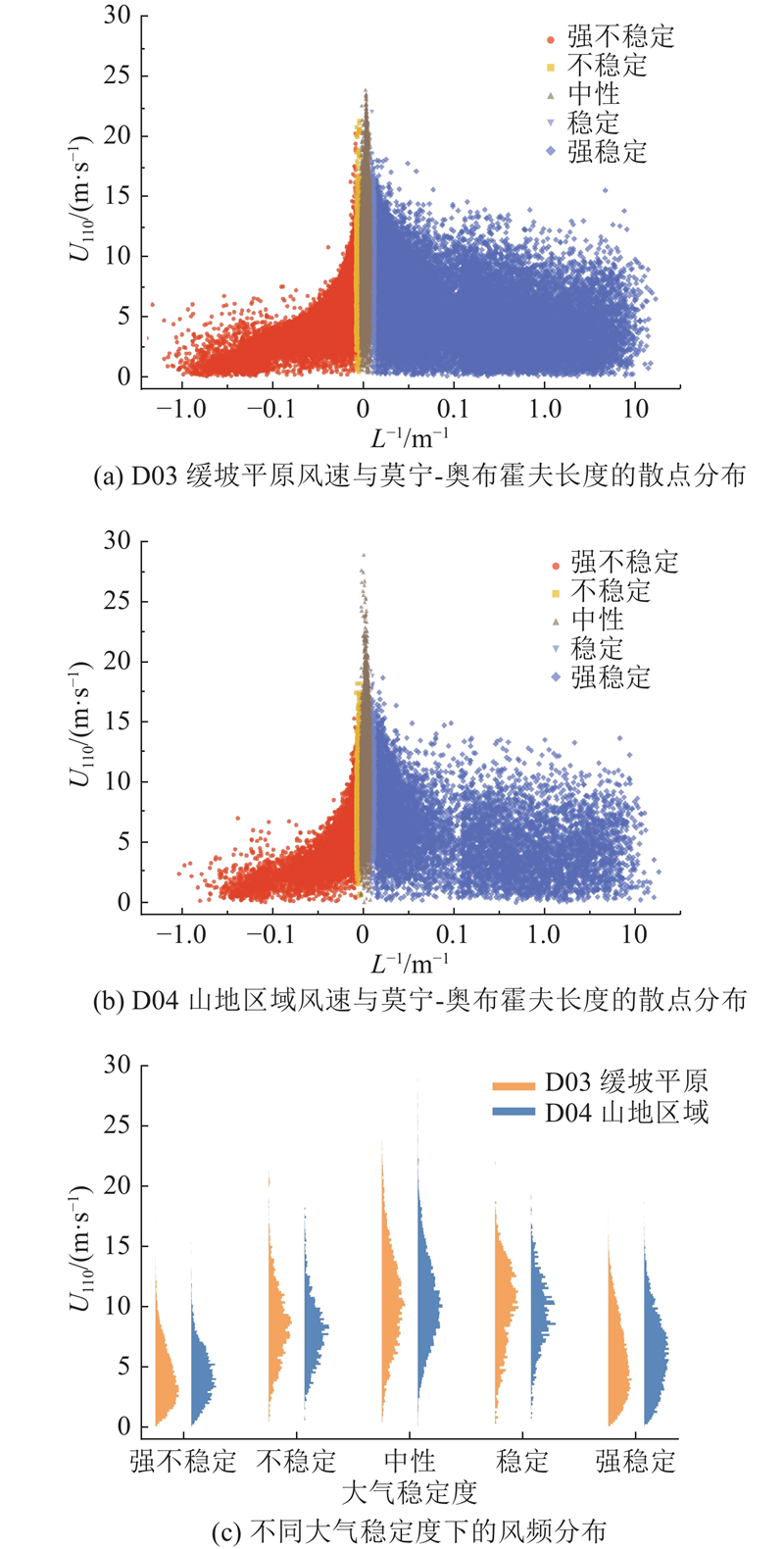
风速是风资源的直观体现形式,为此进行大气稳定度与风速的关联性分析,分别以D03和D04内所有的虚拟测风塔为统计对象. 如图4所示为虚拟测风塔风速与莫宁-奥布霍夫长度的分布散点图及不同大气稳定状态下的风频分布直方图,其中U110为各虚拟测风塔110 m处的水平风速. 可以看出,随着大气稳定度趋近中性,高风速出现的可能性增加. 具体来说,当大气稳定度为中性时,95%的风速分布范围为3.0~19.0 m/s,其中高风速的占比更大,风速超过20 m/s的情况几乎只会出现在中性大气状态下;当大气稳定度趋向强稳定或强不稳定时,风速相对较低. 相比之下,当大气稳定度趋向强稳定时,95%的风速分布范围为0.8~12.5 m/s,在强不稳定大气状态下,95%的风速分布范围为0.7~10.0 m/s,强稳定大气状态出现高风速的概率比强不稳定状态高. 总的来说,风速随大气稳定度变化,由高到低的顺序依次为中性状态、稳定状态和不稳定状态. 因此,高海拔山地区域中性大气状态占比更高,山地区域风能潜力更大. 分析结果表明,D04的风速分布比D03的更集中,这对于风力机的稳定运行和发电作业具有显著优势. 例如,在中性大气状态下,D03的95%的风速分布范围为3.0~19.0 m/s,D04的95%的风速分布范围为3.8~18.4 m/s,D04的风速波动幅度更小,更有利于风电机组的稳定运行. 在中性和强稳定大气状态下,D04风速均值分别为10.46和6.15 m/s,略高于D03区域的10.45和5.75 m/s. 这表明D04区域在这些大气状态下具备更高的风能潜力. 中性和强稳定大气状态在各虚拟测风塔处占比之和在57.8%~63.3%,是风电基地主要的大气稳定状态. 因此,D04高海拔山地区域风能潜力更大;D03低海拔缓坡平原风能潜力略低,且风速分布范围更广,需要更多针对风力机组的适应性设计. 分析D03缓坡平原和D04山地区域风速分布差异的成因. D04的最大风速显著高于D03,尤其在中性大气状态下. 此时,空气的垂直运动主要受地形诱导的机械湍流影响,热力因素的作用减弱. 山地地形的复杂性导致风在穿越山脊、峡谷和坡面时遭遇强烈的地形扰动和加速. 尤其是在风流进入狭窄山谷时,出现收缩效应,使得风速显著增强[21, 24]. 当风流经过山脊时,由于地形的抬升作用,气流会被压缩,流速会随之增加,这种现象被称为狭管效应[21]. 相对而言,平原地区地形较为平坦,缺乏这种加速效应,因此最大风速较低. 尽管山地地区的湍流强度大于平原地区,但风速受地形影响,风速波动主要集中在较高的均值区间. 相比之下,平原地区风速受下垫面粗糙度的影响,风速的整体分布可能较为均匀,导致95%风速的分布区间相对较宽.
图 4
图 4 风速随大气稳定度变化的散点与直方分布
Fig.4 Scatterplot and histogram of wind speed variation with atmospheric stability
4.3. 大气稳定度与空气密度
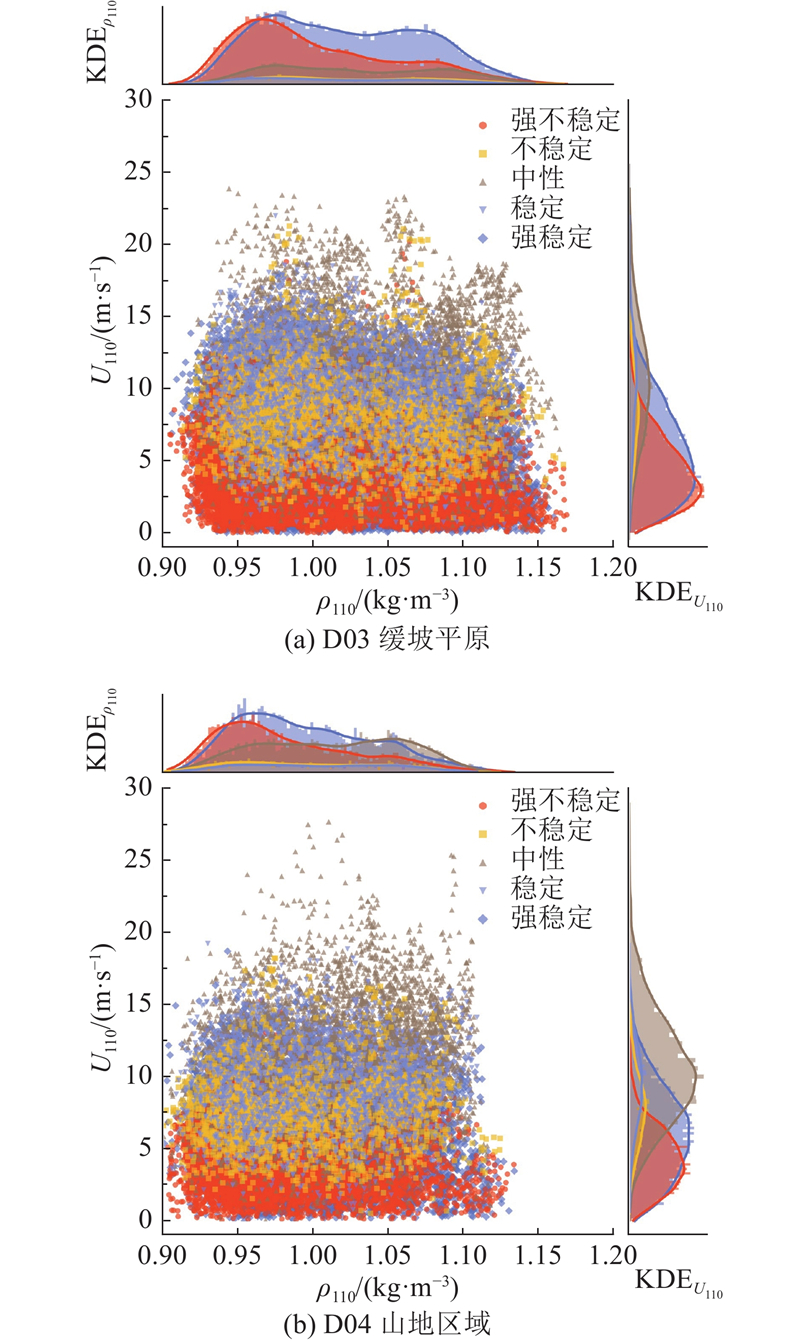
风资源等级的划分标准是风功率密度,风功率密度的主要自变量为风速和空气密度,有必要探究大气稳定度对空气密度的影响. 如图5所示为不同大气稳定状态下风速与空气密度的散点分布及各参数的核密度(kernel density estimation, KDE)分布情况,其中U110、ρ110为各虚拟测风塔110 m处的水平风速和空气密度. 从空气密度的KDE分布情况可以发现,D03缓坡平原和D04山地区域的空气密度分布有共性特征. 在中性大气状态下,空气密度呈双峰分布,且在双峰之间分布较为均匀;强不稳定大气状态空气密度呈单峰分布,且峰值处空气密度偏小,在D03、D04中分别为0.965、0.952 kg/m3. 在强稳定大气状态下,D03缓坡平原和D04山地区域的空气密度在不同的地形下呈现不同特征. D03的空气密度呈双峰分布,峰值处空气密度分别为0.974、1.066 kg/m3; D04的空气密度第2峰不明显,可认为是偏单峰分布,峰值处空气密度为0.958 kg/m3. 这表明,在缓坡平原区域,空气密度更容易受到大气稳定度的影响,山地地区由于地形对流场的复杂干扰,导致空气密度分布趋于更加稳定的单一值. 无论是D03还是D04,强稳定大气状态的峰值空气密度均高于强不稳定状态下的峰值空气密度. 因此,相比强不稳定状态的空气密度分布,强稳定状态下的空气密度分布趋向高值. D03中性、强稳定、强不稳定状态下空气密度的平均值分别为1.028、1.021、1.003 kg/m3;D04中性、强稳定、强不稳定状态下空气密度的平均值分别为1.012、0.995、0.983 kg/m3. D04由于整体海拔较高,空气密度低于D03. 结合空气密度在不同大气状态下的分布及平均值,将大气稳定状态按空气密度由大到小排列如下:中性、强稳定、强不稳定. 分析原因,在中性大气状态下,温度和密度分布最接近大气的标准状态,因此密度相对最大;强稳定状态限制了热量传递和对流,由于空气层间隔较少混合,虽然局部可能会有较大的密度,但整体空气密度分布会因为逆温效应而略低于中性状态;在强不稳定状态下,上升的暖空气会导致整个大气柱的平均密度降低. 从风速的KDE分布图可以看出,各种大气稳定状态下风速均呈现单峰分布,按风速由高到低的排序为中性、强稳定、强不稳定.
图 5
图 5 空气密度与风速的散点及参数核密度分布
Fig.5 Scatterplot and parametric kernel-density-estimated distribution of air density versus wind speed
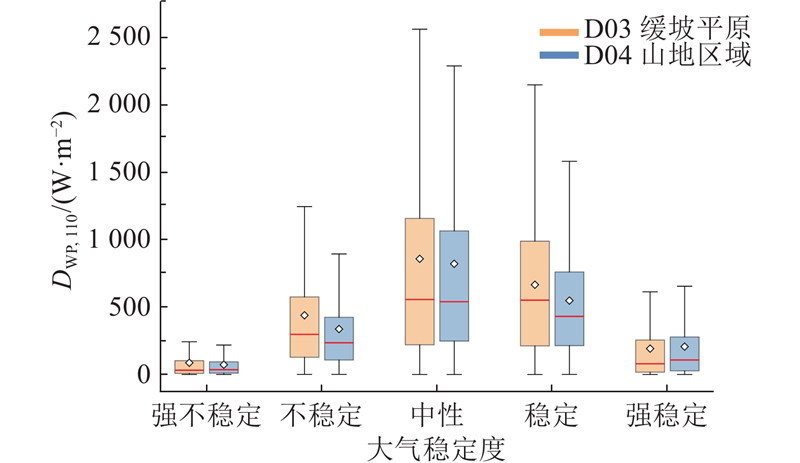
风速和空气密度在不同大气稳定度下表现出相似的变化规律,因此风功率密度的变化趋势也与风速和空气密度的变化趋势一致. 如图6所示为风功率密度随大气稳定度分布箱线图,其中DWP,110为风电场110 m处的风功率密度. 可以看出,在中性大气状态下,D03、D04的平均风功率密度分别为857 和820 W/m2,是强稳定状态平均风功率密度的4.5倍和4.0倍,是强不稳定状态平均风功率87和72 W/m2的9.8倍和11倍. 总体来说,中性大气状态的平均风功率密度约为强稳定和强不稳定大气状态的4倍和10倍. 可以看出,中性大气状态下的风资源条件最佳,强稳定大气状态优于强不稳定大气状态. 由图6还可以看出,D04的风功率密度分布比D03的更集中,但D04风功率密度的平均值与中位数大多比D03的小. D04多塔平均的年均风功率密度为363 W/m2,远高于D03的279 W/m2,这是D04中性大气状态占比更高导致的. 分析结果表明,在风力机选址时应优选中性大气状态占比高的区域,不能仅关注某一大气状态下风功率的高低. 不同稳定度下的风速和风功率特征直接影响风电机组的运行:1)在中性大气状态下,高频次的高风速有助于提升容量因子. 山地区域的中性大气状态占比显著高于缓坡平原的,同时风速分布更为集中. 从全年风资源状况来看,山地区域的风资源更为优越;2)除部分山地区域外,强稳定大气状态是所有大气状态中占比最高的,在强稳定大气状态下,山地区域的风功率密度高于缓坡平原. 综合来看,山地区域的风资源较缓坡平原的更具优势. 此外,山地区域风速的集中分布有助于优化机组的切入/切出控制,较小的风速波动可有效降低功率输出的波动性.
图 6
图 6 风功率密度随大气稳定度分布箱线图
Fig.6 Box plot of wind power density distribution with atmospheric stability
4.4. 大气稳定度与垂直风速、湍流强度
在风电场运行过程中,不稳定大气状态下的尾流距离会减小[25]. 尾流恢复主要受到垂直风速、湍流强度影响,为此进行大气稳定度和垂直风速、湍流强度的关联性分析. 如图7所示为大气稳定度、水平风速、垂直风速的关联分析图与各参数KDE分布情况,其中w110为各虚拟测风塔110 m处的垂直风速. 从垂直风速的KDE分布上看,强稳定、强不稳定状态基本处于0 m/s附近的单核分布,中性状态向负方向偏离,说明在中性大气状态时空气更倾向于下沉运动. 图7的散点图中,从强稳定到强不稳定,D03的垂直风速的95%分布范围由−0.09~0.14 m/s扩大到−0.39~0.41 m/s,D04的垂直风速的95%分布范围由−0.15~0.23 m/s扩大到−0.38~0.44 m/s. 在强稳定状态下,大气的浮力抑制湍流运动,导致垂直方向的空气运动几乎被抑制. D03缓坡平原较为开阔,地形起伏较小,因此垂直风速的变化较为平缓,主要受大气稳定度影响;D04山地区域的复杂地形对垂直风速的影响更加明显,即使在强稳定状态下,地形引发的局部湍流仍可能增强空气的垂直运动. D04在强稳定状态下95%的垂直风速波动范围是D03的1.65倍. 在强不稳定状态下,地面强烈加热使浮力成为主导,湍流运动增强,垂直风速出现大幅波动. D03由于地形较为平坦,垂直风速的变化范围主要取决于大气稳定度;在D04,不稳定大气状态会加剧垂直风速波动,此时地形影响相对较弱. D04在强不稳定状态95%的垂直风速波动范围只有D03的1.03倍. 这表明,在偏向稳定的大气状态时,山地地形会加强垂直风速的波动,风速波动范围显著高于缓坡平坦地形. 在偏向不稳定的大气状态时,地面强烈加热使浮力成为主导,山地地形与缓坡平原的垂直风速波动范围相近. 根据过往的研究,山地地形相对于缓坡平原地形更有利于尾流的恢复,原因是山地增强了大气的垂直运动,气流的垂直掺混能力得到增强[25]. 分析结果进一步明确,在强稳定大气状态下,山地地形诱导的垂直风速波动远大于缓坡平原地形,对尾流恢复的促进作用更为显著;在强不稳定大气状态下,山地地形的垂直风速波动依然较大,对尾流恢复的促进作用也较强,但与缓坡平原地形相近,2种地形的垂直风速波动都主要由不稳定大气状态下的热力因素驱动.
图 7
图 7 垂直风速与风速的散点及参数核密度分布
Fig.7 Scatterplot and parametric kernel-density-estimated distribution of vertical wind speed versus wind speed
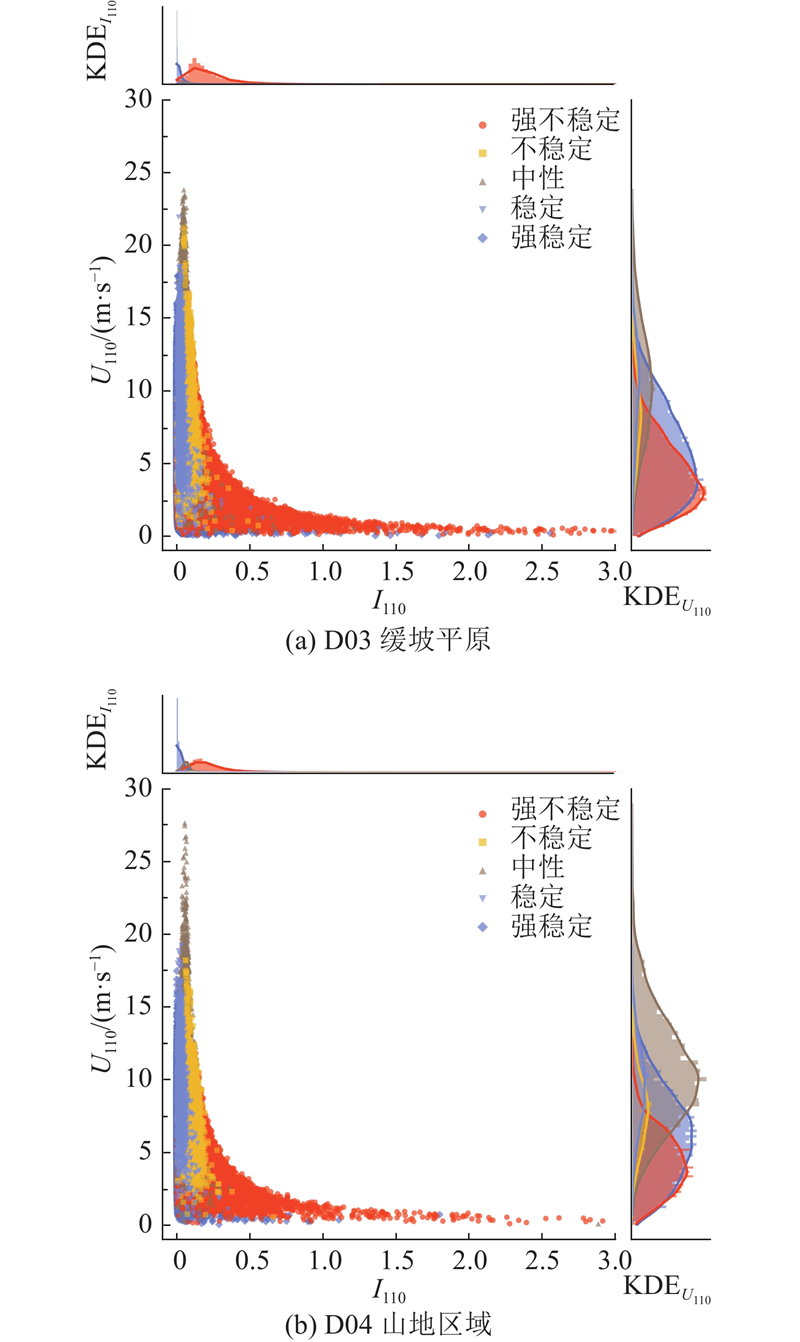
如图8所示为大气稳定度、水平风速、湍流强度的关联分析图与各参数KDE分布情况,其中I110为各虚拟测风塔110 m处的湍流强度. D03和D04的分布特征基本一致,水平风速与湍流强度呈现明显的负相关,这与基本的常识相符,在国际电工委员会(international electrotechnical commission, IEC)标准中,通常将15 m/s风速下包含90%湍流强度点的湍流强度作为代表湍流强度[26]. 从湍流强度的KDE分布来看,所有大气状态下湍流强度都呈现单峰分布,大气越稳定,湍流强度越集中分布于小湍流强度区域;大气越不稳定,湍流强度分布越宽泛,湍流强度也越大. 因此,大气越不稳定越会导致湍流强度增大,且发生大范围变化.
图 8
图 8 湍流强度与风速的散点及参数核密度分布
Fig.8 Scatterplot and parametric kernel-density-estimated distribution of turbulence intensity versus wind speed
综合大气稳定度对垂直风速和湍流强度的影响,从尾流角度来看,在不稳定大气状态下,空气掺混能力和混乱程度增强,有利于大气掺混和尾流恢复,减弱尾流对风电场发电量的影响;在稳定和中性大气状态下,热力作用导致空气垂直掺混减弱,地形在垂直风速和湍流强度的增强中起主导作用,山地区域的尾流恢复能力明显优于缓坡平原地区. 从风电场运行角度来看,山地的风速能得到更高效的利用. 从风力机结构疲劳载荷的角度来看,垂直风速与湍流的增强会使风力机承受更大的载荷强度,进而降低风力机的疲劳寿命. 因此,山地区域的风力机设计强度通常高于缓坡平原.
5. 结 语
本研究采用天气研究与预报模式,以内蒙古自治区阿拉善盟陆上风电基地为研究对象,探究了大气稳定度与关键风参数之间的关联性,揭示了大气稳定度对风资源分布的影响机理. 主要结论如下:1)大气稳定度在不同地形上呈现不同的分布特征,山地区域中性大气状态占比高,缓坡平原强稳定和强不稳定状态占比高. 山地区域中性大气占比最高可达缓坡平原中性大气占比的2.6倍. 2)大气稳定度对陆上大基地风资源特性影响显著,风速、空气密度与大气稳定度呈现一致的关联性,即按照中性、强稳定、强不稳定的大气稳定状态顺序,风速、空气密度和风功率密度均依次递减,中性大气状态下的平均风功率密度约为强稳定和强不稳定大气状态下的4倍和10倍. 高海拔山地区域中性大气状态占比更高,风能潜力更大. 因此,风电场布机时推荐选择高海拔山地区域. 3)大气稳定度显著影响大气掺混,地形在稳定大气状态下对大气掺混和尾流恢复的影响尤为显著. 在不稳定大气状态下,垂直风速波动和湍流强度增加,促进大气掺混,加快风力机尾流恢复. 在稳定大气状态下,地形对风参数的影响更为显著,山地地形有助于形成更强风速和更集中的空气密度分布,同时垂直风速波动显著高于缓坡平原区域. 因此,山地的风功率密度和大气掺混强度往往高于缓坡平原. 本研究分析了中尺度大气稳定度对风电场风参数的影响,尚难揭示在微尺度上的具体作用机制. 未来可引入微尺度模拟,实现中微尺度耦合,更准确地反映复杂地形下的风场特征,深化大气稳定度对风力机运行特性与结构响应的认识.
参考文献
High-resolution mesoscale wind-resource assessment of Fiji using the weather research and forecasting (WRF) model
[J].DOI:10.1016/j.energy.2021.121047 [本文引用: 1]
Performance evaluation of the weather research and forecasting (WRF) model for assessing wind resource in Greece
[J].DOI:10.1016/j.renene.2016.10.033 [本文引用: 1]
耦合风电场参数化模型的天气预报模式对风资源的评估和验证
[J].
Wind resource assessment of weather research and forecasting model coupled with wind farm parameterization model
[J].
A coupled turbine-interaction wind farm parameterization in the weather research and forecasting model
[J].DOI:10.1016/j.enconman.2023.116919 [本文引用: 1]
基于中尺度WRF模式的海上风电场尾流影响评估
[J].
Impact assessment of offshore wind farm wakes based on mesoscale WRF model
[J].
Integration of atmospheric stability in wind resource assessment through multi-scale coupling method
[J].DOI:10.1016/j.apenergy.2023.121402 [本文引用: 1]
The variability of wind resources in complex terrain and its relationship with atmospheric stability
[J].DOI:10.1016/j.enconman.2020.113249 [本文引用: 1]
Influence of atmospheric stability on wind turbine energy production: a case study of the coastal region of yucatan
[J].DOI:10.3390/en16104134 [本文引用: 1]
Influence of atmospheric stability on wind farm layout optimization based on an improved Gaussian wake model
[J].DOI:10.1016/j.jweia.2021.104548 [本文引用: 1]
A workflow for including atmospheric stability effects in wind resource and yield assessment and its evaluation against wind measurements and SCADA
[J].DOI:10.1088/1742-6596/2507/1/012018 [本文引用: 1]
Impact of atmospheric stability on wind turbine wake evolution
[J].DOI:10.1016/j.jweia.2018.03.014 [本文引用: 1]
The impact of stable atmospheric boundary layers on wind-turbine wakes within offshore wind farms
[J].DOI:10.1016/j.jweia.2014.12.011 [本文引用: 1]
Atmospheric stability and topography effects on wind turbine performance and wake properties in complex terrain
[J].DOI:10.1016/j.renene.2018.03.048 [本文引用: 1]
Offshore wind farm wake recovery: airborne measurements and its representation in engineering models
[J].
Influence of atmospheric stability on wind farm performance in complex terrain
[J].DOI:10.1016/j.apenergy.2020.116149 [本文引用: 1]
大气稳定度对山地风力机功率影响研究
[J].
A study of the influence of atmospheric stability on wind turbine power in complex terrain
[J].
Flux-profile relationships in the atmospheric surface layer
[J].DOI:10.1175/1520-0469(1971)028<0181:FPRITA>2.0.CO;2 [本文引用: 1]
Analysis of various schemes for the estimation of atmospheric stability classification
[J].DOI:10.1016/S1352-2310(98)00109-5 [本文引用: 2]
On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer
[J].DOI:10.1007/s10546-007-9166-9 [本文引用: 1]
Field measurements and wind tunnel investigation of wind characteristics at a bridge site in a Y-shaped valley
[J].DOI:10.1016/j.jweia.2020.104199 [本文引用: 3]
On the vertical exchange of heat, mass, and momentum over complex, mountainous terrain
[J].
Evaluation of wind resource potential in mountainous region considering morphometric terrain characteristics
[J].DOI:10.1177/0309524X16689445 [本文引用: 1]
The impact of valley geometry on daytime thermally driven flows and vertical transport processes
[J].
Influence of atmospheric stability on wind-turbine wakes: a large-eddy simulation study
[J].DOI:10.1063/1.4913695 [本文引用: 2]