在我国北方地区,煤电机组大部分是抽凝式热电联产机组[3-4]. 近年来,为了充分利用乏汽余热,提高燃料利用效率,诸多火电厂对厂内机组进行了高背压供热改造. 改造后,这些机组在供暖期可以通过更换低压缸转子切换至高背压模式运行[5-6];也可以选择不更换转子,依然在传统抽凝模式下运行[7]. 当机组选择高背压模式运行时,机组的冷源损失全部用于供热,燃料利用效率高,发电煤耗低,但是发电容量和调峰能力会显著受阻;当机组选择抽凝模式运行时,存在冷源损失,燃料利用效率低于高背压模式,但是发电容量损失可能较小,调峰灵活性更高,容量和调峰收益可能高于高背压模式. 因此,在容量电价机制发布后,如何折中考虑容量、电量及调峰收益,在供暖期来临之前机组选择合适的运行模式,已成为热电厂面临的新问题.
对于上述问题,相关研究大多集中在高背压运行模式与抽凝运行模式的节能效果与经济效益的对比[8-10]、高背压机组与抽凝机组的配合运行[11-14]、高背压机组改造后的运行特性[15-18]等. 张攀等[8]针对高背压供热方式下的经济性进行分析,指出供热参数和背压变化对机组在供热期的经济性影响最大,为运行过程中供热方式的选择提供了依据. 王凤良[9]提出高背压供热改造技术的3种宏观经济效益评价方法,同时以工程实例为基础,验证了经济性评价方法的科学性. 王力等[10]通过高背压供热改造后的热力性能试验,分析得出改造后机组的节能降耗效果显著的结论,验证了改造方案的可行性. 上述文献仅考虑了高背压运行模式经供热改造后热耗与发电煤耗大幅降低的优势,而未考虑该模式在运行中损失调节灵活性的劣势. 且这些研究均未涉及容量电价机制下供热机组运行模式的选择问题,难以为当下的热电厂运行决策提供指导.
以含有高背压供热机组的热电厂为对象,考虑其在整个供暖期的容量收益、电量收益、调峰收益、供热收益以及燃料成本,构建2种模式下的综合效益比较模型,为热电厂在供暖期来临之前机组运行模式的选择提供决策工具.
1. 问题分析与解决思路
1.1. 机组运行模式选择问题分析
双背压双转子互换改造技术[19]是将抽凝供热机组原来的低压双层缸更换为新设计的低压单层整体内缸,从而提高低压缸排汽背压和排汽温度,以实现背压排汽供热,避免冷源损失,因此相较于传统抽凝模式,其燃料利用效率更高. 机组改造后,在供暖期来临时,既可以选择不更换转子,继续采取抽凝模式运行,亦可以选择更换转子,在高背压模式下运行. 若选择更换转子,则在供暖期结束后,需要再次更换转子,以适应非供暖期纯凝工况下的运行,因此相对于抽凝模式,高背压模式的选择会增加一段停机更换转子的时间.
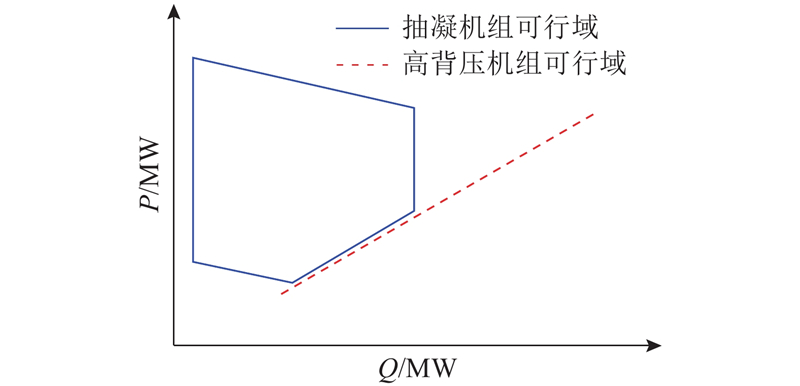
图 1
图 1 高背压机组和抽凝机组的电热关系
Fig.1 Electricity-heat relationship of high backpressure units and extraction-condensing mode
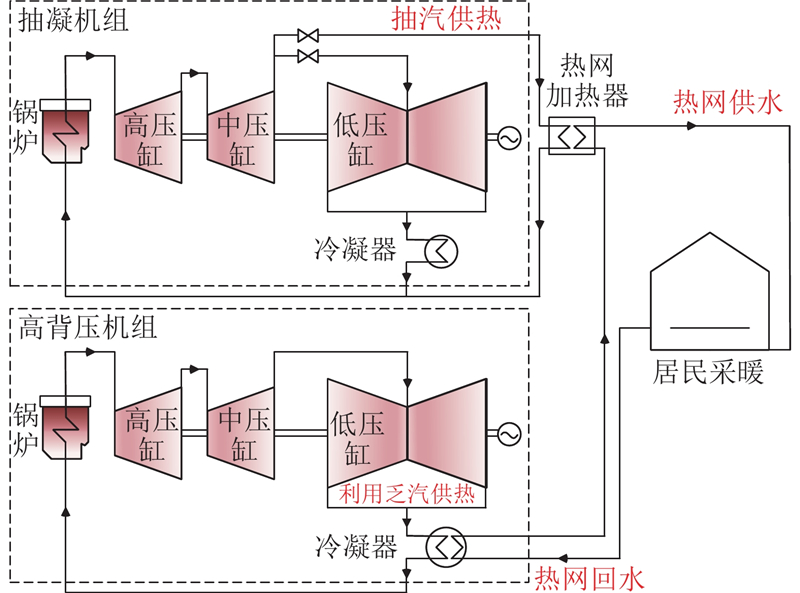
高背压机组通常需要与抽凝机组配合运行(2种机组的结构如图2所示),以保证热电厂整体具有一定的调峰能力,满足系统调峰的需求. 因此,热电厂在改造时不会把所有机组都改造为高背压机组.
图 2
图 2 高背压机组与抽凝机组协同供热方式示意图
Fig.2 Schematic diagram of coordinated heating mode of high backpressure unit and extraction-condensing unit
1.2. 问题解决思路
在供暖期来临之前,存在运行模式的选择问题. 该问题的本质是对2种模式下的收益和成本进行比较. 在容量电价机制施行之后,热电厂的收益包括售电收益、售热收益、容量电费收益、调峰辅助服务市场补偿,成本主要是燃料成本和转子更换成本. 此外,需要考虑更换转子导致机组停机所产生的容量电费损失.
在上述收益中,可以认为2种模式下热电厂在供暖期的供热量和发电量是一致的. 原因在于:在城市热网中,热电厂往往对应特定的供热区域,且该区域没有其他替代热源,因此无论采用何种运行模式,热电厂的供热量可以被认为是相同的;对于发电量,尽管2种模式下机组的调节灵活性有差异,但是考虑到不同机组之间的配合及中长期电量合约的存在,可以认为供暖期全厂发电量基本相同. 因此,只需要比较2种模式下的其他收益和成本.
另外,由于高背压模式的调节灵活性较低,热电厂不会将全部机组改造为高背压机组,而会保留足够的抽凝机组以满足电网调峰要求. 2类机组在运行时因供热而相互耦合,且具有一定的互补性,从而提升了整体的运行灵活性. 例如,高背压机组在热负荷越低时受阻容量越大,而抽凝机组在热负荷越高时受阻容量越大,在进行顶峰调节时,可以让高背压机组较多地承担热负荷,抽凝机组较少地承担热负荷;若在低谷深调,则反之. 因此,收益和成本的比较需要从全厂角度考虑.
基于上述分析,构建热电厂内供热机组在供暖期选择不同模式时的容量收益差、深调收益差和燃料成本差的计算模型,并进一步考虑转子更换成本,形成不同模式下的全厂综合效益比较模型.
2. 全厂综合效益比较模型
考虑到模型的通用性,假设热电厂内改造后的热电机组可以在高背压、抽凝、纯凝3种模式下运行(由于厂内多台机组互补供热,单台供热机组的运行可以采取纯凝模式). 热电厂的运行方案由厂内机组不同模式的选择与组合确定. 根据1.2节的分析,在不同运行方案下,热电厂的售电收益和售热收益相等,方案之间的效益差异主要体现在容量电费、深度调峰收益、燃料成本以及转子更换成本上. 通过构建涵盖各项收益和成本的模型,全面比较热电厂在不同运行方案下的整体收益和成本差异;通过计算不同方案间的容量电费差、深调电费差、燃料成本差和更换转子成本差,筛选出最优运行方案.
2.1. 容量电费差计算模型
比较供热机组选择不同运行模式时全厂的容量收益,实质上是计算热电厂在满足相同电、热负荷下所获的容量电费之差.
2.1.1. 月度容量电费计算模型
根据煤电容量电价机制[22],煤电机组须按月申报最大出力,热电厂每月可以获得的容量电费为
式中:
可以看出,热电厂的容量收益主要取决于当月申报的最大出力. 按照规定,如果实际运行时热电厂无法按照调度指令提供申报的最大出力,需要对容量电费进行扣减. 实际运行时月内各日的热负荷存在差异,引起的供热受阻容量不同,而且在有高背压供热机组的前提下,并非热负荷越大,受阻总容量就越大. 因此,基于对下一个供暖期预测的热负荷进行计算. 预测热负荷由热电厂依据历史热负荷数据、供暖面积变化以及气象条件变化情况推算得出. 每月的申报值定义为在满足预测热负荷需求的前提下,热电厂在该月能够实现的最大出力的最小值:
式中:
2.1.2. 给定热负荷下热电厂最大电出力计算模型
在机组选定运行模式后,热电厂的容量收益取决于在满足热负荷前提下的整体最大电出力,可以由下述优化模型计算得到.
1)目标函数. 以热电厂内所有机组的发电能力之和最大化为目标函数:
式中:Pplant为热电厂的总发电能力,
2)约束条件.
(a)全厂热负荷平衡约束:
式中:
(b)抽凝机组可行运行区间约束:考虑到机组发电功率上下限、供热能力上下限、抽汽供热对发电功率的影响,抽凝模式下机组的可行运行区间为
式中:
(c)高背压机组可行运行区间约束:考虑机组发电功率上下限,高背压模式下机组的可行运行区间为
式中:
(d)纯凝机组可行运行区间约束:考虑机组出力上下限,纯凝运行模式下机组的可行运行区间为
式中:
2.1.3. 供暖期容量电费差计算模型
在选定机组运行模式后,给定目标月份内各日的热负荷数据,即可计算出该月内每日的全厂最大出力,进而取其最小值作为申报容量,用于计算该月的容量电费.
以
式中:
2.2. 深度调峰电费差计算模型
2.2.1. 给定热负荷下深度调峰能力差计算模型
深度调峰交易是热电厂开机机组通过调减出力,使热电厂机组平均负荷率降至有偿调峰基准值及以下时提供辅助服务的交易. 以东北调峰市场[23]为例,以46%为义务调峰基准,36%与26%分别为1、2档和2、3档分界线基准. 热电厂的最小发电能力决定了热电厂能够参与的深度调峰的档位,进而决定了热电厂在辅助服务市场的收益情况.
式中:
式中:
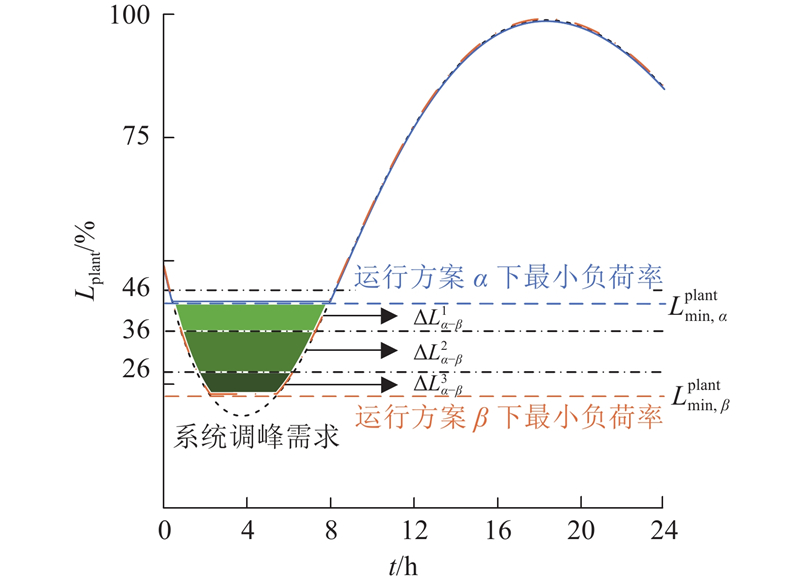
由于机组在高背压或抽凝、纯凝模式下运行时,其深度调峰能力不同,进而影响热电厂在深度调峰市场的获利,因此需要进一步构建给定热负荷下的全厂最小出力模型. 通过计算给定热负荷下的全厂最小出力,计算不同方案下的最小出力率差值及其在不同档位的分布,如图3所示. 其中,Lplant为热电厂的负荷率,t为运行时间. 2种不同运行方案下的最小出力率差可以表示为
图 3
图 3 不同运行方案下热电厂深度调峰能力示意图
Fig.3 Schematic diagram of deep peak-shaving capability of thermal power plant under different operating schemes
式中:
式中:
2.2.2. 给定热负荷下的热电厂最小电出力模型
以包含高背压、抽凝、纯凝3种运行模式的供热机组的热电厂为对象,构建给定全厂热负荷下的热电厂最小电出力计算模型. 与2.1.2节中的模型相比,仅是目标函数不同.
1)目标函数. 以热电厂内所有机组的发电能力之和最小化为目标函数:
2)约束条件与2.1.2节中的最大出力模型相同.
2.2.3. 供暖期深调电费差计算模型
热电厂在得到供暖期各日在不同方案下的深度调峰能力后,须进一步考虑调峰能力的调用情况,才能估算深调电费差.
采用最近1个供暖期各日各时段的调峰情况进行估计. 若该时段属于深调时段,则认为新增的调峰容量被完全调用. 故而,整个供暖期的深度调峰电费差可以由下式估算:
式中:
2.3. 燃料成本差
2.3.1. 燃料成本差计算模型
供热机组采用高背压模式运行的主要原因在于,在该模式下运行时没有余热损失,可以充分利用发电余热进行供热,进而降低了供热能耗和成本. 由于热电联产机组的发电和供热煤耗高度耦合,采用好处归热法[24],将发电煤耗和供热煤耗进行分解,从而在给定热电厂供热负荷的情况下,计算不同运行方案下的燃料成本差.
好处归热法假定发电能耗为纯凝工况下的发电能耗,将余热利用的好处全部归属于供热环节. 假设不同供热方案下整个供暖期的发电量和供热量相同,那么根据好处归热法,2种方案下的发电煤耗量相同. 因此,燃料成本的差异完全体现在供热煤耗量的差异上. 供热煤耗量的差异主要源于背压供热和抽汽供热在煤耗率和供热量方面的不同.
热电厂在整个供暖期的供热成本为
式中:
运行方案
式中:
2.3.2. 抽凝和高背压模式下的供热煤耗计算模型
1)抽凝机组. 抽凝机组
式中:
考虑到供暖期电负荷波动带来的供热煤耗率波动,采用平均负荷进行估计:
式中:
在整个供暖期内,抽凝机组
式中:
2)高背压机组. 高背压机组
式中:
在好处归热法下,高背压模式下机组的发电成本为该机组在纯凝运行模式下的度电成本. 其中,高背压机组在纯凝运行模式下的煤耗为
式中:
考虑到供暖期电负荷波动带来的供热煤耗率波动,采用平均负荷计算高背压机组的供热边际煤耗:
式中:
在整个供暖期内,机组
式中:
2.3.3. 高背压供热量和抽凝供热量确定方法
对于给定机组运行模式,由于供暖期各日热负荷不同,先通过对供暖期各日热负荷进行分配,确定高背压机组和抽凝机组的日供热量,再通过对整个供暖期数据进行累计计算,得到各机组在整个供暖期内的平均供热量,具体过程如下.
考虑到抽凝运行模式下机组的供热煤耗高于高背压运行模式,且高背压模式具有“以热定电”的运行特性,根据热电厂的实际运行规律,采用如下分配方法对各日热负荷进行分配.
1)抽凝机组在满足电负荷及加热器最小抽汽流量的前提下,尽可能地减少供热抽汽,供热量由运行于高背压模式的机组提供.
2)当高背压运行模式下的机组的热出力达到上限时,剩余供热量由运行于抽凝模式的机组按照加热器数量均摊.
2.4. 转子更换成本模型
在整个供暖期,运行方案
式中:
式中:
本研究针对已完成高背压改造的机组在供暖期前是否更转转子的运行决策问题进行分析,因此无须计及机组改造的前期投资成本,该成本属于沉没成本.
2.5. 综合效益差模型
式中:
3. 算例分析
3.1. 基础数据
以中国东北某热电厂为研究对象,利用上述模型对1号机组在供暖期采取2种不同运行模式时的综合收益情况进行计算和对比.
该热电厂有4台热电联产机组,其中1号机组由纯凝机组经高背压改造后成为高背压机组,剩余3台为抽凝供热机组. 2号机组安装有3个加热器,而3号和4号机组各安装了2个加热器. 机组参数如表1、2所示. 其中,a、b、c为机组的煤耗特性常系数,
表 1 机组经济参数(定参数模型)
Tab.1
| 机组 | 类型 | a/(t·MW−2·h−1) | b/(t·MW−2·h−1) | c/(t·h−1) | |
| 1# | 高背压 | — | — | — | 92 |
| 1# | 纯凝 | 11.397 | — | ||
| 2# | 抽凝 | 6.006 | — | ||
| 3# | 抽凝 | 8.774 | — | ||
| 4# | 抽凝 | 6.820 | — |
表 2 机组运行参数(定参数模型)
Tab.2
| 机组 | 类型 | z/MW | |||||
| 1# | 高背压 | 280 | 70 | — | — | 0.53 | 0.04 |
| 1# | 纯凝 | 350 | 100 | — | — | — | — |
| 2# | 抽凝 | 350 | 100 | 200 | 0.218 | 0.62 | −24.4 |
| 3# | 抽凝 | 350 | 100 | 200 | 0.218 | 0.62 | −24.4 |
| 4# | 抽凝 | 350 | 100 | 220 | 0.218 | 0.62 | −24.4 |
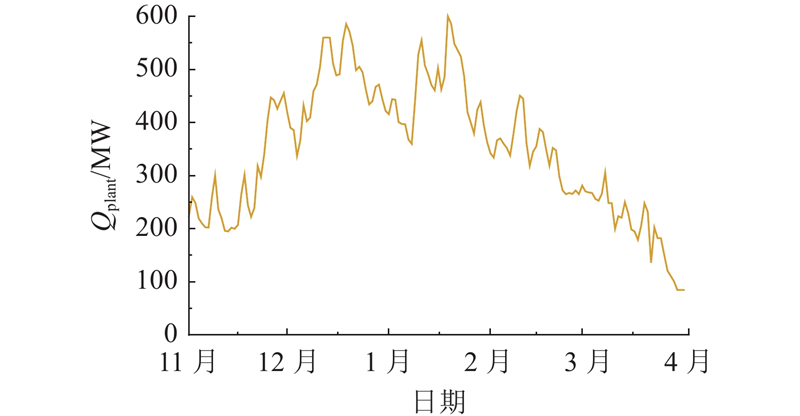
在算例分析中,供热负荷、发电负荷及调峰标志采用某年供暖期5个月的历史数据,取每小时平均供热量作为当日的平均热负荷,其变化曲线如图4所示.
图 4
按照100元/(kW·a)的容量电价进行计算[2]. 为了方便计算,算例中涉及到的其余价格均取平均值:设标煤单价为
3.2. 不同运行方案下最大/最小发电能力分析
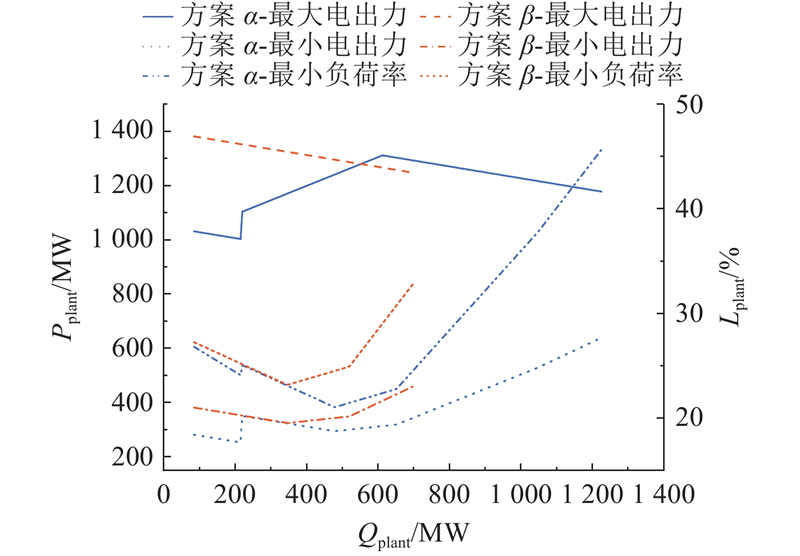
图5展示了不同方案下热电厂在不同热负荷下的最大和最小电出力.
图 5
图 5 不同运行方案下热电厂的边界电出力
Fig.5 Boundary power output of thermal power plant under different operating schemes
对于方案β,由于该方案下承担供热任务的机组均为抽凝机组,热电厂的全厂特性与单台机组的特性基本一致. 随着热负荷的增大,最大电出力因抽汽量增加而下降;最小电出力刚开始随着抽汽量增加而下降,当热负荷达到一定阈值后,又会逐步上升.
方案α下的情况比较复杂. 当热负荷较小时,由于1号机组无法开机,全厂最大和最小出力均低于方案β. 但是随着热负荷的增大,在1号机开机之后,当1号机组可以承担全部热负荷时,为了实现全厂出力最大化,所有热负荷被分配给1号机组,而2~4号机组的容量不会受阻,因而在热负荷变化初期,全厂最大出力会随着热负荷的增大(即1号机组发电量的增加)而增大;当热负荷超过1号机组发电能力上限后,抽凝机组的发电能力因抽汽量的增加而下降,导致全厂最大出力下降. 但是对于最小出力,为了使全厂出力最小,会给1号机分配最小热负荷,使其在最小电出力点运行,而将剩余热负荷分配给2~4号机组(2~4号机组中联产部分的电热比更小,在相同的热负荷下“以热定电”的功率更小). 因此,其最小出力特性类似于方案β,首先随着热负荷的增大而下降,待热负荷超过某个阈值后,再随着热负荷的增大而上升.
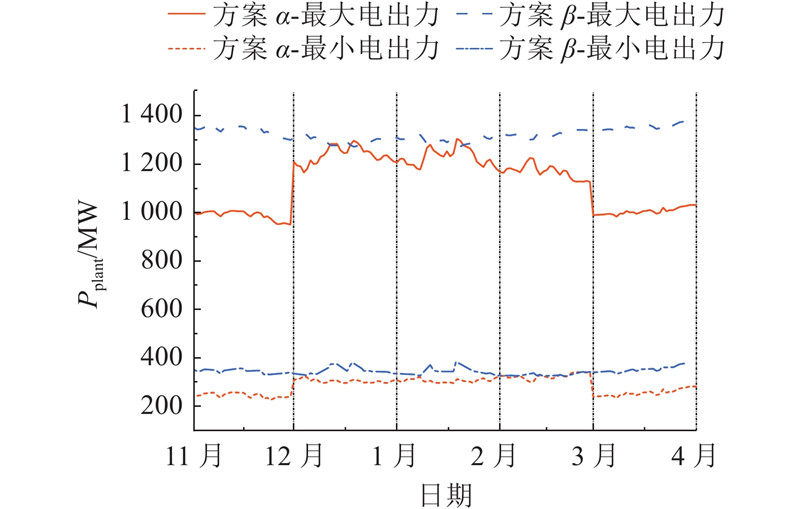
图 6
图 6 不同运行方案下热电厂在供暖期的最大/最小电出力
Fig.6 Maximum/minimum power output of thermal power plant during heating season under different operating schemes
在供热中期,由于热负荷水平较高(约330~560 MW),2种方案下最大和最小出力相差不大,特别是在12月份和1月份. 相对而言,2月份的热负荷在12~2月中处于最低水平,运行方案β下该月的最大电出力更高一些.
3.3. 不同运行方案的全厂收益对比
3.3.1. 容量电费收益差分析
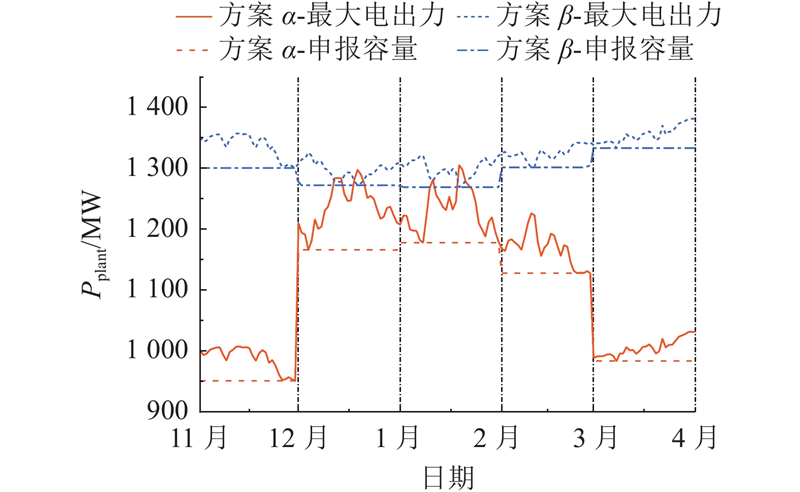
图 7
图 7 不同运行方案下热电厂的最大电出力及申报容量
Fig.7 Maximum power output and declared capacity of thermal power plant under different operating schemes
表 3 不同运行方案下的每月申报容量
Tab.3
| 方案 | |||||
| 11月 | 12月 | 1月 | 2月 | 3月 | |
| α | 951 | 1 166 | 1 178 | 1 128 | 983 |
| β | 1 301 | 1 272 | 1 269 | 1 302 | 1 333 |
表 4 不同运行方案下的每月容量电费
Tab.4
| 方案 | Rcap/万元 | ||||
| 11月 | 12月 | 1月 | 2月 | 3月 | |
| α | 781 | 990 | 1 001 | 865 | 862 |
| β | 1 069 | 1 081 | 1 078 | 999 | 1 169 |
3.3.2. 调峰电费差收益分析
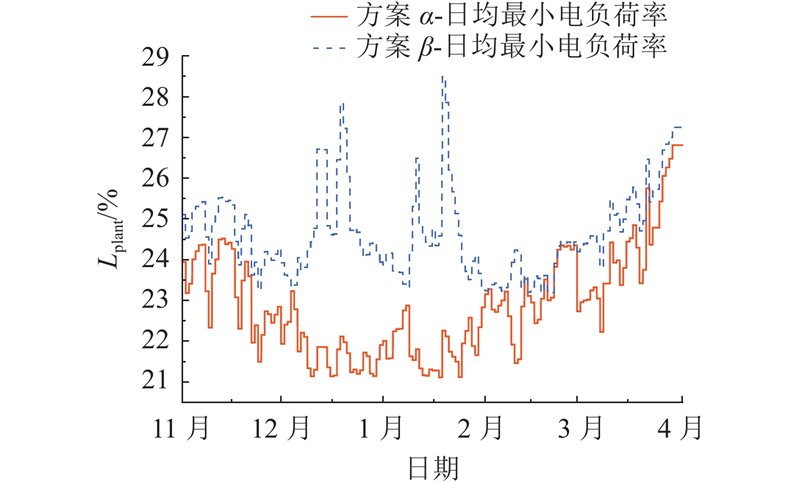
图 8
图 8 不同运行方案下热电厂的最小电负荷率
Fig.8 Minimum electrical load rate of thermal power plant under different operating schemes
基于上述最小负荷率结果,结合历史数据中供暖期各日各时段是否属于调峰时段的信息,可以估算得到整个供暖期2种运行方案下分布在深度调峰3个档位的调峰电量差,如表5所示. 其中,
表 5 不同运行方案下的每月调峰电量
Tab.5
| 方案 | |||
| 1档 | 2档 | 3档 | |
| α | 35 365 | 19 843 | 4 911 |
| β | 39 123 | 21 676 | 3 137 |
| α–β | –3 758 | –1 833 | 1 774 |
3.3.3. 不同运行方案下的供热成本分析
表 6 不同运行方案下每台机组每月承担的供热量
Tab.6
| 方案 | 机组 | Qunit/(104 GJ) | ||||
| 11月 | 12月 | 1月 | 2月 | 3月 | ||
| α | 1# | — | 104.1 | 100.5 | 62.5 | — |
| α | 2# | 31.2 | 9.6 | 9.6 | 8.7 | 24.0 |
| α | 3# | 20.8 | 6.4 | 6.4 | 5.8 | 16.0 |
| α | 4# | 20.8 | 6.4 | 6.4 | 5.8 | 16.0 |
| β | 1# | — | — | — | — | — |
| β | 2# | 31.2 | 54.2 | 52.7 | 35.5 | 24.0 |
| β | 3# | 20.8 | 36.2 | 35.1 | 23.7 | 16.0 |
| β | 4# | 20.8 | 36.2 | 35.1 | 23.7 | 16.0 |
表 7 不同运行方案下每台机组每月的单位供热煤耗率
Tab.7
| 方案 | 机组 | Φunit/(kg·GJ−1) | ||||
| 11月 | 12月 | 1月 | 2月 | 3月 | ||
| α | 1# | — | 11.6 | 11.4 | 8.5 | — |
| α | 2# | 17.1 | 17.0 | 17.0 | 17.0 | 17.0 |
| α | 3# | 16.8 | 16.7 | 16.6 | 16.7 | 16.7 |
| α | 4# | 17.4 | 17.4 | 17.4 | 17.4 | 17.4 |
| β | 1# | — | — | — | — | — |
| β | 2# | 17.1 | 17.1 | 17.1 | 17.1 | 17.1 |
| β | 3# | 16.8 | 16.8 | 16.7 | 16.8 | 16.7 |
| β | 4# | 17.4 | 17.4 | 17.4 | 17.4 | 17.4 |
表 8 不同运行方案下的每月供热成本
Tab.8
| 方案 | Rcoal/万元 | ||||
| 11月 | 12月 | 1月 | 2月 | 3月 | |
| α | |||||
| β | |||||
| α–β | 0 | −684 | −678 | −642 | 0 |
3.3.4. 不同运行方案下的全厂收益差分析
综上,可以得到2种运行方案下热电厂在整个供暖期的容量电费收益差
3.4. 不同热负荷需求下的收益与成本差分析
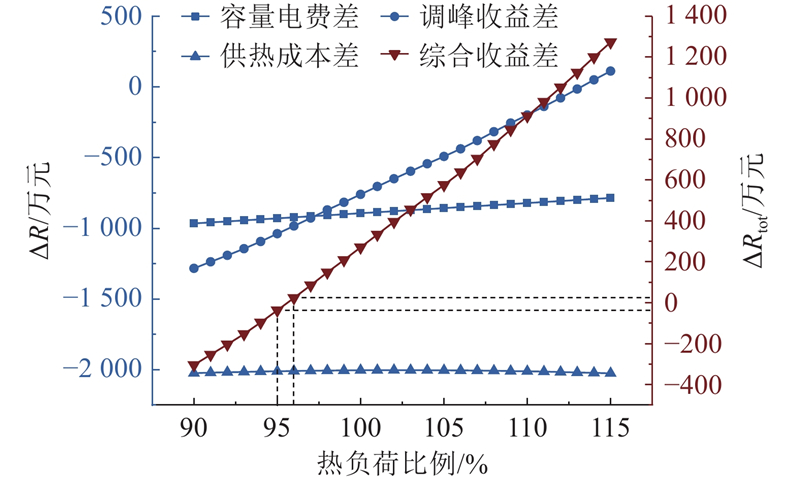
根据上述分析,热负荷是影响机组运行灵活性和节煤效果的主要参数. 因此,在考虑热电厂现有加热器数量及其额定参数的基础上,计算α、β这2种运行方案下,当热负荷从当前热负荷的90%提高到115%时,运行方案α、β间的各项经济效益指标的差值(
图 9
图 9 不同热负荷需求下2种运行方案的热电厂成本与收益差
Fig.9 Differences in costs and benefits of thermal power plant between two operating schemes under different heat load demands
从图9中可以看出,当热负荷需求低于95%时,2种方案的综合收益差为负值,即方案β相比于方案α能够获得更高的综合收益. 但是随着热电厂承担的热负荷继续增加,相较于方案β,热电厂在方案α下运行时能够获得更多的收益. 热负荷需求每增加1%,综合收益差增加约50~70万元.
综上所述,热电厂在不同热负荷条件下,需要采用不同的运行方案,以获得更高的综合收益. 当热负荷较高时,应优先采用方案α,利用高背压机组供热的低能耗特性来获得更可观的综合收益;当热负荷较低时,应采用方案β,以确保热电厂的运行灵活性,更有效地响应市场需求变化,从而获得更可观的综合收益.
4. 结 论
在容量电价机制的新背景下,综合考虑供热机组的运行特性、容量收益、深度调峰收益、供热成本以及高背压机组更换转子的成本,提出用于计算和比较热电厂在不同运行方案下经济效益的模型. 理论分析和算例分析结果表明:
(1)热电厂的整体电出力上、下限受热负荷变化的影响,并与运行方案的选择相关. 整体而言,高背压机组和抽凝机组具有一定的互补性. 选择高背压机组和抽凝机组联合运行的方案既能够保证一定的运行灵活性,又可以提高运行效率,从而在供暖期获得更高的综合收益.
(2)热电厂在不同运行方案下可以获得的综合收益与供暖期热负荷需求紧密相关,且存在临界值. 当热负荷超过临界值时,高背压模式供热的低能耗特性带来的节煤效益更显著,应优先采用高背压机组和抽凝机组联合运行的方案;当热负荷低于临界值时,高背压模式供热的节煤效益低于纯凝模式带来的灵活性效益,应采用纯凝机组和抽凝机组联合运行的方案.
(3)构建的模型适用于含有不同类型供热机组的热电厂,能够计算不同运行方案下的经济效益,辅助热电厂在供暖期前选择合适的运行方案,为热电厂的生产运行部门提供了决策参考,为热电厂在容量电价的新背景下获得更好的收益提供了理论依据.
参考文献
基于能源转型的中国特色电力市场建设的分析与思考
[J].
Analysis and reflection on the marketization construction of electric power with Chinese characteristics based on energy transformation
[J].
大型汽轮机供热改造方案研究
[J].DOI:10.3969/j.issn.1001-5884.2016.03.011 [本文引用: 1]
Research of heating retrofitting schemes for large steam turbine
[J].DOI:10.3969/j.issn.1001-5884.2016.03.011 [本文引用: 1]
高背压供热汽轮机低压转子模态分析
[J].DOI:10.3969/j.issn.1001-5884.2019.03.002 [本文引用: 1]
Modal analysis of low pressure rotor of high back pressure heating turbine
[J].DOI:10.3969/j.issn.1001-5884.2019.03.002 [本文引用: 1]
高参数大流量供热改造汽轮机推力系统控制研究
[J].DOI:10.3969/j.issn.1001-5884.2022.03.006 [本文引用: 1]
Research on thrust system control of steam turbine for high parameter and large flow heating transformation
[J].DOI:10.3969/j.issn.1001-5884.2022.03.006 [本文引用: 1]
直接空冷机组高背压供热技术经济性分析
[J].DOI:10.3969/j.issn.1001-5884.2014.03.014 [本文引用: 2]
The economy analysis of the high back pressure heating technology on direct air-colled unit
[J].DOI:10.3969/j.issn.1001-5884.2014.03.014 [本文引用: 2]
高背压供热改造关键技术及经济性评价探讨
[J].DOI:10.3969/j.issn.1001-5884.2016.02.016 [本文引用: 1]
The key technology and economic research for high-back pressure heat-supply transformation
[J].DOI:10.3969/j.issn.1001-5884.2016.02.016 [本文引用: 1]
300 MW机组高背压供热改造方案及试验分析
[J].
Reconstruction scheme and test analysis for heating supply with high back pressure of a 300 MW unit
[J].
高背压-抽凝机组耦合运行优化技术对深度调峰性能影响及经济性分析
[J].DOI:10.3969/j.issn.1001-5884.2020.04.017 [本文引用: 1]
Effect of coupling operation optimization technology of high back pressure-condensing cogeneration unit on peak regulation performance and economic analysis
[J].DOI:10.3969/j.issn.1001-5884.2020.04.017 [本文引用: 1]
高背压双抽热电联产机组联合运行特性及负荷分配
[J].DOI:10.11930/j.issn.1004-9649.202203078
Operation characteristics and load distribution of CHP units with extraction-condensate and extraction-high back pressure mode
[J].DOI:10.11930/j.issn.1004-9649.202203078
基于PC-GWO的高背压抽凝热电联供系统负荷优化研究
[J].
Research on load optimization of high backpressure extraction CHP units based on PC-GWO
[J].
双机联调抽汽-高背压联合供热㶲分析与优化
[J].
Exergy analysis and optimization of steam extraction-high back pressure combined heating for dual cogeneration units
[J].
大型汽轮机组高背压供热改造适用性分析
[J].
Applicability analysis of high back-pressure heating retrofit for large-scale steam turbine unit
[J].
高背压抽凝供热机组不同供热期运行背压调整优化研究
[J].
Optimization study on the adjustment of back pressure for the operation of high back pressure pumped condensing heating units in different heating periods
[J].
基于单耗理论的抽汽耦合高背压供热优化
[J].DOI:10.11930/j.issn.1004-9649.201911007
Optimization of steam extraction combined high back pressure heating based on specific consumption theory
[J].DOI:10.11930/j.issn.1004-9649.201911007
质–量并行调节下直接空冷高背压供热机组弹性运行与优化
[J].
Flexible operation and optimization of direct air-cooled high pressure heat supply power units in quality-volume regulation
[J].
300 MW汽轮机供热改造双低压转子互换技术应用
[J].
Application of double LP rotor interchangeable technology for heating improving in 300 MW steam turbines
[J].
计及灵活性提升的热电厂日前市场竞价策略
[J].
Bidding strategy of day-ahead market for combined heat and power plant considering flexibility improvement
[J].
300 MW机组厂级供热优化调度方式及性能分析
[J].DOI:10.3969/j.issn.1001-5884.2023.02.017 [本文引用: 1]
Heating supply optimization and performance analysis with plant-level for 300 MW cogeneration unit
[J].DOI:10.3969/j.issn.1001-5884.2023.02.017 [本文引用: 1]
热电联产机组热电成本分摊理论综述
[J].DOI:10.3969/j.issn.1004-7948.2012.08.003 [本文引用: 1]
Summary of thermoelectric cost-sharing theory of cogeneration units
[J].DOI:10.3969/j.issn.1004-7948.2012.08.003 [本文引用: 1]