光伏阵列、储能单元、DC/DC变换器及变流器作为光伏混合储能系统的主要成分[8-9],经直流母线耦合后汇入交流电网. 光储系统具有非线性、多变量、强耦合等特点[10],传统线性控制策略难以满足其控制需求,因此研究者针对构网型变流器的控制策略展开了深入研究. 众多方案中,自抗扰控制(active disturbance rejection control, ADRC)因其优异的抗扰能力、不依赖精确数学模型等优势备受关注. 王新菊等[11]将自抗扰控制和模型预测算法相结合,降低了双重化PWM整流器系统的网侧电流谐波,但是模型预测计算量大,不适用于快速变化系统. 王舒等[12]将角加速率自适应前馈控制与自抗扰控制相结合,提高了磁悬浮系统的抗扰能力,但是自适应控制的实现较为复杂,对传感器和算力要求较高. 谭草等[13]针对非线性干扰下永磁直线电机的响应恶化问题,提出深度模糊滑模-自抗扰控制,提高了直线电机的控制精度与响应速度,但是深度神经网络依赖于高性能算力,训练成本较高. 上述复合控制策略的参数整定复杂,计算量大,而滑模控制(sliding mode control, SMC)因物理实现简单、鲁棒性强,尤其适用于非线性系统,在高超声速飞行器[14]、永磁同步电机[15]、无人机轨迹跟踪[16]等领域得到了广泛研究. 皇金锋等[17]针对光储直流微网的母线电压波动及功率失稳问题,提出基于有限时间观测器的互补滑模控制策略,提升了光储系统的动态性能及抗扰能力. 杨玉杰等[18]针对自动厚度控制系统的鲁棒稳定性问题,基于拟连续高阶滑模控制方法,设计厚度控制器,减小了系统抖振. 沈艳霞等[19]提出永磁同步直线电机无模型控制策略,设计超螺旋滑模观测器,对模型未知量进行辨识和补偿,改善了电机的动态响应性能. 然而,由于SMC中控制信号的高频切换,输出信号会出现振荡,如何有效抑制抖振仍然是关键挑战.
针对上述问题,提出基于拟连续算法的改进滑模自抗扰控制策略,并将其应用于光伏混合储能变流器(photovoltaic hybrid power conversion system, PV-HPCS)中. 引入前馈误差系统,设计高阶超螺旋滑模观测器(higher-order super-twisting sliding mode observer, HO-STSMO),对系统状态量及内外总扰动进行观测估计;在控制器部分,采用双滑模切换控制律,引入二阶拟连续积分终端滑模控制器(quasi-continuous integrating terminal sliding mode controller, QC-ITSMC)作为反馈控制器,并设计改进指数趋近律,与拟连续算法配合工作,有效改善了传统SMC中的抖振问题.
1. 光伏混合储能变流器拓扑分析
光伏混合储能系统主要由光伏阵列、储能单元、双向DC/DC变换器、变流器及配电网等单元构成,核心环节为前级变换器和后级变流器,负责将光伏阵列所产的直流电转换为与电网同频兼容的交流电,并对储能单元进行充放电控制.
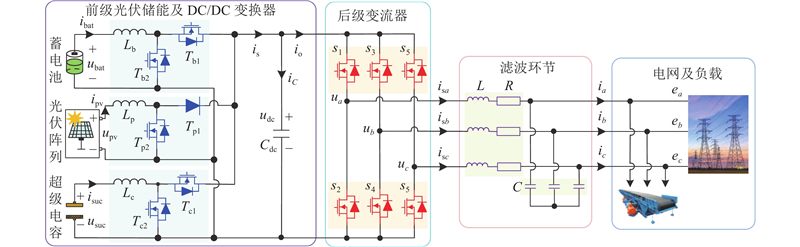
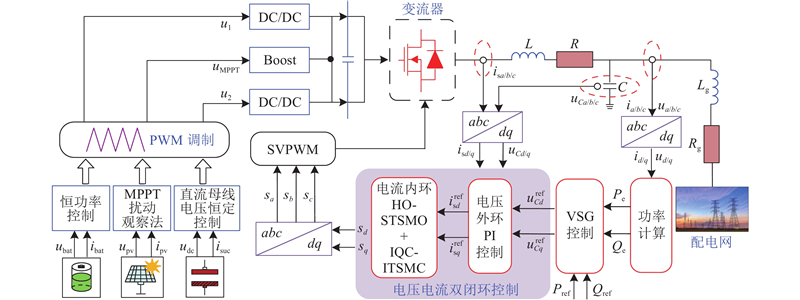
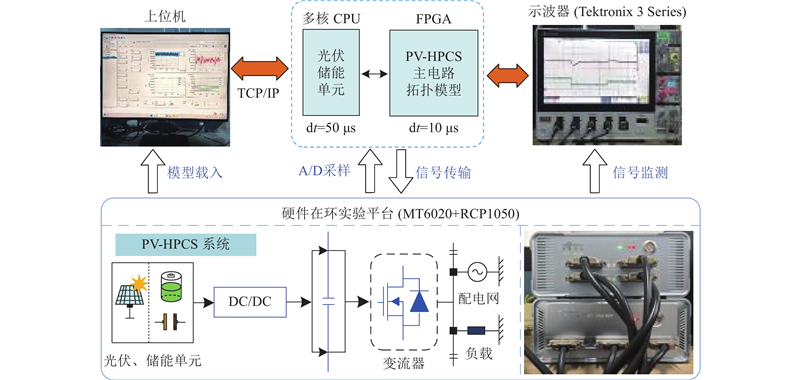
PV-HPCS结构如图1所示. 其中,ua、ub、uc和isa、isb、isc为变流器交流侧三相电压、电流,ia、ib、ic为滤波后电流,ea、eb、ec为电网电压,udc、iC为母线电压、电流,L、C为滤波电感、电容,R为线路等效电阻,s1~s6为变流器上、下桥臂的6个开关管,is为直流侧输出电流,io为变流器输入电流,Cdc为稳压电容,ubat、usuc、upv和ibat、isuc、ipv分别为蓄电池、超级电容、光伏阵列两端的输出电压、电流,Tb1、Tb2与Tc1、Tc2为2对互补导通的开关管,Tp1、Tp2为光伏模块前级Boost变换器中的开关管. 假定电网电压波形对称且没有发生畸变,根据基尔霍夫定律,由图1可得光伏混合储能变流器在a、b、c三相静止坐标系下的数学模型:
图 1
图 1 光伏混合储能变流器主电路拓扑
Fig.1 Main circuit topology of photovoltaic hybrid power conversion system
式中:uCa、uCb、uCc为交流侧电容C两端电压,ska、skb、skc为三相桥臂开关管控制信号.
对式(1)进行Park变换,可得变流器在d-q旋转坐标系下的数学模型:
式中:ω为电网电压的角频率;ed、id、uCd、sd与eq、iq、uCq、sq分别为d、q轴的电网电压、电流、电容电压和开关函数.
前级DC/DC变换器状态方程为
式中:Lb、Lp、Lc分别为蓄电池组、光伏阵列、超级电容前级DC变换器侧的电感,D1、D2分别为开关管Tb1、Tc1的导通占空比,D3为开关管Tp2的关断占空比.
由上述模型可知,PV-HPCS具有多变量、非线性、强耦合的特性,传统线性控制策略难以达到理想的控制效果,因此提出改进滑模自抗扰控制策略,以提升光储变流器的工作性能.
2. 构网型VSG控制设计
VSG控制通过将同步机的数学模型嵌入控制算法,使静止的电力电子装置能够模拟旋转电机的行为. 通过调节变流器的输出电压和电流,实现对有功和无功功率的控制.
2.1. P-f调速控制器
根据牛顿第二定律,虚拟同步发电机的机械方程即转子运动方程可以表示为
式中:J为转动惯量,D为阻尼系数,Pm、Pe为机械功率、电磁功率,
为了模拟同步发电机的调频特性,在VSG控制中应用调速器,即P-f下垂特性:
式中:Pref为参考有功功率,kf为P-f下垂系数.
将式(5)代入式(4),并进行拉氏变换:
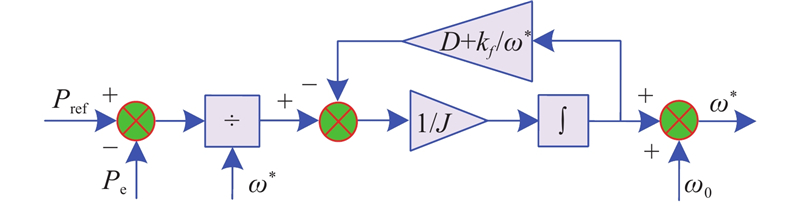
式中:s为拉氏变换中的复频域变量. 根据式(6),可得VSG机端电压的相位参考信息ω*. P-f调速控制框图如图2所示.
图 2
2.2. Q-E励磁控制器
同步发电机通过调节励磁来调节输出无功功率以及机端电压,同理,可以通过控制虚拟同步机的虚拟电势Em的幅值和相位来调节输出无功功率,以保证机端电压稳定. 因此,在VSG无功环中引入电压偏差来对系统无功功率进行调节. VSG无功功率和电压下垂特性如下:
式中:Q*为无功-电压下垂特性调节后的VSG输出无功功率,Qref为无功功率参考值,Un为机端电压有效值,Us为VSG实际输出电压,kQ为Q-E下垂系数.
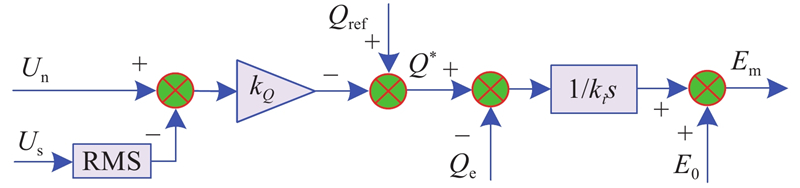
通过调节VSG输出电压幅值和相位,可以对系统无功指令进行跟踪,为光伏混合储能系统提供一定的无功支撑. 将Q*与电磁无功功率Qe进行比较,经过积分,最终可以得到虚拟电势Em的幅值. 控制框图如图3所示,其中,E0为空载电势,ki为积分系数.
图 3
3. 光储变流器控制设计
3.1. 变流器控制设计
VSG控制通常采用电压电流双闭环控制策略. 电压外环用于控制输出电压的幅值和相位,维持电网电压稳定;电流内环用于快速调节输出电流,以实现对有功和无功功率的精确控制. 对电流内环部分进行设计,具体内容如下.
3.1.1. 高阶超螺旋滑模观测器设计
为了提升观测器对系统状态量与集总扰动的观测精度及速度,基于前馈思想,对高阶超螺旋滑模观测器进行改良设计. 假设有如下二阶受控对象:
式中:x为系统状态,u(t)为控制输入,b为控制量增益,f(x,u)为系统中所有不确定项及未知扰动.
令
针对式(8)中的系统,可以构造如下HO-STSMO:
式中:e1为观测误差,z1、z2、z3为x1、x2、f(x,u)的估计值,
由于
由于实际工程中b值一般是未知的,为了简化控制器设计,将d、q轴电流耦合项和未建模部分视为集总扰动,分别用fd、fq表示. 对式(11)求导,并转换为二阶ADRC范式:
式中:bo为b的估计值.
针对上述系统取前馈误差信号
选取状态变量
针对式(15)所示的前馈误差系统,将d、q轴集总扰动fd、fq扩张为新的状态变量zd3、zq3,则可以分别对d、q轴观测器进行设计.
d、q轴高阶超螺旋滑模观测器设计如下:
式中:ed1、eq1为状态观测误差,zd1、zd2、zd3与zq1、zq2、zq3分别为xd1、xd2、fd与xq1、xq2、fq的估计值,φd1、φd2、φd3与φq1、φq2、φq3分别为d、q轴观测器增益. 双曲线函数F(ei)如下式所示:
式中:
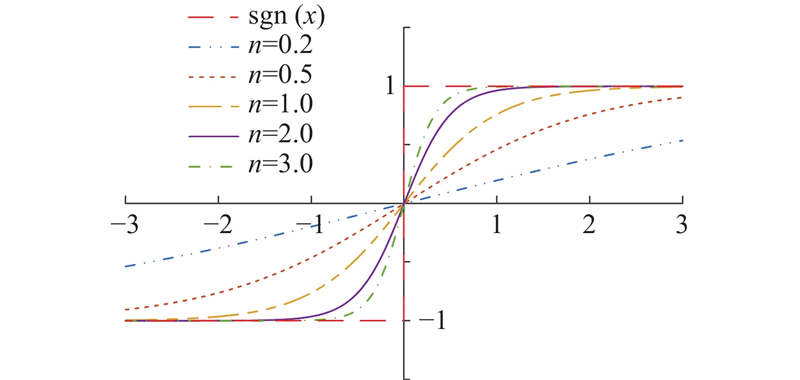
如图4所示,切换函数F(ei)连续且光滑,滑模面趋近至零点时振荡幅度降低,有效削弱了抖振现象.
图 4
图 4
双曲线函数
Fig.4 Comparison of hyperbolic function F(ei) with sgn (x)
3.1.2. 控制器设计
拟连续算法作为一种高阶滑模算法,能够产生连续的控制信号;ITSMC收敛速度快,可以保证系统在有限时间内收敛. 为了平抑抖振现象,提升系统鲁棒性,结合两者思想设计改进二阶拟连续积分终端滑模控制器(IQC-ITSMC).
令
式中:
式中:
式中:
对式(20)进行微分,并将式(15)代入:
由于系统在有限时间内收敛,根据等效控制理论,令
式(23)中滑模面
式中:
式中:
由式(25)可知,当系统远离滑模面时,上述算法可以提供连续控制信号,使系统实现无抖振控制;当系统状态达到并保持在预先设计的滑模面上时,算法出现零点,使得系统出现较大抖振. 因此,设计一种改进指数趋近律,作为滑模运动第二阶段的切换控制器.
传统指数趋近律为
针对传统指数趋近律的不足,设计新型改进指数趋近律:
式中:
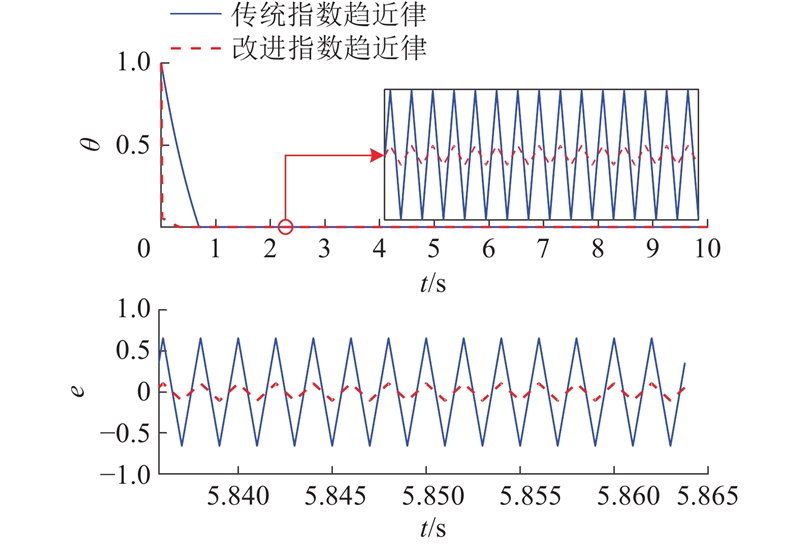
为了验证改进指数趋近律的可行性与优越性,保持滑模面参数α、β与指数项增益系数
图 5
图 5 滑模抖振与跟踪误差对比
Fig.5 Comparison of sliding mode chattering and tracking error
根据图5与式(26)可知,当系统运动状态远离滑模面,即θ→∞时,f(θ)→∞,系统收敛速度加快;当θ→0时,f(θ)→1,等速项增益系数
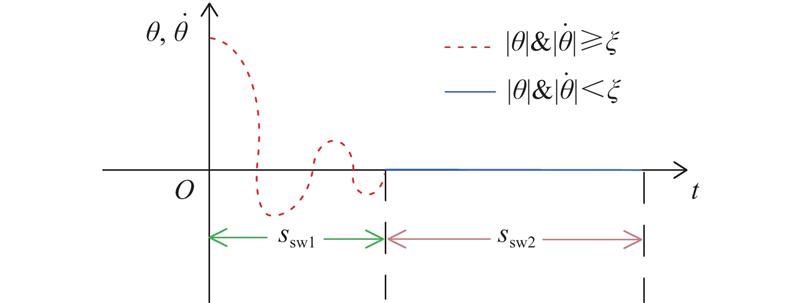
综上,系统切换控制器ssw可以设计为
式中:γ为切换项,保证切换控制律ssw1和ssw2在下述条件下进行工作状态的切换.
式中:
图 6
联立式(24)与式(28),可得光伏混合储能变流器系统的二阶拟连续滑模控制律:
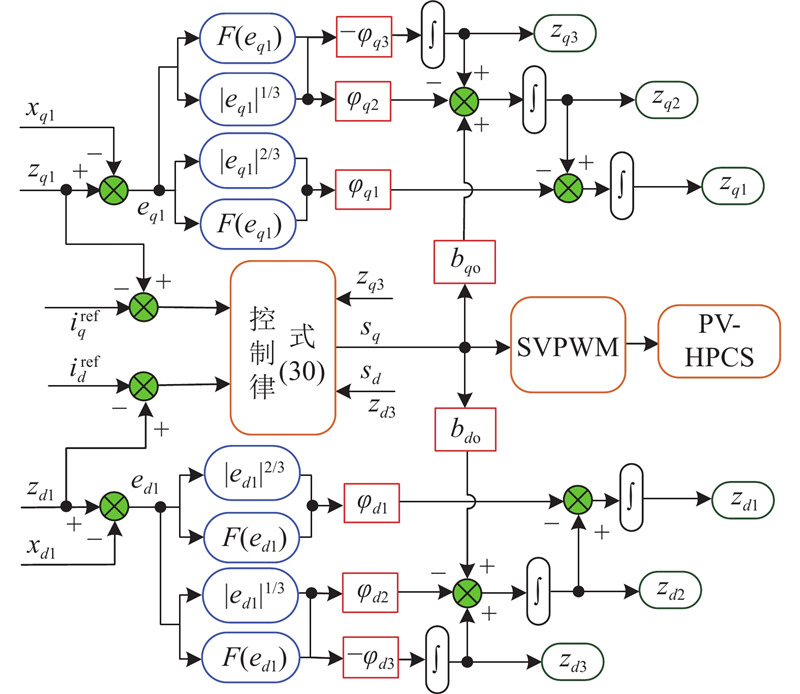
综上可得电流内环控制结构,如图7所示.
图 7
3.2. 前级DC变换器控制设计
为了平抑高、低频功率波动,维持母线电压稳定,对光伏储能模块前级DC/DC变换器进行有效控制至关重要. 本研究中,光伏单元采用最大功率点跟踪(MPPT)算法中的扰动观察法来指导Boost变换器工作;为了减少充放电能耗,蓄电池变换器采用恒功率控制策略.
超级电容由于功率密度高,充放电响应快,可以迅速响应母线电压波动,因此对其变换器部分采用母线电压恒定控制策略,设计过程如下.
对式(3)求导,转换为二阶自抗扰形式:
式中:bsc为控制量增益,u2为变换器开关管控制信号,fsc为系统内外集总扰动.
选取状态量
式中:e2为直流母线电压状态的观测误差,z1、z2、z3为x1、x2、fsc的估计值,φsc1、φsc2、φsc3为增益系数.
选取如下线性滑模面:
式中:
令系统误差
式中:u2为开关管Tc1、Tc2的控制信号.
综上可得系统整体控制结构,如图8所示,其中u1为Tb1、Tb2的控制信号,uMPPT为Tp2的导通占空比.
图 8
图 8 光伏混合储能系统控制结构图
Fig.8 Control structure diagram of photovoltaic hybrid power conversion system
4. 稳定性分析
4.1. 观测器稳定性分析
根据式(16),观测器可以等效为1个二阶微分器[20]. 状态估计误差可以定义为
式中:
当微分器收敛至0时,式(33)中第3项为0,跟踪项zd3可以对集总扰动fd进行精确追踪:
综上,由式(16)和(37)可知,跟踪项zd3为连续值,其估计误差可由观测器直接估计,因此理论上观测器可以实现对状态量的精确跟踪,能够在有限时间收敛于实际状态.
4.2. 控制器稳定性分析
令辅助变量
式中:M和
当
对式(41)进行微分,可得
将拟连续切换控制律ssw1代入式(42):
为了保证控制器稳定,Lyapunov函数须满足
当l满足上述条件时
5. 仿真及实验验证
5.1. 仿真分析
表 1 电路模型参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| Lb、Lp、Lc/mH | 6 | fn/Hz | 50 | |
| Cdc/mF | 20 | ω0/(rad·s−1) | 100π | |
| udc/V | 1 500 | L/mH | 4 | |
| ug/V | 380 | C/μF | 10 | |
| Lg/mH | 1.2 | R/Ω | 0.05 |
表 2 控制器参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| J/(kg·m2) | 3.2 | κ | 4 | |
| D/(N·s·m−1) | 47.75 | λ | 20 | |
| kf/(W·Hz−1) | 25.46 | 15 | ||
| kQ/(var·V−1) | 1 154.7 | 50 | ||
| n | 3 | ld | 5 | |
| bdo、bqo | 22 | lq | 300 | |
| ωdo、ωqo/(rad·s−1) | 300 | η | 33 | |
| ξ | 0.1 | 0.1 |
5.1.1. 直流母线电压动态响应
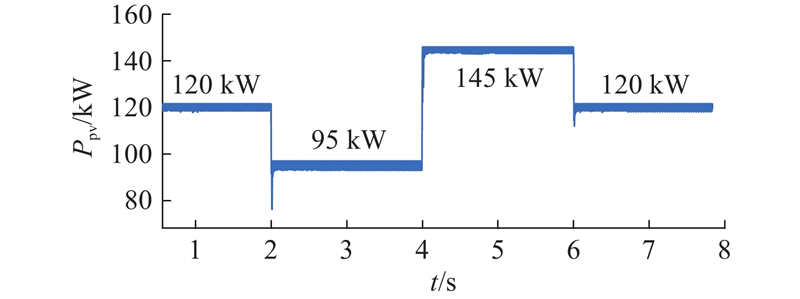
在并网状态下,为了对比光照强度发生变化时系统的暂态性能,在仿真模型中设置相应光伏变化. 光照强度E变化时对应的光伏输出功率Ppv如图9所示.
图 9
图 9 光照强度变化时的光伏电源输出功率
Fig.9 Output power of photovoltaic power supply under varying solar irradiance
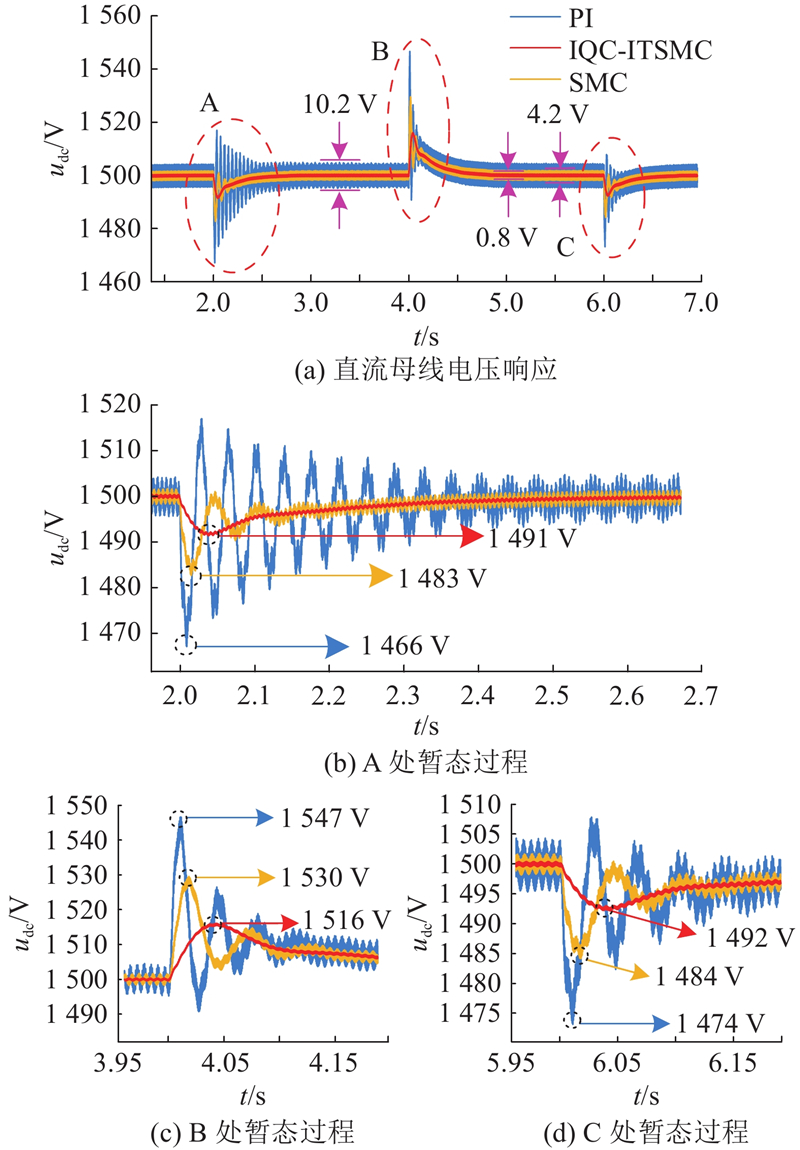
在不同控制策略下母线电压的响应情况如图10所示. 设置温度为25 ℃;初始光照强度为1 000 W/m2,2 s时降为800 W/m2,4 s时升至1 200 W/m2,6 s时恢复至初始光照;变流器输出功率为150 kW.
图 10
图 10 光伏波动下直流母线电压响应
Fig.10 Response of DC bus voltage under photovoltaic fluctuation
由图10可知,当光伏功率发生波动时,采用3种控制策略均能实现对系统状态的有效跟踪. 但是PI控制策略在启动阶段以及光伏功率发生跳变时,出现明显的超调现象;改进控制策略有效抑制了超调问题,同时将纹波脉动抑制在了0.8 V左右,使系统更快地恢复至稳定运行状态. 在3次暂态过程中,无论面对光伏功率跌落或是上升的情况,在保证收敛速度的前提下,改进策略在减小超调量、平抑纹波方面的性能均为最佳,传统SMC策略次之,PI控制效果最差.
5.1.2. 输出功率动态响应
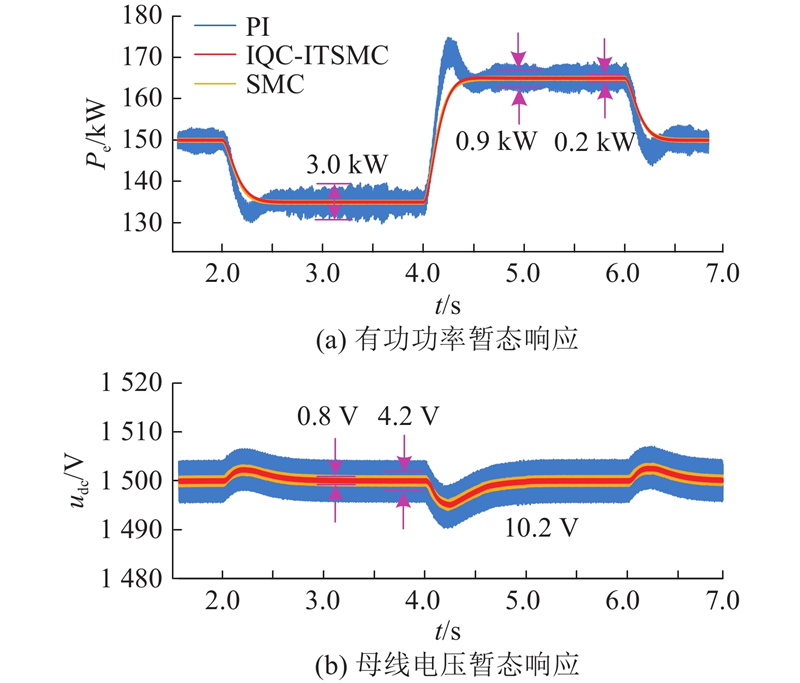
为了验证负载投切对系统动态性能的影响,通过设置相应有功指令突变对系统进行模拟. 保持光照强度为1 000 W/m2,光伏输出功率为120 kW,设置变流器输出的有功指令初始值为150 kW,2 s时降为135 kW,4 s时升至165 kW,6 s时恢复至初始指令. 由于光伏混合储能系统前、后级变换器经直流母线相耦合,有功指令的变化会引起母线电压波动. 在不同控制策略下系统的响应情况如图11所示.
图 11
图 11 有功功率指令突变时系统暂态响应
Fig.11 Transient response of system to sudden changes in active power command
因此,在有功指令突变过程中,改进控制策略的抗干扰能力更强,能够有效限制功率超调,抑制功率及母线电压脉动,保证系统更快、更稳定地运行在设定状态,从而有效提升变流器的控制性能.
5.2. 实验验证
图 12
5.2.1. 光伏波动下直流母线电压暂态实验
图 13
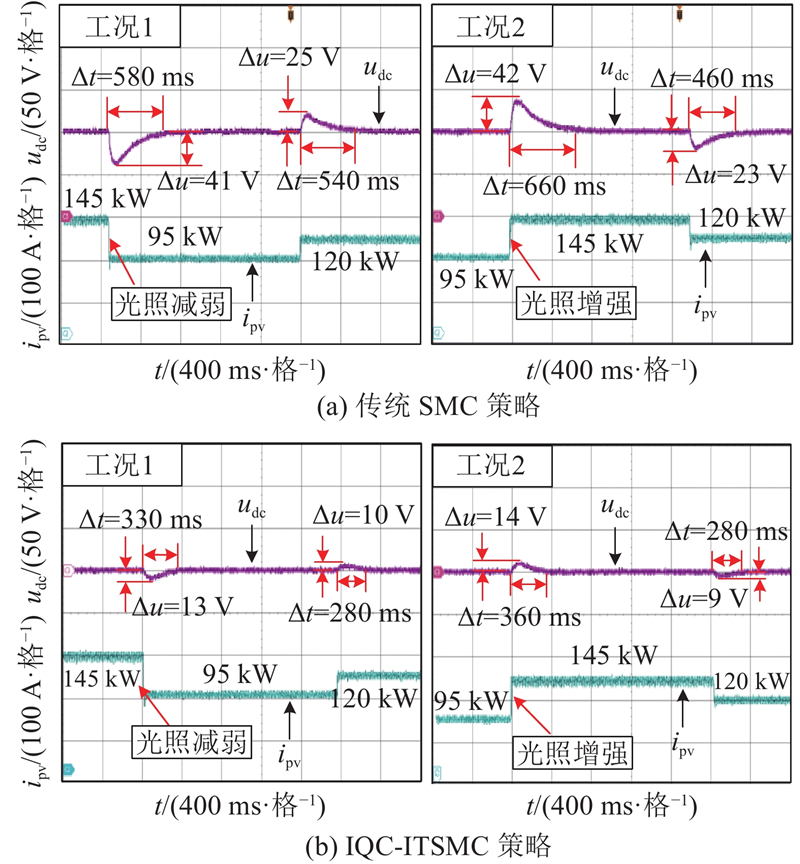
图 13 光伏波动下母线电压实验波形
Fig.13 Experimental waveforms of bus voltage under photovoltaic fluctuation
表 3 光伏波动下母线电压暂态性能对比
Tab.3
| E/(W·m−2) | 控制策略 | Δu/V | Δt/ms | ||
| 1 200→800→1 000 (工况1) | 传统SMC | 41 | 25 | 580 | 540 |
| IQC-ITSMC | 13 | 10 | 330 | 280 | |
| 800→1 200→1 000 (工况2) | 传统SMC | 42 | 23 | 660 | 460 |
| IQC-ITSMC | 14 | 9 | 360 | 280 | |
工况1:模拟光照强度突降状况,光照强度按照1 200→800→1 000 W/m2指令切换;工况2:模拟光照强度突增状况,光照强度按照800→1 200→1 000 W/m2指令切换.
5.2.2. 有功功率指令突变暂态实验
图 14
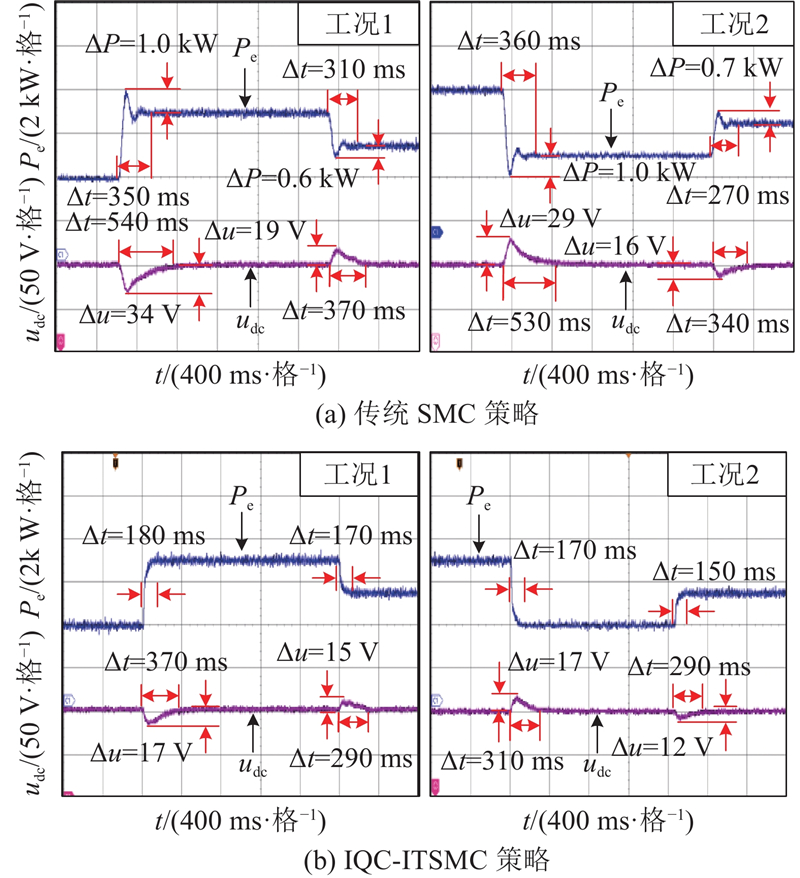
图 14 功率指令突变时系统响应实验波形
Fig.14 Experimental waveforms of system response to abrupt power command changes
表 4 有功指令突变时系统有功功率响应暂态性能对比
Tab.4
| Pref/kW | 控制策略 | ΔP/kW | Δt/ms | ||
| 135→165→150 (工况1) | 传统SMC | 1 | 0.6 | 350 | 310 |
| IQC-ITSMC | — | — | 180 | 170 | |
| 165→135→150 (工况2) | 传统SMC | 1 | 0.7 | 360 | 270 |
| IQC-ITSMC | — | — | 170 | 150 | |
工况1:模拟负载加重,有功功率按照135→165→150 kW指令切换;工况2:模拟负载减轻,有功功率按照165→135→150 kW指令切换.
当有功指令突变时,在传统SMC控制下,变流器输出有功超调量(ΔP)以及直流母线电压超调量(Δu)均较大,且过渡时间较长;改进控制策略下,系统有功功率暂态超调量几乎为0,且暂态时间较短,母线电压超调量及暂态时间均显著减小. 因此,在有功指令突变时,改进控制策略可以有效抑制超调,提升系统暂态性能,使系统更快地运行至稳定状态.
表 5 有功指令突变时系统电压响应暂态性能对比
Tab.5
| Pref/kW | 控制策略 | Δu/V | Δt/ms | ||
| 135→165→150 (工况1) | 传统SMC | 34 | 19 | 540 | 370 |
| IQC-ITSMC | 17 | 15 | 370 | 290 | |
| 165→135→150 (工况2) | 传统SMC | 29 | 16 | 530 | 340 |
| IQC-ITSMC | 17 | 12 | 310 | 290 | |
通过上述不同工况下的实验结果可得,将本研究的控制策略应用于光伏混合储能变流器时,改善了变流器直流母线电压暂态响应能力,抑制了功率波动及超调问题,有效提升了光伏并网系统的暂态性能,提升了系统稳定性.
6. 结 论
针对构网型储能系统网侧功率及母线电压波动较大的问题,基于VSG技术,设计基于拟连续算法的改进滑模自抗扰控制策略,以提升光伏混合储能变流器的动态性能. 通过理论分析、仿真实验验证,得到以下结论.
(1)基于前馈思想对HO-STSMO进行改良设计,提升了观测精度与速度,从而能够应对不同光照条件、负载变化等复杂工况,可以更精准地对系统功率及电压扰动进行跟踪补偿,且响应速度更快.
(2)相较于PI控制和传统SMC策略, IQC-ITSMC控制策略采用双滑模切换控制器,可以在PV-HPCS运行时提供连续平滑的控制信号,有效抑制了功率与母线电压的波动及超调问题,降低了因电压波动而导致的系统故障风险. 同时,稳定的电压环境可以减少电力系统设备应力,延长设备寿命,降低维护成本,并增强系统运行稳定性.
(3)后续研究中,将在现有工作的基础上,对构网型混合储能系统工作于不平衡电网下的控制策略展开进一步研究,以避免变流器运行时出现振荡以及输出电压、电流质量下降的问题.
参考文献
面向同步稳定性的电力电子并网变流器分析与控制研究综述
[J].
A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters
[J].
高比例电力电子电力系统强度的定义、分类及分析方法
[J].
Definition, classification, and analysis method of the strength of power system integrated with high penetration of power electronics
[J].
“双碳”目标下我国能源电力系统发展趋势分析: 绿电替代与绿氢替代
[J].
Analysis of the development trend of China’s energy and power system under the dual carbon target: green electricity substitution and green hydrogen substitution
[J].
“双高”配电系统的挑战与应对措施探讨
[J].
Discussion on challenges and countermeasures of “double high” power distribution system
[J].
基于滑模自抗扰的储能变流器控制策略
[J].
Control strategy of power conversion system based on sliding mode active disturbance rejection control
[J].
基于有功微分补偿与虚拟惯量自适应的光储VSG控制策略
[J].
Control strategy for a PV energy storage VSG based on active power differential compensation and virtual inertia adaptive strategy
[J].
Factors influencing the efficiency of photovoltaic system
[J].DOI:10.1016/j.rser.2018.11.012 [本文引用: 1]
光储一体化变流器改进滑模自抗扰控制
[J].
Improved sliding mode active disturbance rejection control strategy for PV-storage integrated converter
[J].
A novel cooperative control for SMES/battery hybrid energy storage in PV grid-connected system
[J].
双重化PWM整流器自抗扰模型预测直接功率控制
[J].
Active disturbance rejection control-based model predictive direct power control for dual PWM rectifiers
[J].
基于复合控制的磁悬浮CMG动框架效应抑制
[J].
Composite control method for gimbal excitation effect suppression of magnetically suspended CMGs
[J].
直驱式永磁直线电机深度模糊滑模-自抗扰控制
[J].DOI:10.7652/xjtuxb202301018 [本文引用: 1]
Depth fuzzy sliding-mode active disturbance rejection control method of permanent magnet linear motor for direct drive system
[J].DOI:10.7652/xjtuxb202301018 [本文引用: 1]
一种高超声速飞行器固定时间滑模控制方法
[J].DOI:10.3873/j.issn.1000-1328.2024.04.008 [本文引用: 1]
A fixed-time sliding-mode control method for hypersonic vehicle
[J].DOI:10.3873/j.issn.1000-1328.2024.04.008 [本文引用: 1]
一种永磁同步电机无模型超螺旋快速终端滑模控制方法
[J].
A model-free super-twisting fast terminal sliding mode control method for a permanent magnet synchronous motor
[J].
基于NLESO的倾转动力无人机垂直起降模态轨迹跟踪控制
[J].DOI:10.3969/j.issn.1000-2758.2023.01.001 [本文引用: 1]
Trajectory tracking control of tilt-propulsion UAV vertical take-off and landing mode based on NLESO
[J].DOI:10.3969/j.issn.1000-2758.2023.01.001 [本文引用: 1]
基于有限时间观测器的光储系统母线电压互补滑模控制
[J].
Finite-time observer-based sliding mode control of bus voltage complementarity in optical storage systems
[J].
基于拟连续高阶滑模方法的AGC系统控制
[J].DOI:10.3969/j.issn.1000-386x.2019.09.024 [本文引用: 1]
Control of AGC system based on quasi-continuous high-order sliding mode method
[J].DOI:10.3969/j.issn.1000-386x.2019.09.024 [本文引用: 1]
基于超螺旋滑模观测器的永磁同步直线电机无模型控制
[J].
Model-free control of a permanent magnet linear synchronous motor based on a super-twisting sliding mode observer
[J].
Output feedback tracking control of uncertain robot manipulators via higher-order sliding-mode observer and fuzzy compensator
[J].DOI:10.1007/s12206-013-0636-3 [本文引用: 1]
Implementation of super-twisting control: super-twisting and higher order sliding-mode observer-based approaches
[J].DOI:10.1109/TIE.2016.2523913 [本文引用: 1]