目前,PMSM无位置传感器控制策略中位置估算算法主要分为2类:一类是基于反电动势的位置自检测的位置估测算法,另一类是适用于零低速域下的高频电压注入位置估算算法[4],前者在中高速域下有较好的估算效果,但是在零低速域时,由于反电动势过小,难以实现准确估算[5]. 后者采用高频电压注入的方法,使得凸极追踪不依赖于电机反电动势和具体参数信息,在零低速域下仍能保持较好的估算效果[6]. 根据注入方式的不同,高频电压注入可分为2类:在静止参考系下的旋转高频电压注入和在估计转子参考系下的脉振高频电压注入[7]. 相比于旋转高频电压注入,脉振高频电压注入对逆变器非线性和参数变化更具鲁棒性[8],另外脉振高频电压注入不仅适用于内置式永磁同步电机 (interior permanent magnet synchronous motor, IPMSM),也适用于表贴式永磁同步电机(surface-mounted permanent magnet synchronous motor, SPMSM),具有更好的通用性[9].
高频电压注入、位置误差信号的提取和转子位置估计是组成脉振高频电压注入的3个重要环节[10]. 传统脉振高频电压注入在位置误差信号的提取和转子位置估计环节上使用了带通滤波器(band pass filter, BPF)和低通滤波器(low pass filter, LPF)[11],由于这2种滤波器在处理信号的过程中产生了相位延迟,导致了电流环路和位置观测环带宽的降低,从而严重影响了系统位置估算精度和动态性能[12]. 为此,已有研究提出许多改进方法. Yang等[13] 使用无须使用低通滤波器的方波注入方法,提高电流环带宽,提升系统的动态性能. 但是,随着注入方波信号频率的上升,电机电感损耗和电流谐波都有所增大[14]. 周奇勋等[15]提出基于二阶广义积分器 (second order generalized integrator, SOGI)的新型电流基频信号提取策略,利用SOGI的滤波特性替换传统脉振高频电压注入使用的LPF和BPF,解决了两者产生的相位延迟问题. 但是,SOGI在面对直流分量和谐波畸变时存在振荡纹波,不利于对转子的位置估计[16]. 张开继等[17]提出利用滑动平均滤波算法解决电流环上LPF导致的延时问题. 但是,滑动平均算法复杂,不利于硬件实现[18]. 杜思宸等[19]利用可以降低滤波延时的二阶广义积分器实现了对高频位置信号的提取. 但是,并未给出二阶广义积分器的参数整定过程. 李东昇等[20]为了解决使用BPF和LPF导致相位偏移和位置估计误差大的问题, 提出级联SOGI和单频陷波器(single frequency notch filter, SFNF)的改进方法,但是,SOGI滤波特性耦合严重,参数整定困难. 针对降低传统脉振高频电压注入滤波器相位延迟对系统动态性能和位置估计精度的影响的问题,上述研究都取得了一定成果,但是,未能实现在兼顾滤波性能的同时增强系统动态性能、增加位置估算精度和减少硬件计算负担.
本研究基于三参数陷波器 (three parameter notch filter, TPNF)改进脉振高频电压注入无位置传感器控制,在分析传统脉振高频电压注入原理的基础上,给出LPF+BPF滤波策略导致系统观测精度低、动态性能差的原因;利用TPNF的陷波特性,保证对电流环中存在的高频信号的滤除,同时提高电流环带宽;采用四阶广义积分器提取含有位置信息的高频信号,克服传统位置信息提取处理策略产生的信号时延;通过MATLAB/Simulink仿真和电机实验,对所提策略的有效性进行验证.
1. 传统脉振高频电压注入法
1.1. 脉振高频电压注入法原理
PMSM在低速运行时,注入电压的频率远远高于转子电角速度,故可以忽略电压方程中含电角速度项和定子电阻压降,PMSM在
式中:h表示高频特征;ush、ish、Lsh(s为d、q)分别为
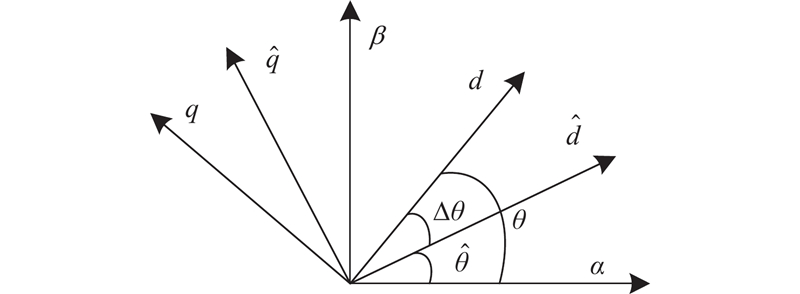
估计两相旋转坐标为
图 1
图 1 3个坐标系关系示意图
Fig.1 Schematic diagram of relationship between three coordinate systems
向估计坐标系d轴上注入高频正弦电压信号:
式中:Umh和 ωh分别为注入高频电压的幅值和角频率.
由式(1)、(2)得出
式中:
由式(3)可知,转子位置估计误差可从估计交轴高频电流分量
图 2
图 2 传统位置误差信号解调策略结构框图
Fig.2 Structure block diagram of conventional position error signal demodulation strategy
式中: ke为位置误差估计系数,ke=−Umh/(ωh(
当转子位置估计误差较小时,sin (2∆θ)≈2∆θ,此时
1.2. 传统脉振高频电压注入法存在的问题
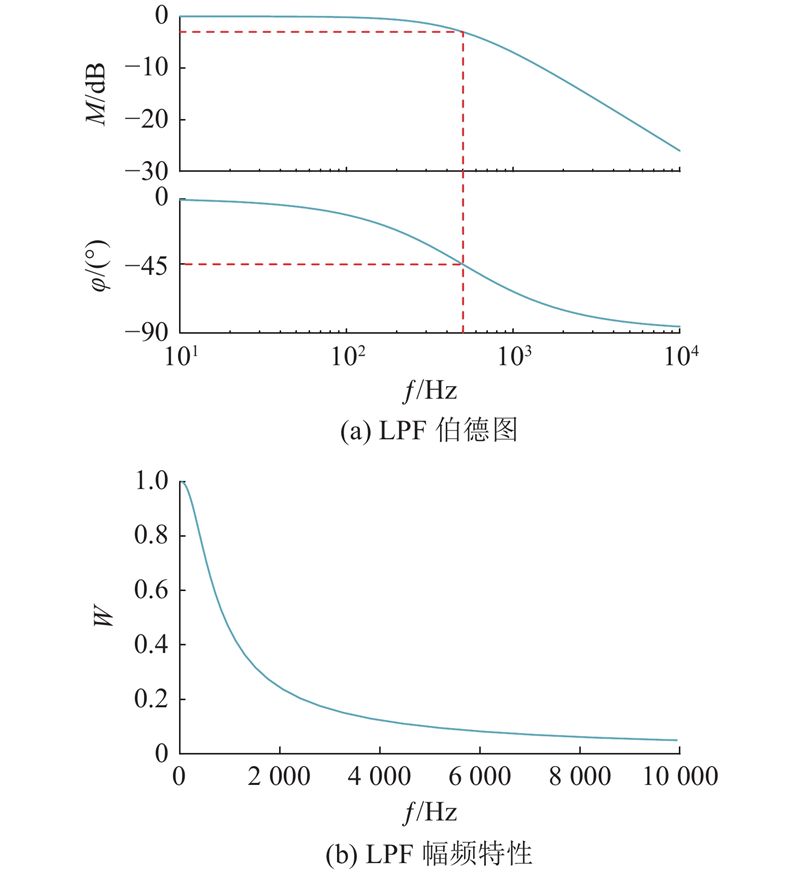
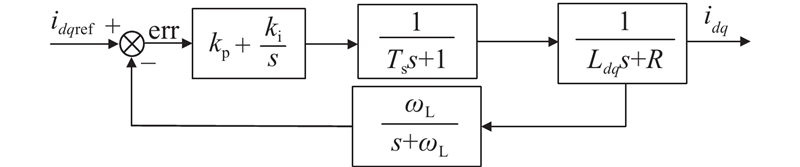
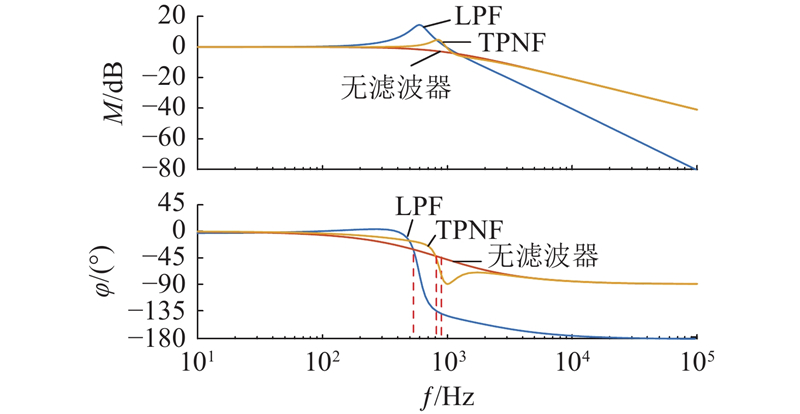
传统脉振高频电压注入法通过高频电压信号注入获取转子位置信息,因此,须采用LPF将注入的高频成分滤除,滤除后的基频电流用于完成电流环反馈. 然而,LPF的使用将不可避免地导致电流环上的反馈信号产生相位滞后,造成系统的延迟时间增加,降低电流环带宽,从而影响电流环的动态性能. 此外,LPF无法完全滤除注入的高频电压信号,导致
图 3
图 3 LPF的伯德图与幅频特性曲线
Fig.3 Bode plot and phase-frequency characteristic curve of LPF
图 4
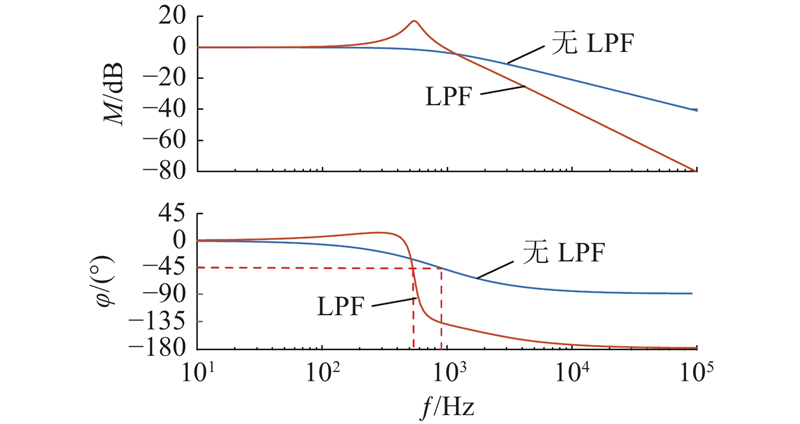
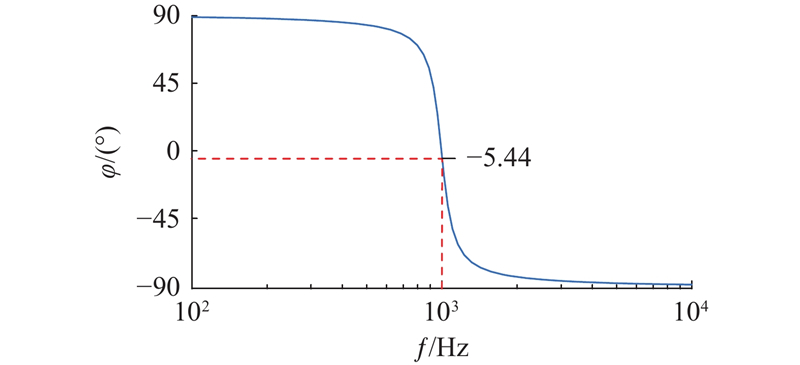
设定电流环带宽ωc为900 Hz,LPF截止频率为500 Hz,分别得到系统有、无LPF时的电流环闭环传递函数伯德图,如图5所示. 可以看出,加入LPF后电流环带宽由原来的900 Hz降到528 Hz. 此外,在传统脉振高频电压注入法中,速度环的转子位置误差信息提取环节使用了BPF和LPF. BPF的作用是提取含有位置信息的高频信号. 但是,BPF的使用与LPF一样都会产生相位延迟的问题,会影响速度环的带宽,造成系统的动态性能下降. 如图6所示为提取频率为1 000 Hz时,BPF通带设置为900~1 100 Hz的幅频特性曲线. 可以看出,BPF在提取频率处产生了约5.44°的相位延迟.由上述分析可知,为了获取电流基频信号和携带转子位置信息的高频信号,传统脉振高频电压注入法使用了LPF和BPF. 虽然可以满足将高频注入信号从系统中滤除和提取的要求,但两者的使用会极大地影响系统动态性能. 因此,研究如何消除系统中滤波器带来的影响,提高系统的动态性能显得尤为重要.
图 5
图 5 系统有无LPF时电流环闭环伯德图
Fig.5 Closed-loop Bode plot of current loop with and without LPF for system
图 6
2. 基于新型信号处理策略的脉振高频电压注入法
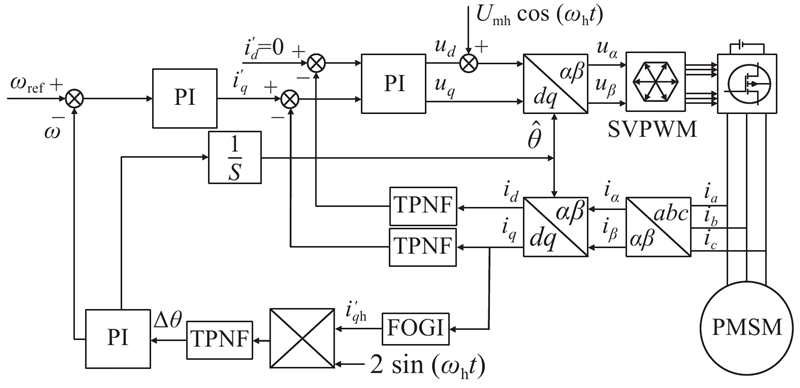
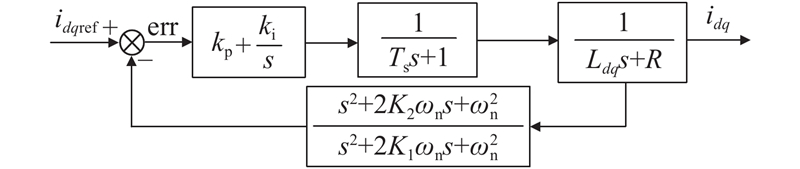
传统脉振高频电压注入法使用BPF和LPF,导致系统存在严重的信号延时问题. 为了解决这一问题,本研究提出改进方法:采用TPNF取代电流环上用于滤除高频注入信号的LPF;在位置信息解调环节,使用FOGI+TPNF的方式取代传统位置信息解调环节使用的BPF+LPF解调方法,从而有效克服信号延迟的问题,实现对转子位置的精确跟踪,并提升系统动态性能. 改进前、后的无位置传感器控制系统中,均采用PID控制策略,改进后的脉振高频电压注入法控制框图如图7所示.
图 7
图 7 改进后的脉振电压高频注入法控制框图
Fig.7 Improved control block diagram of high-frequency pulsating voltage injection method
2.1. 电流环高频电流信号处理策略
在传统脉振高频电压注入法中,LPF被用于滤除电流回路中注入的高频电流信号. 然而,LPF的使用不仅无法完全将高频信号滤除,又会导致电流回路中信号幅值衰减和相位延迟,严重影响系统的动态性能. 为了弥补传统脉振高频电压注入法的不足,采用三参数陷波器将高频电流信号滤除. 相比于传统的LPF策略,TPNF可实现对特定高频信号的完全滤除,同时无幅值衰减和相位延迟地保留基波低频信号. 相比于其他陷波结构,TPNF可以在不增加陷波器阶数的前提下改变陷波深度,陷波带宽、陷波中心频率适应性更强. TPNF传递函数为
式中:
图 8
图 9
利用TPNF将传统脉振高频电压注入电流环上的LPF替换后,电流环结构框图如图10所示.
图 10
图 11
2.2. 位置信息提取处理策略
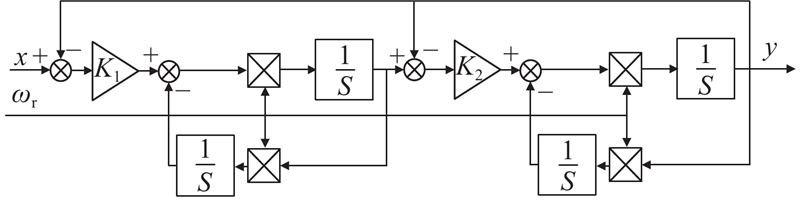
传统位置信息提取采用BPF+LPF结构,导致位置信息存在延时、信噪比低的问题. 为了弥补传统方法的不足,本研究采用四阶广义积分器和三参数陷波器的方法. FOGI是一种可以对特定频率信号实现零延迟提取的滤波结构,其结构图如图12所示. 其中,x为输入信号,ωr为待处理的信号频率,y为经过滤波处理后的信号. FOGI包含2个广义积分环节,K1、K2为比例系数,调节其值可以改变其选频特性.
图 12
四阶广义积分器传递函数为
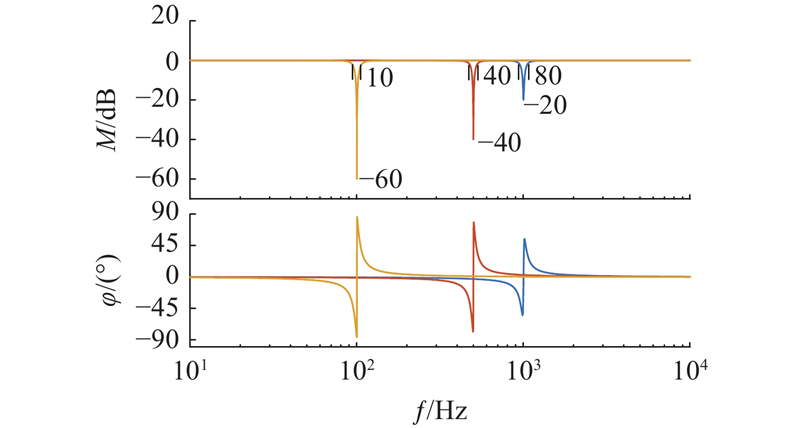
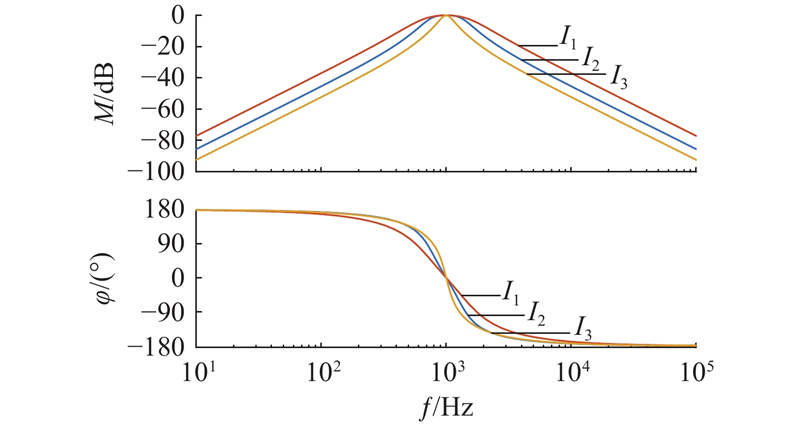
如图13所示为FOGI在不同参数下的伯德图. 提取信号频率为1 kHz,I1参数如下:K1=0.70、K2=2.00;I2参数如下:K1=0.48、K2=1.10;I3参数如下:K1=0.20、K2=1.20. 从图中可以看出,虽然不同K1、K2影响了FOGI的带宽,但在特征频率点处,不同参数对系统响应的幅值并无影响,且无相位偏移. 因此,FOGI可以改善系统由BPF所引起的相位延迟的问题. 从图中也不难看出K1、K2的改变会引起FOGI带宽的改变,从而影响到对特定频率信号的提取. 因此,须合理设计四阶广义积分器参数.
图 13
为了简化复杂的参数整定过程,根据黄守道等[21]提出的广义积分器参数整定方法,引入控制原理中标准四阶特征方程,将四阶广义积分器的特征方程与之比较得到最佳的参数选择. 标准四阶特征方程表达式如下:
式中:ξ为阻尼因子,ξ=0.707; ωn1、ωn2、ωn3为标准特征方程各个极点振荡的固有频率;c1、c2、c3为常数. 为了简化参数整定过程,令c1=c2=1.00、c3=0.05,假定所有极点振荡频率为ωn1=ωn2=ωn3=314 rad/s. 将上述参数代入式(7)中,与FOGI的特征方程比较,最终整定四阶广义积分器参数如下:K1=0.48,K2=1.10.
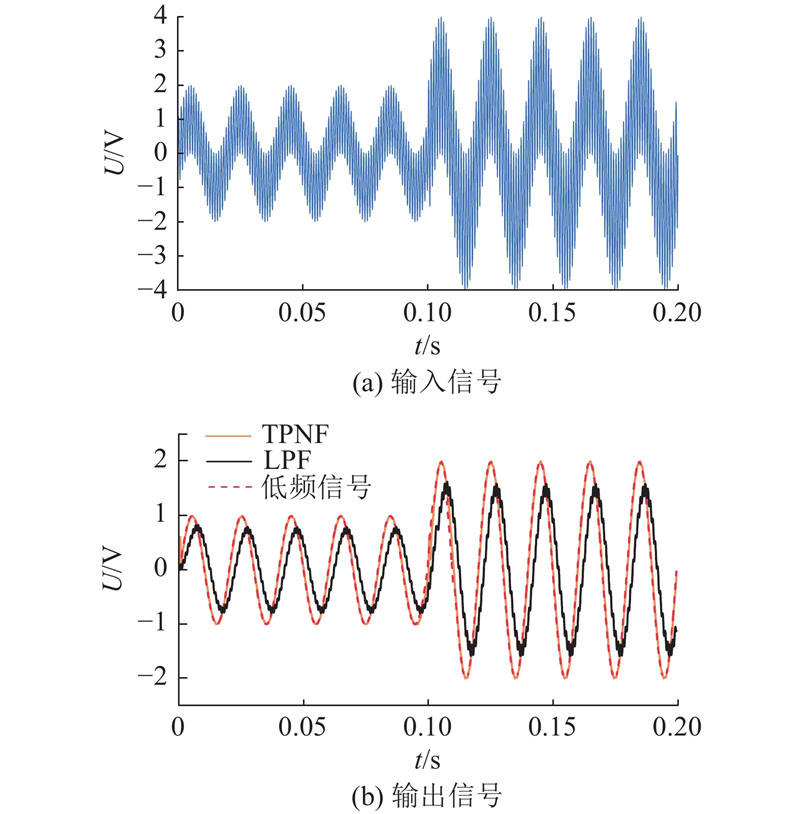
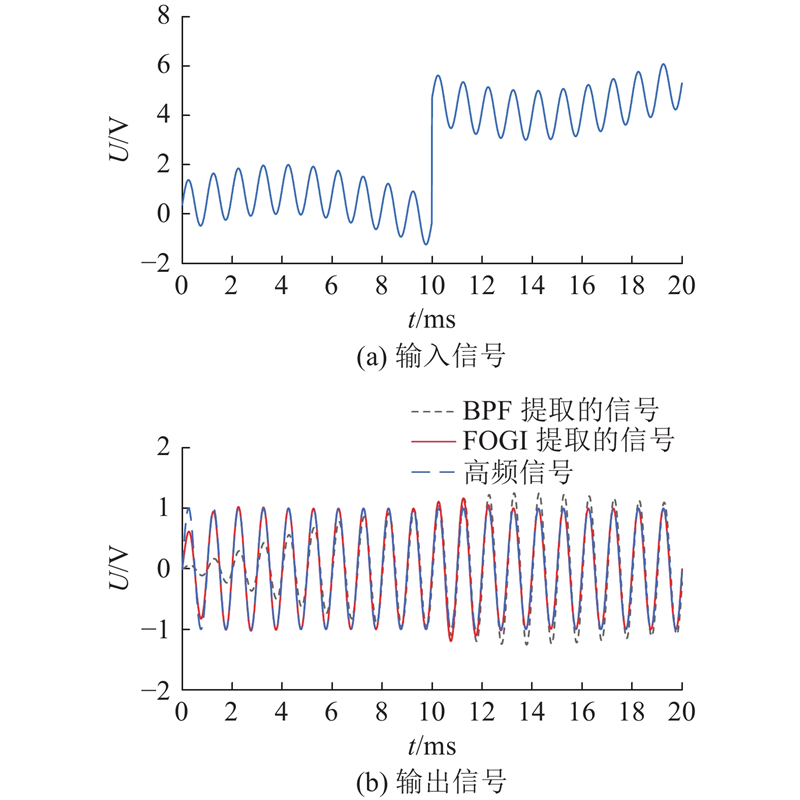
如图14所示为FOGI与BPF信号提取能力的结果比较,其中设定输入信号频率为1 kHz,幅值为1 V的正弦信号,叠加频率为50 Hz,幅值为1 V的正弦信号,并在10 ms时增加一个幅值为 5 V的阶跃信号. 如图14(a)所示为输入信号波形图,如图14(b)所示为经过提取后的信号输出波形图. 从图中可以看出,BPF和FOGI都能实现对高频信号的提取,但是,BPF有明显的信号延时,而FOGI不存在这种问题,此外,在阶跃信号的作用下,BPF和FOGI都产生了一定的高频振荡,但FOGI可以更快地恢复对高频信号的正常提取,时间约为2.5 ms,并且无相位延迟,而BPF不仅有相位延时,恢复正常提取的时间也更长. 因此,FOGI在消除相位延迟的同时,可有效提高系统的动态性能.
图 14
图 14 FOGI和BPF信号提取对比
Fig.14 Comparison of signal extraction between FOGI and BPF
由上述可知,当电机q轴响应电流经过所设计的基于四阶广义积分器的新型位置信号解调方法处理后,可得到如下所示包含位置信息的位置误差信号:
改进位置误差信号解调策略结构框图如图15所示.
图 15
图 15 改进位置误差信号解调策略结构框图
Fig.15 Structure block diagram of improved position error signal demodulation strategy
3. 仿真与实验验证
3.1. 仿真验证
使用MATLAB软件,搭建Simulink仿真模型,分别对传统脉振高频电压注入和改进后的脉振高频电压注入进行仿真验证. 如表1所示为仿真中使用的电机参数. 改进前、后注入电压均为15 V的1 kHz的高频正弦电压.
表 1 仿真电机参数
Tab.1
| 参数 | 数值 |
| 直轴电感/mH | 1.74 |
| 交轴电感/mH | 2.08 |
| 直流侧电压/V | 24 |
| 定子电阻/Ω | 0.6 |
| 极对数/Pn | 2 |
| 转动惯量/(kg·m2) |
3.1.1. 启动与转速突变性能仿真
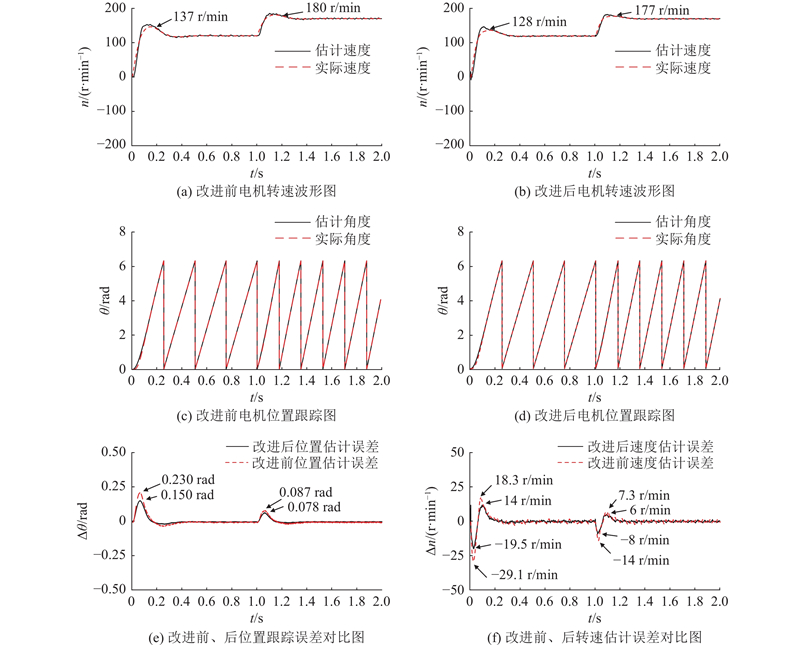
仿真实验时间为2 s,空载状态下,电机初始给定转速为120 r/min,在1 s时将给定转速调整为170 r/min,电机的仿真波形图如图16所示. 在启动时,传统脉振高频电压注入法的转速估计误差最大约为29.1 r/min、转子位置跟踪误差最大约为0.230 rad,转速最高约为137 r/min;在转速突变时,转速估计误差最大约为14 r/min,转子位置跟踪误差最大约为0.087 rad,转速最高约为180 r/min. 相比之下,改进脉振高频电压注入法,在启动时,转速估计误差最大约为19.5 r/min、转子位置跟踪误差最大约为0.150 rad,转速最高约为128 r/min;在转速突变时,转速估计误差最大约为8 r/min,转子位置跟踪误差最大约为0.078 rad,转速最高约为177 r/min,此外,在转速平稳时,转速波动得到明显的改善,较平滑. 通过分析可知,改进后的脉振高频电压注入法相较于传统脉振高频电压注入法,在启动和目标转速突变的瞬间,转速误差、位置误差都更小,动态性能更好,具有更优的控制性能.
图 16
图 16 启动与转速突变工况下改进前、后仿真对比
Fig.16 Comparison of simulation results before and after improvement under start-up and abrupt speed change conditions
3.1.2. 负载突变抗干扰性能仿真
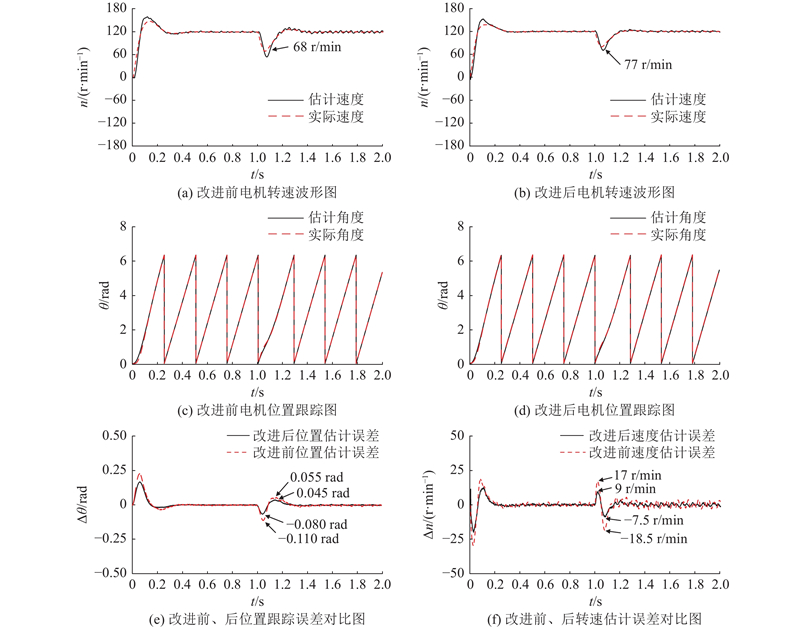
为了验证改进后的脉振高频电压注入法抗干扰性能强于传统脉振高频电压注入法,针对负载突变工况进行如下仿真验证. 仿真实验时间为2 s,电机起始转速为120 r/min,在稳定运行1 s后,突然增加额定转矩的50%(0.11 N·m)并持续到仿真验证结束,仿真波形图如图17所示,对比改进后脉振高频电压注入法和传统脉振高频电压注入法的电动机转速、转子位置、转子位置误差来进行结果分析. 由图17可以看出,电机加载后,改进前、后电机控制系统都能达到控制效果. 然而,传统脉振高频电压注入法下,加负载后电机转速下降到约68 r/min,并且转速估计误差波动最大约为18.5 r/min,位置估计误差最大约为0.110 rad. 相比之下,改进后的脉振高频电压注入下加载后电机转速下降到约为77 r/min,并且转速估计误差波动较小(最大约为9 r/min),位置估计误差最大约为0.080 rad. 综上,改进后方法的抗干扰性能优于传统方法.
图 17
图 17 负载突变工况下改进前、后对比结果
Fig.17 Comparison of simulation results before and after improvement under load mutation conditions
3.2. 实验验证
为了进一步验证本研究所提基于三参数陷波器的脉振高频电压注入永磁同步电机无位置传感器控制策略的有效性,构建了实验验证平台. 该平台以STM32F446RE芯片为主控单元,包括PMSM以及驱动板、上位机、示波器、直流电源、加负载用磁粉制动器及其数显控制器KTC800A,如图18所示. PMSM电机参数如表2所示. 实验过程中,通过电机内置的编码器获取电机转子的实际位置和转速信息,并与估计的转子位置和转速信息作比较. 实验中产生的数据由控制器通过串口通信实时发送到上位机中实时显示并保存,实验结束后将数据导出进行分析. 实验中,母线电压为24 V,注入脉振高频电压幅值为15 V,注入脉振高频电压频率为1 kHz.
表 2 PMSM电机参数
Tab.2
| 参数 | 数值 |
| 额定功率/W | 70 |
| 额定电压/V | 24 |
| 额定电流/A | 3 |
| 电感/mH | 2.08 |
| 定子电阻/ | 0.6 |
| 额定转速/(r·min−1) | |
| 极对数/Pn | 2 |
| 额定转矩/(N | 0.22 |
图 18
3.2.1. 启动性能验证
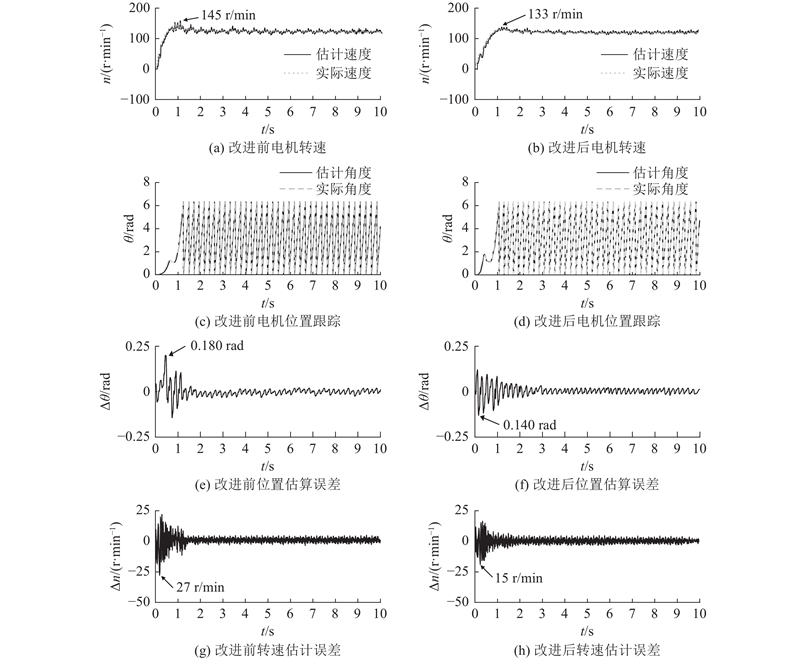
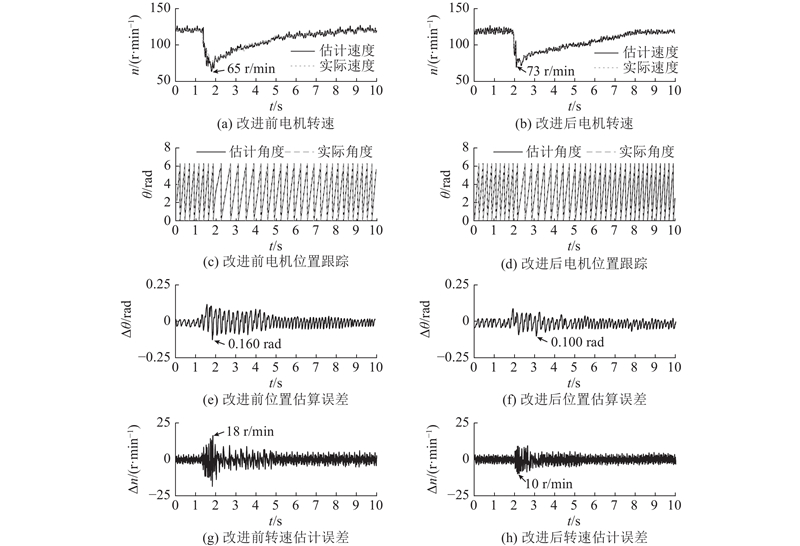
在空载状态下,改进后脉振高频电压注入与改进前的脉振高频电压注入电机启动实验对比如图19所示. 起始状态下电机处于静止状态,0 s时,给予电机启动命令,目标转速为120 r/min. 从图中可以看出,改进前的脉振高频电压注入启动所用时间约为1.8 s,转速最高约为145 r/min,转子位置估算误差最大约为0.180 rad,转速估计误差最大约为27 r/min. 改进后的脉振高频电压注入启动所用时间约为1.40 s,转速最高约为133 r/min,转子位置估算误差最大约为0.140 rad,转速跟踪误差最大约为15 r/min. 由上述分析可知,改进前、后的脉振高频电压注入均实现了在低速域状态下的电机启动,并且,位置估计误差和速度估计误差均经历先增大、后减小、最终趋于平稳的过程,但是,改进后的脉振高频电压注入在电机启动过程中的动态性能和转子位置估计精度均优于改进前的脉振高频电压注入,然而,在电机启动时的动态性能和转子位置估计精度上,改进后的脉振高频电压注入优于改进前的脉振高频电压注入.
图 19
图 19 启动工况下改进前、后电机启动实验对比
Fig.19 Comparison of motor start-up experiments before and after improvement under start-up condition
3.2.2. 负载突变抗干扰性能验证
为了验证本研究所提策略的抗干扰性能优于传统策略,对改进前、后脉振高频电压注入的电机进行负载突变抗干扰性能对比实验,结果如图20所示. 令PMSM无位置传感器控制系统实验平台中的电机处于空载状态下以120 r/min运行,经过一段时间后突加额定负载的50%(0.11 N∙m). 从图中可以看出,当电机加载后,改进后的脉振高频电压注入展现了更强的抗干扰能力,从加载到恢复转速所用的时间约为6 s,实际转速下降到73 r/min,转速估计误差最大为10 r/min,位置估算误差最大为0.100 rad,并且恢复到平稳跟踪精度的速度较快. 作为对比,改进前的脉振高频注入从加载到恢复转速所用时间约为8 s,实际转速下降到65 r/min,转速估计误差最大为18 r/min,位置估算误差最大为0.160 rad,恢复到平稳跟踪精度的速度相较于改进后的脉振高频电压注入较慢.
图 20
图 20 负载突变工况下改进前、后电机转速突变实验对比
Fig.20 Comparison of motor speed abrupt change experiments before and after improvement under load mutation conditions
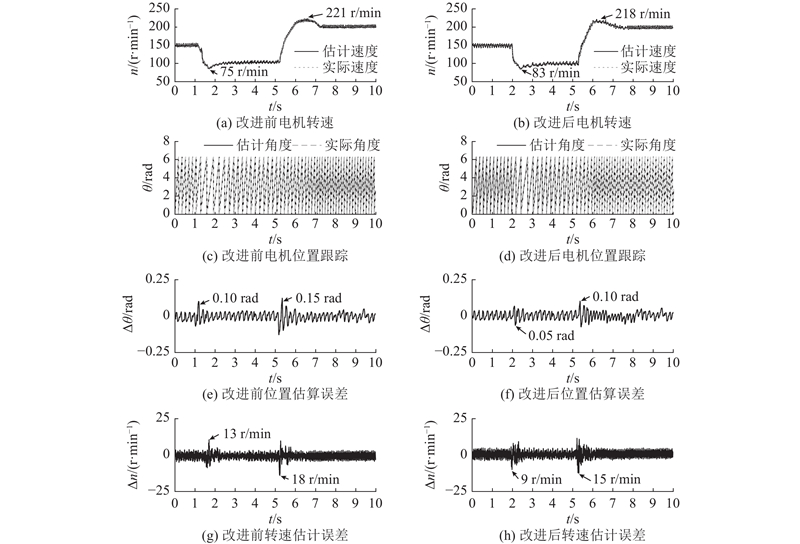
3.2.3. 带载加减速动态性能验证
为了验证本研究所提策略的速度响应能力优于传统方法,在电机在加额定负载50%(0.11 N∙m)的状态下,对改进前、后脉振高频电压注入的电机进行转速突变对比实验,结果如图21所示. 令PMSM无位置传感器控制系统实验平台中的电机以150 r/min运行,经过减速后以100 r/min运行一段时间,随后加速到200 r/min. 从图中可以看出,在150 r/min到100 r/min减速阶段,改进前所用时间约为1.8 s,转速最低约为75 r/min,转速估计误差最大约为13 r/min,位置估算误差最大约为0.100 rad. 改进后所用时间约为1.3 s,转速最低约为83 r/min,转速估计误差最大约为9 r/min,位置估算误差最大约为0.050 rad. 从100 r/min到200 r/min加速阶段,改进前所用时间大概为2.2 s,转速最高约为221 r/min,转速估计误差最大约为18 r/min,位置估算误差最大约为0.150 rad. 改进后所用时间约为1.8 s,转速最高约为218 r/min,转速估计误差最大约为15 r/min,位置估算误差最大约为0.100 rad. 由上述分析可知,改进前后系统均可以有效跟踪转速和位置的变化,虽然转速估计误差和位置估计误差在转速突变时最大,但经过一段时间后均可恢复平稳,此外,相比于改进前,改进后的脉振高频电压注入能更有效且更快速地跟踪真实转速,动态性能更优.
图 21
图 21 带载加减速工况下改进前、后电机带载转速突变实验对比
Fig.21 Experimental comparison of motor load speed transients before and after improvement under loaded acceleration and deceleration conditions
4. 结 论
(1)在电机启动、负载突变、带载变速等工况下,本研究所提策略在转子位置估算精度上明显优于传统脉振高频电压注入法,其中,转子位置估计误差分别降低了0.04、0.06、0.05 rad,转速估计误差分别降低了12、8、4 r/min .
(2)与传统方法相比,本研究所提策略有效解决了滤波延时问题,提高了系统的动态性能和鲁棒性,在电机带载变速的工况下,电机最高转速由传统方法下的221 r/min下降到218 r/min,在电机突加负载的工况下,电机转速下降极值由传统方法的65 r/min提高到了73 r/min,展现出更优的抗干扰能力.
本研究提出的策略为脉振高频电压注入法提供了新的优化思路,在转子位置估计精度和电机系统动态性能提升方面具有显著优势,对提升永磁同步电机低速域无位置传感器控制性能具有一定意义. 然而,本策略无法有效抑制高频电压信号产生高次谐波对电流环稳定性的影响,后续研究将以此展开.
参考文献
Universal full-speed sensorless control scheme for interior permanent magnet synchronous motors
[J].
Speed sensor fault tolerant PMSM machines: from position-sensorless to sensorless control
[J].DOI:10.1109/TIA.2019.2908337 [本文引用: 1]
基于高频信号注入的永磁同步电机无传感器控制技术综述
[J].
Review on sensorless control of permanent magnet synchronous motor based on high-frequency signal injection
[J].
基于共振扩张状态观测器的内置式永磁同步电机统一全速域无位置传感器控制
[J].
Unified full speed sensorless control of interior permanent magnet synchronous motor based on resonance extended state observer
[J].
采用免疫高频脉动信号注入的PMSM转速辨识方法
[J].
High frequency pulsating signal injection for permanent magnet synchronous machines based on immune algorithm
[J].
永磁同步电机无位置传感器控制技术研究综述
[J].
Position-sensorless control technology of permanent-magnet synchronous motor-a review
[J].
Improved initial rotor position estimation for PMSM drives based on HF pulsating voltage signal injection
[J].DOI:10.1109/TIE.2017.2772204 [本文引用: 1]
Initial rotor position detection method of SPMSM based on new high frequency voltage injection method
[J].DOI:10.1109/TPEL.2018.2850318 [本文引用: 1]
PMSM sensorless control by injecting HF pulsating carrier signal into estimated fixed-frequency rotating reference frame
[J].
Sensorless operation capability of surface-mounted permanent-magnet machine based on high-frequency signal injection methods
[J].
Robust position sensorless control of nonsalient PMSM at standstill and low speeds
[J].DOI:10.1109/JESTPE.2014.2307277 [本文引用: 1]
Design consideration on the square-wave voltage injection for sensorless drive of interior permanent-magnet machines
[J].
基于高频方波注入的永磁同步电机转子初始位置辨识
[J].
Initial position identification of permanent magnet synchronous motor rotor based on high-frequency square wave injection
[J].
基于广义二阶积分器的高频脉振电压注入PMSM无位置传感器控制
[J].
Sensorless control of PMSM with HF pulsating voltage injection based on second-order generalized integrator
[J].
基于高阶广义积分器的改进型直线振荡电机无位置传感器控制
[J].
Improved position sensorless piston stroke control for linear oscillatory machine based on high-order generalized integrator
[J].
基于滑动平均滤波的永磁电机无位置传感器控制策略
[J].
Sensorless control strategy of permanent magnet motor based on moving average filtering
[J].
基于高频注入的永磁同步电机零低速下位置传感器失效故障容错控制
[J].
Fault-tolerant control of position sensor failure for PMSM at zero and low speed based on high frequency injection
[J].
SOGI级联SFNF的高频注入无传感器电机控制方法
[J].
High frequency injection sensor-less motor control method with cascade of SOGI and SFNF
[J].
基于五阶广义积分器的内置式永磁同步电机转子位置观测法
[J].
Rotor position estimation method for fifth-order generalized integrator based interior permanent magnet synchronous motors
[J].