随着国家“碳达峰,碳中和”目标的提出,交通与能源的融合正在成为能源和交通领域创新发展的重要趋势[1]. 在交通运输系统迅猛发展的同时,越来越多学者开始涉足交通领域的综合评价,Li等[2]结合熵法与独立GL法构建多能微电网能效评估模型,解决了多种能源互补场景下指标权重难以确定的问题. Cui等[3]采用层次分析法(analytic hierarchy process,AHP)和熵法相结合的组合赋权方法,以及灰色关联分析法(grey relational analysis,GRA),解决了京津冀区域政府引导基金政策效率的定量化评价问题. Saxena等[4]提出新的基于CRITIC和TOPSIS的方法,用于软件可靠性增长模型(SRGM)的最优选择. 该方法通过综合考虑指标的客观权重和主观偏好,解决了软件可靠性模型选择中的多准则决策问题. Zhao等[5]采用层次分析法确定光伏系统能效指标权重,再通过模糊综合评估解决评估过程中的主观性和不确定性问题. 刘义艳等[6]提出高速公路自洽能源系统的综合能效评估方法,通过建立多指标评估体系,结合层次分析法和熵法,对高速公路自洽能源系统的整体能效进行量化评估,解决了自洽能源系统在实际应用中的能效评价问题. 霍千辰等[7]构建基于改进组合权重的高速公路微电网运维评价指标体系,通过优化权重分配,结合客观数据和主观判断,对微电网的运维状态进行综合评价,解决了微电网运维管理中的指标量化和状态评估问题. Li等[8]运用层次分析法确定光伏系统能效指标权重,再通过模糊综合评估解决评估过程中的主观性和不确定性问题. Zhou等 [9]提出基于神经网络的演员-评论家方法,用于求解高维静态哈密顿-雅可比-贝尔曼(high-dimensional static Hamilton-Jacobi-Bellman,HJB)偏微分方程,该方法通过结合强化学习和深度学习技术,解决了高维偏微分方程的数值求解问题,提高了求解效率和精度.
高速公路作为现代交通运输体系的重要组成部分,其能源消耗会对环境和经济产生深远影响. 目前研究在交通能源领域取得了一定的进展,尤其是在多能微电网、光伏系统以及区域能源评价等方面积累了丰富的经验. 然而,高速公路能源系统的能效评价研究仍相对不足,现有方法多依赖于单一的主观或客观赋权方法,未能有效融合两者优势. 为此,本研究提出基于改进德尔菲法和熵权法的高速公路自洽能源系统能效评价体系,综合考虑主客观因素,理论分析与实证研究相结合,力求构建更具科学性和适用性的能效评价模型.
1. 能效评价指标选取
1.1. 高速公路自洽能源系统
高速公路自洽能源系统是依托高速公路沿线的通过可再生能源实现自给自足供电的综合能源系统. 通过在服务区和沿线安装风力和光伏发电设备,结合储能技术,实现能源的高效利用和稳定供应,减少对国家电网的依赖.
该系统采用“源-网-储-荷”4大组成部分模型:电源侧包括风光发电设施,电网侧可接入国家电网,储能侧包括电化学和机械储能,负荷侧涵盖服务区和沿线的用电设备. 这种设计确保了系统在高速公路沿线实现清洁能源的高效生产、储存和消耗.
高速公路自洽能源系统不仅降低了供电成本,还提高了供电的可靠性和环保性,有助于高速公路沿线区域的绿色低碳发展. 高速公路自洽能源系统有“源-网-储-荷”4大组成部分,如图1所示.
图 1
1.2. 评价指标选取方法
在评价交通自洽能源系统能效时,须构建完整指标评价体系,采用自顶向下方法逐级选取指标,从高级别指标到最底层指标[10]. 为了使所建立评价指标体系的评价结果真实准确、客观可信,须满足7点选取原则:目的性原则、科学性原则、可衡量性原则、独立性原则、系统性原则、可比性原则、实用性原则.
1.3. 能效指标选取结果
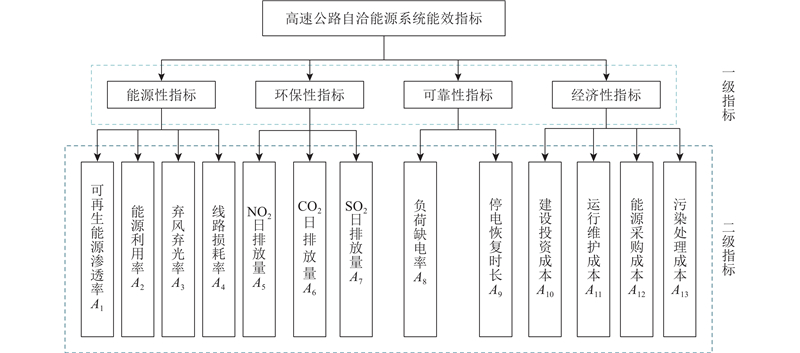
在对具体的评价指标进行选取时,首先,确定交通自洽能源系统能效评估的目的;其次,确定能源性指标、环保性指标、可靠性指标和经济性指标4项一级指标;最后,依据选取的4项一级指标分别确定其所包含的二级指标. 高速公路自洽能源系统能效评价指标树如图2所示.
图 2
图 2 高速公路自洽能源系统能效评价指标树
Fig.2 Efficiency evaluation index tree of self-consistent energy system for highways
在本研究所建立评价指标体系中,二级指标即为最底层指标,均可通过简单计算或是直接记录量化获取. 各类指标具体计算方法如下.
1)能源性指标. 可再生能源渗透率是指自洽能源系统中可再生能源实际发电量占系统总发电量的比例,可再生能源渗透率表达式如下:
式中:
能源利用率表达式如下:
式中:
系统弃风弃光率表达式如下:
式中:
线路损耗率表达式如下:
式中:
2)环保性指标. NO2日排放量A5、CO2日排放量A6、SO2日排放量A7可通过连续监测设备采集,其中NO2采用紫外差分吸收光谱法(DOAS)或化学发光法(CLD),CO2采用非分散红外(NDIR)传感器,SO2采用紫外荧光法或电化学法. 采样点应具备代表性,数据每小时记录一次,异常数据须剔除. 数据处理包括清洗和标准化,最终生成每日平均排放量.
3)可靠性指标. 负荷缺电率表达式如下:
式中:
停电恢复时长A9是从故障停电开始到恢复正常供电的时间,一般通过电力调度系统实时记录,停电起始和恢复时间自动标记,手动记录应确保时间精确至分钟. 数据处理包括异常修正(如人为误录)和标准化,最终生成各次停电的平均恢复时长.
4)经济性指标. 投资建设成本表达式如下:
式中:
运行维护成本表达式如下:
式中:
能源采购成本表达式如下:
式中:
污染处理成本表达式如下:
式中:
2. 指标权重求解方法
不同评价指标的重要性各异,须通过权重系数反映其影响. 在确定指标及计算方法后,须科学赋权以构建完整评价体系,确保其准确性和科学性[14]. 本研究采用改进德尔菲法(基于CRITIC法修正专家经验)和修正熵权法(相似性误差改进)分别作为主客观评价方法,通过方差最小化组合赋权,实现主客观权重的综合优化,并运用集对分析遴选最优建设方案.
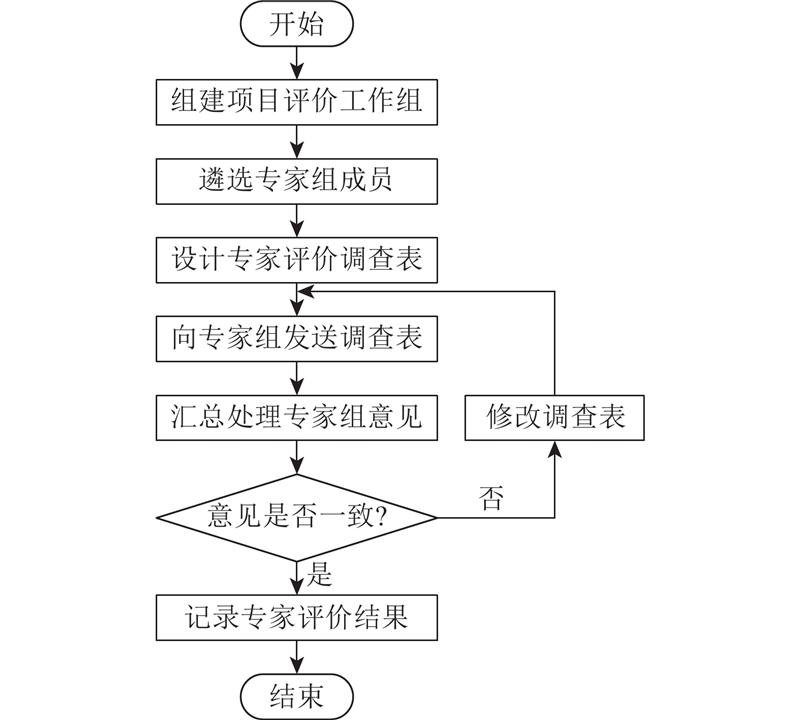
2.1. 德尔菲法
德尔菲法(Delphi)是匿名函询法[15]. 通过多轮反馈信函分享专家打分和意见,使评价结果趋于一致,确保结论统一.
图 3
2.2. 基于CRITIC法改进的德尔菲法
在传统德尔菲法的基础上引入CRITIC法原理[17]优化专家评价数据:剔除异常打分,并基于专家资历(年限/职称/论文)设计权重得分表,实现加权评价,提升方法科学性.
CRITIC法与德尔菲法结合,通过专家资历赋予不同权重,优化专家评价数据,降低水平差异对结果的影响,提升主观权重的科学性和可靠性. 这种融合充分发挥了德尔菲法的独立性与CRITIC法的客观性,使主观评价更具说服力. 然而,专家权重分配存在局限. 其依赖于资历之类的静态指标,可能低估新兴技术专家意见;若假设专家在所有指标上专业水平均匀,则缺乏灵活性;数据获取难度大,可能导致意见过度集中或分散,影响评价全面性.
CRITIC法是客观赋权方法,旨在根据各指标间的对比强度和相互矛盾性来确定多属性决策(MAGDM)中各指标的权重. 具体来说,它结合了各指标的标准差(S.D.)和相关系数(C.C.).
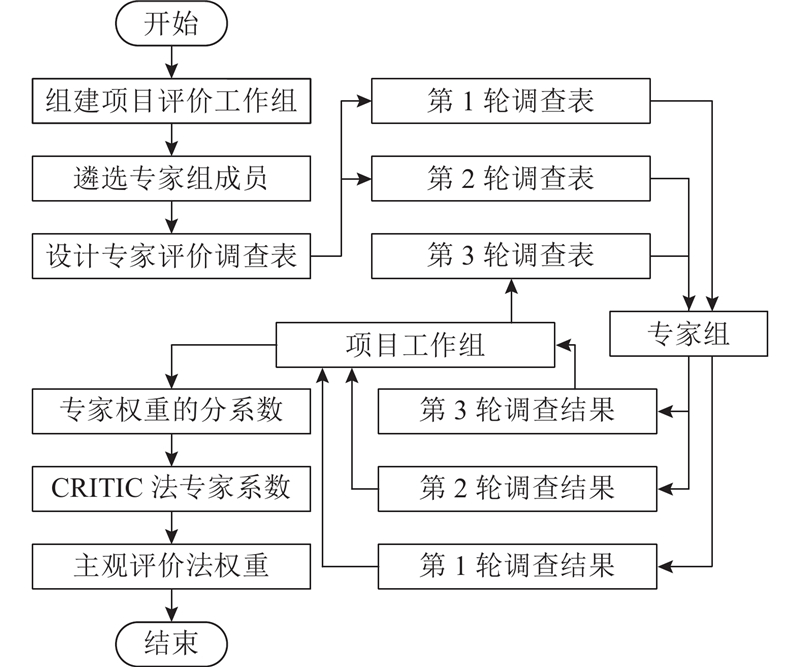
如图4所示,考虑专家经验水平的基于CRITIC法改进的德尔菲法包括8个步骤.
图 4
图 4 考虑专家经验水平的基于CRITIC法改进的德尔菲法流程图
Fig.4 Flowchart of Delphi method improved by CRITIC considering expert experience
1)根据评价项目研究所需专业范围,选择确定专家组人员.
2)制定德尔菲调查表,分发给各位专家进行评价.
3)将整理后的打分结果反馈给全部专家,各专家综合其余专家打分结果,提出修改意见.
4)结合专家提出的修改意见进一步改进调查表,并再次发给专家进行评价.
5)重复以上步骤,直到获得专家组普遍认可的评价结果.
6)使用专家权重得分表求得专家组中不同专家的权重系数
表 1 专家权重得分表
Tab.1
| 工作年限 | 分值A | 职称 | 分值B | 论文 | 分值C |
| >30 | 30 | 教授/正高工 | 30 | SCI一、二区 | 2.0 |
| 20~30 | 20 | 副教授/高工 | 25 | SCI三区 | 1.0 |
| 10~20 | 10 | 讲师/工程师 | 15 | SCI四区 | 0.8 |
| <10 | 5 | 博士在读 | 10 | EI | 0.5 |
7)使用CRITIC法求各个专家权重系数
8)计算各个指标的主观评价权重结果.
通过上述步骤最终得到专家组普遍认可的指标体系中,各评价指标的主观权重向量
该方法在传统德尔菲法基础上,引入专家权重评分表和CRITIC法计算专家权重系数,能有效降低专家水平差异对评价结果的影响,显著提升指标主观权重的准确性和可靠性.
2.3. 改进熵权法
熵是热力学的概念,熵越大,系统越混乱;熵越小,系统越有序. 在数学上将信息排除了冗余之后的平均信息量称为信息熵[18].
熵权法是基于信息熵原理的客观赋权方法[19],采用改进熵权法,通过信息熵计算指标权重,并引入熵误差修正. 主要步骤如下.
1)构建熵权法评价决策矩阵.
决策矩阵
2)对决策矩阵
标准化处理须区分3类指标:效益型(正向)、成本型(逆向)和固定型(适度). 本研究高速公路自洽能源系统能效评价仅涉及效益型和成本型指标.
当评价指标为效益型指标时,该指标标准化
当评价指标为成本型指标时,该指标标准化
由式(11)、(12)可以得到标准化后矩阵
3)利用标准化矩阵,求解各指标对应熵.
4)对熵权法进行误差修正,求各指标熵权.
改进后熵权法的评价指标Qj所对应的熵权
5)将式(14)求得的评价指标熵权结果进行归一化处理,得到权重指标向量.
改进熵权法求各指标客观权重可通过如下公式计算得到:
通过上述步骤可以得到各个评价指标基于改进熵权法的客观权重向量
2.4. 主客观综合评价方法
在获取主客观权重后,采用组合赋权法进行融合,综合不同方法的优势,避免单一方法的局限性,从而提升权重结果的准确性与科学性[20].
常用的组合赋权法有:加权平均、乘积组合、方差最小化等. 本研究采用方差最小化组合赋权法[21]. 该方法通过最小化样本点与均值的离差平方和求解综合权重,以数值计算降低不确定性,使权重结果更科学准确.
在利用方差最小化组合赋权法求解时,首先须将采用考虑专家经验水平的基于CRITIC法改进的德尔菲法得到的主观权重向量
式中:
在求解组合权重系数
由微分性质可以得到最优一阶导数条件:
将其进行线性化转化可以得到:
由式(18) 可以通过计算得出待求组合权重系数
2.5. 集对分析法
采用集对分析法基于综合评价结果对本研究不同方案进行筛选分析,主要包括以下4个步骤:
1)构建集对分析模型:
式中:
2)确定最优和最劣方案.
3)确定指标联系度.
4)计算评价方案优劣距离. 计算各评价方案与最优方案集
式中:
各方案按贴近度排序,贴近度越高则越接近最优方案集,表现越优.
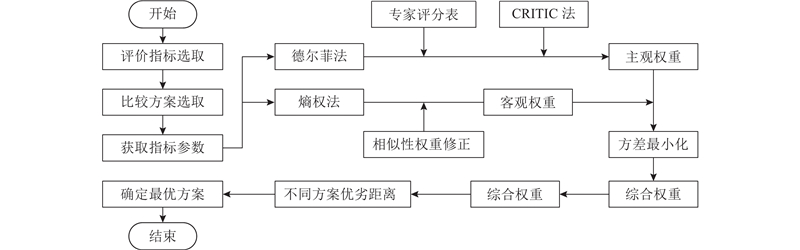
综上所述,本研究提出高速公路自洽能源系统高能效评价指标体系模型,如图5所示.
图 5
图 5 高速公路自洽能源系统高能效评价指标体系模型
Fig.5 Efficiency evaluation index system model for self-consistent energy systems in highways
3. 能效评价算例分析
以某高速公路路段服务区以及收费站为例,该路段具有丰富的太阳光以及风力资源,供电条件良好. 服务区分为2个区域,第1个区域占地面积为
方案1:电网搭配
方案2:结合电网、700片光伏板和15台风力发电机,储能需求为2.318×105 kW·h,充电需求同样为
方案3:电网搭配800片光伏板和10台风力发电机,储能需求最低,仅为2.106×105 kW·h,充电需求为
方案4:电网、1台柴油发电机、400片光伏板以及15台风力发电机的组合,储能需求为2.765×105 kW·h,充电需求为
方案5:电网、1台柴油发电机、500片光伏板和8台风力发电机的配置,储能需求为2.425×105 kW·h,充电需求为
方案6:电网、2台柴油发电机、400片光伏板和6台风力发电机,储能需求为2.212×105 kW·h,充电需求为
这些方案涵盖了多种可再生能源(光伏、风能)与传统能源(柴油发电机)的混合配置,旨在通过对比分析,筛选出在能源利用效率、成本控制和环保性能等方面表现最优的方案.
方案中所用到的光伏板、风力发电机、柴油发电机参数如表2所示.
表 2 相关设备信息清单
Tab.2
| 名称 | 功率 | 成本 | 其他 |
| 隆基Hi-MO X10光伏板 | 635~650 W | 850~900 元/片 | 转换效率最高可达24.8% |
| 广州红鹰能源科技股份有限公司HY-10 kW风力发电机 | 额定功率10 kW | 10~20 万元/台 | 一般达到80%负荷出力 |
| 潍柴600 kW柴油发电机组(6M33D725E310) | 600 kW(常用)、650 kW(备用) | 37.6 万元/台 | 耗油量约为148.24 L/h |
使用第1章中所述的计算公式,求各个指标具体参数. 如表3所示展示了不同自洽能源系统方案下各评价指标的具体参数.
表 3 不同自洽能源系统方案下各评价指标的具体参数
Tab.3
| 评价指标 | A1/% | A2/% | A3/% | A4/% | A5/g | A6/g | A7/g | A8/% | A9/h | A10/万元 | A11/万元 | A12/万元 | A13/万元 |
| 方案1 | 93.5 | 66.8 | 24.6 | 5.43 | 251.4 | 910.3 | 49.5 | 3 | 1.06 | 334.5 | 638.4 | 98.6 | |
| 方案2 | 92.6 | 65.4 | 35.8 | 3.28 | 266.9 | 890.4 | 50.7 | 6 | 0.95 | 896.7 | 367.8 | 549.6 | 103.5 |
| 方案3 | 94.1 | 63.7 | 18.2 | 4.36 | 247.8 | 894.4 | 45.6 | 2 | 1.15 | 984.6 | 485.2 | 635.4 | 117.3 |
| 方案4 | 83.6 | 58.4 | 26.3 | 5.61 | 385.8 | 70.1 | 5 | 1.08 | 593.1 | 716.5 | 109.8 | ||
| 方案5 | 76.8 | 71.9 | 38.2 | 5.17 | 389.2 | 72.6 | 8 | 0.91 | 482.7 | 506.7 | 124.7 | ||
| 方案6 | 69.7 | 67.3 | 23.9 | 4.98 | 398.3 | 77.2 | 4 | 0.86 | 401.6 | 498.6 | 105.1 |
3.1. 主观权重计算
在求取各评价指标主观权重时,选取6名专家:2位教授, 1位副教授, 1位讲师,2名博士在读生. 打分表如表4所示.
表 4 专家组打分结果
Tab.4
| 评价指标 | 打分 | |||||
| 专家1 | 专家2 | 专家3 | 专家4 | 专家5 | 专家6 | |
| A1 | 90 | 85 | 70 | 95 | 85 | 65 |
| A2 | 85 | 95 | 65 | 80 | 80 | 70 |
| A3 | 80 | 90 | 60 | 90 | 92 | 60 |
| A4 | 45 | 80 | 55 | 85 | 90 | 45 |
| A5 | 40 | 50 | 40 | 55 | 65 | 35 |
| A6 | 35 | 45 | 35 | 50 | 60 | 40 |
| A7 | 30 | 35 | 30 | 45 | 55 | 30 |
| A8 | 75 | 40 | 50 | 35 | 75 | 55 |
| A9 | 70 | 55 | 45 | 40 | 70 | 50 |
| A10 | 65 | 75 | 85 | 65 | 50 | 90 |
| A11 | 60 | 70 | 80 | 70 | 45 | 80 |
| A12 | 55 | 65 | 90 | 75 | 40 | 85 |
| A13 | 50 | 60 | 75 | 60 | 35 | 75 |
由表4中专家打分结果经过计算,得到各评价指标
表 5 专家权重系数
Tab.5
| 专家组 | |||
| 专家1 | |||
| 专家2 | |||
| 专家3 | |||
| 专家4 | |||
| 专家5 | |||
| 专家6 |
各评价指标的主观权重评价结果
评价指标的主观权重向量表达式如下:
3.2. 客观权重计算
利用表3评价指标参数,通过客观评价法得到改进熵权法决策矩阵
本研究中选取的13项评价指标中
客观权重向量表达式如下:
3.3. 主客观综合权重计算
根据式(21)、(22)的客观权重向量,使用平方差最小化组合赋权法,解得组合权重系数θ1=
主客观综合权重计算结果如表6所示. 其中,Ssub、Sobj、Scom分别表示主观、客观、综合权重.
表 6 主客观综合权重评价结果
Tab.6
| 指标 | Ssub | Sobj | Scom |
| A1 | |||
| A2 | |||
| A3 | |||
| A4 | |||
| A5 | |||
| A6 | |||
| A7 | |||
| A8 | |||
| A9 | |||
| A10 | |||
| A11 | 0.0850 | ||
| A12 | 0.0850 | ||
| A13 |
3.4. 权重计算结果分析
通过式(19)所述集对分析模型,分别构建出所有方案最优指标集和最劣指标集.
图 6
图 8
计算联系度
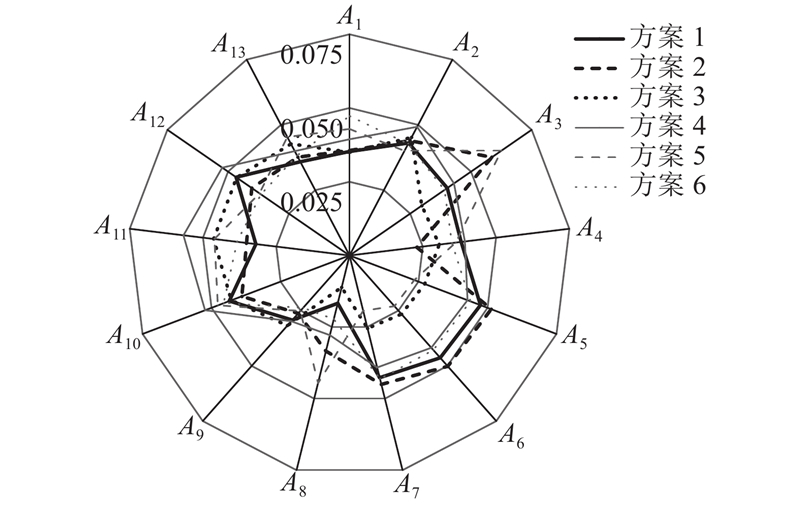
由图6可知,方案3相较于其他5种方案在停电恢复时长(
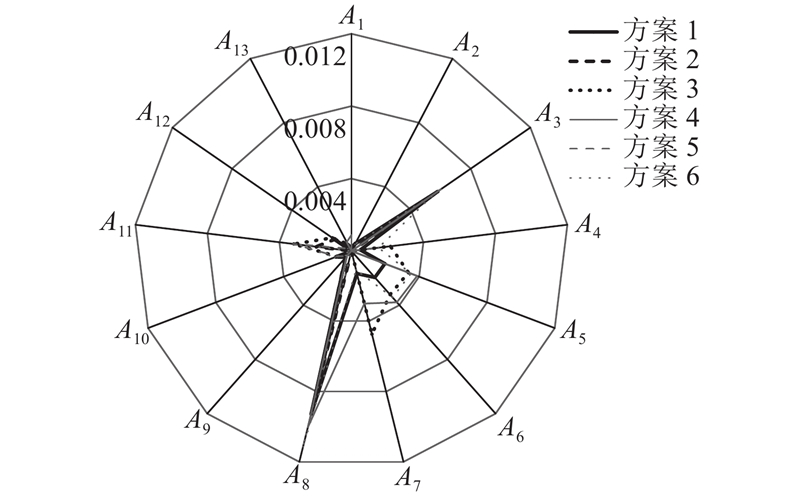
如图7所示,在SO2日排放量指标上,方案3与其他方案存在显著差异(差异度较高),但在其他评价指标中均保持较低差异水平. 综合差异度分析结果表明,方案3在各方案比较中具有明显优势.
图 7
由图8可以看出,方案3与其他5个方案的对立度普遍偏低,各指标间未出现显著对立情况. 说明方案3与其他方案在评价指标上具有较好的协调性,能兼顾不同方案之间的关联性,从而获得更可靠的评估结论.
图 9
图 9 各评价方案与最优方案相对贴近度
Fig.9 Relative closeness of each evaluation scheme to optimal scheme
本研究提出的改进德尔菲-熵权法在传统方法的基础上进行了优化,具有显著优势. 首先,通过引入CRITIC法改进德尔菲法,考虑专家资历分配不同权重,剔除异常评分,提升了主观评分的科学性和代表性. 其次,采用相似性误差修正的熵权法,使得客观权重计算更加稳健,减少了异常数据对结果的干扰. 最后,通过方差最小化组合主客观权重,实现了主客观因素的有效融合,确保评价结果兼具主观判断的合理性和客观数据的准确性. 相比传统方法,该改进方法不仅能够提升评价结果的科学性和公正性,而且在多种高速公路能源系统方案的对比中表现出更高的区分度和一致性. 通过集对分析法对6种方案进行综合评价,筛选出最优方案.
4. 结 语
构建了适用于高速公路自洽能源系统的高能效评价指标体系模型,并将其应用于实际系统方案的评价分析. 首先从能源性、环保性、可靠性和经济性4大维度出发,选取了13项关键评价指标,搭建起系统的高能效评价指标树框架. 结合主观与客观方法:一方面,借助专家打分表和CRITIC法对德尔菲法进行优化,形成有效的主观权重确定方案;另一方面,对熵权法进行相似性权重修正,得到精准的客观权重确定方法,并运用方差最小化方法将两者有机结合,最终精准计算出各评价指标的组合权重. 在此基础上,运用集对分析法对不同方案的评价结果进行深入剖析,成功锁定最优方案,从而完善了整个高速公路自洽能源系统高能效评价指标体系模型. 将该模型应用于6种不同的高速公路自洽能源系统高能效优化方案的分析,经过严谨的评估与比对,成功筛选出最优方案,充分验证了模型的科学性、实用性和高效性,为高速公路自洽能源系统的高能效发展提供了有力的理论支持与实践指导.
参考文献
能源交通融合下的弹性公路能源系统发展技术要点及展望
[J].
A review on the development of resilient highway energy system under the integration of energy and transportation
[J].
The policy efficiency evaluation of the Beijing-Tianjin-Hebei regional government guidance fund based on the entropy method
[J].DOI:10.2478/amns.2021.1.00049 [本文引用: 1]
A novel CRITIC-TOPSIS approach for optimal selection of software reliability growth model (SRGM)
[J].DOI:10.1002/qre.3087 [本文引用: 1]
高公路自洽能源系统综合能效评估方法
[J].
Comprehensive energy efficiency evaluation method for expressway self-contained energy systems
[J].
Actor-critic method for high dimensional static Hamilton-Jacobi- Bellman partial differential equations based on neural networks
[J].DOI:10.1137/21M1402303 [本文引用: 1]
Quality evaluation of solution sets in multiobjective optimisation
[J].
Construction of nursing care quality evaluation indicators for post-anaesthesia care unit in China
[J].
A comparative survey of VANET clustering techniques
[J].DOI:10.1109/COMST.2016.2611524 [本文引用: 1]
Investigation on the novel high-performance copper/graphene composite conductor for high power density motor
[J].
基于德尔菲法和TOPSIS法的垃圾焚烧发电厂综合评价方法
[J].
A comprehensive evaluation method of waste incineration power plant based on Delphi method and topsis method
[J].
Laboratory implementation of direct torque controller based speed loop pseudo derivative feedforward controller for PMSM drive
[J].
Information and entropy
[J].DOI:10.1103/PhysRevE.47.4010 [本文引用: 1]
Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: a critical review
[J].DOI:10.1016/j.jmrt.2020.12.114 [本文引用: 1]
基于组合赋权法和模糊综合评价的电力设备状态数据质量评估
[J].
Data quality assessment for power equipment condition based on combination weighing method and fuzzy synthetic evaluation
[J].
A proximal stochastic gradient method with progressive variance reduction
[J].DOI:10.1137/140961791 [本文引用: 1]
TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment
[J].DOI:10.1007/s40314-016-0402-0 [本文引用: 1]