[2]
BENZ T. Small strain stiffness of soils and its numerical consequences [D]. Stuttgart: University of Stuttgart, 2006.
[本文引用: 2]
[3]
上海市住房和城乡建设管理委员会. 基坑工程技术标准: DG/TJ 08-61—2018 [S]. 上海: 同济大学出版社, 2018.
[本文引用: 1]
[4]
王浩然. 上海软土地区深基坑变形与环境影响预测方法研究[D]. 上海: 同济大学, 2012.
[本文引用: 3]
WANG Haoran. Prediction of deformation and response of adjacent environment of deep excavations in Shanghai soft deposit [D]. Shanghai: Tongji university, 2012.
[本文引用: 3]
[5]
王卫东, 王浩然, 徐中华 上海地区基坑开挖数值分析中土体HS-Small模型参数的研究
[J]. 岩土力学 , 2013 , 34 (6 ): 1766 - 1774
[本文引用: 5]
WANG Weidong, WANG Haoran, XU Zhonghua Study of parameters of HS-Small model used in numerical analysis of excavations in Shanghai area
[J]. Rock and Soil Mechanics , 2013 , 34 (6 ): 1766 - 1774
[本文引用: 5]
[6]
陈峰. 无锡地铁基坑典型地层本构模型适应性研究[D]. 上海: 同济大学, 2011.
[本文引用: 1]
CHEN Feng. Adaptability of constitutive model for typical soil layers in Wuxi metro excavation [D]. Shanghai: Tongji University, 2011.
[本文引用: 1]
[7]
楼春晖. 软土地区深开挖空间变形特性及环境影响分析 [D]. 杭州: 浙江大学, 2019.
[本文引用: 2]
LOU Chunhui. Investigation of spatial deformation characteristics and environmental effects due to deep excavation in soft soil area [D]. Hangzhou: Zhejiang University, 2019.
[本文引用: 2]
[8]
白时雨, 王文军, 谢新宇, 等 考虑扰动影响的土体小应变硬化模型参数试验研究及其在基坑工程中的应用
[J]. 岩土力学 , 2023 , 44 (1 ): 206 - 216
[本文引用: 1]
BAI Shiyu, WANG Wenjun, XIE Xinyu, et al Experimental study on HS-small model parameters of soil considering disturbance and its application in foundation pit engineering
[J]. Rock and Soil Mechanics , 2023 , 44 (1 ): 206 - 216
[本文引用: 1]
[9]
李连祥, 刘嘉典, 李克金, 等 济南典型地层HSS参数选取及适用性研究
[J]. 岩土力学 , 2019 , 40 (10 ): 4021 - 4029
[本文引用: 4]
LI Lianxiang, LIU Jiadian, LI Kejin, et al Study of parameters selection and applicability of HSS model in typical stratum of Jinan
[J]. Rock and Soil Mechanics , 2019 , 40 (10 ): 4021 - 4029
[本文引用: 4]
[10]
李子健. 天津市区HSS模型参数及其在深基坑变形分析中的应用 [D]. 天津: 天津大学, 2022.
[本文引用: 6]
LI Zijian. Determination of parameters for the Hardening Soil-Small model and application in deformation analysis for foundation pit in Tianjin [D]. Tianjin: Tianjin University, 2022.
[本文引用: 6]
[12]
顾晓强, 吴瑞拓, 梁发云, 等 上海土体小应变硬化模型整套参数取值方法及工程验证
[J]. 岩土力学 , 2021 , 42 (3 ): 833 - 845
[本文引用: 3]
GU Xiaoqiang, WU Ruituo, LIANG Fayun, et al On HSS model parameters for Shanghai soils with engineering verification
[J]. Rock and Soil Mechanics , 2021 , 42 (3 ): 833 - 845
[本文引用: 3]
[13]
HARDIN B O, BLACK W L Vibration modulus of normally consolidated clay
[J]. Journal of the Soil Mechanics and Foundations Division , 1968 , 94 (2 ): 353 - 369
DOI:10.1061/JSFEAQ.0001100
[本文引用: 1]
[14]
BRINKGREVE R B J, BROERE W. PLAXIS material models manual [M]. Delft: PLAXIS B. V. , 2006.
[本文引用: 1]
[15]
VARDANEGA P J, BOLTON M D Stiffness of clays and silts: normalizing shear modulus and shear strain
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2013 , 139 (9 ): 1575 - 1589
DOI:10.1061/(ASCE)GT.1943-5606.0000887
[16]
OZTOPRAK S, BOLTON M D Stiffness of sands through a laboratory test database
[J]. Géotechnique , 2013 , 63 (1 ): 54 - 70
[17]
JURČEK T, PULKO B, MAČEK M Small strain shear modulus of the Ljubljana marsh soil measured with resonant column and bender elements under isotropic and anisotropic stress conditions
[J]. Applied Sciences , 2024 , 14 (5 ): 1984
DOI:10.3390/app14051984
[本文引用: 1]
[18]
郑刚, 杜一鸣, 刁钰, 等 基坑开挖引起邻近既有隧道变形的影响区研究
[J]. 岩土工程学报 , 2016 , 38 (4 ): 599 - 612
DOI:10.11779/CJGE201604003
[本文引用: 2]
ZHENG Gang, DU Yiming, DIAO Yu, et al Influenced zones for deformation of existing tunnels adjacent to excavations
[J]. Chinese Journal of Geotechnical Engineering , 2016 , 38 (4 ): 599 - 612
DOI:10.11779/CJGE201604003
[本文引用: 2]
[19]
周强, 高洁, 郑刚, 等 软土地区超深基坑引发邻近重要建筑沉降的倾斜注浆主动控制方案: 以天津地铁7号线某地下四层站工程为例
[J]. 科学技术与工程 , 2023 , 23 (23 ): 10049 - 10058
ZHOU Qiang, GAO Jie, ZHENG Gang, et al Active control scheme of inclined grouting for settlement of adjacent important buildings caused by ultra-deep excavation in soft soil area: taking a four floors underground station project of Tianjin metro line 7 as an example
[J]. Science Technology and Engineering , 2023 , 23 (23 ): 10049 - 10058
[20]
赵挚南, 王寒晖, 郝龙, 等 基于HSS模型的基坑开挖对近邻地铁影响数值分析
[J]. 低温建筑技术 , 2021 , 43 (1 ): 125 - 129
ZHAO Zhinan, WANG Hanhui, HAO Long, et al Numerical analysis of the influence of foundation pit excavation neighboring subway based on hss model
[J]. Low Temperature Architecture Technology , 2021 , 43 (1 ): 125 - 129
[21]
邓旭, 甄洁, 林森斌, 等 基坑开挖引起地铁结构隆起的堆载控制研究
[J]. 铁道科学与工程学报 , 2024 , 21 (6 ): 2417 - 2429
DENG Xu, ZHEN Jie, LIN Senbin, et al Loading control for the uplift of subway structures induced by adjacent excavation
[J]. Journal of Railway Science and Engineering , 2024 , 21 (6 ): 2417 - 2429
[22]
信磊磊. 基于变形控制标准的基坑开挖对邻近既有建筑物和隧道变形影响研究 [D]. 天津: 天津大学, 2016.
XIN Leilei. Analysis of response of the existing tunnel and building in excavation based on deformation control criterions [D]. Tianjin: Tianjin University, 2015.
[23]
陈磊. 小应变本构模型在留有反压土的基坑开挖变形中的应用 [D]. 天津: 天津大学, 2014.
[本文引用: 2]
CHEN Lei. Application of Hardening Soil Small in deformation analysis of foundation pit with earth berms [D]. Tianjin: Tianjin University, 2014.
[本文引用: 2]
[24]
天津市勘察设计院集团有限公司. 天津地铁8号线一期工程岩土工程勘察报告: 下瓦房站[R]. 天津: 天津市勘察设计院集团有限公司, 2020.
[本文引用: 3]
[25]
BOLTON M D The strength and dilatancy of sands
[J]. Géotechnique , 1986 , 36 (1 ): 65 - 78
[本文引用: 1]
[26]
BRINKGREVE R B J, VERMEER P A. PLAXIS reference manual connect edition V20 [M]. Delft: PLAXIS B. V. , 2019.
[本文引用: 2]
[27]
YANG J, GU X Q Shear stiffness of granular material at small strains: does it depend on grain size?
[J]. Géotechnique , 2013 , 63 (2 ): 165 - 179
[本文引用: 1]
[28]
夏峰, 宋成科, 孟庆筱, 等 天津地区覆盖层土动力学参数统计分析
[J]. 地震工程学报 , 2015 , 37 (1 ): 48 - 54
[本文引用: 4]
XIA Feng, SONG Chengke, MENG Qingxiao, et al Analysis of soil dynamic parameters of overburden in the Tianjin area
[J]. China Earthquake Engineering Journal , 2015 , 37 (1 ): 48 - 54
[本文引用: 4]
[29]
刘念武, 龚晓南, 楼春晖 软土地区基坑开挖对周边设施的变形特性影响
[J]. 浙江大学学报: 工学版 , 2014 , 48 (7 ): 1141 - 1147
[本文引用: 2]
LIU Nianwu, GONG Xiaonan, LOU Chunhui Deformation behavior of nearby facilities analysis induced by excavation in soft clay
[J]. Journal of Zhejiang University: Engineering Science , 2014 , 48 (7 ): 1141 - 1147
[本文引用: 2]
[30]
乔世范, 蔡子勇, 张震, 等 南沙港区软土狭长深基坑围护体系性状
[J]. 浙江大学学报: 工学版 , 2022 , 56 (8 ): 1473 - 1484
[本文引用: 1]
QIAO Shifan, CAI Ziyong, ZHANG Zhen, et al Behavior of retaining system of narrow-long deep foundation pit in soft soil in Nansha Port Area
[J]. Journal of Zhejiang University: Engineering Science , 2022 , 56 (8 ): 1473 - 1484
[本文引用: 1]
[31]
TAN Y, WEI B, DIAO Y, et al Spatial corner effects of long and narrow multipropped deep excavations in Shanghai soft clay
[J]. Journal of Performance of Constructed Facilities , 2014 , 28 (4 ): 04014015
DOI:10.1061/(ASCE)CF.1943-5509.0000475
[本文引用: 2]
[32]
郑刚, 赵悦镔, 程雪松, 等 复杂地层中基坑降水引发的水位及沉降分析与控制对策
[J]. 土木工程学报 , 2019 , 52 (Suppl.1 ): 135 - 142
[本文引用: 1]
ZHENG Gang, ZHAO Yuebin, CHENG Xuesong, et al Strategy and analysis of the settlement and deformation caused by dewatering under complicated geological condition
[J]. China Civil Engineering Journal , 2019 , 52 (Suppl.1 ): 135 - 142
[本文引用: 1]
[33]
曾超峰, 王硕, 袁志成, 等 考虑邻近结构阻隔影响的基坑开挖前降水引发地层变形的特性
[J]. 浙江大学学报: 工学版 , 2021 , 55 (2 ): 338 - 347
[本文引用: 1]
ZENG Chaofeng, WANG Shuo, YUAN Zhicheng, et al Characteristics of ground deformation induced by pre-excavation dewatering considering blocking effect of adjacent structure
[J]. Journal of Zhejiang University: Engineering Science , 2021 , 55 (2 ): 338 - 347
[本文引用: 1]
敏感环境下基坑数值分析中土体本构模型的选择
1
2010
... 在建筑物密集的复杂城市环境下,须重点关注深基坑开挖的变形特性和开挖对周边环境的影响. 数值分析方法是设计和分析深基坑工程的有效手段之一,但其计算准确的前提是选择合适的本构模型以及模型参数的合理确定[1 ] ,盲目的参数选取极易导致不合理的数值结果. 小应变硬化(hardening soil model with small strain,HSS)本构模型[2 ] 由于能考虑土体的小应变阶段剪切模量的应力相关性和非线性,近年来在基坑工程领域得到广泛的应用,并已纳入部分地方规范[3 ] 中. ...
敏感环境下基坑数值分析中土体本构模型的选择
1
2010
... 在建筑物密集的复杂城市环境下,须重点关注深基坑开挖的变形特性和开挖对周边环境的影响. 数值分析方法是设计和分析深基坑工程的有效手段之一,但其计算准确的前提是选择合适的本构模型以及模型参数的合理确定[1 ] ,盲目的参数选取极易导致不合理的数值结果. 小应变硬化(hardening soil model with small strain,HSS)本构模型[2 ] 由于能考虑土体的小应变阶段剪切模量的应力相关性和非线性,近年来在基坑工程领域得到广泛的应用,并已纳入部分地方规范[3 ] 中. ...
2
... 在建筑物密集的复杂城市环境下,须重点关注深基坑开挖的变形特性和开挖对周边环境的影响. 数值分析方法是设计和分析深基坑工程的有效手段之一,但其计算准确的前提是选择合适的本构模型以及模型参数的合理确定[1 ] ,盲目的参数选取极易导致不合理的数值结果. 小应变硬化(hardening soil model with small strain,HSS)本构模型[2 ] 由于能考虑土体的小应变阶段剪切模量的应力相关性和非线性,近年来在基坑工程领域得到广泛的应用,并已纳入部分地方规范[3 ] 中. ...
... 采用如下公式[2 ] 对表2 中数据进行拟合: ...
1
... 在建筑物密集的复杂城市环境下,须重点关注深基坑开挖的变形特性和开挖对周边环境的影响. 数值分析方法是设计和分析深基坑工程的有效手段之一,但其计算准确的前提是选择合适的本构模型以及模型参数的合理确定[1 ] ,盲目的参数选取极易导致不合理的数值结果. 小应变硬化(hardening soil model with small strain,HSS)本构模型[2 ] 由于能考虑土体的小应变阶段剪切模量的应力相关性和非线性,近年来在基坑工程领域得到广泛的应用,并已纳入部分地方规范[3 ] 中. ...
3
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... 王浩然等[4 -5 ] 研究指出,$ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m 是影响基坑变形的最重要的3个参数(即小应变参数),其余参数对基坑变形的影响相对较小. 然而如引言所述,现有文献中数值模拟大多采用的是$ G_{\text{0}}^{{\text{ref}}} = n{E_{{\text{s1-2}}}} $ n 为拟合参数)的倍数经验方法,且将γ 0.7 认为是定值. 考虑到取样扰动对土体小应变剪切模量的影响[12 ] ,合理的方法应当为采用现场原位波速试验的结果来确定$ G_{\text{0}}^{{\text{ref}}} $ m ,并考虑γ 0.7 受土层深度变化的影响. ...
3
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... 王浩然等[4 -5 ] 研究指出,$ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m 是影响基坑变形的最重要的3个参数(即小应变参数),其余参数对基坑变形的影响相对较小. 然而如引言所述,现有文献中数值模拟大多采用的是$ G_{\text{0}}^{{\text{ref}}} = n{E_{{\text{s1-2}}}} $ n 为拟合参数)的倍数经验方法,且将γ 0.7 认为是定值. 考虑到取样扰动对土体小应变剪切模量的影响[12 ] ,合理的方法应当为采用现场原位波速试验的结果来确定$ G_{\text{0}}^{{\text{ref}}} $ m ,并考虑γ 0.7 受土层深度变化的影响. ...
上海地区基坑开挖数值分析中土体HS-Small模型参数的研究
5
2013
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... HSS模型共有13个参数,强度参数c' 、φ' 和K 0 可根据勘察报告确定. 剪胀角ψ 参考Bolton[25 ] 的研究,对砂土有ψ =φ' −30° ,当φ' <30° 时,ψ =0;对于黏性土,ψ =0. 破坏比R f ,通常取PLAXIS建议值0.9[5 ,9 ,26 ] . 根据PLAXIS用户手册,参考应力p ref =100 kPa,加卸载泊松比v ur =0.2[5 ,9 ,26 ] . 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... [5 ,9 ,26 ]. 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... 王浩然等[4 -5 ] 研究指出,$ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m 是影响基坑变形的最重要的3个参数(即小应变参数),其余参数对基坑变形的影响相对较小. 然而如引言所述,现有文献中数值模拟大多采用的是$ G_{\text{0}}^{{\text{ref}}} = n{E_{{\text{s1-2}}}} $ n 为拟合参数)的倍数经验方法,且将γ 0.7 认为是定值. 考虑到取样扰动对土体小应变剪切模量的影响[12 ] ,合理的方法应当为采用现场原位波速试验的结果来确定$ G_{\text{0}}^{{\text{ref}}} $ m ,并考虑γ 0.7 受土层深度变化的影响. ...
上海地区基坑开挖数值分析中土体HS-Small模型参数的研究
5
2013
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... HSS模型共有13个参数,强度参数c' 、φ' 和K 0 可根据勘察报告确定. 剪胀角ψ 参考Bolton[25 ] 的研究,对砂土有ψ =φ' −30° ,当φ' <30° 时,ψ =0;对于黏性土,ψ =0. 破坏比R f ,通常取PLAXIS建议值0.9[5 ,9 ,26 ] . 根据PLAXIS用户手册,参考应力p ref =100 kPa,加卸载泊松比v ur =0.2[5 ,9 ,26 ] . 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... [5 ,9 ,26 ]. 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... 王浩然等[4 -5 ] 研究指出,$ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m 是影响基坑变形的最重要的3个参数(即小应变参数),其余参数对基坑变形的影响相对较小. 然而如引言所述,现有文献中数值模拟大多采用的是$ G_{\text{0}}^{{\text{ref}}} = n{E_{{\text{s1-2}}}} $ n 为拟合参数)的倍数经验方法,且将γ 0.7 认为是定值. 考虑到取样扰动对土体小应变剪切模量的影响[12 ] ,合理的方法应当为采用现场原位波速试验的结果来确定$ G_{\text{0}}^{{\text{ref}}} $ m ,并考虑γ 0.7 受土层深度变化的影响. ...
1
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
1
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
2
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
2
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
考虑扰动影响的土体小应变硬化模型参数试验研究及其在基坑工程中的应用
1
2023
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
考虑扰动影响的土体小应变硬化模型参数试验研究及其在基坑工程中的应用
1
2023
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
济南典型地层HSS参数选取及适用性研究
4
2019
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... HSS模型共有13个参数,强度参数c' 、φ' 和K 0 可根据勘察报告确定. 剪胀角ψ 参考Bolton[25 ] 的研究,对砂土有ψ =φ' −30° ,当φ' <30° 时,ψ =0;对于黏性土,ψ =0. 破坏比R f ,通常取PLAXIS建议值0.9[5 ,9 ,26 ] . 根据PLAXIS用户手册,参考应力p ref =100 kPa,加卸载泊松比v ur =0.2[5 ,9 ,26 ] . 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... ,9 ,26 ]. 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
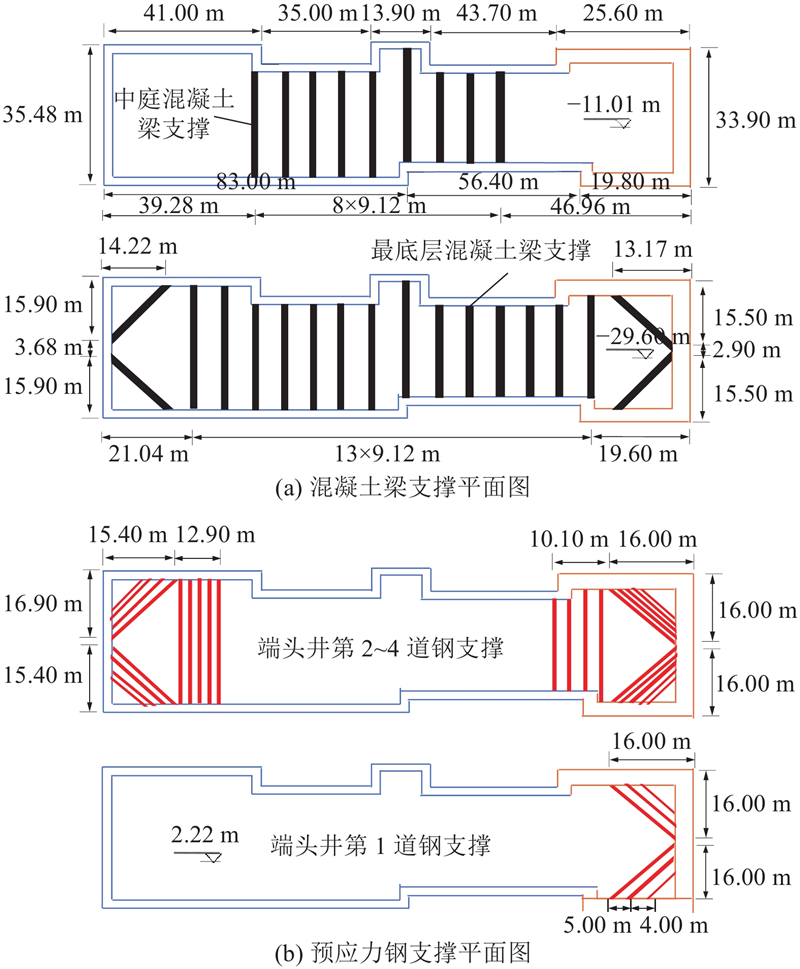
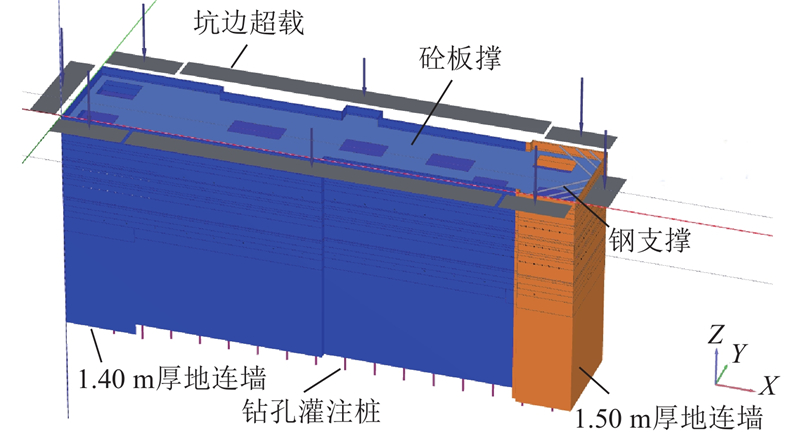
... 为了合理反映基坑的空间特征,采用PLAXIS 3D建立下瓦房站基坑开挖三维有限元模型. 为了减小边界条件对计算结果的影响,模型高度宜大于基坑开挖深度的2~4倍,模型一侧宽度宜大于基坑开挖深度的3~4倍[9 ] . 因此,三维数值模型尺寸设为360 m×280 m×110 m. 基坑开挖过程中考虑坑边2~10 m范围内的超载,其中标准段为20 kPa,端头井为30 kPa. 网格采用超细网格,并在坑内进行局部加密,模型共666 904个节点,447 369个单元. 如图6 所示为基坑围护结构的模型示意图. ...
济南典型地层HSS参数选取及适用性研究
4
2019
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... HSS模型共有13个参数,强度参数c' 、φ' 和K 0 可根据勘察报告确定. 剪胀角ψ 参考Bolton[25 ] 的研究,对砂土有ψ =φ' −30° ,当φ' <30° 时,ψ =0;对于黏性土,ψ =0. 破坏比R f ,通常取PLAXIS建议值0.9[5 ,9 ,26 ] . 根据PLAXIS用户手册,参考应力p ref =100 kPa,加卸载泊松比v ur =0.2[5 ,9 ,26 ] . 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... ,9 ,26 ]. 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... 为了合理反映基坑的空间特征,采用PLAXIS 3D建立下瓦房站基坑开挖三维有限元模型. 为了减小边界条件对计算结果的影响,模型高度宜大于基坑开挖深度的2~4倍,模型一侧宽度宜大于基坑开挖深度的3~4倍[9 ] . 因此,三维数值模型尺寸设为360 m×280 m×110 m. 基坑开挖过程中考虑坑边2~10 m范围内的超载,其中标准段为20 kPa,端头井为30 kPa. 网格采用超细网格,并在坑内进行局部加密,模型共666 904个节点,447 369个单元. 如图6 所示为基坑围护结构的模型示意图. ...
6
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
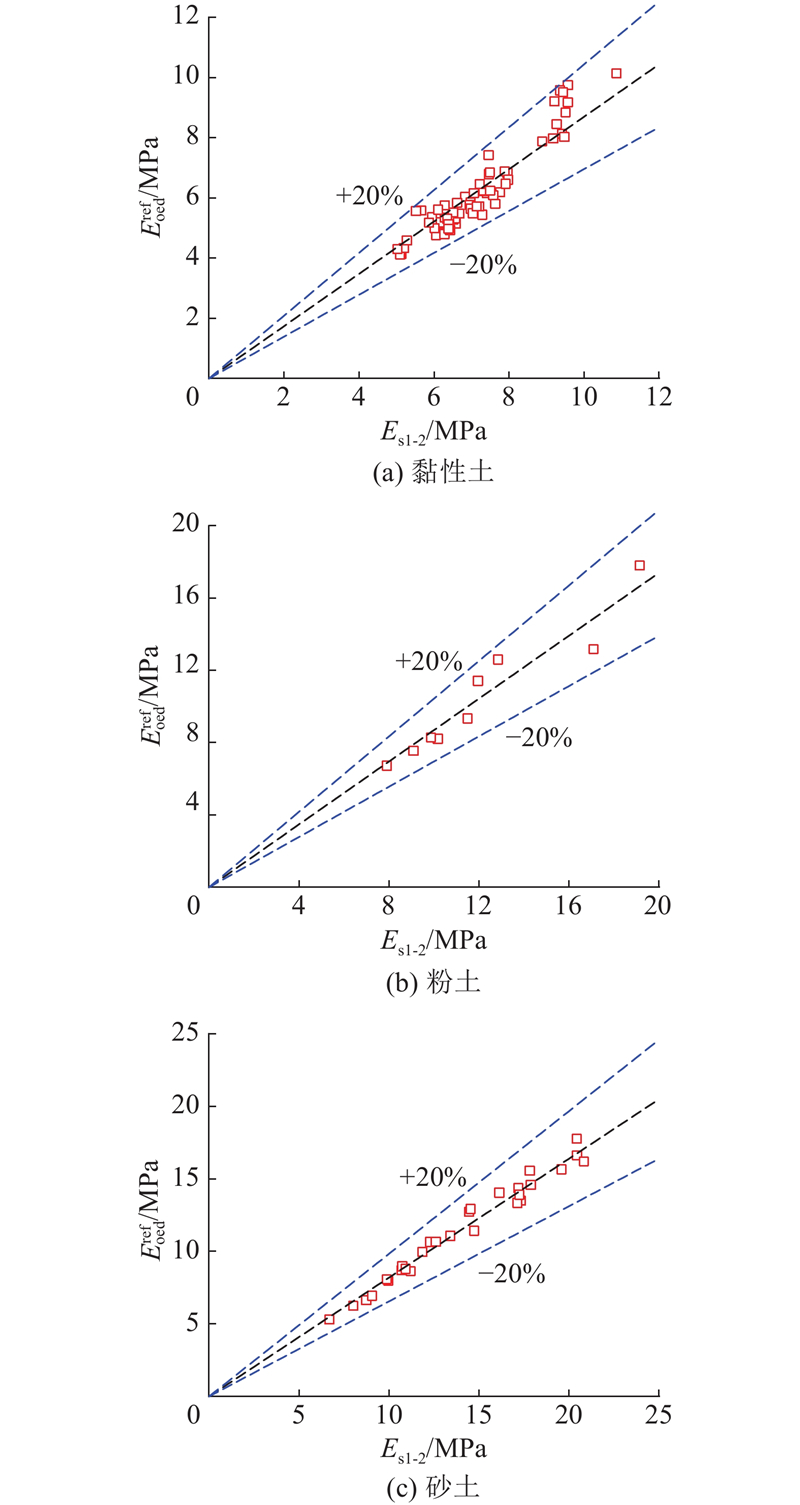
... 对本场地上百组标准固结试验中的应力-应变曲线进行乘幂拟合[10 ] ,相关系数R 2 >0.99,求得拟合曲线在100 kPa处的斜率即为土体参考切线模量$ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ E s1-2 的经验关系:$ E_{{\text{oed}}}^{{\text{ref}}} = 0.87{E_{{\text{s1-2}}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} = 0.82{E_{{\text{s1-2}}}} $ 图4 . 结果表明,$ E_{{\text{oed}}}^{{\text{ref}}} $ E s1-2 的线性关系较好,拟合公式的误差小于20%. ...
... 对于$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [10 ,18 -23 ] ,计算表达式如下: ...
... 地连墙和混凝土楼板撑采用板单元模拟,地连墙表面添加正负界面单元以模拟墙土相互作用,界面参数R inter 取0.7[10 ] . 钻孔灌注桩采用Embedded桩单元模拟,钢支撑、混凝土梁支撑采用点对点锚杆单元模拟. 相关结构尺寸见2.2节,结构弹性模量如表4 所示. 其中,E 为弹性模量. ...
6
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
... 对本场地上百组标准固结试验中的应力-应变曲线进行乘幂拟合[10 ] ,相关系数R 2 >0.99,求得拟合曲线在100 kPa处的斜率即为土体参考切线模量$ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ E s1-2 的经验关系:$ E_{{\text{oed}}}^{{\text{ref}}} = 0.87{E_{{\text{s1-2}}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} = 0.82{E_{{\text{s1-2}}}} $ 图4 . 结果表明,$ E_{{\text{oed}}}^{{\text{ref}}} $ E s1-2 的线性关系较好,拟合公式的误差小于20%. ...
... 对于$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [10 ,18 -23 ] ,计算表达式如下: ...
... 地连墙和混凝土楼板撑采用板单元模拟,地连墙表面添加正负界面单元以模拟墙土相互作用,界面参数R inter 取0.7[10 ] . 钻孔灌注桩采用Embedded桩单元模拟,钢支撑、混凝土梁支撑采用点对点锚杆单元模拟. 相关结构尺寸见2.2节,结构弹性模量如表4 所示. 其中,E 为弹性模量. ...
The geotechnical properties of soils
1
1970
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
上海土体小应变硬化模型整套参数取值方法及工程验证
3
2021
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... 王浩然等[4 -5 ] 研究指出,$ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m 是影响基坑变形的最重要的3个参数(即小应变参数),其余参数对基坑变形的影响相对较小. 然而如引言所述,现有文献中数值模拟大多采用的是$ G_{\text{0}}^{{\text{ref}}} = n{E_{{\text{s1-2}}}} $ n 为拟合参数)的倍数经验方法,且将γ 0.7 认为是定值. 考虑到取样扰动对土体小应变剪切模量的影响[12 ] ,合理的方法应当为采用现场原位波速试验的结果来确定$ G_{\text{0}}^{{\text{ref}}} $ m ,并考虑γ 0.7 受土层深度变化的影响. ...
上海土体小应变硬化模型整套参数取值方法及工程验证
3
2021
... 考虑到土体具有强烈的区域性特征,学者们对各地的HSS模型参数取值开展相关研究. 王浩然等[4 -5 ] 较早开展了上海地区HSS模型参数取值的研究,通过室内试验和反分析,将HSS模型中众多的模量参数(如$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 类似地,学者们陆续建立了无锡[6 ] 、杭州[7 ] 、宁波[8 ] 、济南[9 ] 、天津[10 ] 等地区的HSS参数选取方法,均将$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ E s1-2 建立倍数经验关系. 但是该方法存在模量间倍数关系浮动范围较大的问题,且土体越软,$ E_{{\text{ur}}}^{{\text{ref}}} $ $ E_{{\text{50}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [11 -12 ] ,简单的倍数关系如$ {G}_{\text{0}}^{\text{ref}}=n{E}_{\text{s1-2}}或{G}_{\text{0}}^{\text{ref}}=n{E}_{\text{50}}^{\text{ref}} $ n 为拟合参数),可能无法准确反映土体的小应变刚度特性. ...
... 参考Hardin公式,顾晓强等[12 ] 对上海土体开展了大量室内和原位试验,并结合文献中的试验数据,提出一套$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ e 0 的计算关系式,通过实际基坑案例的计算,验证了该取值方法的可靠性. 然而尚未有适用于天津软土地区的$ G_{\text{0}}^{{\text{ref}}} $ e 0 的试验统计结果. 由于土体模量具有应力相关特性,模量应力水平相关幂指数m 的准确选取对基坑变形分析至关重要,以往研究多采用经验方法[4 ,5 ,7 -10 ] ,未根据现场波速试验结果确定幂指数m . ...
... 王浩然等[4 -5 ] 研究指出,$ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m 是影响基坑变形的最重要的3个参数(即小应变参数),其余参数对基坑变形的影响相对较小. 然而如引言所述,现有文献中数值模拟大多采用的是$ G_{\text{0}}^{{\text{ref}}} = n{E_{{\text{s1-2}}}} $ n 为拟合参数)的倍数经验方法,且将γ 0.7 认为是定值. 考虑到取样扰动对土体小应变剪切模量的影响[12 ] ,合理的方法应当为采用现场原位波速试验的结果来确定$ G_{\text{0}}^{{\text{ref}}} $ m ,并考虑γ 0.7 受土层深度变化的影响. ...
Vibration modulus of normally consolidated clay
1
1968
... Hardin等[13 ] 指出,土的小应变剪切模量G 0 与初始孔隙比e 0 、平均有效主应力、结构性等有关,随之提出适用于黏性土的Hardin公式,$ {G_0} = 3\;230{({\mathrm{OCR}})^k}{(\sigma _{\mathrm{m}}^{'})^{0.5}}{(2.97 - e)^2}/(1+e) $ G 0 为小应变剪切模量,e 为土体孔隙比,OCR为超固结比,$ \sigma _{\mathrm{m}}^{'} $ k 为影响系数,与塑性指数I p 有关. ...
1
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
Stiffness of clays and silts: normalizing shear modulus and shear strain
0
2013
Stiffness of sands through a laboratory test database
0
2013
Small strain shear modulus of the Ljubljana marsh soil measured with resonant column and bender elements under isotropic and anisotropic stress conditions
1
2024
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
基坑开挖引起邻近既有隧道变形的影响区研究
2
2016
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
... 对于$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [10 ,18 -23 ] ,计算表达式如下: ...
基坑开挖引起邻近既有隧道变形的影响区研究
2
2016
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
... 对于$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [10 ,18 -23 ] ,计算表达式如下: ...
软土地区超深基坑引发邻近重要建筑沉降的倾斜注浆主动控制方案: 以天津地铁7号线某地下四层站工程为例
0
2023
软土地区超深基坑引发邻近重要建筑沉降的倾斜注浆主动控制方案: 以天津地铁7号线某地下四层站工程为例
0
2023
基于HSS模型的基坑开挖对近邻地铁影响数值分析
0
2021
基于HSS模型的基坑开挖对近邻地铁影响数值分析
0
2021
基坑开挖引起地铁结构隆起的堆载控制研究
0
2024
基坑开挖引起地铁结构隆起的堆载控制研究
0
2024
2
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
... 对于$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [10 ,18 -23 ] ,计算表达式如下: ...
2
... Brinkgreve等[14 -17 ] 的研究均表明,剪切模量衰减参数γ 0.7 (剪切模量衰减到初始剪切模量72.2%时对应的剪应变)受围压或者平均有效应力变化的影响,γ 0.7 随着围压增大而增大,即不同深度处的γ 0.7 应当不同. 但是目前大部分数值模拟中,将各深度土层的γ 0.7 设为相同值,如天津地区经验值为0.000 2或0.000 3[10 ,18 -23 ] . ...
... 对于$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ [10 ,18 -23 ] ,计算表达式如下: ...
3
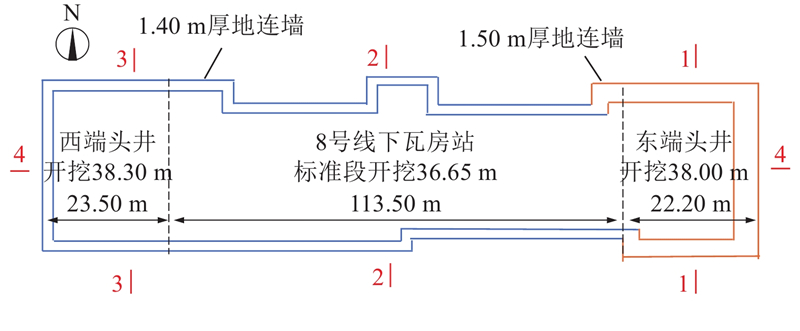
... 在场地110 m的深度范围内,共有21层土层,根据勘察报告[24 ] ,各土层的基本物理力学指标如表1 所示. 其中,e 0 为土体初始孔隙比,γ 为土的重度,c' 为有效黏聚力,φ' 为有效内摩擦角. 场地潜水水位埋深为−1.10~−1.50 m,基坑坑内降水为开挖面以下1.0 m. 基坑开挖范围内涉及3组承压含水层,第1承压含水层为砂质粉土层(⑧2 ),粉砂层(⑨2 ),承压水位标高约为−2.52 m,;第2承压含水层为粉砂层(⑪2 、⑪4 ),承压水位标高约为−2.72 m;第3承压含水层为粉砂层(⑬2 ),承压水位标高约为−14.27 m. 相应的隔水层分别为⑦、⑧1 、⑩1 、⑪1 、⑪5 、⑫1 、⑬3 、⑭1 层. ...
... 依据勘察报告[24 ] 以及第3章中的参数取值关系式,该场地21层土层的HSS模型参数和土层厚度如表5 和表1 所示. 其中,$\Delta{d} $
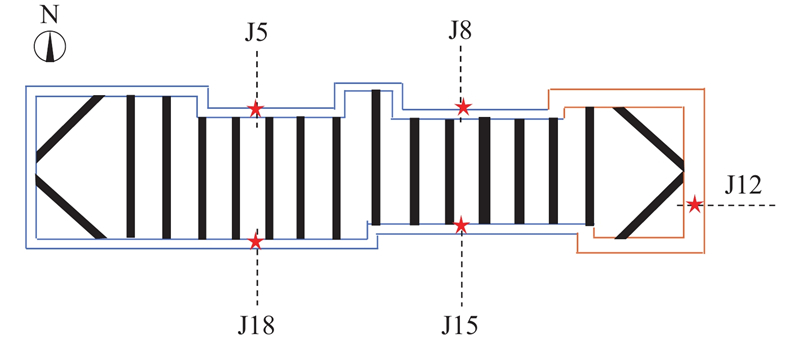
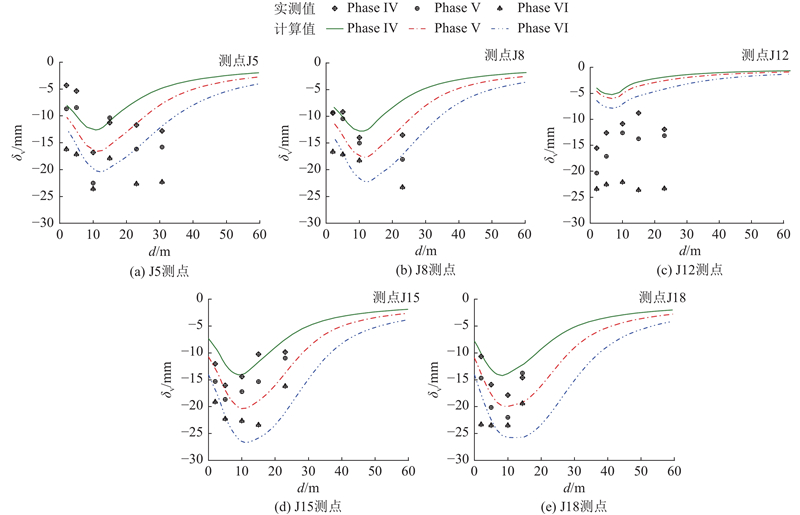
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...
The strength and dilatancy of sands
1
1986
... HSS模型共有13个参数,强度参数c' 、φ' 和K 0 可根据勘察报告确定. 剪胀角ψ 参考Bolton[25 ] 的研究,对砂土有ψ =φ' −30° ,当φ' <30° 时,ψ =0;对于黏性土,ψ =0. 破坏比R f ,通常取PLAXIS建议值0.9[5 ,9 ,26 ] . 根据PLAXIS用户手册,参考应力p ref =100 kPa,加卸载泊松比v ur =0.2[5 ,9 ,26 ] . 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
2
... HSS模型共有13个参数,强度参数c' 、φ' 和K 0 可根据勘察报告确定. 剪胀角ψ 参考Bolton[25 ] 的研究,对砂土有ψ =φ' −30° ,当φ' <30° 时,ψ =0;对于黏性土,ψ =0. 破坏比R f ,通常取PLAXIS建议值0.9[5 ,9 ,26 ] . 根据PLAXIS用户手册,参考应力p ref =100 kPa,加卸载泊松比v ur =0.2[5 ,9 ,26 ] . 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
... ,26 ]. 因此,HSS模型参数取值的关键在于准确确定以下6个参数:$ E_{{\text{50}}}^{{\text{ref}}} $ $ E_{{\text{oed}}}^{{\text{ref}}} $ $ E_{{\text{ur}}}^{{\text{ref}}} $ $ G_{\text{0}}^{{\text{ref}}} $ γ 0.7 和m . ...
Shear stiffness of granular material at small strains: does it depend on grain size?
1
2013
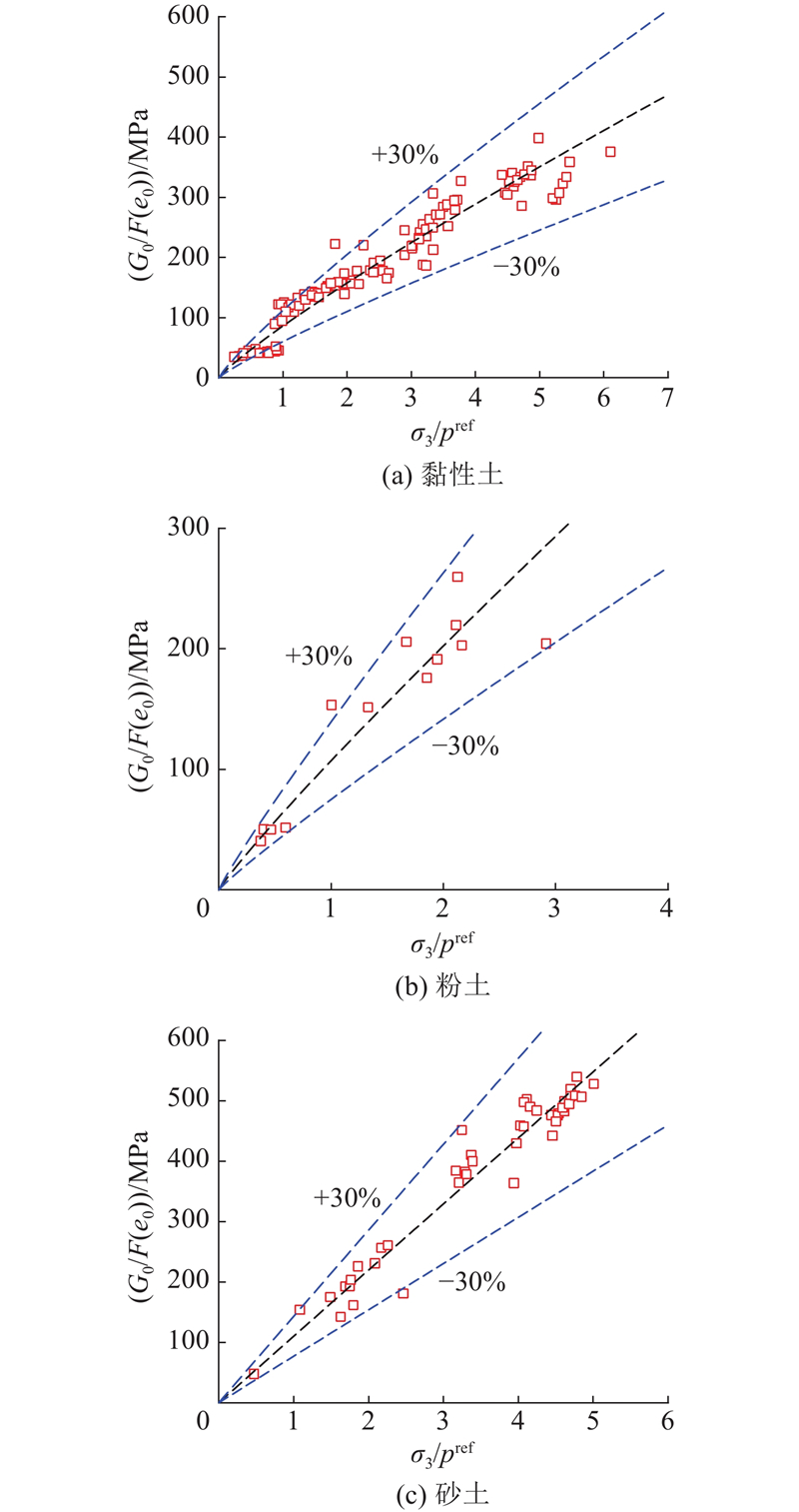
... 对下瓦房站3个钻孔共160余个不同深度处的波速数据进行统计分析,将不同深度处土体的G 0 与初始孔隙比e 0 以及水平向有效围压σ 3 建立经验关系:$ {G_0} = 86.21e_0^{ - 0.29}{({\sigma _3}/{p^{\rm{ref}}})^{0.872}} $ $ {G_0} = 107.24e_0^{ - 0.29}{({\sigma _3}/{p^{\rm{ref}}})^{0.917}} $ $ {G_0} = 110.13e_0^{ - 0.29}\;\times {({\sigma _3}/{p^{\rm{ref}}})^{0.997}} $ 图5 所示,其中F (e 0 )为孔隙比的函数,反映初始孔隙比对G 0 的影响,本研究采用F (e 0 )=$e_0^{-n} $ [27 ] ,n 为拟合参数,p ref 为参考应力,取100 kPa. 由图5 可见,拟合公式的误差总体小于30%. PLAXIS软件默认采用水平向围压σ 3 对不同深度的G 0 进行换算,因此本研究采用σ 3 作为应力相关的参数,σ 3 为土体上覆有效应力σ 1 与静止土压力系数K 0 的乘积. 图5 公式取σ 3 =100 kPa得到的G 0 ,即为HSS模型中的$ G_{\text{0}}^{{\text{ref}}} $ . ...
天津地区覆盖层土动力学参数统计分析
4
2015
... 关于γ 0.7 的取值,夏峰等[28 ] 根据1 480组动三轴试验数据,统计了天津地区埋深120 m以内的土动力学参数,其统计的G -γ 平均值见表2 . ...
... 天津地区不同深度粉质黏土剪切模量随剪应变衰减规律统计[28 ] ...
... Statistics of shear modulus degradation with shear strain under different depths for silty clays in Tianjin area[28 ] ...
... 较为遗憾的是,夏峰等[28 ] 仅给出粉质黏土的模量衰减数值,并未给出砂土和粉土的数值大小,但其文中指出不同土类的模量衰减关系相似. 因此,本研究将粉土和砂土的γ 0.7 也近似按粉质黏土取值. ...
天津地区覆盖层土动力学参数统计分析
4
2015
... 关于γ 0.7 的取值,夏峰等[28 ] 根据1 480组动三轴试验数据,统计了天津地区埋深120 m以内的土动力学参数,其统计的G -γ 平均值见表2 . ...
... 天津地区不同深度粉质黏土剪切模量随剪应变衰减规律统计[28 ] ...
... Statistics of shear modulus degradation with shear strain under different depths for silty clays in Tianjin area[28 ] ...
... 较为遗憾的是,夏峰等[28 ] 仅给出粉质黏土的模量衰减数值,并未给出砂土和粉土的数值大小,但其文中指出不同土类的模量衰减关系相似. 因此,本研究将粉土和砂土的γ 0.7 也近似按粉质黏土取值. ...
软土地区基坑开挖对周边设施的变形特性影响
2
2014
... 本研究方法的有限元变形结果如图8 (a)所示,基坑围护墙实测变形和有限元计算结果均呈现出中间大,两端小的三维空间特征[29 -30 ] ,这与Tan等[31 ] 在软土地区长条形地铁深基坑中的实测结果类似,即基坑端部的围护墙变形小于基坑长边中部的变形. 图8 (b)~图8 (f)分别对比了不同位置测点处,从开挖至−20.60 m到坑底(Phase IV至VI)阶段,围护结构在不同深度z 处的围护墙侧移δ h 的计算值与实测值. ...
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...
软土地区基坑开挖对周边设施的变形特性影响
2
2014
... 本研究方法的有限元变形结果如图8 (a)所示,基坑围护墙实测变形和有限元计算结果均呈现出中间大,两端小的三维空间特征[29 -30 ] ,这与Tan等[31 ] 在软土地区长条形地铁深基坑中的实测结果类似,即基坑端部的围护墙变形小于基坑长边中部的变形. 图8 (b)~图8 (f)分别对比了不同位置测点处,从开挖至−20.60 m到坑底(Phase IV至VI)阶段,围护结构在不同深度z 处的围护墙侧移δ h 的计算值与实测值. ...
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...
南沙港区软土狭长深基坑围护体系性状
1
2022
... 本研究方法的有限元变形结果如图8 (a)所示,基坑围护墙实测变形和有限元计算结果均呈现出中间大,两端小的三维空间特征[29 -30 ] ,这与Tan等[31 ] 在软土地区长条形地铁深基坑中的实测结果类似,即基坑端部的围护墙变形小于基坑长边中部的变形. 图8 (b)~图8 (f)分别对比了不同位置测点处,从开挖至−20.60 m到坑底(Phase IV至VI)阶段,围护结构在不同深度z 处的围护墙侧移δ h 的计算值与实测值. ...
南沙港区软土狭长深基坑围护体系性状
1
2022
... 本研究方法的有限元变形结果如图8 (a)所示,基坑围护墙实测变形和有限元计算结果均呈现出中间大,两端小的三维空间特征[29 -30 ] ,这与Tan等[31 ] 在软土地区长条形地铁深基坑中的实测结果类似,即基坑端部的围护墙变形小于基坑长边中部的变形. 图8 (b)~图8 (f)分别对比了不同位置测点处,从开挖至−20.60 m到坑底(Phase IV至VI)阶段,围护结构在不同深度z 处的围护墙侧移δ h 的计算值与实测值. ...
Spatial corner effects of long and narrow multipropped deep excavations in Shanghai soft clay
2
2014
... 本研究方法的有限元变形结果如图8 (a)所示,基坑围护墙实测变形和有限元计算结果均呈现出中间大,两端小的三维空间特征[29 -30 ] ,这与Tan等[31 ] 在软土地区长条形地铁深基坑中的实测结果类似,即基坑端部的围护墙变形小于基坑长边中部的变形. 图8 (b)~图8 (f)分别对比了不同位置测点处,从开挖至−20.60 m到坑底(Phase IV至VI)阶段,围护结构在不同深度z 处的围护墙侧移δ h 的计算值与实测值. ...
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...
复杂地层中基坑降水引发的水位及沉降分析与控制对策
1
2019
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...
复杂地层中基坑降水引发的水位及沉降分析与控制对策
1
2019
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...
考虑邻近结构阻隔影响的基坑开挖前降水引发地层变形的特性
1
2021
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...
考虑邻近结构阻隔影响的基坑开挖前降水引发地层变形的特性
1
2021
... 然而,已有研究和同类狭长地铁基坑实测结果[29 -31 ] 均表明,坑外地表沉降通常呈现出显著的三维空间特征,本研究的有限元模拟结果与此规律一致(图9 中J12测点计算值小于其余测点的). 现场勘察[24 ] 发现,本场地工程地质较为复杂,局部存在较多的含水透镜体,导致各土层间水力联系密切,易引发基坑内外出现水力联通现象[32 ] ,这可能是基坑端部(J12测点)实测地表沉降较大的原因之一. 另外一方面,为了精确探究地表沉降的影响因素,还应考虑邻近地下结构阻隔效应的影响[33 ] . ...