脑-机接口(brain-computer interface, BCI)是一种创新的通信技术,允许用户通过脑信号直接控制外部设备,无须依赖传统的外周神经系统和肌肉通路[1-3]. 在BCI研究领域,基于稳态视觉诱发电位(steady-state visual evoked potential, SSVEP)的BCI,相较于运动想象、P300和其他基于脑电图(electroencephalogram, EEG)的BCI范式,因其出色的信噪比(signal-to-noise radio, SNR)和信息传输率(information transfer rate, ITR)而受到青睐[4-8],现已广泛应用于机器人控制[9]、智能家居控制[10]以及字符拼写[11]等多个领域.
在SSVEP-BCI领域,开发高效的SSVEP解码方法是实现其实际应用的关键所在. 早期研究尝试利用单通道EEG数据和频率密度分析(power spectrum density analysis, PSDA)来识别SSVEP,但由于对背景噪声的敏感性,这种方法的识别准确率有限[12]. 近年来,多种基于多通道EEG数据的空间滤波技术被引入以提高识别准确率,包括最小能量组合(minimum energy combination, MEC)[13]、多元同步指数(multivariate synchronization index, MSI)[14]和典型相关分析(canonical correlation analysis, CCA)[15]等. 特别是,Lin等[15]提出利用CCA对SSVEP进行解码,通过空间滤波技术有效利用多通道EEG数据的空间信息,并结合人工构建的正余弦参考模板来识别SSVEP. 该方法增强了信号的信噪比,并取得了不错的性能. Chen等[16]提出滤波器组典型相关分析(filter bank CCA, FBCCA)方法,通过整合谐波信息进一步提升SSVEP解码的性能,该技术已被广泛应用于解码算法中[17-21]. 然而,这些无需训练的方法在识别SSVEP频率时易受到自发性大脑活动的干扰,限制了其ITR.
面对这一挑战,研究人员基于CCA进一步开发了利用个体校准试验的空间滤波技术. 结合个体特定的校准试验,提出多集典型相关分析(multi-set CCA, MsetCCA)[17]和扩展典型相关分析(extended CCA, ECCA)[18],以增强SSVEP频率的检测性能. 同时,Nakanishi等[19]提出任务相关成分分析(task-related component analysis, TRCA)及其集成策略(ensemble TRCA, eTRCA),通过最大化校准试验间的重现性来训练空间滤波器,实现了识别性能的显著提升. 此外,Huang等[22]结合相邻位置刺激数据训练空间滤波器,以及Wong等[23]提出的多刺激学习策略,进一步提升了SSVEP-BCI的目标识别性能. 但这些方法须收集充足的校准试验,过程既耗时又费力,对于实用的SSVEP-BCI系统而言,迫切需要一种基于有限校准试验的高效学习策略.
为了在校准试验不足的情况下维持高识别性能,研究者引入迁移学习至SSVEP解码中,通过将源受试者的公共知识迁移至目标受试者,提升目标受试者的解码性能. 这主要涉及2种迁移学习策略:基于转移模板的迁移学习和基于转移空间滤波器的迁移学习. 例如,Yuan等[24]提出基于转移模板的典型相关分析(transfer template-based CCA, tt-CCA),以及Waytowich等[25]提出自适应组合CCA(adaptive-C3A),旨在将源受试者的SSVEP模板迁移至目标受试者. Yan等[26-27]提出跨受试者空间滤波器转移(cross-subject spatial filter transfer, CSSFT)方法及其改进版本,将模板和空间滤波器从源受试者迁移至目标受试者. 尽管这些方法取得了一定的性能提升,但长时间的校准过程仍限制了SSVEP-BCI系统的实际应用.
为了使校准时间更短,并保持高识别性能,研究者基于源受试者和目标受试者共享的公共知识,提出了多种方法. Wang等[28]提出的受试者内和受试者间最大相关性(inter- and intra-subject maximal correlation, IISMC),Lan等[29]提出的转移相关成分分析(transfer-related component analysis, TransRCA)和Wei等[30]提出的受试者内和受试者间典型相关分析(intra- and inter-subject CCA, IISCCA),均取得了良好成绩. 但这些方法仍受限于目标受试者的校准试验,尤其是在仅单一校准试验时,识别准确率会受到严重影响. Chiang等[31]提出的最小二乘变换(least-squares transformation, LST)方法以及Bian等[32]提出的小数据最小二乘变换(small data-LST, sd-LST),通过转换源受试者的数据以匹配目标受试者的数据,补充目标受试者的校准数据集. Luo等[33]采用源混叠矩阵估计(source aliasing matrix estimation, SAME)方法,利用有限的已知校准试验生成反映个体特异性的人工合成校准试验,以此扩展数据集. 这些方法均为数据增强技术,解决了校准试验不足的问题,但受试者的视觉疲劳、注意力失误以及认知负荷等个体差异因素可能会阻碍试验的可转移性[34-35].
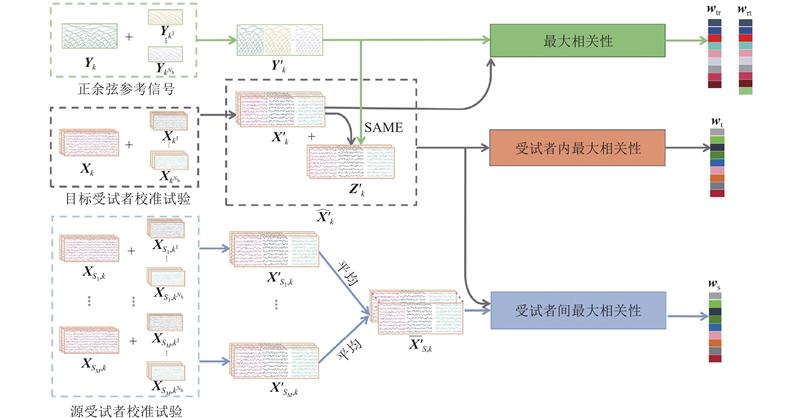
针对校准试验不足,尤其是仅有单一校准试验,以及个体差异因素的挑战,提出跨受试者邻近刺激学习方法. 该方法旨在从受试者的目标刺激及其邻近刺激数据中提取相关信息,包含2个核心组成部分. 1)为了充分利用目标受试者的校准试验并降低个体差异的影响,采取2种策略进行信息融合. 一方面,通过最大化与正余弦参考信号的相关性,提取SSVEP的基波和谐波特征,构建邻近刺激共享空间滤波器;另一方面,通过对目标受试者的校准试验施加SAME增强方法,再最大化其增强后校准试验间的协方差,提取任务相关成分,构建受试者内邻近刺激共享空间滤波器. 2)通过引入源受试者与目标受试者校准试验间的协方差最大化策略,从源受试者数据中提取与目标受试者相似的信号信息,构建受试者间邻近刺激共享空间滤波器. 本方法的优势在于结合了CCA提取信号基波和谐波特性与TRCA提取任务相关信息的优点,能够有效提取SSVEP信号中的基波、谐波特征及任务相关信息,从而提高系统的鲁棒性.
1. 跨受试者邻近刺激学习方法
假设目标受试者第k类刺激的第j次试验的校准试验表示为
在所提方法中,采用不同信号之间的相关性设计了4种邻近共享空间滤波器,用以提取和增强邻近刺激的公共频率信息;构建了2个信号模板,以便对测试试验进行模板匹配. 训练过程如图1所示. 其中,
图 1
1.1. 最大相关性
由于目标刺激下产生的SSVEP信号可以通过与目标刺激相同频率的正余弦信号的线性组合及其谐波叠加来近似表示[15],针对扩展校准试验构造了对应的正余弦扩展参考信号. 与目标受试者的校准试验处理方式一样,正余弦扩展参考信号定义为
式中:fk 表示目标刺激频率;根据文献[16],最大谐波数
模板信号
因此,邻近共享空间滤波器
1.2. 受试者内最大相关性
为了充分提取目标受试者任务相关信息,首先对目标受试者的所有扩展校准试验应用SAME数据增强方法,然后最大化增强后试验间的协方差,学习邻近刺激之间共享空间滤波器,并平均目标受试者所有校准试验以获得SSVEP个体模板.
SAME数据增强方法利用目标受试者有限的已知校准试验,生成能反映其个体特异性的人工合成校准试验,以此扩展数据集. SSVEP的理论模型可以定义为
式中:
最后,人工合成校准试验
式中:
采用SAME对目标受试者扩展校准试验进行数据增强. 具体来说,通过最小二乘变换计算正余弦扩展参考信号
因此,受试者内邻近共享空间滤波器
根据广义瑞利商,受试者内邻近共享空间滤波器
1.3. 受试者间最大相关性
从源受试者数据中提取与目标受试者相似的信号信息,通过最大化目标受试者与源受试者扩展校准试验之间的最大相关性,学习邻近刺激之间共享的跨受试者邻近共享空间滤波器,并通过平均源受试者所有校准试验以获得SSVEP迁移模板. 具体来说,假设
式中:
因此,通过最大化源受试者与目标受试者扩展校准试验之间所有交叉协方差之和来学习受试者间邻近共享滤波器. 源受试者与目标受试者扩展校准试验间所有交叉协方差之和
源受试者扩展校准试验与目标受试者扩展校准试验的自协方差矩阵之和
所求受试者间邻近共享空间滤波器
在本研究中,SAME数据增强并未应用于训练基于邻近刺激最大相关性的滤波器
1.4. SSVEP识别
式中:
式中:sign表示从负相关系数中保留判别信息.
1.5. 空间滤波器集成策略和滤波器组分析
空间滤波器集成策略[19]基于假设来自不同目标的空间滤波器彼此相似,旨在通过结合所有刺激目标的空间滤波器来提升空间滤波的性能. 因此,集成空间滤波器
式中:集成空间滤波器
滤波器组技术将SSVEP分解为子带分量,然后提取嵌入在谐波分量中的高信噪比独立信息,从而促进目标分类. 在这项研究中,第b个子带的下截止频率和上截止频率设置为8b Hz和90 Hz,其中b的范围为1~5[16]. 之后,从切比雪夫I型无限脉冲响应(IIR)带通滤波器过滤的第b个子带信号中提取特征向量
将特征向量
2. 结果与讨论
2.1. SSVEP数据集
选用2个广泛使用的公共数据集:Benchmark数据集[36]和BETA数据集[37]. 这2个数据集均包含由40种不同频率闪烁刺激引发的64通道SSVEP数据. 刺激频率范围为8.0~15.8 Hz,步长为0.2 Hz,相位范围为0~1.5π,步长为0.5π. Benchmark数据集包含了35名受试者的数据,每个刺激目标进行6次试验,共计记录了
2.2. 实验设置
为了验证所提方法的可行性并评估其性能,将其与当前最先进的eTRCA算法以及2种迁移学习算法eIISMC和eTransRCA进行比较. 在参数设置上,eTRCA算法在Benchmark和BETA数据集中均使用5个子频带滤波器,其最终分类准确率和ITR是基于所有受试者的平均值计算得出的. eIISMC算法的子频带滤波器数量与eTRCA相同,目标受试者依次从数据集中选取,同时随机选择5位剩余受试者作为源受试者,此过程重复8次以获得分类准确率和ITR. eTransRCA算法的子频带滤波器数量与eTRCA的相同,目标受试者依次从数据集中选取,但随机选择10位源受试者,重复10次以计算最终结果.
通过平均分类准确率和ITR这2个业界公认的指标,评估基于SSVEP-BCI系统的性能. ITR(单位为bits/min)的计算公式如下:
式中:
准确率和ITR是通过留一法交叉验证得出的. 在具体操作中,数据集划分为目标受试者和源受试者组,目标受试者是从数据集中依次选取的,其余受试者构成源受试者组. 具体而言,对于Benchmark数据集,目标受试者为1名,源受试者组包含34名受试者;对于BETA数据集,目标受试者为1名,源受试者组包含69名受试者. 为了训练空间滤波器和构建信号模板,从源受试者组中随机选择
2.3. 算法性能比较
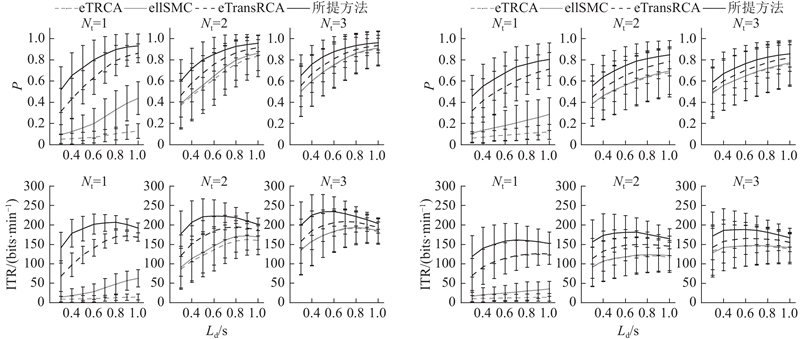
如图2(a)、(b)所示分别展示了在Benchmark数据集和BETA数据集上,各算法在不同数据长度和校准试验数量
图 2
图 2 不同数据长度和校准试验数量下的分类准确率和ITR的比较
Fig.2 Comparison of classification accuracy and ITR against different data lengths and numbers of calibration trials
对于Benchmark数据集,随着数据长度的增加,所提出方法的准确率呈现上升趋势,并明显优于其他算法. 具体而言,在
对于BETA数据集,所提方法的准确率和ITR同样优于其他比较算法. 在
从图2可以看出,算法在Benchmark数据集上的性能优于BETA数据集上的. 这主要是因为Benchmark数据集的采集是在电磁屏蔽的实验室环境中进行的,而BETA数据集则更贴近实际应用场景,未在电磁屏蔽室内采集,因此Benchmark数据集的SNR显著高于BETA的. 尽管算法在BETA数据集上的性能相对较低,但这更能反映出算法在实际应用中的表现.
为了深入探究4种算法的复杂度,进行详尽的分析. 在训练阶段,这些算法均致力于训练如图1所示的空间滤波器,并计算出信号模板;而在测试阶段,则主要聚焦于相关系数的计算以及进行频率识别. 为了验证计算成本的普遍适用性,在一台搭载Intel(R) Core(TM) i7-9700K CPU @ 3.60 GHz处理器(8核)、16GB RAM,并运行64位Windows 10操作系统的计算机上对这些算法进行评估. 评估结果显示,TRCA、eIISMC、eTransRCA以及所提方法的训练时间分别为0.20、0.64、0.45、0.38 s,而相应的预测时间则分别为0.11、0.32、0.17、0.15 s. 鉴于这些算法所展现出的时间复杂度,可以确认该方法能满足在线实验的需求.
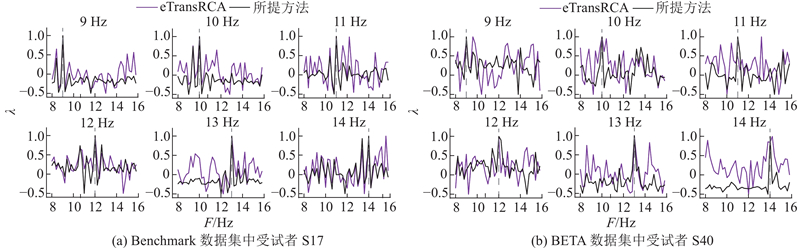
鉴于eTransRCA算法与所提方法的性能差异较小,对这2种方法进一步深入比较. 如图3所示展示了Benchmark数据集中的受试者S17和BETA数据集中的受试者S40使用所提方法和eTransRCA方法时获得的特征值. 每个子图代表一个不同的测试试验,测试试验涵盖了9 ~14 Hz的频率,共计6个子图. 其中,λ为特征值,F为频率. 在每个测试试验中,计算40个特征值并将最大特征值对应的刺激频率定为目标SSVEP识别频率. 各子图中的特征值是通过式(17)计算得到的,并已归一化至[0,1.0]. 数据长度统一设定为0.6 s,且每个受试者的
图 3
图 3 受试者在所提方法和eTransRCA方法下获得的特征值
Fig.3 Feature values obtained by eTransRCA and proposed method from an example subject
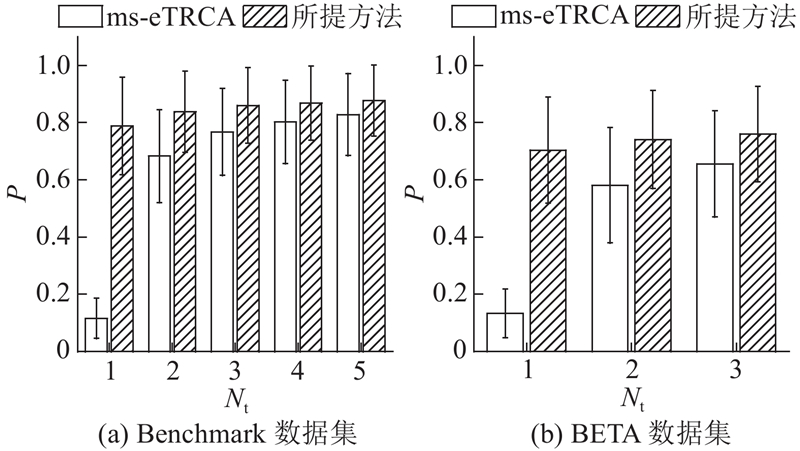
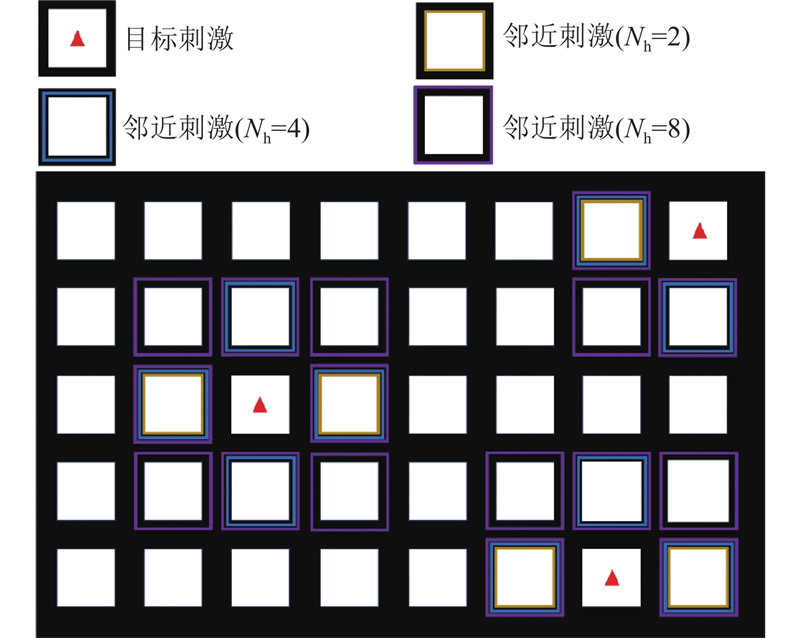
ms-eTRCA方法通过多刺激学习,从目标刺激及其频率相邻的刺激中提取空间滤波器来提高识别准确率,但未能考虑那些在空间上相邻而非频率上相邻的刺激所提供的信息. 在实际应用中,用户的视线可能不完全集中在目标刺激,而是可能受到空间上相邻刺激的影响. 如图4所示展示了所提方法与ms-eTRCA在不同校准试验数量下的平均识别准确率(数据长度在0.3~1.0 s取平均). 结果表明,在所有校准试验条件下,所提方法的识别准确率优于ms-eTRCA的,尤其是在仅进行单一校准试验时,所提方法仍能保持较高的识别准确率.
图 4
图 4 多刺激学习与邻近刺激学习算法对比
Fig.4 Comparison between multi-stimulus learning and neighboring stimulus learning
2.4. 算法性能评估
2.4.1. 源受试者数量的影响
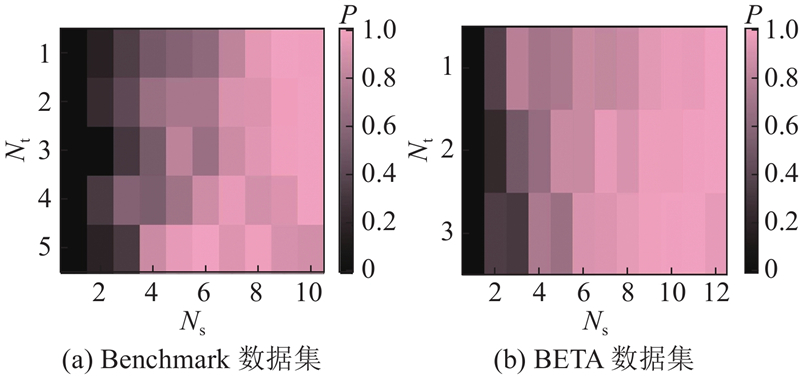
为了探究源受试者数量
图 5
图 5 不同校准试验数量和源受试者数量条件下的分类准确率
Fig.5 Classification accuracy against different numbers of calibration trials and source subjects
2.4.2. 校准试验数量的影响
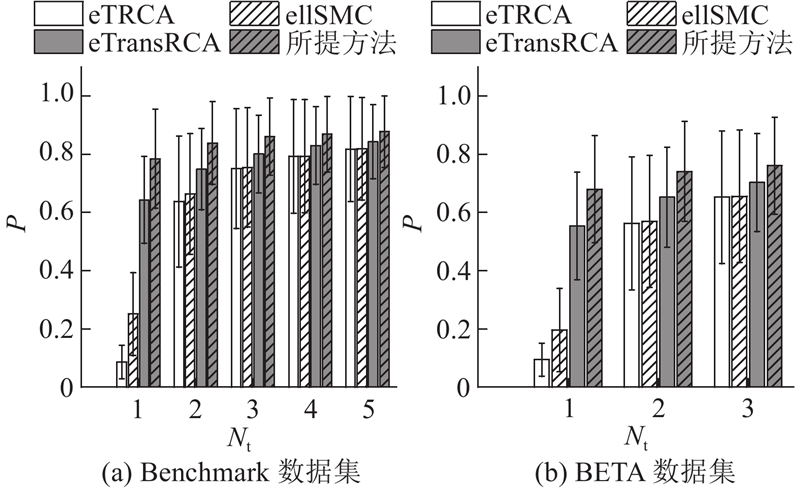
如图6所示比较了不同数量的校准试验对分类准确率的影响,结果在受试者和数据长度上取平均值. 随着
图 6
图 6 不同校准试验数量的分类准确率对比
Fig.6 Comparison of classification accuracy against different numbers of calibration trials
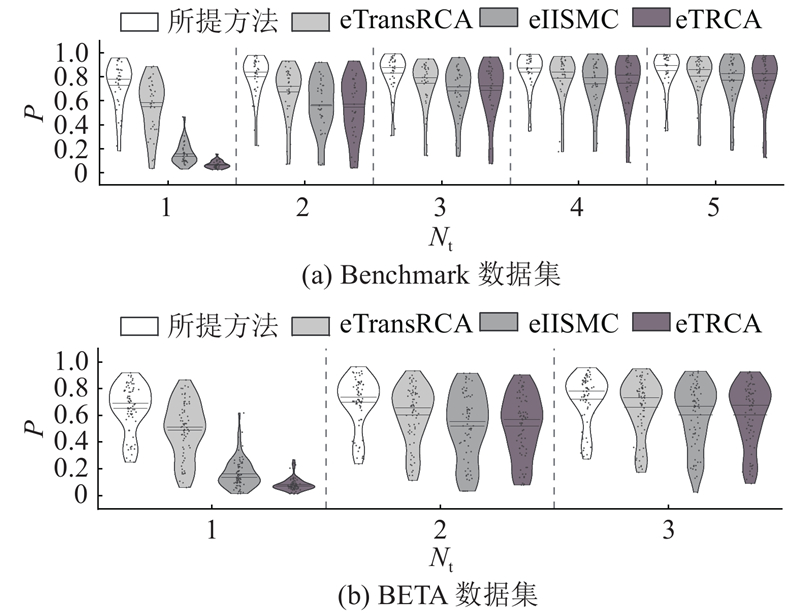
如图7所示,通过小提琴图展示了在0.5 s数据长度下,不同
图 7
图 7 不同算法下受试者分类正确率分布
Fig.7 Distribution of classification accuracy across subjects under different algorithms
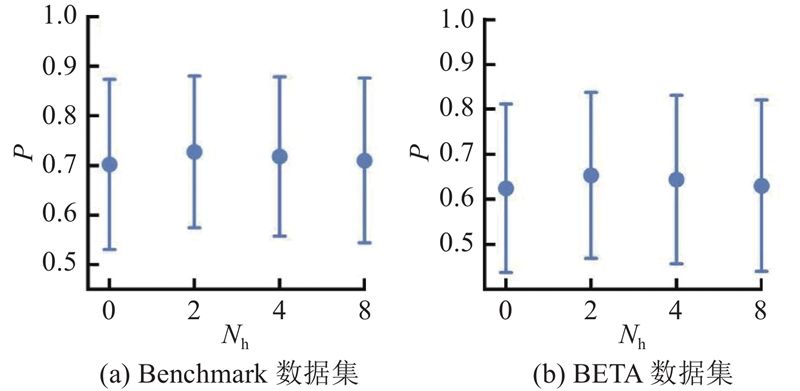
2.4.3. 邻近刺激数量的影响
图 8
图 9
图 9 不同邻近刺激数量下的分类准确率
Fig.9 Classification accuracy against different numbers of neighboring stimulus
2.5. 讨论
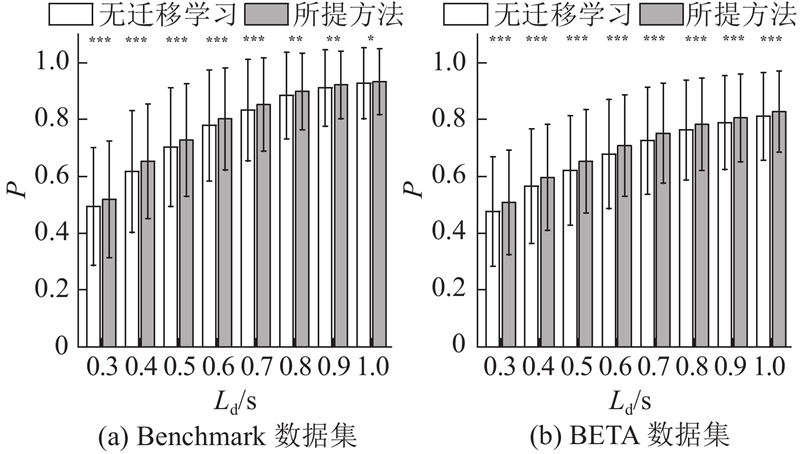
由式(16)可知,特征向量由5种相关系数构成,其中2种仅关联目标受试者,其余3种涉及源受试者. 为了进一步探索所提方法与仅基于目标受试者特征向量的方法在分类准确率上的差异,如图10所示展示了在单一校准试验下,本方法与未使用迁移学习方法在2个数据集上的性能对比. 其中,星号表示配对t检验获得的2种方法之间的显著差异,*表示p < 0.05,**表示p < 0.01,***表示p < 0.001. 结果表明,与未采用迁移学习的方法相比,本方法在SSVEP识别性能提升上更为明显. 同时,配对t检验的结果也表明,在Benchmark数据集和BETA数据集中,本方法与无迁移学习方法的准确率差异均有统计学意义(Benchmark数据集p < 0.05;BETA数据集p < 0.001). 这表明,源受试者的迁移信息对于提升目标受试者的识别性能是有益的.
图 10
图 10 不同数据长度的分类准确率对比
Fig.10 Comparison of classification accuracy against different data lengths
进一步进行消融实验以探索每个相关性在所提方法中的具体贡献. 如表1所示展示了在单一校准试验情况下,数据长度为0.6 s的消融实验结果. 实验结果表明,通过CCA和TRCA从目标受试者提取相关性特征以及从源受试者提取相关性特征均能提高识别准确率. 此外,实验结果证实相关系数
表 1 不同相关系数组合的消融实验
Tab.1
| 情况 | 相关系数选择 | P/% | ||||
| Benchmark | BETA | |||||
| (a) | √ | √ | √ | 80.17 | 70.83 | |
| (b) | √ | √ | − | 77.62 | 67.74 | |
| (c) | √ | − | √ | 70.21 | 61.78 | |
| (d) | − | √ | √ | 79.13 | 68.43 | |
具体来说,对Benchmark数据集中编号S09~S35的受试者,选取0.5 s数据长度进行平均分类准确率的比较分析. 在随机选择条件下,从26名非目标受试者中随机选取了8位作为源受试者. 而在选择经验丰富的源受试者时,则直接选取编号S01~S08的8位经验丰富的受试者作为源受试者. 如表2所示,选择经验丰富的受试者作为源受试者能够为目标受试者提供更有价值的信息,从而提升分类准确率.
表 2 2种源受试者选择方法的分类准确率对比
Tab.2
| 选择方法 | P/% | ||||
| Nt = 1 | Nt = 2 | Nt = 3 | Nt = 4 | Nt = 5 | |
| 随机选择 | 70.34 | 76.40 | 79.54 | 80.13 | 81.34 |
| 有经验选择 | 71.43 | 78.15 | 80.63 | 81.54 | 82.82 |
| p值 | ** | ** | ** | *** | *** |
3. 结 语
提出跨受试者邻近刺激学习方法,旨在在较少校准试验下,提升SSVEP-BCI系统的性能. 该方法通过最大化目标受试者、源受试者以及正余弦参考信号之间的相关性,提取目标刺激以及其邻近刺激的基波和谐波特性,以及任务相关信息,从而构建空间滤波器和信号模板进行目标识别. 在Benchmark和BETA这2个公开的SSVEP数据集上的实验结果表明,即使在仅有单一校准数据的情况下,相较于eTRCA、eIISMC和eTransRCA,所提出的方法也能明显提高分类准确率和ITR,证明了其有效性和实用性. 此外,本研究还探讨了源受试者数量、校准试验数量以及邻近刺激数量对分类准确率的影响,为优化BCI系统提供了有价值的见解. 未来研究将继续探索迁移学习策略的优化,其中,如何精确地选择更有价值的源受试者以及从源受试者中提取更有价值的特征进行迁移学习是未来研究的关键任务.
参考文献
Enhanced system robustness of asynchronous BCI in augmented reality using steady-state motion visual evoked potential
[J].DOI:10.1109/TNSRE.2022.3140772 [本文引用: 1]
Brain-computer interfaces for communication and control
[J].DOI:10.1016/S1388-2457(02)00057-3
A comprehensive assessment of brain computer interfaces: recent trends and challenges
[J].DOI:10.1016/j.jneumeth.2020.108918 [本文引用: 1]
An online multi-channel SSVEP-based brain-computer interface using a canonical correlation analysis method
[J].DOI:10.1088/1741-2560/6/4/046002 [本文引用: 1]
A speedy hybrid BCI spelling approach combining P300 and SSVEP
[J].
High-speed spelling with a noninvasive brain-computer interface
[J].
A pre-gelled EEG electrode and its application in SSVEP-based BCI
[J].DOI:10.1109/TNSRE.2022.3161989
Design and implementation of a brain-computer interface with high transfer rates
[J].DOI:10.1109/TBME.2002.803536 [本文引用: 1]
基于SSVEP信号的下肢外骨骼机器人控制系统研究
[J].
Research on lower limb exoskeleton robot control system based on SSVEP signals
[J].
A hybrid BCI-controlled smart home system combining SSVEP and EMG for individuals with paralysis
[J].DOI:10.1016/j.bspc.2019.101687 [本文引用: 1]
Brain-computer interface spellers: a review
[J].DOI:10.3390/brainsci8040057 [本文引用: 1]
Control of an electrical prosthesis with an SSVEP-based BCI
[J].DOI:10.1109/TBME.2007.897815 [本文引用: 1]
Multiple channel detection of steady-state visual evoked potentials for brain-computer interfaces
[J].DOI:10.1109/TBME.2006.889160 [本文引用: 1]
Multivariate synchronization index for frequency recognition of SSVEP-based brain-computer interface
[J].DOI:10.1016/j.jneumeth.2013.07.018 [本文引用: 1]
Frequency recognition based on canonical correlation analysis for SSVEP-based BCIs
[J].DOI:10.1109/TBME.2006.886577 [本文引用: 3]
Filter bank canonical correlation analysis for implementing a high-speed SSVEP-based brain-computer interface
[J].DOI:10.1088/1741-2560/12/4/046008 [本文引用: 3]
Frequency recognition in SSVEP-based BCI using multiset canonical correlation analysis
[J].DOI:10.1142/S0129065714500130 [本文引用: 2]
High-speed spelling with a noninvasive brain-computer interface
[J].
Enhancing detection of SSVEPs for a high-speed brain speller using task-related component analysis
[J].DOI:10.1109/TBME.2017.2694818 [本文引用: 3]
Improving the performance of individually calibrated SSVEP-BCI by task- discriminant component analysis
[J].DOI:10.1109/TNSRE.2021.3114340
Enhancing SSVEP identification with less individual calibration data using periodically repeated component analysis
[J].DOI:10.1109/TBME.2023.3333435 [本文引用: 1]
Incorporating neighboring stimuli data for enhanced SSVEP-based BCIs
[J].
Learning across multi-stimulus enhances target recognition methods in SSVEP-based BCIs
[J].DOI:10.1088/1741-2552/ab2373 [本文引用: 1]
Enhancing performances of SSVEP-based brain–computer interfaces via exploiting inter-subject information
[J].DOI:10.1088/1741-2560/12/4/046006 [本文引用: 1]
Cross-subject spatial filter transfer method for SSVEP-EEG feature recognition
[J].DOI:10.1088/1741-2552/ac6b57 [本文引用: 1]
An improved cross-subject spatial filter transfer method for SSVEP-based BCI
[J].DOI:10.1088/1741-2552/ac81ee [本文引用: 1]
Cross-subject assistance: inter- and intra-subject maximal correlation for enhancing the performance of SSVEP-based BCIs
[J].DOI:10.1109/TNSRE.2021.3057938 [本文引用: 4]
Cross domain correlation maximization for enhancing the target recognition of SSVEP-based brain-computer interfaces
[J].DOI:10.1109/TNSRE.2023.3309543 [本文引用: 2]
A canonical correlation analysis-based transfer learning framework for enhancing the performance of SSVEP-based BCIs
[J].DOI:10.1109/TNSRE.2023.3288397 [本文引用: 3]
Small data least-squares transformation (sd-LST) for fast calibration of SSVEP-based BCIs
[J].
Data augmentation of SSVEPs using source aliasing matrix estimation for brain-computer interfaces
[J].DOI:10.1109/TBME.2022.3227036 [本文引用: 2]
Concurrent recording of steady-state and transient event-related potentials as indices of visual-spatial selective attention
[J].DOI:10.1016/S1388-2457(00)00371-0 [本文引用: 1]
SSVEP and ERP measurement of cognitive fatigue caused by stereoscopic 3D
[J].DOI:10.1016/j.neulet.2012.07.049 [本文引用: 1]
A benchmark dataset for SSVEP-based brain-computer interfaces
[J].DOI:10.1109/TNSRE.2016.2627556 [本文引用: 3]
BETA: a large benchmark database toward SSVEP-BCI application
[J].DOI:10.3389/fnins.2020.00627 [本文引用: 2]
Human EEG responses to 1–100Hz flicker: resonance phenomena in visual cortex and their potential correlation to cognitive phenomena
[J].