随着贸易全球化推进，数十亿吨货物通过海路运输，精准可靠的定位变得愈加重要. 与陆运可以依托地面基站和道路网络协同定位不同，海上导航系统的高度依赖全球导航卫星系统(global navigation satellite system, GNSS)，但易受大气条件变化和人为信号干扰的影响^[1-2]，导致定位可靠性下降.

传感技术和物联网的发展使得动态定位船舶(dynamic-positioning vessel, DP-vessel)能够通过先进传感器和计算机控制系统^[3]实现高精度定位. 在当前的海运系统中，大多数普通船舶(common vessel, C-vessel) 配备基础设备. 如何在保持DP-vessel高精度定位的同时，提升装备简陋的C-vessel的定位性能，成为亟待解决的问题.

区块链技术和物联网应用的结合为这一问题提供了思路. 物联网设备收集精确的定位和环境数据，借由区块链实现安全透明的位置数据共享和导航优化^[4-5]. Song等^[6]提出通过车辆区块链协同定位校正，提高定位精度. Li等^[7]提出安全高效的全球定位系统定位误差演进共享框架. Song等^[8]通过深度神经网络算法校正车辆的GPS位置，通过区块链的数据共享降低了同一路段上普通车辆的GPS定位误差.

在追求定位精度的同时，位置数据作为高度敏感的特殊数据，其隐私保护至关重要. Luo等^[9-10]采用K匿名算法创建匿名区域，防止第三方定位特定车辆，利用区块链技术构建信任模型，以增强位置隐私保护. 申自浩等^[11]实现了用户自定义的位置共享，以保护隐私. 现有针对陆上交通位置共享的研究往往忽略了数据请求的不可链接性问题，即未能实现数据与其请求者链接关系的隐匿. 目前，Gai等^[12]提出基于zk-SNARKs的海运安全位置共享方案，确保数据隐私和不可链接性. zk-SNARKs在提供高级别隐私保护的同时，带来了更大的计算和通信开销，难以满足资源受限船只对实时操作的需求. 如何在保障安全性的前提下，实现配置异质的DP-vessel和C-vessel之间的公平数据共享，并最小化通信和计算成本，成为海运位置数据共享领域亟须解决的关键问题.

不同于现有方案使用zk-SNARKs实现不可链接性，本文提出新的方法，利用one-out-of-many proofs^[13]断开数据与请求者的链接. one-out-of-many proofs是部分知识证明^[14]的一种特殊实现，允许证明者以零知识的方式证明N个承诺中的某个打开为0. Benjamin^[15]将one-out-of-many推广到了many-out-of-many. Bootle等^[16-19]注重效率的提升. Aram等^[19]提出分层方法，大大降低了计算开销，但通信开销增加至$O\left( {n{{\log }_2}n+M{{\log }_2}m+m} \right)$.

针对上述问题，本文给出结构紧致的轻量级零知识证明协议(compressing zero-knowledge proofs of 1-out-of-t，CZKP-1t). 提出基于该零知识证明协议的海上位置数据共享方案(maritime positioning sharing based on CZKP-1t，CZKP-1t-MPS).

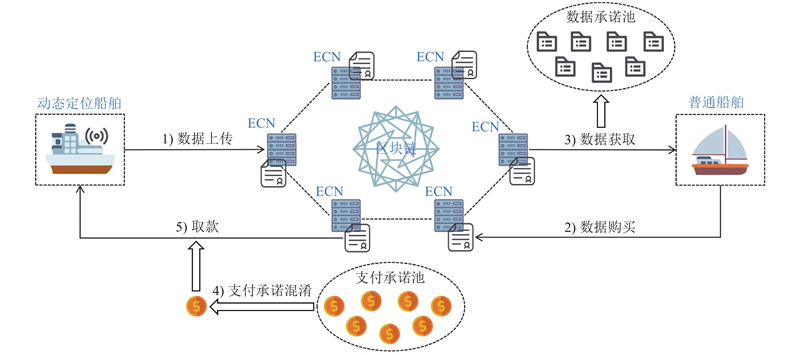
基于紧凑零知识证明的海上位置数据共享系统模型如图1所示，系统实体包括边缘计算节点(edge computing nodes，ECNs)、动态定位船舶(DP-vessel)、普通船舶(C-vessel)和区块链.

1) ECNs：拥有足够的存储空间和计算能力，在其上维护区块链账本. 在ECNs上部署了智能合约，作为透明的第三方仲裁方，确保数据交易过程的正确进行.

2) DP-vessel：能够利用其丰富的船载传感器来纠正位置，生成GNSS定位误差数据.

3) C-vessel：只能通过GNSS获得位置信息,因此需要请求来自DP-Vessel的GNSS定位误差数据来更新其位置.

4)区块链：由所有ECNs共同维护，记录共享数据的相关信息.

ECNs被部署在海上的地标上，存储该地标的确切位置. 当绕过一个地标时，DP-vessel利用复杂的传感器，通过该地标的准确位置来纠正位置，生成当前的GNSS定位误差数据. DP-vessel将定位误差数据提交给部署在该地标上的ECN，该数据随后存储在该ECN上. 当C-vessel到达同一位置时，首先支付酬金，生成相应的支付承诺. 然后请求GNSS定位误差数据. 最后，DP-vessel获取对应的数据酬金.

本文研究的关键难点在于如何断开位置数据共享双方的、位置数据与其持有者之间的链接关系. 受到UTXO模型区块链中混币思想和Bao等^[20]提出的支票池构造的启发，建立数据承诺集和支付承诺池集，结合提出的特殊零知识证明协议CZKP-1t来解决上述问题. 其中，数据承诺集包括交易过程中DP-vessel上传数据产生的所有数据承诺，支付承诺集包括由C-vessel购买数据产生的所有支付承诺.

构造用于海上位置数据共享方案中的高效零知识证明协议.

在one-out-of-many proofs中，证明者和验证者持有承诺密钥$g、h \in {G}$及N个承诺${c_0},\cdots ,{c_{N - 1}}$，其中${c_i} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({v_i},{r_i}) = {g^{{r_i}}}{h^{{v_i}}}$. 证明者需要证明其中一个承诺打开为0，即有${c_l} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}(0,r) = {g^r}{h^0}$，但不暴露是哪个承诺.

当构造证明时，需要隐藏的关键信息（承诺序号l）被编码为n位二进制数，即$l = {l_1}{l_2}\cdots {l_n}$. Groth等^[13]构造n个承诺来证明每一位${l_i} \in \{ 0,1\} $，以确保${c_l}$是N个承诺中的一个. 本文基于聚合承诺对证明过程进行压缩，重构证明和验证过程，提出紧凑的零知识证明协议CZKP-1t. 协议定义为$ {L_{{\text{CZKP - 1t}}}} = \{ (l,r)|{c_0},\cdots ,{c_{N - 1}} \in C \wedge l \in [0,N - 1] \wedge {c_l} = $$ {g^r}{h^0}\} $.

聚合承诺描述为$ C: = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({x_1},\cdots ,{x_n};r) = {g^r}{h^{ \sum\nolimits_{i = 1}^n {{x_i}} }} $，其中ck表示承诺密钥 $g、h$.

接下来对协议进行具体描述.

1）承诺. 证明者选取随机数${r_{\text{A}}},{r_{\text{B}}}{\text{,}}{r_{\text{C}}},{a_1},\cdots ,{a_n},$${\rho _1},\cdots , {\rho _n} \in {{Z}_q}$（其中Z_q为整数模q的环）. 计算承诺

$ {C_{\text{L}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({l_1},\cdots ,{l_n};r) . $

$ {C_{\text{A}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({a_1},\cdots ,{a_n};{r_{\text{A}}}) . $

$ {C_{\text{B}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({a_1}(1 - 2{l_1}),\cdots ,{a_n}(1 - 2{l_n});{r_{\text{B}}}) . $

$ {C_{\text{C}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}( - {a_1}^2,\cdots , - {a_n}^2;{r_{\text{C}}}) . $

$ {C_k} = \prod\nolimits_{i = 0}^{N - 1} {c_i^{{p_{i,k}}}{\text{Co}}{{\text{m}}_{{\text{ck}}}}(0,{\rho _k}} ) ; \;k = 0,\cdots ,n - 1. $

证明者将承诺$\{ {{{C}}_{{{\mathrm{L}}}}},{{{C}}_{{{\mathrm{A}}}}},{{{C}}_{{{\mathrm{B}}}}},{{{C}}_{{{\mathrm{C}}}}},{{{C}}_{{k}}}\} $发送给验证者.

2）挑战. 验证者返回挑战$x \leftarrow {\{ 0,1\} ^\lambda }$.

3）响应. 证明者根据挑战生成响应：

$ \begin{gathered} {f_j} = {l_j}x+{a_j}. \\ {z_{\text{A}}} = rx+{r_{\text{A}}}. \\ {z_{\text{B}}} = {r_{\text{B}}}x+{r_{\text{C}}}. \\ \end{gathered} $

$ z = r{x^n} - \sum\nolimits_{k = 0}^{n - 1} {{\rho _k}{x^k}} . $

其中，$j = 0,\cdots ,n - 1$. 证明者将响应$\{ \{ {f_j}\} _{j = 0}^{j = n - 1}, {z_{\text{A}}},{z_{\text{B}}},z\} $发送给验证者.

4）验证. 验证者验证以下3个等式是否成立.

(1)$ C_{\text{L}}^x{C_{\text{A}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({f_1},\cdots {f_n};{z_{\text{A}}}). $

(2)$ C_{\text{B}}^x{C_{\text{C}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({f_1}(x - {f_1}),\cdots, {f_n}(x - {f_n});{z_{\text{B}}}). $

(3)$ \prod\nolimits_{i = 0}^{N - 1} {{{{c}}_i}^{\prod\nolimits_{j = 1}^n {{f_{j,{i_j}}}} } \cdot \prod\nolimits_{k = 0}^{n - 1} {{\text{C}}_k^{ - {x^k}}} } = {\text{Co}}{{\text{m}}_{{\text{ck}}}}(0;z). $

若成立，则接受，即零知识证明通过；反之不通过. 式中：$ {f_{j,0}} = x - {f_j} = (1 - {l_j})x - {a_j} = {\delta _{0{l_j}}}x - {a_j} $，$ {f_{j,1}} = $$ {f_j} = {l_j}x+{a_j} = {\delta _{1{l_j}}}x+{a_j} $，其中${\delta _{il}}$为克罗内克函数，当$i = l$时${\delta _{il}} = 1$， 当$i \ne l$时${\delta _{il}} = 0$.

定义6种类型的数据集. 所有的数据集都可以从当前的区块链账本中获得.

${\text{SNSet}}({\mathrm{pk}})$ ：包含用户pk的所有交易的序列号，序列号只能使用一次，唯一标识一笔交易.

TAGSet：包含所有的支付承诺TAG，支付承诺和TAG唯一绑定，用于限制每个支付承诺只能使用一次. 其中，$\text { TAG }:=k^{-r},\; k \in G,\; r \in {Z}_q^*$ .

${\text{EDSET}}$：包含所有位置数据的序列号${\mathrm{ED}}_j$.

数据承诺集：包含所有的数据承诺$\delta _i^{{\mathrm{ED}}_j}$.

数据承诺池：包含来自数据承诺集的t−1个承诺和用户构建的1个承诺，表示为$\{ {\delta ^{{\mathrm{ED}}_0}},\cdots , {\delta ^{{\mathrm{ED}}_l}},\cdots ,{\delta ^{{\mathrm{ED}}_{t - 1}}}\} $.

支付承诺集：包含所有的支付承诺${C_R}$.

支付承诺池：包含来自支付承诺集的t个承诺，其中1个为用户持有，t−1个从支付承诺集中随机选择.

CZKP-1t-MPS由初始化、位置数据上传、位置数据购买、位置数据获取、支付承诺混淆和取款6个算法组成.

ECNs和用户运行${\text{CPK}}{\text{.Setup}}({1^\lambda })$、${\text{HE}}{\text{.Setup}}({1^\lambda })$和${\text{NIZK}}{\text{.Setup}}({1^\lambda })$，得到公共参数列表${\text{pp}}: = ({\text{p}}{{\text{p}}_{{\text{cpk}}}},{\text{p}}{{\text{p}}_{{\text{he}}}},{\text{p}}{{\text{p}}_{{\text{nizk}}}})$. 其中，CPK算法为联合公钥系统^[21]，本文使用Twisted ElGamal加密和Schnorr 2种公钥体制组成的联合公钥系统，该系统的安全性在文献[22]中已证明. HE算法为Hash ElGamal^[23]，能够实现快速且有效的解密，用于加密不需要支持同态的共享内容. 用户运行${\text{CPK}}{\text{.KeyGen}} ({\text{p}}{{\text{p}}_{{\text{ise}}}})$，生成用于签名交易和加密关键信息的密钥对$({\mathrm{pk}},{\mathrm{sk}})$，并生成余额承诺${C_{{v_{{U}}}}} \leftarrow {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}{\text{,}}{v_{{\text{init}}}};r)$，其中$r \in {Z}_q$. 选择初始序列号${\mathrm{sn}} \in {\{ 0,1\} ^n}$，则用户的初始化账户余额为$ {\text{zk\_balance}}: = ({C_{{v_{{U}}}}},{\mathrm{pk}},{v_{{\text{init}}}},{\mathrm{sn}},r) $. 用户生成零知识证明${\pi _{{\text{create}}}}$，保证余额承诺的正确性. 用户生成签名$\sigma \leftarrow {\text{CPK}}{\text{.Sign}}({\mathrm{sk}},({\mathrm{pk}},{\mathrm{sn}},{C_{{v_{{U}}}}}, {\pi _{{\text{create}}}}))$和交易${\text{Tran}}{{\text{s}}_{{\text{Create}}}}: = \{ {\mathrm{pk}},{\mathrm{sn}},{C_{{v_{{U}}}}},{\pi _{{\text{create}}}},\sigma \} $.

如下所示的智能合约被部署到ECNs上. ECNs 验证${\pi _{{\text{create}}}}$和$\sigma $有效后，该用户可以参与后续位置的共享过程.

动态定位船舶${{V}}_{{R}}^{{{{\mathrm{DP}}}}}$将GNSS错误数据${D_j}$发布到网络上，并生成该数据的唯一序列号${\mathrm{ED}}_j$. ${{V}}_{{R}}^{{\text{DP}}}$为该数据生成数据承诺$\delta _i^{{\mathrm{ED}}_j}$，指明数据所有者${\mathrm{pk}}_{{R}}$和数据价格${v_j}$. 具体如算法1所示.

算法1　PublishData　　●输入：　　- 公共参数pp　　- 数据持有者的公钥${\mathrm{pk}}_{{R}}$　　●输出：　　- 数据承诺$\delta _i^{{\mathrm{ED}}_{{j}}}$　　- 交易$ {\text{Tran}}{{\text{s}}_{{\text{Publish}}}} $　　1) 计算 $\delta _i^{{\mathrm{ED}}_j} \leftarrow {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}_{{R}},{v_j};{r_1})$.　　2) 生成零知识证明 ${\pi _{{\text{pubdate}}}} \leftarrow {\text{NIZK}}\{ ({r_1},{v_j})|\delta _i^{{\mathrm{E}}{{\mathrm{D}}_j}} = {\text{CPK}}{\text{.Enc}}({\mathrm{p}}{{\mathrm{k}}_{{R}}},{v_j};{r_1})\} $　　3) 计算签名${\sigma _{\text{R}}} \leftarrow {\text{CPK}}{\text{.Sign}}({\mathrm{sk}}_{{R}},({\mathrm{pk}}_{{R}},{\pi _{{\text{pubdata}}}}))$.　　4) 生成交易$ {\text{Tran}}{{\text{s}}_{{\text{PubData}}}}: = \{ {\mathrm{ED}}_j,\delta _i^{{\mathrm{ED}}_j},{v_j},{\mathrm{pk}}_{{R}},{\pi _{{\text{publish}}}},{\sigma _{{R}}}\} $.　　5) 输出$(\delta _i^{{\mathrm{ED}}_j},{\text{Tran}}{{\text{s}}_{{\text{PubData}}}})$.

在获取位置数据之前，普通船舶$V_U^C$需要支付相应的酬金. 为了断开数据收发双方的链接关系，$V_U^C$将购买数据所需的酬金${v_j}$从自己的账户余额${\text{zk\_balanc}}{{\text{e}}_U}$转到支付承诺${C_v}$中，后续数据持有者对其进行混淆后再转入自己账户. 同时，$V_U^C$用数据持有者的公钥加密共享参数$({r_3},{v_j},{\mathrm{ED}}_j)$. 具体如算法2所示.

算法2　PurchaseData　　称数据请求者为U, 称数据持有者为R.　　●输入：　　- 公共参数${\text{pp}}$　　- 发送者的余额zk_balance　　- 发送方的私钥sk　　- 金额为$V_{{U}}^C$的承诺　　- 接收方的公钥${\mathrm{pk}}_{{R}}$　　●输出：　　- 收款人的支付承诺${C_{{v}}}$　　- 发送者的新余额 $ V_{{U}}^C $　　- 交易${\text{Tran}}{{\text{s}}_{{\text{Purdata}}}}$　　1) 解析${\mathrm{zk}}\_{\mathrm{balanc}}{{\mathrm{e}}_{{U}}}$为$({C_{{v_{{U}}}}},{\mathrm{pk}}_{{U}},{v_{{U}}},{\mathrm{sn}}_{{U}},r)$.　　2) 检查是否$V_U^C$. 如果失败, 则返回⊥.　　3) 生成2个随机数$V_U^C$, 计算$ C_{{v_{{U}}}}^* \leftarrow {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}_{{U}}, $$v_{{U}}^*;{r_2}) $, $ {C_{{v}}} \leftarrow {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}_{{R}},{v_j};{r_3}) $, 其中$V_{{U}}^* = {v_U} - {v_j}$.　　4) 选择序列号$V_U^C$, 其中${\mathrm{sn}} \notin {\text{SNSet}}({\mathrm{pk}} _{{U}})$.　　5) 令$ {\mathrm{zk}}\_{\mathrm{balance}}^* = (C_{{v_{{U}}}}^*,{\mathrm{pk}}_{{U}},v_{{U}}^*,{\mathrm{sn}},{r_2}) $.　　6) 计算$ {\mathrm{aux}}_{{R}} \leftarrow {\text{HE}}.{\text{Enc}}({\mathrm{pk}}_{{R}},({r_3},{v_j},{\mathrm{ED}}_j)) $.　　7) 生成零知识证明>$ {\pi _{{\text{purdata}}}} \leftarrow {\text{NIZK}}\{ (r,{r_2},{r_3},{v_{{U}}},v_{{U}}^*,{v_j})|{C_{{v_{{U}}}}}{\text{ = CPK}}{\text{.Enc}}({\mathrm{pk}}_{{U}},{v_{{U}}};r) \wedge $$ C_{{v_{{U}}}}^*{\text{ = CPK}}{\text{.Enc}}({\mathrm{p}}{{\mathrm{k}}_{{U}}},v_{{U}}^*;{r_2}) \wedge {C_v}{\text{ = CPK}}{\text{.Enc}}({\mathrm{p}}{{\mathrm{k}}_R},{v_j};{r_3}) \wedge v_{{U}}^* =$$ {v_{{U}}} - {v_j} \wedge v_{{U}}^*,{v_j} \in V\} . $　　8) 计算签名$ {\sigma _U} \leftarrow {\text{CPK}}{\text{.Sign}}({\mathrm{sk}}_U,({\mathrm{pk}}_{{U}},{\mathrm{sn}},{C_{{v_{{R}}}}},C_{{v_{{U}}}}^*,{\mathrm{aux}}_{{R}},{\pi _{{\text{purdata}}}})). $　　9) 令$ {\text{Tran}}{{\text{s}}_{{\text{PurData}}}}: = \{ {\mathrm{pk}}_{{U}},{\mathrm{sn}},{C_v},C_{{v_{{U}}}}^*,{\mathrm{aux}}_{{R}}, {\pi _{{\text{purdata}}}}, {\sigma _{{U}}}\} $.　　10) 输出$({C_v},{\mathrm{zk}}\_{\mathrm{balance}}^*,{\text{Tran}}{{\text{s}}_{{\text{PurData}}}})$.

在付款完成后，普通船舶$V_U^C$可以请求获得相应的位置数据. 通过CZKP-1t协议构造零知识证明${\pi _{{\text{fetchdata}}}}$，证明自己拥有${\text{DateCommitPool}}$中的某个承诺. 证明随后在智能合约中进行验证，若验证通过，则ECN将对应的${\mathrm{ED}}_j$返回给$V_U^C$. 具体如算法3所示.

算法3　FetchData　　●输入：　　- 公共参数${\text{pp}}$　　- 用户R私钥${\mathrm{sk}}_{{U}}$　　●输出：　　- 交易${\text{Tran}}{{\text{s}}_{{\text{FetchData}}}}$　　1) 从数据承诺集中取t−1个承诺, 数据承诺池表示为$ \{ \delta _0^{{\mathrm{ED}}_0},\cdots ,\delta _l^{{\mathrm{ED}}_l},\cdots ,\delta _{t - 1}^{{\mathrm{ED}}_{t - 1}}\} $, 其中$ \delta _l^{{\mathrm{ED}}_l} $为$V_{{U}}^C$支付过的承诺.　　2) 生成零知识证明$ \begin{gathered} {\pi _{{\text{fetdata}}}} \leftarrow {\text{NIZK}}\{ ({r_3},{v_j})|{\text{CPK}}{\text{.Dec}}(\delta _0^{{\mathrm{ED}}_0} - {C_v}) = 0 \vee \cdots \vee \\ {\text{CPK}}{\text{.Dec}}(\delta _{t - 1}^{{\mathrm{ED}}_{t - 1}} - {C_v}) = 0 \wedge \delta _i^{{\mathrm{ED}}_j} \leftarrow {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}_{{R}},{v_j};{r_3}) \\ \wedge {\mathrm{tag}} = {k^{ - r}} \wedge {v_j} \in V\} . \\ \end{gathered} $　　3) 计算签名$ {\sigma _{\text{U}}} \leftarrow {\text{CPK}}{\text{.Sign}}({\mathrm{sk}}_{{U}},({\mathrm{pk}}_{{R}},{\pi _{{\text{fetdata}}}})) $.　　4) 令$ {\text{Tran}}{{\text{s}}_{{\text{FetData}}}}: = \{ {\mathrm{pk}}_{{U}},{\pi _{{\text{fetdata}}}},{\sigma _{{R}}}\} $.　　5) 输出${\text{Tran}}{{\text{s}}_{{\text{FetData}}}}$.

为了实现数据收发双方的不可链接性，该算法获取属于动态定位船舶$V_{{R}}^{{\text{DP}}}$的支付承诺${C_v}$，生成支付承诺池$ {\text{PaymentPool}(t)}: = \{ {C_{({R_0},0)}},\cdots , {C_{({R_l},l)}},{C_{({R_{t - 1,t-1}})}}\} $，其中${C_{({R_l},l)}} = {C_v}$. 输出新的支付承诺$C_v^*$， ${\pi _{{\text{refresh}}}}$确保同时满足以下3个条件. 1）$V_{{R}}^{{\text{DP}}}$拥有$ {\text{PaymentPool}(t)} $中的某个承诺. 2）该承诺与原承诺${C_v}$金额一致. 3）原承诺${C_v}$未被使用过. 具体如算法4所示.

算法4　RefreshPayment　　●输入：　　- 公共参数${\text{pp}}$　　- 用户R私钥${\mathrm{sk}}_{{R}}$　　- 支付承诺$\{ {C_{{v_i}}}\} _0^{t - 1}$　　●输出：　　- 用户的新支票$C_v^*$　　- 交易${\text{Tran}}{{\text{s}}_{{\text{Refresh}}}}$　　1) 从当前账本中获取$ {\text{Tran}}{{\text{s}}_{{\text{PurData}}}} $, 解析为$ ({\mathrm{pk}}_{{U}},{\mathrm{sn}}, {C_v},C_{{v_{{U}}}}^*,{\mathrm{aux}}_{{R}},{\pi _{{\text{purchase}}}},{\sigma _{{U}}}) $.　　2) 计算$({r_3},{v_j},{\mathrm{ED}}_j) \leftarrow {\text{HE}}{\text{.Dec}}({\mathrm{sk}}_{{R}},{\mathrm{aux}}_{{R}})$.　 3) 生成随机数 $r^* \in {Z}_q$, 计算$C_v^* \leftarrow {\text{CPK}}{\text{.Enc}} $ $ ({\mathrm{pk}}_{{R}},{v_j};{r_4}).$ 　　4) 从支付承诺集中取t−1个支付承诺, 数据承诺池表示为$ \{ {C_{({R_0},0)}},\cdots ,{C_{({R_l},l)}},\cdots ,{C_{({R_{t - 1,t-1}})}}\} $, 其中属于用户的支票密文表示为${C_{({R_l},l)}}$. 即${C_{({R_l},l)}} = {C_v}$.　　5) 计算${\mathrm{tag}}: = {k^{ - {r_3}}}$.　　6) 生成零知识证明$ \begin{gathered} {\pi _{{\text{refresh}}}} \leftarrow {\text{NIZK}}\{ ({r_3},{r_4},{v_j})|{\text{CPK}}{\text{.Dec}}({C_{({R_0},0)}} - C_v^*)= \\ 0 \vee \cdots \vee {\text{CPK}}{\text{.Dec}}({C_{({R_{t - 1}},t - 1)}} - C_v^*) = 0 \wedge {C_v}^*= \\ {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}_R,{v_j};{r_4}) \wedge {\mathrm{tag}} = {k^{ - {r_3}}} \wedge {v_j} \in V\}. \\ \end{gathered} $　　7) 计算签名$ {\sigma _{\text{R}}} \leftarrow {\text{CPK}}{\text{.Sign}}({\mathrm{sk}}_{{R}},({\mathrm{pk}}_{{R}},{\mathrm{tag}},C_v^*,{\pi _{{\text{refresh}}}})) $.　　8) 令$ {\text{Tran}}{{\text{s}}_{{\text{Refresh}}}}: = \{ {\mathrm{pk}}_{{R}},{\mathrm{tag}},C_v^*,{\pi _{{\text{refresh}}}},{\sigma _{{R}}}\} $.　　9) 输出$(C_v^*,{\text{Tran}}{{\text{s}}_{{\text{RefreData}}}})$.

该算法将$C_v^*$中的金额存进动态定位船舶${{V}}_{{R}}^{{\text{DP}}}$的账户余额$ {\mathrm{zk}}\_{\mathrm{balance}}_{{R}}$. 具体如算法5所示.

算法5　DepositPayment　　●输入：　　- 公共参数${\text{pp}}$　　- 用户余额${\mathrm{zk}}\_{\mathrm{balance}}_{{R}}$　　- 用户私钥sk　　- 用户更新后的支付承诺$C_{{v_R}}^*$　　●输出：　　- 支票持有人的新余额${\mathrm{zk}}\_{\mathrm{balance}}_{{R}}^*$　　- 转账交易$ {\text{Tran}}{{\text{s}}_{{\text{Deposit}}}} $　　1) 从当前账本中获取$ {\text{Tran}}{{\text{s}}_{{\text{Refresh}}}} $, 解析为 $ \{ {\mathrm{pk}}_{{R}}, {\mathrm{tag}},C_v^*,{\pi _{{\text{refresh}}}},{\sigma _{{R}}}\} $.　　2) 解析${\text{zk\_balanc}}{{\text{e}}_R}$为$({C_{{v_{{R}}}}},{\mathrm{pk}}_{{R}},{v_{{R}}},{\mathrm{sn}}_{{R}},r)$.　　3) 生成随机数${r_5} \in {Z}_q$, 计算$C_{{v_{{R}}}}^* \leftarrow {\text{CPK}}{\text{.Enc}} $ $({\mathrm{pk}}_{{R}},v_{{R}}^*; {r_5})$，其中$v_R^* = {v_R}+{v_j}$.　　4) 生成零知识证明$ \begin{gathered} {\pi _{{\text{deposit}}}} \leftarrow {\text{NIZK}}\{ (r,{r_4},{r_5},{v_{{R}}},v_{{R}}^*,{v_j})|{C_{{v_{{R}}}}} = {\text{CPK}}{\text{.Enc}} \\ ({\mathrm{pk}}_{{R}},{v_{{R}}};r) \wedge {C_{{v_{{R}}}}}^* = {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}_{{R}},{v_{{R}}}^*;{r_5}) \wedge C_v^* = \\ {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}_{{R}},{v_j};{r_4}) \wedge v_{{R}}^* = {v_{{R}}}+{v_j} \wedge v_{{R}}^* \in V\} . \\ \end{gathered} $　　5) 选择序列号${\mathrm{sn}}^* \in {\{ 0,1\} ^n}$, 满足${\mathrm{sn}}^* \notin {\text{SNSet}}({\mathrm{pk}}_{{R}})$.　　6) 计算签名$ {\sigma _{{R}}} \leftarrow {\text{CPK}}{\text{.Sign}}({\mathrm{sk}}_{{R}},({\mathrm{pk}}_{{R}},{\mathrm{sn}}^*,C_v^*,C_{{v_{{R}}}}^*,{\pi _{{\text{deposit}}}})) $.　　7) 令${\text{zk\_balance}}_{{R}}^*: = ({C_{{v_{{R}}}}}^*,{\mathrm{pk}}_{{R}},{v_{{R}}}^*,{\mathrm{sn}},{r^*})$.　　8) 令$ {\text{Tran}}{{\text{s}}_{{\text{Deposit}}}}: = \{ {\mathrm{pk}}_{{R}},{\mathrm{sn}},C_{{v_{{R}}}}^*,{\pi _{{\text{deposit}}}},{\sigma _{{R}}}\} $.　　9) 输出${\text{(Tran}}{{\text{s}}_{{\text{Deposit}}}},{\mathrm{zk}}\_{\mathrm{balance}}_{{R}}^{\text{*}})$.

定理1：若陈述为真，且证明者遵循协议进行证明，验证者将总是能够成功验证该证明，则零知识证明协议满足完备性.

证明：对于式(1)，有

$\begin{split} C_{\text{L}}^x{C_{\text{A}}} =& {({g^r}{h^{\sum\nolimits_{i = 1}^n {{l_i}} }})^x} \cdot ({g^{{r_{\mathrm{A}}}}}{h^{\sum\nolimits_{i = 1}^n {{a_i}} }})= \\ & {g^{rx+{r_{\mathrm{A}}}}}{h^{\sum\nolimits_{i = 1}^n {{l_i}} x+{a_i}}} =\\ &{\text{Co}}{{\text{m}}_{{\text{ck}}}}({f_1},\cdots ,{f_n};{z_{\text{A}}}). \end{split} $

对于式(2)，等号左边为

$ \begin{split} C_{\text{B}}^x{C_{\text{C}}} =& {({g^{{r_{\text{B}}}}}{h^{\sum\nolimits_{i = 1}^n {{a_i}(1 - 2{l_i})} }})^x} \cdot ({g^{{r_{\text{C}}}}}{h^{\sum\nolimits_{i = 1}^n { - {a_i}^2} }}) =\\ & {g^{{r_{\text{B}}}x+{r_{\text{C}}}}}{h^{\sum\nolimits_{i = 1}^n { (- 2{l_i}{a_i}x+{a_i}x - a_i^2 )} }}. \end{split}$

等号右边为

$ \begin{gathered} {\text{Co}}{{\text{m}}_{{\text{ck}}}}({f_1}(x - {f_1}),\cdots ,{f_n}(x - {f_n});{z_{\text{B}}})= \\ {g^{{r_{\text{B}}}x+{r_{\text{C}}}}}{h^{\sum\nolimits_{i = 1}^n {{x^2}{l_i}(1 - {l_i}) - 2{l_i}{a_i}x+{a_i}x - a_i^2} }} .\\ \end{gathered} $

当且仅当$ {l_i} \in \{ 0,1\} $，即${x^2}{l_i}(1 - {l_i}) = 0$时，有$ C_{\text{B}}^x{C_{\text{C}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({f_1}(x - {f_1}),\cdots ,{f_n}(x - {f_n});{z_{\text{B}}}) $恒成立.

对于式(3)，有

$ \begin{split} & \prod\limits_{i = 0}^{N - 1} {c_i^{\prod\nolimits_{j = 1}^n {{f_{j,{i_j}}}} }} \cdot \prod\limits_{k = 0}^{n - 1} {c_k^{ - {x^k}}}= \\ & \prod\limits_{i = 0}^{N - 1} {c_i^{{p_{i(x)}}}} \cdot \prod\limits_{k = 0}^{n - 1} {\left(\prod\limits_{i = 0}^{N - 1} {c_i^{{p_{i,k}}} \cdot {\text{Co}}{{\text{m}}_{{\text{ck}}}}(0;{\rho _k}} )\right)^{ - {x^k}}} =\\ & \prod\limits_{i = 0}^{N - 1} {c_i^{{\delta _{il}}{x^n}}} \cdot \prod\limits_{i = 0}^{N - 1} {\prod\limits_{k = 0}^{n - 1} {c_i^{{p_{i,k}}{x^k}}} } \cdot \prod\limits_{i = 0}^{N - 1} {\prod\limits_{k = 0}^{n - 1} {c_i^{ - {p_{i,k}}{x^k}}} }, \\ & \prod\limits_{k = 0}^{n - 1} {{\text{Co}}{{\text{m}}_{{\text{ck}}}}{{(0;{\rho _k})}^{ - {x^k}}}} = c_l^{{x^n}} \cdot {\text{Co}}{{\text{m}}_{{\text{ck}}}}\left(0; - \sum\limits_{k = 0}^{n - 1} {{\rho _k}{x^k}} \right) =\\ & {\text{Co}}{{\text{m}}_{{\text{ck}}}}(0;r{x^n}) \cdot {\text{Co}}{{\text{m}}_{{\text{ck}}}}\left(0; - \sum\limits_{k = 0}^{n - 1} {{\rho _k}{x^k}} \right) = \\ &{\text{Co}}{{\text{m}}_{{\text{ck}}}}(0;z). \end{split}$

可知，若陈述为真且证明过程无误，则以上3个验证等式总是成立，完备性得证.

定理2：若验证者可以在获得来自证明者的多个模拟证明后，从证明者给定的证明中提取出陈述，则零知识证明协议满足可靠性.

证明：假设证明者对2个不同的挑战$x$和$x'$进行响应，响应分别为$({f_0},\cdots ,{f_{n - 1}},{z_{\text{A}}},{z_{\text{C}}})$和$(f_0',\cdots ,f_{n - 1}', z_{\text{A}}',z_{\text{C}}')$. 由于有

$\begin{split} &C_{\text{L}}^x{C_{\text{A}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({f_0},\cdots ,{f_{n - 1}};{z_{\text{A}}}),\\&C_{\text{L}}^{x'}{C_{\text{A}}} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}(f_0',\cdots ,f_{n - 1}';z'_{\text{A}}),\end{split}$

可得

$ C_{\text{L}}^{x - x'} = {\text{Co}}{{\text{m}}_{{\text{ck}}}}({f_0} - f_0',\cdots ,{f_{n - 1}} - f_{n - 1}';{z_{\text{A}}} - z_{\text{A}}'). $

${C_{\mathrm{L}}}$可以被打开，得到${l_i} = ({{{f_i} - f_i'}})/({{x - x'}})$，$ r = (z_{\text{A}} - z_{\text{A}}')/ ( {{x - x'}}) $以及${a_j} = {f_j} - {l_j}x,{r_{\mathrm{A}}} = {z_{\mathrm{A}}} - rx$. 同理，${C_{\text{B}}}$也可以被打开，得到$ {b_j} = [{{{f_j}(x - {f_j}) - f_j'(x - f_j')}}]/ ({{x - x'}}) $，$ {r_{\text{B}}} = ({{{z_{\text{B}}} - z_{\text{B}}'}})/({{x - x'}}) $，$ {c_j} = - a_j^2 $和$ {r_{\text{C}}} = {z_{\text{B}}} - {r_{\text{B}}}x $. 可靠性得证.

定理3：若存在一个模拟器能够生成一个交互记录，使得验证者无法区分它是来自真实的证明过程，还是由模拟器生成的，则零知识证明协议满足零知识性.

证明：根据挑战$x \leftarrow {\{ 0,1\} ^\lambda }$，模拟器随机选取${f_1},\cdots {f_n},{z_{\text{A}}},{z_{\text{B}}},z \leftarrow {{Z}_q}$和$ {C_{\text{A}}},{C_{\text{C}}} \leftarrow {{G}} $，根据验证等式可以计算得到

$ {C_{\text{L}}} = C_{\text{A}}^x{\text{Co}}{{\text{m}}_{{\text{ck}}}}{({f_1},\cdots ,{f_n};{z_{\text{A}}})^{ - x}}. $

$ {C_{\text{B}}} = C_{\text{C}}^x{\text{Co}}{{\text{m}}_{{\text{ck}}}}{({f_1}(x - {f_1}),\cdots ,{f_n}(x - {f_n});{z_{\text{A}}})^{ - x}}. $

$ {C_0} = \prod\limits_{i = 0}^{N - 1} {c_i^{\prod\nolimits_{j = 1}^n {{f_{j,{i_j}}}} }} \cdot \prod\limits_{k = 1}^{n - 1} {C_k^{ - {x^k}}} \cdot {\text{Co}}{{\text{m}}_{{\text{ck}}}}(0; - z). $

返回的模拟器初始消息和响应为$({C_{\text{L}}},{C_{\text{A}}},{C_{\text{B}}}, {C_{\text{C}}},$$ {C_0},\cdots ,{C_{n - 1}},{f_1},\cdots, {f_n},{z_{\text{A}}},{z_{\text{B}}},z) $.

在真实证明和模拟器中，${f_1},\cdots ,{f_n},{z_{\mathrm{A}}},{z_{\mathrm{B}}},z \leftarrow {{Z}_q}$是不可区分的. 在这些值和给定x的条件下，验证等式在真实证明和模拟证明中唯一确定${C_{\text{L}}}$、${C_{\text{B}}}$和${C_0}$. 这表明真实证明和模拟证明具有相同的概率分布. 零知识性得证.

从2个角度分析公平性. 恶意数据请求者可能试图不支付费用获取数据. 本文方案要求请求者生成正确零知识证明，并由部署在ECN上的智能合约验证. 零知识证明的可靠性确保未付费者无法生成有效的证明，智能合约的确定性和自动执行特性保证仅合法请求者可以获取相应的位置数据.

另一方面，恶意的位置数据提供者可能试图获取不当酬金. 本方案中，请求者使用提供者公钥加密共享参数${\text{au}}{{\text{x}}_{{R}}}$，仅对应私钥持有者可解密并构造零知识证明. HE加密算法的安全性^[23]确保攻击者无法获取共享参数或私钥信息，零知识证明的可靠性保证只有持有正确私钥和共享参数的数据持有者才能获得费用，从而保证了交易公平性.

定理4：若CPK加密算法满足IND-CPA安全性，$\Sigma $协议和CZKP-1t协议满足零知识性，则CZKP-1t-MPS满足机密性，即账户余额不会被账户所有者以外的人获得，且交易金额无法被第三方获得.

证明：账户余额始终以$ {C_{{v_{\text{U}}}}} \leftarrow {\text{CPK}}{\text{.Enc}}({\mathrm{pk}}{\text{,}}{v_{{U}}};r) $的形式存在，若敌手要获得账户余额的明文信息，则只能从${C_{{v_{{U}}}}}$中解密得到${v_{{U}}}$. CPK加密算法满足IND-CPA安全性，敌手无法从多项式时间内有效地区分不同的密文，因此敌手无法从${C_{{v_{{U}}}}}$中获得账户余额明文${v_{{U}}}$.

为了证明交易金额的机密性，以 PurchaseData算法为例进行分析. 敌手可以a)从${C_v}$中解密得到${v_j}$，b)从$ {\pi _{{\text{purchase}}}} $中提取出${v_j}$. 对于a)来说，由于CPK加密算法满足IND-CPA安全性，在多项式时间内，敌手无法解密得到交易金额. 对于b) 来说，由于$\Sigma $协议和CZKP-1t协议满足零知识性，即使敌手参与了零知识证明的交互过程，也无法通过此过程获得交易金额的明文. CZKP-1t-MPS满足机密性.

不可链接性分为交易不可链接性和数据请求不可链接性. 其中交易不可链接性保证交易双方的身份隐私，即交易双方以外的任何人无法区分$ {\text{Tran}}{{\text{s}}_{{\text{Purdata}}}} $对应的$ {\text{Tran}}{{\text{s}}_{{\text{Deposit}}}} $. 数据请求不可链接性保证除数据请求者以外的任何人无法知道请求的是哪个数据. 所提的CZKP-1t-MPS满足不可链接性，证明如下.

1）交易不可链接性. 构造游戏${G^{{\mathrm{UL}}}}$：将区块链网络抽象为预言机$\varOmega $，它提供与CZKP-1t-MPS中定义的操作进行交互的接口. 区块链账本$L$包含了$\varOmega $中包含和管理的所有交易. 假设敌手A可以在游戏${G^{{\mathrm{UL}}}}$进行期间对$\varOmega $进行问询. $\varOmega $响应A的询问直到A返回一组交易$({\text{tx}},{\text{tx}}^*) \in L$，该组交易满足：①tx和tx^*的交易类型相同，②$ {\text{tx}} \ne {\text{tx}}^* $，③敌手A没有参与到交易tx或tx*中. 若满足以下一种情况，则$\varOmega $输出1，即敌手赢得游戏.

情况1：若$ {\text{tx、t}}{{\text{x}}^*} \in {\text{Tran}}{{\text{s}}_{{\text{Purdata}}}} $，则交易中的接收者即DP-vessel相同.

情况2：若$ {\text{tx、t}}{{\text{x}}^*} \in {\text{Tran}}{{\text{s}}_{{\text{Deposit}}}} $，则交易中的发起者即C-vessel相同.

以PurchaseDate算法为例，若方案满足交易不可链接性，则对于多项式时间敌手A来说，概率$ {{P}} [{G^{{\mathrm{UL}}}}(\lambda ,A)] = 1 $可以忽略.

证明：假设A输出的交易组$({\mathrm{t}}{\mathrm{x}},{\mathrm{t}}{\mathrm{x}}^*) \in L$，其中tx表示为

$ {\text{Tran}}{{\text{s}}_{{\text{purchase}}}}: = \{ {\mathrm{pk}}_{{U}},{\mathrm{sn}},{C_v},C_{{v_{{U}}}}',{\mathrm{aux}}_{{R}},{\pi _{{\text{purchase}}}},{\sigma _{{U}}}\} , $

Tx^*表示为

$ {\mathrm{Trans}}_{{\text{purchase}}}^*: = \{ {\mathrm{pk}}_{{U}}^*,{\mathrm{sn}}^*,C_v^*,C_{{v_{{U}}}}^{'*},{\mathrm{aux}}_{{R}}^*,\pi _{{\text{purchase}}}^*,\sigma _{{U}}^*\} . $

若要赢得游戏，则A必须找到${\mathrm{pk}}_{{R}} = {\mathrm{pk}}_{{R}}^*$. A可以a) 从${C_v}$和$C_v^*$中解密获得${\mathrm{pk}}_{{R}}$和${\mathrm{pk}}_{{R}}^*$，b) 从${\text{au}}{{\text{x}}_{{R}}}$和${\text{aux}}_{{R}}^{\text{*}}$中解密获得${\mathrm{pk}}_R$和${\mathrm{pk}}_R^*$，c) 从零知识证明${\pi _{{\text{purchase}}}}$和$\pi _{{\text{purchase}}}^{\text{*}}$中提取出${\mathrm{pk}}_{{R}}$和${\mathrm{pk}}_{{R}}^{\text{*}}$. 对于a) 和b) 来说，由于Twisted Elgamal算法满足IND-CPA安全性，多项式时间敌手A无法以不可忽略的概率赢得游戏. 对于c) 来说，由于构造的零知识算法满足零知识性，敌手无法赢得游戏，即$ {{P}} [{G^{{\mathrm{UL}}}}(\lambda ,A)] = 1 $的概率可以忽略，交易不可链接性得证.

2）数据请求的不可链接性. 在交易$ {\text{Tran}}{{\text{s}}_{{\text{fetchdata}}}}: = \{ {\mathrm{pk}}_{{U}},{\pi _{{\text{fetchdata}}}},{\sigma _{{R}}}\} $中，若敌手想要知道${\mathrm{pk}}_{{U}}$获取的是哪一条数据，则须从零知识证明$ {\pi _{{\text{fetchdata}}}} $中提取出$ \delta _l^{{\mathrm{E}}{{\mathrm{D}}_l}} $，由于构造的零知识算法满足零知识性，敌手无法赢得游戏. 数据请求的不可链接性得证.

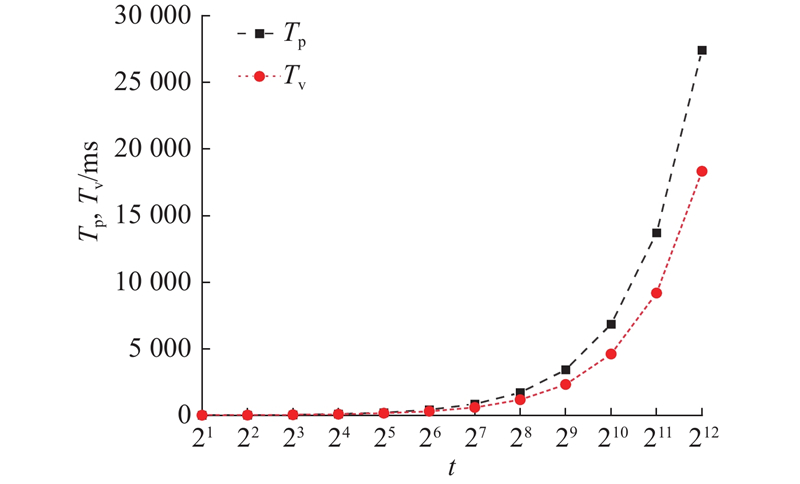
CZKP-1t算法支持对匿名集的规模进行动态调整. 参数t定义了匿名集的规模，它直接影响匿名性的程度. 为了在匿名性与计算效率之间取得平衡，对匿名集规模t与协议执行时间之间的关系进行测试. 测试结果如图2所示. 经过综合考量，选择t = 256作为匿名集的最优规模，这一选择在确保较低计算成本的同时，提供了较高的匿名性保障.

当选用t = 256时, 对文献[13]、[19]和本文方案CZKP-1t的计算开销进行仿真对比. 采用OpenSSL-1.0.1密码学库，在配置为AMD Ryzen 7 5825U with Radeon Graphics 2.00 GHz处理器和16 GB RAM的Windows 11操作系统上进行实验. 实验环境配置为Python 3.5，选用512位的椭圆曲线. 从表1可知，改进后算法的证明过程计算开销T_p较文献[13]降低了62.98%，验证过程计算开销T_v降低了8.21%.

选择以太坊来构建CZKP-1t-MPS. 模拟实验采用Golang编写的以太坊客户端Go-Ethereum实现. 为了兼容所提的海上位置共享方案，在原始Go-Ethereum的基础上增加${\text{Tran}}{{\text{s}}_{{\text{PubData}}}}$、${\text{Tran}}{{\text{s}}_{{\text{PurData}}}}$、${\text{Tran}}{{\text{s}}_{{\text{FetData}}}}$、${\text{Tran}}{{\text{s}}_{{\text{Refresh}}}}$、${\text{Tran}}{{\text{s}}_{{\text{Deposit}}}}$ 5种交易类型. 在Go-Ethereum中部署相应的智能合约.

尽管陆上交通领域已有许多针对位置共享的方案提出，但海运领域相关文献极其有限. 其中，Gai等^[12]构建了具有隐私保护的位置共享方案，与本文的研究方向一致，接下来主要与文献[12]进行对比.

如表2所示为文献[12]与本文方案CZKP-1t-MPS在数据共享全过程各个阶段的计算开销T对比. 为了方便起见，将本文方案中的支付承诺混淆阶段并入取款阶段. 交易验证时间在表2中以Verify阶段进行表示. 与文献[12] 相比，CZKP-1t-MPS各阶段的总计算开销降低了78.5%. 此外，文献[12]的初始化算法需要124.13 s，而本文算法只需要20.31 s. 只有验证阶段的效率稍具劣势，但执行时间只有0.273 s. 总体而言，本文方案的计算效率较文献[12]优势明显.

为了定义通信开销，使用$|{G}|$表示群${G}$元素的大小，$|{{Z}_q}|$表示${{Z}_q}$元素的大小，$|V|$表示交易金额的大小，$|{\mathrm{sn}}|$表示序列号大小. $|{{Z}_q}|$=32 B，$|V|$=4 B，$|{\mathrm{sn}}|$=32 B. 由于使用椭圆曲线点的压缩形式，$|{G}|$=33 B.

当t = 256时，匿名性和计算性能可以得到较好的平衡. 表3给出t = 256时CZKP-1t-MPS中各种交易类型的大小.

对本文方案CZKP-1t-MPS与文献[12]的BP3-MPS方案的通信开销c进行对比.从表4可知，本文方案CZKP-1t-MPS在通信成本方面略高于BP3-MTS^[12]. 这一差异归因于后者采用了zk-SNARKs，该零知识证明算法具有较小的证明大小. zk-SNARKs依赖于信任设置过程，一旦信任设置存在缺陷，则需要对系统进行更新或修改，这将带来额外的复杂性和潜在风险. 本文方案不存在上述风险，具有较高的鲁棒性. 另一方面，在海上环境中，由于船只的分布密度较陆地交通小，交易的发起频率更低，因此对通信带宽需求更低. 在船只配置异构的海上环境，即便配置较低的C-vessel的网络带宽仅为10 Mbit/s，本文方案CZKP-1t-MPS相较于BP3-MTS在数据传输时间上的差异仅为μs级别.

综上所述，本文方案CZKP-1t-MPS的计算效率较仅有的海上位置共享方案BP3-MTS显著提升，处理时间从s级降至ms级，而通信效率下降带来的μs级传输时延是可以忽略的. 总体效率提升80%左右，更适合船只资源配置异质的海运场景.

(1） 利用位置数据共享方法，实现了账户模型区块链下数据共享双方的身份不可链接性和数据与其持有者的不可链接性.

(2） 改进后的零知识证明协议计算复杂度从$O\;(t\log t)$降至$O\;(t)$.

(3） 位置数据共享方案处理时间从s级降至ms级，总体效率提高80%左右.