IEEE 802.15.7标准提供了开关键控、脉冲位置调制、脉冲振幅调制和色移键控(color-shift keying,CSK)等多种调制方案. CSK通过变化红/绿/蓝(R/G/B)LED光强度形成不同调制符号来传输数据. 作为恒定光强度调制方式,CSK可以有效避免人眼感知的LED闪烁特性[3]. 同时,相比于白光LED,多色LEDs的光谱效率更高[4]. 学者对基于恒定光强度平面的CSK进行了深入研究,以最大化最小欧式距离(minimum Euclidean distance,MED)为目标函数优化设计CSK星座来改善VLC系统性能[5-9]. 为了充分利用三维光强度空间的特性,Chen等[10-13]对基于多强度平面的CSK星座进行优化设计,提高了VLC系统的传输质量. Wang等[14]研究用户随机接入方向下的CSK星座设计方法. 一般情况下,当最大光强度闪烁时间周期小于5 ms时,人眼察觉不到闪烁变化[15];VLC作为高数据传输系统满足最大光强度闪烁时间周期要求. 由于VLC系统受限于强度调制/直接检测方式,发送信号仅能取实正值. 为了克服该问题,Wang等[16-19]通过研究VLC系统中改进的空间调制(spatial modulation,SM)来提高系统的频谱效率与可靠性. 调制技术的研究工作主要集中于基于振幅调制的VLC系统. CSK作为VLC中的高效调制方式,与SM结合进行星座设计对提高系统性能具有重要意义.
本研究基于三维光强度空间和SM原理,提出分别对应恒定光强度和多强度面约束的CSK设计方案(SM-CSK),无需估计发送LED的索引. 1) 针对室内工作学习场景在恒定光强度约束下的SM-CSK能够增加CSK符号间的MED,该方案通过增加LED的数量来扩展三维光强度空间中CSK符号坐标的取值,并将双极性信号转换为单极CSK信号. 2) 针对无人值守的电磁敏感区域和室外场景在三维光强度空间和白光约束下的SM-CSK以最大化CSK符号间的MED为目标函数,基于序列二次规划(sequential quadratic programming,SQP)算法进行多球面(multi-sphere partitioning, MSP)建模,该方案通过设定初始值和步长来迭代优化运算,得到不同半径下的同心球面SM-CSK星座结构. 此外,本研究将给出恒定光强度和多强度平面的多进制SM-CSK星座性能参数,评估SM-CSK误比特率(bit error rate, BER)性能,并通过仿真实验验证BER性能的可靠性.
1. 系统模型
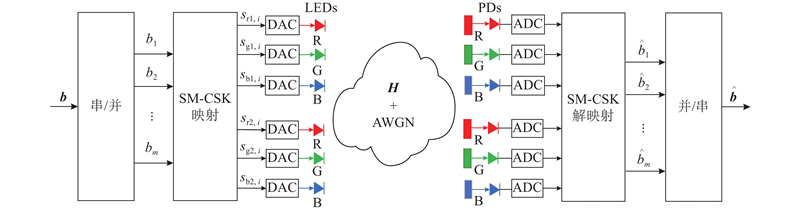
为了提高基于CSK调制的VLC系统传输质量,引入SM来传输三维光强度空间的扩展CSK符号. 如图1所示为基于SM-CSK映射的VLC系统模型. 发送的数据序列
图 1
图 1 空间调制-CSK映射的可见光通信系统模型
Fig.1 Visible light communication system model mapped by spatial modulation-CSK
表 1 LED选取与空间调制-CSK信号的关系
Tab.1
| 扩展CSK信号 | LED索引 | SM-CSK信号 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
表 2 四进制空间调制-CSK的映射规则
Tab.2
| 比特子序列 | LED索引 | |
| 00 | 1 | |
| 01 | 2 | |
| 10 | 3 | |
| 11 | 4, 5, 6 |
式中:
式中:
2. 恒定强度面空间调制-CSK星座设计
2.1. 问题建模
恒定强度面SM-CSK(constant intensity plane-based SM-CSK, CIP-SM-CSK)星座的主要设计思路:在恒定光强度和白光约束下,通过增大三维光强度空间中CIP-SM-CSK符号的MED来提高VLC系统的信号传输质量. CIP-SM-CSK星座的MED为
将CIP-SM-CSK星座设计问题建模为
式中:
2.2. 星座设计
CIP-SM-CSK星座的设计步骤:1) 选择基于二维三角形平面的三角划分CSK符号集[22].
式中:
2.2.1. 4-CIP-SM-CSK设计
选取3-CSK,设计数据速率为2 bits/符号的CIP-SM-CSK星座结构. 基于3-CSK符号集,依据符号子集划分准则,得到
2.2.2. 8-CIP-SM-CSK设计
选取6-CSK,设计数据速率为3 bits/符号的CIP-SM-CSK星座结构. 基于6-CSK符号集,依据符号子集划分准则,得到
2.2.3. 16-CIP-SM-CSK设计
选取15-CSK,设计数据速率为4 bits/符号的CIP-SM-CSK星座结构. 基于15-CSK符号集,依据符号子集划分准则,得到
图 2
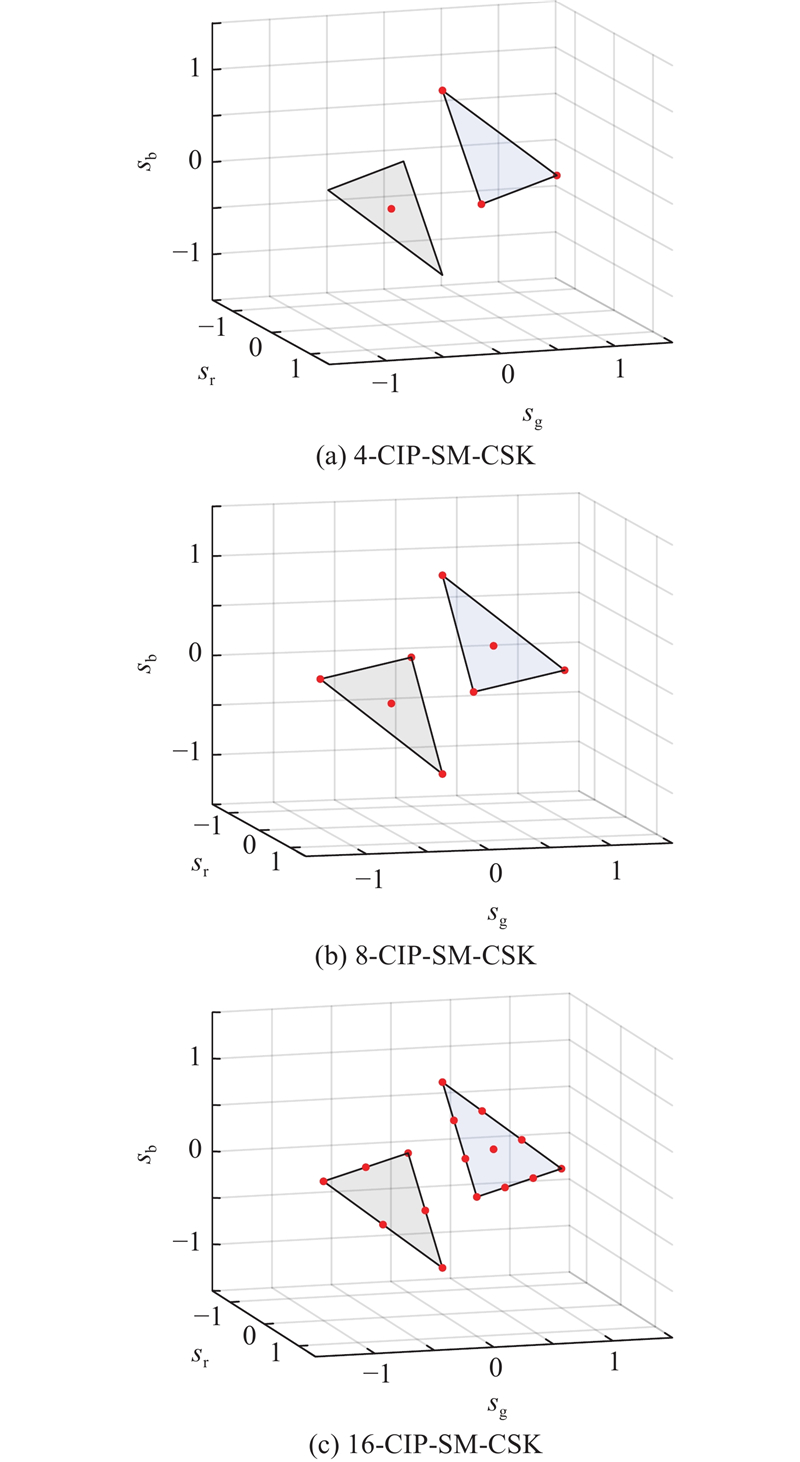
图 2 恒定强度面空间调制-CSK的星座示意图
Fig.2 Constellation diagram of constant intensity plane-based spatial modulation-CSK
表 3 恒定强度面空间调制-CSK的符号坐标
Tab.3
| M | 星座点 |
| 4 | |
| 8 | |
| 16 |
3. 多球面空间调制-CSK星座设计与性能分析
3.1. 问题建模
多球面SM-CSK(multi-sphere partitioning-based SM-CSK,MSP-SM-CSK)星座的主要设计思路:基于三维多强度面CSK星座结构和白光约束,通过设计多球面的SM-CSK星座结构来增大对应的MED. MSP-SM-CSK星座的MED为
将MSP-SM-CSK星座设计问题建模为
其中式(7b)同式(4b),表示满足白光约束,
3.2. 星座设计
观察可知,MSP-SM-CSK星座设计问题是非凸的,很难进行直接优化处理. 基于文献[22]中三角形划分的CSK星座结构,引入SQP迭代算法来解决优化设计问题,优化的MSP-SM-CSK星座符号生成步骤如下. 1) 设定光强度变化范围为
基于3-CSK符号集分析可知,4-MSP-SM-CSK与4-CIP-SM-CSK星座结构相同,因此重点介绍8-MSP-SM-CSK和16-MSP-SM-CSK的星座设计.
3.2.1. 8-MSP-SM-CSK设计
选取6-CSK,设计数据速率为3 bits/符号的MSP-SM-CSK星座结构. 基于6-CSK符号集,依据符号子集划分方法得到
图 3
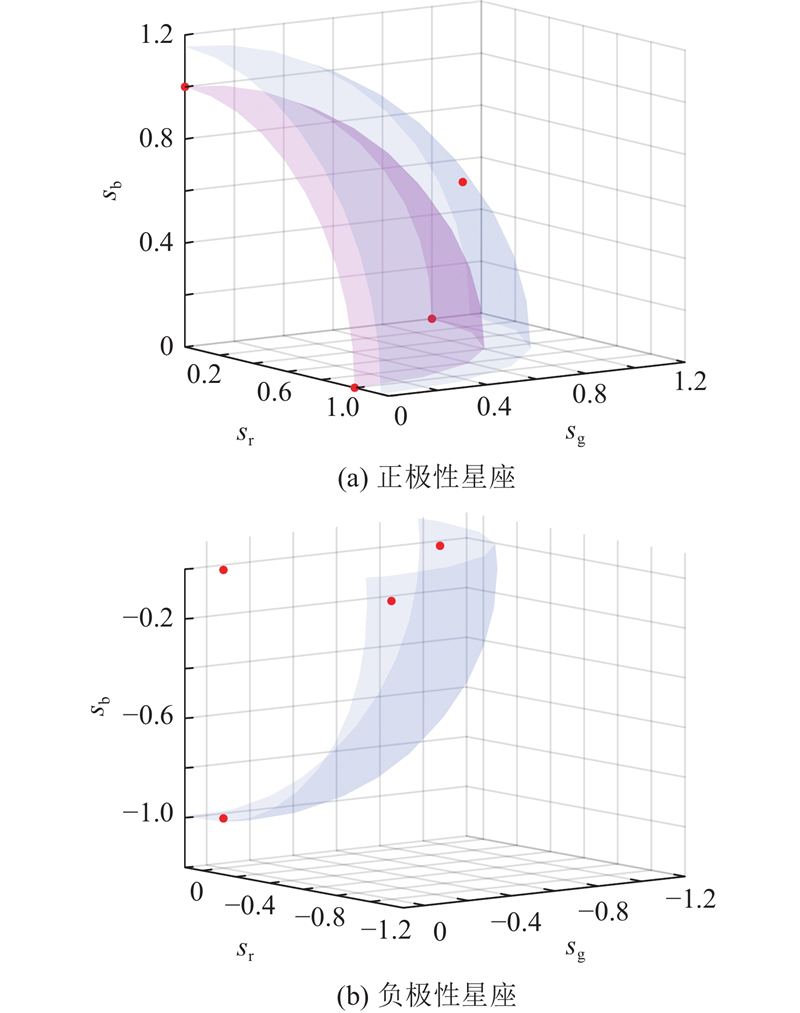
图 3 八进制多球面空间调制-CSK的星座示意图
Fig.3 Constellation diagram of octal multi-sphere partitioning-based spatial modulation-CSK
3.2.2. 16-MSP-SM-CSK设计
选取15-CSK,设计数据速率为4 bits/符号的MSP-SM-CSK星座结构. 基于15-CSK符号集,依据符号子集划分方法得到
图 4
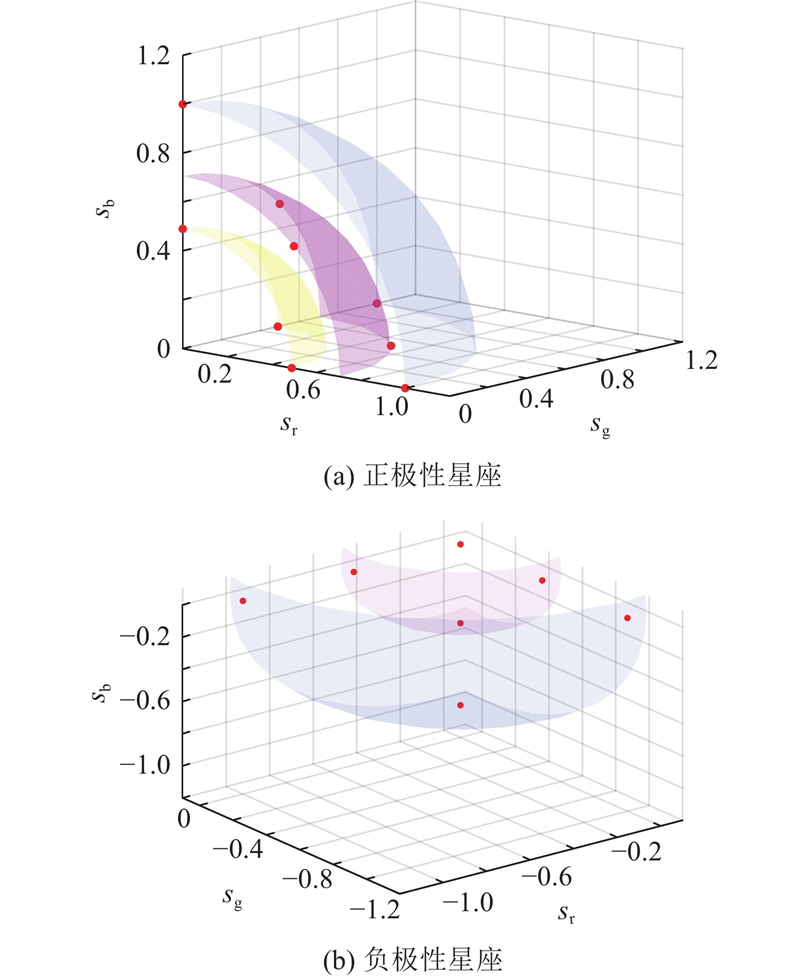
图 4 十六进制多球面空间调制-CSK的星座示意图
Fig.4 Constellation diagram of hexadecimal multi-sphere partitioning-based spatial modulation-CSK
8-MSP-SM-CSK和16-MSP-SM-CSK的符号坐标如表4所示.
表 4 多球面空间调制-CSK的符号坐标
Tab.4
| M | 星座点 |
| 8 | |
| 16 |
3.3. 性能分析
使用最大似然检测(maximum likelihood detection,MLD)算法,将SM-CSK的误符号率描述为
其中
式中:
其中
式中:
4. 仿真结果
如表5所示为不同数据率
表 5 不同CSK方案的参数对比
Tab.5
| 方案 | 方案 | 方案 | |||||||||||
| 4-CSK | 2 | 1.5 | 0.67 | 8-CSK | 3 | 2.25 | 0.22 | 16-CSK | 4 | 2.25 | 0.07 | ||
| 4-SCSK | 2 | 1.5 | 0.93 | 8-SCSK | 3 | 2.00 | 0.27 | 16-SCSK | 4 | 2.00 | 0.11 | ||
| 4-MIP-CSK | 2 | 3.0 | 0.89 | 8-MIP-CSK | 3 | 2.25 | 0.34 | 16-MIP-CSK | 4 | 3.38 | 0.18 | ||
| 4-CIP-SM-CSK | 2 | 3.0 | 1.78 | 8-CIP-SM-CSK | 3 | 1.75 | 0.67 | 16-CIP-SM-CSK | 4 | 2.25 | 0.22 | ||
| — | — | — | — | 8-MSP-SM-CSK | 3 | 2.25 | 1.00 | 16-MSP-SM-CSK | 4 | 0.75 | 0.43 |
如图5所示为不同数据率下理论与仿真的BER随信噪比RSN的变化曲线. 图5(a)中,当BER=10−5时,与4-MIP-CSK、4-SCSK、4-CSK相比,4-CIP-SM-CSK分别实现约3.25、3.31、4.25 dB的性能增益. 图5(b)中,当BER=10−5时,与8-MIP-CSK、8-SCSK、8-CSK相比,8-CIP-SM-CSK分别实现约3.16、3.91、5.83 dB的性能增益,8-MSP-SM-CSK分别实现约4.66、5.41、7.33 dB的性能增益. 图5(c)中,当BER=10−5时,与16-MIP-CSK、16-SCSK、16-CSK相比,16-CIP-SM-CSK分别实现约1.31、2.56、4.71 dB的性能增益;16-MSP-SM-CSK分别实现约4.41、5.66、7.81 dB的性能增益.
图 5
图 5 不同CSK方案的误比特率随信噪比的变化曲线
Fig.5 Variation curve of bit error rate of different CSK schemes with signal-to-noise ratio
5. 结 语
本研究通过空间域来发送双极性的扩展CSK信号,将二维光强度平面的CSK星座结构扩展至三维光强度空间,提出基于空间调制的CSK设计方案. 在恒定光强度和白光约束下,建模CIP-SM-CSK设计问题,生成最大化符号间MED的CIP-SM-CSK设计步骤. 提出MSP-SM-CSK优化设计方案来增大MED,使用顺序二次规划迭代算法来求解符号坐标. 参数对比和仿真结果显示:在高信噪比条件下,与CSK、SCSK方案相比,所提方案的误比特率明显降低. 为了提升多强度面CSK星座性能,后续将进一步研究CSK星座结构.
参考文献
IMT-2030(6G)推进组正式发布《6G总体愿景与潜在关键技术》白皮书
[J].
IMT-2030 (6G) Promotion Group officially released the white paper on 6G vision and candidate technologies
[J].
Design and implementation of color-shift keying for visible light communications
[J].DOI:10.1109/JLT.2014.2314358 [本文引用: 1]
Joint constellation-labeling optimization for VLC-CSK systems
[J].
Design and analysis of probabilistic shaping in color shift keying modulation schemes
[J].DOI:10.1109/JSYST.2020.3007391 [本文引用: 1]
Spherical quasi-physical model-based color-shift keying for visible light communication
[J].DOI:10.1109/TWC.2020.3019107 [本文引用: 1]
Optical wireless communications that exploits the human vision’s tolerance of light fluctuations in intensity and chromaticity
[J].
Multi-intensity planes constellation and code design-based color-shift keying for visible light communications
[J].DOI:10.1109/JIOT.2023.3281497 [本文引用: 1]
Sensing-aided CSK constellation design for multi-color VLC system with random receiver orientation
[J].DOI:10.1109/TWC.2024.3382039 [本文引用: 1]
Human electroretinogram responses to video displays, fluorescent lighting, and other high frequency sources
[J].DOI:10.1097/00006324-199108000-00012 [本文引用: 1]
SM and NOMA joint assisted indoor multi-user VLC downlink
[J].
Design of protograph LDPC-coded MIMO-VLC systems with generalized spatial modulation
[J].
Capacity, convergence, and complexity improvements for LDPC-coded MIMO-VLC systems with generalized spatial modulation
[J].DOI:10.1109/TCOMM.2024.3366114
On the capacity region of optical mobile communication systems with spatial light modulation
[J].DOI:10.1109/TVT.2024.3499321 [本文引用: 1]
Wireless in-house data communication via diffuse infrared radiation
[J].DOI:10.1109/PROC.1979.11508 [本文引用: 1]
Coding for visible light communication using color-shift keying constellations
[J].DOI:10.1109/TCOMM.2019.2907939 [本文引用: 2]
Symbol error rate analysis for colour-shift keying modulation in visible light communication system with RGB light-emitting diodes
[J].DOI:10.1049/iet-opt.2014.0152 [本文引用: 1]