电网系统中常有故障发生,确定故障类型和位置的传统方法有阻抗法、行波法. Liao[1]提出基于阻抗的故障检测方法,使用阻抗矩阵检测电网故障. Naidu等[2]利用单端行波数据基于行波技术检测故障位置. 为了更快速地诊断故障类型并进行精确定位,Petri网[3]、多源信息融合技术[4]以及优化方法[5]被广泛应用[6]. Tan等[7]提出基于模糊Petri网和多源数据的配电网故障段识别方法. Lu等[8]提出基于开关量和电气量多源特征融合的电网智能故障诊断方法,有效提高了电网的故障诊断效率和容错性. 何瑞江等[9]通过建立线性整数规划模型来定位断路故障区段. 上述方法可解释性较强,但特征的学习能力不足. 它们通常依赖电网的精确参数来建立数学模型,这些参数在电网中可能会因设备老化、负载波动而发生变化,导致故障诊断的准确率下降.
针对节点数较多的电网,基于机器学习和深度学习的方法因具有从数据中学习并通过训练自动调整权重和参数的特点而被广泛关注. 在利用机器学习方法进行电网故障诊断的应用方面,Biju等[10]利用基于长短期记忆网络(long short-term memory, LSTM)模型进行故障分类;王发麟等[11]结合改进的自适应遗传算法与BP神经网络,提高了线缆断路故障定位的准确率;刘科研等[12]基于支持向量机(support vector machine, SVM)模型,通过提取测量点相电压基波及2-7次谐波分量,实现故障类型判别及定位. 随着深度学习技术的快速发展,特别是卷积网络[13-14]的引入,电网故障诊断方法进一步得到优化. 有研究利用图注意力网络[15-16]定位配电网故障,充分考虑网络拓扑和节点间影响,增强了特征提取能力;邓丰等[17]提出CNN-LSTM模型,分别提取频率分布特征和时间关联特征,用于配电网故障定位;Liang等[18]通过改进池化模型的自适应卷积神经网络(convolutional neural networks, CNN)方法,提升了故障线选择的特征提取能力;魏东等[19]采用2个softmax分类器的CNN架构,实现区内外故障判断与故障选相的联合分类;许可等[20]提出结合图卷积神经网络(graph convolutional networks, GCN)[21-22]的端到端模型,利用该模型进行的故障定位和类型识别准确率较高. 上述模型未能同时挖掘电力数据的时间与空间特征,导致故障的诊断准确率不高. Hu等[23]提出具有时空卷积块的深度学习模型,综合考虑时间和空间特征,实现用于故障定位和故障类型分类的学习框架. 上述模型未能形成完整的故障诊断系统,不能兼顾故障类型判断、故障线路定位和故障距离判断3个关键任务.
本研究提出基于快速傅里叶变换(fast Fourier transform, FFT)-CNN-GCN的电网故障诊断新模型,同时实现故障类型分类、故障线路定位和故障距离判断. 该模型利用FFT进行电压和电流信号分解,提取时域和频域特征;利用CNN的特征提取能力,从时间序列中提取局部关键特征;利用GCN融合空间特征与时序特征,从整体上提升模型的诊断能力. 模型设计力求减少对电网参数准确性的依赖,进行三相电压和电流信号的多维度特征提取,直接从数据中学习故障模式,以提高模型的故障诊断准确性和效率.
1. 电网故障判别与定位
1.1. 故障类型
电网故障包括单相接地故障、两相短路故障、两相接地故障、三相短路故障,细分类型如表1所示.
表 1 电网故障类型
Tab.1
| 故障类型 | 故障类型细分 |
| LG(单相接地故障) | AG、BG、CG |
| LL(两相短路故障) | AB、AC、BC |
| LLG(两相接地故障) | ABG、ACG、BCG |
| LLL(三相短路故障) | ABC |
1.2. 故障线路定位
母线是电网的核心组件,负责将电能从发电站或变电站输送到各个分支线路、变压器和终端负荷点. 本研究以母线为节点,以线路为连接节点的纽带构造拓扑图,展示电网的物理连接结构. 故障线路定位是指考虑各母线之间的相互影响,通过检测和分析各个母线的电压和电流以确定故障发生位置的过程.
1.3. 故障距离判断
故障距离判断在故障线路定位的基础上进行,通过进一步分析电压和电流信号,确定故障点在特定线路上的具体位置. 故障距离判断能够帮助维修人员迅速找到故障点,及时进行维修,减少停电时间,保障电力系统的稳定运行.
2. 基于FFT-CNN-GCN的电网故障诊断模型
本研究所提模型由FFT、CNN和GCN3个功能模块组成. 原始三相电压和三相电流数据输入后,先由FFT模块提取原始数据的基波频率和基波相位,再由CNN模块提取基波频率和相位的时序特征,并通过归一化层处理特征数据,进而利用GCN模块对拓扑结构的处理能力来捕捉电网节点间的空间关联,最终确定故障类型和故障发生的具体位置.
2.1. 基于快速傅里叶变换模块的数据处理
FFT是用于计算离散信号频率成分的快速算法. 对长度为
式中:
1)采集信号:在采样时间
2)根据式(1)对采集到的信号进行FFT,得到三相电压和三相电流的频域表示,即
3)基波的幅值和相角计算: IEEE39节点系统的标准频率为60 Hz,因此三相电压和三相电流的基波对应的频率
2.2. 卷积神经网络
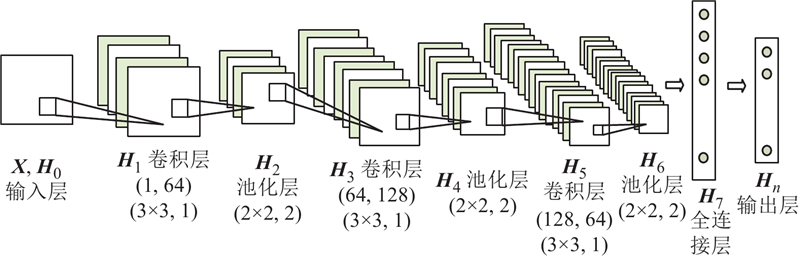
图 1
在CNN模型中,将系统故障发生后短时间内母线电压和电流经FFT处理后得到的幅值和相角作为输入,以故障类型、故障线路以及故障距离为标签. 观测窗口内完整的数据排列为
式中:
式中:
式中:
CNN 的训练目标是最小化损失函数. 将CNN用于多分类问题时,采用交叉熵损失函数:
式中:
2.3. 归一化层
为了减少内偏移协变、加快后续模型收敛速度、提高模型的鲁棒性和泛化能力,展平通过CNN提取的特征,采用层归一化(layer normalization, LN)方法对展平的特征进行处理. 1)层归一化层沿着通道的维度
2.4. 图卷积神经网络
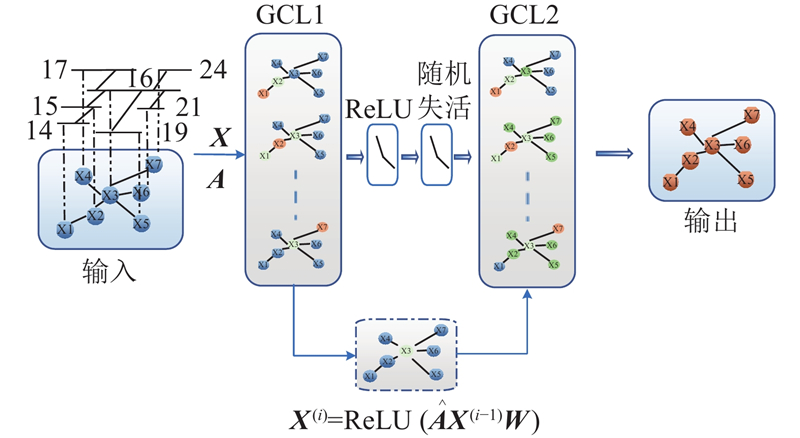
GCN充分利用节点之间的关联信息对节点间的电压和电流特征进行更新和聚合,并通过优化模型的损失函数来提高故障诊断的准确性. GCN是用于处理图数据的深度学习模型,结构如图2所示. 输入层的输入一般有2个:1)特征矩阵
图 2
式中:
式中:
式中:
3. 仿真与实验
3.1. 数据选取及预处理
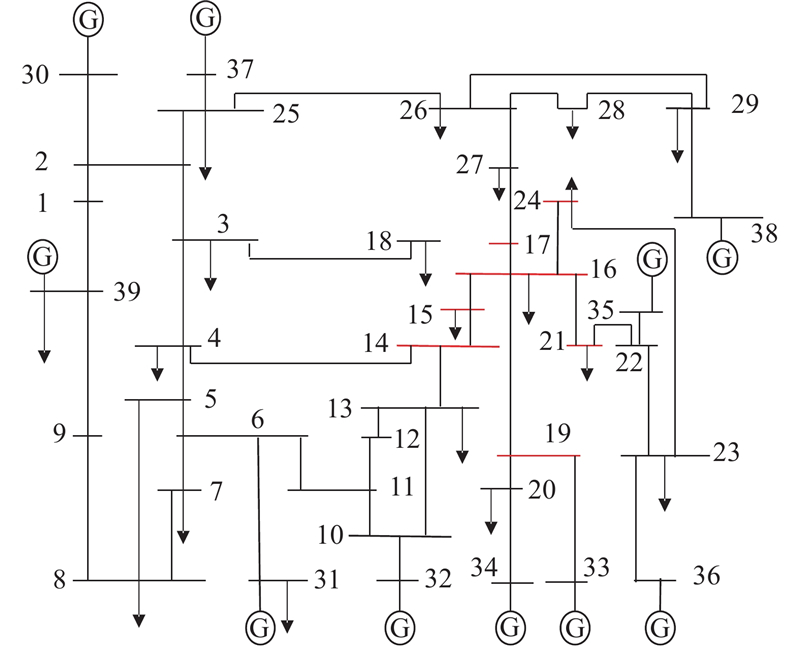
利用PSCAD对如图3所示的已知拓扑的IEEE 39节点电网系统[25]进行仿真. 设置电网故障电阻为0.01 Ω,在母线14、15、16、17、19、21和24处安装电压和电流测量装置,现实电网中关键母线处通常已安装测量装置,因此该方法不会显著增加的额外成本. 虽然仿真仅考虑部分区域,但是本研究所提模型具有较强的扩展性,随着节点数的增加,调整模型的输入数据和邻接矩阵,即可适应更大的图结构数据[26]. 为了获得样本数据,假设母线在0.35 s发生如表1所示的10种类型的故障之一,故障持续0.15 s. 测量装置从0.3~0.6 s以0.001 s的间隔采样三相电流和三相电压值. 为了精准定位不同位置的故障,在母线9个不同位置(分别距离母线节点10%,20%,···,90%)上模拟生成10种类型故障. 针对原始故障数据,对数据进行采样,采样时间窗口为50,滑动步长为5,每个故障位置发生1种故障,得到51个样本[23]. 50个时间点包含0.05 s的故障数据,在这种情况下,所提模型可以利用故障发生后不超过0.15 s的任意0.05 s的数据确定故障类型、故障线路和故障距离. 如果在该时间窗口内有任何时间点发生故障,则认为该窗口对应的样本为故障样本,从而解决故障和非故障样本不平衡的问题. 以IEEE39节点系统中的部分区域为例进行故障类型分类和故障线路定位,共得到92 780个数据样本,选择80%的样本进行模型训练,剩余样本用于模型测试.
图 3
图 3 IEEE 39节点电网系统的拓扑结构
Fig.3 Topological structure of IEEE 39-bus power grid system
3.2. 模型构建
如图4所示,本研究所提模型用于建立系统故障发生前后一段时间内的电力系统测量数据与故障类型、故障线路以及故障距离之间的映射关系. 为了使FFT后三相电压和三相电流的基波幅值和相位适合CNN的网格状拓扑,将这些数据预处理成形状为(16,7,50,12)的图像,其中16表示批量大小,7表示节点数,50表示样本包含50个时间点,12表示特征的数量. 图像数据先通过3层卷积-池化操作逐步提取高层次的特征,再通过展平层对特征进行处理,将每个特征图降维到标量. 应用层归一化技术对池化后的特征进行标准化,提升训练过程的稳定性和模型的收敛性,减少特征的复杂性并为后续的图卷积层提供输入. 图卷积层对特征数据进行处理,进一步增强感知能力. 输入数据的大小为(16,7,384),图卷积层将卷积提取的特征与图结构信息结合,生成新的特征矩阵. 这些提取的特征向量被输入全连接层,由Log-softmax函数将提取的特征向量转化为每个类别的归一化概率,最终输出故障类型、故障线路以及故障距离的标签.
图 4
图 4 基于FFT-CNN-GCN的电网故障诊断模型结构
Fig.4 Structure of power grid fault diagnosis model based on FFT-CNN-GCN
3.3. 实验结果及分析
为了确保结果的准确性和可靠性,进行多次实验,并对评价指标的值进行平均处理.
3.3.1. 模型收敛性验证
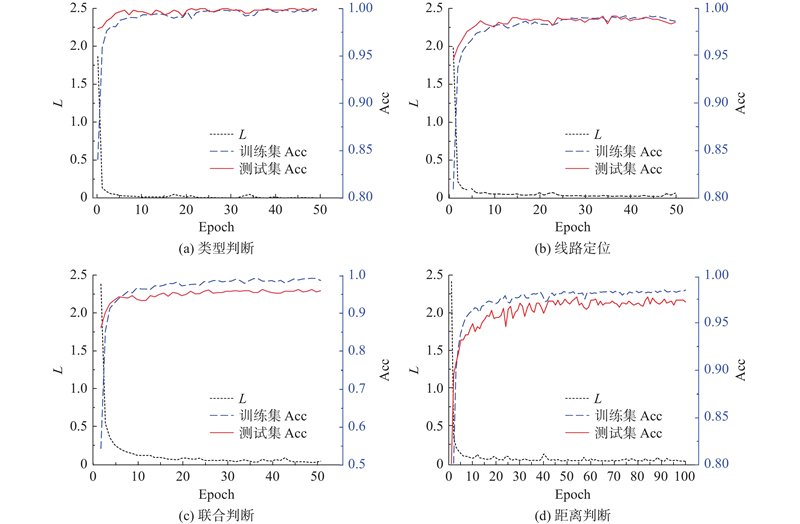
构造提取时序特征的CNN和含有GCL的GCN的混合网络模型,针对包含表1中故障类型的数据集进行训练与测试. 所提模型执行不同任务的准确率和损失值如图5所示. 其中Acc为诊断准确率,Epoch为迭代轮次. 可以看出,在初始的几轮训练中,模型的训练损失迅速下降,表明模型开始成功捕捉到数据的主要特征. 随着迭代轮数的增加,模型的损失率逐渐趋于稳定,表明模型具有良好的收敛性. 训练集和测试集的准确率在初期迅速上升,并在后期保持较高水平,未出现过拟合或欠拟合现象,表明模型具有出色的学习效果和泛化能力. 使用训练好的模型进行故障样本检测时,在实验室条件下,每个任务的计算时间均不超过0.5 ms,证明所提模型具备较好的实时性.
图 5
图 5 基于FFT-CNN-GCN的电网故障诊断模型执行不同任务的损失值和准确率折线图
Fig.5 Line chart of loss value and accuracy for different tasks of power grid fault diagnosis model based on FFT-CNN-GCN
3.3.2. 模型性能验证
开展消融实验,通过分析FFT模块和CNN-GCN混合网络对整体性能的影响,验证两者在所提模型中的有效性及贡献. 将所提模型与FFT-CNN-LSTM模型[27]进行对比,验证模型在线路故障诊断上性能.
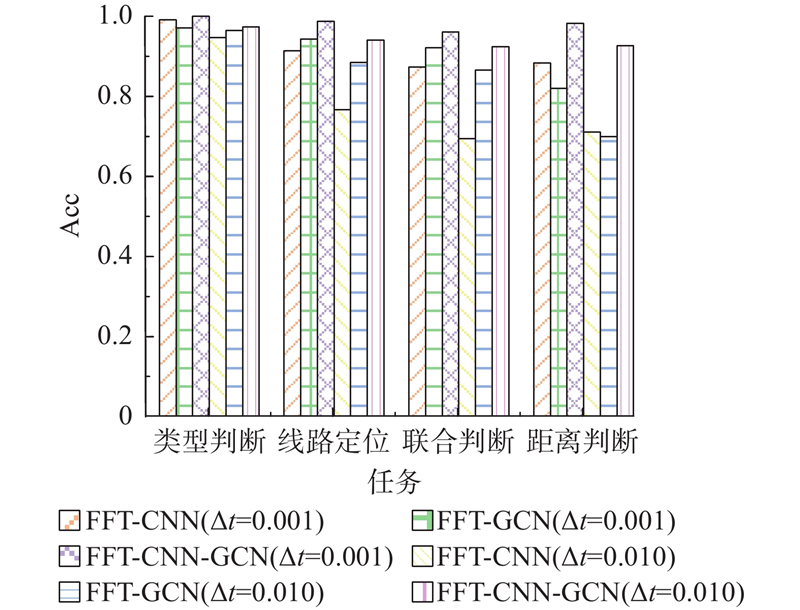
比较多模块组合模型在不同任务上的性能,参与模型包括FFT-CNN、FFT-GCN、FFT-CNN-GCN、CNN、GCN和CNN-GCN. 如图6所示,FFT-CNN和FFT-GCN的Acc比未使用FFT的CNN和GCN模型的高,FFT-CNN-GCN的Acc比未使用FFT的融合网络模型CNN-GCN的高,这说明加入FFT后的模型在频域特征的提取上表现更佳. 在故障类型判断任务中,所提模型的Acc=0.998 4,优于其他模型. 对于故障线路定位任务,所提模型同样表现出色,Acc=0.985 3. 在故障类型判断和线路定位的联合判断任务中,所提模型的Acc=0.959 2,证明了该模型在综合特征提取方面的强大能力. 在故障距离判断任务中,所提模型的Acc=0.980 4,高于其他模型组合. 本研究所提模型综合利用FFT和深度学习技术,在参与对比的模型中综合性能最佳,进一步验证了该模型在提升模型精度和鲁棒性方面的有效性.
图 6
如表2所示,所提模型的Acc、F1分数、精确率P和召回率R均优于FFT-CNN-LSTM模型的对应指标. 分析原因:所提模型通过GCN有效捕捉数据的拓扑结构,并结合CNN的时序特征处理能力,提升了模型的准确性;FFT-CNN-LSTM模型虽然在时序数据处理上有优势,但对图结构的建模能力较弱,因此Acc较低.
表 2 不同电网故障诊断模型的性能对比
Tab.2
| 任务 | FFT-CNN-GCN | FFT-CNN-LSTM | |||||||
| Acc | F1 | P | R | Acc | F1 | P | R | ||
| 类型判断 | |||||||||
| 线路定位 | |||||||||
| 联合判断 | |||||||||
| 距离判断 | 0. | ||||||||
3.3.3. 模型适应性验证
评估不同采样间隔和噪声条件下,FFT-CNN、FFT-GCN和FFT-CNN-GCN模型在故障诊断任务中的表现,探讨采样频率和噪声对模型性能的影响.
如图7所示,3种模型采样间隔Δt=0.001 s的Acc均高于Δt=0.010 s的Acc. 较低采样频率下噪声更容易混入有用信号,导致Δt=0.010 s时部分重要的信号特征会失真,从而降低模型的学习效果. 更高的采样频率可以更好地平滑噪声提高信号质量,因此Δt=0.001 s提供了更多的时序信息,模型能够捕捉到更多的信号变化和细节信息. 在这2种采样间隔下,所提模型始终表现出比其他模型更高的诊断准确率,其复杂的特征提取能力使其能够充分利用高采样频率下的信号特征,从而在各类任务中展现出较强的鲁棒性.
图 7
图 7 不同采样间隔下3种模型的准确率对比
Fig.7 Comparison of accuracy among three models under different sampling intervals
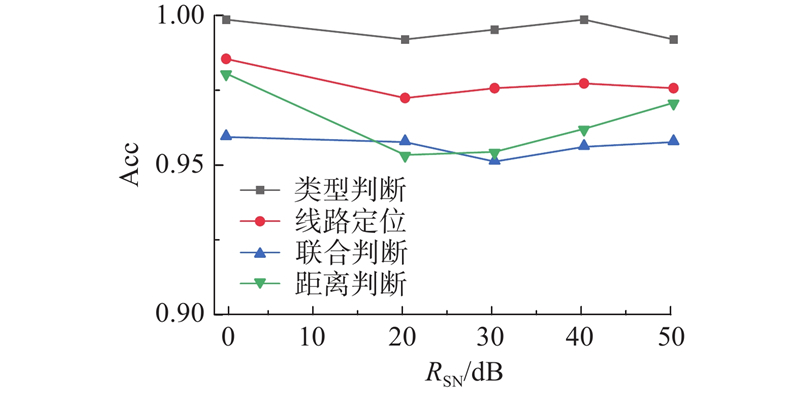
如图8所示,对比所提模型在无噪声及信噪比RSN=20、30、40、50 dB条件下的故障诊断类型识别、故障线路定位、类型和线路联合识别、准确率. 可以看出,所提模型在噪声影响下的Acc相对稳定,展示出较强的鲁棒性,能够有效适应不同噪声水平. 该模型通过在训练过程中自我调整以适应含噪声的数据,能够从数据中提取时域、频域、时间和空间的复杂特征,从而在噪声环境下仍然性能表现良好.
图 8
图 8 不同噪声水平下基于FFT-CNN-GCN的电网故障诊断模型执行不同任务的准确率
Fig.8 Accuracy of power grid fault diagnosis model based on FFT-CNN-GCN for different tasks under various noise levels
4. 结 语
本研究提出可同时实现故障类型判断、故障线路定位和故障距离判断的新模型,克服了现有模型在参数精度要求高、准确率不足以及适应性不强等问题. 与现有的基于人工智能的模型相比,所提模型结合信号处理、卷积神经网络和图卷积网络的优势,在时域和频域上以及时间和空间上对数据进行特征提取,具有较高的准确性. 仿真结果表明,所提模型既能实现故障类型判断、故障线路定位、故障距离判断等单一任务,又能同时支持故障类型判断与故障线路定位的联合任务,在电网线路故障诊断中表现出较好的性能. 所提模型处理单一任务的准确率都超过98%,处理联合任务的准确率超过95%,模型受采样间隔和噪声干扰的影响较小,具有良好的适应性. 所提模型在处理大规模电网时存在计算效率不足的问题,未来研究将聚焦算法优化,以提升模型在实时监测与故障响应中的速度.
参考文献
基于IAGA-BP的复杂机电产品线缆故障定位方法研究
[J].
Research on cable fault location method for complex mechatronic products based on IAGA-BP
[J].
基于电压数据SVM分类的有源配电网故障判别及定位
[J].
Fault identification and location of active distribution network based on SVM classification of voltage data
[J].
A new two-level hierarchical diagnosis network based on convolutional neural network
[J].DOI:10.1109/TIM.2019.2896370 [本文引用: 1]
A real-time fault localization in power distribution grid for wildfire detection through deep convolutional neural networks
[J].DOI:10.1109/TIA.2021.3083645 [本文引用: 1]
基于图注意力网络的配电网故障定位方法
[J].
Distribution network fault location based on graph attention network
[J].
CNN-LSTM全景故障特征挖掘的配电网单端定位方法
[J].
Single-ended traveling wave location method for distribution network based on CNN-LSTM panoramic fault feature mining
[J].
Two-terminal fault location method of distribution network based on adaptive convolution neural network
[J].DOI:10.1109/ACCESS.2020.2980573 [本文引用: 1]
Fault location for single-circuit line based on bus-impedance matrix utilizing voltage measurements
[J].DOI:10.1109/TPWRD.2008.915799 [本文引用: 1]
Precise traveling wave-based transmission line fault location method using single-ended data
[J].DOI:10.1109/TII.2020.3027584 [本文引用: 1]
A hierarchical power grid fault diagnosis method using multi-source information
[J].DOI:10.1109/TSG.2019.2946901 [本文引用: 1]
基于改进麻雀算法的配电网故障定位
[J].
Fault localization of distribution network based on improved sparrow algorithm
[J].
电网故障诊断的研究历程及展望
[J].
Research course and prospects of power grid fault diagnosis
[J].
含分布式电源配电网故障区段定位的线性整数规划方法
[J].
Fault section location method for DG-DNs based on integer linear programming
[J].
Hyperparameter optimization of long short term memory models for interpretable electrical fault classification
[J].DOI:10.1109/ACCESS.2023.3330056 [本文引用: 1]
基于卷积神经网络的输电线路区内外故障判断及故障选相方法研究
[J].
Research on internal and external fault diagnosis and fault-selection of transmission line based on convolutional neural network
[J].
基于图卷积网络的配电网故障定位及故障类型识别
[J].
Distribution network fault location and type identification based on graph convolution neural network
[J].
Fault location and classification for distribution systems based on deep graph learning methods
[J].DOI:10.35833/MPCE.2022.000204 [本文引用: 2]
Bi-objective reactive power reserve optimization to coordinate long- and short-term voltage stability
[J].
Data-driven short-term voltage stability assessment based on spatial-temporal graph convolutional network
[J].DOI:10.1016/j.ijepes.2020.106753 [本文引用: 1]
基于1D-CNN-LSTM混合神经网络模型的双桥并联励磁功率单元故障诊断
[J].
Fault diagnosis of double bridge parallel excitation power unit based on 1D-CNN-LSTM hybrid neural network model
[J].