泵阀联合调控旨在协调控制水泵与阀门,确保输水系统全线运行的安全可靠性. Zhang等[3]提出结合溢流式调压池和调节阀的新型防护方案. Wan等[4]研究水泵在不同启动时差下的瞬态过程,提出泵阀最优协同调控方案. 丁梓恒等[5]针对加压输水与重力自流结合的输水工程,进行事故停泵工况下的水锤防护方案分段研究. Liu等[6]构建含多水利设施的泵阀联合优化模型,得到水泵相继停机工况下风险指数最小的运行方案. Feng等[7]提出FLUENT与RELAP5的耦合方案,对并联泵阀系统中的水锤现象进行数值研究,为水锤防护提供了指导. Zhang等[3-7]的研究结果表明,泵阀联合调控策略在降低停泵水锤危害方面成效显著. 在包含高位水池的有压输水工程方面,这些研究多采取分段策略,未能充分反映泵阀联合调控对系统整体的影响. 泵阀联合调控求解过程为包含多个目标函数的复杂过程,人工计算不仅耗时耗力,而且难以保证找到最优解. 智能优化算法为解决此类工程问题提供了有效手段. Yan等[8-9]将非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)、多目标粒子群优化算法(multi-objective particle swarm optimization, MOPSO)应用于泵站优化运行研究. 这2种算法各有其优缺点[10],为了更高效地获取最优解,寻求更优算法并致力于算法与实际工程问题结合日益成为行业的普适性追求. 人工兔优化算法(artificial rabbits optimization algorithm, ARO)由Wang等[11]提出,是新型元启发式算法,已在热电联产经济调度[12]、微电网配置[13]、建筑物能源预测[14]等领域得到应用,且相比其他算法展现出更优的收敛速度及全局搜索能力. 鉴于泵阀联合优化调控为多目标优化问题,选择合适的策略进行单目标到多目标的改进是求解的核心. Tian等[15]引入非支配排序策略,提出改进的人工兔多目标优化算法,并将其应用于求解车辆动力系统优化问题. 非支配排序及拥挤度距离被广泛应用于多目标问题求解,可更好地保持算法收敛性与多样性的平衡[16-17]. ARO求解多目标优化问题的研究鲜少,且暂无ARO被引入泵阀联合优化调控研究的相关报道. 多目标优化还面临在实际决策中如何从Pareto解集中选择最佳方案的问题. 常见的决策方法如加权和法[18]难考虑指标间相互影响,层次分析法[19]构建判断矩阵复杂且计算量大,目标函数排序法[20]难以量化目标重要性. 灰色关联度分析法[21](grey relational analysis, GRA)是快速而有效的决策分析工具,通过比较系统内部各因素之间的几何形状相似度来评估各因素之间的关联程度,能够有效避免传统方法的主观偏差,已在化学工艺[22]、电力系统[23]以及供应链管理[24]等领域得到广泛应用.
本研究提出基于非支配排序及拥挤度距离[25]的非支配排序人工兔优化算法(non-dominated sorting artificial rabbits optimization algorithm, NSARO),并构建NSARO-GRA的优化求解决策模型. 以中国北方某地区的有压输水工程为例,研究3个并联泵、3个泵后阀及1个末端控制阀的联合优化调控,通过优化模型所得方案与现状方案对比,验证所提泵阀联合调控优化-决策方法的有效性.
1. 泵阀联合调控多目标优化模型及求解决策方法
泵站加压提水结合重力输水工程通常在输水管道最高处建设高位水池,将输水工程分为加压提水段与重力输水段,布置示意图如图1所示. 加压提水段的运行状态取决于水泵的启停运行控制与泵后阀的关闭规律,重力输水段的运行调控主要受末端控制阀影响. 此外,为了协调加压提水段及重力输水段运行,避免高位水池出现漏空或漫溢现象,须综合考虑水泵启停、泵后阀关闭及末端控制阀调节的协调运行. 本研究以瞬变过程管道系统压力极值最小及高位水池水位波动最小为目标,构建连续停机工况下泵阀联合优化调控模型,以协调优化泵阀调控间隔及调控规律,确保输水系统安全稳定运行. 1)通过建立的泵阀联合优化调控模型生成决策变量,驱动水力计算模型计算得到目标函数所需变量值,返回至优化调控模型计算得到目标函数. 2)采用NSARO求解优化调控模型,得到Pareto解集. 3)采用GRA获得优选的泵阀联合调控方案.
图 1
2. 耦合水力计算模型的泵阀联合优化调控模型
2.1. 优化模型
2.1.1. 决策变量
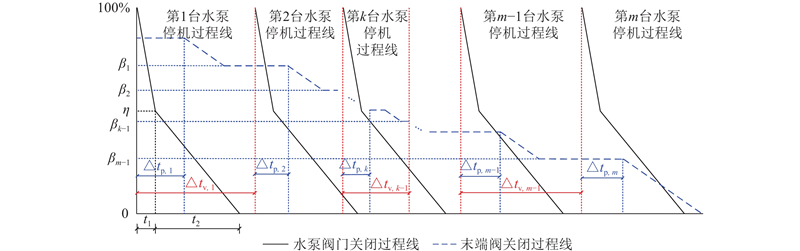
以包含m台水泵的输水系统为例,其连续停机过程如图2所示,决策变量包含:1)水泵之间的停机间隔Δtv=(Δtv,1,···,Δtv,k−1,···,Δtv,m−1);2)在实践中,先快后慢的阀门关闭规律是避免压头急剧变化和减少水锤的最佳选择[26],因此,泵后阀采用两阶段关闭规律CR,包含快关时长t1、快关开度η(η为关闭角度占总关角度的百分比,为无量纲参数)、慢关时长t2,CR=( t1,η,t2);3)考虑末端控制阀的调控与m台水泵停机相互配合,末端阀调控规律包含阀门调控时刻同m台水泵停机时刻之间的响应时间差Δtp=(Δtp,1,Δtp,2,···,Δtp,k,···,Δtp,m),以及每次调控对应的阀门开度β=(β1,β2,···,βk−1,···,βm−1). 决策变量向量描述为
图 2
2.1.2. 目标函数
综合考虑加压提水结合重力输水工程的特点,为了保证系统整体安全稳定运行,管道压力不能超过其承受能力,水泵倒转不得超过规定速度的1.2倍,并使高位水池不漏空不漫溢. 鉴于在连续停机过程中,水泵不发生倒转,选取以下3个目标函数:1)管道系统最大正压最小,
2)管道系统最大负压最小,
3)高位水池水位波动值最小,
式中:Hmax、Hmin分别为瞬变过程中沿线的最大、最小压力水头,Zmax、Zmin分别为高位水池的最高、最低水位.
2.1.3. 约束条件
约束条件包括显式约束、隐式约束. 显式约束是指决策变量可行域约束,隐式约束是指系统水锤压力约束和高位水池水位约束.
1)显式约束:(a)水泵停机间隔约束,
式中:Δtmin、Δtmax分别为水泵间的最大、最小时间停机间隔. (b)对于先快后慢的关阀模式,泵后阀关闭规律须满足以下约束条件:
式中:t1,max、t1,min分别为阀门的最大、最小允许控制时间,t2,max、t2,min为泵阀机组中阀门允许的最大和最小慢关时间. 鉴于快关不完全关闭,
式中:β0为末端阀初始阀相对开度.
2)隐式约束:(a)管道系统压力约束,根据泵站设计规范要求,“水锤综合防护设计后的输水管道系统不应出现水柱分离,瞬时最高压不应大于稳态最大压力的1.3~1.5倍”[27],即
管道任何部位不应出现水柱断裂或负压;对于立式或斜式轴流泵,虹吸式出水流道驼峰顶部的压力不应低于−7.5 m,
式中:Hw,max为沿线稳态最大压力值. (b)高位水池水位约束,为了保证高位水池不发生漏空或漫溢现象,高位水池水位须满足:
式中:ZS,max、ZS,min分别为高位水池的设计最高、最低运行水位.
2.2. 有压输水系统水力计算模型
基于有压管道非恒定流的基本方程,结合工程运行条件与实测数据资料,将阀门、水泵、调节池等作为边界条件,建立有压输水系统的水力计算模型,采用特征线法进行求解,实现不同工况下水力瞬变过程模拟计算,解得系统的最大最小压力值及水位波动值.
2.2.1. 水锤计算的特征相容方程
有压输水管路系统模型的基本数学方程[28]为
式中:H为测压管水头,qV为体积流量,D为管道直径,A为管道直面积,tf为过流时间,g为重力加速度,x为节点坐标,cwh为水锤波速,φ为管道坡度,f为沿程摩擦阻力系数. 将式(14)、(15)简化为标准双曲型偏微分方程,由特征线法得到特征相容方程为
计算系数
式中:Δx为距离步长,Hi,t、qV,i,t分别为t时刻i节点的水头、体积流量,Hi−1,t−1、Hi+1,t−1分别为t−1时刻i−1和i+1节点的水头,qV,i−1,t−1、qV,i+1,t−1分别为t−1时刻i−1和i+1节点的体积流量.
2.2.2. 水泵边界条件
水泵的边界条件[29]由水头平衡方程FⅠ和转动方程FII组成:
式中:HR、qV,R分别为额定扬程和额定体积流量,Hsy为泵装置扬程,α、μ分别为相对流量、相对转速,下标0表示上一时刻数值,
2.2.3. 阀门边界条件
阀门的过流方程[28]为
式中:qV,p为阀门的体积流量,τ为阀门相对开度,Cr为全开时流量系数,Ar为全开时过流面积,ΔHP为阀门两侧的压力水头差.
2.2.4. 调节池边界条件
调节池的边界条件由连续方程及水头平衡方程得到
流量与水位关系方程为
式中:qV,d为调节池进口体积流量,qV,up为调节池出口体积流量,qV,S为体积流量变化量,ZS为调节池水位,HT为调节池底部测管水头,α1为水头损失系数,AS为调节池断面面积.
2.2.5. 上下游水库边界条件
假定水力瞬变过程中上下游水库水位恒定,水位边界方程为
式中:HC为定水位值.
3. 泵阀联合调控多目标优化求解及决策方法
3.1. 基于非支配排序人工兔优化算法的泵阀联合调控模型求解方法
本研究引入非支配排序与拥挤度距离,提出基于NSARO的泵阀联合优化调控求解方法.
3.1.1. 人工兔优化算法
ARO模拟兔子的生存策略,其寻优过程主要包括2个阶段,即全局勘探阶段(迂回觅食)和局部开发阶段(随机隐藏). 在迂回觅食阶段,兔子倾向于在种群中随机选择个体并添加扰动,进行位置更新,数学模型为
式中:X为个体位置,Xu、Xv分别为第u个个体和第v个个体的位置,N为种群规模,r1、r2和r3均为[0,1]的随机数,d为当前迭代次数,J为移动步长,c的取值为0或1,round为四舍五入取整函数. 在随机隐藏阶段,兔子沿着搜索空间的每个维度在周围制造若干个洞穴,并且从中随机选择1个进行隐藏,以降低被捕食的概率,数学模型为
式中:Y为隐藏参数,在迭代过程中随机从1线性减小到1/T;r4、r5均为[0,1]的随机数;ζ的取值为0或1;T为最大迭代次数. 随着时间的推移,兔子的能量逐渐减少,引入能量因子E模拟从勘探阶段到开发阶段的自动转换,
式中:r6为[0,1]的随机数.
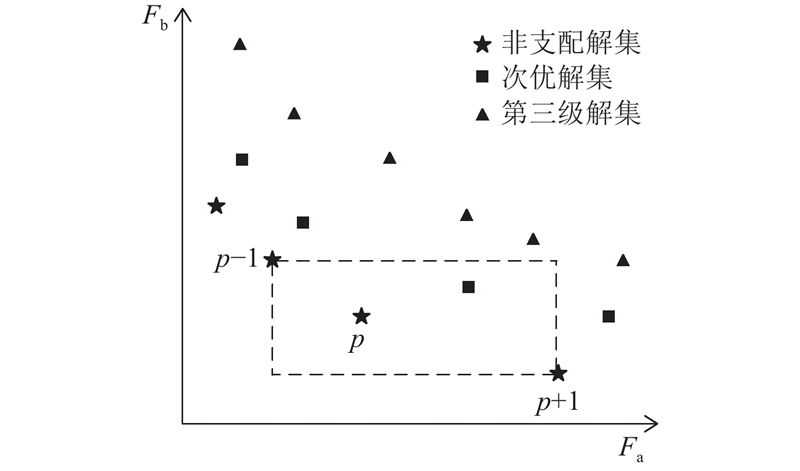
3.1.2. 非支配排序人工兔优化算法
图 3
图 3 非支配排序及拥挤度距离示意图
Fig.3 Schematic diagram of non-dominated sorting and crowding distance
3.1.3. 求解流程
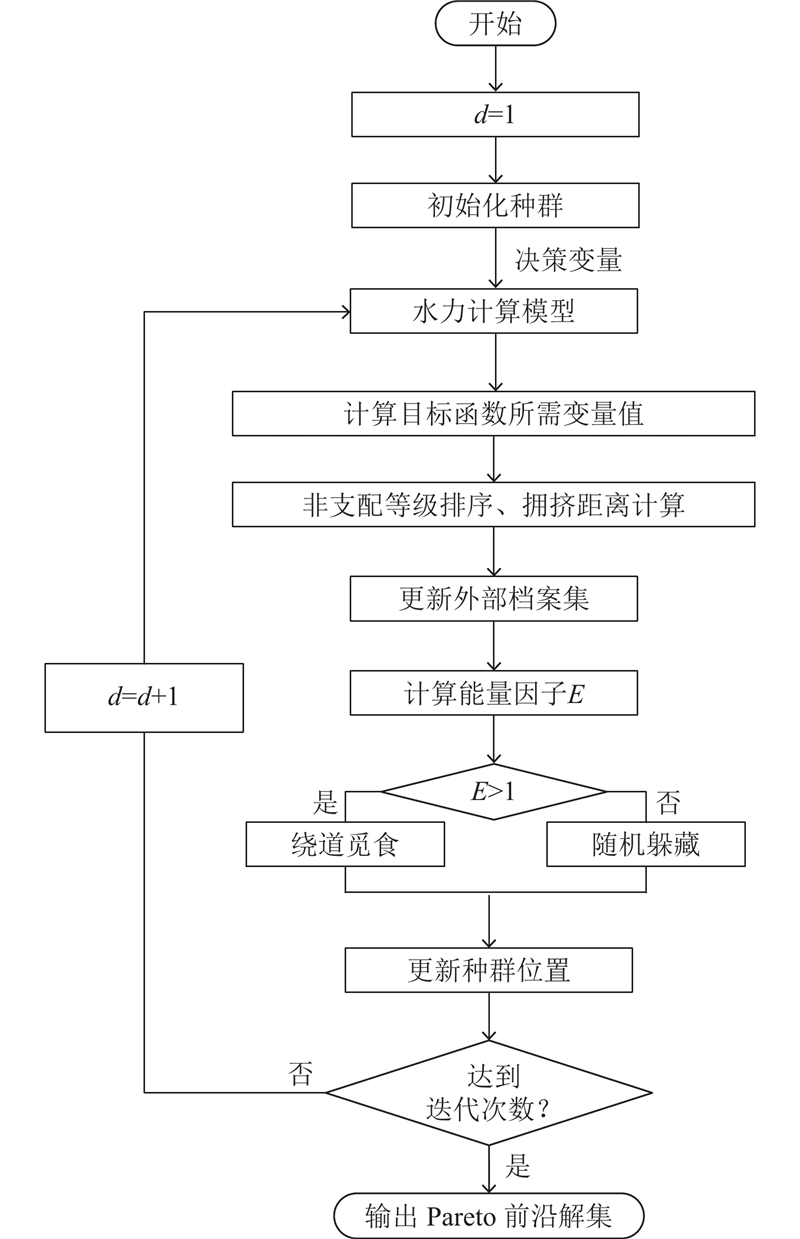
结合已建立的泵阀联合优化调控模型,采用NSARO求解的流程如图4所示,主要步骤如下.
图 4
图 4 非支配排序人工兔优化算法的泵阀联合优化调控求解流程
Fig.4 Solution process of pumps and valves joint optimization control using non-dominated sorting artificial rabbits optimization algorithm
1)初始化种群. 对于m台并联水泵连续关闭,各决策变量初始化位置为
式中:ub、lb分别为解空间的上、下界,rand为[0,1]的随机数.
2)计算目标函数及约束处理. 将初始种群传入水力计算模型,求解得到目标函数所需的变量值,返回至优化调控模型计算目标函数. 若个体的目标函数值超出约束范围,则通过罚函数将其放大10 000倍.
3)非支配排序及拥挤度距离计算. 遍历种群中个体,通过非支配关系得出非支配个体,并根据拥挤度距离对非支配个体进行排序,更新外部档案集.
4)更新种群位置. 利用式(33)计算能量因子E,根据能量高低选择不同的更新方式,当E>1时,选择迂回觅食策略,根据式(29)计算;反之,则采取随机躲藏,通过式(31)计算更新种群位置,并根据式(5)~(9)进行显式约束处理.
5)迭代寻优. 更新种群后,返回步骤2)继续求解,当达到最大迭代次数,算法优化结束,获得Pareto前沿解集.
3.2. 基于灰色关联度的决策方法
GRA是基于灰色系统理论的决策分析方法,主要过程是通过建立评价指标体系,计算每个Pareto前沿解与所确定参考方案间的关联度,最终根据关联度高低进行综合评价和排序,从而识别出灰色关联度σ最大的方案,主要计算步骤[30]如下.
1)确定分析初始数据. 将3个目标函数作为GRA的影响因素,由Pareto解集得到影响因素集,对于无偏折中策略,将各影响因素的权重ω1、ω2、ω3均设为1/3.
2)无量纲化处理. 采用初值法对3个目标函数值进行无量纲化处理,消除各数据的物理意义和量纲不同造成的影响.
3)参考方案确定. 按照最大正压取最小值、最大负压取绝对值最小值、高位水池波动值最小值的原则,选出各影响因素值的最优数据构成参考方案.
4)灰色关联系数计算. 各联合调控方案Wb与参考方案W0关于影响因素χ的灰色关联系数计算式为
式中:γ为灰色关联系数;Δb(χ)为Wb与W0关于影响因素χ的绝对差;δ为分辨系数(0≤δ≤1),取δ=0.5.
5)灰色关联度计算. 将各目标函数的权重ω1、ω2、ω3与灰色关联度系数加权求和,得到灰色关联度σ.
4. 实例应用
4.1. 工程概况
某加压提水结合重力输水工程组成如图1所示. 泵站由4台同型号离心泵组成(3用1备),每台水泵后设有液控蝶阀,单泵设计体积流量为1.86 m3/s,单泵扬程为65.69 m,效率为85%,额定转速750 r/min,电机轴功率1 425 kW. 输水管线全长36.59 km,上游水库的设计水位为30.68 m,下游水库的设计水位为50.44 m. 距离泵站4 799 m处设有1座高位水池,其平面净尺寸为20 m×10 m(长×宽),底板底高程为83.00 m,设计水位为87.53 m,允许最高运行水位为95 m,允许最低运行水位为84 m. 管道末端控制阀的开启和关闭为直线关闭规律,总关时长为27 min.
对于连续停机工况,工程实际运行现状调控方案:3台泵停机间隔为10 min,泵后阀采用第1阶段30 s快关67%,第二阶段60 s慢关余下的33%;末端控制阀于第1台机组关机时从初始开度74%以6.17%/min定速关闭. 该方案下输水系统管道的最大正压力水头为106.13 m,最大负压力水头为4.67 m,高位水池的最高水位为94.22 m,最低水位为86.24 m.
4.2. 基于非支配排序人工兔优化算法的优化结果
图 5
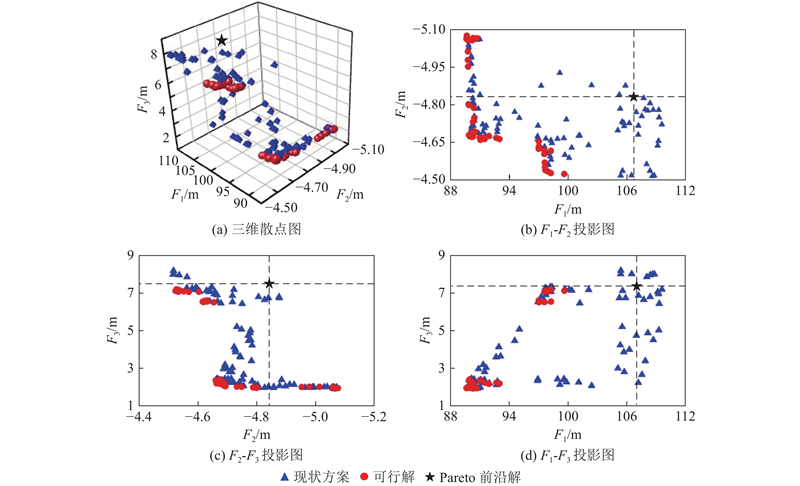
利用NSARO计算得到的泵阀联合优化调控模型优化结果如图6所示,共包含157个可行方案,有45个为Pareto前沿解Pf. 由图6(a)可以看出,Pareto解集分布均匀,表明该算法能够较好平衡3个目标,从而在空间中找到一系列非劣解,证明该算法的全局搜索能力较优. 多目标优化结果中可行解的数量仅占模拟解总数的6.16%,原因在于,满足显式约束的决策变量驱动水力计算模型所得的目标函数未能满足隐式约束. 隐式约束较为复杂,涉及多个目标的相互作用和影响,难以在模型中准确体现,故可行解占比较低. 因此,仅依靠决策者的经验难以同时兼顾显式及隐式约束,无法高效找到最优调控方案,本研究提出的泵阀联合优化调控模型可有效解决实际调控过度依赖决策者经验的问题. 分析优选方案在3个维度中的具体表现,三维空间数据点的二维投影图见图6. 以现状方案为原点,将投影图划分为4个象限. 位于第1象限的解在2个目标函数上均大于现状方案,意味着劣于现状方案;位于第2、4象限的解仅有1个目标函数值低于现状方案;位于第3象限的解在2个目标函数上均小于现状方案,即更优解. 观察投影图可知,在F1-F2投影图中,大部分可行解位于第2、3象限;在F2-F3投影图中,第3、4象限承载了绝大多数可行解;在F1-F3投影图中,大部分可行解位于第3象限. 上述情况说明,这些解不仅在某些单一指标上有所提升,在多个维度上亦优于现状调控方案.
图 6
图 6 泵阀联合优化调控模型的优化结果
Fig.6 Optimization results of pump and valve joint optimization control model
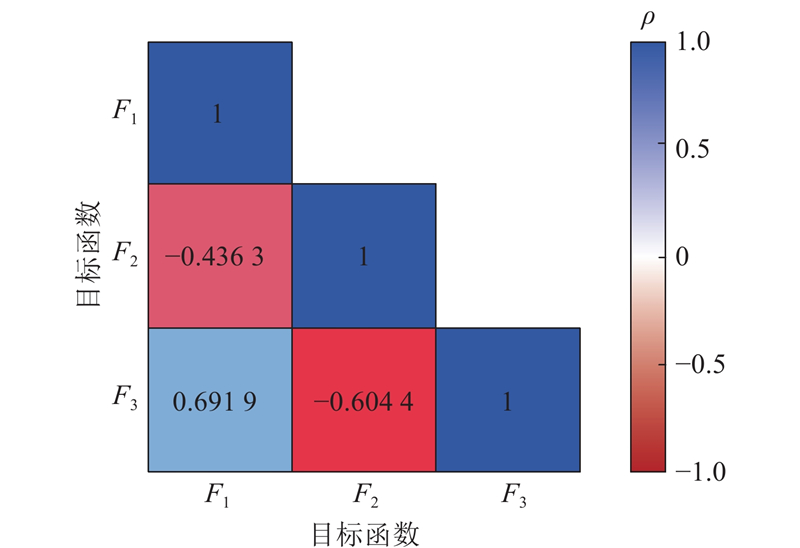
图 7
图 7 目标函数的Spearman相关系数矩阵图
Fig.7 Matrix plot of Spearman’s correlation coefficient for objective function
4.3. 方案对比
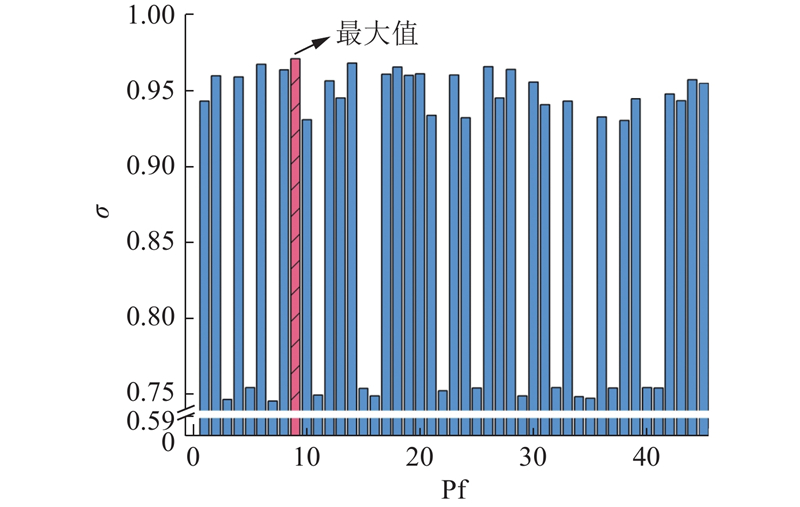
Pareto解集3个优化目标相互制衡,无法同时达到最优,故利用GRA对得到的Pareto解集进行无偏折中决策,计算各调控方案的灰色关联度如图8所示. Pareto解集的灰色关联度介于0.730~0.972,选取灰色关联度最高(σ = 0.971 2)的方案为泵阀联合调控的优选方案.
图 8
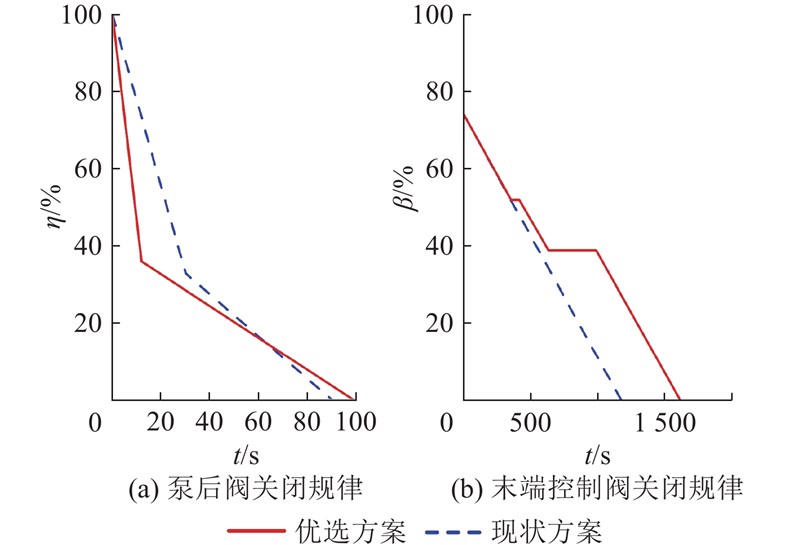
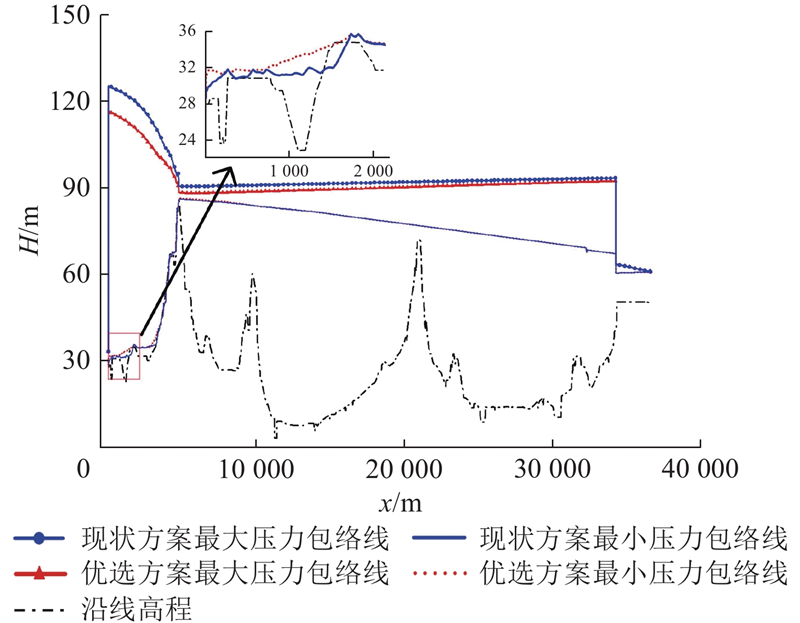
为了具体说明泵阀联合调控优选方案对管道系统压力极值及高位水池水位波动的影响,将该方案与现状方案进行对比分析,优选方案及现状方案的具体调控策略如表1所示,泵后阀及末端控制阀调控规律如图9所示,得出全线管道压力包络线如图10所示. 由图10及表1可知,优选方案的压力水头峰值比现状方案降低了13.57 m. 造成该现象的原因在于,相较于现状运行方案,优选方案泵后阀总关时间延长,且快关时间缩短进一步增加了慢关时间,从而避免了因流速变化过大而导致的压力激增. 此外,末端控制阀关闭速度恒定,故2种方案下高位水池后的重力自流段压力变化幅度相似. 结合图9(a)可知,优选方案在第1次调节末端控制阀后,阀门保持第1次调控至的开度共63 s,开度较大,因此,高位水池后管道压力整体较原方案有所下降. 对于加压提水段,管道内出现多处负压,如图10所示,优选方案中慢关阶段阀门关闭时间延长,使得流体速度和压力波动变缓,进而在地势起伏较大的管段最大负压力水头降低了0.29 m. 因此,优选方案在调控过程中能够显著降低管道压力极值,大幅提升输水系统的安全性.
表 1 现状方案与优选方案的联合调控策略
Tab.1
| 方案 | 决策变量 | 目标函数 | |||||||||
| t1/s | η/% | t2/s | ∆t1/s | ∆t2/s | β1/% | β2/% | Hmax/m | Hmin/m | Zmax−Zmin/m | ||
| 现状方案 | 30 | 33 | 60 | 600 | 600 | — | — | 106.13 | −4.67 | 7.98 | |
| 优选方案 | 12 | 36 | 87 | 414 | 572 | 35 | 13 | 92.56 | −4.38 | 2.19 | |
图 9
图 9 不同方案泵后阀及末端控制阀的调控规律对比
Fig.9 Control law comparison of pump discharge valve and terminal control valve of different schemes
图 10
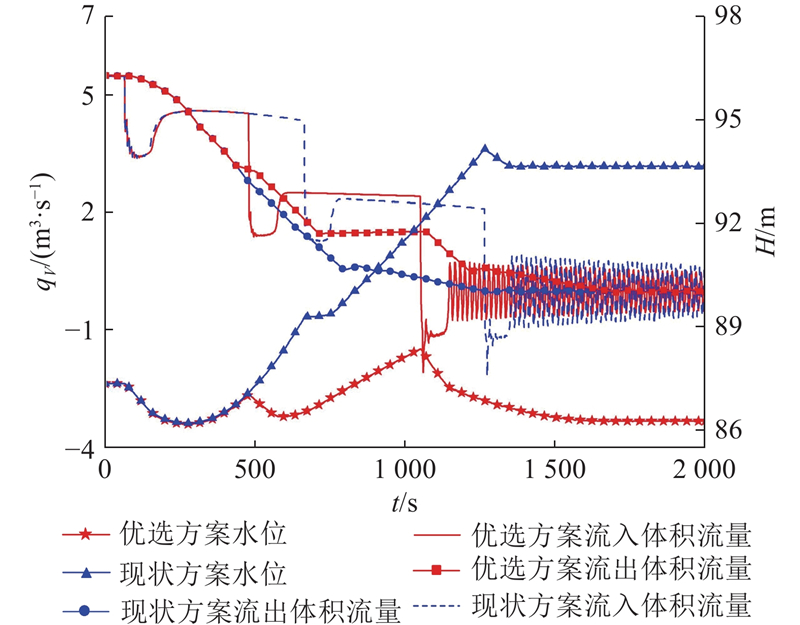
如图11所示为2种方案的高位水池水位、体积流量变化过程曲线. 可以看出,优选方案与现状方案的水位波动变化趋势较为相似,均发生2次先降后升的变化,现状方案下高位水池内的最高水位为94.22 m,与最高运行水位仅相差0.78 m,安全裕量极小;优选方案的高位水池内最高水位为88.41 m,相较现状方案下降了5.81 m. 由于水位波动情况由水池流入流量、流出流量差决定,须进一步结合高位水池流量变化过程进行水位波动情况分析. 由图11可知,现状方案中末端阀门未与水泵的连续停机同步调节,导致高位水池长时间流入流量大于流出流量,水位持续上升. 由表1可知,优选方案缩短了水泵停机间隔,考虑了与水泵停机时刻之间的响应时间差,使得流入与流出流量相差较小,水位波动值降低. 由此可见,优选方案更具安全性及可靠性.
图 11
图 11 高位水池水位和体积流量变化曲线
Fig.11 Water level and volume flow rate curves of high-elevated pool
5. 结 语
本研究建立连续停机工况泵阀联合调控多目标优化模型,提出新的优化-决策方法,并将所提方法应用于某加压提水结合重力输水工程. 1)引入非支配排序和拥挤度距离,提出基于非支配排序及拥挤度距离的非支配排序人工兔优化算法,应用于泵阀联合调控优化研究,得到157组可行解,其中Pareto解集占28.7%,Pareto解集在多个维度上均优于现状调控方案. 2)利用Spearman方法得出3个目标函数之间的相关性,结果表明管道最大正压与最大负压存在竞争关系,管道最大正压与高位水池波动值具有很强的协同关系,管道最大负压与高位水池波动值之间存在竞争关系. 3)通过灰色关联度分析法得到优选方案,与现状方案相比,管道最大压力水头降低了13.57 m,最大负压力水头降低了0.29 m,高位水池水位波动值降低了5.79 m. 优选方案对提升输水系统的稳定性具有重要意义,但在降低最大负压方面优化空间相对有限,原因在于最大负压主要受输水系统管道布置的影响,难以仅通过阀门启闭的调控来完全优化. 未来,将考虑采用工程措施来进一步降低管道最大负压.
参考文献
长距离多支线输水系统稳压塔降高方案研究
[J].
Study on reducing height of surge tank in long-distance and multi-branch water conveyance system
[J].
基于Bentley Hammer的气囊式空气罐的水锤防护研究
[J].
Water hammer protection effect of gasbag-type pneumatic tank based on the analysis using the Bentley Hammer software
[J].
Multi-objective optimization and decision-making of the combined control law of guide vane and pressure regulating valve for hydroelectric unit
[J].DOI:10.1002/ese3.1038 [本文引用: 2]
Sensitivity analysis of operational time differences for a pump–valve system on a water hammer response
[J].DOI:10.1115/1.4031202 [本文引用: 1]
泵站加压与重力自流联合供水工程的停泵水锤防护
[J].
Pump failure water hammer protection of pumping station pressurization and gravity combined water supply project
[J].
A parallel multi-objective optimization based on adaptive surrogate model for combined operation of multiple hydraulic facilities in water diversion project
[J].DOI:10.2166/hydro.2024.285 [本文引用: 1]
Numerical research on water hammer phenomenon of parallel pump-valve system by coupling FLUENT with RELAP5
[J].DOI:10.1016/j.anucene.2017.05.049 [本文引用: 2]
A multi-objective optimal control model of cascade pumping stations considering both cost and safety
[J].DOI:10.1016/j.jclepro.2022.131171 [本文引用: 1]
多目标粒子群优化算法及其应用研究综述
[J].
Survey of multi-objective particle swarm optimization algorithms and their applications
[J].
改进量子粒子群算法在水电站群优化调度中的应用
[J].
Improved quantum-behaved particle swarm optimization and its application in optimal operation of hydropower stations
[J].
Artificial rabbits optimization: a new bio-inspired meta-heuristic algorithm for solving engineering optimization problems
[J].DOI:10.1016/j.engappai.2022.105082 [本文引用: 1]
Optimal solution of the combined heat and power economic dispatch problem by adaptive fitness-distance balance based artificial rabbits optimization algorithm
[J].DOI:10.1016/j.eswa.2023.122272 [本文引用: 1]
Designing an optimal hybrid microgrid system using a leader artificial rabbits optimization algorithm for domestic load in Guelmim city, Morocco
[J].DOI:10.1016/j.renene.2024.120011 [本文引用: 1]
A novel prediction model for integrated district energy system based on secondary decomposition and artificial rabbits optimization
[J].DOI:10.1016/j.enbuild.2024.114106 [本文引用: 1]
Non-dominated sorting artificial rabbit multi-objective sizing optimization for a conceptual powertrain of a 6×4 battery electric tractor truck
[J].DOI:10.1016/j.energy.2024.132009 [本文引用: 1]
Approximate non-dominated sorting for evolutionary many-objective optimization
[J].DOI:10.1016/j.ins.2016.06.007 [本文引用: 1]
Effectiveness and efficiency of non-dominated sorting for evolutionary multi- and many-objective optimization
[J].DOI:10.1007/s40747-017-0057-5 [本文引用: 1]
Localized weighted sum method for many-objective optimization
[J].DOI:10.1109/TEVC.2016.2611642 [本文引用: 1]
The analytic hierarchy process supporting decision making for sustainable development: an overview of applications
[J].DOI:10.1016/j.jclepro.2018.11.270 [本文引用: 1]
Deriving decision makers’ weights in group decision making: an overview of objective methods
[J].DOI:10.1016/j.inffus.2018.11.009 [本文引用: 1]
Research on optimal decision-making of cloud manufacturing service provider based on grey correlation analysis and TOPSIS
[J].DOI:10.1080/00207543.2019.1600760 [本文引用: 1]
A multi-criterion decision making for sustainability assessment of hydrogen production technologies based on objective grey relational analysis
[J].DOI:10.1016/j.ijhydene.2019.11.039 [本文引用: 1]
计及碳排放的风-光-抽水蓄能系统容量优化配置方法
[J].
Optimal capacity configuration method for wind-photovoltaic-pumped-storage system considering carbon emission
[J].
A fuzzy multi attribute decision framework with integration of QFD and grey relational analysis
[J].DOI:10.1016/j.eswa.2018.08.017 [本文引用: 1]
A fast and elitist multiobjective genetic algorithm: NSGA-II
[J].DOI:10.1109/4235.996017 [本文引用: 1]
长距离供水工程的关阀水锤与线路充填
[J].
Study on water-hammer and line packing in long-distance water-supply project
[J].
长距离输水系统停泵水锤防护多目标优化研究
[J].
Multi-objective optimization method for water hammer protection against pump failure in long-distance water transfer systems
[J].
超驼峰工况下轴流泵站事故停泵防护方案寻优
[J].
Optimizing protection scheme for accident shutdown of axial flow pumping station under super hump conditions
[J].
泵后管线先降后升的长距离输水系统水锤防护
[J].
Long-distance water hammer protection of pipeline after pump being first lowered and then raised
[J].
The use of grey relational analysis in solving multiple attribute decision-making problems
[J].DOI:10.1016/j.cie.2007.12.002 [本文引用: 1]
Stock price prediction with optimized deep LSTM network with artificial rabbits optimization algorithm
[J].DOI:10.1016/j.eswa.2023.120346 [本文引用: 1]
An enhanced binary artificial rabbits optimization for feature selection in medical diagnosis
[J].DOI:10.1007/s00521-023-08812-6 [本文引用: 1]
The hypervolume indicator: computational problems and algorithms
[J].