复杂产品主要涉及工程密集型产品、系统和网络等，具有高成本、高附加值、高技术水平和多主体参与等典型特点^[1-2]. 这些属性增加了开发复杂产品的风险，也对其风险评估活动提出了更高的要求. 失效模式与影响分析 (failure mode and effects analysis, FMEA) 是挖掘潜在风险，进行风险评估并对风险进行优先定级的有效逻辑分析方法^[3]. 作为保障产品开发过程安全性和可靠性的重要方法^[4-5]，FMEA既可用于风险的事前预防，也可用于事后改进，已被广泛应用于航空航天^[6]、信息系统^[7]、核工业^[8]以及医疗服务^[9]等领域的复杂产品开发. 在传统FMEA方法中，每个失效模式的风险评估信息使用1到10的数字量表进行量化^[10]. 数值难以准确刻画专家的评价信息，人们习惯采用“致命”、“严重”、“较低”等主观或定性的语言术语^[11]，因此越来越多的学者开始关注语言型FMEA方法.

现有语言型FMEA方法按照语言评价形式的不同可分为2种类型. 1）采用直接语言评价的FMEA方法：Zhao等^[12]提出基于全乘比例分析多目标优化法和区间直觉模糊集的方法，用以处理FMEA评价中主观语言的不确定性和模糊性，使得失效模式的最终排序更为准确可靠；Liu等^[13]采用混合平均算子构建群评估矩阵，利用改进的和谐性分析方法分析群区间二元组语言数据，解决了不同类型FMEA团队成员的评估信息差异问题，并在最终排序时考虑了风险因素的权重差异；Nie等^[14]利用混合风险评估模型和多粒度语言分布评估来解决FMEA团队成员知识背景和经验的差异问题，采用最佳-最差和最大化推导方法来确定风险因素权重. 2）采用两两对比语言评价的FMEA方法：王睿等^[15]利用直觉乘法加权平均算子集结失效模式的偏好矩阵并修正专家极端语言偏好信息，运用专家评价法和理想解模型法确定风险因素权重，有效提高了语言型FMEA风险评估的准确度；Carpitella等^[16]结合可靠性分析和多准则决策方法来优化语言型FMEA方法，通过利用模糊逼近理想解排序法评估风险因子完成失效模式的排序，运用层次分析法评估不同专家的能力和经验差异，用以提高语言评价结果的准确性与可靠性.

上述方法在克服传统FMEA方法的缺陷方面发挥了积极作用，但在面向复杂产品开发情境时仍然存在以下不足. 1）在语言信息表达方面，现有语言型FMEA方法多假定专家能够直接绝对地给出失效模式的评价信息，未考虑复杂情境下，评价问题通常复杂晦涩. 复杂产品开发过程中存在众多交互影响的子模块，由于知识、经验有限，评价专家难以直接给出准确的绝对评价^[17]. 2）在语言建模方面，已有研究假定不同评价专家对同一语言术语具备同样的理解，忽略了评价专家间可能存在的个性化语义差异；在复杂产品开发过程中，由于教育背景、地域分布不同，不同评价专家对于同一个语言术语集的理解可能存在差异^[18-20]，须考虑语义理解的一致性. 3）在因子赋权方面，现有研究多假定风险因子同等重要^[21]，较少同时考虑FMEA评价成员和风险因子的综合权重对结果的影响，忽略了风险因子和评价专家的重要性差异^[22-23]. 在复杂产品开发过程中，利益相关者众多，存在不同的项目角色、从业经验、知识结构等因素，不同风险因子以及评价专家对结果的影响程度不尽相同.分布式语言偏好关系(distributed linguistic preference relation, DLPR)具有优越的成对比较信息表达能力，被广泛应用于医疗服务、故障诊断领域^[24-25]. 本研究将分布式语言偏好关系作为专家表达评价信息的工具，构建针对专家评价信息的一致性驱动个性化语义模型，引入高级管理者对评价专家和风险因子的相对重要性分别进行评价以获得最终权重.

模糊偏好关系 (fuzzy preference relation, FPR)是经典的偏好信息表达结构. FPR的一致性通常通过加性传递性来表达^[25]，根据Orlovsky^[26]给出的模糊偏好关系以及Herrera-Viedma等^[27]给出的加性转移属性，存在定义1与定义2.

定义1　令X = {x₁, x₂, ···, x_n}为给定方案集，N = {1, 2, ···, n}；X上的FPR为${\boldsymbol{F}} = {\left[ {{f_{lk}}} \right]_{n \times n}} \subset X \times X$，满足对任意的$l,k \in N$，有f_lk ≥ 0, f_lk+f_kl = 1, f_ll = 0.5，其中f_lk为x_l相对于x_k的偏好值. 当f_lk = 0.5时，表示x_l与x_k同等重要；当f_lk > 0.5时，表示x_l优于x_k，且f_lk越大，说明x_l比x_k越优；当f_lk = 1时，表示x_l完全优于x_k.

定义2　令F = [f_lk]_n×n为定义在X上的FPR，若存在加性传递性 (f_lk – 0.5)+(f_kr – 0.5) = (f_lr – 0.5), 即f_lr = f_lk+f_kr – 0.5, $ \forall $l, k, r = 1, 2, ···, n，则称F是加性一致的.

DLPR在成对比较信息上的优势使其被广泛用于语言决策背景^[28]，根据Zhang等^[29]对于DLPR的相关界定，存在定义3.

定义3　令X = {x₁, x₂, ···, x_n}为方案集，L = {p₁, p₂, ···, p_T}为语言术语集，n为方案的数量，T为表示语言术语集L粒度的奇数，使用L定义在X上的DLPR为${\boldsymbol{D}} \subset X \times X,$ D = [d^lk]_n×n, d^lk = {(p₁, β^lk(p₁)), ···, (p_T, β^lk(p_T))}. 称${\boldsymbol{D}}$为L的语言分布，d^lk为x_l相较于x_k的偏好程度，β^lk(p_T) (t = 1, 2, ···, T) 为p_T的数值比例，并且满足0 < β^lk(p_T) < 1, $\displaystyle\sum\nolimits_{t = 1}^T {{\beta ^{lk}}\left( {{p_T}} \right) = 1} $. 特别地，d^ll = {(p_(T+1)/2, 1)}，存在逆运算：Neg(d^lk) = d^kl = {(Neg(p₁), β^lk(p₁)), ···, (Neg(p_T), β^lk(p_T))}, 其中Neg(p_t) = p_T+1−t, $ \forall $l, k = 1, 2, ···, n.

根据Dong等^[30]对数值刻度模型 (numerical scale model, NS)的相关界定，存在定义4.

定义4　令L = {p₁, p₂, ···, p_T}为语言术语集，则映射NS: L → R称为L的数值刻度. 如果NS严格单调递增，则称NS为L的有序数值刻度.

NS(p_t)表示语言术语p_t的数值索引，描述了p_t的语义. 考虑不同专家对于相同术语集中的语义理解程度存在差异，NS(p_t)的数值通常是因人而异的，个性化NS(p_t)可以是语言术语集p_t的个性化语义.

对于FMEA问题，假设存在n种失效模式，表示为FM = {FM₁, FM₂, ···, FM_n}；$h$个风险因子，表示为RF = {RF₁, RF₂, ···, RF_h}. $ {\boldsymbol{\omega}} {\text{ = }}{\left[ {{\omega _1},{\omega _2},\cdots ,{\omega _h}} \right]^{\text{T}}} $为风险因子RF的权重向量，满足${\omega _i} \geqslant 0\left( {i = 1,2,\cdots ,h} \right)$且$\sum_{i = 1}^h {{\omega _i}} {\text{ = }}1$. 由m位专家构成的团队EX = {EX₁, EX₂, ···, EX_m}对FM的每个风险因子进行评估. 令${\boldsymbol{\lambda}} {\text{ = }}{\left[ {{\lambda _1},{\lambda _2},\cdots ,{\lambda _m}} \right]^{\text{T}}}$为EX的权重向量，满足${\lambda _j} \geqslant 0 \left( {j = 1,2,\cdots ,m} \right)$且$\sum_{j = 1}^m {{\lambda _j} = 1} $. 针对每个风险因子，每位专家通过分布式语言偏好关系对所有失效模式进行两两对比形式的评估. 具体地，给定包含T_i (i = 1, 2, ···, h) 个语言术语的语言术语集L_i, EX_j在RF_i上为n个失效模式提供两两对比的分布式语言偏好关系$ {\boldsymbol{D}}_i^j = {\left[ {d_{lk}^{ij}} \right]_{n \times n}} $，其中$ d_{lk}^{ij} = \{ (p_t^{ij},\beta _t^{ij})|t = 1,\cdots , {T_i} \} $为EX_j在RF_i上对FM_l和FM_k的分布式语言偏好，$\beta _t^{ij}$为语言术语集L_i中第t个语言术语$p_t^{ij}$的比率. 通过上述评估形式获得h×m个分布式语言偏好关系.另有一个管理者以分布式语言偏好关系的形式对所有专家与风险因子的相对重要性进行两两对比. 具体地，以专家为例，给定包含T_e个语言术语的语言术语集L_e，管理者提供两两比较的分布式语言偏好关系矩阵D_e = ${\left[ {d_{jq}^{\mathrm{e}}} \right]_{m \times m}}$，其中$d_{jq}^{{\mathrm{e}}}$ = {(p_t^e, β_t^e) | t = 1, 2, ···, T_e}为管理者对专家EX_j和EX_q的分布式语言偏好，$\beta _t^{{\mathrm{e}}}$为$p_t^{{\mathrm{e}}}$的比率. 同理，给定包含T_r个语言术语的语言术语集L_r，管理者能够给出针对风险因子相对重要性的分布式语言偏好关系$ {{\boldsymbol{D}}_{{\mathrm{r}}}} = {\left[ {d_{ip}^{{\mathrm{r}}}} \right]_{h \times h}} $.

给定含有T个语言术语的语言术语集L = {p₁, p₂, ···, p_T}及其数值刻度NS(p_t). 个性化语义是指每个个体对L中的每个语言术语p_t都具有不同的语义理解，即NS(p_t)具有不同的值. 基于个性化语义的分布式语言偏好关系量化，是指采用NS(p_t)将分布式语言偏好关系D = [d_lk]_n×n转换为对应的数值偏好关系F = [f_lk]_n×n，其中d_lk = {(p_t , β_t) | t = 1, ···, T}. 具体地，

(1)$ {f_{lk}} = \sum\limits_{t = 1}^T {{\text{NS}}\left( {{p_t}} \right) \times {\beta _t}} . $

在实际的决策过程中，更优的NS(p_t)可使D的量化更加合理，因此通过最大化D的一致性来获得更优的NS(p_t). F与D表达了同样的信息，为此通过计算F的一致性来间接反映D的一致性. 由加性转移属性的定义可知，决策者偏好结果完全一致的F应满足等式：

(2)$ \begin{split}& \left( {{f_{lk}} - 0.5} \right)+\left( {{f_{kr}} - 0.5} \right) = \left( {{f_{lr}} - 0.5} \right); \\&\quad\;\; l,k,r = 1,2,\cdots ,n. \end{split} $

(3)$ {f_{lr}} = {f_{lk}}+{f_{kr}} - 0.5;\; l,k,r = 1,2,\cdots ,n. $

在实际的决策过程中，由于决策问题的复杂性和决策者知识的有限，式（3）一般难以成立，因此，令

(4)$ {{E}}({f_{lr}}) = {f_{lk}}+{f_{kr}} - 0.5, $

(5)$ {{D}}({f_{lr}}) = \left| {{f_{lr}} - {{E}}({f_{lr}})} \right|. $

D(f_lr)反映决策者在x_l和x_r之间的不一致水平. 由于D(f_lr)可能不落在 [0,1]，对其进行如下修正：

(6)$ {\text{AD}}({f_{lr}}) = {\mathrm{Me}}\left\{ {0,1,{{D}}({f_{lr}})} \right\}. $

1−AD(f_lr)刻画了决策者在方案x_l和x_r之间的一致性水平. 决策者在方案x_l上的一致性水平表示为

(7)$ {\text{C}}{{\text{D}}_l} = \frac{1}{{n - 1}}\sum\limits_{r = 1,l \ne r}^n {\left( {1 - {\text{AD}}({f_{lr}})} \right)} . $

决策者在所有方案上的一致性水平表示为

(8)$ {\text{CD = }}\frac{1}{n}\sum\limits_{l = 1}^n {({\text{C}}{{\text{D}}_l})} . $

L中的语言术语具有对称性， NS(p_t)须满足以下约束：

(9)$ {\text{NS}}({p_t})+{\text{NS}}({p_{T+1 - t}}) = 1, $

(10)$ {\text{NS}}({p_1}) = 0, $

(11)$ {\text{NS}}({p_{(T+1)/2}}) = 0.5, $

(12)$ {\text{NS}}({p_T}) = 1. $

考虑到L中语言术语的有序性，NS(p_t)须满足以下约束：

(13)$ \text{NS}({p}_{t{'}}) > \text{NS}({p}_{t''}),\; t{'} > t'' . $

考虑到L中语言术语分布的合理性，NS(p_t)须满足以下约束：

(14)$ \frac{{t - 1}}{T} \leqslant {\text{NS}}({p_t}) \leqslant \frac{{t+1}}{T};\;t = 2,3,\cdots ,T - 1 . $

构建分布式语言偏好关系量化的个性化语义模型M1，表达式为

$ \left. \begin{gathered} {\text{M1 = max CD}}{\text{.}} \\ {\text{s}}{\text{.t}}{\text{. NS}}\left( {{p_t}} \right)+{\text{NS}}\left( {{p_{T+1 - t}}} \right) = 1;{\text{ }}t = 1,2, \cdot \cdot \cdot ,T. \\ \;\;\;\;\;\;{\text{ NS}}\left( {{p_1}} \right) = 0. \\ \;\;\;\;\;\;{\text{ NS}}\left( {{p_{\left( {T+1} \right)/2}}} \right) = 0.5. \\ \;\;\;\;\;\;{\text{ NS}}\left( {{p_T}} \right) = 1. \\ \;\;\;\;\;\;{\text{ NS}}\left( {{p_{t+1}}} \right) - {\text{NS}}\left( {{p_t}} \right) \geqslant \xi ;{\text{ }}t = 1, \cdot \cdot \cdot ,T - 1. \\ \;\;\;\;\;\;{\text{ }}\frac{{t - 1}}{T} \leqslant {\text{NS}}\left( {{p_t}} \right) \leqslant \frac{{t+1}}{T};{\text{ }}t = 2,3, \cdot \cdot \cdot ,T - 1. \\ \end{gathered} \right\} $

基于M1，分别构建针对D_e、D_r和$ {\boldsymbol{D}}_i^j,i = 1,2,\cdots ,h; j = 1,2,\cdots ,m $量化的个性化语义模型. 量化${\boldsymbol{D}}_i^j$依赖于对D_e、D_r的量化，为此称D_e、D_r的量化为第一阶段，${\boldsymbol{D}}_i^j$的量化为第二阶段.

令L为用以评价领域专家重要性的语言术语集L_e，D为D_e = ${\left[ {d_{jq}^{{\mathrm{e}}}} \right]_{m \times m}}$，NS(p_t)为NS_e(p_t^e)，F为F_e = ${\left[ {f_{jq}^{{\mathrm{e}}}} \right]_{m \times m}}$. 由式 (8)得到D_e的一致性水平CD_e，根据M1构建D_e量化的个性化语义模型Me，表达式为

$ \left. \begin{gathered} {\text{Me = max C}}{{\text{D}}_{\text{e}}}{\text{.}} \\ {\text{s}}{\text{.t}}{\text{. N}}{{\text{S}}_{\text{e}}}\left( {p_{_t}^{\text{e}}} \right)+{\text{NS}}\left( {p_{{T_{\text{e}}}+1 - t}^{\text{e}}} \right) = 1;{\text{ }}t = 1,2, \cdot \cdot \cdot ,{T_{\text{e}}}. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_{_1}^{\text{e}}} \right) = 0. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_{_{\left( {{T_{\text{e}}}+1} \right)/2}}^{\text{e}}} \right) = 0.5. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_{_{{T_{\text{e}}}}}^{\text{e}}} \right) = 1. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_{_{t+1}}^{\text{e}}} \right) - {\text{N}}{{\text{S}}_{\text{e}}}\left( {p_{_t}^{\text{e}}} \right) \geqslant \xi ;{\text{ }}t = 1, \cdot \cdot \cdot ,{T_{\text{e}}} - 1. \\ \;\;\;\;\;\;{\text{ }}\frac{{t - 1}}{{{T_{\text{e}}}}} \leqslant {\text{N}}{{\text{S}}_{\text{e}}}\left( {p_{_t}^{\text{e}}} \right) \leqslant \frac{{t+1}}{{{T_{\text{e}}}}};{\text{ }}t = 2,3, \cdot \cdot \cdot ,{T_{\text{e}}} - 1. \\ \end{gathered} \right\} $

令L为用以评价风险因子重要性的语言术语集L_r，D为D_r = ${\left[ {d_{ip}^{{\mathrm{r}}}} \right]_{h \times h}}$，NS(p_t)为NS_r$(p_t^{\mathrm{r}}) $，F为F_r = ${\left[ {f_{ip}^{{\mathrm{r}}}} \right]_{h \times h}}$. 由式 (8)得到D_r的一致性水平CD_r，根据M1构建D_r量化的个性化语义模型Mr，表达式为

$ \left. \begin{gathered} {\text{Mr = max C}}{{\text{D}}_{\text{r}}}{\text{.}} \\ {\text{s}}{\text{.t}}{\text{. N}}{{\text{S}}_{\text{r}}}\left( {p_{_t}^{\text{r}}} \right)+{\text{NS}}\left( {p_{{T_{\text{r}}}+1 - t}^{\text{r}}} \right) = 1;{\text{ }}t = 1,2, \cdot \cdot \cdot ,{T_{\text{r}}}. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_{_1}^{\text{r}}} \right) = 0. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_{_{\left( {{T_{\text{r}}}+1} \right)/2}}^{\text{r}}} \right) = 0.5. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_{_{{T_{\text{r}}}}}^{\text{r}}} \right) = 1. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_{_{t+1}}^{\text{r}}} \right) - {\text{N}}{{\text{S}}_{\text{r}}}\left( {p_{_t}^{\text{r}}} \right) \geqslant \xi ;{\text{ }}t = 1, \cdot \cdot \cdot ,{T_{\text{r}}} - 1. \\ \;\;\;\;\;\;{\text{ }}\frac{{t - 1}}{{{T_{\text{r}}}}} \leqslant {\text{N}}{{\text{S}}_{\text{r}}}\left( {p_{_t}^{\text{r}}} \right) \leqslant \frac{{t+1}}{{{T_{\text{r}}}}};{\text{ }}t = 2,3, \cdot \cdot \cdot ,{T_{\text{r}}} - 1. \\ \end{gathered} \right\} $

求解Me和Mr，得到管理者针对专家与风险因子语言术语集L_e和L_r的一致性最优个性化语义*NS_e$(p_t^{\mathrm{e}} )$和*NS_r$(p_t^{\mathrm{r}} ) $.

基于*NS_e$(p_t^{\mathrm{e}} ) $和*NS_r$(p_t^{\mathrm{r}} ) $，由式 (1) 将D_e、D_r转换为最优的数值偏好关系*F_e =${\left[ {*f_{jq}^{{\mathrm{e}}}} \right]_{m \times m}}$和*F_r = ${\left[ {*f_{ip}^{{\mathrm{r}}}} \right]_{h \times h}}$. 根据平均加权算子^[31]的权重计算方法，通过最优数值偏好关系计算获得专家权重${\lambda _j}$和风险因子权重${\omega _i}$，计算式为

(15)$ {\lambda _j} = {{\displaystyle\sum\limits_{i = 1}^m {*f_{jq}^{{\mathrm{e}}}} }}\bigg/{{\displaystyle\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {*f_{jq}^{{\mathrm{e}}}} } }};\;j = 1,2,\cdots ,m , $

(16)$ {\omega _i} = {{\displaystyle\sum\limits_{j = 1}^h {*f_{ip}^{{\mathrm{r}}}} }}\bigg/ {{\displaystyle\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^h {*f_{ip}^{{\mathrm{r}}}} } }};\;i = 1,2,\cdots ,h . $

令L为用以评价风险类型或失效模式的语言术语集L_i，D为D_i^j =${\left[ {d_{lk}^{ij}} \right]_{n \times n}}$，NS(p_t)为NS(p_t^ij)，F为F_i^j = ${\left[ {f_{lk}^{ij}} \right]_{n \times n}}$，由式 (8) 计算得到D_i^j的一致性水平为CD_i^j. 考虑到专家和风险因子的重要性差异对D_i^j量化的影响，对CD_i^j进行加权平均，得到D_i^j量化的个性化语义模型目标函数：

(17)$ O = \sum\limits_{i = 1}^h {\sum\limits_{j = 1}^m {{\lambda _j}{\omega _i}{\text{CD}}_i^j} } . $

根据M1构建D_i^j量化的个性化语义模型Mf，表达式为

$ \left.\begin{array}{l}{\mathrm{Mf}}=\mathrm{max}{\displaystyle \sum _{i=1}^{h}{\displaystyle \sum _{j=1}^{m}{\lambda }_{j}{\omega }_{i}{\text{CD}}_{i}^{j}.}}\\ \text{s}\text{.t}.{\text{ NS}}_{i}^{j}\left({p}_{t}^{ij}\right)+{\text{NS}}_{i}^{j}\left({p}_{{T}_{i}+1-t}^{ij}\right)=1;\;t=1,2,\mathrm{\cdots },{T}_{i}.\\ \;\;\;\;\;\;{\text{ NS}}_{i}^{j}\left({p}_{1}^{ij}\right)=0.\\ \;\;\;\;\;\;{\text{ NS}}_{i}^{j}\left({p}_{({T}_{i}+1)/2}^{ij}\right)=0.5.\\ \;\;\;\;\;\;{\text{ NS}}_{i}^{j}\left({p}_{{T}_{i}}^{ij}\right)=1\text{.}\\ \;\;\;\;\;\;{\text{ NS}}_{i}^{j}\left({p}_{t+1}^{ij}\right)-{\text{NS}}_{i}^{j}\left({p}_{t}^{ij}\right)\geqslant \xi ;\;t=1,\mathrm{\cdots },{T}_{i}-1.\\ \;\;\;\;\;\;\text{ }\dfrac{t-1}{{T}_{i}}\leqslant {\text{NS}}_{i}^{j}\left({p}_{t}^{ij}\right)\leqslant \dfrac{t+1}{{T}_{i}};\;t=2,3,\mathrm{\cdots },{T}_{i}-1.\\ \;\;\;\;\;\;\text{ }i=1,2,\mathrm{\cdots },h;\;j=1,2,\mathrm{\cdots },m.\end{array}\right\} $

求解Mf得到专家EX_j对风险类型语言术语集L_i中的语言术语p_t^ij的个性化语义理解*NS_i^j(p_t^ij), 其中i = 1, 2, ···, h; j = 1, 2, ···, m; t = 1, 2, ···, T_i.

基于获得的*NS_i^j，由式 (1) 得到最优的数值偏好关系*F_i^j = ${\left[ {*f_{lk}^{ij}} \right]_{n \times n}}$. 根据$ {\omega _i} $和$ {\lambda _j} $聚合所有的*F_i^j，得到集体偏好关系F^c，表达式为

(18)$ {{\boldsymbol{F}}^{{\mathrm{c}}}} = {\omega _i}{\lambda _j}*{\boldsymbol{F}}_i^j = {\left[ {f_{lk}^{{\mathrm{c}}}} \right]_{n \times n}}, $

(19)$ f_{lk}^{{\mathrm{c}}} = {\omega _i}{\lambda _j}*f_{lk}^{ij}. $

基于F^c计算每个失效模式的得分S (FM_l), l = 1, 2, ···, n, 并进行排序.

(20)$ S\left( {{\text{F}}{{\text{M}}_l}} \right) = {{\displaystyle\sum\limits_{k = 1}^n {f_{lk}^{{\mathrm{c}}}} }}\bigg/{{\displaystyle\sum\limits_{l = 1}^n {\displaystyle\sum\limits_{k = 1}^n {f_{lk}^{{\mathrm{c}}}} } }}. $

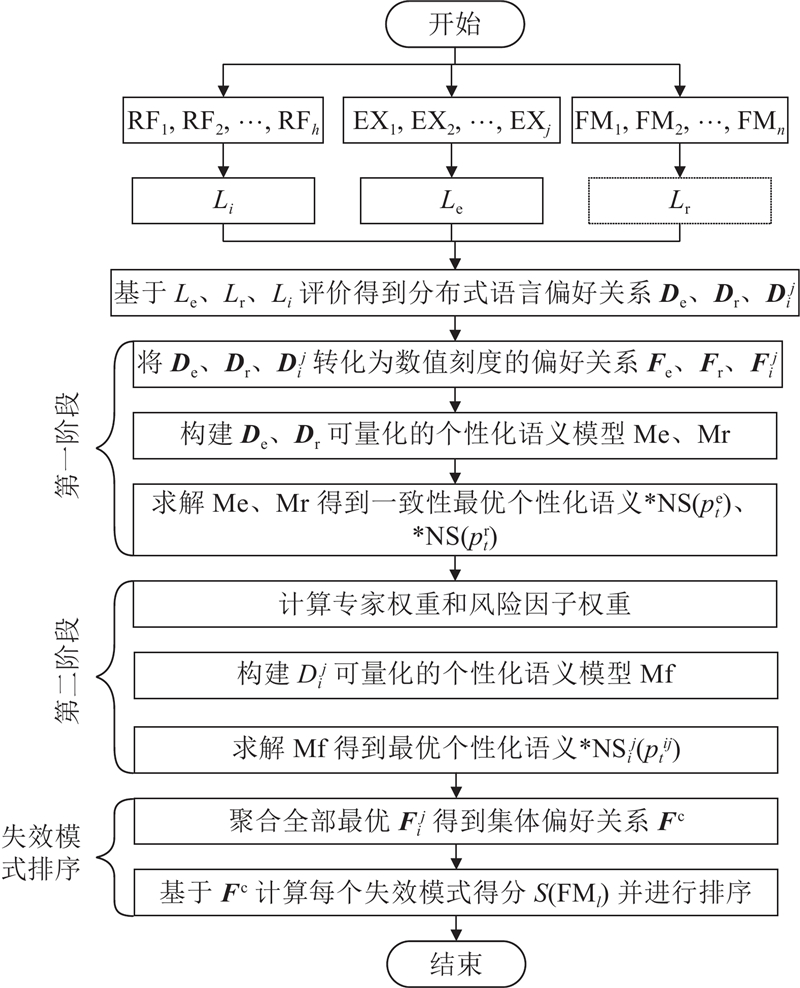
如图1所示为本研究所提方法的模型框架. 根据相应的基础数据输入进行评价，得到针对专家、风险因子以及失效模式的分布式语言偏好信息. 1）通过数值关系转换与最大化一致性水平构建量化D_e、D_r的个性化语义模型Me、Mr，求解模型得到针对专家、风险因子的一致性最优的个性化语义. 2）利用加权平均算子，计算得到专家、风险因子的权重数值，构建并求解个性化语义模型Mf，得到针对失效模式评价的最优个性化语义. 3）聚合全部的最优数值偏好关系得到集体偏好关系，进一步计算每个失效模式的数值得分并排序.

航空发动机研制是国防建设与经济社会发展的重要组成部分，集中体现国家的工业基础、科技水平与综合国力^[32]. 航空发动机的研制技术难度高、投资成本大、研制周期长，项目风险远远高于一般的装备产品研发^[33]. 由于航空发动机研制项目无法取得大量条件一致的历史风险数据，很难通过数理统计获得相关参数的概率分布，风险管理的原始数据一般由专家凭专业知识和工程经验进行主观评分的方法收集，对评价专家的经验具有较高的依赖性，且风险数据多是不确定的、模糊的. 在航空发动机研制过程中的各类风险活动复杂晦涩，风险之间往往牵一发而动全身^[34-35]，专家通常难以对某类风险给出直接绝对的评价，适合采用两两比较的语言评价方式. 航空发动机研制的主体众多，在知识结构、地域分布上均存在差异，使得来自不同领域、不同地域的专家在评价风险类型时存在不同的语言认知与经验感受. 不同专家的从业背景及其经验能力存在差异，风险因子对整体的影响与重要性也不同^[36]. 采用分布式语言偏好评价航空发动机研制过程中的风险类型，考虑专家的个性化语义影响，同时考虑评价专家和风险因子的重要性差异，有助于提升航空发动机研制过程中风险评估的准确性与可靠性.

某型航空发动机为改进改型类型项目，须根据客户需求对产品进行迭代升级，最终达到交付标准. 该类型项目虽然具有一定的历史经验可参考，但研发过程仍然具有相当高的不确定性. 型号总师通常负责设计制造验证阶段的总协调、总决策，根据以往研制项目判断研制过程中可能存在的风险类型. 风险可分为6类：技术难度过大、进度延期、政策频繁变化、市场需求突然改变、费用超支、成员能力不足，表示为FM = {FM₁, FM₂, FM₃, FM₄, FM₅, FM₆}. 传统上，每个风险类型的评估与发生率 (Occurrence, O)、严重度 (Severity, S) 和难检度 (Detection, D) 这3个具体风险因子相关^[37]，风险因子表示为RF = {RF₁, RF₂, RF₃}. 由型号总师选择几个主要领域（设计、制造、采购、质量）的专家EX = {EX₁, EX₂, EX₃, EX₄}组成FMEA评价团队，根据如表1所示的语言术语集L_i, i = 1, 2, 3，对6类风险类型的3个风险因子进行评价. 型号总师需根据如表2所示的L_e从每位专家的知识背景、从业经验、部门环境等方面对4位专家进行重要性评价，再根据表2中的L_r从风险因子的影响程度、管控难度对3个风险因子进行重要性评价.

第一阶段：根据型号项目总师对风险因子和评价专家的重要性评价结果，以及4个领域专家对某型航空发动机研制过程中6类风险类型的分布式语言偏好信息，基于M1构建量化D_e、D_r的个性化语义模型分别为

$ \left. \begin{gathered} {\text{Me = max C}}{{\text{D}}_{\text{e}}}{\text{.}} \\ {\text{s}}{\text{.t}}{\text{. N}}{{\text{S}}_{\text{e}}}\left( {p_{_t}^{\text{e}}} \right)+{\text{NS}}\left( {p_{6 - t}^{\text{e}}} \right) = 1;{\text{ }}t = 1,2, \cdot \cdot \cdot ,5. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_{_1}^{\text{e}}} \right) = 0. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_{_{\text{3}}}^{\text{e}}} \right) = 0.5. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_5^{\text{e}}} \right) = 1. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{e}}}\left( {p_{_{t+1}}^{\text{e}}} \right) - {\text{N}}{{\text{S}}_{\text{e}}}\left( {p_{_t}^{\text{e}}} \right) \geqslant \xi ;{\text{ }}t = 1, \cdot \cdot \cdot ,4. \\\;\;\;\;\;\; {\text{ }}\frac{{t - 1}}{5} \leqslant {\text{N}}{{\text{S}}_{\text{e}}}\left( {p_{_t}^{\text{e}}} \right) \leqslant \frac{{t+1}}{5};{\text{ }}t = 2,3, \cdot \cdot \cdot ,4. \\ \end{gathered} \right\} $

$ \left. \begin{gathered} {\text{Mr = max C}}{{\text{D}}_{\text{r}}}{\text{.}} \\ {\text{s}}{\text{.t}}{\text{. N}}{{\text{S}}_{\text{r}}}\left( {p_{_t}^{\text{r}}} \right)+{\text{NS}}\left( {p_{8 - t}^{\text{r}}} \right) = 1;{\text{ }}t = 1,2, \cdot \cdot \cdot ,7. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_{_1}^{\text{r}}} \right) = 0. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_{\text{4}}^{\text{r}}} \right) = 0.5. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_7^{\text{r}}} \right) = 1. \\ \;\;\;\;\;\;{\text{ N}}{{\text{S}}_{\text{r}}}\left( {p_{_{t+1}}^{\text{r}}} \right) - {\text{N}}{{\text{S}}_{\text{r}}}\left( {p_{_t}^{\text{r}}} \right) \geqslant \xi ;{\text{ }}t = 1, \cdot \cdot \cdot ,6. \\ \frac{t-1}{7}\leqslant \text{N}{{\text{S}}_{\text{r}}}\left( p_{_{t}}^{\text{r}} \right)\leqslant \frac{t+1}{7};\text{ }t=2,3,\cdots ,6.\end{gathered} \right\} $

其中$ \xi $ = 0.001. 采用无速度约束的多群粒子群优化方法求解Me和Mr^[38]，得到型号总师对语言术语集L_e和L_r的一致性最优个性化语义解*NS_e$(p_t^{\mathrm{e}})$和*NS_r$(p_t^{\mathrm{r}}) $，分别为Me在0.8330的最优一致性下的个性化语义解[0.0001, 0.4991, 0.5001, 0.5011, 0.9999]，以及Mr在0.8332的最优一致性下的个性化语义解[0, 0.3749, 0.4989, 0.5001, 0.5011, 0.6250, 0.9999].

第二阶段：基于 *NS_e$(p_t^{\mathrm{e}}) $和*NS_r$(p_t^{\mathrm{r}}) $，由式（1）将分布式语言偏好矩阵D_e、D_r转换为最优的数值偏好关系*F_e = ${\left[ {*f_{jq}^{{\mathrm{e}}}} \right]_{m \times m}}$和*F_r = ${\left[ {*f_{ip}^{{\mathrm{r}}}} \right]_{h \times h}}$：

$ {\text{*}}{{\boldsymbol{F}}_{{\mathrm{e}}}} = \left[ \begin{gathered} 0.500\;1 \quad 0.199\;7 \quad 0.500\;7 \quad 0.600\;7 \\ 0.800\;4 \quad 0.500\;1 \quad 0.399\;4 \quad 0.499\;4 \\ 0.499\;5 \quad 0.600\;7 \quad 0.500\;1 \quad 0.500\;8 \\ 0.399\;4 \quad 0.500\;8 \quad 0.499\;4 \quad 0.500\;1 \\ \end{gathered} \right] $

$ {\text{*}}{{\boldsymbol{F}}_{{\mathrm{r}}}} = \left[ \begin{gathered} 0.500\;1 \quad 0.550\;7 \quad 0.513\;1 \\ 0.449\;3 \quad 0.500\;1 \quad 0.712\;7 \\ 0.487\;0 \quad 0.287\;2 \quad 0.500\;1 \\ \end{gathered} \right] $

根据式 (15) 、 (16)，求解专家权重${\lambda _j}$和风险因子权重${\omega _i}$，得到4位领域评价专家的权重分别为0.2749, 0.2251, 0.2374, 0.2626；3个风险因子RF₁, RF₂, RF₃的权重分别为0.3192, 0.2973, 0.3835. 根据M1构建D_i^j的个性化语义模型为

$ \left. \begin{gathered} {\text{M1 = }}\max \sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^5 {{\lambda _j}{\omega _i}{\text{CD}}_i^j.} } \\ {\text{s}}{\text{.t}}.{\text{ NS}}_i^j\left( {p_t^{ij}} \right)+{\text{NS}}_i^j\left( {p_{8 - t}^{ij}} \right) = 1;\;t = 1,2,\cdots ,7. \\ \;\;\;\;\;\;{\text{ NS}}_i^j\left( {p_1^{ij}} \right) = {\text{0}}{\text{.}} \\ \;\;\;\;\;\;{\text{ NS}}_i^j\left( {p_4^{ij}} \right) = 0.5. \\ \;\;\;\;\;\;{\text{ NS}}_i^j\left( {p_7^{ij}} \right) = {\text{1}}. \\ \;\;\;\;\;\;{\text{ NS}}_i^j\left( {p_{t+1}^{ij}} \right) - {\text{NS}}_i^j\left( {p_t^{ij}} \right) \geqslant \xi ;\;t = 1,\cdots ,6. \\ \;\;\;\;\;\;{\text{ }}\frac{{t - 1}}{7} \leqslant {\text{NS}}_i^j\left( {p_t^{ij}} \right) \leqslant \frac{{t+1}}{7};\;t = 2,3,\cdots ,6. \\ \;\;\;\;\;\;{\text{ }}i = 1,\cdots ,3;{\text{ }}j = 1,2,\cdots ,4. \\ \end{gathered} \right\} $

求解Mf 得到航空发动机研制过程中不同领域专家基于语言术语集L_i评价风险类型的一致性最优下的个性化语义解*NS_i^j(p_t^ij)，最优一致性及其个性化语义结果如表3、表4所示.

通过Mf获得的*NS_i^j和数值转化公式，得到航空发动机研制过程中风险类型评估的最优数值偏好关系*F_i^j. 以4位专家对于风险因子RF₁的语言评价结果为例，依据本研究所提方法得到的最优数值偏好关系${\text{*}}{\boldsymbol{F}}_1^1 $、${\text{*}}{\boldsymbol{F}}_1^2 $、${\text{*}}{\boldsymbol{F}}_1^3 $、${\text{*}}{\boldsymbol{F}}_1^4 $结果分别为

${\text{*}}{\boldsymbol{F}}_1^1 = \left[ \begin{gathered} {\text{0}}{\text{.499 9 0}}{\text{.963 6 0}}{\text{.072 7 0}}{\text{.608 4 0}}{\text{.578 0 0}}{\text{.628 0}} \\ {\text{0}}{\text{.036 4 0}}{\text{.499 9 0}}{\text{.742 9 0}}{\text{.625 0 0}}{\text{.594 7 0}}{\text{.667 3}} \\ {\text{0}}{\text{.927 3 0}}{\text{.257 2 0}}{\text{.499 9 0}}{\text{.380 9 0}}{\text{.299 4 0}}{\text{.397 6}} \\ {\text{0}}{\text{.391 6 0}}{\text{.375 0 0}}{\text{.619 1 0}}{\text{.499 9 0}}{\text{.422 0 0}}{\text{.664 2}} \\ {\text{0}}{\text{.422 0 0}}{\text{.405 3 0}}{\text{.700 6 0}}{\text{.578 0 0}}{\text{.499 9 0}}{\text{.594 7}} \\ {\text{0}}{\text{.372 0 0}}{\text{.332 7 0}}{\text{.602 4 0}}{\text{.435 6 0}}{\text{.594 7 0}}{\text{.499 9}} \\ \end{gathered} \right]\\$

$ \begin{split} *{\boldsymbol{F}}_1^2 = \left[ \begin{gathered} {\text{0}}{\text{.500 0 0}}{\text{.962 5 0}}{\text{.074 9 0}}{\text{.566 2 0}}{\text{.681 9 0}}{\text{.531 6}} \\ {\text{0}}{\text{.037 5 0}}{\text{.500 0 0}}{\text{.644 5 0}}{\text{.588 2 0}}{\text{.728 7 0}}{\text{.553 6}} \\ {\text{0}}{\text{.925 1 0}}{\text{.355 5 0}}{\text{.500 0 0}}{\text{.455 8 0}}{\text{.528 5 0}}{\text{.430 6}} \\ {\text{0}}{\text{.433 8 0}}{\text{.411 8 0}}{\text{.544 2 0}}{\text{.500 0 0}}{\text{.544 2 0}}{\text{.481 0}} \\ {\text{0}}{\text{.318 1 0}}{\text{.271 3 0}}{\text{.471 6 0}}{\text{.455 8 0}}{\text{.500 0 0}}{\text{.374 4}} \\ {\text{0}}{\text{.468 4 0}}{\text{.446 4 0}}{\text{.569 4 0}}{\text{.519 0 0}}{\text{.625 6 0}}{\text{.500 0}} \\ \end{gathered} \right] \\*{\boldsymbol{F}}_1^3 = \left[ \begin{gathered} {\text{0}}{\text{.499 9 0}}{\text{.330 7 0}}{\text{.340 3 0}}{\text{.650 2 0}}{\text{.561 9 0}}{\text{.594 3}} \\ {\text{0}}{\text{.669 3 0}}{\text{.499 9 0}}{\text{.303 6 0}}{\text{.594 3 0}}{\text{.535 4 0}}{\text{.558 2}} \\ {\text{0}}{\text{.659 8 0}}{\text{.696 5 0}}{\text{.499 9 0}}{\text{.455 0 0}}{\text{.405 7 0}}{\text{.428 6}} \\ {\text{0}}{\text{.349 9 0}}{\text{.405 7 0}}{\text{.544 9 0}}{\text{.499 9 0}}{\text{.419 0 0}}{\text{.477 9}} \\ {\text{0}}{\text{.438 1 0}}{\text{.464 6 0}}{\text{.594 3 0}}{\text{.581 0 0}}{\text{.499 9 0}}{\text{.535 4}} \\ {\text{0}}{\text{.405 7 0}}{\text{.441 8 0}}{\text{.571 5 0}}{\text{.522 1 0}}{\text{.464 6 0}}{\text{.499 9}} \\ \end{gathered} \right] \\*{\boldsymbol{F}}_1^4 = \left[ \begin{gathered} 0.499\;9{\text{ 0}}{\text{.298 2 0}}{\text{.805 9 0}}{\text{.701 8 0}}{\text{.641 9 0}}{\text{.591 6}} \\ {\text{0}}{\text{.155 7 0}}{\text{.499 9 0}}{\text{.029 9 0}}{\text{.641 9 0}}{\text{.586 4 0}}{\text{.551 2}} \\ {\text{0}}{\text{.194 1 0}}{\text{.970 2 0}}{\text{.499 9 0}}{\text{.433 7 0}}{\text{.393 3 0}}{\text{.358 1}} \\ {\text{0}}{\text{.298 2 0}}{\text{.358 1 0}}{\text{.566 2 0}}{\text{.499 9 0}}{\text{.469 0 0}}{\text{.378 3}} \\ {\text{0}}{\text{.358 1 0}}{\text{.413 5 0}}{\text{.606 7 0}}{\text{.531 0 0}}{\text{.499 9 0}}{\text{.463 8}} \\ {\text{0}}{\text{.408 4 0}}{\text{.448 8 0}}{\text{.641 9 0}}{\text{.621 7 0}}{\text{.536 2 0}}{\text{.499 9}} \\ \end{gathered} \right]\end{split} $

基于式（18）得到航空发动机研制过程中风险类型的集体偏好关系F^c，

$ {{\boldsymbol{F}}^{{\mathrm{c}}}} = \left[ \begin{gathered} {\text{0}}{\text{.500 0 0}}{\text{.513 0 0}}{\text{.504 9 0}}{\text{.649 8 0}}{\text{.613 0 0}}{\text{.613 2}} \\ {\text{0}}{\text{.525 1 0}}{\text{.500 0 0}}{\text{.269 3 0}}{\text{.639 2 0}}{\text{.597 6 0}}{\text{.623 2}} \\ {\text{0}}{\text{.495 1 0}}{\text{.730 7 0}}{\text{.500 0 0}}{\text{.418 5 0}}{\text{.438 2 0}}{\text{.460 0}} \\ {\text{0}}{\text{.357 1 0}}{\text{.360 8 0}}{\text{.581 5 0}}{\text{.500 0 0}}{\text{.436 3 0}}{\text{.481 8}} \\ {\text{0}}{\text{.387 0 0}}{\text{.402 4 0}}{\text{.561 8 0}}{\text{.597 2 0}}{\text{.500 0 0}}{\text{.507 8}} \\ {\text{0}}{\text{.386 8 0}}{\text{.427 8 0}}{\text{.540 1 0}}{\text{.527 0 0}}{\text{.508 8 0}}{\text{.500 0}} \\ \end{gathered} \right] $

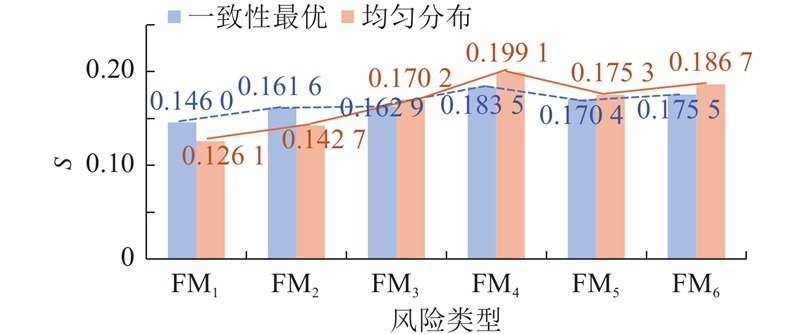
将F^c代入式（20）计算得到某型航空发动机研制过程中6类风险类型的最终得分，分别为0.146 0、0.161 6、0.162 9、0.183 5、0.170 4、0.175 5. 由此可得，在航空发动机研制过程中，基于分布式语言偏好评价并考虑专家权重、风险因子权重与个性化语义的风险类型排序：FM₄ > FM₆ > FM₅ > FM₃ > FM₂ > FM₁. 市场需求突然改变是首要风险类型，航空发动机研制过程中客户的需求变动频率较大，若未能及时有效沟通协调，可能面临如产品无法顺利交付、费用与资源的大量损失的严重后果. 在风险管控过程中，管理者应当增加关注程度，通过充分的跟踪与及时的沟通主动寻求适当的预防与解决办法.

在不需要对语言进行精确刻画以及不需要考虑个性化语义的背景下，已有关于语言量化的研究多数假设语言分布为均匀分布的形式以此来简化语言信息处理工作^[39]. 本研究考虑个性化语义在语言评价中的影响作用，通过构建模型与求解方法得到一致性最优下的个性化语义结果. 选择通常不涉及个性化语义背景的均匀分布方法与所提方法进行对比，论证所提方法的有效性与可行性.

若假设语义分布为均匀分布，即专家重要性语言术语集L_e的均匀分布解为[0, 2/4, 2/4, 3/4, 1]、风险因子重要性语言术语集L_r的均匀分布解为[0,1/6, 2/6, 3/6, 4/6, 5/6, 1]，型号总师对L_e和L_r的一致性水平分别为0.7000和0.6889，本研究基于Me和Mr求解得到的最优一致性分别为0.8330和0.8332. 由此可知，在型号总师评价专家和风险因子重要性时，所提方法获得的解在一致性方面存在优势. 在权重的均匀分布方法下，通过数值转换与权重公式计算得到的4位专家权重分别为0.2469、0.2562、0.2125、0.2844，重要性排序为EX₄ > EX₂ > EX₁ > EX₃，本研究基于一致性驱动的个性化语义模型求解得到的专家权重排序为EX₁ > EX₄ > EX₃ > EX₂；3个风险因子的权重分别为0.2556、0.3074、0.4370，重要性排序为RF₃ > RF₂ > RF₁，所提方法求解的风险因子重要性排序为RF₃ > RF₁ > RF₂. 由此可知，所提方法获取的权重结果与均匀方法解下的结果存在重要性排序上的差异.

4位领域专家根据语言术语集L_i对6类风险类型进行语言评价，假设语义分布为均匀分布 [0, 1/6, 2/6, 3/6, 4/6, 5/6, 1]，求解得到相应的一致性水平，如表5所示. 对比所提方法获得的最优一致性水平可以看出，无论是不同专家对各个风险因子的一致性水平，还是对语言术语集L_i的加权一致性，均低于所提方法得到的一致性水平. 因此，当领域专家对风险类型进行语言评价时，所提方法在一致性方面同样具有优越性.

由一致性水平与相关权重求解得到相应的数值偏好关系以及最终的集体偏好关系，代入式（20）计算得到假设语义均匀分布下的风险类型得分值，分别为0.1261、0.1427、0.1702、0.1991、0.1753、0.1867，风险类型排序为FM₄ > FM₆ > FM₅ > FM₃ > FM₂ > FM₁. 如图2所示，虽然均匀分布与一致性最优的结果存在数值上的差异，但不影响风险类型的优先级排序情况. 综合对比结果可以看出，本研究在考虑个性化语义背景下得到的一致性水平更优，语言评价结果的可靠性与准确性得到提升.

为了进一步对比所提方法的优越性，采用传统FMEA方法计算预处理后的数据集，即最终风险模式排序根据风险类型的绝对数值乘积大小依次列出，得到风险排序结果为FM₁ > FM₂ > FM₆ > FM₅ > FM₄ > FM₃. 排序结果与所提方法存在差异. 主要原因：传统FMEA方法使用绝对数值对风险类型进行直接评价，未考虑评价专家或者风险类型重要性差异的影响. 在实际情况中，评价专家的权威性、在项目中负责的领域、经验能力均存在差异；型号总师更倾向于综合考虑全局因素，对风险类型的关注程度也存在差异. 例如，传统FMEA方法的排序首位为“技术难度过大”的管理风险，考虑航空发动机自身的产品技术特点，这一风险模式具有普遍性. 所提方法排序较前的风险是“客户需求突然改变”“成员能力不足”，考虑本研究案例数据的来源是改进改型的航空发动机研制项目，客户需求改变以及项目组成员能力能否完成任务更符合案例实际背景特征，也更能体现不同情境下的风险关注重点. 因此，与传统的FMEA风险评估方法对比，本研究提出的语言型FMEA评价方法更符合实际评估情况和专家评价习惯. 尤其是在面向复杂产品开发领域，本研究改进的语言型FMEA方法更适合在复杂晦涩情境进行风险评价活动，可以获得更为可靠的风险评估结果.

如表6所示为已有研究使用语言表达方式改进传统FMEA方法的文献梳理. 与改进的语言型FMEA风险评估方法相比，所提方法在语言信息的表达形式、信息的处理方式和权重的确定方面均有适应复杂产品开发情境的改进与提升. 由表6可知，已有改进型FMEA方法大多采用直接数值/语言评价，直接的语言或者数值评价虽然简便易行，但往往难以匹配复杂情境，对于一些难以直接判断的情况适应性不足. 本研究结合具体情境，选择间接的语言偏好形式评价，在信息表达形式方面丰富了既有FMEA方法. 在语言型FMEA的信息处理过程中，鲜少文献考虑语义影响，本研究基于个性化语义的风险评估结果更适合评价专家背景差异较大的复杂情境. 语言型FMEA更多关注风险因子的权重影响，较依赖单一的主观或客观赋权方法，所提方法不仅采用主客观结合的综合赋权方法，还同时考虑风险因子以及评价专家的权重影响，进一步补充了语言型FMEA方法中权重确定的研究.

本研究面向复杂产品开发过程的典型特征与实际需求，针对已有语言型FMEA评价方法在风险管理问题中的不足，基于个性化语义并考虑专家与风险因子的权重差异，提出改进的语言型FMEA方法. 以航空发动机研制为例，通过开展实践数据的验证对比试验，论证了所提方法的可行性与有效性，表明该方法有助于增强结果的可信性与准确性. 所提方法的3个主要优势：1）采用分布式语言偏好关系改进语言FMEA评估中的语言信息表达方式，适用于晦涩复杂的复杂产品风险管理实践背景；2）考虑个性化语义对评价结果的影响，优化语言FMEA方法中语言建模与求解过程，有助于解决现实中语义感受与认知存在差异的问题；3）采用综合赋权法同时考虑评价专家与风险因子的重要性差异问题，增加了语言FMEA方法中权重赋予的整体性与客观性，有助于提高评价结果的可信性与准确性. 总体而言，与现有语言型FMEA方法相比，所提方法不仅能够较好地处理复杂背景下的风险评价问题，也充分考虑了语言的个性化、风险因子与评价者的差异性对评价结果的影响.

本研究提出的语言型FMEA方法的应用背景适合复杂产品研制情境，对于一些技术成熟度较高的产品与行业背景，所提方法在应用层面的可操作性与简便性或有不足. 所提方法暂未涉及后续的共识达成阶段，主要原因是设计制造协同问题一直是行业痛点，不同开发领域间存在固有矛盾. 调整偏好达成共识容易产生违背专家初始意愿的后续问题，现有共识达成方法难以解决该复杂情境下的共识与意愿问题. 所提方法在风险识别部分的改进存在不足，仍然基于专家直接评价得到，未来计划结合人工智能领域的前沿方法进行更加全面的风险模式识别.