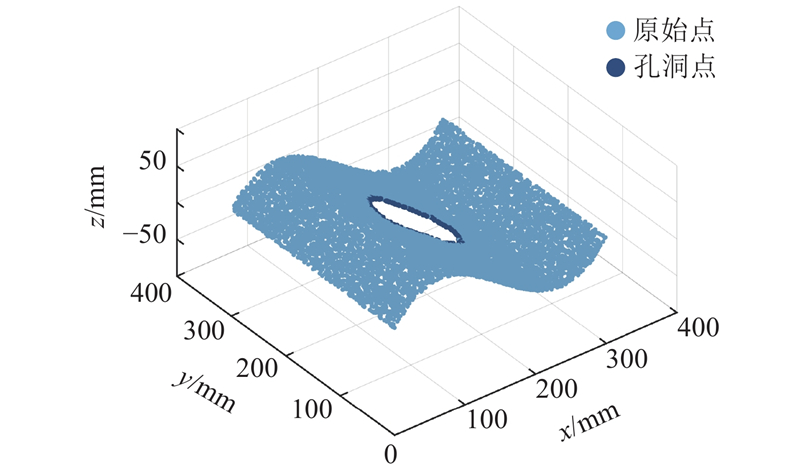
现有点云孔洞修复算法主要分为2个类别:基于网格点的方法和基于无序点的方法. 基于网格的点云孔修复算法采用泊松(Poisson)法或德劳内(Delaunay)法生成三角网格,标记处于单个三角网格中的边界线得到孔洞轮廓,通过三角网格的几何或特征信息完成点云孔洞的修复[12-17]. 该类方法简单易行,但严重依赖三角网格精度,鲁棒性差、计算时间长. 崔文等[13]针对激光点云中的孔洞,遍历三角网格得到孔洞边界,融合最小二乘网格与径向函数隐式曲面完成孔洞修复. Chen等[15]为了提高基于三角网格的孔洞修复的效率,提出保留特征的网格简化方法,结果显示该方法虽然提升了修复效率,但牺牲了修复精度. 基于无序点的方法无需拓扑重建的预处理,储存效率和执行效率得到提升. 这类方法主要基于局部微切面识别孔洞边界,结合边界及其邻域点的几何特征信息,使用不同的点插值方法完成孔洞修补[18-23]. Lin等[18]针对具有尖锐特征的孔洞提出基于张量投票填充方法,通过恢复特征曲线将特征孔划分为非特征孔后分别填充. 该方法修复能力较好,但文献没有给出如何利用特征线分割孔的方法. Zhang等[21]针对有边界曲面点云孔洞提出基于模糊推理系统的修复方法,该方法对点云上小孔的修复效率高于样条曲线算法,而且2种方法的修复精度相当;该方法的模糊系统采用经验性参数,只能通过不断试错达成较好的修复效果. 随着人工智能的发展,神经网络被用于孔洞修复[24-28]. 王春香等[25]提出基于遗传算法(genetic algorithm,GA)-反向传播(back propagation, BP)神经网络的无序点云孔洞自动修补方法,以鼠标表面上的小孔修复为例,展示了该方法较高的修复精度;当修复目标表面增大时,该方法的修复误差会增加. Duan等[26]提出基于径向基函数(radial basis function, RBF)神经网络映射的点云孔洞修复算法,以Matlab生成的曲面孔洞模型为例,证明该方法的修复精度高于样条曲面拟合插值算法,但修复时间较长. 可以看出,基于神经网络的修复方法修复较小孔洞的精度较高,但模型训练过程大大降低了方法效率.
基于无序点云的研究大多集中在单一孔洞的识别与修复上,本研究提出无序点云多孔洞自动修补方法. 1)针对基于微切面的边界识别方法在复杂曲面处的误识别问题,以整体点云数据拟合的平面为投影面,采用角度判别法提取边界点. 2)推导出点云密度公式,使所提方法适用不同分辨率的点云和非均匀分布的数据点. 3)构建曲面方程,还原大小、点云测量精度与所在表面形状不同的孔洞的几何信息. 4)设计迭代求解映射点方法,减小计算机截断误差与舍入误差.
1. 无序点云孔洞边界识别
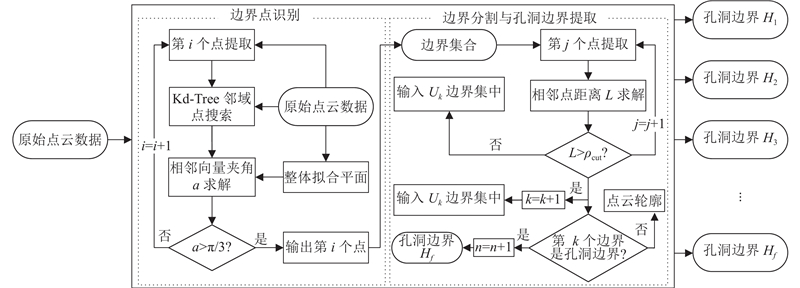
为了方便描述,约定孔洞边界点和点云轮廓点均为边界点,孔洞边界和点云轮廓均为边界. 约定通过整体点云数据拟合的平面称为整体拟合平面,以边界点拟合的平面称为边界拟合平面. 采用2个循环算法分别实现边界点的识别与孔洞边界的提取:循环1)遍历原始点云中所有点,采用角度阈值法判定边界点,得到边界集合点集;循环2)遍历集合点集中所有点,分割点集得到独立边界点集并判断边界是否为孔洞边界. 循环2)是实现多孔洞修复的重要环节;当原始点云数据存在轮廓且因点云缺失存在多个点云孔洞时,该循环实现多个边界的分割并识别出真正的孔洞边界. 由如图1所示的多孔洞上边界识别流程得到若干独立孔洞边界点集.
图 1
1.1. 边界点识别
判别点及其邻域点是否投影在同一平面,这是判断能否使用邻域点角法进行孔洞点判别的前提. 设平面方程
构建目标函数
式中:n为点数,当基于整体点云数据拟合平面时,n表示曲面所有点数;当以边界点拟合平面时,n表示边界点数. s(a, b, c)分别对a、b和c求偏导并等于零,得到系数方程组
求解式(3)得到拟合平面系数. 以判别点在拟合平面上的投影点为起点,该判别点的邻域投影点为终点,在投影面上形成若干向量. 角度判别法的原理是求解2个相邻向量夹角,当该夹角超过阈值时,判定该判别点为边界点. 通过点云密度选择邻域范围,考虑到不同原始点云数据的分辨率可能相差较大,推导点云密度求解公式为
式中:n1为整体点云数量,
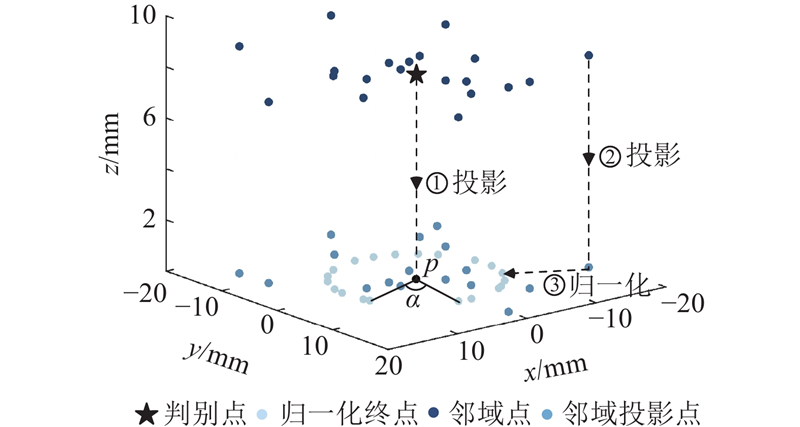
为了提高算法效率,构建K维树(Kd-Tree)算法来查找判别点的邻域点. Kd-Tree算法的核心:通过递归的方式将三维空间划分为嵌套的子空间,每个子空间对应树中的1个节点. 在搜索邻域点时从Kd-Tree的根节点开始,通过比较查询点与当前节点的切分维度值,确定搜索方向(左子树或右子树),递归地在所选子树中记录已找到的邻域点及其距离. 如图2所示,将采用Kd-Tree算法得到的判别点的邻域点投影到整体拟合平面上,为了在确定相邻向量时根据邻域点之间形成的向量确定单一的搜索方向,对点p与其邻域点形成的向量进行归一化处理,归一化公式为
图 2
式中:M为邻域投影点与点p之间的距离,h为归一化后的向量长度,取h=10 mm,上标(1)表示投影点坐标分量,上标(2)表示投影点归一化后的坐标分量. 归一化的目的是使向量的长度一致以便于计算相邻向量的夹角. 归一化的长度可以任意确定,不会影响最终结果. 1)从归一化点云中任选一点作为初始点,将其标记为已处理;2)通过Kd-Tree查找初始点的最近邻点,将该点也标记为已处理. 这2个点分别与点p构成的向量称为相邻向量,将从初始点指向其最近邻点的向量记为该步的指向向量;3)在未标记的点中,查找当前被搜索点(上一步的最近邻点)的2个最近邻点,分别生成2个新的指向向量;4)计算这2个新向量与上一轮指向向量之间的夹角,选择夹角较小的向量所对应的点作为本轮的搜索目标,标记该点并记录其对应的相邻向量;5)重复步骤3)和4),依次迭代搜索与标记,直到最终回到初始点. 计算各相邻向量之间的夹角,
式中:p、q为相邻向量. 将这些夹角排序,得到夹角的最大值记为а.
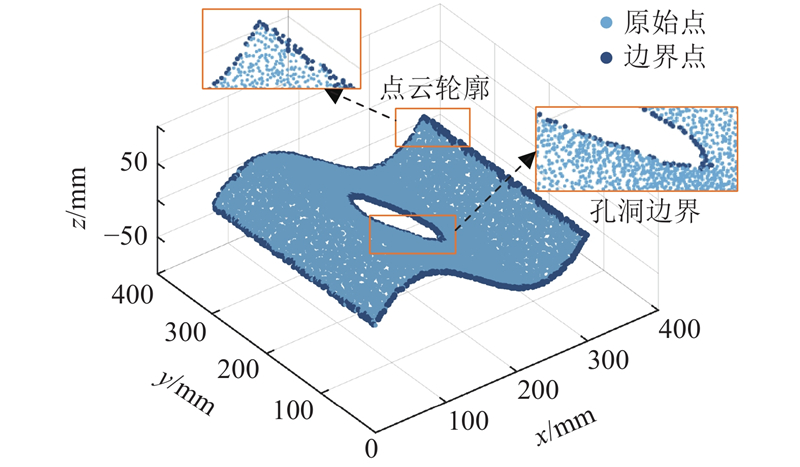
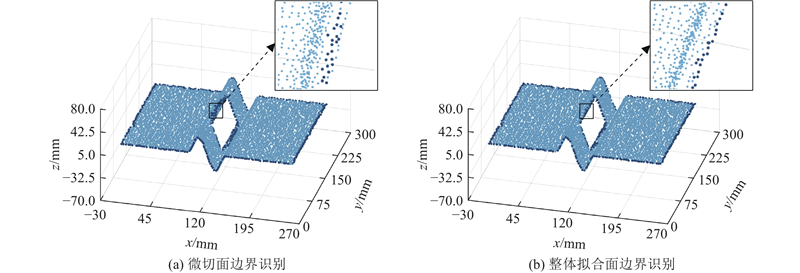
如图3所示为使用基于点云密度的边界识别效果图. 数据点的x、y坐标落在区间[0, 300]内,以π/3为阈值,а≥π/3的判别点为边界点,识别出的边界点包括孔洞边界点和点云轮廓点.
图 3
1.2. 边界分割与孔洞边界提取
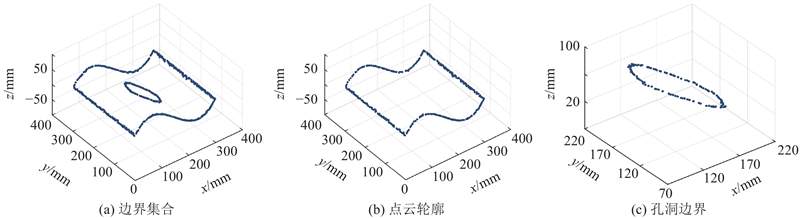
导出的边界点集还不能描述单一孔洞的边界,为此进行边界分割. 分割后的边界中包含点云轮廓,基于边界形心、边界、边界邻域三者之间的位置关系提取出孔洞边界,实现不同孔洞的定位与修复. 采用距离法分割边界,以图4(a)所示边界点集为例:1)从边界点集中任选一点作为起始搜索点,将其复制至新集合(如U1)中,并对其进行标记;2)在剩余未处理的边界点中,使用Kd-Tree查找当前搜索点的最近点(被搜索点);3)判断搜索点与被搜索点之间的距离是否小于或等于云密度ρcut(点云密度ρ的3倍):若满足条件,则将被搜索点复制到当前搜索点所在的同一集合(如U1);否则,创建新集合(如U2、U3),并将被搜索点复制至该集合;4)标记当前被搜索点,以避免重复访问,并将其作为下一步的搜索点;5)重复步骤2)~4),依次处理每个新确定的被搜索点,直到边界集中所有点都被复制完毕;6)不同的边界区域将被存储于多个子集中. 点云的边界分割效果如图4(b)和(c)所示.
图 4
子集中的点构成点云轮廓或孔洞边界,考虑孔洞边界和点云轮廓的位置关系,以边界形心为参考点提出边界判别方法:将边界及其邻域点(边界中所有点的邻域点的并集)投影到边界拟合平面上. 计算投影边界的形心:
式中:c为形心坐标向量,m1为投影边界点总数,bi为投影边界点坐标向量. 计算边界点到形心的平均距离:
邻域投影点到形心的平均距离:
式中:nj为边界邻域点坐标向量,m2为边界邻域投影点总数. 当l1≤l2时,进行判别的子集中的边界为孔洞边界,否则为点云轮廓. 如图5所示为使用边界判别方法区分并排除点云轮廓后的效果,图中的深色边界定位了单一孔洞.
图 5
2. 无序点云的孔洞修补
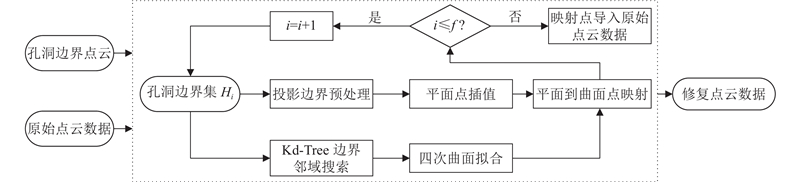
在提取出各独立孔洞边界后,通过循环依次处理每个孔洞:利用Kd-Tree在原始点云中搜索当前边界的邻近点以确定拟合邻域;通过邻域点拟合曲面方程,并将插值点映射至该曲面,生成孔洞填充点. 处理完所有孔洞后,将填充点集成至原始点云,实现自动修复. 单一孔洞修补的循环执行流程为多孔洞修补的关键环节,如图6所示.
图 6
2.1. 投影边界预处理
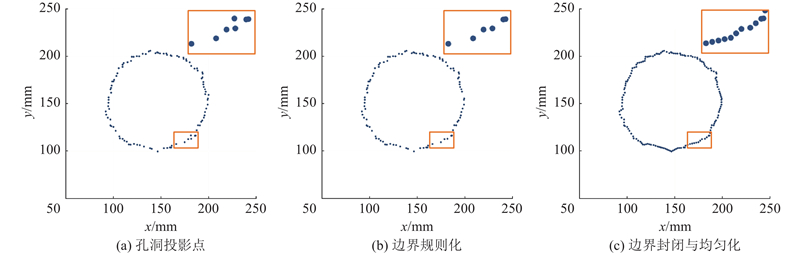
当原始点云的不同区域点云分辨率、位置孔洞的形状不同时,存在边界点漏识别与错误识别的问题. 漏识别会加大孔洞边界上点与点间距离的不均匀性,错误识别会使孔洞边界上出现边界邻域点. 在填充孔洞之前须进行边界规则化与均匀化预处理. 规则化方法:1)从投影边界点集中依次取3个点,以第2个点为基准,计算该点与第1和第3个点形成的向量,称2个向量为边界相邻向量;2)计算边界相邻向量夹角,当夹角大于π/2时,删除中间点. 3)后退1个点重新开始检查,直到边界任意相邻向量夹角都在区间[0, π/2]内. 规则化后的投影边界在平面点插值时不会出现局部稠密问题,保证了再次依次取点时,所有相邻的3个点均按顺序单向环绕. 均匀化方法:从投影边界中依次取点,计算相邻2个点的间距,当间距大于局部投影点云密度时,插入点计算式为
式中:η=[L/ρn]+1,L为相邻点的间距,ρn为边界邻域投影点云密度,[L/ρn]为不大于L/ρn的整数. nu、nv为2个相邻投影点的坐标,
图 7
2.2. 投影边界内点插值
图 8
图 8 基于三角片法的点插值过程
Fig.8 Point interpolation process using triangular patch method
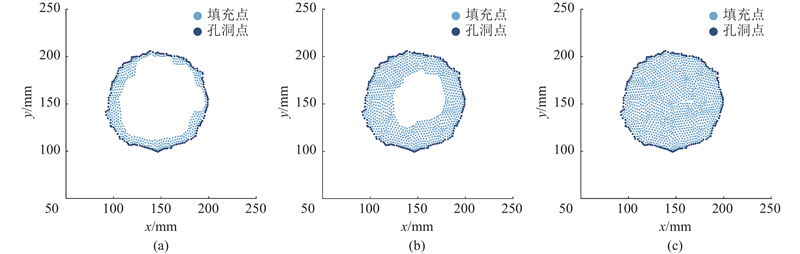
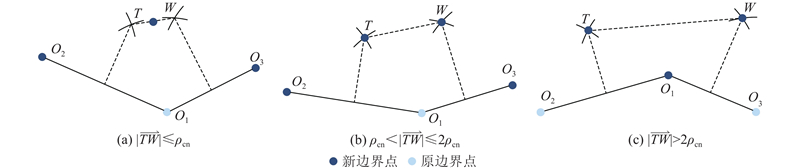
如图9所示为平面内基于三角片方法的点插值原理. 点O1、O2、O3为边界点上的3个相邻点;点T和W是2条边的中垂线和圆心为O1、半径为边界点及其邻域点的密度ρcn的圆的交点,被称为候补填充点. 当点间距小于ρcn时,以点T和W的中点为新的边界点,且在新的边界中不保留点O1;当间距大于ρcn小于2ρcn时,以点T、W为新的边界点,不保留点O1;当间距大于2ρcn时,以点T、W为新的边界点,并在新的边界点中保留点O1. 实际上,中垂线与圆的交点有4个,在孔洞内的交点才被称为候补填充点,基于边界相邻向量叉积模判断候补填充点. 对依次从点集中取点的环绕方向使用右手定则,得到的方向定义为边界的特征方向. 假设特征方向为Г,依次取点计算边界相邻向量的叉积与叉积模,当叉积的方向与Г相同时,叉积模为正,反之为负. 对所有叉积模求和,当总值大于零时,Г便为边界实际特征方向,反之实际特征方向为−Г. 当
图 9
2.3. 曲面方程拟合与点映射
在孔洞边界投影面内得到平面填充点后,建立曲面模型还原孔洞的几何特征;计算机存在截断误差与舍入误差,直线与高次曲面方程的联立求解存在较大误差,为此设计基于参数方程的方法,将平面点映射到曲面上,完成无序点云模型的孔洞填充. 考虑不同孔洞大小、点云测量精度与孔洞所在表面形状等条件下多孔洞修复方法的适用性,以曲面方程拟合修复,参数方程为
其中λ=[λ0, λ1, ···, λg]为系数矩阵,β=[1, x, y, x2, xy, y2, ···, x2yh−2, xyh−1, yh],g=(h+1)(h+2)/2−1. h越大,曲面方程所能拟合的曲面越复杂,拟合曲面也越容易受到点云噪点的干扰. 取g=14、h=4,既能够拟合修复复杂形状表面上的孔洞,也能够在激光雷达点云测量不光滑的条件下使几何还原不受干扰. 采用最小二乘法拟合曲面方程,
式中:n2为孔洞边界及其邻域中点的总数. 系数方程组式(13)常因出现奇异性而无法按照矩阵运算求解,本研究选择Levenberg-Marquardt算法[30]求解系数方程组. 平面点到曲面的映射方法采用参数方程:
式中:
随着t的变化,当w=0或w变号时,xt、yt、zt即为平面坐标x映射到曲面上的坐标.
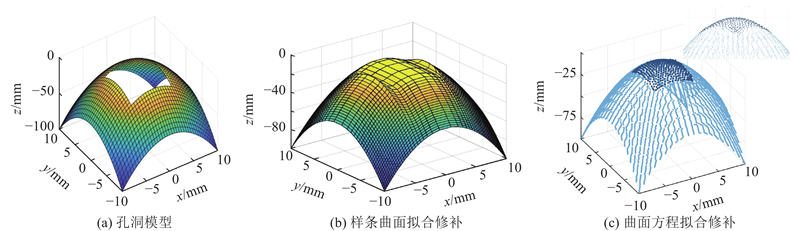
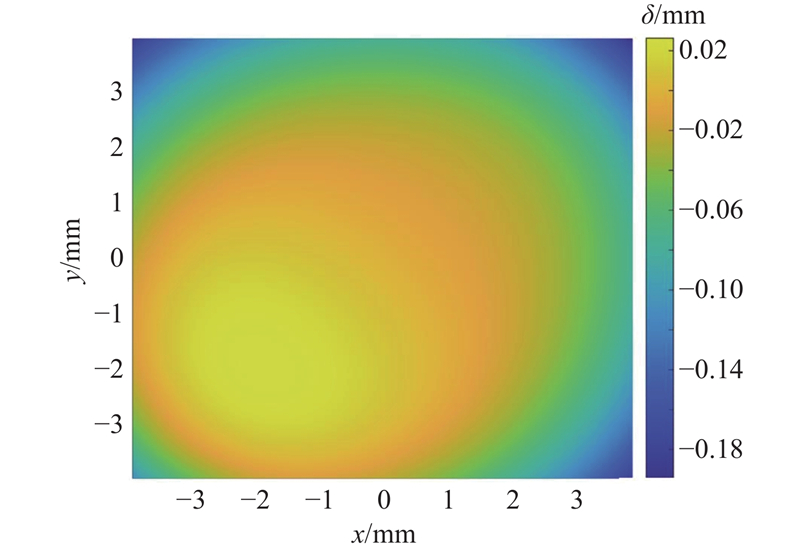
如图10所示为采用曲面拟合及点映射方法修复的孔洞以及绝对修复误差δ(x, y)的分布云图.
图 10
式中:z(x, y)与zt分别为x、y坐标下的真实z坐标和拟合插值坐标. 图10(b)中的孔洞区域通过人工删除原始点云数据构建,因此该区域的真实点坐标(x, y, z(x, y))已知,将已有真实点的x、y代入拟合曲面方程得到zt. 由云图可知最大误差为0.15 mm.
3. 算法分析与对比
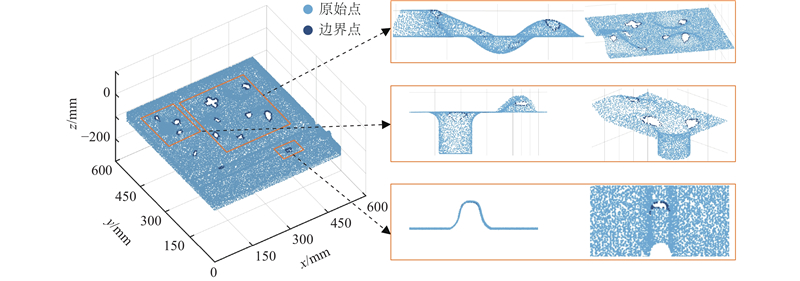
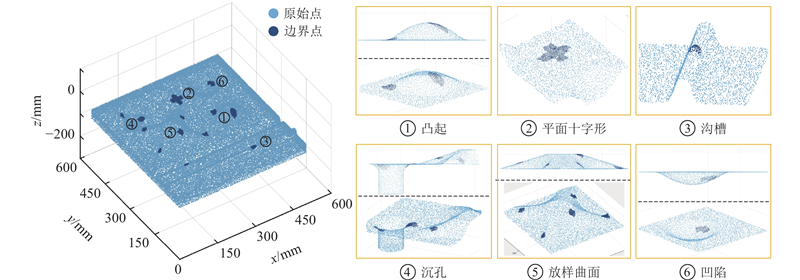
通过绘制带孔洞CAD模型验证本研究所提方法对多孔洞自动识别与修补的能力. CAD模型的x、y、z坐标范围分别为0~600、 0~600、 −100~30 mm,该模型上有凸起、沟槽、放样曲面、凹陷和沉孔等特征. 在模型的不同位置人为删除部分点,构建不同大小、不同边界形状的孔洞,不同孔洞所在的点云表面形状也不同. 采用所提方法对模型的孔洞识别与修补情况分别如图11和图12所示. 可以看出,经过孔洞预处理后的三维填充点分布均匀,密度与邻域点云密度相近,在填充点云与邻域点云之间没有缝隙. 不同形状点云表面上的孔洞修复效果不同,平面与弧面上的孔洞填充点云准确还原了原始点云的几何与特征信息(如凸起、平面十字形、沉孔和凹陷);复杂曲面的孔洞填充点云与周围点云相比,仅在大曲率过渡处有微小的偏移,但仍能恢复原始模型的形状(如沟槽和放样曲面). 验证结果表明了多孔洞修复流程与算法的有效性.
图 11
图 12
图 13
图 14
如图15所示为曲面方程拟合方法绝对修复误差. 在计算修复误差时,z轴真实值由孔洞区域填充点的x、y坐标代入模型方程得到,z轴修复值则由拟合点坐标直接获得. 可以发现,绝对误差范围为−0.190~0.025 mm.
图 15
图 15 曲面方程拟合方法的绝对修复误差
Fig.15 Absolute repair error of surface-equation fitting method
4. 无序点云孔洞修补实验
现场采集无序点云开展无序点云孔洞修复实验,验证无序点云孔洞识别与修补方法的实际应用效果. 实验平台主要由具有1.60GHz i5-8250U CPU、8.00GB内存和QT、Visual Studio软件的PC机,LIVOX Mid-40激光雷达,R4A路由器,Livox转换器和待测目标物等组成,如图16所示. Livox Mid-40激光雷达发射905 nm激光波长、采用非重复式扫描方式,每秒获得1.0×105个点,20 m内距离精度为2 cm、角度精度小于0.1°,当雷达与被测物体小于1 m时测量失效.
图 16
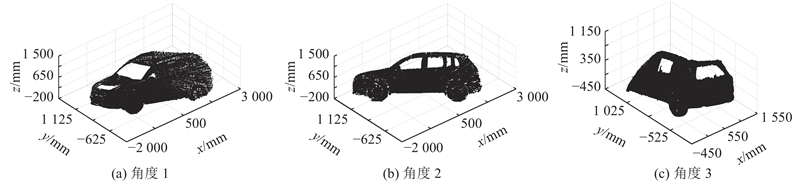
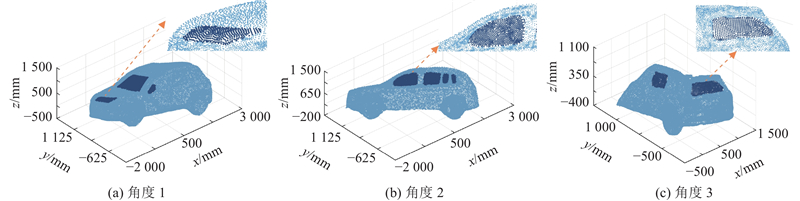
汽车是生活中常见的目标物,镜面反射使汽车的三维成像测量容易因点云缺失产生孔洞. 以汽车为扫描对象,采用激光雷达从3个角度且每个角度固定扫描3 s得到汽车表面点云图,如图17所示. 可以看到,激光雷达在一些角度下测不到玻璃表面点云,孔洞由此产生. 由于激光雷达的局限与车辆周围环境因素的干扰,原始点云数据存在大量体外孤点、离群点缺陷. 对原始点云数据进行点云降采样、平滑降噪与体外孤点去除等相关操作后[31-32],采用本研究提出的孔洞识别与修补方法对孔洞进行修复,结果如图18所示. 其中中浅色点为数据处理后得到的汽车表面点云,深色点为孔洞三维修复点. 结果表明,基于无序点云的孔洞修补方法在实际应用中具有较为稳定的多孔洞自动修补能力,能够较高精度还原汽车的原始外表面.
图 17
图 18
图 19
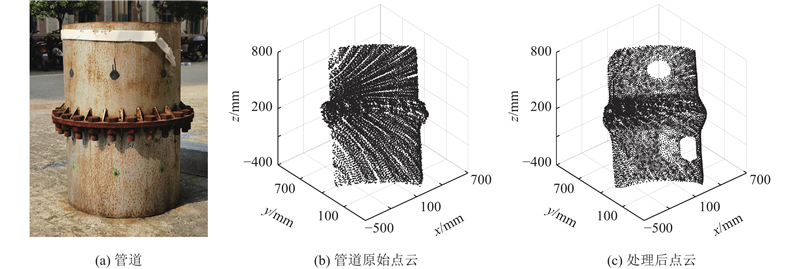
图 19 管道原貌及其点云图
Fig.19 Original appearance of pipeline and its point cloud image
图 20
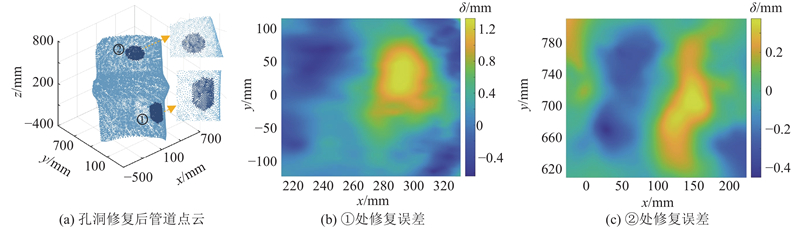
图 20 管道点云的孔洞修补结果与绝对修复误差
Fig.20 Hole-repair results and absolute error of pipeline point clouds
5. 结 语
三维传感点云数据的孔洞修复对于如缺陷检测、目标识别的下游应用具有重要科研价值和工程意义. 本研究提出基于无序点云的孔洞自动修补方法,基于CAD点云模型进行方法分析和对比,通过激光雷达扫描得到的点云数据对所提方法进行实验验证,主要结论如下. 1)在整体拟合平面上采用角度判别法识别边界,避免了传统方法在复杂曲面处的误识别问题. 对投影边界规则和均匀化处理,采用三角片法在边界内实现点插值,基于参数方程方法完成点映射,得到与原始点云密度特征相同的三维插值点. 2)构建四次曲面方程模型,以孔洞边界及其邻域点拟合方程,有效还原了不同孔洞的原始几何信息. 以大曲率曲面上的孔洞为例,该方法的修复精度高于样条曲面插值拟合算法,且具有较高的修复效率. 3)考虑数据点分布不均匀,推导出点云密度公式,有效反映了原始数据的分辨率. 定义边界形心公式,基于边界形心、边界、边界邻域的位置关系提取孔洞边界. 设计基于边界分割、孔洞提取、曲面拟合等算法的多维循环流程,实现无序点云上多孔洞的自动修补. 4)采用激光雷达并以汽车和管道为扫描对象进行方法性能验证实验,结果表明所提方法在测量数据不光滑的情况下仍然具备多孔洞的自动修补能力,方法的修复精度可以达到毫米级. 确定不同大小和形状的孔洞边界邻域范围,才能使无序点云多孔洞修复方法达到最佳的孔洞识别和修复效精度,如何让所提方法根据孔洞的特征自动调整Kd-Tree搜索参数以确定对应邻域范围是今后工作的重点.
参考文献
An octree-based two-step method of surface defects detection for remanufacture
[J].DOI:10.1007/s40684-022-00433-z [本文引用: 1]
Lidar sensor-based object recognition using machine learning
[J].DOI:10.1007/s10946-021-09986-x
A comparative study of visual identification methods for highly similar engine tubes in aircraft maintenance, repair and overhaul
[J].
Accurately identifying the defects of bubbles and foreign objects under the protective films of electric vehicle batteries by using 3D point clouds
[J].DOI:10.1088/1361-6501/ad57e1 [本文引用: 1]
Three-dimensional face point cloud hole-filling algorithm based on binocular stereo matching and a B-spline
[J].DOI:10.1631/FITEE.2000508 [本文引用: 1]
Hole repairing algorithm for 3D point cloud model of symmetrical objects grasped by the manipulator
[J].
Automatic pipe and elbow recognition from three-dimensional point cloud model of industrial plant piping system using convolutional neural network-based primitive classification
[J].DOI:10.1016/j.autcon.2020.103236
Reparation with moving least squares sampling and extraction of body sizes of beef cattle from unilateral point clouds
[J].DOI:10.1016/j.compag.2024.109208
3D facial recognition using local feature-based methods and accuracy assessment
[J].
Matching point clouds with STL models by using the principle component analysis and a decomposition into geometric primitives
[J].
Research on point cloud processing and grinding trajectory planning of steel helmet based on 3D scanner
[J].
A region-growing algorithm using parallel computing for surface reconstruction from unorganized points
[J].DOI:10.1016/j.advengsoft.2013.03.002 [本文引用: 1]
激光三角网格点云孔洞曲面修补方法
[J].
Hole surface repairing for laser triangular mesh point cloud
[J].
基于多向波前法的岛屿孔洞修补
[J].
Island hole repairing based on multi-directional advancing method
[J].
Holes filling of scattered point cloud based on simplification
[J].DOI:10.1007/s11042-021-11019-3 [本文引用: 1]
结合间接邻域的散乱点云三角网格曲面重构
[J].
Surface reconstruction algorithm with indirect neighborhood point set from scattered point cloud
[J].
Fast self-repairing region growing surface reconstruction algorithm for unorganised point cloud data
[J].DOI:10.1504/IJCAT.2017.087330 [本文引用: 1]
附加增值条件的移动最小二乘法的点云孔洞修补
[J].
Additional value-added conditional moving least squares method for point cloud hole repair
[J].
改进哈里斯鹰优化算法在匹配地面点云孔洞修补中的应用
[J].
Application of improved Harris Hawks optimization algorithm in patching cloud holes at matching ground points
[J].
A method for identifying and repairing holes on the surface of unorganized point cloud
[J].DOI:10.1016/j.measurement.2023.112575 [本文引用: 1]
Point cloud repair method via convex set theory
[J].
Improved hole repairing algorithm for livestock point clouds based on cubic B-spline for region defining
[J].DOI:10.1016/j.measurement.2021.110668 [本文引用: 1]
SSA-BP神经网络在无人机点云孔洞修补的应用
[J].
Application of SSA-BP neural network in UAV point cloud hole repair
[J].
基于GA-BP神经网络的散乱点云孔洞自动修补
[J].
Automatic repair of scattered point cloud hole based on GA-BP neural network
[J].
Ship hull surface reconstruction from scattered points cloud using an RBF neural network mapping technology
[J].
Point cloud data hole repair aggregation algorithm based on optimized neural network
[J].
Filling the holes on 3D heritage object surface based on automatic segmentation algorithm
[J].DOI:10.1111/exsy.13749 [本文引用: 1]
三角网格模型孔洞修补算法研究
[J].
Research on the algorithm of hole repairing in mesh surfaces
[J].
A Levenberg–Marquardt algorithm with correction for singular system of nonlinear equations
[J].DOI:10.1016/j.amc.2013.03.026 [本文引用: 1]
综合多种算法的点云精简优化策略与实验研究
[J].DOI:10.3788/LOP57.231402 [本文引用: 1]
Point cloud simplification optimization strategy and experimental research based on multiple algorithms
[J].DOI:10.3788/LOP57.231402 [本文引用: 1]
Point cloud reduction and denoising based on optimized downsampling and bilateral filtering
[J].DOI:10.1109/ACCESS.2020.3011989 [本文引用: 1]