不同地区的FRPs市场交易时间尺度存在一定差异,例如美国中部电力系统运营商(midcontinent independent system operator, MISO)在日前与实时2个时段开展FRPs交易,而加州独立系统运营商(California independent system operator, CAISO)仅在实时运行阶段进行FRPs交易[15]. Khoshjahan等[10] 仅在实时市场中交易和调度FRPs,在FRPs价格过高时考虑调度部分旋转备用容量. 本研究同时在日前与实时2个时段开展FRPs交易. 针对灵活性资源日前预留和实时调用决策,Cornelius [16]对比日前和实时市场对系统调节能力的需求,指出实际运行中的净负荷波动比日前市场预测值更加剧烈. Ghaljehei等 [17-18]改进日前火电FRPs需求预留的设计模型,提高了系统实时灵活性. Hu等[13]以储能聚合商收益最大化为目标进行电能-调频市场中提供FRPs的竞标模型的优化. Huang等[19]利用风储系统参与多市场投标,利用分布鲁棒方法处理价格和风电的不确定性. 朱西平等[20]将能源枢纽作为FRPs,并构建低碳环境下FRPs的机会成本和风险成本,实现低碳经济调度. 成明洋等[21]利用风光储场站来缓解实时市场不确定性,并参与两阶段电能量和灵活爬坡市场联合出清. Toubeau等 [22]通过数据驱动方法来估计实时市场中储能的部署概率,从而为储能的日前调度问题提供概率约束. Ai等[23]根据日前市场的报价场景,利用模型预测控制策略得到实时市场的预期部署概率. 然而,上述研究忽略了系统灵活性缺失严重、无法进行调控的极端情况,也缺乏对FRPs参与市场交易时的各种情况的直观、系统的分析. 同时,大多数研究仅针对单一主体参与FRPs的情况进行收益讨论,并未涉及多灵活性资源参与时的决策问题. 在高比例可再生能源并网导致源荷波动加剧的背景下,如何实现灵活性缺失风险可控的调度决策值得更进一步的研究.
随着灵活爬坡服务市场的完善,储能作为颇具潜力的灵活性资源,将逐步进入FRPs市场,但是对于满足日前和实时两时段交易的FRPs,目前针对日前市场和实时市场如何进行成本和机会收益的结算尚待研究. 因此,引入实时市场FRPs缺失概率,构建涵盖日前与实时市场全环节的交易决策树模型,建立考虑包括储能和火电的多类型灵活性资源提供FRPs的日前市场经济调度模型;在日前市场经济调度计算结果的基础上,通过FRPs日前市场接受概率和实时市场预期部署概率来进行机会成本和FRPs收益结算,系统性量化风险偏差成本与灵活性偏差惩罚成本,在利用储能提供FRPs获得收益的同时降低了系统成本.
1. FRPs交易决策树模型
由于可再生能源出力和负荷预测存在误差,系统的实际净负荷与预测净负荷之间出现偏差,此时需要通过市场手段来调用灵活性资源,以抵御净负荷的不确定性. FRPs旨在增强系统灵活性,可以将灵活性资源以预留容量的市场化方式引入系统,获取实时灵活性爬坡能力. FRPs的需求确定和成本分析已成为爬坡市场中的重要问题.
1.1. FRPs需求构成和机会成本分析
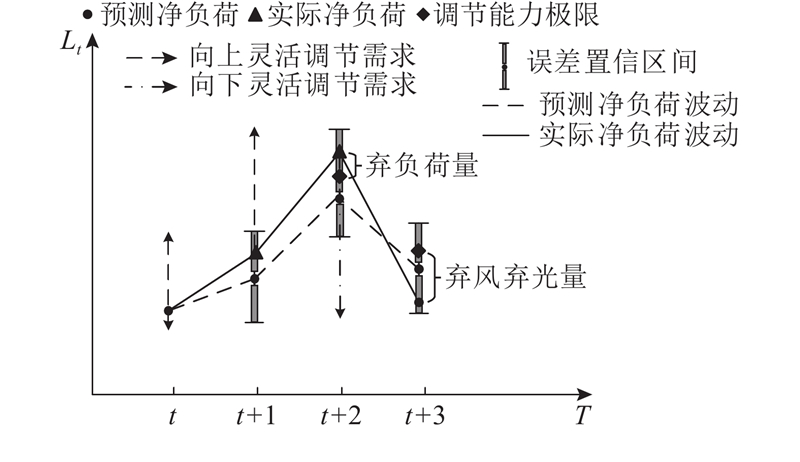
FRPs的需求由系统爬坡需求的变化量确定:一是系统在下一个时段的净负荷相较于当前时段的净负荷的变化量,即预测净负荷波动;二是为了满足系统风、光出力与负荷预测误差在一定置信区间内的偏差而额外产生的需求量,即不确定性需求. 在考虑不确定性的情况下,系统的灵活爬坡需求如图1所示. 图中Lt和T分别为净负荷与时刻.
图 1
以表1中参与灵活爬坡的机组G1~G6的电能量报价
表 1 FRPs机会成本与电能量市场报价的关系
Tab.1
| 机组 | |||
| G1 | 20 | 20 | 0 |
| G2 | 18 | 20 | 2 |
| G3 | 16 | 10 | 4 |
| G4 | 12 | 10 | 8 |
| G5 | 10 | 10 | 10 |
| G6 | 25 | 10 | — |
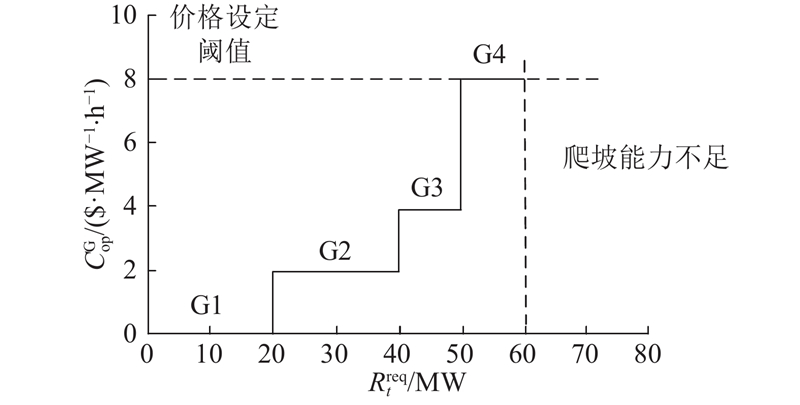
当系统爬坡需求小于20 MW时,系统仅仅依靠机组G1就能够预留出足够的FPRs,此时系统预留FRPs并未产生机会成本,故灵活爬坡产品价格为0. 当系统爬坡需求在[20, 40] MW之间,G2作为预留FRPs的边际机组,此时灵活爬坡产品价格为2 $/(MW·h). G3、G4作为爬坡边际机组的定价与此类似. 需要注意的是,当爬坡价格大于其价格设定的阈值时,系统认为预留爬坡并不能带来收益,此时机组不会倾向于提供FRPs. 如图2所示,当爬坡需求大于60 MW时,尽管机组能够为系统提供向上的FRPs,但是预留FRPs产生的成本已经超过预期收益,仍然会造成系统爬坡能力不足. 图2中
图 2
图 2 FRPs机会成本和爬坡需求的关系
Fig.2 Relationship between opportunity cost of FRPs and ramping demand
1.2. 基于概率模型的FRPs决策树
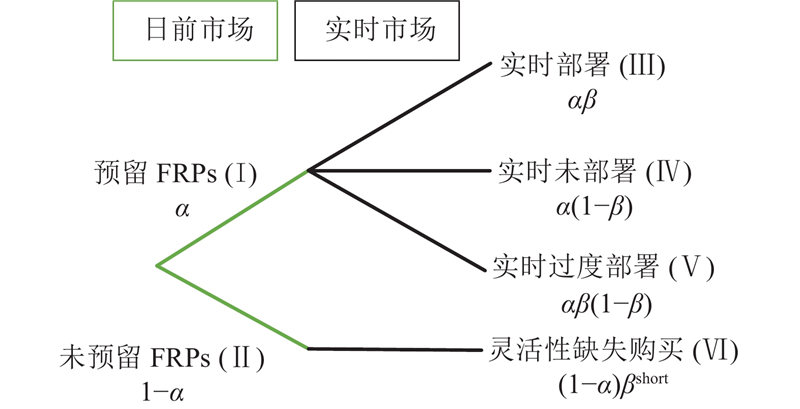
图 3
图 3 FRPs参与日前和实时市场的决策树
Fig.3 Decision tree for FRPs participation in day-ahead and real-time markets
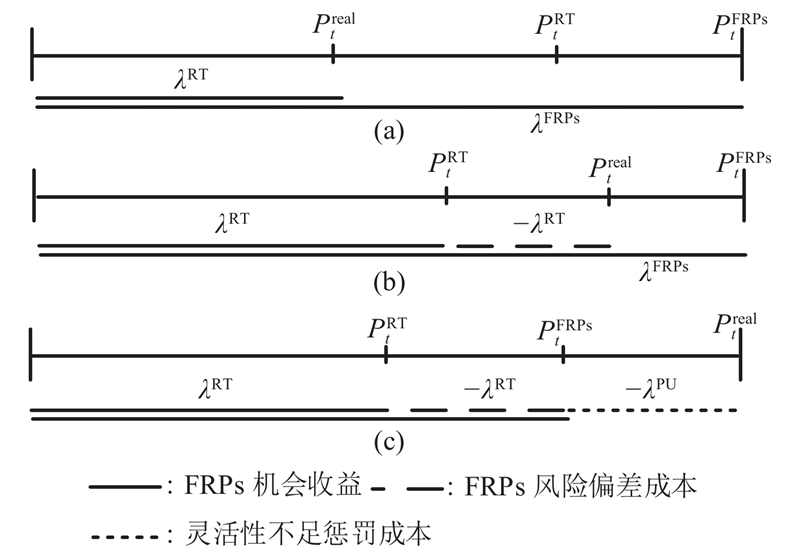
图 4
图 4 FRPs参与市场结算的成本和收益
Fig.4 Costs and revenues of FRPs participating in market settlement
在分支(I)中,系统有
图4中(a)展示的是分支(Ⅲ)和分支(Ⅳ)中FRPs在实时市场的部署情况. 分支(Ⅲ)展示了实时市场以
图4中(b)和 (c)展示了系统灵活性缺失的情况. 当日前市场以
概率
2. 考虑灵活爬坡产品的经济调度模型
2.1. 目标函数
用FRPs在日前市场的接受概率、在实时市场的预期部署概率来模拟系统灵活性预留和实时使用情况,引入灵活性不足惩罚成本,以量化系统灵活性缺失的风险. 基于多时段的确定性机组组合模型,建立考虑储能提供FRPs的日前市场经济调度模型:
式中:
式中:
式中:
对于储能来说,可以利用日前能量市场中不同时段的电价差异,通过充放电来获得收益. 在日前能量市场中的收益为
式中:
当系统的实时爬坡需求大于日前预留的FRPs量时,系统需要额外追加灵活性偏差惩罚成本. 灵活性不足量为
式中:
2.2. 约束条件
1) 功率平衡约束
系统满足的功率平衡约束为
式中:
2) 火电机组约束
火电机组需要满足启停约束和运行约束. 停机状态下的火电机组在启动时需要一定时间,无法实时提供FRPs. 运行状态下的火电机组能够利用其爬坡能力提供FRPs,提供的FRPs量不能大于自身的向上、向下调节能力,其约束主要包括机组出力上下限约束、爬坡约束、灵活爬坡容量约束以及考虑灵活爬坡备用的容量约束:
式中:
3) 储能设备约束
储能设备主要通过预留充放电功率来提供向上和向下灵活性爬坡能力,系统满足的储能约束主要包括储能充放电约束和电量约束:
式中:
4) 灵活爬坡约束与实时市场调用
系统在日前市场需要购买的FRPs由火电机组和储能提供的FRPs共同构成. 在日前市场中,系统需要设置日前市场接受概率,并预留对应容量,在此基础上应该满足
系统预期部署在实时市场的灵活爬坡容量由火电机组和储能提供的FRPs共同构成,在预期部署设想中,其满足
式中:
在实时市场预期部署下,能够调用的FRPs容量不超过日前市场预留容量,此时需要满足以下要求:
在实时市场,系统仍须满足灵活性平衡. 当能够调用的FRPs不满足实时爬坡需求时,灵活性不足的缺额需要以其他惩罚形式进行补偿,系统需要满足
3. 算例分析
3.1. 算例数据
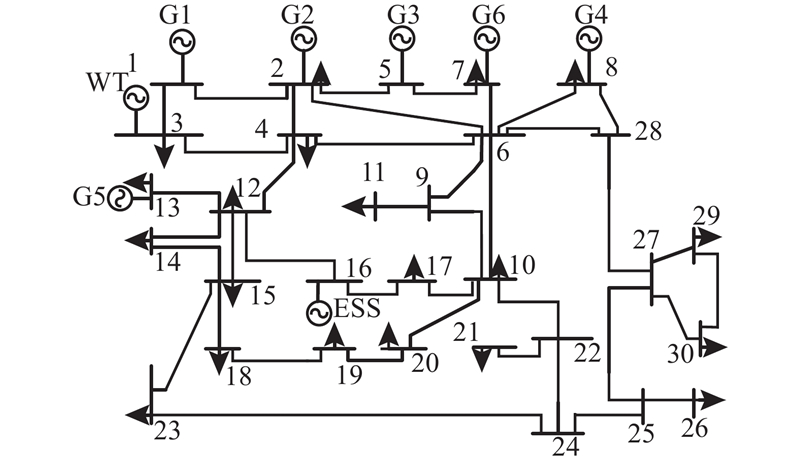
为了验证所建模型的有效性,采用改进的IEEE 30节点系统,参照文献[25],在不考虑网络堵塞的情况下设置6台火电机组和1个风电场,并设置目前常用的磷酸铁锂储能设备,结构详见图5. 其中储能(energy storage system, ESS)参数设定如下:储能功率和能量容量为25 MW和100 MW·h,储能自放电率为0.02,储能充/放电效率为0.95,储能荷电状态上、下限为0.95、0.10,储能初始荷电状态设定为0.5. 火电机组参数见表2. 表中,
图 5
表 2 火电机组参数
Tab.2
| 机组 | MW | MW | (MW·h−1) | ($·MW−1) | |||
| G1 | 200 | 100 | 25 | 16 | 10 | 10 | 10 |
| G2 | 100 | 40 | 30 | 20 | 8 | 8 | 8 |
| G3 | 80 | 40 | 20 | 24 | 6 | 6 | −6 |
| G4 | 40 | 20 | 30 | 26 | 4 | 4 | 4 |
| G5 | 50 | 20 | 20 | 28 | 3 | 3 | 3 |
| G6 | 20 | 10 | 40 | 30 | 1 | 1 | −1 |
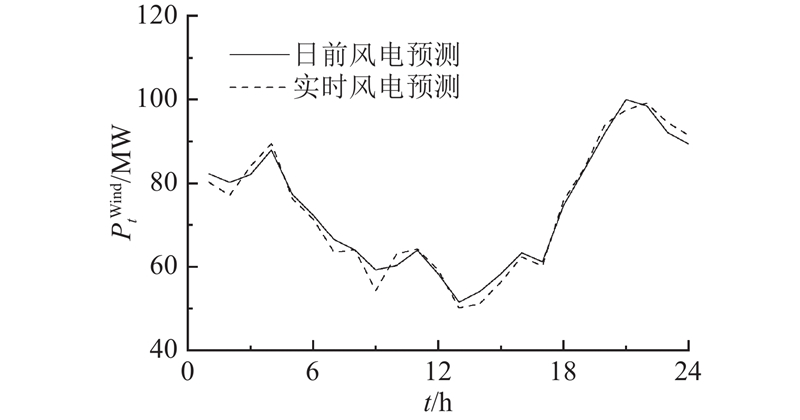
图 6
图 6 日前风电出力和实时风电出力预测结果
Fig.6 Forecast results of day-ahead wind power output and real-time wind power output
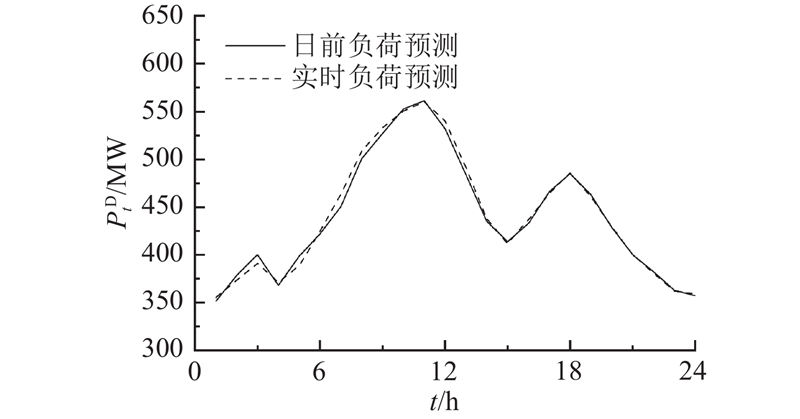
图 7
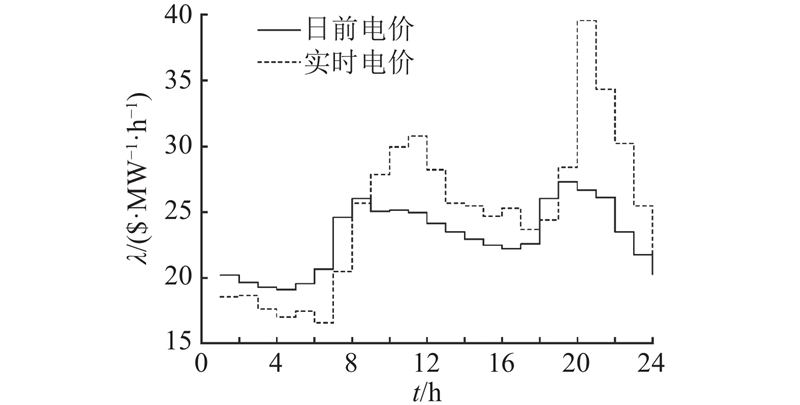
图 8
图 8 日前市场和实时市场电价
Fig.8 Electricity prices in day-ahead market and real-time market
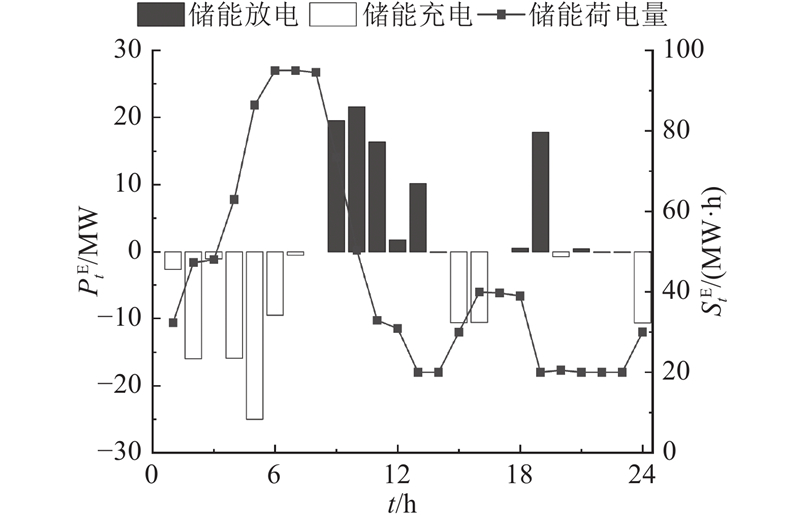
3.2. FRPs和储能对调度结果的影响分析
设计3类场景,并对其进行仿真验算.
场景1:系统仅在日前市场进行经济调度,没有预留FRPs;场景2:只考虑火电机组在日前市场提供FRPs;场景3:考虑火电机组和储能在日前市场共同提供FRPs.3种场景下的系统运行成本如表3所示. 表中,
表 3 不同场景下的系统运行成本对比
Tab.3
| 场景 | ||||
| 1 | 19.41 | 0.00 | 0.00 | 4.57 |
| 2 | 16.04 | 1.25 | 1.78 | 1.79 |
| 3 | 14.56 | 1.41 | 2.54 | 0.45 |
由式(3)可知,在日前市场接受概率和实时市场预期部署概率固定的前提下,提供FRPs的机会收益和FRPs价格阈值成正比. 以8 $/(MW·h)的FRPs价格为例,随着负荷高峰期系统边际成本增加,低价火电机组预留爬坡容量的成本大于设定的价格阈值,不倾向于预留FRPs,此时场景3比场景2能够提供更多容量的FRPs.
在系统总运行成本方面,场景1中因为日前市场未预留FRPs,所以没有FRPs风险偏差成本和机会收益,在实时市场产生较大的灵活性偏差,其惩罚成本占比很高,约占总成本的24%. 场景2考虑火电机组参与FRPs,系统通过火电机组提供日前市场所需的FRPs量,从而满足实时市场的FRPs需求,因此相较于场景1,场景2的灵活性偏差惩罚成本大幅减少,约为场景1的39%. 但是系统不能通过火电机组提供所有市场所需的FRPs量,因此仍然有一定的灵活性偏差惩罚成本. 场景3中储能和火电共同提供FRPs,能够在日前市场提供更多的FRPs. 尽管产生的风险偏差成本较场景2略有上涨,但是FRPs带来的机会收益更大,同时使得灵活性偏差惩罚大大下降,约为场景2的25%,说明当火电机组和储能共同提供FRPs时,能够减少系统因灵活性不足所造成的损失,从而更好地保障系统的实时灵活性,也能够有效降低系统总成本. 此外,当FRPs参与市场时,其风险偏差成本和机会收益是相互对立的;伴随着预留FRPs容量的提升,其机会收益和风险偏差成本均会提高,但是通过合理的调度决策可以使机会收益大于风险偏差成本.
图 9
图 10
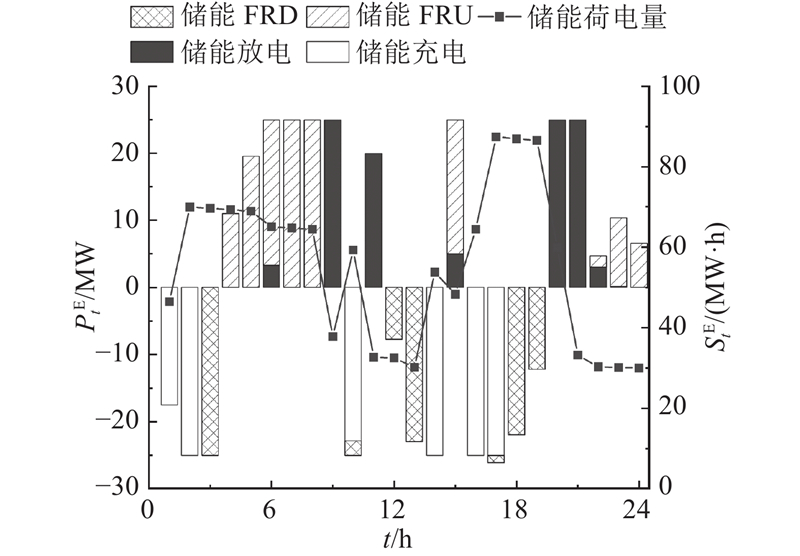
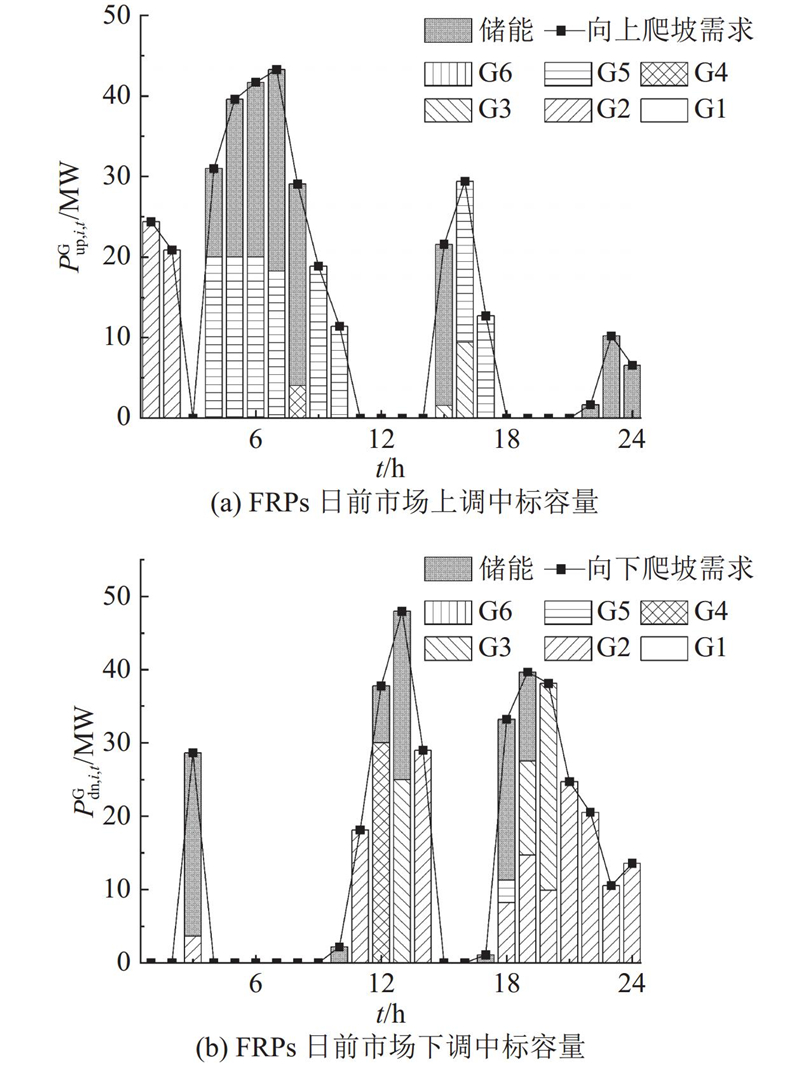
以场景3为例,图11中(a)和 (b)展示了日前市场中标的FRPs上调和下调容量. 可以看出,机组G1不参与FRPs预留,这是因为在大部分时刻G1因预留FRPs损失的机会成本大于设定的FRPs阈值8 $/(MW·h). 而储能在上调和下调FRPs中分别占比41.1%和26.1%,说明储能更倾向于提供向上灵活性,这是因为提供向上FRPs可以使储能在实时市场中也有概率获得一定收益. 不同于场景1和场景2,场景3中的储能收益不仅仅是电能量市场的能量收益,也有部分收益为FRPs的机会收益. 在该算例中,储能通过预留FRPs获得的机会收益成为储能的主要收益来源,这丰富了储能的收益方式.
图 11
图 11 FRPs在日前市场的上调和下调中标容量
Fig.11 Upward and downward awarded quantities of FRPs in day-ahead market
3.3. 日前市场接受概率灵敏度分析
以场景3为例,假设实时市场的预期部署概率取中位数0.5,日前市场FRPs接受概率反映了市场主体预留FRPs的意愿,会影响灵活性偏差惩罚成本、FRPs收益以及风险成本,对储能决策也会产生一定影响. 表4展示了日前市场接受概率和FRPs中标容量之间的关系. 其中,
表 4 日前市场接受概率与容量之间的关系
Tab.4
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.1 | 33.5 | 46.5 | 11.6 | 0.0 | 45.1 | 46.5 |
| 0.2 | 65.6 | 93.1 | 24.7 | 0.0 | 90.3 | 93.1 |
| 0.3 | 99.0 | 125.6 | 36.2 | 12.2 | 135.2 | 138.2 |
| 0.4 | 130.5 | 151.0 | 50.6 | 35.0 | 181.1 | 186.0 |
| 0.5 | 154.1 | 176.9 | 71.5 | 55.8 | 225.6 | 232.8 |
| 0.6 | 179.2 | 213.8 | 90.1 | 65.4 | 270.1 | 279.2 |
| 0.7 | 195.7 | 244.6 | 120.1 | 82.2 | 315.8 | 325.8 |
| 0.8 | 202.1 | 264.5 | 158.0 | 107.8 | 360.1 | 372.3 |
| 0.9 | 197.6 | 264.5 | 208.4 | 154.4 | 406.0 | 418.9 |
| 1.0 | 184.5 | 264.5 | 266.7 | 200.5 | 451.2 | 465.0 |
随着日前市场接受概率增大,系统预留的上调和下调灵活爬坡容量增加. 以火电机组为例,场景3中提供的向下灵活调节产品最多为264.5MW,无法满足系统下调灵活爬坡需求,此时储能的介入弥补了灵活性预留的不足. 相比而言,储能更倾向于参与向上灵活调节产品的预留,这是因为0.5的实时市场部署概率会给向上灵活调节产品带来一定的收益.
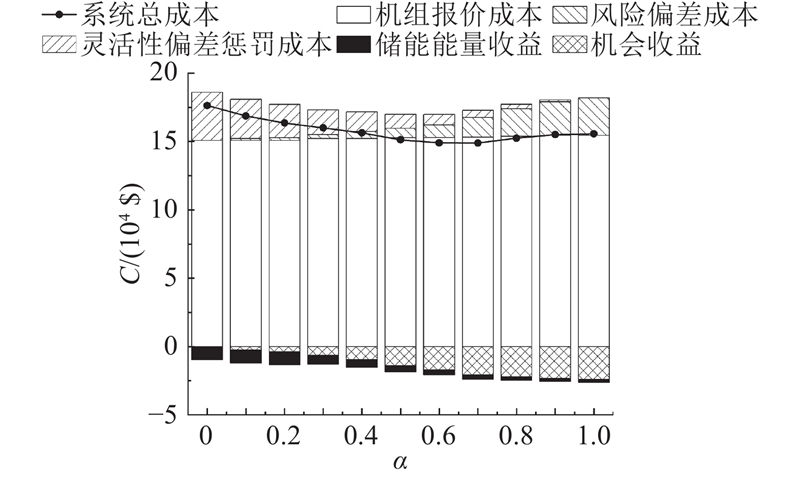
由图12可知,随着日前市场接受概率的提高,通过预留FRPs带来的机会收益增加. 这是由于FRPs收益是各机组因提供灵活爬坡产品容量而不参加电能量市场所损失的机会成本的补偿,无论在实时市场中是否调用,机组都将获得收益. 一方面,随着日前市场接受概率提高,系统需要预留的FRPs容量增大,此时,需要储能在部分时段中提供FRPs,才能弥补需求缺额. 另一方面,日前市场接受概率的提高使得FRPs被部署到实时市场的可能性增大,导致系统灵活性偏差惩罚成本降低,但是与此同时,过度部署造成的风险偏差成本迅速增加.
图 12
图 12 日前市场接受概率对成本的影响
Fig.12 Impact of acceptance probability of day-ahead market on costs
结合表4分析,储能通过能量市场获取的利润很低,因此通过预留FRPs获取机会收益. 市场主体预留的FRPs容量越大,灵活性偏差惩罚成本越小,使得系统总运行成本下降;但是当接受概率超过0.7时,FRPs部署的风险偏差成本大于机会收益,运行成本将上升. 如何在实时市场部署概率确定的前提下保障最优预留量已成为灵活爬坡服务市场的研究重点.
3.4. 实时市场预期部署概率灵敏度分析
以场景3为例,假设固定日前市场接受概率为0.75,此时系统总成本接近于最低值. 在实时市场中,系统预留的FRPs无法完全应对系统爬坡,此时实时市场预期部署概率将会对机组的机会收益、风险偏差成本和灵活性不足补偿成本产生影响.
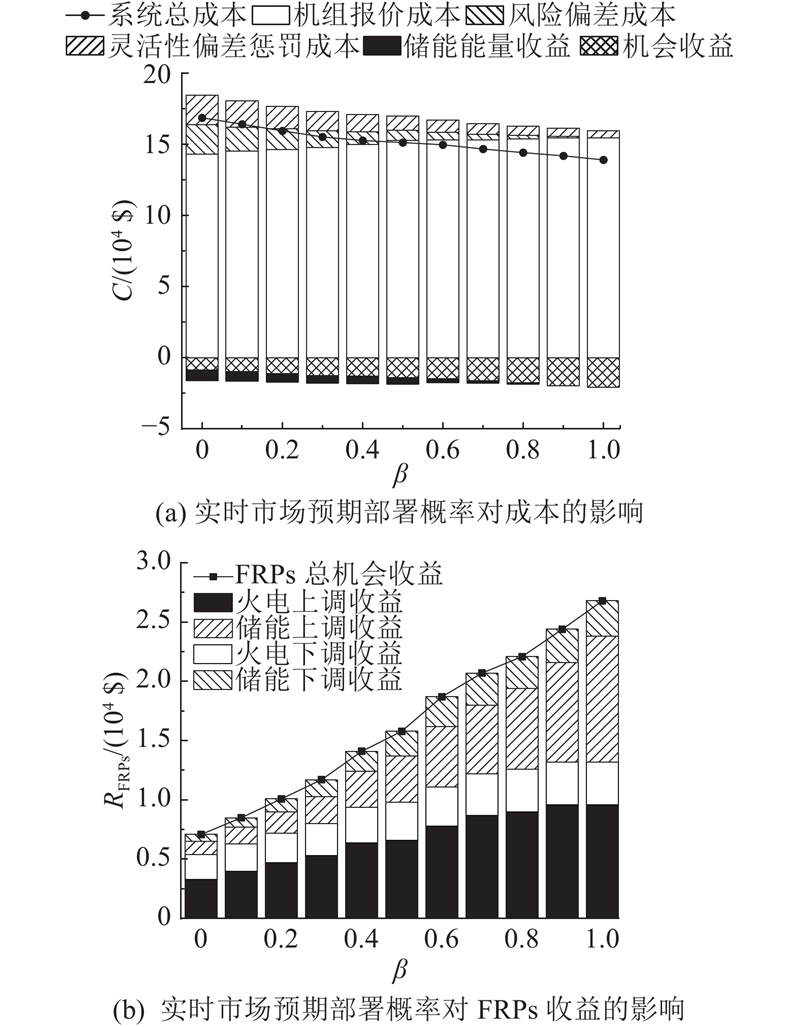
如图13(a)所示,随着实时市场预期部署概率的提高,系统总成本将逐渐减小. 一方面,这是由于实时预期部署概率的提高使得日前市场保留的FRPs被部署到实时市场的可能性更大,系统风险偏差成本显著下降. 另一方面,日前市场预留的FRPs将通过实时市场部署给系统带来更高的机会收益,但是与此同时,灵活性偏差惩罚成本并未降至0,这是因为日前市场接受概率为0.75的FRPs在实时市场中仍然存在缺额,系统需要对短缺的灵活性偏差做出惩罚. 本质上,FRPs作为新型辅助服务产品,其在实时市场部署概率越高,能获取的收益越多. 实时市场部署概率每增加0.1,可以减少约2%的系统总成本.
图 13
图 13 实时市场预期部署概率对成本和收益的影响
Fig.13 Impact of expected deployment probability in real-time market on costs and revenues
当实时市场不调用FRPs时,系统风险偏差成本最高,此时FRPs仅能够通过日前市场预期部署带来收益. 随着实时市场预期部署概率的提高,部署FRPs带来的实时上调收益显著增加,储能和火电提供上调FRPs的收益约为提供下调FRPs的收益的3~4倍,如图13(b)所示. 值得一提的是,当部署概率提高,系统更倾向于在日前市场利用储能预留上调FRPs. 参与日前电能量市场不再是储能的主要收益来源,储能的电能量收益将从0.21万美元减少到0.12万美元,而储能预留FRPs带来的收益从0.17万美元增加到1.37万美元.
4. 结 语
对能量-灵活爬坡联合市场中利用储能和火电机组提供FRPs的过程进行研究,分析日前市场的FRPs预留和实时市场的FRPs调用决策对系统偏差成本、机会收益和灵活性偏差惩罚成本的影响. 基于日前市场接受概率和实时市场预期部署概率,提出了考虑储能参与灵活爬坡的日前市场经济调度模型. 通过算例仿真和因素分析验证了所提模型的有效性,并得到了以下结论:
(1)日前市场中FRPs中标容量与系统设置的爬坡价格阈值以及各类灵活性资源能提供的上调、下调能力有关. 日前市场对FRPs的接受概率越高,其风险偏差成本和机会收益越高,灵活性偏差惩罚成本越低,系统总成本则先减小后增加. 实时市场预期部署概率越高,机会收益越高,系统风险偏差成本和灵活性偏差惩罚成本越低,系统总成本越低.
(2)当储能参与能量-灵活爬坡联合市场时,虽然会略微增加风险偏差成本,但能够带来更多的机会收益并减少系统灵活性偏差惩罚成本,从而降低系统总成本. 储能通过能量市场获得的收益很少,随着日前市场接受概率和实时市场部署概率的提高,储能更倾向于通过提供FRPs来获取收益,且更倾向于预留上调灵活性,以便于在实时市场中获取更高的机会收益.
本研究并未考虑火电机组参与灵活爬坡市场的报价策略,不同报价策略对日前市场接受概率和实时市场预期部署概率的影响将是下一步的研究重点.
参考文献
高比例可再生能源并网的电力系统灵活性评价与平衡机理
[J].
Flexibility evaluation and supply/demand balance principle of power system with high-penetration renewable electricity
[J].
基于两阶段随机优化建模的新能源电网灵活性资源边际成本构成的机理分析
[J].
Mechanism analysis of flexible resources’ marginal price in new energy grid based on two-stage stochastic optimization modeling
[J].
Enhancing power systems operational flexibility with ramp products from flexible resources
[J].DOI:10.1016/j.jpgr.2021.107599 [本文引用: 1]
面向新型电力系统灵活性提升的国内外辅助服务市场研究综述
[J].
A review of domestic and foreign ancillary services market for improving flexibility of new power system
[J].
Enhanced flexible ramping product formulation for alleviating capacity shortage in look-ahead commitment
[J].DOI:10.35833/MPCE.2020.000942 [本文引用: 1]
高比例新能源接入下电网灵活性爬坡能力市场化获取机制现状分析及思考
[J].
Status analysis and thoughts of market-oriented acquisition mechanism on flexible ramp capability for power grid with high proportion of renewable energy
[J].
Optimal scheduling of flexible ramp product and emerging flexible resources considering short-term variability impacts in power system with high RESs penetration: a novel robust UC approach
[J].DOI:10.1016/j.ijepes.2022.108279 [本文引用: 1]
Enhancing electricity market flexibility by deploying ancillary services for flexible ramping product procurement
[J].DOI:10.1016/j.jpgr.2020.106878 [本文引用: 2]
基于分布鲁棒优化的灵活爬坡备用调度方法
[J].
Distributionally robust optimization based dispatch methodology of flexible ramping products
[J].
Local energy and planned ramping product joint market based on a distributed optimization method
[J].
Provision of flexible ramping product by battery energy storage in day-ahead energy and reserve markets
[J].DOI:10.1049/iet-gtd.2017.1522 [本文引用: 3]
计及灵活爬坡的气-电耦合综合能源系统低碳经济调度研究
[J].
Low carbon economic scheduling of gas-electric coupling integrated energy system considering flexible ramping products
[J].
电力市场中的灵活调节服务: 基本概念、均衡模型与研究方向
[J].
Flexible ramping product in electricity markets: basic concept, equilibrium model and research prospect
[J].
Day-ahead operational scheduling with enhanced flexible ramping product: design and analysis
[J].DOI:10.1109/TPWRS.2021.3110712 [本文引用: 1]
An integrated scheduling approach to underpin flexibility in European power systems
[J].DOI:10.1109/TSTE.2015.2497081 [本文引用: 1]
Portfolio management for a wind-storage system based on distributionally robust optimisation considering a flexible ramping product
[J].DOI:10.1049/iet-rpg.2019.0964 [本文引用: 1]
考虑灵活爬坡产品的能源枢纽低碳经济调度
[J].
Low-carbon economic dispatching of energy hub considering flexible ramping product
[J].
电力系统灵活调节服务与市场机制研究综述
[J].
A review of power system flexible ramping product and market mechanism
[J].
考虑火电调峰主动性与需求响应的含储能电力系统优化调度
[J].
Optimal dispatch of power system with energy storage considering deep peak regulation initiative of thermal power and demand response
[J].