随着全站仪、电子测距仪、激光测距仪、微波测距装置等先进测绘技术的迅速发展,传统的测量方法被逐步取代. 先进测量设备显著提升了测量精度,但测量结果对大气环境参数波动的敏感性增加. 如何实现高精度的大气折射率修正是测距装置进行检定校准的关键因素[1].
野外环境获取大气折射率主要依赖大气环境参数测量法,该方法原理简单,精度可达10−8[2],理论上能够满足大部分测量装置的校准精度要求. 由于野外环境的大气参数抖动、参数分布不均匀性及大气参数处理算法不足,该方法在实际应用中的长距离测量不确定度很难达到10−7[3]. 传统的大气折射率补偿方法为两点法[4],即在检测环境两端分别架设环境参数检定装置. 一般情况下,两点法在短距离测距校准时能够满足需求,但随着距离的增加,两点法的测量结果不足以代表该距离段内的平均温度. 为了监测环境场的局部梯度,德国联邦物理技术研究所PTB[5]采用多点法布置60个Pt-100温度传感器以确保环境参数的高采样密度. 该方法距离测量的不确定度为8.2×10−7,误差修正结果较两点法优越. 陈杨等[6]提出基于传感器阵列的环境参数自动测量系统,采用等效面积法处理传感器阵列采集的数据,距离测量不确定度优于3.0×10−7. 刘学德等[7]对1.2 km自动测量系统进行改进升级,在沿线附近布置82个传感器并采用分组并行采集传感器数据的改进方案,大幅降低了传感器采样周期,控制折射率修正误差不超过5×10−8. 谷友艺等[8]提出基于多点法的分段线性插值融合径向基神经网络方法,在保证精度的前提下,提升了温度场曲线整体平滑性和曲率渐变性,比分段线性插值法更符合实际环境参数变化情况.
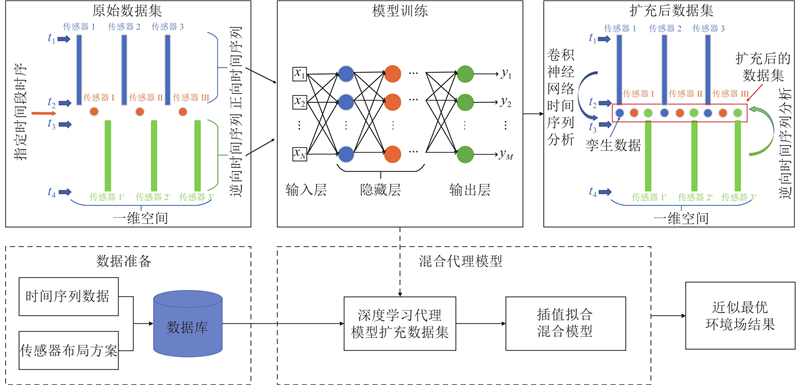
综上所述,提高物理场测量精度比较简单的方法是增加传感器阵列的密集程度. 野外测量地形影响、高精度传感器和辅助测量设备的成本限制,降低了通过提高传感器精度或数量来提升环境参数测量精度的可行性. 深度学习技术在时序预测、序列分类及信号处理等时间序列分析领域展现出强大的能力[9-11]. 在测量系统进行大气折射率修正时,本研究将传感器在指定时间段的前后时间段置于其他点位,将前后时间段的时间序列预测得出的孪生数据扩充至修正时间段,以扩充传感器阵列观测点位. 这种经深度学习改进的传感器布局模型能够充分利用有限的传感器资源,降低长距离测量时大气折射率补偿的不确定度. 针对当前高精度测量装置的大气环境参数校准模型的需求与现有方法的缺陷,本研究在扩充传感器阵列的基础上,提出径向基插值融合多项式拟合的混合代理模型,结合2种模型的优势并加入正则化分析. 所提模型能够避免函数拟合时的龙格现象和过拟合现象,使环境场的可解释性增强,较好地应用于高精度测量装置的大气折射修正领域.
1. 融合深度学习的高精度物理场拟合模型
基于深度学习的高精度物理场拟合方法充分发挥了深度学习的优势,在使用正逆向时间序列分析的基础上,扩充一维环境场上的传感器阵列,使物理场拟合时的观测点位更为密集;径向基插值融合多项式拟合的混合代理模型在拟合前加入径向基插值处理,增强物理场拟合前的平滑性,避免发生龙格现象;将正则化加入混合代理模型的多项式迭代损失函数中进行最优化处理,选定最佳多项式拟合次数.
1.1. 卷积神经网络扩充传感器阵列
1.1.1. 正向时间序列扩充传感器阵列
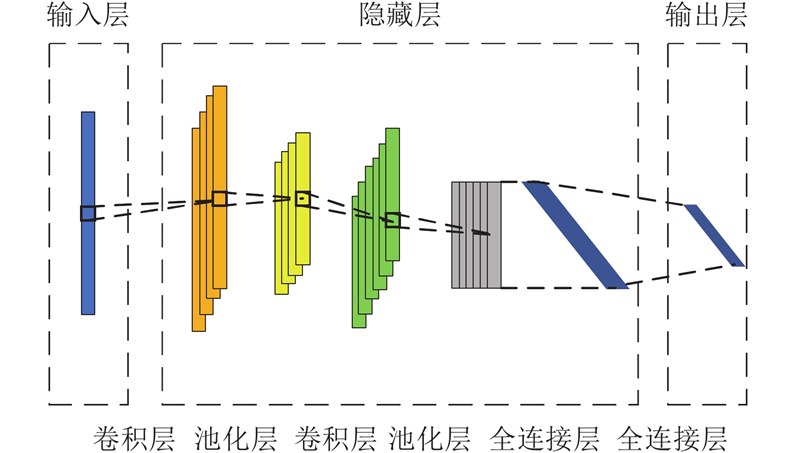
图 1
图 1 典型一维卷积神经网络架构图
Fig.1 Architecture diagram of typical 1D convolutional neural network
式中:
式中:
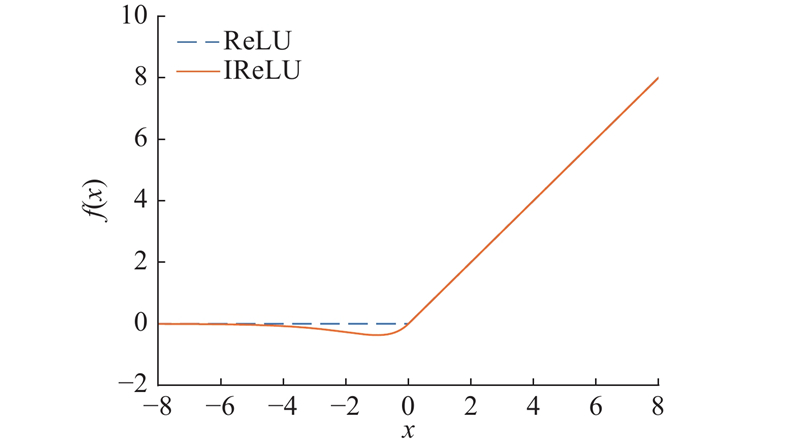
如图2所示,IReLU激活函数在负半轴引入指数增长,使负半轴上的非线性剧烈,有利于捕捉数据中的复杂结构,避免一些情况下的梯度消失问题.
图 2
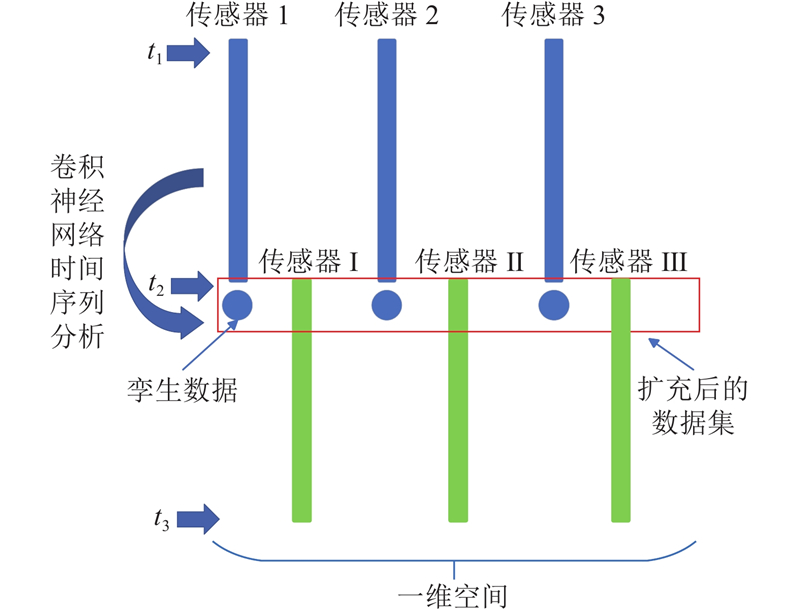
池化层主要用于减小特征向量的空间维度并降低计算量. 常见的池化操作有最大池化和平均池化,最大池化选择每个池化窗口中的最大值作为输出,有助于提取时间序列中的主要特性. 本研究采用最大池化法,以保留特征向量中最显著的特征. 结合改进后的一维卷积神经网络,基于深度学习正向时间序列扩充一维空间环境传感器阵列的方法如图3所示. 以三点传感器阵列为例,通过标注传感器1~3的点位,使传感器点位在一维空间中均匀分布,并实时测量
图 3
图 3 基于深度学习的扩充传感器阵列模型
Fig.3 Model for expanding sensor array based on deep learning
1.1.2. 逆向时间序列扩充传感器阵列
提出基于逆向时间序列扩充传感器阵列的方法,通过逆向时间序列分析进一步扩充传感器观测点位. 一组离散时间序列:
式中:
式中:
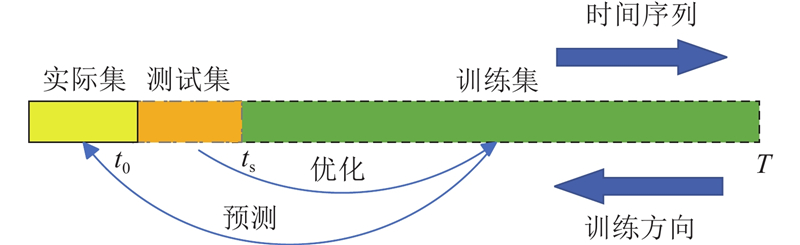
图 4
为了获得较好的训练模型,将均方根误差RMSE作为评估指标,测试集中预测值与实际值之间的偏差:
式中:
算法1 逆向时间序列划分算法
输入:正向时间序列
1. 初始化划分时间
2. 对时间序列进行逆向处理
3.
4.
5. 设置滑动窗口
6.
7.
输出:逆向时间序列的训练集和测试集
经过对时间序列的逆向处理及划分,逆向时间序列转化为正向时间序列. 如图5所示为改进后的正逆向时间序列扩充传感器阵列的整体模型. 模型在仅考虑正向时间序列扩充传感器阵列的基础上,于
图 5
图 5 基于正逆向时间序列扩充传感器阵列的模型
Fig.5 Model of expanding sensor array based on forward and backward time series
1.2. 融合径向基函数插值的多项式物理场拟合优化
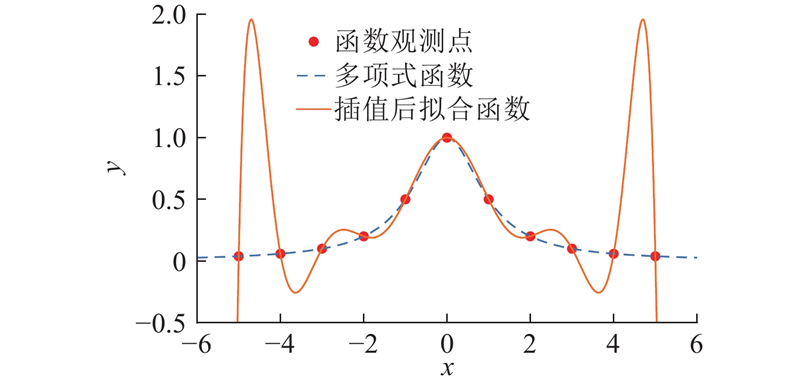
一般而言,多项式拟合时次数越高,对未知区域预测越准确. 在实际应用中,使用高次多项式预测时,拟合函数两端附近有时会出现剧烈的振荡,导致较大的误差,这种现象被称为龙格现象[17](Runge phenomenon).
对式(9)进行多项式拟合,若拟合次数过高,会出现如图6所示的龙格现象. 为了提高物理场拟合的精度,本研究在拟合函数之前引入插值以实现平滑处理. 插值是常用的数值分析方法,广泛应用于计算机图形学、地理信息系统(geographic information system,GIS)、信号处理等领域[18-20]. 传统的插值方法包括多项式插值、拉格朗日插值、最小二乘法插值等. 本研究的应用场景要求高精度的插值,即使插值过程中产生的极小偏差也可能导致拟合的环境场与实际情况存在显著差异,为此提出融合径向基插值与多项式拟合的多物理场拟合方法. 采用径向基插值作为函数拟合前的数据处理模型,径向基函数表达式为
图 6
式中:
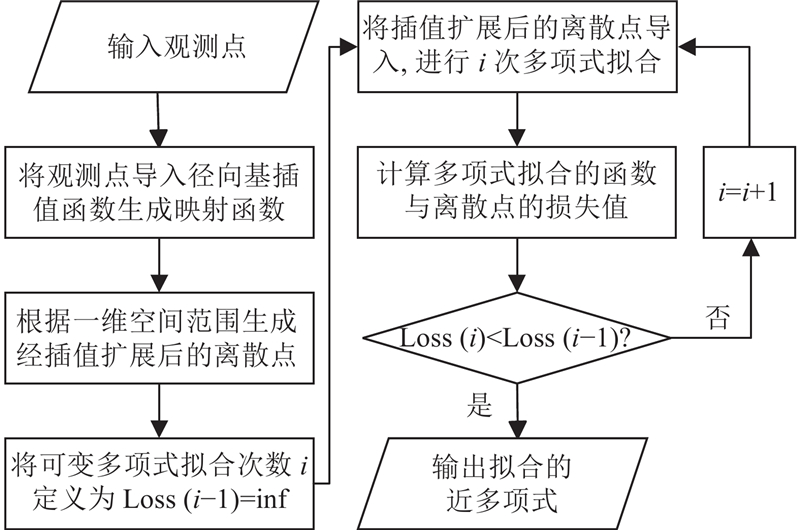
1.3. 物理场拟合时的最优化
一般而言,在径向基插值融合多项式拟合的多物理场拟合方法中,多项式次数越大,拟合函数与插值后的物理场趋势越接近,对实际物理场的模拟也更精确. 然而,随着多项式次数进一步增加,模型对训练数据的拟合程度会提高,导致过拟合现象出现,即模型对于噪声或随机变化过度敏感,对新数据失去泛化能力. 过拟合对多项式拟合产生的主要负面影响如下:1)不稳定性. 多项式阶数过高时,会扩大噪声对拟合的影响,使拟合出的多项式不具可靠性. 2)解释性差. 高次项几乎没有实际意义,随着拟合阶数的增加,当拟合次数为30时,甚至会产生量级为10−50的多项式系数,这些高阶特征对目标变量的预测贡献极小,使得解释模型结果更加困难. 3)浪费计算资源. 多项式反复迭代优化会增加模型性能的计算负担,在高次多项式拟合中,由于参数数量增加,优化算法可能需要更长时间才能收敛到最优解,增加了训练模型的时间成本.
考虑高阶多项式中的过拟合问题,结合神经网络中的正则化方法进行优化处理:
式中:
式中:
图 7
图 7 融合径向基函数插值与多项式拟合的算法框架
Fig.7 Algorithm framework for combination of radial basis function interpolation and polynomial fitting
2. 仿真环境搭建与实验分析
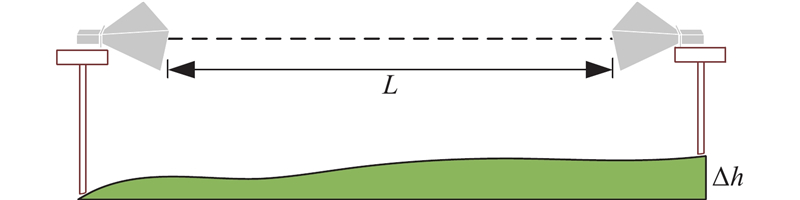
电磁波测距精度受大气折射率的影响,温度、湿度、气压等因素显著影响大气折射率,从而严重影响测量装置的测距精度. 进行测距结果折射率修正,需要高精度的温度、湿度和气压场数据,本研究提出基于深度学习扩展传感器阵列构建物理场的方法. 以温度场的构建为例,介绍如何根据应用环境建立仿真环境. 建立如图8所示的测距环境仿真模型. 为了满足远距离测量需求,选取仿真时测距的间距
图 8
式中:
2.1. 扩充传感器阵列前后的对比分析
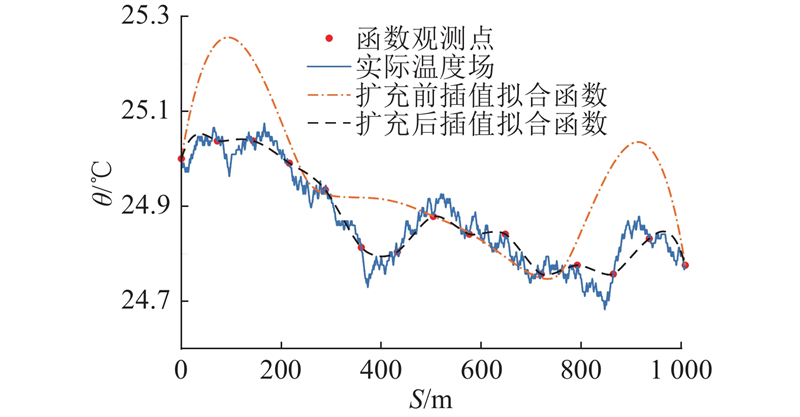
采用基于深度学习扩展传感器阵列的方法对比分析2种情况下的仿真实验结果. 如图9所示为直接使用现有5个传感器阵列和通过深度学习扩充传感器阵列扩充至15个观测点后进行物理场拟合的仿真结果,其中
图 9
图 9 扩充传感器阵列的仿真对比图
Fig.9 Simulation comparision chart of expanding sensor array
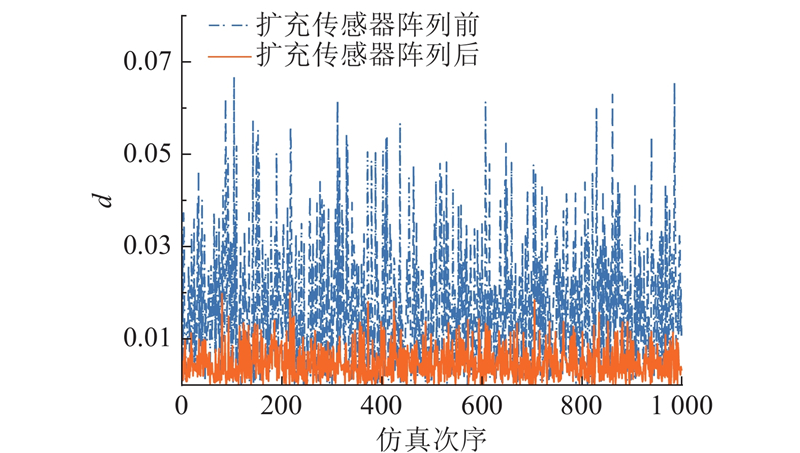
为了验证扩充传感器阵列的普适性,采用蒙特卡洛法模拟1 000组随机温度场,对所有模拟情况进行仿真分析. 以平均温度偏差为参考量,如图10所示为扩充传感器阵列前后各组仿真温度偏差d. 可以看出,扩充传感器阵列后的平均温度更为稳定可靠.
图 10
图 10 扩充传感器阵列前后的平均温度偏差对比
Fig.10 Comparison of average temperature deviation before and after expanding sensor array
2.2. 插值方法对比分析
为了避免龙格现象并证明插值的必要性,基于正逆向时间序列扩充传感器阵列的物理场拟合方法,利用扩充后的15个传感器阵列进行多项式拟合. 由于宏观环境因素的影响,仿真时温度变化缓慢. 为了使实验结果更直观,采用均方根误差的对数形式表述拟合情况:
多次仿真实验得到不同多项式次数的温度场拟合结果对数均方根误差情况如表1所示. 理论上,多项式次数越大,误差越小,但由表可知,在多项式次数较高时,函数发生过拟合. 当多项式次数
表 1 不同多项式次数拟合的对数均方根误差
Tab.1
| d | log (RMSE) | d | log (RMSE) | |
| 5 | −3.04 | 11 | −3.18 | |
| 7 | −3.41 | 13 | −1.39 | |
| 9 | −3.47 | — | — |
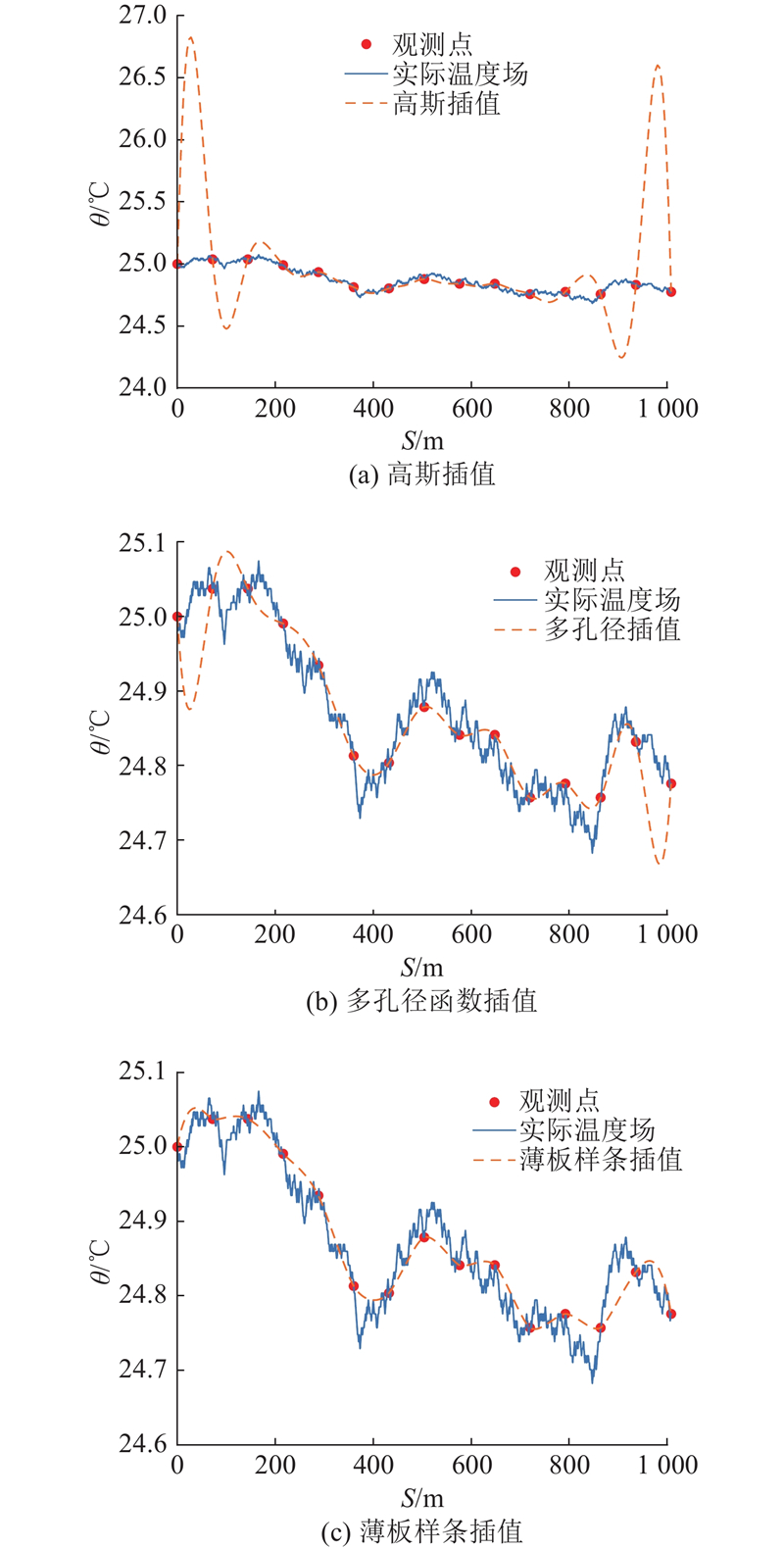
插值后物理场的观测点变得密集,进一步分析不同径向基插值函数的优劣,以确认最佳的径向基插值函数. 在径向基插值中,有多种具有良好平滑性的插值方法. 为了筛选出适用于本研究应用环境的插值方法,以高斯径向基插值、多孔径函数径向基插值和薄板样条径向基插值为例,在保证插值点数相同的情况下进行仿真实验分析,3种方法拟合出的温度场离散点偏差的对数均方根误差分别为−0.70、−0.306和−3.54,拟合结果如图11所示. 高斯插值出现明显的振荡现象,表明高斯插值不适用于高精度物理场拟合;多孔径插值方法比高斯插值的效果好,但在物理场两侧预测效果仍不理想;相比之下薄板样条插值的对数均方根误差小,拟合趋势表现最佳,且优于仅通过多项式拟合函数的情况. 该结果证明了多项式拟合融合径向基插值理论的优越性,本研究最终选择薄板样条插值作为拟合函数前的预处理函数.
图 11
2.3. 物理场拟合的正则化分析
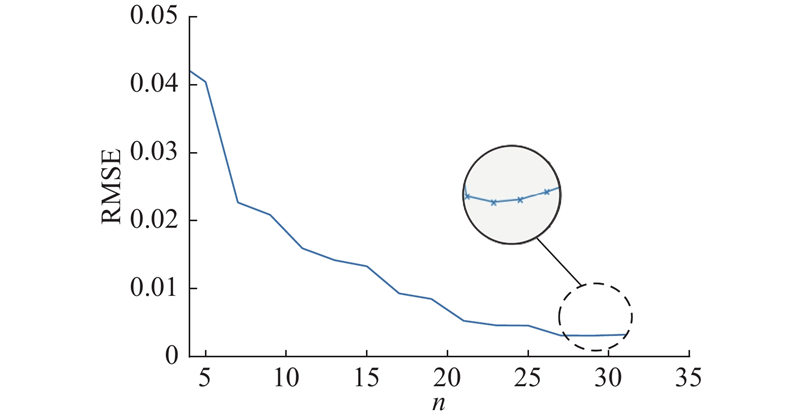
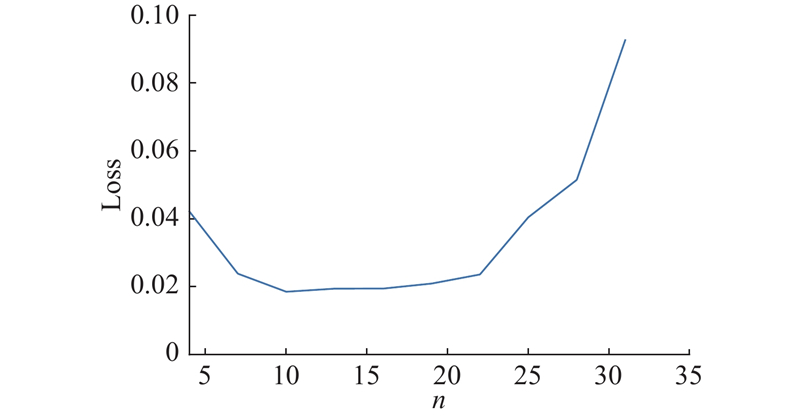
针对本研究提出的拟合方法,随着多项式次数的增加,函数拟合情况更接近插值后的物理场变化趋势. 多项式次数超过最优阶数后,拟合函数在采样点外的区域震荡剧烈,此时判定为过拟合. 为了避免过拟合现象的发生,引入损失函数对拟合情况进行评估. 如图12所示为均方根误差作为损失函数的情况. 当多项式次数较高时,函数的偏差几乎不变,甚至出现过拟合现象,继续增加多项式阶数不仅会降低函数的解释性,还可能导致拟合情况不佳. 如图13所示,使用自适应正则化方法对模型进行惩罚. 图中,损失函数极小值为1.85×10−2,对应的函数阶次为10. 加入正则化后误差呈现先下降后上升的趋势,表明多项式拟合阶数小会导致欠拟合,阶数大会导致过拟合. 该结果表明,所提拟合方法既提高了拟合精度,又避免了龙格现象和过拟合现象发生,是优良的拟合方法.
图 12
图 12 多项式拟合时的损失函数(以均方根误差为损失函数)
Fig.12 Loss function during polynomial fitting (root mean square error as loss function)
图 13
如图14所示,去除部分插值点后,在函数两端未知区域进行仿真,以评估自适应正则化在消除函数过拟合方面的效果. 由图可知,在未加入正则化优化的情况下,多项式次数很高时(
图 14
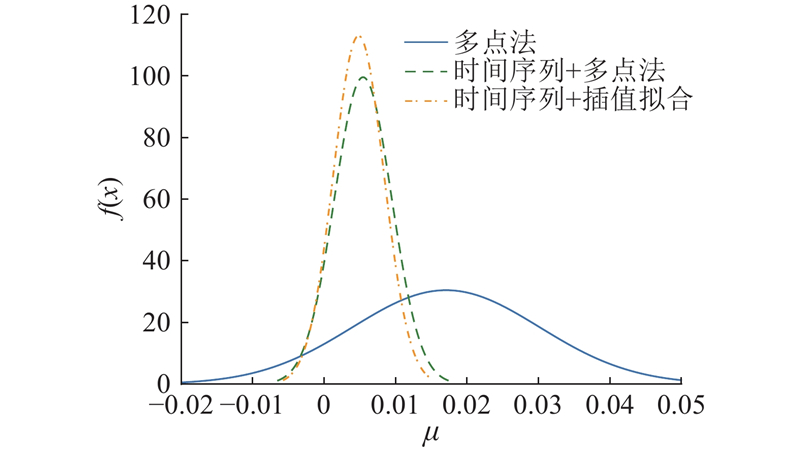
如图15所示为依据中心极限定理改进前后3种方法平均温度偏差的正态分布情况. 图中,
图 15
图 15 蒙特卡洛法仿真的正态分布分析
Fig.15 Normal distribution analysis of Monte Carlo simulation
表 2 正态分布的均值及标准差
Tab.2
| 方法 | ||
| 多点法 | ||
| 时间序列+多点法 | ||
| 时间序列+插值拟合 |
一系列仿真实验证实了基于深度学习扩展传感器阵列并融合插值拟合模型混合的方法能够较好地应用于高精度物理场仿真,有效辅助高精度测量装置在大气折射误差修正中的应用.
3. 实测平台搭建与实验验证
进一步验证基于深度学习的高精度物理场拟合模型的优越性,通过现有的传感器阵列系统进行大气参数的获取实验,结合课题组参考星间通信技术研发的某微波测距系统进行测距实验验证[21].
3.1. 大气参数拟合对比实验
利用如图16所示的传感器补偿系统进行高精度大气环境参数获取实验. 实验在某室内测绘中心进行,室内环境的温度、湿度、气压等大气参数变化趋势稳定,传感器的精度高.
图 16
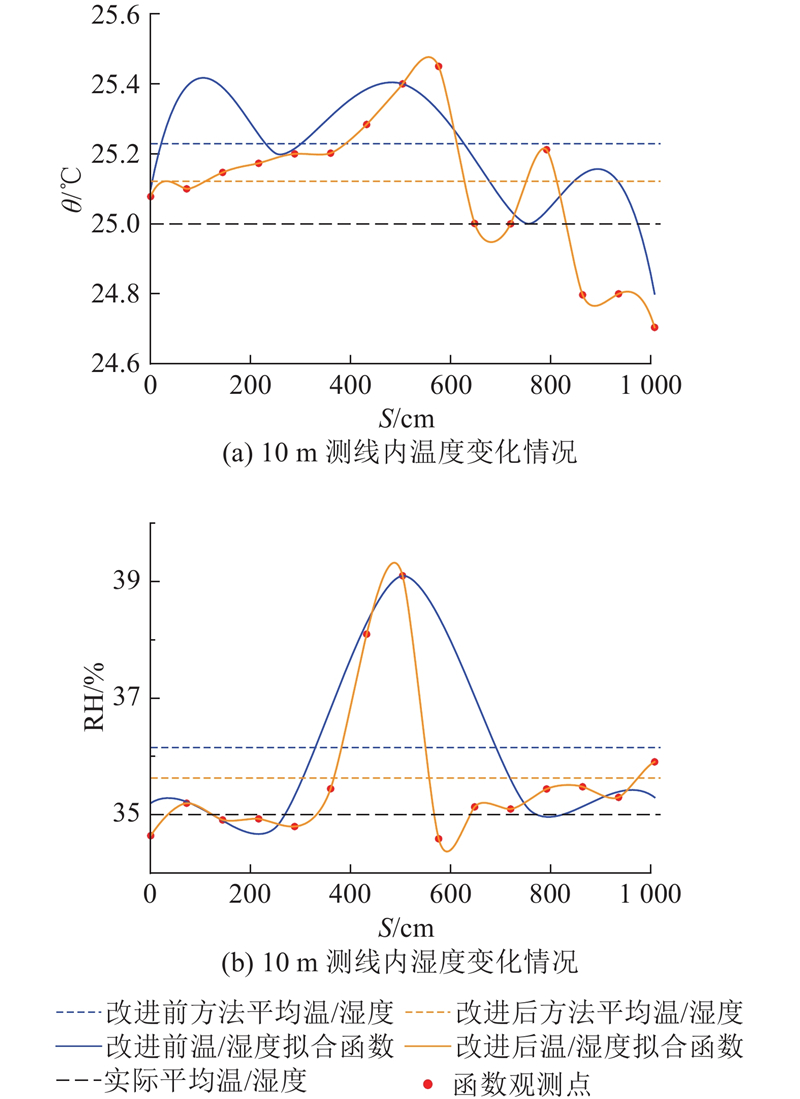
以测距距离10 m的情况为例,对比分析改进前后方法得出的测线内温度、湿度情况,测线场内的实际平均温度、相对湿度分别为25.00 ℃、35.00%. 改进前方法得出的平均温度、相对湿度分别为25.23 ℃、36.15%,改进后方法得出的平均温度、相对湿度分别为25.12 ℃、35.63%. 运用改进后的方法后,平均温度的精度提高了47.8%,平均湿度的精度提高了45.2%.
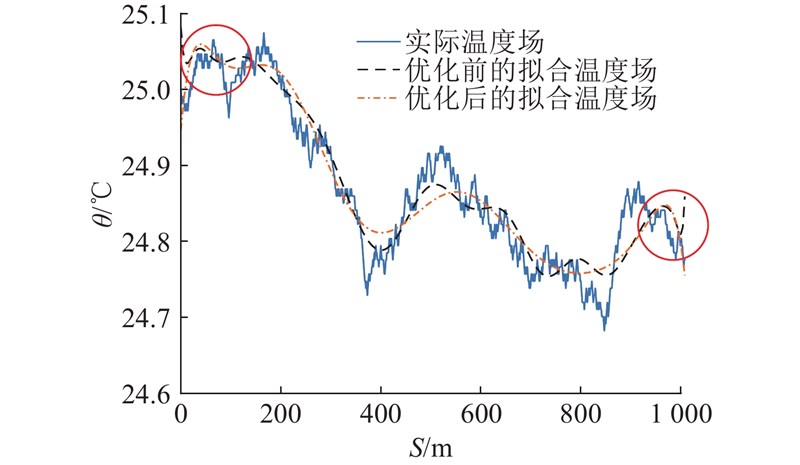
如图17所示为不同测线内的温度、相对湿度的变化情况,其中改进前后方法得出的测线内平均温度、相对湿度情况以虚线形式展示,实际平均温度、相对湿度值由更高精度的传感器数据得出. 可以看出,运用基于深度学习的物理场混合代理拟合模型得出的平均温度、相对湿度情况更接近实际情况. 受限于实验设备和实验条件的影响,实测中难以像仿真实验一样重复多组实验进行验证,并且实测中某些传感器测点数据难免出现异常波动现象,这会对实验的结果产生影响.
图 17
图 17 测线内的温湿度变化监测结果
Fig.17 Monitoring results of temperature and humidity variations in measurement line
3.2. 测距实验验证
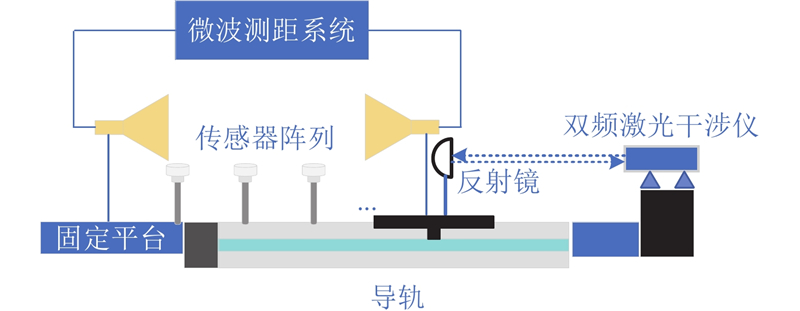
设计测距实验,室内测试整体实验平台如图18所示,由微波测距系统、精密可移动导轨及高精度双频激光测距仪组成. 平台上布设高精度传感器,利用纳米级双频激光干涉仪对大气折射修正效果进行检验. 真实距离
图 18
式中:
表 3 修正前后的测距偏差
Tab.3
| 10 | 2.98 | 6.54 |
| 20 | 5.99 | 6.83 |
| 30 | 8.93 | 8.53 |
| 40 | 11.88 | 7.02 |
| 50 | 14.87 | 11.62 |
4. 结 论
(1)相比传统测距测量大气折射率中常用的多点法,基于深度学习的正逆向时间序列扩充传感器阵列的方法将传感器观测点位扩充至原来的3倍. 改进后的深度学习融合插值拟合的代理模型显著提升了环境参数的测量精度. 以大气环境参数中的温度场为例,根据蒙特卡洛仿真的1 000组温度场模拟数据验证了改进方法的平均温度精度相较传统多点法提升了71.8%.
(2)径向基插值融合多项式拟合的物理场混合代理模型有效避免了单纯多项式拟合时的龙格现象. 蒙特卡洛仿真结果表明,混合代理模型的正态分布标准差更小,相较传统的多点法,改进方法的标准差降低了73.1%,证明本研究模型所得环境参数数据的稳定性和可靠性更高.
(3)分析并提出适用于本实验环境的多项式正则化改进模型,确保最终拟合的物理场模型具有较高的解释性与稳定性,并且优化了计算资源的运用.
(4)基于深度学习的高精度物理场拟合模型能够很好地应用于高精度测量装置的大气补偿修正系统中,应用于课题组研发的某微波测距系统时能够使测距精度从毫米级提升至微米级,具有较好的实际应用意义.
实验结果表明,基于深度学习的高精度物理场拟合模型显著提升了测量装置中大气折射率修正模型的精度,减少了大气折射率误差对高精度测量装置带来的不确定度影响. 该模型在全站仪、电子测距仪、激光测距仪、微波测距装置等先进测量设备的校准中具有极大的应用潜力,已应用于浙江大学研发的某微波测距大气补偿修正系统中. 本研究的传感器阵列扩充倍数主要受限于硬件布设密度与数据耦合机制,下一步将重点针对传感器自身误差建模与传感器阵列拓扑结构优化,突破现有测量精度瓶颈.
参考文献
基于空气环境参数自动测量系统的全站仪测距精度校准技术
[J].DOI:10.3969/j.issn.1000-1158.2019.z1.03 [本文引用: 1]
Ranging accuracy calibration technology of total station based on automatic measurement system of air environment parameters
[J].DOI:10.3969/j.issn.1000-1158.2019.z1.03 [本文引用: 1]
提高环境参量法测量空气折射率精度的研究
[J].
The improvement of measuring precision for refractive index of air using the method of Edlén equation calculating with environmental parameters of air
[J].
Transportable distance measurement system based on superheterodyne interferometry using two phase-locked frequency-doubled Nd: YAG lasers
[J].DOI:10.1063/1.3428729 [本文引用: 1]
野外基线温度测量方法探讨
[J].
Exploration of methods for measuring baseline temperature in the field
[J].
The upgraded PTB 600 m baseline: a high-accuracy reference for the calibration and the development of long distance measurement devices
[J].DOI:10.1088/0957-0233/23/9/094018 [本文引用: 1]
基于传感器阵列的野外基线环境参数自动测量系统研制
[J].DOI:10.3969/j.issn.1000-1158.2018.04.02 [本文引用: 1]
Development of outdoor baseline environment parameters measurement system based on sensor array
[J].DOI:10.3969/j.issn.1000-1158.2018.04.02 [本文引用: 1]
1.2 km标准基线环境参数自动测量系统研制
[J].DOI:10.3969/j.issn.1000-1158.2020.08.01 [本文引用: 1]
Development of environmental parameters automatic measurement system for 1.2 km standard baseline
[J].DOI:10.3969/j.issn.1000-1158.2020.08.01 [本文引用: 1]
野外基线测温方法的比较研究
[J].
Comparative study on thermometry methods of outdoor baseline
[J].
A state of art review on time series forecasting with machine learning for environmental parameters in agricultural greenhouses
[J].DOI:10.1016/j.inpa.2022.10.005 [本文引用: 1]
Deep learning for time series forecasting: a survey
[J].
Audio signal based danger detection using signal processing and deep learning
[J].DOI:10.1016/j.eswa.2023.121646 [本文引用: 1]
CNN-LSTM deep learning architecture for computer vision-based modal frequency detection
[J].DOI:10.1016/j.ymssp.2020.106885 [本文引用: 1]
Set-CNN: a text convolutional neural network based on semantic extension for short text classification
[J].DOI:10.1016/j.knosys.2022.109948
CNN variants for computer vision: history, architecture, application, challenges and future scope
[J].DOI:10.3390/electronics10202470 [本文引用: 1]
基于一维卷积神经网络的钻杆故障诊断
[J].
Drill pipe fault diagnosis method based on one-dimensional convolutional neural network
[J].
基于改进1DCNN-GRU的滚动轴承故障诊断
[J].DOI:10.3969/j.issn.1000-1158.2023.09.16 [本文引用: 1]
An improved 1DCNN-GRU for rolling bearing fault diagnosis
[J].DOI:10.3969/j.issn.1000-1158.2023.09.16 [本文引用: 1]
Research on Runge phenomenon
[J].DOI:10.12677/AAM.2019.88175 [本文引用: 1]
Non-smooth interpolation of graph signals
[J].DOI:10.1016/j.sigpro.2022.108480 [本文引用: 1]
Research on a visual thermal landscape model of underground space based on the spatial interpolation method: a case study in Shanghai
[J].
Cardinal MK-spline signal processing: spatial interpolation and frequency domain filtering
[J].DOI:10.1016/j.ins.2019.04.056 [本文引用: 1]
用于星间通信的高灵敏度快捕算法
[J].DOI:10.11918/202208112 [本文引用: 1]
High sensitivity fast acquisition algorithm for inter-satellite communication
[J].DOI:10.11918/202208112 [本文引用: 1]