“跑、冒、滴、漏”是液压系统中被广为诟病的问题. 据美国军方统计表明,在飞机作动器失效的情形中,90%以上是作动器主密封件——往复密封失效引起的[1]. 往复密封的性能直接关系到整个液压系统的工作效率,是液压系统作动器的关键基础元件.
因往复密封为轴对称结构,目前往复密封的研究均是以密封截面为研究对象展开研究. 密封研究面临材料非线性、结构非线性和接触非线性以及大变形的问题,研究过程较复杂,无法通过解析方法直接获得宏微观特性. 往复密封研究主要利用有限元方法,所搭建的有限元模型主要包括二维轴对称模型和平面应变模型[2].
二维轴对称模型广泛应用于O形密封、格莱圈、VL圈等密封的特性研究中. 郭媛等[3]通过建立格莱圈组合密封结构的二维轴对称模型,对格莱圈进行动态数值模拟,获得内部应力分布和接触压力分布,分析格莱圈的不同密封参数对密封性能的影响. 蔡智媛等[4]建立液压格莱圈密封二维轴对称几何模型,对比研究模拟密封圈安装过程中采用的轴向推进和径向压缩2种预压缩有限元模型的计算结果. 徐璁等[5]针对格莱圈密封材料密封性能研究不足的问题,使用二维轴对称模型对氟硅橡胶和氟橡胶制成的O形圈的密封性能进行仿真研究. 刘凤麒等[6]利用轴对称模型,研究流体压力和滑环圆角半径对格莱圈接触压力的影响,得到密封件的最优参数. 张妙恬等[7]以斯特封为研究对象,使用二维轴对称单元,完成斯特封在不同工况下的有限元仿真.
经理论和仿真数据验证可知,二维轴对称单元在密封建模中能够达到与三维实体模型非常接近的结果,二维轴对称模型的准确性得到验证[8]. 相比于二维轴对称模型,平面应变单元因建模更加自由和方便,无须选择轴对称和确定绝对坐标,大量的研究利用平面应变单元展开. 欧阳小平等[9]使用平面应变单元,研究O形密封的失效规律. 王冰清等[10-12]使用平面应变单元建立油水两相液压杆密封的热弹性流体动力学混合润滑模型,探究宽温环境和含水率对O形密封特性的影响,利用平面应变单元研究材料参数(橡胶硬度和聚四氟乙烯弹性模量)对斯特封性能的影响,提出在不同工况下的最佳硬度范围. 笔者等[13-14]利用平面应变模型建立双唇级联密封宏观变形,探究双唇密封级间压力对密封宏观变形和应力分布的影响.
目前,二维轴对称单元和平面应变单元大量交叉使用,共同用于往复密封件宏观特性的分析,但平面应变模型和二维轴对称模型之间计算结果的差距目前没有相关研究,为往复密封特性的分析带来较大的困扰. 本文以典型往复密封结构O 形密封为研究对象,分别利用二维平面模型和二维轴对称模型对往复密封展开仿真研究. 对比分析往复密封在不同压缩率下的宏微观特性,揭示平面应变单元与二维轴对称单元结果的差异性,有助于更深入地理解往复密封机理,指导往复密封的优化设计.
1. 二维平面与轴对称单元特性
二维平面单元与轴对称单元均为对原三维模型的简化,因三维实体单元的建模过程复杂,在压缩过程中需要考虑密封材料非线性、接触非线性和几何大变形等问题,造成计算规模很大. 将密封三维模型简化为二维模型,可以大大减小计算时间.
在有限元建模方法中,平面应变单元节点在
式中:
图 1
二维轴对称单元是由简单二维平面单元转化而来,该单元有2个独立的位移分量
图 2
当轴对称单元被应用时,沿弧度方向积分的单元刚度矩阵如下:
式中:
不同于简单的二维平面单元,轴对称单元增加了圆周方向的应变参量. 轴对称单元在圆周方向的应变被线性简化为
图 3
图 3 轴对称单元的本质表达示意图
Fig.3 Schematic of essential expression of axisymmetric element
由上述分析可知,二维轴对称模型理论上更适合于密封的建模,但建模过程没有平面应变模型灵活. 二维轴对称模型建模时必须竖直建立(对称轴为
2. 建模方法
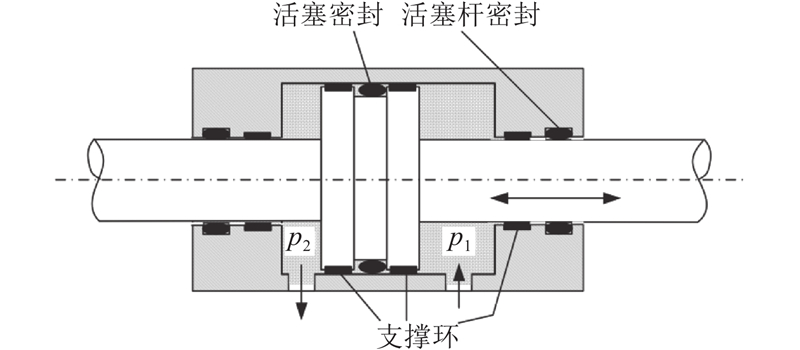
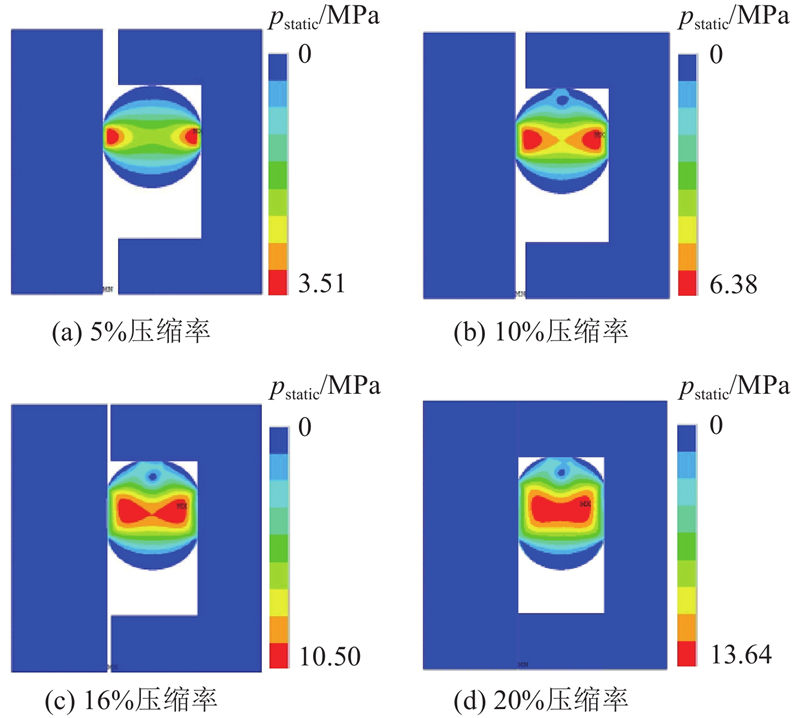
为了探究二维轴对称单元与平面单元在密封建模中的差距,以O形密封为研究对象,利用二维轴对称单元和简单二维平面单元对O形密封进行建模,开展不同压缩率下的密封特性仿真对比研究. 如图4所示为液压缸结构图,往复密封件在安装过程中,会被沟槽底部和活塞杆(缸筒内壁)挤压. 图中,p1为进口油压,p2为出口油压.
图 4
压缩率
图 5
为了对比分析2种建模方法的准确性,当讨论压缩率的影响时,需要消除宏观拉伸对密封性能的影响,密封内径和活塞杆直径保持一致,在不同压缩率条件下对比平面应变模型和二维轴对称模型的计算结果. O形密封的参数如表1所示.
表 1 O形密封、沟槽、活塞杆和流体的基本参数
Tab.1
| 参数 | 数值 |
| 密封材料 | 聚氨酯 |
| 弹性模量E/MPa | 49 |
| 截面直径d/mm | 1.708 |
| 穆尼-瑞林系数/MPa | 0.202、6.958 |
| 密封内径DSeal/mm | 无拉伸:25.35 |
| 沟槽底径DGroove/mm | 28.08/28.21/28.42/28.60 |
| 活塞杆直径DRod/mm | 25.35 |
| 表面粗糙度Ra/μm | 1.6 |
| 往复行程长度L/mm | 100 |
| 速度u/ (m·s−1) | 0.1 |
| 经验摩擦系数 f | 0.2 |
| 参考黏度 μ0/ (Pa·s) | 0.038 7 |
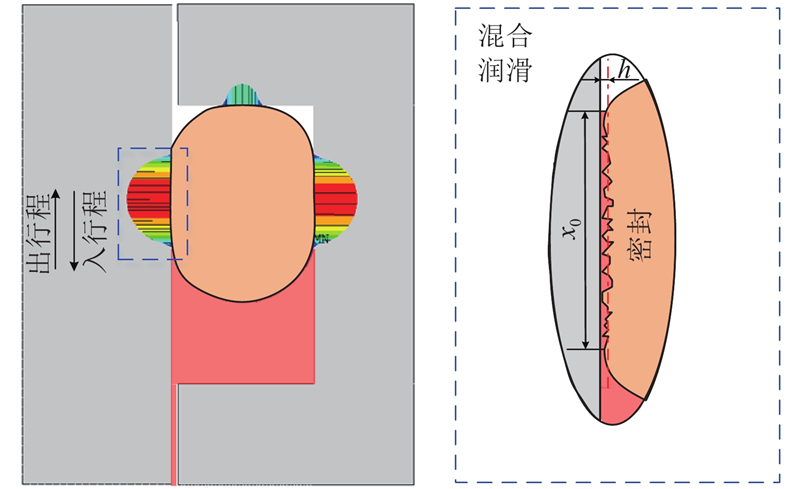
往复密封界面因流体动压效应,密封接触区域并非干摩擦,而是存在一层流体膜. 在往复密封的建模过程中涉及密封整体特性的宏观分析和往复密封接触界面的微观特性研究,如图6所示. 宏观特性如内部应力、接触压力分布和密封接触长度等参数会直接影响密封使用过程中的磨损情况,进而影响密封寿命.宏观接触压力的分布会影响往复密封接触界面的微观特性. 往复密封界面的最小油膜厚度约为几百纳米,界面润滑状态往往会影响往复密封摩擦和泄漏特性. 往复密封特性分析须综合宏、微观两个方面分析,建立往复密封跨尺度模型.
图 6
2.1. 宏观有限元分析模型
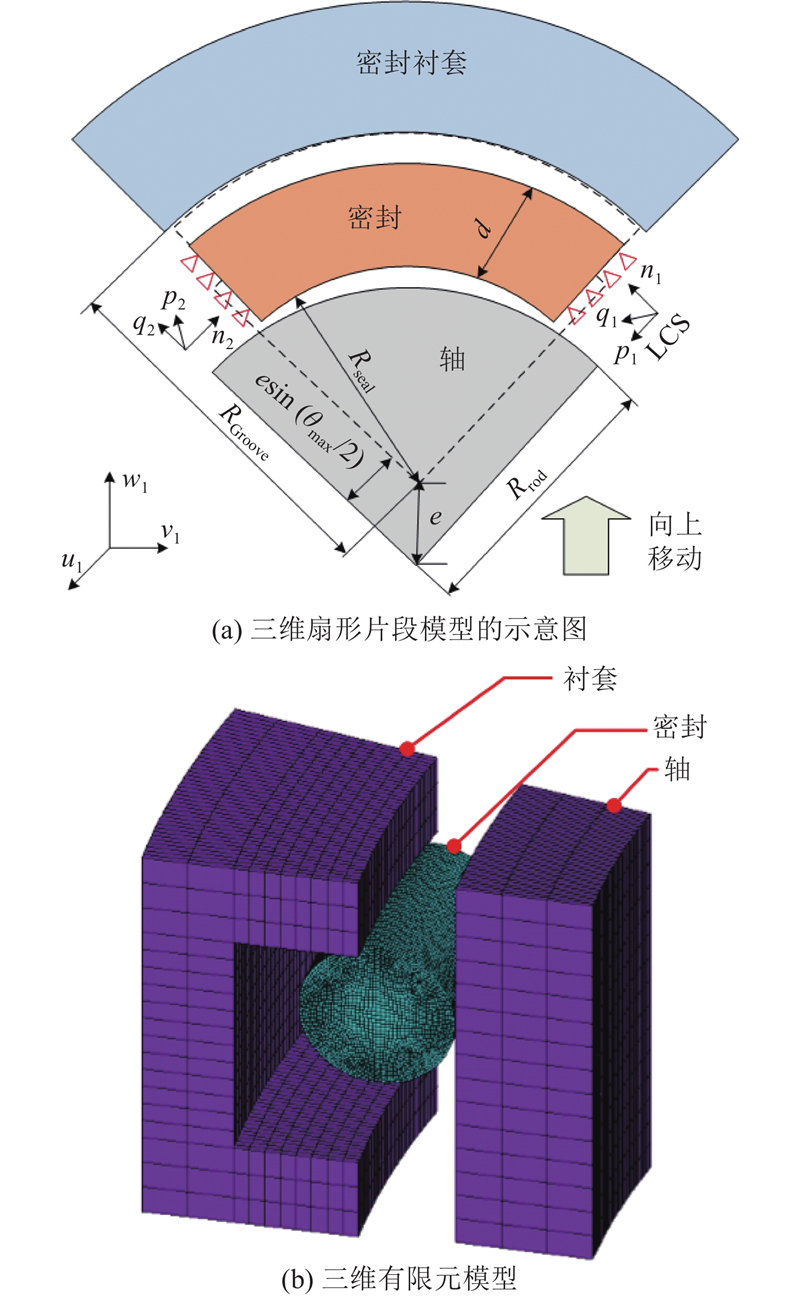
研究对象为O形密封件,通过商业软件ANSYS建立往复密封有限元模型. 为了验证平面应变模型与二维轴对称模型在往复密封计算中的结果准确性,建立三维实体模型进行模型对比验证. 与平面应变单元和二维轴对称单元相比,三维实体单元拥有3个方向的位移分量,能够真实反映对应的应力应变状态. 三维模型的网格数量远超二维模型,考虑到密封材料、接触非线性,造成全周三维密封模型的计算量过大. 为了便于计算,截取密封圈的一段,以三维扇形片段结构来表征密封整体的性能. 为了考虑密封件压缩过程中的周向应变影响,对扇形片段的截面进行特殊边界条件的设置,基本原理如下. 密封在拉伸或者压缩过程中,虽然它的弧长缩小了,但每一段的弧度
图 7
通过相关单元类型的设置,分别建立O形密封的简单二维平面和二维轴对称模型,如图8所示,设置衬套、活塞杆和密封材料属性(如弹性模量、泊松比和Mooney-Rivlin系数). 接触单元选择CONTA172(接触面)和TARGE169(目标面)2种单元类型,通过接触向导设置接触副,将接触单元分别设置为平面应变模型和二维轴对称模型. 因活塞杆和衬套相对较硬(弹性模量大),将其设置为目标面. 聚氨酯橡胶的弹性模量小,故设置为接触面,接触算法采用增广拉格朗日方法.
图 8
因在该工况中O形密封未被拉伸,活塞杆外径与密封圈内径相同,故活塞杆固定,将衬套向左移动,压紧O形圈,完成密封圈安装步骤的模拟. 在轴对称模型的建立过程中,对称轴必须为y轴,故竖直方向y轴为轴向方向,x轴为径向方向. 针对安装变形后的O形密封圈,在轴和活塞间的密封表面单元或节点上施加流体压力,实现液压系统压力的加载仿真. 在整个模型的建立过程中,有限元网格模型共含有18 012个网格节点,与细化后的含有22 507个网格节点的模型相比,两者的计算误差小于0.2%,验证了本文所用有限元模型的网格无关性.
2.2. 微观混合润滑模型
大量理论和试验表明,混合润滑广泛存在于往复密封接触区域中. 基于混合润滑理论,探究往复密封界面的润滑状态,分析不同压缩率下的密封界面微观特性,对比分析简单二维平面模型和二维轴对称模型在混合润滑计算结果上的差异,应用2种建模方法开展往复密封微观特性的研究. 微观混合润滑模型主要由界面流体组成模型、微观接触机理和变形方程3个子模型组成. 3个子模型通过耦合和迭代,直到计算收敛,获得密封界面的微观特性,分析微观固体接触压力分布和油膜压力,计算往复密封总摩擦力和泄漏量.
2.2.1. 密封界面流体模型
在密封界面流体模型中,使用修正后的雷诺方程[17]. 在该模型中,同时考虑了空化和表面粗糙度的影响.
在流体区中,
式中:
在空化区中,
求解式(4),可得密封界面的流体运输速度和泄漏量.
流体黏性摩擦力可由下式获得:
在数值迭代中,油液黏度随流体压力的变化而变化,Roelands方程用于描述油液的黏压特性:
式中:
2.2.2. 微观接触机制
式中:
式中:
2.2.3. 变形分析
将油膜压力和固体接触压力之和与静态接触压力进行比较,两者压力差会轻微改变密封件的变形,从而改变油膜厚度. 与密封的总尺寸相比,油膜厚度非常小. 假设流体动压效应引起的轻微变形与压力差成正比,使用半无限空间的方法计算密封的变形:
式中:
各节点的膜厚可以表示为
式中:
2.2.4. 混合润滑的计算过程
由于流体动压效应,密封被轻微抬起. 随着迭代次数的增加,油膜厚度趋于稳定. 收敛薄膜厚度的计算需要综合G-W模型、流体方程、变形方程,3个子模型反复迭代. 根据式(12)可知,一旦膜厚稳定,静态接触压力同油膜压力和微观接触压力之和之间的差值应趋于稳定. 提出如下所示的收敛准则:
式中:
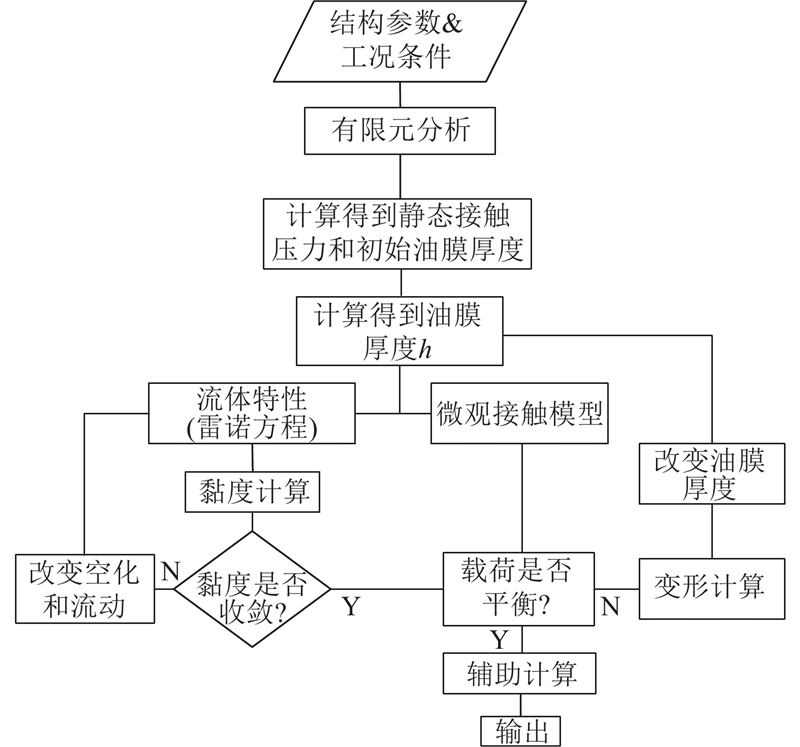
2.3. 建模流程
混合润滑计算过程的算法如图9所示. 利用有限元模型得到的静接触压力计算初始膜厚,在混合润滑过程中,采用有限体积方法对雷诺方程进行数值计算. 在考虑空化效应和黏压效应的情况下,可以得到相应的油膜压力分布,计算该油膜厚度下的微观接触压力. 将微观接触压力与油膜压力之和同静态接触压力进行比较,两者之间的压力差促使油膜厚度发生变化,利用变形方程更新油膜厚度,改变后的油膜分布对油膜压力和微观接触压力的分布产生影响,迭代计算油膜压力和微观接触压力,整个循环迭代,直至达到收敛准则. 在循环完成后,计算并输出流体运输速率(泄漏量)和摩擦力.
图 9
图 9 往复密封流固耦合的数值计算流程
Fig.9 Numerical calculation process of fluid-structure interaction for reciprocating seal
3. 结果分析与讨论
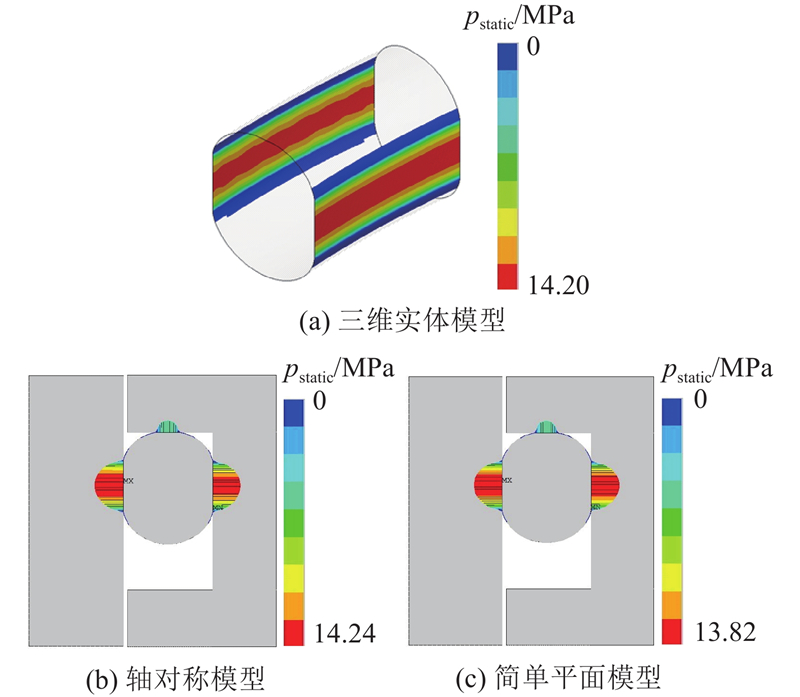
3.1. 二维轴对称、平面应变模型和三维模型的对比验证
通过二维平面与轴对称单元的特性可知,轴对称单元的特性从理论上更适合往复密封的建模. 为了验证二维轴对称和平面应变模型的准确性,以三维实体模型的计算结果为基准,对比上述2个模型. 从影响密封性能最关键的接触压力(见图10)可以看出,二维轴对称模型的计算结果与三维实体模型结果一致,利用平面应变模型计算得到的接触压力小于前两者的计算结果,主要原因是靠近沟槽底部的密封部分在压缩过程中向左移动,即处于负拉伸状态. 密封件在安装和使用过程中,如果弧长变大,则密封件被视为正拉伸,正拉伸会造成密封件同活塞杆和沟槽底部的接触压力逐渐变小[10]. 本文中密封件的内径同活塞杆的直径相同,外径大于沟槽的底径,所以在安装过程中O形圈除了同活塞杆接触的边界,密封件整体都是向弧长缩小的方向移动,称为负拉伸. 与正拉伸相反,负拉伸会使密封件同活塞杆的接触压力增大.
图 10
图 10 二维轴对称、平面应变模型与三维实体模型计算的接触压力对比
Fig.10 Comparison of contact pressure calculation between 2D axisymmetric model, plane strain model and 3D solid model
相比于平面应变模型,二维轴对称模型多了一个圆周方向的应变分量
3.2. 不同压缩率下密封宏观特性的有限元分析
图 11
图 11 不同压缩率条件下的接触压力分布(轴对称模型)
Fig.11 Contact pressure distribution under different compression ratio (axisymmetric model)
图 12
图 12 不同压缩率条件下的内部应力分布(轴对称模型)
Fig.12 Internal stress distribution under different compression ratio (axisymmetric model)
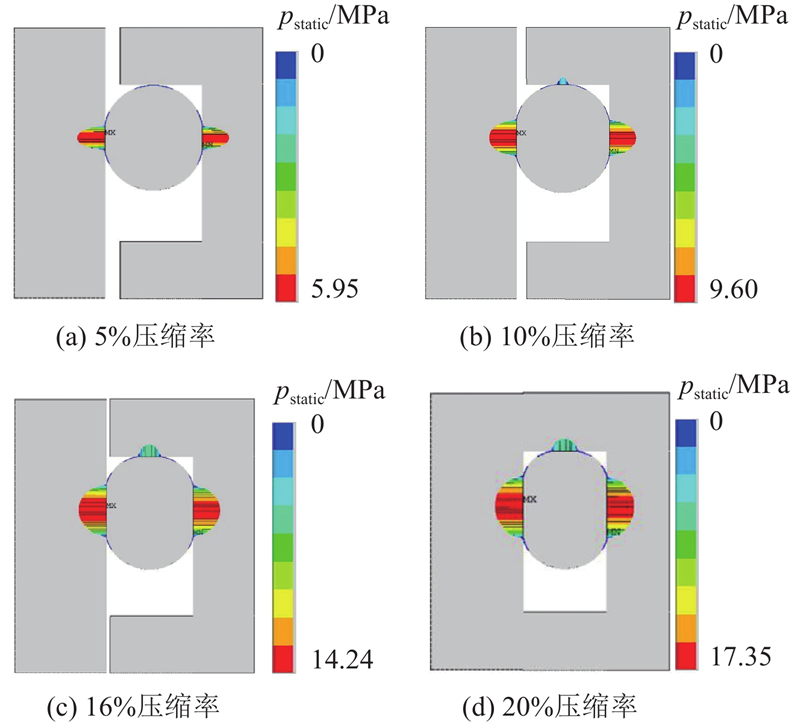
如图13、14所示分别为利用二维平面模型计算得到的各压缩率下的内部应力和接触压力分布情况. 最大接触压力和应力均随着压缩率的增大而增大,但在同一压缩率下,由于负拉伸效应,二维轴对称模型的接触压力和内部应力均高于二维平面模型的计算结果. 在往复密封被挤压的过程中,虽然密封件内径同活塞杆贴合,O形密封整体处于宏观零拉伸率下,但在沟槽压缩过程中,对于密封件局部位置,如沟槽-密封接触区域在径向会产生流动,造成密封外径尺寸缩小(负拉伸). 在二维轴对称模型中,密封件同活塞杆的接触压力和沟槽底部的压力分布有一定的差距,活塞杆的接触压力大于沟槽底部的接触压力. 在二维平面模型中,因无负拉伸作用,两者分布基本一致,计算结果差距不大.
图 13
图 13 不同压缩率条件下的接触压力分布(平面模型)
Fig.13 Contact pressure distribution under different compression ratio (plane model)
图 14
图 14 不同压缩率条件下的内部应力分布(平面模型)
Fig.14 Internal stress distribution under different compression ratio (plane model)
3.3. 不同压缩率下的密封界面润滑特性(2D模型和轴对称模型)
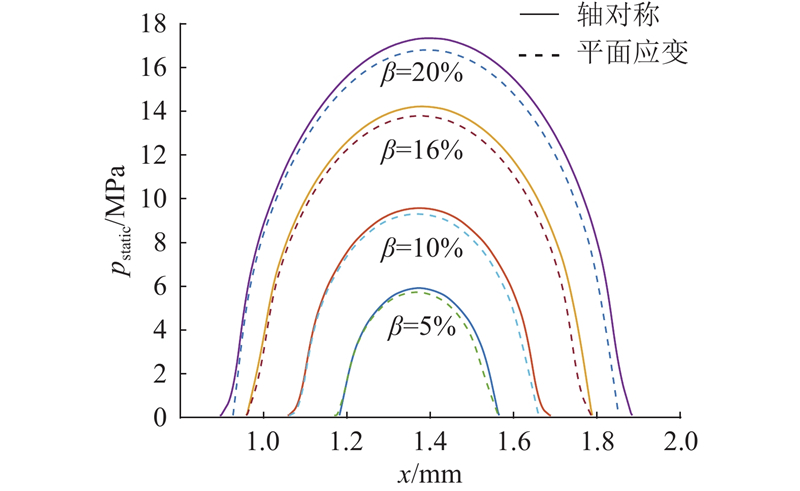
如图15所示为利用轴对称模型和二维平面模型得到的各压缩率下的接触压力分布对比. 随着压缩率的增大,接触压力和密封宽度均逐渐增大. 通过ANSYS计算所得的静态接触压力
图 15
图 15 不同压缩率下的静态接触压力
Fig.15 Static contact pressure at different compression ratio
图 16
图 16 当压缩率为16%时不同压力下的静态接触压力
Fig.16 Static contact pressure at different pressure with same compression ratio of 16%
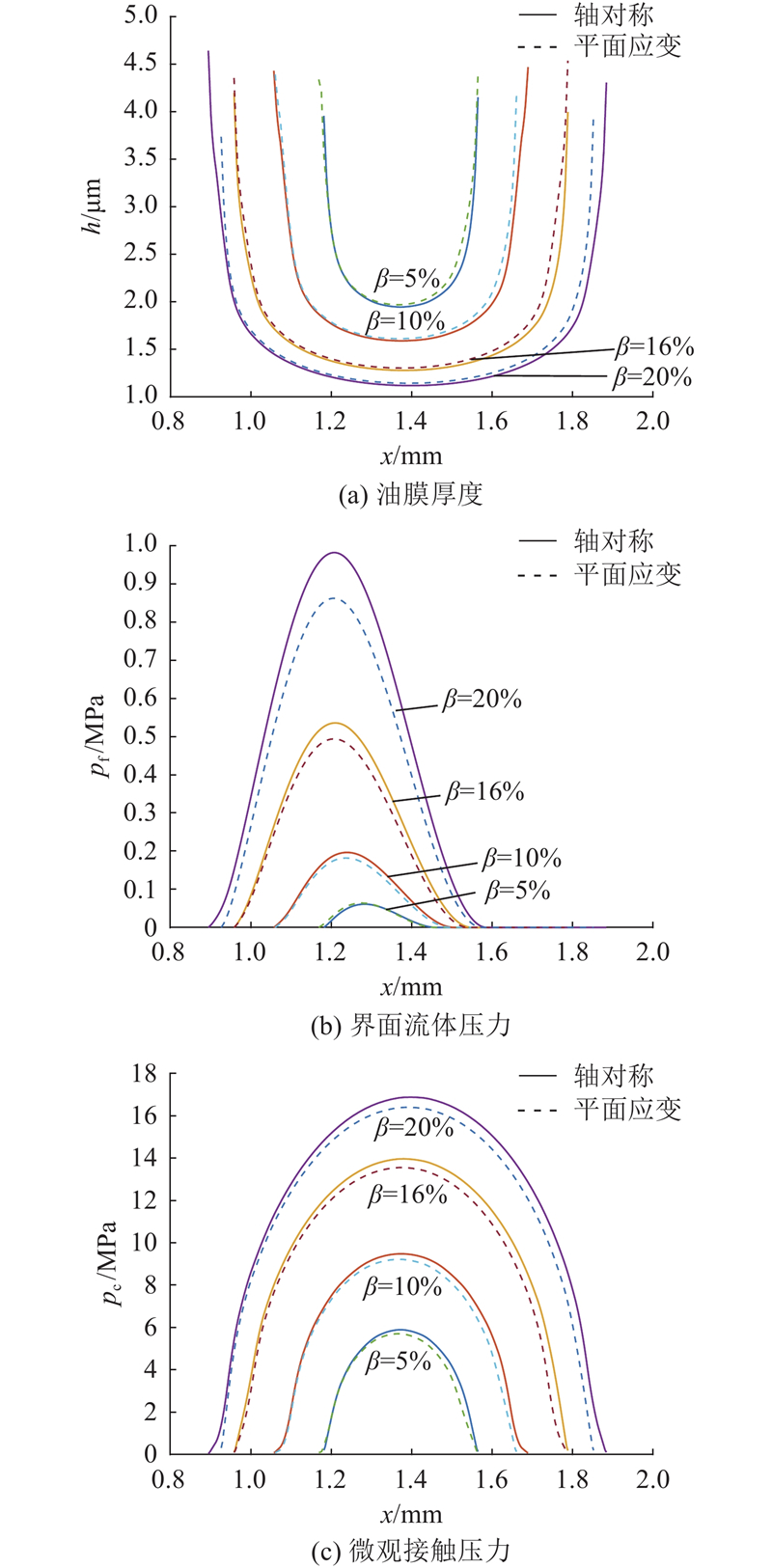
因密封油膜厚度
图 17
图 17 不同压缩率下的密封微观特性
Fig.17 Microscopic sealing characteristics under different compression ratio
二维轴对称模型和平面应变模型在宏观摩擦力
图 18
图 18 利用2种模型计算得到的不同压缩率下摩擦力和泄漏量
Fig.18 Friction and leakage under different compression ratios calculated by two models
4. 结 语
在现有的往复密封研究中,二维轴对称单元和平面应变单元交叉使用,共同用于往复密封件特性的分析. 为了分析平面应变模型和二维轴对称单元模型在密封特性计算结果上的差异,在宏观零拉伸率下,利用二维轴对称模型和平面应变模型,对O形密封的宏微观特性展开系统性分析.
研究结果表明,二维轴对称模型的计算精度与三维实体模型结果一致. 虽然平面应变模型与轴对称模型的计算结果趋势相同,但在同一压缩率下,二维平面应变模型的接触压力、内部应力和摩擦力均小于轴对称模型的计算结果. 随着压缩率的增大,两者的相差幅度逐渐增大. 原因在于平面应变模型忽略了靠近沟槽底部密封部分的负拉伸效应.
本文基于往复密封三维模型的计算结果,验证平面应变模型和轴对称模型的准确性. 在未来的研究中,将探索相关试验方法如摩擦力测量、接触压力检测、表面形貌分析等手段,更全面地揭示往复密封的机理.
参考文献
格莱圈动密封性能分析及密封参数优化
[J].
Analysis of dynamic sealing performance of Glyd ring and optimization of parameters
[J].
基于2种预压缩模型的格莱圈静密封性能
[J].
Static sealing performance of Glyd-ring seal with two precompression models
[J].
氟硅橡胶与氟橡胶O形圈密封性能仿真
[J].
Simulation of sealing performance of fluorosilicone rubber O-ring and fluoro rubber O-ring
[J].
滑环圆角半径对液压往复格莱圈接触压力的影响
[J].
Influence of slip ring radius on contact pressure of hydraulic reciprocating Glyd-ring
[J].
基于斯特封的飞机作动器主密封有限元分析
[J].
Finite element analysis of aircraft actuator’s main seal based on Sterling seal
[J].
Investigation into the influence of stretching on reciprocating rod seals based on a novel 3-D model vs axisymmetric model
[J].
航空作动器O形密封材料失效分析
[J].
Analysis of material fault of O-ring seal in aircraft cylinder
[J].
宽温高湿环境下油水两相O形液压杆封性能分析
[J].
Performance analysis of oil-water two-phase O-ring hydraulic rod seals under the wide-temperature high-humidity environments
[J].
Influence of nitrile butadiene rubber (nbr) shore hardness and polytetrafluoroethylene (ptfe) elastic modulus on the sealing characteristics of step rod seals
[J].DOI:10.3390/lubricants11090367
Effect of nitrile butadiene rubber hardness on the sealing characteristics of hydraulic O-ring rod seals
[J].DOI:10.1631/jzus.A2200612 [本文引用: 1]
Investigation into the inter-lip characteristics of combined seals with double lips in different working conditions
[J].
Numerical and experimental study on combined seals with the consideration of stretching effects
[J].DOI:10.1115/1.4048496 [本文引用: 1]
A computational method for cavitation in a wavy mechanical seal
[J].DOI:10.1115/1.2920861 [本文引用: 2]
An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication
[J].DOI:10.1115/1.3453103 [本文引用: 4]
The contact sport of rough surfaces
[J].DOI:10.1126/science.aaq1814 [本文引用: 1]
The contact of two nominally flat rough surfaces
[J].