$ \begin{split} {{{\bf\textit{Ξ}} }_1} =& {\text{diag}}\;\{ \alpha {{{\boldsymbol{P}}}_i},{{\boldsymbol{I}}}\} , \\ {{{\bf\textit{Ξ}} }_2} = &\left[ {\begin{array}{*{20}{l}} {{{\overline {\boldsymbol{A}}}_i}},{{\overline{\boldsymbol{ E}}}} \end{array}} \right], \\ {{{\bf\textit{Ξ}} }_3} =& {\text{diag}}\;\{ {{{\boldsymbol{P}}}_1},{{{\boldsymbol{P}}}_2},{{{\boldsymbol{P}}}_3},{{{\boldsymbol{P}}}_4}\} , \\ {{\bf\textit{ƞ}} } =& {\left[ {\begin{array}{*{20}{l}} {\sqrt {{\pi _{i1}}} },{\sqrt {{\pi _{i2}}} },{\sqrt {{\pi _{i3}}} },{\sqrt {{\pi _{i4}}} } \end{array}} \right]^{\mathrm{T}}}. \\\end{split} $
注2 由于式(14)中矩阵$ {\overline {\boldsymbol{A}}_i},i = 1,2 $ ${\boldsymbol{ K}} $ $ {\tilde {\boldsymbol{B}}_i}{\boldsymbol{K}}{\overline{\boldsymbol{ I}}_i},i = 1,2 $ $ {\overline {\boldsymbol{I}}_i},i = 1,2 $ ${{\boldsymbol{M}}_i},i = 1,2$ ${{\overline {\boldsymbol{I}}}_i}{{\boldsymbol{{M}}}_i} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{I}}},{\boldsymbol{0}} \end{array}} \right],i = 1,2$ . 一般来说,对应的矩阵${{{\boldsymbol{M}}}_i}$ [38 ] .
其中$ {{{\boldsymbol{\varOmega}} }_i} = - \,{\overline {\boldsymbol{G}}} \,-\, {{{\overline {\boldsymbol{G}}}}^{\mathrm{T}}}\,+\,{\alpha ^{ - 1}}\,{{{\boldsymbol{X}}}_i}\,,\, {{{\overline{\boldsymbol{ I}}}}_3} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{I}}},\,{{\boldsymbol{0}}} \end{array}} \right],\,\, {\boldsymbol{\varLambda}}_i=\overline{\boldsymbol{A}}_i \overline{\boldsymbol{G}}_i+ \tilde{\boldsymbol{B}}_i{\boldsymbol{Y}}\overline{\boldsymbol{I}}_3 {\boldsymbol{M}}_i^{\mathrm{T}}$ . 则系统式(8)是随机有限时间有界的,并满足${\ell _2} - {\ell _\infty }$ $ \gamma = \sqrt {{{\overline \gamma }^2}{\alpha ^N}} $ .
$\begin{split} & {{{\boldsymbol{K}}}_2} = \left[ {\begin{array}{*{20}{l}} {0.154\,3}&{0.267\,3} \\ { - 0.277\,2}&{ - 0.481\,7} \end{array}} \right],\\&{{\boldsymbol{K}}_3} = \left[ {\begin{array}{*{20}{l}} {0.219\,8}&{0.229\,0} \\ { - 0.281\,9}&{ - 0.357\,5} \end{array}} \right],\end{split} $
[1]
HU Z, CHEN K, DENG F, et al ${H_\infty }$
[J]. IEEE Transactions on Cybernetics , 2024 , 54 (3 ): 1661 - 1670
DOI:10.1109/TCYB.2022.3233065
[本文引用: 3]
[2]
QIU L, SHI Y, YAO F, et al Network based robust ${H_2}/{H_\infty }$
[J]. IEEE Transactions on Cybernetics , 2015 , 45 (8 ): 1450 - 1462
DOI:10.1109/TCYB.2014.2352291
[本文引用: 1]
[3]
JIAO S, XU S Observed-mode-dependent nonfragile control of networked control systems under hidden DoS attacks
[J]. IEEE Transactions on Control of Network Systems , 2024 , 11 (1 ): 139 - 149
DOI:10.1109/TCNS.2023.3272824
[本文引用: 2]
[4]
GUO L, ZHANG D. ${H_\infty }$ Proceedings of the IECON 2018 - 44th Annual Conference of the IEEE Industrial Electronics Society . Washington: IEEE, 2018: 5889–5894.
[本文引用: 1]
[6]
WU W, GAO W, LIN J. Data-based predictive control with delay compensation for networked nonlinear systems with packet dropouts and delays in two channels [C]// Proceedings of the Chinese Automation Congress . Jinan: IEEE, 2017: 2888–2893.
[本文引用: 1]
[7]
李志强. 拒绝服务攻击下信息物理系统的事件触发安全控制研究 [D]. 北京: 北京科技大学, 2022: 1–155.
[本文引用: 2]
LI Zhiqiang. Event-triggered security control of cyber-physical systems under denial-of-service attacks [D]. Beijing: University of Science and Technology Beijing, 2022: 1–155.
[本文引用: 2]
[8]
ZENG P, DENG F, ZHANG H, et al Event-based ${H_\infty }$
[J]. IEEE Transactions on Fuzzy Systems , 2022 , 30 (6 ): 1853 - 1863
DOI:10.1109/TFUZZ.2021.3069345
[本文引用: 3]
[9]
程志键. 攻击环境下网络化系统的状态估计问题研究[D]. 合肥: 中国科学技术大学, 2022: 1–127.
[本文引用: 1]
CHENG Zhijian. Research on state estimation of networked systems in attack environment [D]. Hefei: University of Science and Technology of China, 2022: 1–127.
[本文引用: 1]
[10]
MA L, ZHANG Y, YANG C, et al Security control for two-time-scale cyber physical systems with multiple transmission channels under DoS attacks: the input-to-state stability
[J]. Journal of the Franklin Institute , 2021 , 358 (12 ): 6309 - 6325
DOI:10.1016/j.jfranklin.2021.05.017
[本文引用: 1]
[11]
WANG X, YANG H, ZHONG S Improved results on consensus of nonlinear MASs with nonhomogeneous Markov switching topologies and DoS cyber attacks
[J]. Journal of the Franklin Institute , 2021 , 358 (14 ): 7237 - 7253
DOI:10.1016/j.jfranklin.2021.07.044
[12]
CHENG G, LIU H Asynchronous finite-time ${H_\infty }$
[J]. Journal of the Franklin Institute , 2023 , 360 (3 ): 1495 - 1522
DOI:10.1016/j.jfranklin.2022.12.025
[14]
GUO H, PANG Z, SUN J, et al An output-coding-based detection scheme against replay attacks in cyber-physical systems
[J]. IEEE Transactions on Circuits and Systems II: Express Briefs , 2021 , 68 (10 ): 3306 - 3310
[本文引用: 1]
[15]
HE H, CHEN Y, QI W, et al Observer-based resilient control of positive systems with heterogeneous DoS attacks: a Markov model approach
[J]. Journal of the Franklin Institute , 2022 , 359 (1 ): 272 - 293
DOI:10.1016/j.jfranklin.2021.04.034
[本文引用: 1]
[16]
HUANG L, GUO J, LI B Observer-based dynamic event-triggered robust ${H_\infty }$
[J]. IEEE Access , 2021 , 9 : 145626 - 145637
DOI:10.1109/ACCESS.2021.3121689
[本文引用: 1]
[17]
ZHENG X, ZHANG H, WANG L, et al Dynamic event-based distributed piecewise filtering over sensor networks under periodic DoS attacks
[J]. IEEE Transactions on Control of Network Systems , 2023 , 10 (2 ): 853 - 864
DOI:10.1109/TCNS.2022.3210858
[本文引用: 1]
[18]
TIAN E, WANG X, PENG C Probabilistic-constrained distributed filtering for a class of nonlinear stochastic systems subject to periodic DoS attacks
[J]. IEEE Transactions on Circuits and Systems I: Regular Papers , 2020 , 67 (12 ): 5369 - 5379
DOI:10.1109/TCSI.2020.3007953
[本文引用: 1]
[19]
XU Q, ZHANG N, QI W Finite-time control for discrete-time nonlinear Markov switching LPV systems with DoS attacks
[J]. Applied Mathematics and Computation , 2023 , 443 : 127783
DOI:10.1016/j.amc.2022.127783
[本文引用: 1]
[20]
YE Z, ZHANG D, YAN H, et al A semi-Markovian jumping system approach to secure DPC of nonlinear networked unmanned marine vehicle systems with DoS attack
[J]. Journal of the Franklin Institute , 2023 , 360 (16 ): 12552 - 12575
DOI:10.1016/j.jfranklin.2021.07.054
[本文引用: 1]
[21]
QI W, HOU Y, PARK J, et al SMC for discrete-time networked semi-Markovian switching systems with random DoS attacks and applications
[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems , 2023 , 53 (3 ): 1982 - 1993
DOI:10.1109/TSMC.2022.3211322
[本文引用: 2]
[22]
SHI T, SHI P, CHAMBERS J Dynamic event-triggered model predictive control under channel fading and denial-of-service attacks
[J]. IEEE Transactions on Automation Science and Engineering , 2024 , 21 (4 ): 6448 - 6459
DOI:10.1109/TASE.2023.3325534
[本文引用: 2]
[23]
YUAN Y, YUAN H, HO D, et al Resilient control of wireless networked control system under denial-of-service attacks: a cross-layer design approach
[J]. IEEE Transactions on Cybernetics , 2020 , 50 (1 ): 48 - 60
DOI:10.1109/TCYB.2018.2863689
[本文引用: 2]
[24]
ZHAO N, SHI P, XING W, et al Resilient adaptive event-triggered fuzzy tracking control and filtering for nonlinear networked systems under denial-of-service attacks
[J]. IEEE Transactions on Fuzzy Systems , 2022 , 30 (8 ): 3191 - 3201
DOI:10.1109/TFUZZ.2021.3106674
[本文引用: 2]
[25]
GENG Q, YANG H, LI L, et al Hybrid dynamic event-triggered tracking control of wheeled mobile robots against stochastic DoS attacks
[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems , 2023 , 53 (12 ): 7805 - 7813
DOI:10.1109/TSMC.2023.3299269
[本文引用: 2]
[26]
LIAN J, LI H, WU F, et al. Time-triggered control of double channel transmission networked switched systems under DoS attacks [C]// Proceedings of the 42nd Chinese Control Conference . Tianjin: IEEE, 2023: 5263–5268.
[本文引用: 2]
[27]
黄鹤, 谢德晓, 韩笑冬, 等 具有随机丢包的一类网络控制系统的故障检测
[J]. 控制理论与应用 , 2011 , 28 (1 ): 79 - 86
[本文引用: 1]
HUANG He, XIE Dexiao, HAN Xiaodong, et al Fault detection for networked control system with random packet dropout
[J]. Control Theory and Applications , 2011 , 28 (1 ): 79 - 86
[本文引用: 1]
[28]
ZHANG H, XU S Finite-time almost sure stability of a Markov jump fuzzy system with delayed inputs
[J]. IEEE Transactions on Fuzzy Systems , 2022 , 30 (6 ): 1801 - 1808
DOI:10.1109/TFUZZ.2021.3067797
[本文引用: 1]
[29]
WANG Z, SHEN L, XIA J, et al Finite-time non-fragile ${l_2} - {l_\infty }$
[J]. Journal of the Franklin Institute , 2018 , 355 (14 ): 6371 - 6389
DOI:10.1016/j.jfranklin.2018.06.030
[本文引用: 2]
[30]
ZHAO Y, MA Y Adaptive event-triggered finite-time sliding mode control for singular T-S fuzzy Markov jump systems with asynchronous modes
[J]. Communications in Nonlinear Science and Numerical Simulation , 2023 , 126 : 107465
DOI:10.1016/j.cnsns.2023.107465
[本文引用: 1]
[31]
DORATO P. Short-time stability in linear time-varying systems [R]. Brooklyn: Polytechnic Institute of Brooklyn, 1961: 83–87.
[本文引用: 1]
[32]
AMATO F, ARIOLA M, DORATO P Finite-time control of linear systems subject to parametric uncertainties and disturbances
[J]. Automatica , 2001 , 37 (9 ): 1459 - 1463
DOI:10.1016/S0005-1098(01)00087-5
[本文引用: 1]
[33]
LI F, SHEN H, CHEN M, et al Non fragile finite-time ${l_2} - {l_\infty }$
[J]. Applied Mathematics and Computation , 2015 , 271 : 467 - 481
DOI:10.1016/j.amc.2015.09.029
[本文引用: 1]
[34]
CHEN H, GAO F Finite-time asynchronous state estimation for jump systems with partial transition probabilities via redundant channels: a co-design method
[J]. Journal of the Franklin Institute , 2021 , 358 (18 ): 10095 - 10120
DOI:10.1016/j.jfranklin.2021.09.032
[本文引用: 1]
[35]
SHEN H, LIU X, XIA J, et al Finite-time energy-to-peak fuzzy filtering for persistent dwell-time switched nonlinear systems with unreliable links
[J]. Information Sciences , 2021 , 579 : 293 - 309
DOI:10.1016/j.ins.2021.07.081
[本文引用: 1]
[36]
REN H, ZONG G, QIAN X, et al Hybrid event-based asynchronous finite-time control for cyber-physical switched systems under denial-of-service attacks
[J]. Journal of the Franklin Institute , 2023 , 360 (2 ): 1036 - 1057
DOI:10.1016/j.jfranklin.2022.11.028
[本文引用: 1]
[37]
YE Z, ZHANG D, DENG C, et al Finite-time resilient sliding mode control of nonlinear UMV systems subject to DoS attacks
[J]. Automatica , 2023 , 156 : 111170
DOI:10.1016/j.automatica.2023.111170
[本文引用: 2]
[38]
SHI T, LU R, LV Q Robust static output feedback infinite horizon RMPC for linear uncertain systems
[J]. Journal of the Franklin Institute , 2016 , 353 (4 ): 891 - 902
DOI:10.1016/j.jfranklin.2016.01.012
[本文引用: 1]
${H_\infty }$
3
2024
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
... [1 ,4 ]、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
... [1 ,3 ]. 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
Network based robust ${H_2}/{H_\infty }$
1
2015
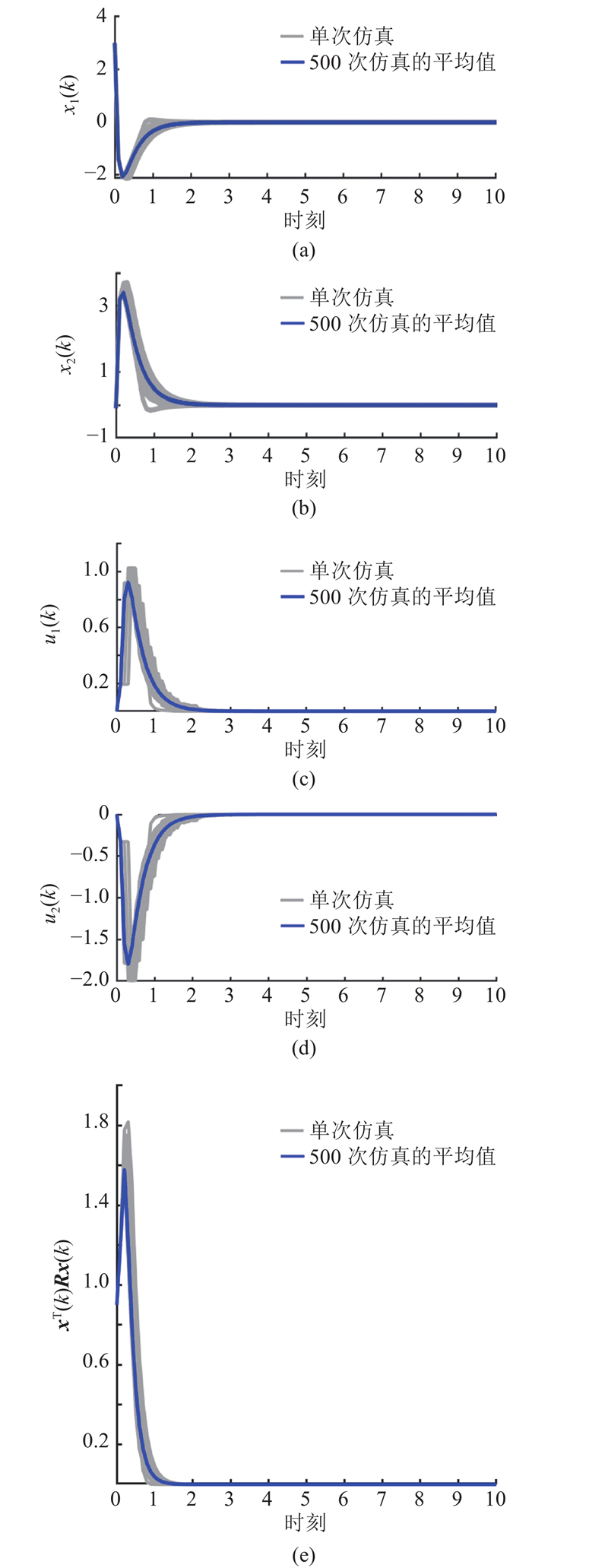
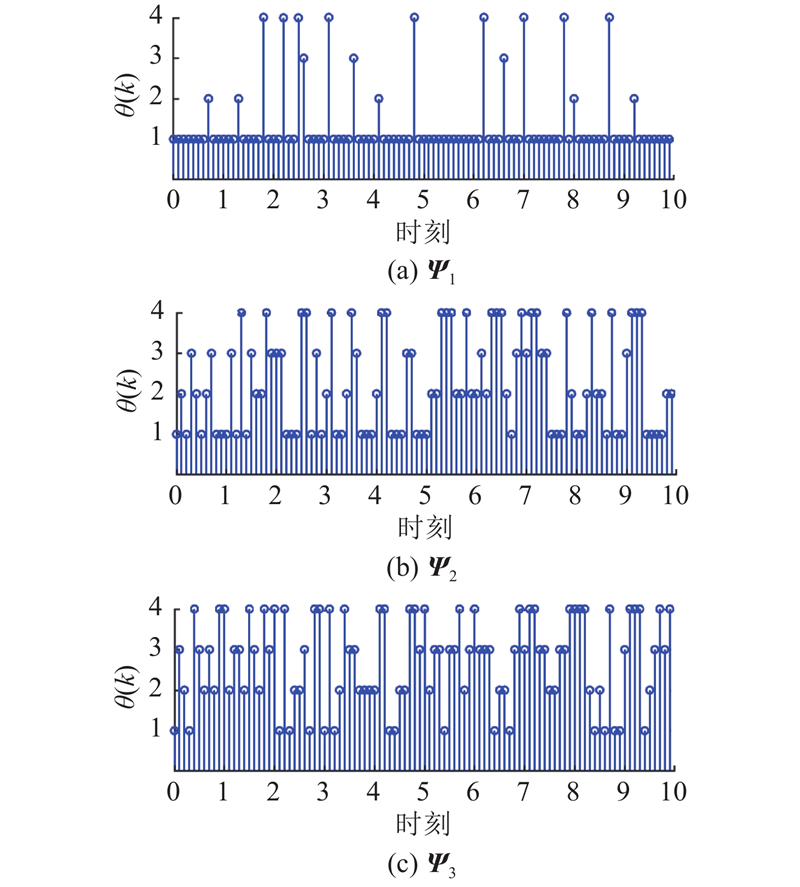
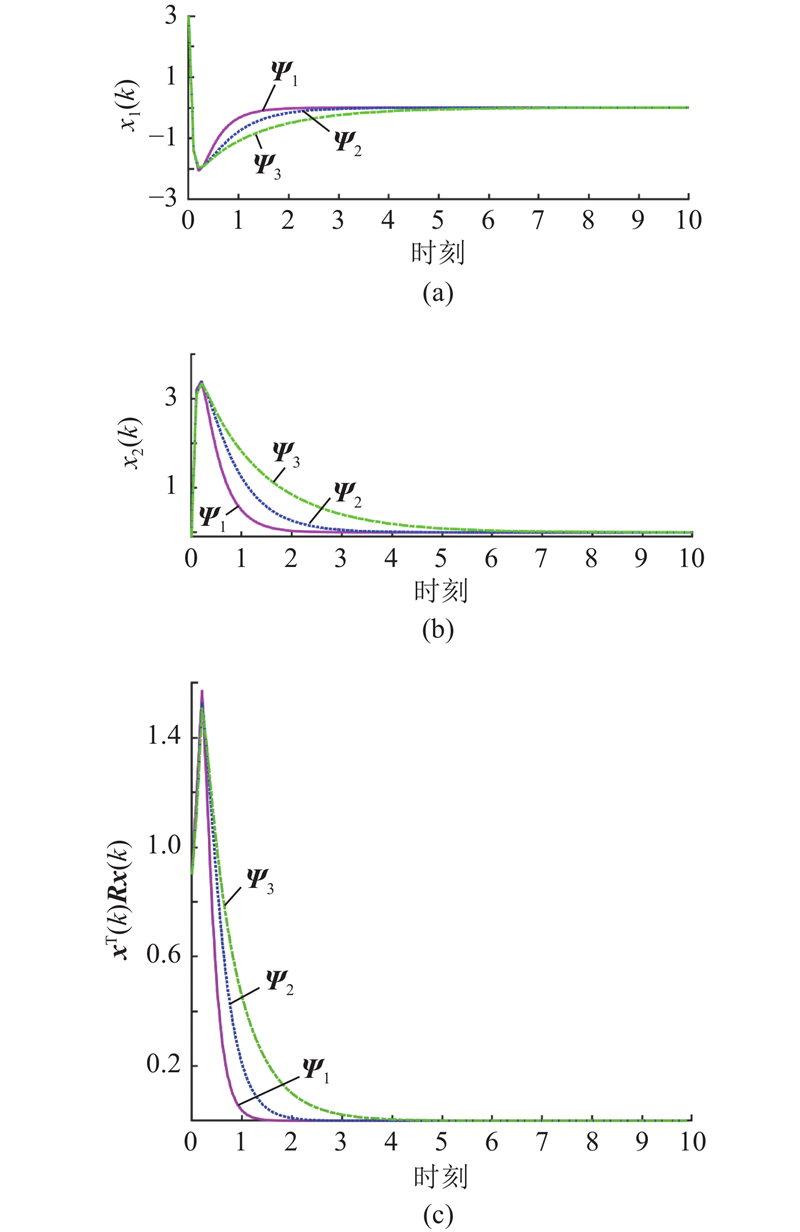
... 示例2 考虑受外部干扰的角度定位系统[2 ] ,该系统的状态空间模型为 ...
Observed-mode-dependent nonfragile control of networked control systems under hidden DoS attacks
2
2024
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
... ,3 ]. 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
1
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
Optimal stationary state estimation over multiple Markovian packet drop channels
1
2021
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
1
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
2
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
... [7 ],乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
2
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
... [7 ],乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
Event-based ${H_\infty }$
3
2022
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
... [8 ,19 ]. DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
1
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
1
... 相比于传统点对点传输的控制系统,网络控制系统(networked control systems,NCSs )具有灵活性高,功耗低,布线体积小等优点,被广泛应用于智能制造、车辆控制、多智能体系统、无人机集群控制等领域[1 -3 ] . 无线网络的共享性和开放性带来的安全隐患包括数据包丢失[1 ,4 ] 、时间延迟[5 -6 ] 和网络攻击[7 -8 ] ,不仅对控制系统安全运行构成严重的威胁,也使NCSs的建模、分析和设计变得复杂. 在这些安全隐患中,网络攻击对NCSs的危害性最大[1 ,3 ] . 葡萄牙电信公司遭受的网络攻击致使数百万人使用的服务中断[7 ] ,乌克兰政府网站遭到网络攻击后大量重要数据泄露[9 ] . 因此,控制器设计时考虑网络攻击的影响,对NCSs的实际应用具有重要意义. ...
Security control for two-time-scale cyber physical systems with multiple transmission channels under DoS attacks: the input-to-state stability
1
2021
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
Improved results on consensus of nonlinear MASs with nonhomogeneous Markov switching topologies and DoS cyber attacks
0
2021
Asynchronous finite-time ${H_\infty }$
0
2023
Distributed filtering under false data injection attacks
1
2019
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
An output-coding-based detection scheme against replay attacks in cyber-physical systems
1
2021
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
Observer-based resilient control of positive systems with heterogeneous DoS attacks: a Markov model approach
1
2022
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
Observer-based dynamic event-triggered robust ${H_\infty }$
1
2021
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
Dynamic event-based distributed piecewise filtering over sensor networks under periodic DoS attacks
1
2023
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
Probabilistic-constrained distributed filtering for a class of nonlinear stochastic systems subject to periodic DoS attacks
1
2020
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
Finite-time control for discrete-time nonlinear Markov switching LPV systems with DoS attacks
1
2023
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
A semi-Markovian jumping system approach to secure DPC of nonlinear networked unmanned marine vehicle systems with DoS attack
1
2023
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
SMC for discrete-time networked semi-Markovian switching systems with random DoS attacks and applications
2
2023
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
... 注1 当$ \alpha (k) \equiv 1 $ 21 ]、[24 ];当$\beta (k) \equiv 1$ 22 ]、[23 ]. ...
Dynamic event-triggered model predictive control under channel fading and denial-of-service attacks
2
2024
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
... 注1 当$ \alpha (k) \equiv 1 $ 21 ]、[24 ];当$\beta (k) \equiv 1$ 22 ]、[23 ]. ...
Resilient control of wireless networked control system under denial-of-service attacks: a cross-layer design approach
2
2020
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
... 注1 当$ \alpha (k) \equiv 1 $ 21 ]、[24 ];当$\beta (k) \equiv 1$ 22 ]、[23 ]. ...
Resilient adaptive event-triggered fuzzy tracking control and filtering for nonlinear networked systems under denial-of-service attacks
2
2022
... 网络攻击通常分为3类: 欺骗攻击、拒绝服务( denial-of-service,DoS )攻击和重放攻击[8 ,10 -13 ] . DoS攻击通过中断信号传输来阻止信号更新,对控制系统最具危险性. DoS攻击的发起对系统的先验性知识要求不高,有越来越多的学者关注与DoS攻击相关的研究[14 -15 ] ,如在周期性DoS攻击下的控制器设计问题[16 ] ,分布式滤波问题[17 -18 ] . 上述研究针对确定性的DoS攻击,但具有随机特性的DoS攻击更为常见[8 ,19 ] . DoS攻击的随机特性建模主要采用2种方法: 伯努利分布模型和马尔可夫分布模型. 在基于伯努利分布模型方面,Ye等[20 ] 针对存在于控制器-执行器(C-A)通道的DoS攻击,研究基于网络的T-S模糊海上无人航行器系统的安全动态定位控制问题;Qi等[21 ] 针对存在于传感器-控制器(S-C)通道的DoS攻击,研究半马尔可夫切换系统的离散时间滑模控制问题. 在基于马尔可夫分布模型方面,Shi等[22 -23 ] 针对存在于C-A通道的DoS攻击,研究动态事件触发机制的模型预测控制问题和无线网络控制系统的弹性控制问题;Zhao等[24 ] 针对存在于S-C通道的DoS攻击,研究非线性系统的自适应事件触发跟踪控制与滤波问题. ...
... 注1 当$ \alpha (k) \equiv 1 $ 21 ]、[24 ];当$\beta (k) \equiv 1$ 22 ]、[23 ]. ...
Hybrid dynamic event-triggered tracking control of wheeled mobile robots against stochastic DoS attacks
2
2023
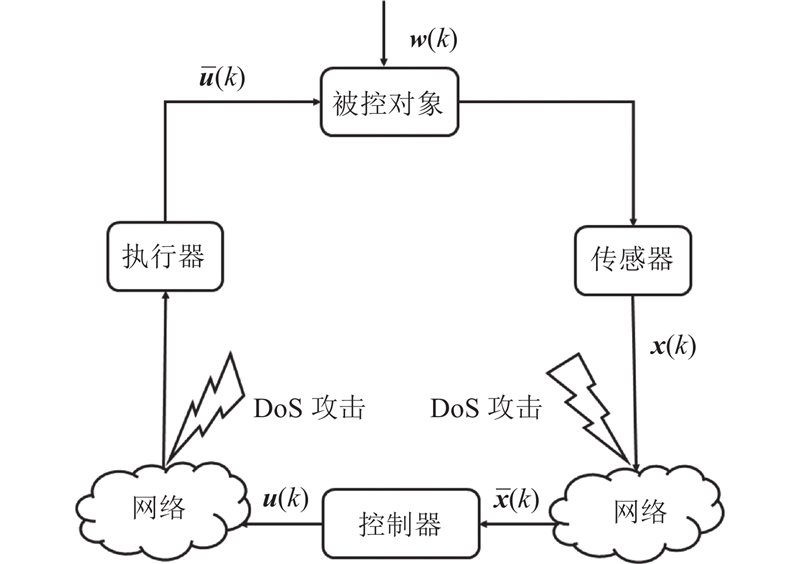
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
... [25 ]视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
2
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
... [26 ]将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
具有随机丢包的一类网络控制系统的故障检测
1
2011
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
具有随机丢包的一类网络控制系统的故障检测
1
2011
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Finite-time almost sure stability of a Markov jump fuzzy system with delayed inputs
1
2022
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Finite-time non-fragile ${l_2} - {l_\infty }$
2
2018
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
... [29 ]、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Adaptive event-triggered finite-time sliding mode control for singular T-S fuzzy Markov jump systems with asynchronous modes
1
2023
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
1
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Finite-time control of linear systems subject to parametric uncertainties and disturbances
1
2001
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Non fragile finite-time ${l_2} - {l_\infty }$
1
2015
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Finite-time asynchronous state estimation for jump systems with partial transition probabilities via redundant channels: a co-design method
1
2021
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Finite-time energy-to-peak fuzzy filtering for persistent dwell-time switched nonlinear systems with unreliable links
1
2021
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Hybrid event-based asynchronous finite-time control for cyber-physical switched systems under denial-of-service attacks
1
2023
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
Finite-time resilient sliding mode control of nonlinear UMV systems subject to DoS attacks
2
2023
... 双通道通信网络常见于NCSs. Geng等[25 ] 研究轮式移动机器人在双通道同步攻击下的轨迹跟踪问题;Lian等[26 ] 研究双通道切换系统在拒绝服务攻击下的时间触发控制问题. Geng等[25 ] 视2个通道的DoS攻击为同步攻击,忽略了通道不同步攻击的情况. Lian等[26 ] 将存在于2个通道的攻击独立建模,黄鹤等[27 ] 指出2个通道通常共享1个通信网络,因此2个通道的DoS攻击相互关联. 本研究考虑双通道存在DoS攻击的情形,将双通道DoS攻击的动态特性进行统一建模,将闭环系统描述为包含4个模态的马尔可夫跳变系统. 现有研究大多集中在传统的李雅普诺夫稳定性概念之下. 该概念描述系统状态在无限时间间隔内的收敛特性[28 -29 ] . 实际系统往往要在短时间内做出响应,如导弹控制系统、机器人运动控制系统、通信网络系统等[30 ] ,李雅普诺夫稳定性解决这类问题时存在局限性. Dorato[31 ] 提出有限时间稳定的概念,探究系统状态在有限时间间隔内的收敛特性,为了使有限时间稳定性概念更具一般性,Amato等[32 ] 进一步提出有限时间有界性的概念. 有限时间控制被广泛应用于随机系统[29 ] 、马尔可夫跳变系统[33 -34 ] 和切换系统[35 ] 等领域. 在应对网络攻击时,有限时间控制的问题研究成果相对有限,Ren等[36 -37 ] 只考虑DoS攻击存在单通道的有限时间问题,鲜见涉及双通道DoS攻击的有限时间控制问题的文献,研究S-C通道和C-A通道可能都存在DoS攻击的有限时间控制问题具有重要的理论意义和实际价值. ...
... 注3 定理2中不等式的保守性可以通过调整给定参数来降低. Ye等[37 ] 指出,式(35)、(36)的保守性可以通过增大$\alpha $ ${\delta _2}$ $\omega $ ${{\boldsymbol{R}}}$ $\gamma $
Robust static output feedback infinite horizon RMPC for linear uncertain systems
1
2016
... 注2 由于式(14)中矩阵$ {\overline {\boldsymbol{A}}_i},i = 1,2 $ ${\boldsymbol{ K}} $ $ {\tilde {\boldsymbol{B}}_i}{\boldsymbol{K}}{\overline{\boldsymbol{ I}}_i},i = 1,2 $ $ {\overline {\boldsymbol{I}}_i},i = 1,2 $ ${{\boldsymbol{M}}_i},i = 1,2$ ${{\overline {\boldsymbol{I}}}_i}{{\boldsymbol{{M}}}_i} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{I}}},{\boldsymbol{0}} \end{array}} \right],i = 1,2$ . 一般来说,对应的矩阵${{{\boldsymbol{M}}}_i}$ [38 ] . ...