孔内深层超强夯(super down-hole dynamic consolidation, SDDC)技术具有处理深度大、适用范围广、工程造价低等特点,在西北地区黄土地基的湿陷性处理中广泛应用. 冯志焱等[5]利用现场静载荷试验对比分析SDDC处理前后黄土地基的湿陷性和承载力,结果表明SDDC技术能够有效消除黄土的湿陷性并将地基承载力提高超过2倍. 黄雪峰等[6]由浸水试验得到不同桩间距下地基土的挤密系数和湿陷系数,通过拟合建立平均挤密系数与桩间距的函数模型. 王小军等[7-8]通过对比3种不同处理措施(SDDC桩法、水泥挤密桩法和强夯法)下地基的沉降量大小和浸水效果,认为SDDC桩法的处理深度最大且处理效果最好. 杨校辉等[9]开展不同深度的SDDC桩复合地基载荷浸水试验,根据不同处理深度下的地基沉降量,提出新的剩余湿陷量控制及湿陷性评价标准. Liu等[10]采用Ansys有限元软件对处理后的渣土桩复合地基进行承载力计算和分析,发现处理后的地基具有半柔性半刚性的特点,桩身土与桩间土之间具有良好的协调性. 孔洋等[11]开展原位浸水试验,研究SDDC桩处理大厚度湿陷性黄土地基的挤密效果,根据挤密区沉降量的变化特性探究水分的运移规律. Xue等[12]将SDDC技术与水泥粉煤灰碎石(cement fly-ash gravel,CFG)桩结合,发现处理后的复合地基不仅满足承载力设计要求,消除了黄土湿陷性,还能够缩短工期,节省经费.
SDDC技术在成桩过程中,由于夯锤的超强夯作用,桩周土体会受到很大的侧向挤密效应. 若将成桩过程视为圆柱形孔扩张的平面应变问题,则桩周土体的挤密效应可通过典型的圆孔扩张理论[13-16]求解. 罗嗣海等[17]推导当初始半径不趋近于0时圆柱形孔扩张的弹塑性解,研究当预钻孔取土打桩时孔径大小对挤土效应的影响. 胡伟等[18-19]结合半球形孔扩张模型和修正剑桥模型,考虑沉桩速度,推导出非饱和土中沉桩后桩周应力和位移的解析解,表明沉桩影响范围与沉桩速度成正比. 韩同春等[20]将沉桩时的挤土过程视为空间轴对称圆柱孔准静态扩张过程,基于Mohr-Coulomb及空间滑动面(spatially mobilized plane,SMP)屈服准则求解塑性区的应力场和位移场的理论解. 贾尚华等[21]利用土体塑性区的边界条件和土体体积变化规律,推导和分析砂土的柱孔扩张问题中初始半径、扩孔半径和扩孔压力三者间的关系. 沈才华等[22]基于圆孔扩张理论,考虑挤密砂桩在挤密过程中砂桩自身的体积变化,建立桩身压缩模量的计算方法,结合桩间土的压缩曲线,构建桩周土平均压缩模量的计算公式.
研究SDDC桩在湿陷性黄土地基中的加固效果大多侧重于理论预测和加固机理,鲜少针对成桩过程中桩周土的加固范围和施工时的参数设计,由于缺少现场实例的验证,存在所得理论难以推广和应用的问题. 本研究基于圆孔扩张理论和Mohr-Coulomb屈服准则,对某湿陷性黄土地基处理项目中SDDC桩的加固范围以及桩周土体的应力场和位移场进行理论分析与计算,开展现场深层水平位移试验以验证理论计算结果,分析不同初始孔径与成桩直径对挤土效应的影响,以期为湿陷性黄土地区SDDC桩的设计和应用提供参考.
1. 圆孔扩张理论的一般解
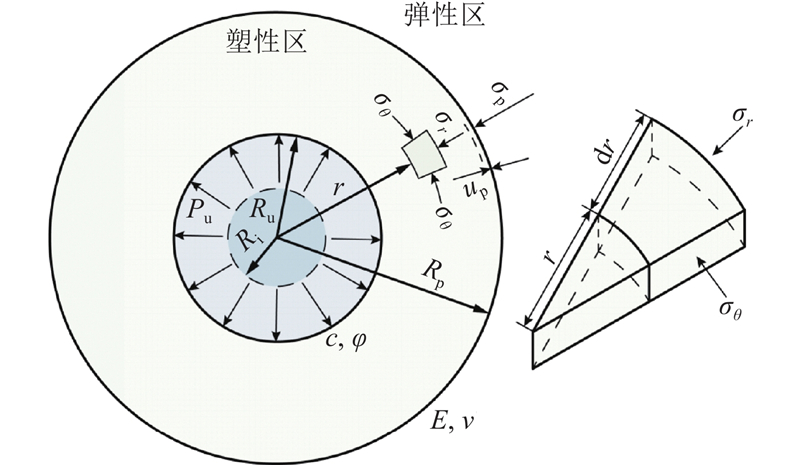
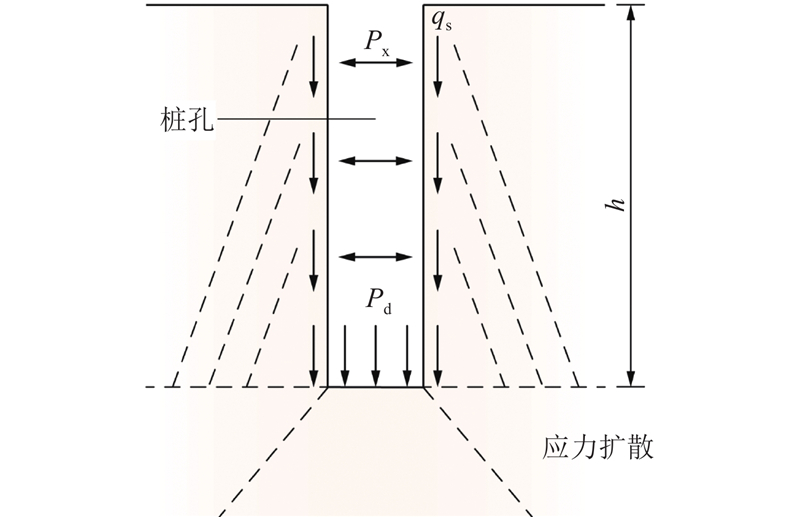
将SDDC桩的成桩过程视为圆柱形孔扩张的平面应变问题,只考虑成桩前、后的理想状态. 由于夯击时间短暂,故将其成桩过程视为不固结、不排水过程. 如图1所示,在c为黏聚力,φ为内摩擦角的无限土体中,具有初始半径Ri的圆柱形孔在超强夯形成的均匀内压p的作用下扩张. 在此扩张过程中,柱孔周围的土体会从弹性变形状态逐渐进入塑性变形状态,孔内填料随着p的增加被不断挤密到周围土体,桩周土体的塑性区不断扩张,塑性区以外的土体仍保持弹性平衡状态. 当土体达到极限状态时,塑性区扩张内压达到pu,冲扩孔半径达到Ru,塑性区半径达到Rp. 此时,冲扩孔形成的半径即为最终SDDC桩体的半径,塑性区半径即为超强夯作用对土体的有效加固区半径. 进行如下基本假定:1)土体是均质且各向同性的理想弹塑性材料,2)土体屈服服从Mohr-Coulomb屈服准则,3)土体在扩孔过程中不考虑竖向压缩变形,4)圆孔在无限大的土体中扩张,5)视圆孔扩张问题为轴对称平面应变问题.
图 1
1.1. 具有初始孔径的圆孔扩张理论弹性解
在SDDC桩加固地基的弹性区,假定土体服从小变形理论,由轴对称得到圆孔扩张问题的平衡微分方程为
式中:σr为径向应力,σθ为切向应力,r为土体到中心轴的径向距离. 非饱和土中柱孔周围土体的总应力平衡微分方程与饱和土类似. 由非饱和土有效应力公式[23]可知
式中:σn为净应力;s为吸力;χ为有效应力参数,与饱和度和吸力有关. 完全饱和土和干土的有效应力参数分别为1和0,非饱和土的有效应力参数表达式[24]为
式中:se为土体从饱和状态过渡到非饱和状态时的吸力. 非饱和土中平衡微分方程的有效应力形式为
土体饱和度与吸力一一对应,在不排水条件下,土体的质量含水率(单位体积土壤中所含水的质量与干土质量的比)不变,由于土中气体的排出使得孔隙在扩孔过程中被压缩,土体饱和度发生变化,导致塑性区的吸力发生变化,此时吸力是变量而非常量,在计算过程中很难考虑,为此忽略塑性区土体饱和度的变化及其对土体吸力的影响. 由应力边界条件得到
式中:σp为圆孔发生塑性变形的临界应力,σ0为土层径向的初始应力. 圆孔扩张的几何方程为
式中:ur为径向位移,εr为径向应变,εθ为切向应变. 消除位移ur得到变形协调条件:
根据广义胡克定律,平面应变问题圆孔扩张的应力-应变关系表示为
式中:E为弹性模量,ν为泊松比. 联立平衡方程、变形协调方程和应力-应变关系,得到径向应力表示的积分方程,其通解形式为
其中A和B均为积分常数. 将式(12)代入式(1),得到切向应力:
由边界条件式(5)、(6),确定
代入式(12)、(13),得到弹性区应力解为
弹性区的径向位移ur由式(11)中的切向应变求得:
1.2. 基于Mohr-Coulomb屈服准则的塑性解
假定土体在塑性区服从大变形理论和Mohr-Coulomb屈服条件,结合弹性区和塑性区的边界条件求解塑性区的应力及变形关系. 圆孔扩张时的Mohr-Coulomb屈服条件:
由此得到
塑性区应力分量应满足平衡方程式(1)和屈服条件式(21),即
对该一阶线性微分方程求解:
其中C为常数,利用边界条件r=Ru时,σr=pu确定:
代入式(20)、(23),得到塑性区应力分量解:
利用弹-塑性界面应力分量的连续性,在r=Rp处,弹性区和塑性区的应力相等,由此得到
利用弹塑性边界式(5),结合式(17)和式(20)得到
将式(28)代入式(27),得到极限扩孔压力与塑性区半径的关系:
假设圆孔扩张后的总体积变化等于弹性区体积变化与塑性区体积变化之和,且本研究只考虑桩长范围内土体的径向位移变化,忽略土体的竖向变形:
式中:up为塑性区边界的径向位移;
在塑性区与弹性区的交界处,即r=Rp时,塑性区边界的径向位移为
将式(28)、(32)代入式(31)得到
解得塑性区半径,
将式(34)代入式(29),得到极限扩孔压力pu与初始孔径Ri和扩孔半径Ru的关系式:
将式(28)代入式(16)~(18),得到弹性区、塑性区应力场和位移场的解:
2. 现场试验概况
2.1. 场地及试桩概况
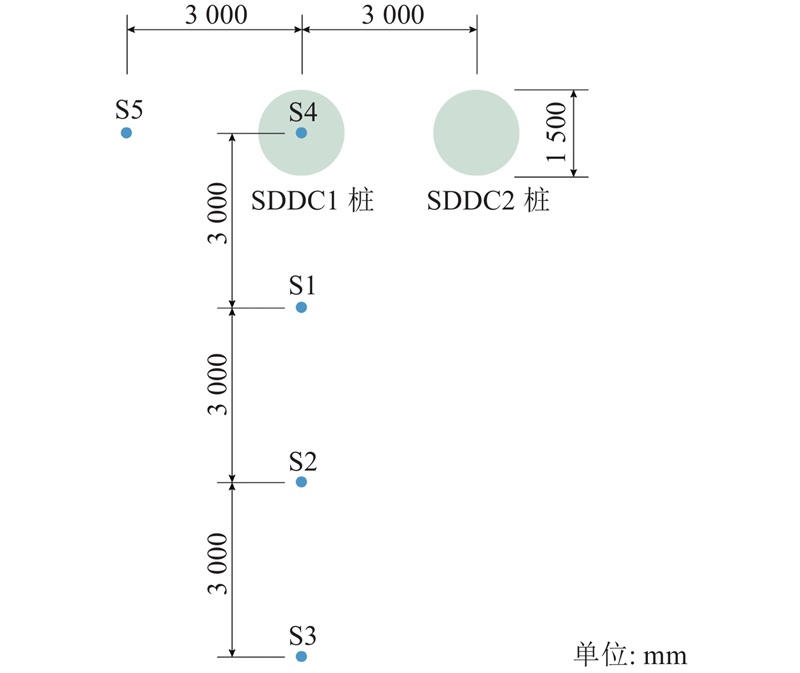
本研究依托某地基处理项目进行现场试验,该项目位于甘肃省兰州新区,距离兰州市区约45 km. 场地原始地貌单元属黄土丘陵地貌,主要呈低丘缓坡与沟壑交错分布,经低丘缓坡沟壑改造,挖填整平后地形开阔,地势较为平坦,土层分布连续. 从该项目场地中选择2根SDDC桩作为试验桩,在成桩前、后分别距离桩心不同位置处开展深层水平位移试验. 2根试验桩均采用长螺旋旋挖钻机成孔,孔内分层回填素土后夯实成桩. 夯锤质量为9.8 t,桩内虚铺厚度为1.5 m,夯击8次,桩身10~20 m夯锤提升高度为15 m,桩身10 m以上夯锤提升高度为10 m. 桩体成孔直径为1 200 mm,成桩直径为1 500 mm,桩长为20 m. 试桩位置如图2所示,其中S1~S5为深层水平位移孔编号.
图 2
图 2 试桩及深层水平位移孔布置
Fig.2 Test piles and deep horizontal displacement holes layout
2.2. 土体物理力学参数
根据场地勘探结果,结合区域地质资料对比分析可知,SDDC桩处理深度内土层以马兰黄土为主,土质较均匀,物理力学性质一般,具有Ⅳ级自重湿陷性. 该土层地表以下约13.0 m为稍密状态,其下为中密状态. 对试验区土层采取土样进行室内土工试验及原位测试,所得试验数据统计如表1所示.
表 1 土体物理力学指标
Tab.1
| 参数 | 数值 | |
| h=0~13 m | h=13~20 m | |
| 密度ρ/(kg·m−3) | 1 440 | 1 620 |
| 泊松比ν | 0.42 | 0.43 |
| 黏聚力c/kPa | 15.7 | 15.7 |
| 内摩擦角φ/(°) | 25.9 | 25.9 |
| 弹性模量E/MPa | 10.0 | 12.0 |
2.3. 深层水平位移试验
为了确定SDDC桩成桩过程中夯扩作用对不同距离桩周土水平位移的影响程度,对理论计算结果进行验证,现场在2根试桩的不同距离对桩周土开展深层水平位移试验(深层水平位移孔布置见图2),如图3所示. 1)在SDDC1桩施工前,分别对距离桩心3.0、6.0、9.0 m处的S1、S2、S3进行深层水平位移孔的钻孔工作,孔深均为20 m,钻孔完成后埋设测斜管,并在钻孔中填砂注水,保证填砂的密实性. 2)进行SDDC1桩的施工,分别在SDDC1桩成孔后尚未填料时和成桩完成后对S1、S2、S3的深层水平位移进行1次测量,测量时待导管稳定后先测取初始读数,之后沿深度方向每隔0.5 m测读1次. SDDC1桩完成后进行S4、S5的钻孔工作,孔深为20 m,钻孔完成后埋设测斜管,并在钻孔中填砂注水. 3)进行SDDC2桩的施工,分别在SDDC2桩成孔后尚未填料时和成桩完成后对S4、S5的深层水平位移进行1次测量.
图 3
3. 理论计算与试验结果分析
3.1. 理论计算
小孔扩张理论的基本假定如下:土体是均质且各向同性的理想弹塑性材料. 采用加权平均数的计算方法对现场试验区土体进行拟合,得到新的物理力学指标作为计算参数:c=15.7 kPa、φ=25.9°、ν=0.42、E=10.7 MPa、初始孔径2Ri=1 200 mm、最终孔径2Ru=1 500 mm. 取
图 4
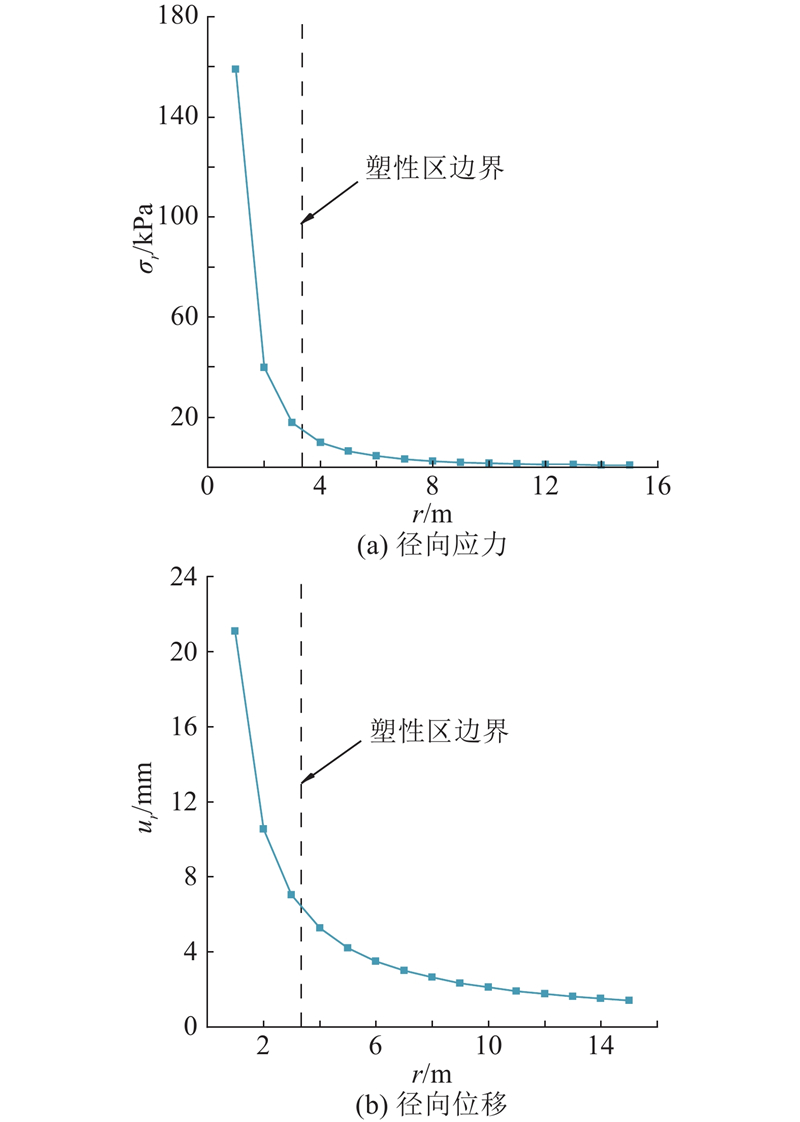
图 4 径向应力和径向位移随径向距离的变化
Fig.4 Variation of radial stress and radial displacement with radial distance
3.2. 现场试验结果
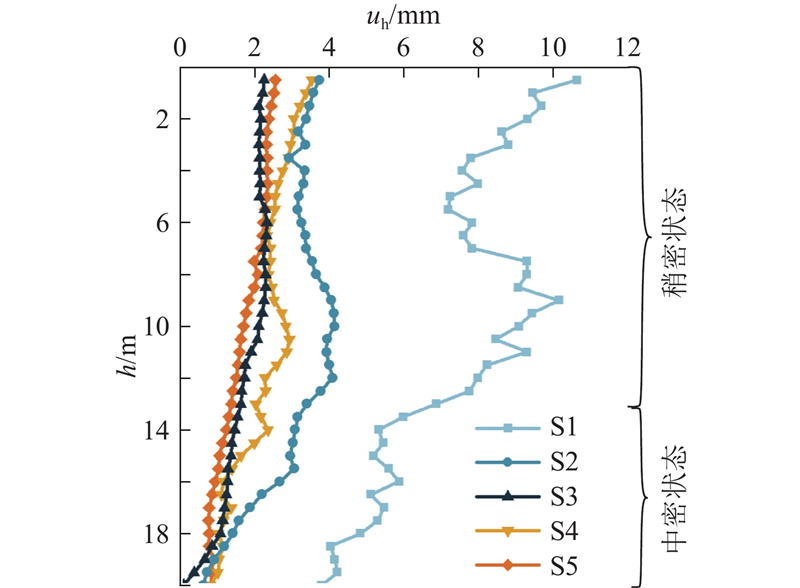
对比成桩完成后深层水平位移试验的测量结果和成孔后尚未填料时的测量结果,得到SDDC1、SDDC2桩成桩过程中各测孔内土体不同深度的水平位移uh变化,如图5所示. 对比图中S1、S2、S3的深层水平位移试验结果可以发现,随着与桩体中心轴距离的增加,桩周土体各深度的水平位移逐渐减小. 在S1处,土体水平位移最大,且由于距离桩孔较近,受施工扰动影响较大,数据离散程度最高;该测孔中土体水平位移的分布形式近似呈双峰形分布,最大值位于地表处,为10.64 mm,在地表以下9.0 m处出现第二次“峰值”,为10.15 mm;在11~14 m深度,水平位移自下而上增速较快. 这是由于该深度范围为上部稍密土层与下部中密土层的分界面,分界面处土体挤压应力会发生剧变,导致土体位移加大[25]. 在S2和S3处,由于距离桩孔较远,深层水平位移较小,且数据离散性较低,不同深度的位移量较为接近;2个测孔中的最大水平位移均位于地表以下,分别为4.13和2.33 mm,地表处的水平位移分别为3.73和2.25 mm. 分别对比图中S1和S4、S2和S5的深层水平位移试验结果可以发现,虽然S1到SDDC1桩的距离和S4到SDDC2桩的距离均为3.0 m,但S4中土体的水平位移远小于S1的,最大位移为3.52 mm,且数据整体的离散程度较低. 这是由于SDDC1桩的桩体密实度高于原状土,且其侧向挤密作用极大地提高了桩间土体的密实度和均匀度,导致SDDC2桩的挤密效果有所降低;在分别距离2根试桩6.0 m的S2和S5处,土体位移的差距相对较小,表明SDDC桩与桩之间的相互影响会随着距离的增加而衰减. 为了避免桩体相互影响导致复合地基的承载力低于设计值,在成桩时应采用间隔成桩的方式(隔行、隔列、跳桩)施工.
图 5
图 5 测孔深层水平位移发展
Fig.5 Development of deep horizontal displacements of measurement holes
图 6
图 7
3.3. 试验结果与理论计算对比
将SDDC桩的成桩过程视为圆柱形孔扩张的平面应变问题,只考虑单桩对桩周土体的影响,为此将理论计算得到的土体径向位移ur,c与现场深层水平位移试验得到的S1、S2、S3中的各深度平均水平位移uh,f进行对比,验证理论分析的正确性. 不同距离土体位移的计算值与实测值对比如表2所示. 可以看出,在r=3.0 m处,土体径向位移的计算值略小于实测的平均水平位移;在r=6.0和9.0 m处,计算值略大于实测值. 本研究没有考虑塑性区土体饱和度的变化及其对土体吸力的影响,且理论计算参数与现场土体参数存在误差,导致计算值与实测值存在少量偏差,但两者的整体变化趋势基本相同. 由此可知,基于圆孔扩张理论研究SDDC桩有效加固范围和桩周土体位移场分布的方法可行.
表 2 土体位移计算值与实测值
Tab.2
| 测孔编号 | r/m | ur,c/mm | uh,f/mm |
| S1 | 3.0 | 7.03 | 7.31 |
| S2 | 6.0 | 3.52 | 3.03 |
| S3 | 9.0 | 2.34 | 1.75 |
4. 初始孔径与成桩直径的影响分析
为了研究初始孔径与成桩直径对SDDC桩加固范围的影响,利用本研究所提计算方法对不同孔径和不同桩径下SDDC桩的有效加固范围以及桩周土体的应力场和位移场分布进行分析,土体计算参数与3.1节相同.
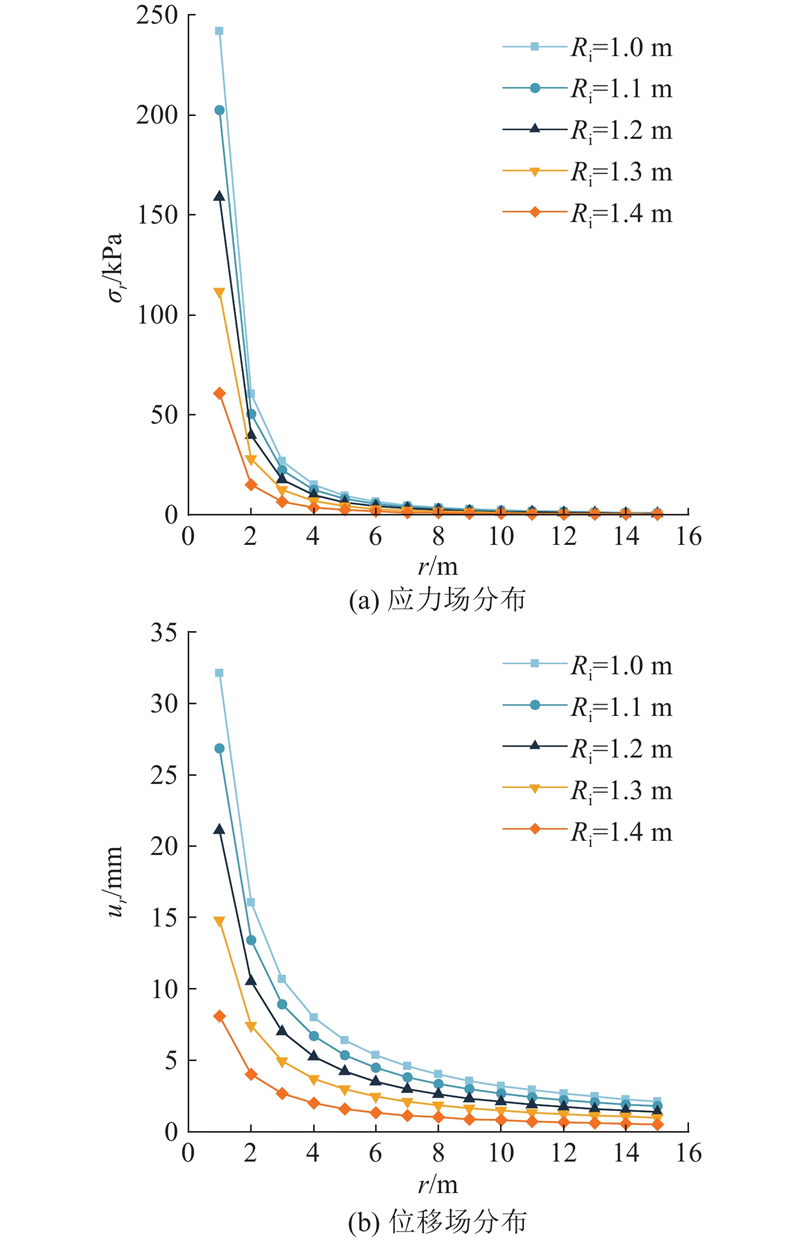
4.1. 不同初始孔径的影响
表 3 不同孔径对孔内深层超强夯桩加固范围的影响(Ru=1.5 m)
Tab.3
| Ri/m | Rp/m | pu/kPa |
| 1.0 | 4.14 | 98.88 |
| 1.1 | 3.78 | 91.95 |
| 1.2 | 3.35 | 83.17 |
| 1.3 | 2.81 | 71.46 |
| 1.4 | 2.08 | 53.99 |
图 8
图 8 不同孔径下的应力场和位移场分布(Ru=1.5 m)
Fig.8 Distribution of stress field and displacement field with different pore diameters (Ru=1.5 m)
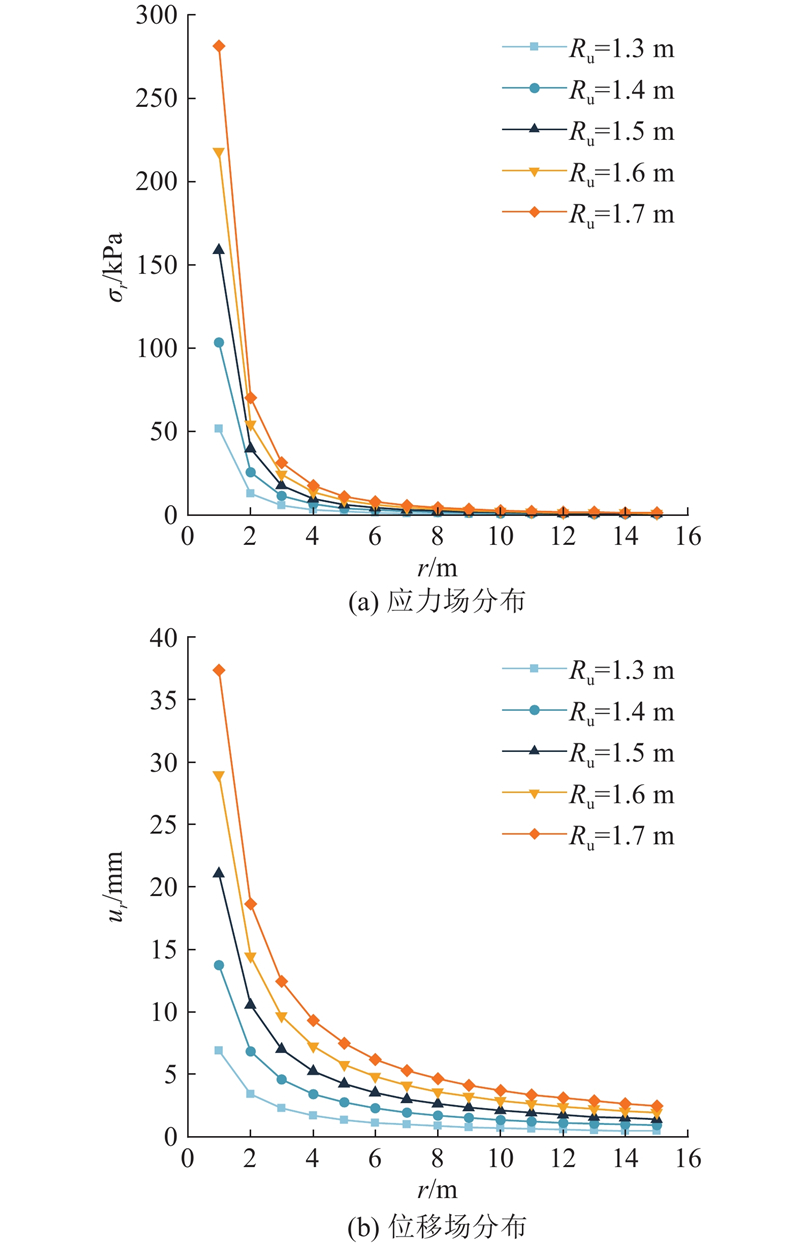
4.2. 不同成桩直径的影响
表 4 不同桩径对孔内深层超强夯桩加固范围的影响(Ri=1.2 m)
Tab.4
| Ru/m | Rp/m | pu/kPa |
| 1.3 | 1.92 | 57.31 |
| 1.4 | 2.71 | 73.39 |
| 1.5 | 3.35 | 83.17 |
| 1.6 | 3.93 | 89.95 |
| 1.7 | 4.46 | 94.99 |
图 9
图 9 不同桩径下的应力场和位移场分布(Ri=1.2 m)
Fig.9 Distribution of stress field and displacement field with different pile diameters (Ri=1.2 m)
对比不同初始孔径与不同成桩直径下SDDC桩的有效加固区半径和最终扩孔压力可以看出,不同桩径下的有效加固区半径变化范围更大,不同孔径下的最终扩孔压力变化范围更大,这表明初始孔径对SDDC成桩时所需的扩孔压力影响更大,成桩直径对SDDC成桩后的有效加固范围影响更大.
5. 结 论
(1)基于平面应变条件下圆孔扩张理论计算得到的湿陷性黄土地基中SDDC桩桩周土体水平位移与现场实测值吻合度较高,可以利用该方法计算SDDC桩有效加固范围和桩周土体位移场分布.
(2)SDDC桩加固地基时,桩周土体越密实,加固效果越差;该地基处理项目中SDDC桩的有效加固区半径为3.35 m,约为设计桩径的2.23倍.
(3)桩周土体的径向应力和径向位移均随着径向距离的增大呈对数衰减,且距离桩体越近,衰减越剧烈;径向应力衰减更快,最终趋于土体的初始应力,径向位移逐渐趋于0.
(4)在设计桩径一定的情况下,应力场和位移场的衰减幅度与初始孔径成反比;在初始孔径一定的情况下,应力场和位移场的衰减幅度与成桩直径成正比.
(5)SDDC桩对土体的加固效果会导致相邻桩的挤土效果减弱. 本研究主要针对SDDC单桩的水平挤土效应,未考虑多根桩之间的相互影响,未来计划针对SDDC桩的群桩效应开展进一步研究.
参考文献
试论我国黄土力学研究中的若干新趋向
[J].DOI:10.3321/j.issn:1000-4548.2001.01.002 [本文引用: 1]
Exploration of some new tendencies in research of loess soil mechanics
[J].DOI:10.3321/j.issn:1000-4548.2001.01.002 [本文引用: 1]
Collapsibility, composition, and microstructure of loess in China
[J].
银西高铁董志塬地区黄土工程特性分析研究
[J].DOI:10.3969/j.issn.1006-2106.2016.12.006 [本文引用: 1]
Analysis and study of loess engineering characteristics of Dongzhiyuan on Xi’an-Yinchuan high-speed railway
[J].DOI:10.3969/j.issn.1006-2106.2016.12.006 [本文引用: 1]
大厚度自重湿陷性黄土地基处理厚度与处理方法研究
[J].
Study on foundation treatment thickness and treatment method for collapse loess with large thickness
[J].
孔内深层强夯法处理湿陷性黄土地基的一个实例
[J].DOI:10.3969/j.issn.1000-7598.2005.11.034 [本文引用: 1]
An example of treating collapsible loess by super down hole deep compaction
[J].DOI:10.3969/j.issn.1000-7598.2005.11.034 [本文引用: 1]
大厚度自重湿陷性黄土湿陷变形特性水分入渗规律及地基处理方法研究
[J].
Research on deformation, permeability regularity and foundation treatment method of dead-weight collapse loess with heavy section
[J].
郑西客运专线湿陷性黄土区试验路堤的沉降观测与预测研究
[J].DOI:10.3969/j.issn.1000-7598.2010.z1.036 [本文引用: 1]
Settlement observation and prediction research of test embankment in collapsible loess area along Zhengzhou-Xi’an passenger dedicated line
[J].DOI:10.3969/j.issn.1000-7598.2010.z1.036 [本文引用: 1]
Ⅳ级自重湿陷性黄土区客运专线铁路路堤处理地基的现场试验研究
[J].
Field test research on treatment effect of embankment foundation in class Ⅳ dead-weight collapsible loess zone along railway passenger dedicated line
[J].
大厚度自重湿陷性黄土地基处理深度和湿陷性评价试验研究
[J].
Experimental study on collapsibility evaluation and treatment depths of collapsible loess upon self weight with thick depth
[J].
DDC法复合黄土地基的原位浸水试验研究
[J].
In-situ soaking test on composite loess foundation with down-hole dynamic compaction (DDC)
[J].
The research on treating collapsible loess by down whole deep compaction and cement fly-ash gravel
[J].DOI:10.30564/frae.v2i1.485 [本文引用: 1]
Expansion of cavities in infinite soil mass
[J].DOI:10.1061/JSFEAQ.0001740 [本文引用: 1]
Finite cavity expansion in dilatant soils: loading analysis
[J].
Rigorous similarity solutions for cavity expansion in cohesive-frictional soils
[J].DOI:10.1061/(ASCE)1532-3641(2002)2:2(233)
基于非线性Mohr-Coulomb强度准则下的扩孔问题解析
[J].DOI:10.3321/j.issn:1000-131X.2009.07.014 [本文引用: 1]
Analytical solution of cavity expansion with the non-linear Mohr-Coulomb failure rule
[J].DOI:10.3321/j.issn:1000-131X.2009.07.014 [本文引用: 1]
预钻孔孔径对部分挤土桩挤土效应的影响研究
[J].DOI:10.3969/j.issn.1000-7598.2002.02.018 [本文引用: 1]
Study on the influence of the diameter of pre-driven borehole on soil-displacement effect of partly soil-displaced piles
[J].DOI:10.3969/j.issn.1000-7598.2002.02.018 [本文引用: 1]
非饱和土中球形孔扩张的弹塑性分析
[J].DOI:10.3321/j.issn:1000-4548.2006.10.022 [本文引用: 1]
Elastic-plastic solution of expansion of sphere cavity in unsaturated soils
[J].DOI:10.3321/j.issn:1000-4548.2006.10.022 [本文引用: 1]
非饱和土中考虑沉桩扩孔速度影响的半球形孔扩张弹塑性分析
[J].
Elastoplastic analysis of expansion of hemisphere cavity in unsaturated soil considering pile driving velocity
[J].
柱孔扩张理论的空间轴对称解在沉桩挤土效应中的应用
[J].DOI:10.3969/j.issn.1000-6915.2012.z1.083 [本文引用: 1]
Application of space axisymmetric solutions of cavity expansion to soil squeezing of pile driving
[J].DOI:10.3969/j.issn.1000-6915.2012.z1.083 [本文引用: 1]
砂土中柱孔扩张问题的扩孔压力与扩孔半径分析
[J].
Analysis of expanded radius and internal expanding pressure of cylindrical hole
[J].
基于扩孔理论的挤密砂桩复合地基桩土应力比计算方法
[J].
Determination of pile-soil stress ratio for compaction foundation using cavity expansion theory
[J].
The principle of effective stress
[J].
Cavity expansion in unsaturated soils exhibiting hydraulic hysteresis considering three drainage conditions
[J].DOI:10.1002/nag.2379 [本文引用: 1]
饱和成层地基中静压单桩挤土效应的有限元模拟
[J].DOI:10.3969/j.issn.1000-7598.2008.11.022 [本文引用: 1]
Squeezing effects of jacked pile in layered soil
[J].DOI:10.3969/j.issn.1000-7598.2008.11.022 [本文引用: 1]
基于高精度全自动监测系统的静压群桩现场试验
[J].
Field test of static pressure pile group based on high precision automatic monitoring system
[J].