[1]
骆冠勇, 潘泓, 曹洪, 等 承压水减压引起的沉降分析
[J]. 岩土力学 , 2004 , 25 (Suppl.2 ): 196 - 200
DOI:10.3969/j.issn.1000-7598.2004.z2.040
[本文引用: 1]
LUO Guanyong, PAN Hong, CAO Hong, et al Analysis of settlements caused by decompression of confined water
[J]. Rock and Soil Mechanics , 2004 , 25 (Suppl.2 ): 196 - 200
DOI:10.3969/j.issn.1000-7598.2004.z2.040
[本文引用: 1]
[2]
LIU J C, LEI G G, MEI G X One-dimensional consolidation of visco-elastic aquitard due to withdrawal of deep-groundwater
[J]. Journal of Central South University , 2012 , 19 (1 ): 282 - 286
DOI:10.1007/s11771-012-1002-9
[本文引用: 1]
[3]
徐进, 王少伟, 杨伟涛 水位变化下可压缩土层的黏弹性耦合变形分析
[J]. 岩土力学 , 2020 , 41 (3 ): 1065 - 1073
XU Jin, WANG Shaowei, YANG Weitao Analysis of coupled viscoelastic deformation of soil layer with compressible constituent due to groundwater level variation
[J]. Rock and Soil Mechanics , 2020 , 41 (3 ): 1065 - 1073
[4]
徐进, 杨伟涛, 陈征, 等 水位下降诱发含水层–弱透水层1维黏弹性固结分析
[J]. 工程科学与技术 , 2021 , 53 (5 ): 89 - 97
XU Jin, YANG Weitao, CHEN Zheng, et al One-dimensional viscoelastic consolidation analysis of aquifer–aquitard due to drawdown of water level
[J]. Advanced Engineering Sciences , 2021 , 53 (5 ): 89 - 97
[5]
谢康和, 陶立为, 王玉林, 等 越流系统中弱透水层的一维固结解及分析
[J]. 沈阳工业大学学报 , 2012 , 34 (5 ): 581 - 585
[本文引用: 1]
XIE Kanghe, TAO Liwei, WANG Yulin, et al One-dimensional consolidation solution and analysis for aquitard in leakage system
[J]. Journal of Shenyang University of Technology , 2012 , 34 (5 ): 581 - 585
[本文引用: 1]
[6]
YAO J F, XIE K H, HUANG D Z. Analytical solution for one-dimensional consolidation of soil layer induced by time-dependent groundwater drawdown [J]. Applied Mechanics and Materials , 2013, 405/406/407/408: 83–88.
[7]
吴浩, 谢康和, 黄大中 第二类越流系统中结构性弱透水土层一维固结解析解
[J]. 岩土工程学报 , 2014 , 36 (9 ): 1688 - 1695
DOI:10.11779/CJGE201409016
WU Hao, XIE Kanghe, HUANG Dazhong Analytical solution for one-dimensional consolidation of structured aquitard soils in second kind of leakage system
[J]. Chinese Journal of Geotechnical Engineering , 2014 , 36 (9 ): 1688 - 1695
DOI:10.11779/CJGE201409016
[8]
张玮鹏, 谢康和, 吕文晓, 等 抽水引起的有起始比降饱和土固结解析解
[J]. 中南大学学报: 自然科学版 , 2016 , 47 (3 ): 875 - 881
[本文引用: 1]
ZHANG Weipeng, XIE Kanghe, LÜ Wenxiao, et al Analytical solution to one-dimensional consolidation of saturated soil with threshold gradient induced by groundwater pumping
[J]. Journal of Central South University: Science and Technology , 2016 , 47 (3 ): 875 - 881
[本文引用: 1]
[9]
CHEN R P, ZHOU W H, CHEN Y M Influences of soil consolidation and pile load on the development of negative skin friction of a pile
[J]. Computers and Geotechnics , 2009 , 36 (8 ): 1265 - 1271
DOI:10.1016/j.compgeo.2009.05.011
[本文引用: 1]
[10]
孔纲强, 陈力恺, 刘汉龙 考虑土体非线性固结沉降的复合地基桩侧负摩阻力研究
[J]. 中国公路学报 , 2013 , 26 (3 ): 37 - 43
DOI:10.3969/j.issn.1001-7372.2013.03.002
KONG Gangqiang, CHEN Likai, LIU Hanlong Study on negative skin friction of pile in composite foundation considering nonlinear consolidation of soil
[J]. China Journal of Highway and Transport , 2013 , 26 (3 ): 37 - 43
DOI:10.3969/j.issn.1001-7372.2013.03.002
[11]
赵明华, 胡倩, 杨超炜, 等 考虑地基土非线性固结的桩侧负摩阻力计算方法研究
[J]. 岩土工程学报 , 2016 , 38 (8 ): 1417 - 1424
DOI:10.11779/CJGE201608008
[本文引用: 1]
ZHAO Minghua, HU Qian, YANG Chaowei, et al Negative skin friction of piles considering nonlinear consolidation of soil
[J]. Chinese Journal of Geotechnical Engineering , 2016 , 38 (8 ): 1417 - 1424
DOI:10.11779/CJGE201608008
[本文引用: 1]
[12]
LIU J, GAO H, LIU H Finite element analyses of negative skin friction on a single pile
[J]. Acta Geotechnica , 2012 , 7 (3 ): 239 - 252
DOI:10.1007/s11440-012-0163-x
[本文引用: 1]
[13]
YAO W, LIU Y, CHEN J Characteristics of negative skin friction for superlong piles under surcharge loading
[J]. International Journal of Geomechanics , 2012 , 12 (2 ): 90 - 97
DOI:10.1061/(ASCE)GM.1943-5622.0000167
[本文引用: 1]
[14]
贾煜, 宋福贵, 王炳龙, 等 基于改进荷载传递法计算降水引起的基桩沉降
[J]. 岩土力学 , 2015 , 36 (1 ): 68 - 74
[本文引用: 1]
JIA Yu, SONG Fugui, WANG Binglong, et al Modified load transfer method for calculation of foundation pile settlement due to dewatering
[J]. Rock and Soil Mechanics , 2015 , 36 (1 ): 68 - 74
[本文引用: 1]
[15]
刘御刚. 抽降水对高速铁路桥梁桩基的影响分析[D]. 长沙: 中南大学, 2014: 1–97.
[本文引用: 1]
LIU Yugang. Analysis on influence imposed by exploiting groundwater on bridges pile foundation of high-speed railway [D]. Changsha : Central South University, 2014: 1–97.
[本文引用: 1]
[16]
江留慧. 抽降水下既有建筑物基桩承载力性状分析[D]. 镇江: 江苏大学, 2020: 1–113.
[本文引用: 2]
JIANG Liuhui. Analysis of bearing capacity behavior of existing building foundation pile by pumping water [D]. Zhenjiang: Jiangsu University, 2020: 1–113.
[本文引用: 2]
[17]
刘红军, 上官士青, 朴春德, 等 基于数学规划算法的单桩沉降计算分析研究
[J]. 岩土工程学报 , 2012 , 34 (5 ): 868 - 873
[本文引用: 1]
LIU Hongjun, SHANGGUAN Shiqing, PIAO Chunde, et al Calculation and analysis of single pile settlement based on mathematical programming algorithm
[J]. Chinese Journal of Geotechnical Engineering , 2012 , 34 (5 ): 868 - 873
[本文引用: 1]
[18]
谢新宇, 王忠瑾, 王金昌, 等 考虑桩土非线性的超长桩沉降计算方法
[J]. 中南大学学报: 自然科学版 , 2013 , 44 (11 ): 4664 - 4671
[本文引用: 1]
XIE Xinyu, WANG Zhongjin, WANG Jinchang, et al Calculation method for settlement of super-long pile considering nonlinearity of pile and soils
[J]. Journal of Central South University: Science and Technology , 2013 , 44 (11 ): 4664 - 4671
[本文引用: 1]
[19]
TERZAGHI K. 1925. Principles of soil mechanics. IV. Settlement and consolidation of clay. [J]. Engineering News-Record , 1925, 95: 874–878.
[本文引用: 1]
[20]
TAO L W, XIE K H, HUANG D Z. Analytical solution for one-dimensional consolidation of soft soil induced by water head difference [C]// Proceedings of the International Conference on E-Product E-Service and E-Entertainment . [S.l.]: IEEE, 2010: 1–4.
[本文引用: 2]
[21]
欧孝夺, 白露, 吕政凡, 等 自平衡试桩Q -s 曲线理论解析方法研究
[J]. 铁道科学与工程学报 , 2022 , 19 (2 ): 399 - 408
[本文引用: 1]
OU Xiaoduo, BAI Lu, LÜ Zhengfan, et al Research on theoretical analytical method of Q -s curves of self-balancing test piles
[J]. Journal of Railway Science and Engineering , 2022 , 19 (2 ): 399 - 408
[本文引用: 1]
[22]
李连祥, 李先军, 成晓阳, 等 考虑圆孔扩张理论的支盘桩荷载传递法
[J]. 中国公路学报 , 2018 , 31 (8 ): 20 - 29
DOI:10.3969/j.issn.1001-7372.2018.08.002
[本文引用: 1]
LI Lianxiang, LI Xianjun, CHENG Xiaoyang, et al Load transfer method for squeezed and branch piles considering cavity expansion theory
[J]. China Journal of Highway and Transport , 2018 , 31 (8 ): 20 - 29
DOI:10.3969/j.issn.1001-7372.2018.08.002
[本文引用: 1]
[23]
李术才, 陈红宾, 张晓, 等 粉质黏土隧道超前支护效应试验研究
[J]. 中南大学学报: 自然科学版 , 2019 , 50 (4 ): 946 - 956
[本文引用: 3]
LI Shucai, CHEN Hongbin, ZHANG Xiao, et al Experimental study on advanced support effect in silty clay tunnel
[J]. Journal of Central South University: Science and Technology , 2019 , 50 (4 ): 946 - 956
[本文引用: 3]
[24]
陈岳林. 温州软土地基桩基变形性状研究[D]. 杭州: 浙江大学, 2005: 1–102.
[本文引用: 3]
CHEN Yuelin. Settlement behavior of pile foundation in Wenzhou soft ground [D]. Hangzhou: Zhejiang University, 2005: 1–102.
[本文引用: 3]
[25]
王宗琴, 张云鹏, 田乙, 等 考虑固结的新近吹填场地桩侧负摩阻力分布特性
[J]. 哈尔滨工业大学学报 , 2022 , 54 (8 ): 108 - 116
DOI:10.11918/202104053
[本文引用: 1]
WANG Zongqin, ZHANG Yunpeng, TIAN Yi, et al Distribution characteristics of negative skin friction on piles installed at dredger fill sites considering consolidation effect
[J]. Journal of Harbin Institute of Technology , 2022 , 54 (8 ): 108 - 116
DOI:10.11918/202104053
[本文引用: 1]
[26]
叶观宝, 郑文强, 张振 大面积填土场地中摩擦型桩负摩阻力分布特性研究
[J]. 岩土力学 , 2019 , 40 (Suppl.1 ): 440 - 448
YE Guanbao, ZHENG Wenqiang, ZHANG Zhen Investigation on distribution of negative friction of frictional piles in large filling sites
[J]. Rock and Soil Mechanics , 2019 , 40 (Suppl.1 ): 440 - 448
[27]
吴爽爽, 胡新丽, 章涵, 等 嵌岩桩负摩阻力现场试验与计算方法研究
[J]. 岩土力学 , 2019 , 40 (9 ): 3610 - 3617
[本文引用: 1]
WU Shuangshuang, HU Xinli, ZHANG Han, et al Field test and calculation method of negative skin friction of rock-socketed piles
[J]. Rock and Soil Mechanics , 2019 , 40 (9 ): 3610 - 3617
[本文引用: 1]
[28]
贺志军, 雷皓程, 夏张琦, 等 多层软土地基中单桩沉降与内力位移分析
[J]. 岩土力学 , 2020 , 41 (2 ): 655 - 666
[本文引用: 1]
HE Zhijun, LEI Haocheng, XIA Zhangqi, et al Analysis of settlement and internal force displacement of single pile in multilayer soft soil foundation
[J]. Rock and Soil Mechanics , 2020 , 41 (2 ): 655 - 666
[本文引用: 1]
[29]
王奎华, 吕述晖, 吴文兵, 等 层状地基中基于虚土桩模型的单桩沉降计算方法
[J]. 工程力学 , 2013 , 30 (7 ): 75 - 83
DOI:10.6052/j.issn.1000-4750.2012.03.0171
[本文引用: 1]
WANG Kuihua, LÜ Shuhui, WU Wenbing, et al A new calculation method for the settlement of single pile based on virtual soil-pile model in layered soils
[J]. Engineering Mechanics , 2013 , 30 (7 ): 75 - 83
DOI:10.6052/j.issn.1000-4750.2012.03.0171
[本文引用: 1]
[30]
陈仁朋, 周万欢, 曹卫平, 等 改进的桩土界面荷载传递双曲线模型及其在单桩负摩阻力时间效应研究中的应用
[J]. 岩土工程学报 , 2007 , 29 (6 ): 824 - 830
DOI:10.3321/j.issn:1000-4548.2007.06.006
[本文引用: 1]
CHEN Renpeng, ZHOU Wanhuan, CAO Weiping, et al Improved hyperbolic model of load-transfer for pile-soil interface and its application in study of negative friction of single piles considering time effect
[J]. Chinese Journal of Geotechnical Engineering , 2007 , 29 (6 ): 824 - 830
DOI:10.3321/j.issn:1000-4548.2007.06.006
[本文引用: 1]
[31]
曹卫平 桩土界面荷载传递双曲线模型的改进及其应用
[J]. 岩石力学与工程学报 , 2009 , 28 (1 ): 144 - 151
DOI:10.3321/j.issn:1000-6915.2009.01.019
[本文引用: 1]
CAO Weiping An improved load transfer hyperbolic model for pile-soil interface and its application
[J]. Chinese Journal of Rock Mechanics and Engineering , 2009 , 28 (1 ): 144 - 151
DOI:10.3321/j.issn:1000-6915.2009.01.019
[本文引用: 1]
承压水减压引起的沉降分析
1
2004
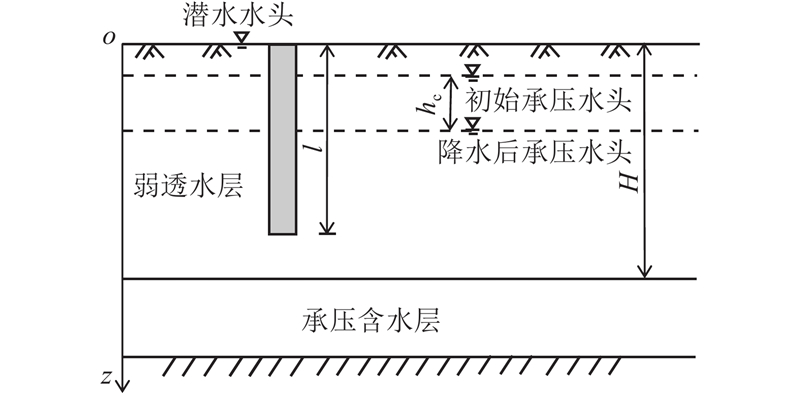
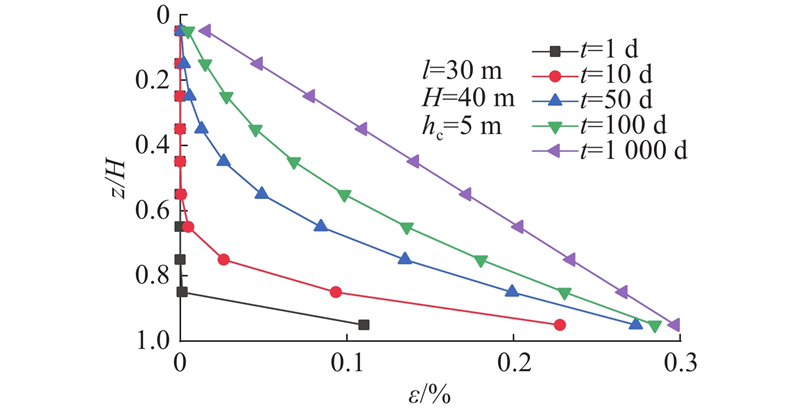
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
承压水减压引起的沉降分析
1
2004
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
One-dimensional consolidation of visco-elastic aquitard due to withdrawal of deep-groundwater
1
2012
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
水位变化下可压缩土层的黏弹性耦合变形分析
0
2020
水位变化下可压缩土层的黏弹性耦合变形分析
0
2020
水位下降诱发含水层–弱透水层1维黏弹性固结分析
0
2021
水位下降诱发含水层–弱透水层1维黏弹性固结分析
0
2021
越流系统中弱透水层的一维固结解及分析
1
2012
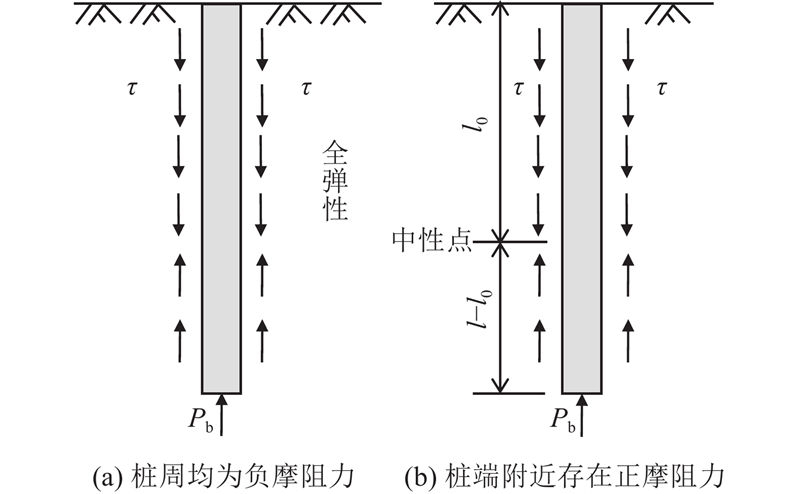
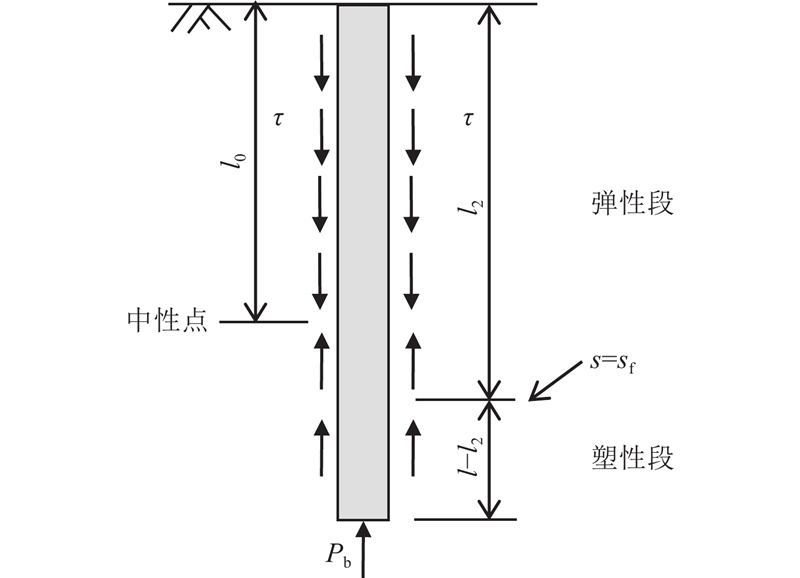
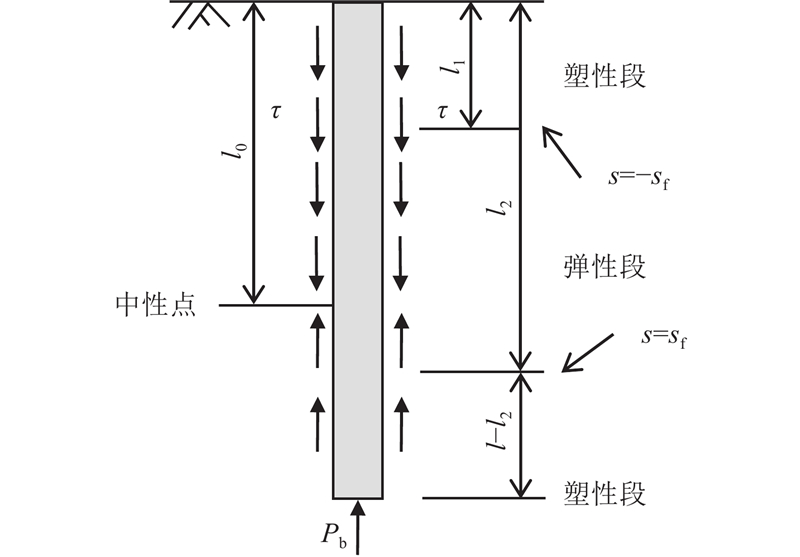
... 与如堆载的常规附加应力引起的土体自上而下的固结不同,抽降承压水引起弱透水层固结是自下而上进行的[5 , 20 ] . 根据固结进程不同,以桩土相对位移达到界限位移作为桩土界面弹塑性分界点,桩土界面的变化和桩的受力可分为3个阶段:1)桩侧土均为弹性,2)桩端附近桩侧土进入塑性,3)桩顶附近桩侧土进入塑性. ...
越流系统中弱透水层的一维固结解及分析
1
2012
... 与如堆载的常规附加应力引起的土体自上而下的固结不同,抽降承压水引起弱透水层固结是自下而上进行的[5 , 20 ] . 根据固结进程不同,以桩土相对位移达到界限位移作为桩土界面弹塑性分界点,桩土界面的变化和桩的受力可分为3个阶段:1)桩侧土均为弹性,2)桩端附近桩侧土进入塑性,3)桩顶附近桩侧土进入塑性. ...
第二类越流系统中结构性弱透水土层一维固结解析解
0
2014
第二类越流系统中结构性弱透水土层一维固结解析解
0
2014
抽水引起的有起始比降饱和土固结解析解
1
2016
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
抽水引起的有起始比降饱和土固结解析解
1
2016
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
Influences of soil consolidation and pile load on the development of negative skin friction of a pile
1
2009
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
考虑土体非线性固结沉降的复合地基桩侧负摩阻力研究
0
2013
考虑土体非线性固结沉降的复合地基桩侧负摩阻力研究
0
2013
考虑地基土非线性固结的桩侧负摩阻力计算方法研究
1
2016
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
考虑地基土非线性固结的桩侧负摩阻力计算方法研究
1
2016
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
Finite element analyses of negative skin friction on a single pile
1
2012
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
Characteristics of negative skin friction for superlong piles under surcharge loading
1
2012
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
基于改进荷载传递法计算降水引起的基桩沉降
1
2015
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
基于改进荷载传递法计算降水引起的基桩沉降
1
2015
... 骆冠勇等[1 ] 提出由承压水减压引起的固结沉降计算方法. Liu等[2 -8 ] 进一步研究了多层土、弱透水层以及承压含水层的流变性、初始水头沿深度非均匀分布、固结和渗透的非线性对承压水减压引起的地层沉降. 土的沉降大于桩的位移会使桩侧产生负摩阻力,继而降低桩身承载力,引起不均匀沉降. 关于负摩阻力的研究多集中于大面积堆载以及潜水降水工程场景. Chen等[9 -11 ] 考虑弱透水层的非均质性,采用不同的荷载传递法研究大面积堆载引起的桩土关系问题;Liu等[12 -13 ] 从二维和三维固结角度分析堆载下的桩土关系问题;贾煜等[14 ] 引入桩体自重,提出潜水水位下降诱发的基桩沉降计算方法. 大面积堆载以及降潜水引起的弱透水层固结均是自上而下进行的,这2种工况下桩土关系的变化有相似的发展规律. ...
1
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
1
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
2
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
... 基于太沙基一维固结理论,瞬时降承压水条件下土体固结沉降随时间发展的计算式[16 ,20 ] 为 ...
2
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
... 基于太沙基一维固结理论,瞬时降承压水条件下土体固结沉降随时间发展的计算式[16 ,20 ] 为 ...
基于数学规划算法的单桩沉降计算分析研究
1
2012
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
基于数学规划算法的单桩沉降计算分析研究
1
2012
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
考虑桩土非线性的超长桩沉降计算方法
1
2013
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
考虑桩土非线性的超长桩沉降计算方法
1
2013
... 针对由承压水减压引起的基桩受力变形问题的研究不多. 刘御刚等[15 -16 ] 初步研究了承压水减压和桩顶同时受荷引起的基桩受力变形问题,由于桩土关系的变化主要受桩顶加载的影响,得出“桩顶附近桩周土先进入塑性,随后在塑性区自上而下扩展”的规律. 该规律与传统桩顶轴向受荷条件下桩土界面的发展趋势相同[17 -18 ] . 承压水降水诱发的弱透水层沉降是由自上而下的越流作用引起的,与如大面积堆载、降潜水的附加应力作用有所不同. 上述研究未能揭示降承压水引起的弱透水层固结对桩土作用机制的影响,对抽降承压水引起的软黏土中未打穿自由单桩受力特性的认识尚不深入. 本研究基于太沙基一维固结理论,采用理想弹塑性荷载传递模型,推导承压水大面积降水诱发软黏土弱透水层中未打穿自由单桩受力变形特性的半解析解,深入分析承压水减压降水引起弱透水层中既有基桩的桩土作用机制. ...
1
... 1)地基为半无限弹性体,忽略桩及桩周土的径向变形;地基土为均质、各向同性材料,土的固结符合太沙基一维线性固结理论[19 ] ,不考虑压缩模量随深度的变化. 2) 桩顶和地基表面无附加荷载,土体和桩的沉降仅由承压含水层减压降水引起. 3) 桩体为可压缩的均质弹性体,应力-应变关系满足虎克定律,忽略成桩施工对地基土的影响. 4) 基桩未打穿弱透水层,桩侧与土相互关系满足理想弹塑性荷载传递规律,桩端土反力与桩端刺入变形采用线弹性假定. 5) 承压水大面积降水且瞬时完成. 6) 下部含水层压缩性远低于上部弱透水层,忽略抽降承压水引起含水层中的沉降. ...
2
... 基于太沙基一维固结理论,瞬时降承压水条件下土体固结沉降随时间发展的计算式[16 ,20 ] 为 ...
... 与如堆载的常规附加应力引起的土体自上而下的固结不同,抽降承压水引起弱透水层固结是自下而上进行的[5 , 20 ] . 根据固结进程不同,以桩土相对位移达到界限位移作为桩土界面弹塑性分界点,桩土界面的变化和桩的受力可分为3个阶段:1)桩侧土均为弹性,2)桩端附近桩侧土进入塑性,3)桩顶附近桩侧土进入塑性. ...
自平衡试桩Q -s 曲线理论解析方法研究
1
2022
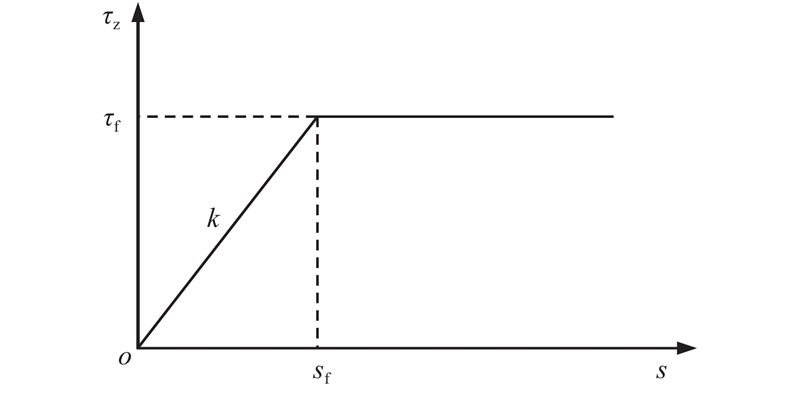
... 式中:s p 为桩身竖向位移,s s 为土的竖向位移,s 为桩土相对位移. 如图2 所示,桩侧荷载传递模型采用理想弹塑性模型[21 ] . 根据桩土相对位移的方向和正、负摩阻力的定义,对应的桩侧土的荷载传递函数表示为 ...
自平衡试桩Q -s 曲线理论解析方法研究
1
2022
... 式中:s p 为桩身竖向位移,s s 为土的竖向位移,s 为桩土相对位移. 如图2 所示,桩侧荷载传递模型采用理想弹塑性模型[21 ] . 根据桩土相对位移的方向和正、负摩阻力的定义,对应的桩侧土的荷载传递函数表示为 ...
考虑圆孔扩张理论的支盘桩荷载传递法
1
2018
... 式中:k 为土体弹性阶段刚度系数,τ f 为弹性阶段桩侧极限摩阻力,s f 为桩侧摩阻力达到极限值时对应的桩-土相对位移. 假定桩端反力P b 与桩端处桩土相对位移s b 满足线性关系[22 ] ,则平衡方程为 ...
考虑圆孔扩张理论的支盘桩荷载传递法
1
2018
... 式中:k 为土体弹性阶段刚度系数,τ f 为弹性阶段桩侧极限摩阻力,s f 为桩侧摩阻力达到极限值时对应的桩-土相对位移. 假定桩端反力P b 与桩端处桩土相对位移s b 满足线性关系[22 ] ,则平衡方程为 ...
粉质黏土隧道超前支护效应试验研究
3
2019
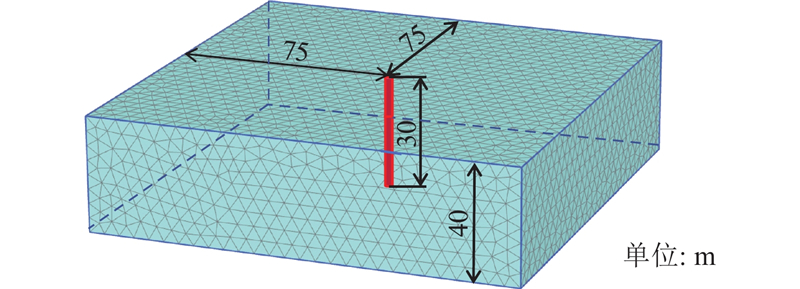
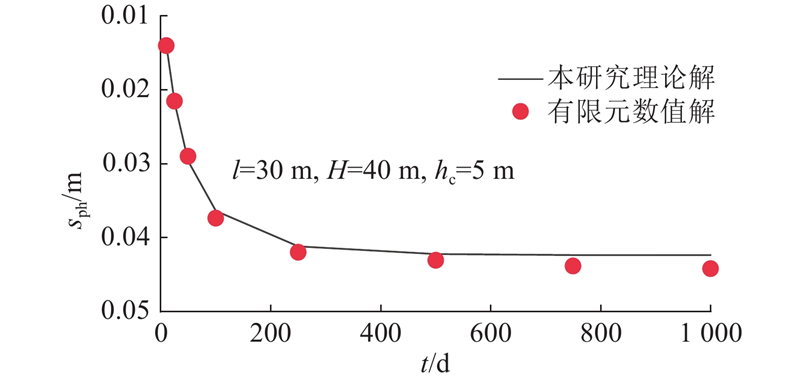
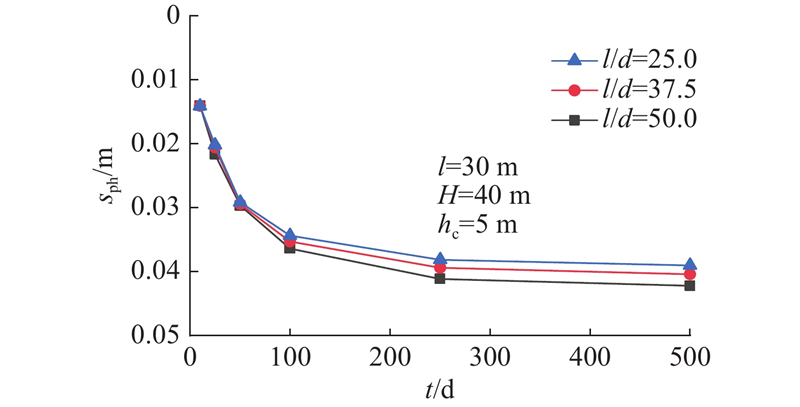
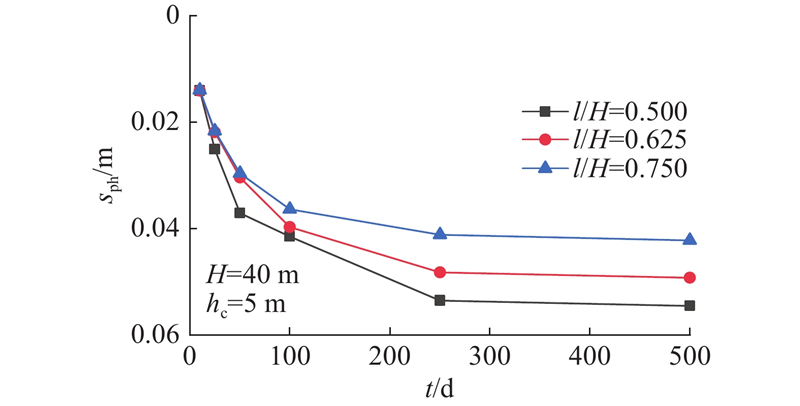
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
... [23 -24 ]相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
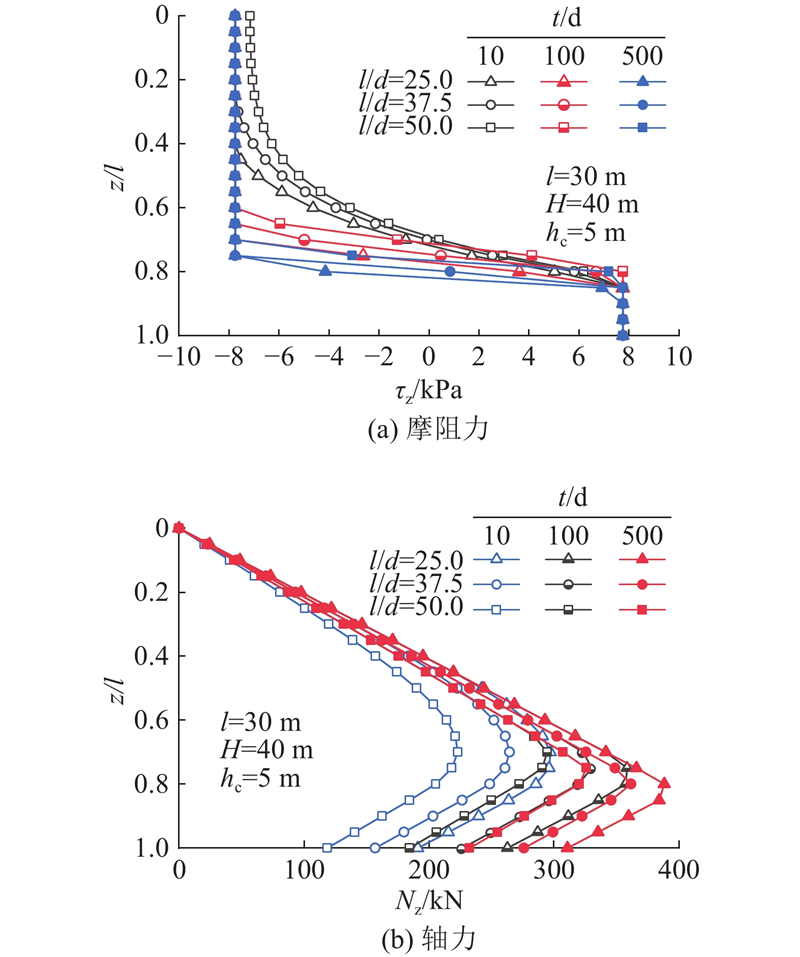
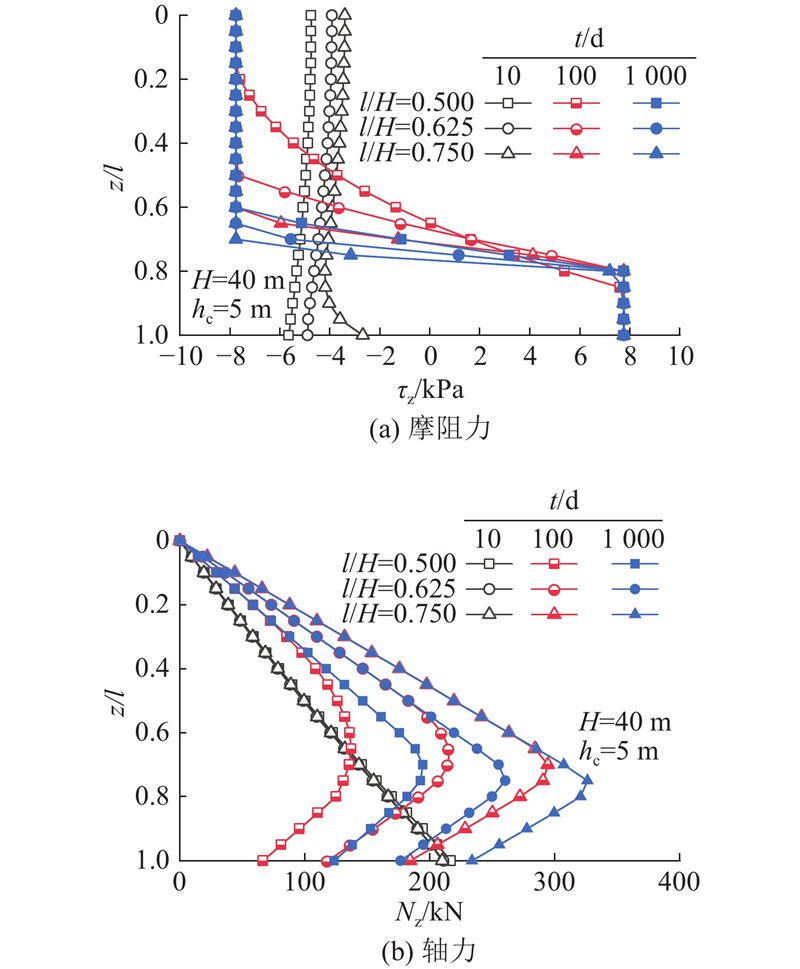
... 以文献[23 ]、[24 ]的地层和桩基静载试验数据为背景构建算例,进一步探讨固结时间、桩长、桩径以及降水深度等参数变化对抽降承压水引发弱透水层中基桩受力变形的影响. ...
粉质黏土隧道超前支护效应试验研究
3
2019
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
... [23 -24 ]相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
... 以文献[23 ]、[24 ]的地层和桩基静载试验数据为背景构建算例,进一步探讨固结时间、桩长、桩径以及降水深度等参数变化对抽降承压水引发弱透水层中基桩受力变形的影响. ...
3
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
... -24 ]相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
... 以文献[23 ]、[24 ]的地层和桩基静载试验数据为背景构建算例,进一步探讨固结时间、桩长、桩径以及降水深度等参数变化对抽降承压水引发弱透水层中基桩受力变形的影响. ...
3
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
... -24 ]相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
... 以文献[23 ]、[24 ]的地层和桩基静载试验数据为背景构建算例,进一步探讨固结时间、桩长、桩径以及降水深度等参数变化对抽降承压水引发弱透水层中基桩受力变形的影响. ...
考虑固结的新近吹填场地桩侧负摩阻力分布特性
1
2022
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
考虑固结的新近吹填场地桩侧负摩阻力分布特性
1
2022
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
大面积填土场地中摩擦型桩负摩阻力分布特性研究
0
2019
大面积填土场地中摩擦型桩负摩阻力分布特性研究
0
2019
嵌岩桩负摩阻力现场试验与计算方法研究
1
2019
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
嵌岩桩负摩阻力现场试验与计算方法研究
1
2019
... 以文献[23 ]、[24 ]为背景构建算例,基本计算参数为弱透水层厚度H =40 m、压缩模量E S =1.6 MPa、泊松比υ =0.35、桩身弹性模量E p =30 GPa、桩长l =30 m、直径d =0.6 m,假定桩顶荷载为0、桩土界限位移s f =0.002 m[25 -27 ] . 承压水降深h c =5 m. 采用Plaxis 3D软件,针对该算例建立有限元数值分析模型,满足第1章中的基本假设,且当土体采用线弹性模型时,Plaxis假定压缩模量为定值. 采用Embeded桩约束考虑桩-土之间理想弹塑性的相互作用,土体与桩身参数与温州金都大厦的地层和桩基静载试验数据[23 -24 ] 相同. 承压含水层大面积瞬时降水通过改变弱透水层底部水头边界进行控制. 模型的有限元网格划分如图6 所示,进行瞬时降承压水下桩土相互作用的过程模拟. 如图7 所示为理论解和有限元数值解得到的桩顶沉降s ph 随固结时间t 的变化,由图可知,理论解与数值解吻合较好,验证了本研究理论解的合理性. ...
多层软土地基中单桩沉降与内力位移分析
1
2020
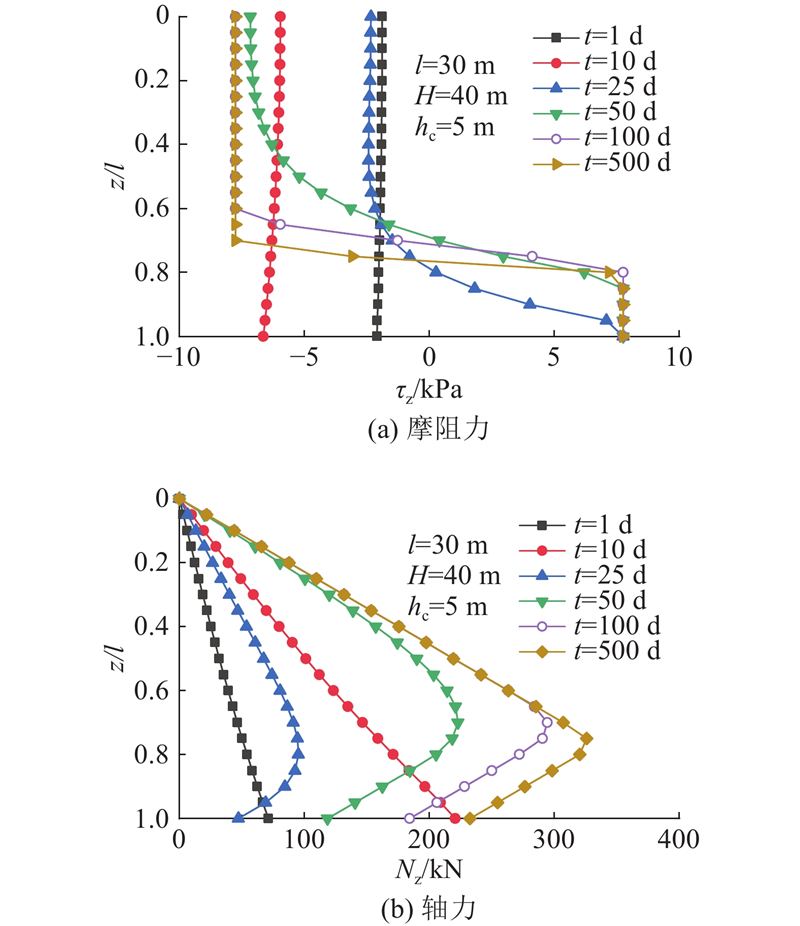
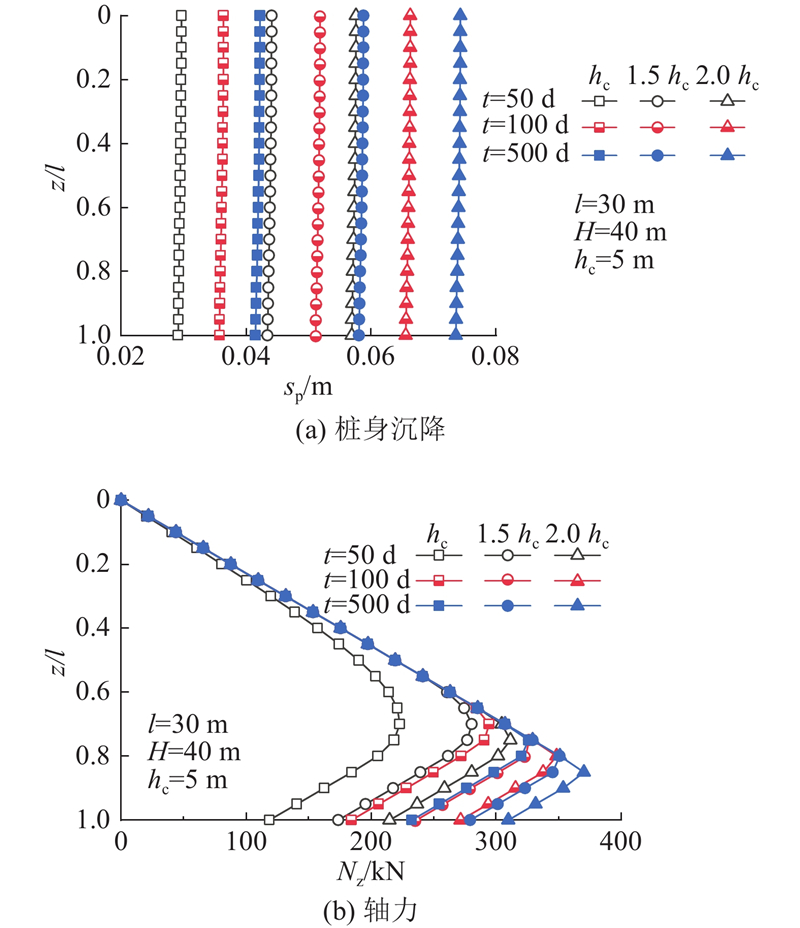
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...
多层软土地基中单桩沉降与内力位移分析
1
2020
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...
层状地基中基于虚土桩模型的单桩沉降计算方法
1
2013
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...
层状地基中基于虚土桩模型的单桩沉降计算方法
1
2013
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...
改进的桩土界面荷载传递双曲线模型及其在单桩负摩阻力时间效应研究中的应用
1
2007
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...
改进的桩土界面荷载传递双曲线模型及其在单桩负摩阻力时间效应研究中的应用
1
2007
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...
桩土界面荷载传递双曲线模型的改进及其应用
1
2009
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...
桩土界面荷载传递双曲线模型的改进及其应用
1
2009
... 将算例参数代入式(1)~ (19),得到抽降承压水引起的弱透水层固结过程中桩侧-土接触面的相对位移s z (桩、土沉降差)和桩身摩阻力τ z . 如图8 所示为固结时间t 对桩土关系的影响. 图8 (a)中,固结前期,桩侧均为负摩阻力,且负摩阻力不断增长,随着固结的进行,桩端附近出现正摩阻力并率先达到极限且逐渐向上扩展,随后桩顶负摩阻力区达到极限并逐渐向下扩展. 这与桩顶加载情况桩长深度范围内只存在正摩阻力[28 -29 ] 的分布不同,正、负摩阻力沿深度的发展进程也与地表堆载情况下“上部先于下部达到极限摩阻力的过程”的认识 [30 -31 ] 有明显区别,其原因主要是承压水降水引起的土体固结进程与地表堆载引发的土体固结进程不同. 图8 (b)中,在固结前期,桩侧均为负摩阻力,轴力N z 随着深度和时间不断增大,随着固结的进行,桩侧出现正摩阻力,此时轴力出现拐点,即中性点,且中性点随着时间发展不断上移并趋于稳定. ...