场地地震响应问题是研究场地地震响应和土-结构地震相互作用的基础和前提,更是地震工程的重点研究课题[1-6]. 针对弹性地基场地地震响应问题的研究大多考虑等温或均质地基的条件,未同时考虑热效应和土体成层特性的影响. 随着温室效应的加重,温度和变形的耦合作用影响波的形成,使得热效应显著影响波的传播特性. 在自然界中,成层弹性地基场地的地震响应与均质地基条件下的差距明显. 因此,考虑热效应和土层的成层特性,建立非等温条件下的成层场地模型并研究弹性地基场地的地震响应,利于科学认识热效应影响下成层弹性地基场地中地震波的传播机理,为已发生的弹性地基场地的地震响应提供理论解释,对地震勘探和地震灾害评估有实际指导价值和现实意义.
Duhamel等[7-8]介绍不耦合热弹性理论,指出在温度变化下,介质中会产生与P波传播特性相似的热波. 该理论有2个缺陷:1)在物理试验中,温度对弹性材料状态的影响显著,该理论认为温度的影响对弹性体的性质几乎不产生影响. 2)该理论认为热波传播速度无限,这在物理上是不合理的. Biot[9]考虑新的热弹性理论,解决了不耦合理论的缺陷1),但仍然无法解决热波传播时速度无限的问题. 为此,2种广义热弹性理论被提出,预测热波以有限速度进行传播. Lord等[10]引入新的傅里叶热传导定律. Green等[11]通过修正Duhamel-Neumann关系和能量平衡方程建立新的热弹性耦合理论来修正以前的热传导定律,使得2种广义热弹性理论可以预测热波传播时的有限速度. Green等[12]建立新的变形介质热力学模型,详细解释了热流以有限速度传播的现象. Green等[13]基于文献[12]的热力学模型构建了新的热弹性理论,将热流定义为有限速度传播的热波. Abouelregal[14]提出弹性介质在无应力边界条件下的波动控制方程.
基于广义热弹性理论,针对热弹性波在弹性介质中的波动特性的研究涌现. Sinha等[15-17]根据热力学的基本理论,研究了均质固体半空间中热弹性波在自由表面上的波动特性. Abd-Alla等[18]研究在S波入射下,各热弹性波在固体半空间上的反射问题. Sharma等[19]基于不同的热弹性理论,研究在等温无应力和刚性固定的边界条件下,固体半空间上热弹性波的反射问题. Singh[20]研究S波在热弹性介质表面的反射问题,发现反射波的反射系数与入射角和热弹性扩散参数有关. Singh[21]继续研究在具有热扩散特性的弹性介质中,平面波在自由表面上的反射特性,计算了在不同材料常数下不同平面波的速度. Kumar等[22]在不考虑能量耗散的条件下,研究热弹性波在热弹性固体半空间边界上的波动特性. Chakraborty等[23]基于广义热弹性介质的控制方程,研究S波入射下各热弹性波在2个不同热弹性固体半空间界面上的透反射问题. Hou等[24]考虑不同的入射波类型和不均匀角度,研究入射在2个各向同性热弹性半空间界面上的平面波的波动特性,分析了平面波的幅度、相位和能量比.
在针对弹性地基场地地震响应问题的研究方面,王相宝等[25]研究单相土体结构的地震响应问题;杨猛[26]建立S波从弹性介质入射至地表的地震动模型,研究S波反射作用下的场地地震效应;王进廷等[27]分析弹性模量以及入射波的角度和频率对上层土动压力的影响;Zhao等[28]研究弹性地基在表面波作用下的地震响应问题. 上述研究未考虑到土层的成层特性. 李志远[29]推导层状弹性地基的刚度矩阵,研究平面波的波动响应问题;Ba等[30]研究层状地基中P波、S波和SH波作用下的地震响应问题;董立东[31]研究双层弹性地基场地在P波和S波入射下的地震响应问题,分析了入射角、泊松比对地震动的影响. 现有研究大多是等温条件下成层弹性地基场地的地震响应,鲜见针对在考虑热效应作用下的平面波入射到弹性地基对地震响应影响问题的研究. Yang等[32]推导了热效应下基岩上覆单一弹性地基层中波动问题的解析解,分析了各热物性参数对场地地震响应产生的影响规律.
1. 场地的波动方程
根据广义热弹性理论,单相热弹性介质的波动方程[33]为
式中:Kb=λ+2μ/3为体积模量,λ、μ均为弹性介质的拉梅常量,α为热膨胀系数,ρ为弹性介质的密度,cs为固相比热容,tq和tθ分别为热通量和温度相位延迟时间,T和T0分别为介质温度和初始温度,K为弹性介质的热传导系数;us为位移矢量. 根据亥姆霍兹矢量分解原理,分解固相位移矢量us为
式中:Ψs和Hs分别为弹性介质的标量和矢量位势函数. 热弹性介质中各个波的势函数假设如下:
式中:A、B分别为P波(包含T波)和S波的波幅系数,T波也叫热波(thermal wave);kp和ks分别为纵波和横波的波数;ω为频率;t为时间. 将式(3)代入式(1)、(2),再结合式(4)~(6)进行理论推导,得到热弹性固体介质中体波的控制方程为
由于式(7)和式(8)有非零解,得到特征方程:
式(9)为单相热弹性介质中压缩波P波(包含T波)的特征方程,式(10)为剪切波(S波)的特征方程,方程中元素表达式详见文献[33]. 求解特征方程得到各热弹性波(P波、T波和S波)的波数. 推导式(7)、(8)得到单相热弹性介质中P波和T波的势函数幅值比例:
式中:i为i层弹性地基层.
2. 成层弹性地基场地模型
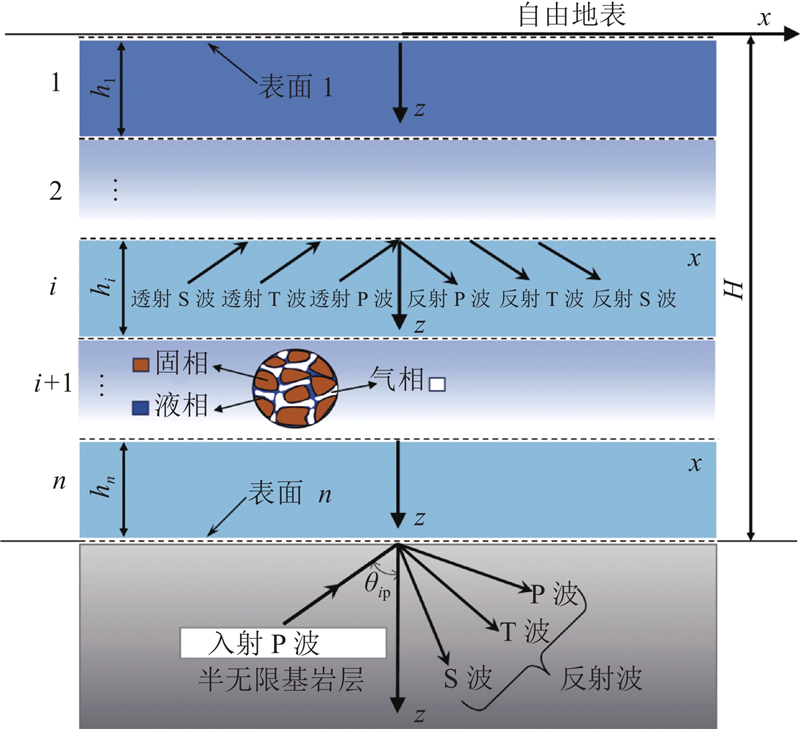
如图1所示为成层弹性地基场地模型示意图,考虑水平均匀半无限基岩层上覆厚度分别为hi (i=1,2,
图 1
3. 弹性地基层中波幅系数转换矩阵
第i层弹性地基中的反射波与透射波的位移势函数表示如下. 上行P波:
上行T波:
上行S波:
下行P波:
下行T波:
下行S波:
式中:Ψ、T和H分别为P波、T波和S波的势函数;r,t分别表示反射波和透射波;n为第i层弹性介质中不同的反射和透射P波(包括T波) (n=1、2);
在弹性地基层中,各应力、位移表达式详见文献[33]. 将波场函数代入应力、位移和温度的势函数表达式,得到第i层弹性地基层中的应力、位移和温度与各波幅系数关系式为
式中:Si为第i层弹性地基层中应力、位移和温度矢量,
为了保证相邻2层弹性介质层交界面紧密接触,假定介质边界处的应力和位移连续,该边界的等温条件通过温度和热通量的连续性来保证,在第i层和第i+1层分界面上,有
将式(19)代入式(20)得到
理论推导式(21)得到
其中
4. 基岩上覆成层弹性地基波动问题解
基岩采用单相热弹性介质来模拟. 基岩层中入射波和反射波的势函数表示如下. P波:
T波:
S波:
式中:kip1x、kip1z分别为基岩层中入射P波在x方向和z方向上的视波数,krpnx和krpnz分别为基岩层中反射P波和反射T波在x方向和z方向上的视波数,krsx和krsz分别为基岩层中反射S波在x方向和z方向上的视波数;
在基岩层中,各应力、位移表达式详见文献[33]. 同理可得,基岩中的应力、位移和温度与各波波幅系数的关系:
式中:Se为基岩层中应力、位移和温度矢量,
交界面上位移连续:
交界面上温度连续和温度变化率相等:
根据基岩层与第n层弹性地基层交界面上的边界条件,得到
式中:Tse11~Tse64的表达式见附录B. 将式(19)、(28)代入式(32),结合波幅系数递推式(23),得到
式中:Tsn11~Tsn66的表达式见附录A. 根据第1层弹性地基层为自由地表,由正应力、剪应力和温度的变化率为0的3个边界条件,得到
在式(33)中,共有6个方程,9个待定的波幅系数,分别为H1(6×1)和Arp1、Arp2、Brs,式(34)中共有3个方程. 上述9个方程对应9个未知波幅系数,可解得基岩层中的3个未知振幅以及第1层弹性地基层中的6个未知波幅. 第n层的波幅系数可由第1层的波幅系数表示,由此确定每层的波幅系数,求得每层中各点的位移和应力.
5. 自由地表位移
波场确定后,场地中的各点位移、应力均可确定,将式(12)~(17)代入自由表面水平方向位移ux和竖向方向位移uz的表达式,得到
利用成层场地自由地表处的位移放大系数ux/u0和uz/u0表征成层弹性地基场地自由地表的位移,位移放大系数为水平和竖向方向的位移幅值与入射波的位移幅值u0之比.
6. 数值计算与分析
6.1. 验证数值解的正确性
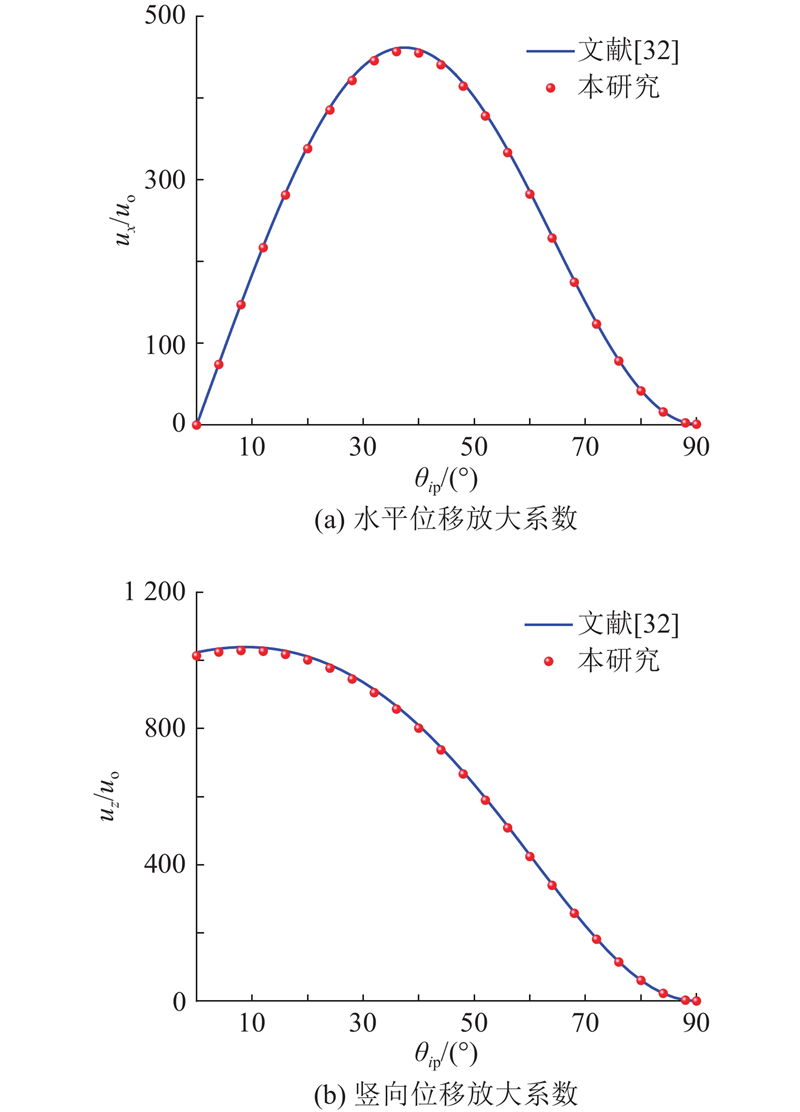
Yang等[32]研究了在热效应作用下平面P波从基岩入射上覆均质弹性地基自由场地中的波动问题. 为了验证本研究求解过程的正确性,设图1中基岩上覆成层弹性地基的层数为2,2层的弹性地基取相同的材料参数,材料参数取值自文献[32],验证时所取参数如表1所示. 此时本研究所提模型退化为基岩上覆均质弹性地基模型(解退化为热效应作用下平面P波入射弹性地基自由场地的地震地面运动问题). 如图2所示为所提模型退化为与文献[32]的模型后,与文献[32]中的水平和竖向位移放大系数的对比图. 可以看出,所提模型与文献[32]模型在地表水平位移和竖向位移放大系数随入射角度变化上基本一致,说明本研究的求解方法正确. 位移放大系数的量级和数值分析图的量级存在差异,原因是取用的验证数据均出自文献[32],在数值分析中,热物性参数的取值主要参考的文献[15]、[32]. 在进行验证计算和数值分析计算时,由于取用参数存在差异,导致热弹性波的振幅、波速、能量和入射波产生的位移显著改变,影响了场地的地震响应. 如公路路面覆盖、大型房屋建筑结构的工程建设将很大程度改变表层弹性地基层的热物性参数,导致成层弹性地基场地出现地震地面运动时可能面临一系列工程灾害. 本研究将成层弹性地基模型划分为基岩层(弹性地基)、弹性地基层I、弹性地基层II. 基岩上覆2层厚度,h1=h2=20 m的弹性地基层,其他参数取值参考文献[15]、[32],详见表2. 通过数值计算研究热效应作用下P波入射成层弹性地基场地地震地面运动的问题,具体分析表层弹性地基层中固相比热容、热传导系数、热膨胀系数等热物性参数对场地地震地面运动所产生的影响. 由于沉积年代的不同以及地理和气候的差异,不同地区成层弹性地基层的热物性参数有所不同,但计算结果的总体趋势与通过数值分析得到的趋势相同,仅存在数值差异.
表 1 成层弹性地基中验证数值解的参数 [32]
Tab.1
| 参数 | 数值 | ||
| 基岩层 | 层I | 层II | |
| tq/s | 2.0×10−7 | 2.0×10−7 | 2.0×10−7 |
| ρ/(kg·m−3) | 2 700 | 2 700 | 2 700 |
| cs/(J·kg−1·K−1) | 1 046 | 1 046 | 1 046 |
| T/K | 293.2 | 293.2 | 293.2 |
| λ/GPa | 12.0 | 9.0 | 9.0 |
| μ/GPa | 8.0 | 4.0 | 4.0 |
| tθ/s | 1.5×10−7 | 1.5×10−7 | 1.5×10−7 |
| α/K−1 | 4.0×10−4 | 4.0×10−4 | 4.0×10−4 |
| K/(J·s−1·m−1·K−1) | 3.0 | 3.0 | 3.0 |
| 土层厚度h/m | — | 10 | 10 |
| ω/Hz | 5 | 5 | 5 |
图 2
图 2 热效应均质弹性地基下的位移放大系数
Fig.2 Displacement magnification factors under thermal effect homogeneous elastic foundations
| 参数 | 数值 | ||
| 基岩层 | 层I | 层II | |
| tq/s | 2.0×10−7 | 2.0×10−7 | 2.0×10−7 |
| ρ/(kg·m−3) | 2 700 | 2 700 | 2 650 |
| cs/(J·kg−1·K−1) | 1 046 | 1 046 | 1 046 |
| T/K | 293.2 | 293.2 | 293.2 |
| λ/GPa | 12.0 | 9.0 | 8.0 |
| μ/GPa | 8.0 | 4.0 | 8.0 |
| tθ/s | 1.5×10−7 | 1.5×10−7 | 1.5×10−7 |
| α/K−1 | 3.0×10−4 | 3.0×10−4 | 3.0×10−4 |
| K/(J·s−1·m−1·K−1) | 3.0 | 3.0 | 3.0 |
6.2. 均质弹性地基和成层弹性地基的对比
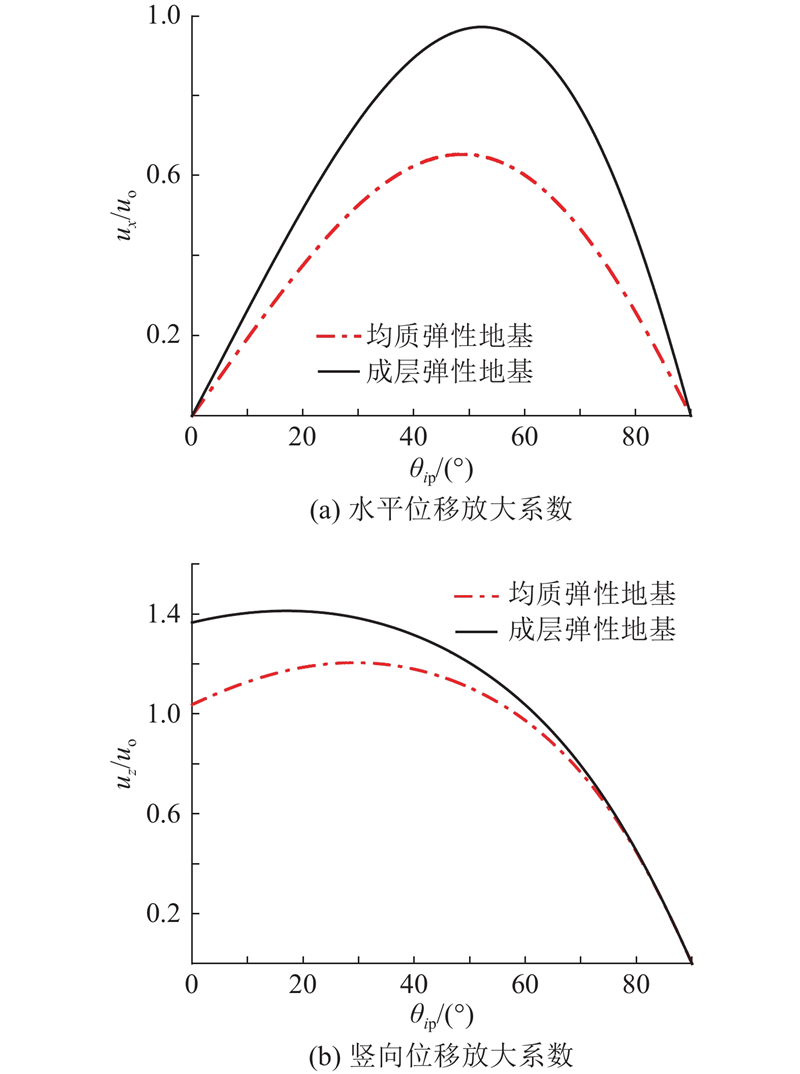
如图3所示,为了对比均质弹性地基和成层弹性地基下地表位移放大系数的差别,绘出频率为30 Hz的基岩上覆均质弹性地基和成层弹性地基中地表位移放大系数随入射角度变化的曲线. 可以看出,均质弹性地基和成层弹性地基的地表位移放大系数的峰值点有差异. 成层弹性地基的水平和竖向位移放大系数的峰值分别相对于均质弹性地基峰值增加了33.17%和38.12%,即成层弹性地基下的地表位移放大系数更大. 分析原因:在自然界中,由于河流、湖泊、海洋、冰川、风及气候变化等动力影响,土层通常以分层的形式存在,在热效应条件下,每层土的热膨胀系数、密度、体积模量等土体参数随土层深度变化而变化,土层沉积后的物理力学性质沿土层深度方向有明显差别. 在均质地基中,土体性质基本相同. 在实际工程实践中,土体地基极少为理想的均质土层,尤其是海洋沉积性土层、火山地带附近和部分干旱和半干旱地区的土层分层现象明显. 当地基含有明显分层时,受分层界面透反射影响,含分层非均质地基对入射地震波表现出明显的选择性滤波,使得地基中地震波动响应与均质土层存在显著差异. 2种地基条件下位移放大系数在数值上的差异说明成层弹性地基的成层特性使不同地基下的地表位移放大系数差异明显,因此在实际工程中将场地简化为均质地基,不考虑场地的成层特性会产生误差.
图 3
图 3 不同弹性地基的位移放大系数对比
Fig.3 Comparison of displacement magnification factors for different elastic foundations
6.3. 不同入射角下热传导系数的影响
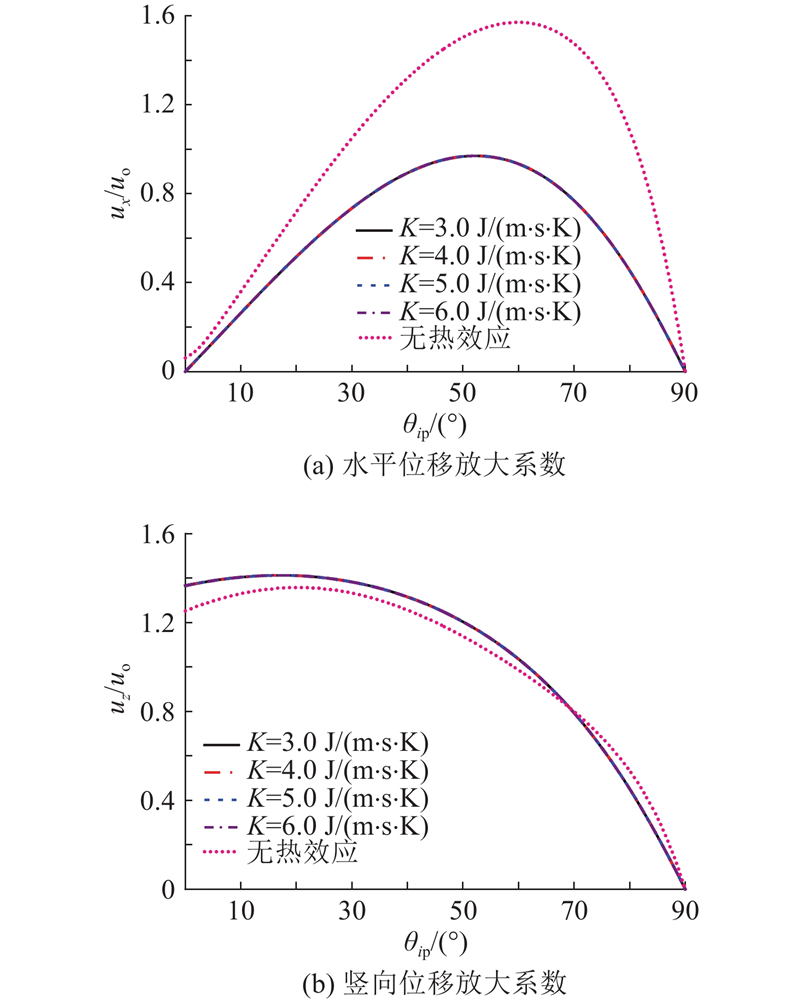
热传导系数表征岩石的导热性,是研究地壳热状态的重要参数,被广泛应用于地震勘探和采矿领域[32]. 如图4所示,为了研究热传导系数变化对地表位移放大系数的影响规律,绘制当
图 4
图 4 不同热传导系数下的位移放大系数
Fig.4 Displacement magnification factors under different heat conduction coefficients
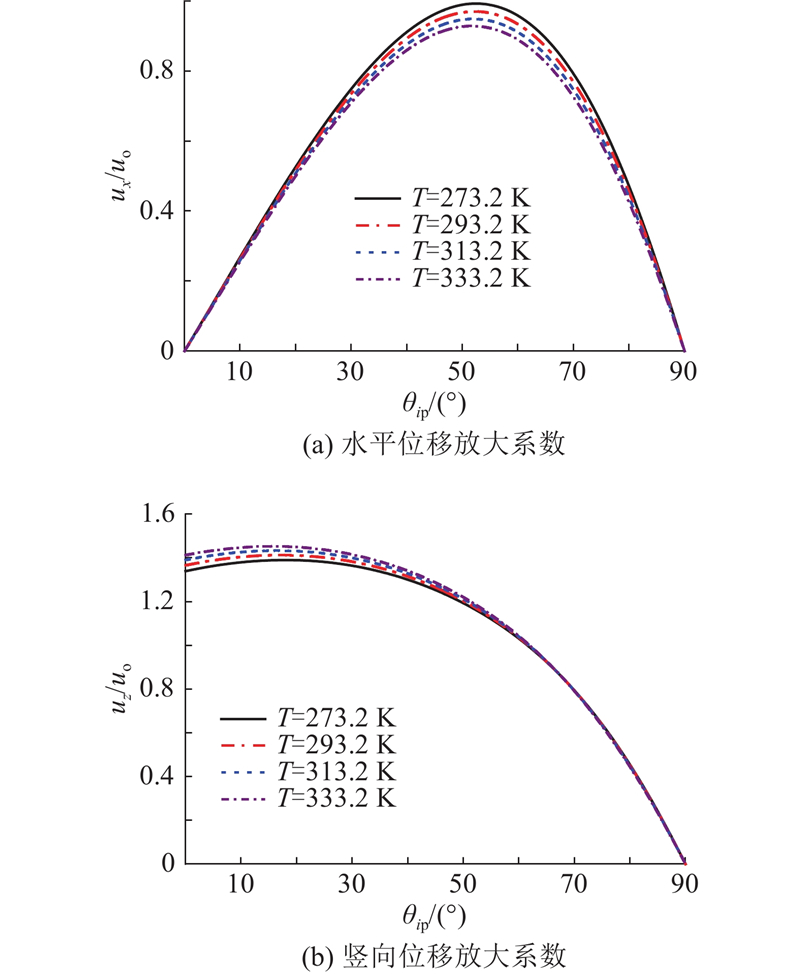
6.4. 不同入射角下介质温度的影响
介质温度与应力应变之间的耦合效应影响波的形成和传播,从而影响场地的地震地面运动. 如图5所示,为了分析介质温度变化对位移放大系数的影响规律,绘制当
图 5
图 5 不同温度下的位移放大系数
Fig.5 Displacement magnification factors under different temperatures
6.5. 固相比热容和热膨胀系数对地表位移放大系数的影响
在热效应下的成层弹性地基中,固相比热容和热膨胀系数是不可或缺的热物性参数. 固相比热容不仅影响热弹性波的波速,也影响波速的变化幅度. 热膨胀系数常用来表征热弹性介质的热膨胀量,不仅可以用来衡量热弹性介质的热稳定性能,还与温度变化时介质所产生的热应力与应变密切相关[34]. 因此固相比热容和热膨胀系数对场地地震响应的影响不可忽视. 如图6所示,为了分析热膨胀系数和固相比热容对地表位移放大系数的影响,绘出当θip=30°、
图 6
图 6 位移放大系数随固相比热容和热膨胀系数变化的三维等高线图
Fig.6 Three-dimensional contour plot of displacement magnification factor with solid specific heat capacity and thermal expansion coefficient
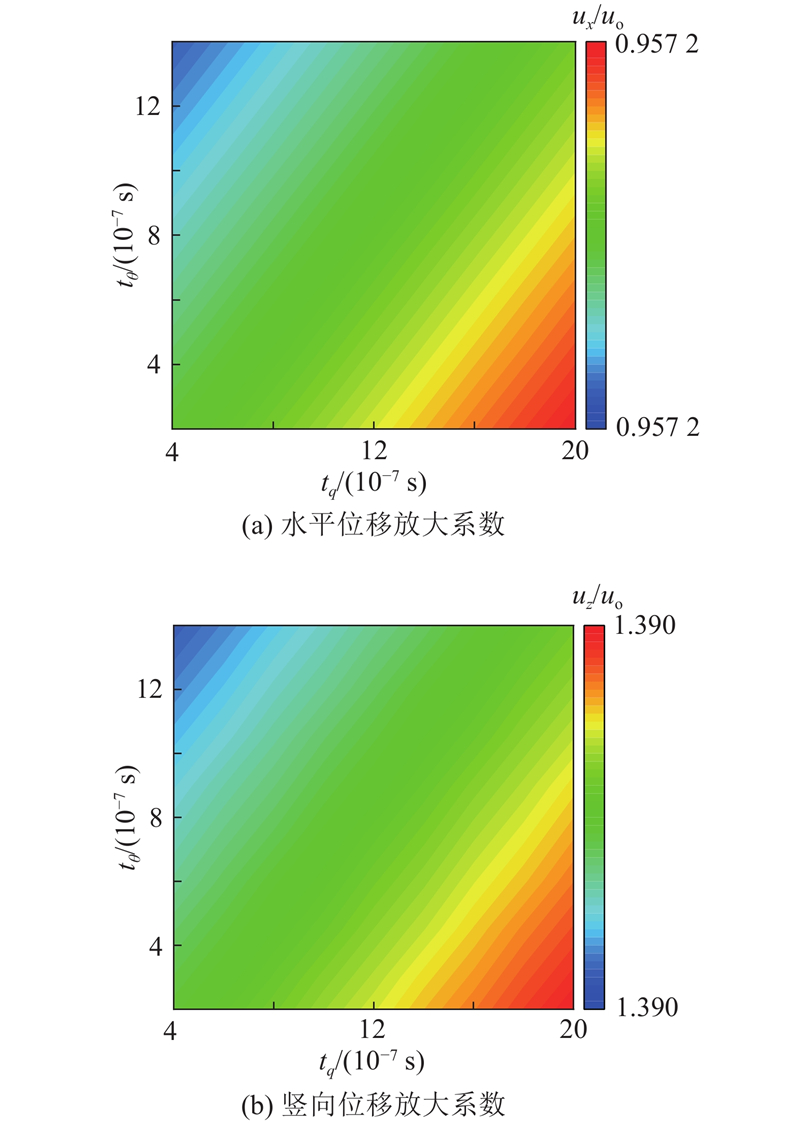
6.6. 热通量和温度梯度相位延迟时间对地表位移放大系数的影响
相对于等温条件下的波动理论,在热弹性理论下,介质中会产生与P波传播特性类似的热波. 热通量和温度梯度相位延迟时间出现在热传导的波动控制方程式(2),控制着T波的产生和传播,对T波的传播特性产生影响. 如图7所示,为了分析热通量和温度梯度相位延迟时间对地表位移放大系数的影响,绘出当θip=30°、
图 7
图 7 位移放大系数随热通量和温度梯度相位延迟时间变化的三维等高线图
Fig.7 Three-dimensional contour plot of displacement magnification factor with heat flux and temperature gradient phase delay time
6.7. 不同入射角下入射频率的影响
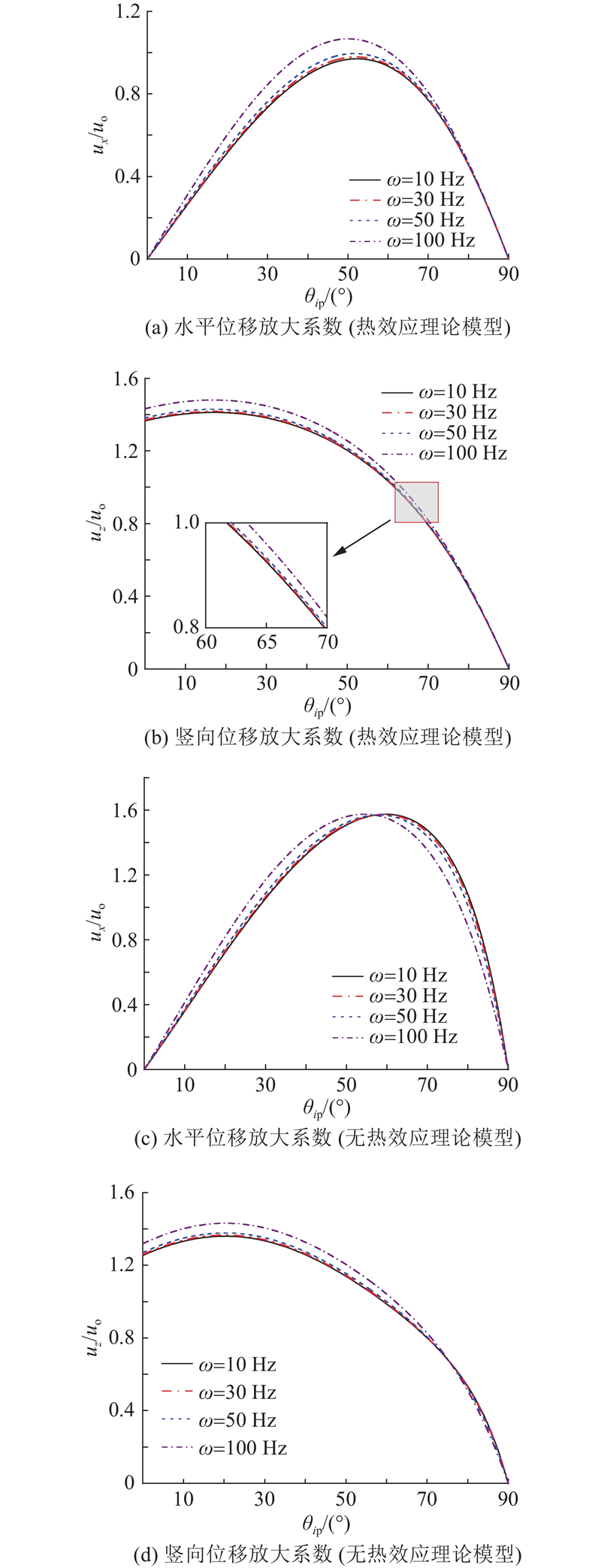
低频震源研究在勘探地震学中具有重要意义. 为了模拟真实的情况,在地震波数值模拟当中,震源子波的主频一般在5~50 Hz(2~100 Hz的频率包含了大部分地震激发的地震波频率[35]),在分析入射频率变化对地表位移放大系数影响的过程中,保持其他参数不变. 如图8所示为频率逐渐增大时在2种理论模型下地基表面位移放大系数随入射角度变化的关系曲线. 由图可知,2种理论模型下,频率变化对地表位移放大系数的影响有所不同. 在热效应条件下,随着频率的增大,水平和竖向位移放大系数逐渐增大. 对于无热效应条件下,竖向位移放大系数随着频率的增大而逐渐增大,当入射角度θip<60°,水平位移放大系数随着频率的增大而增大,当入射角度θip>60°时,水平位移放大系数随着频率的增大而减小. 在相同频率下,热效应下的水平位移放大系数较小,竖向位移放大系数较大. 所得成层弹性地基中频率变化对地表位移放大系数的影响规律与文献[32]所得到的热效应条件下均质弹性地基中频率变化对地表位移放大系数的影响规律相近,再次证明了本研究解的有效性;2种理论模型下地表位移放大系数在数值上的差异性,再次说明在非等温条件下研究成层弹性地基地震地面运动具有重要意义. 由此可见,在进行如小区场地抗震设计的实际工程应用时,入射频率的变化对地表位移放大系数的影响不可忽视.
图 8
图 8 不同入射频率下的位移放大系数(2种理论模型)
Fig.8 Displacement magnification factors under different incident frequencies (two theoretical models)
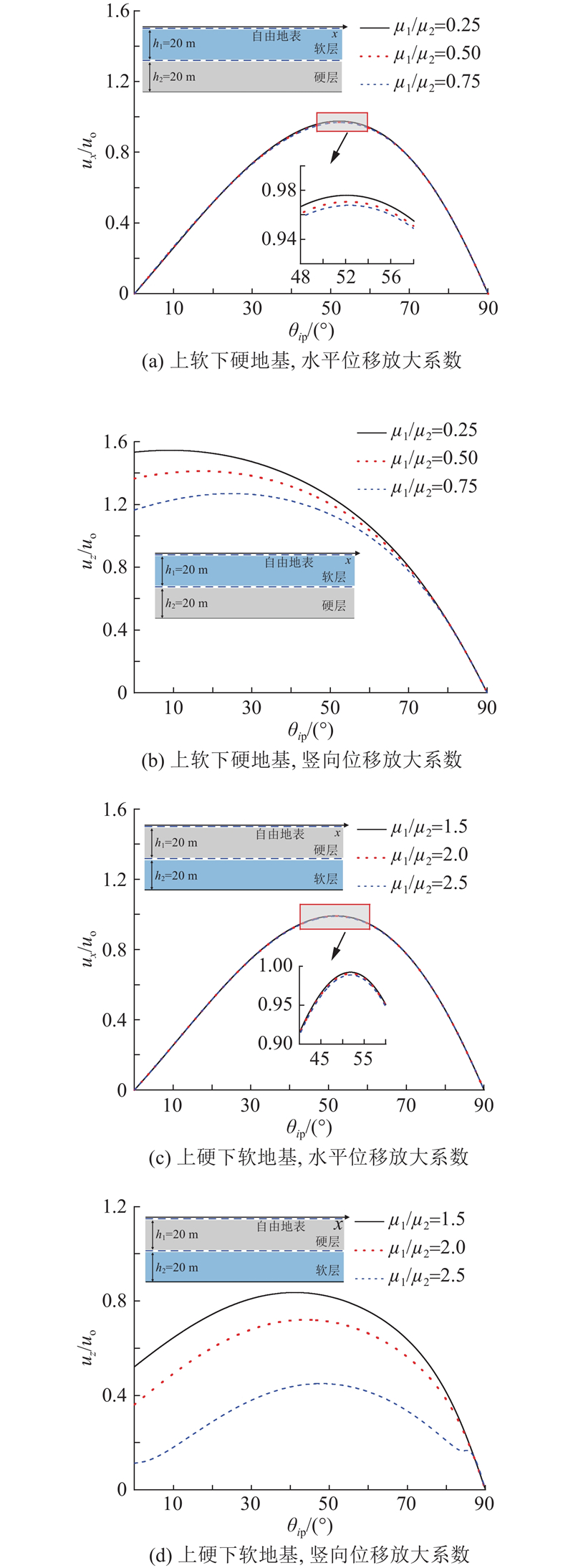
6.8. 不同入射角下软硬土层排列次序的影响
软硬土层的排列次序对地表位移幅值的影响显著[36]. 如图9所示为在2种典型成层弹性地基中当表层剪切模量发生变化时地基表面位移放大系数随入射角度变化的关系曲线. 在上软下硬地基中,由上下土层剪切模量比μ1/μ2=0.25、0.50和0.75分为工况1、2、3;在上硬下软地基中,由μ1/μ2=1.5、2.0和2.5分为工况4、5、6,其中下层土的剪切模量为8.0 GPa,其他参数见表1. 由图可知,无论是上软下硬地基还是上硬下软地基,水平和竖向位移放大系数均随着入射角的增大先增大后减小. 随着表层剪切模量的增大,2种地基下的水平和竖向位移放大系数均逐渐减小,原因是表层土的剪切模量越大,土体的抗剪强度越高,土骨架的相对变形减小. 较软土层处于地表时位移放大系数较硬土层处于地表时的位移放大系数大,说明在上软下硬的地基中应力发生集中,在上硬下软的地基中则发生应力分散. 由此可见,在工程中充分利用硬土层对应力的扩散作用,有望节约成本,增大表层土的剪切模量可有效减小地表位移,再次说明成层弹性地基的成层特性对场地地震响应的影响显著.
图 9
图 9 不同典型成层弹性地基中的位移放大系数
Fig.9 Displacement magnification factors in different typical layered elastic foundations
7. 结 论
本研究探讨介质温度、固相比热容对热效应下成层弹性地基地震响应的影响,基于热力学的基本理论,提出考虑温度的变化和土体在沉积过程中自身成层特性的数学模型. 该模型可用于研究热效应作用下,地震波入射成层弹性地基场地的地震响应问题. 当选取弹性地基层中波速最大,将抗衰减性最强的P波作为对象,研究热效应作用下成层弹性地基场地地震响应问题时,得出以下结论.
(1) 在入射角度范围内,有热效应和无热效应2种理论模型下所得地表位移放大系数差异显著,且土层沉积后的成层特性使得场地的地震响应有别于均质地基的情况. 因此,应重点关注热效应和土层沉积后的成层特性对场地地震响应的影响.
(2) 在热效应作用下,当平面P波入射成层弹性地基场地时,随着介质温度的增大,地表水平位移放大系数逐渐减小,地表竖向位移放大系数逐渐增大. 因此,在实际工程须重点关注和记录土层的温度变化情况.
(3) 固相比热容对位移放大系数的影响主要取决于土体的热稳定性能,热膨胀系数对位移放大系数的影响与土体固相比热容的大小密切相关,这对于考虑热效应作用下成层弹性地基的地震响应研究至关重要.
(4) 热效应条件下的水平和竖向位移放大系数均随着入射频率的增大而逐渐增大,但与无热效应模型下所得到的位移在数值上存在差异. 因此,在进行小区场地抗震设计时,入射频率的变化对地表位移放大系数的影响不可忽视
(5) 软硬土层在土层中的排列次序对地表位移放大系数影响不可忽视,在工程中充分利用硬土层对应力的扩散作用有望节约成本,增大表层土的剪切模量,有效缩短地表位移.
本研究主要是探讨热弹性介质理论框架下成层弹性地基场地的地震动特性. 在自然界中,土骨架的黏性使土体表现出非线性行为. 后续计划研究热效应下土骨架的黏性对于成层弹性地基场地地震响应的影响,为弹性地基场地的抗震设防提供理论指导.
参考文献
梯度饱和多孔材料中弹性波的截止频率
[J].
Analysis of cut-off frequencies for functionally graded fluid-saturated materials
[J].
多空沟对弹性波的散射及隔振性能分析: 平面P-SV波入射
[J].
Analysis of elastic wave scattering and vibration isolation performance of multiple open trenches: plane P-SV wave incident
[J].
起伏地表条件下有限差分地震波数值模拟——基于广义正交曲线坐标系
[J].
Finite-difference method for seismic wave numerical simulation in presence of topography: in generalized orthogonal curvilinear coordinate system
[J].
沉积盆地-山体耦合场地对平面P波、SV波和Rayleigh波的二维散射分析
[J].DOI:10.6052/j.issn.1000-4750.2014.05.0396
Two dimensional scattering analysis of planar P, SV, and Rayleigh waves by coupled alluvial basin-mountain terrain
[J].DOI:10.6052/j.issn.1000-4750.2014.05.0396
The method of fundamental solutions for the elastic wave scattering in a double-porosity dual-permeability medium
[J].
Seismic analysis of a lined tunnel in a multi-layered TI saturated half-space due to qP1-and qSV-waves
[J].DOI:10.1016/j.tust.2021.104248 [本文引用: 1]
A generalized dynamical theory of thermoelasticity
[J].DOI:10.1016/0022-5096(67)90024-5 [本文引用: 1]
Thermoelasticity
[J].DOI:10.1007/BF00045689 [本文引用: 1]
A re-examination of the basic postulates of thermomechanics
[J].
Thermoelasticity without energy dissipation
[J].DOI:10.1007/BF00044969 [本文引用: 1]
Rayleigh waves in a thermoelastic solid half space using dual-phase-lag model
[J].DOI:10.1016/j.ijengsci.2011.03.007 [本文引用: 1]
Reflection of thermoelastic waves at a solid half-space with thermal relaxation
[J].DOI:10.4294/jpe1952.22.237 [本文引用: 5]
Reflection of thermoelastic waves at a solid half-space with two thermal relaxation times
[J].
Reflection and refraction of thermoelastic waves at an interface of two semi-infinite media with two relaxation times
[J].DOI:10.1080/01495739708956095 [本文引用: 1]
The reflection phenomena of SV-waves in a generalized thermoelastic medium
[J].DOI:10.1155/S0161171200004221 [本文引用: 1]
Reflection of generalized thermoelastic waves from the boundary of a half-space
[J].DOI:10.1080/01495730306342 [本文引用: 1]
Reflection of SV waves from the free surface of an elastic solid in generalized thermoelastic diffusion
[J].
Reflection of P and SV waves from free surface of an elastic solid with generalized thermodiffusion
[J].DOI:10.1007/BF02702017 [本文引用: 1]
Reflection of plane waves from the boundaries of a micropolar thermoelastic half-space without energy dissipation
[J].
Reflection and refraction of a plane thermoelastic wave at a solid–solid interface under perfect boundary condition, in presence of normal initial stress
[J].DOI:10.1016/j.apm.2011.04.026 [本文引用: 1]
Reflection and transmission of inhomogeneous plane waves in thermoelastic media
[J].DOI:10.3389/feart.2022.850331 [本文引用: 1]
单相土体与饱和土体地下结构地震反应对比研究
[J].
Comparative study of seismic response of underground structures in single-phase and saturated soils
[J].
位于弹性半空间上的理想流体层动力反应—平面P波入射
[J].DOI:10.3969/j.issn.1000-4750.2003.06.003 [本文引用: 1]
Dynamic response of ideal fluid layer overlying elastic half-space due to P-wave incidence
[J].DOI:10.3969/j.issn.1000-4750.2003.06.003 [本文引用: 1]
Analytical solution for seismic response of tunnels with composite linings in elastic ground subjected to Rayleigh waves
[J].DOI:10.1016/j.soildyn.2021.107113 [本文引用: 1]
Scattering of elastic spherical P, SV, and SH waves by three-dimensional hill in a layered half-space
[J].DOI:10.1016/j.soildyn.2020.106545 [本文引用: 1]
Study on seismic ground motion of P-wave incident elastic foundation free field under thermal effect
[J].
Propagation behavior of homogeneous plane-P1-wave at the interface between a thermoelastic solid medium and an unsaturated porothermoelastic medium
[J].DOI:10.1140/epjp/s13360-021-02144-x [本文引用: 5]
热弹性介质中波传播特征
[J].DOI:10.6038/cjg2021N0458 [本文引用: 1]
Characteristics of wave propagation in thermoelastic medium
[J].DOI:10.6038/cjg2021N0458 [本文引用: 1]
层状非饱和土地基的轴对称稳态动力响应
[J].DOI:10.3969/j.issn.1000-7598.2011.04.027 [本文引用: 1]
Axisymmetric steady state dynamic response of layered unsaturated soils
[J].DOI:10.3969/j.issn.1000-7598.2011.04.027 [本文引用: 1]