随着我国经济的快速发展,冰雪赛事、节日庆典之类临时性活动的举办频率不断增加,举办规模不断扩大. 临时转播塔作为活动场地的重要基础设施,其设计应兼具安全性、适用性与经济性. 然而,现有的临时转播塔常采用钢管支架结构或简易角钢塔结构,具有可建造高度低、用钢质量大的不足. 此外,现有临时转播塔多依赖经验进行设计,存在较大的盲目性,难以适应当前精细化设计的需求. 针对上述问题,须对现有的临时转播塔结构进行优化,并发展相应的结构优化设计方法.
塔架结构的优化设计属于有约束的复杂多极值函数优化问题,对该类问题,浮点数编码遗传算法(float-encoded genetic algorithm, FGA)之类的元启发算法的求解精度高于响应面法之类的传统优化方法[6-7]. 近年来随着元启发算法的更新及应用,塔架结构的优化设计方法得到进一步发展. Sivakumar等[8]采用遗传算法优化格构式塔架中构件的截面尺寸;Musa[9]采用和声搜索算法对角钢塔的构件截面进行优化;Kaveh等[10]利用改进灰狼算法优化格构式塔架的尺寸设计变量. 上述研究对塔架结构进行尺寸优化时计算效率较高,但未考虑结构形状和拓扑关系对受力性能的影响,对复杂结构的优化结果较差. Jawad等[11]采用人工蜂群算法优化格构式塔架的形状和尺寸;Couceiro等[12-13]将一阶灵敏度分析引入模拟退火算法,对塔架的形状和尺寸变量进行优化;Huang等[14]提出混合式塔架结构,并采用遗传算法优化结构的形状和尺寸. 塔架结构的拓扑优化方法分为连续体优化与离散体优化2种. 基于连续变量的拓扑优化计算效率较低,且优化结果须经调整方能满足施工工艺要求[15]. 因此,塔架结构优化常采用离散的拓扑设计变量. De Souza等[16]预先建立塔段的多种拓扑模板,采用元启发算法实现了输电塔的拓扑优化;Degertekin等[17]利用Jaya算法对格构式塔架的形状、尺寸及离散拓扑变量进行优化;Khodzhaiev等[18]提出具有可变长度基因组的遗传算法和塔架结构的两阶段拓扑优化方法;金树等[19]基于蚁群算法,采用离散的尺寸、形状及拓扑设计变量实现了输电塔结构的综合优化. 上述研究中优化对象均是永久性塔架,缺少考虑多设计变量的模块化临时塔架综合优化研究. 而FGA算法、和声搜索算法与灰狼算法等现有元启发算法在结构优化问题上存在早熟性收敛现象,限制了其求解效率与搜索能力[20-22].
本研究设计了模块化临时转播塔结构,提出考虑该结构形状、尺寸及拓扑形式的综合优化方法,采用初始替换策略、初始大种群策略、末位替换策略、差异化策略与自适应遗传策略改进FGA算法的计算效率与寻优能力,结合参数化有限元分析,提出模块化临时转播塔结构的优化设计方法.
1. 模块化临时转播塔结构
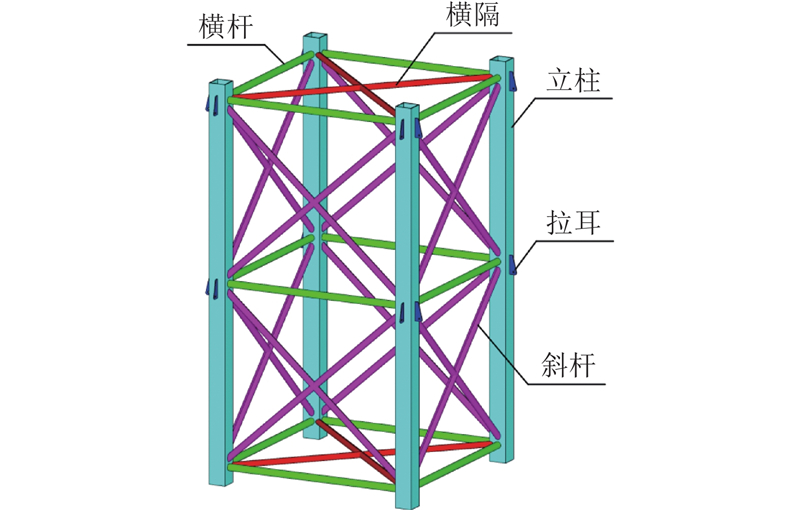
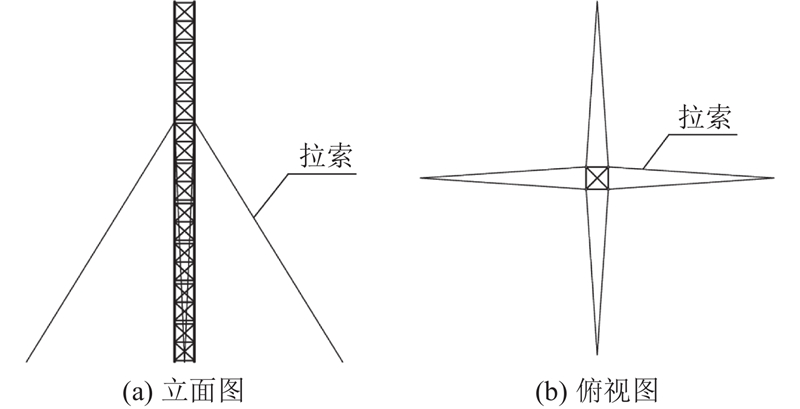
为了更好地约束水平位移,模块化临时转播塔结构采用正方形截面的装配式拉索钢塔架体系,其组成包括若干个标准节与8根预应力钢拉索. 典型标准节的组成见图1,模块化临时转播塔结构的组成见图2. 为了尽量减少构件种类以降低建造成本,将标准节中的杆件分为立柱、横杆、斜杆、横隔4类,同类型杆件的截面尺寸相同. 每个标准节由4根立柱,若干根横杆、斜杆、横隔及其他连接件焊接而成,相邻标准节之间采用高强螺栓连接. 为了充分发挥斜杆的受力性能,标准节高度取为宽度的2倍. 为了减小风荷载作用并降低标准节的加工难度,立柱采用方钢管制作,横隔和斜杆采用圆钢管制作. 为了适应严寒环境,杆件材料均选用Q345E低合金钢,拉索选用多束1860型预应力钢绞线.
图 1
图 2
2. 优化设计基本理论
2.1. 参数化有限元模型
采用ANSYS建立模块化临时转播塔结构的参数化有限元模型. 由于各标准节的组成相同,可根据设计参数分别建立单个标准节与拉索的有限元模型,而后装配标准节与拉索建立临时转播塔结构整体有限元模型. 根据构件的受力特点,采用BEAM188单元模拟各类杆件,CABLE280单元模拟拉索. 塔顶设备等效为集中质量,采用MASS21单元模拟,与格构式塔架的相应节点刚性耦合. 建模所需的设计参数见表1.
表 1 临时转播塔结构设计变量
Tab.1
表 2 有限元模型计算结果对比
Tab.2
| 结果类型 | f1/Hz | f2/Hz | f3/Hz | f4/Hz | w/mm |
| ANSYS | 79.435 | ||||
| SAP2000 | 79.380 | ||||
| midas Gen | 79.222 | ||||
| ε1/% | 3.01 | 3.00 | 3.30 | 3.25 | 0.07 |
| ε2/% | 3.00 | 3.00 | 3.32 | 3.25 | 0.27 |
2.2. 综合优化的数学模型
模块化临时转播塔的综合优化属于有约束的优化问题,其数学模型包括目标函数、设计变量、约束条件3部分. 综合优化为在满足约束条件的前提下,改变设计变量使目标函数最小化的过程.
式中:X={x1, x2,
2.2.1. 目标函数
塔架结构的运输、建造和拆除成本以及结构在全寿命周期的碳排放量均与结构的总质量正相关,因此优化设计的目标通常是在保证安全性、适用性的前提下尽可能减小结构的总质量. 针对模块化临时转播塔结构,选取目标函数如下:
式中:M(X)为结构总质量,nb为构件总数,ρi、li和Ai分别为构件的密度、长度和横截面积. 具体数值可通过有限元模型求解得到.
2.2.2. 设计变量
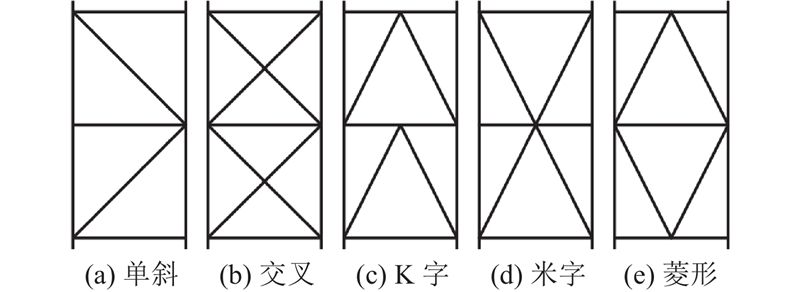
模块化临时转播塔的拓扑形式主要受斜杆布置形式、横隔层数及拉索端部高度3个参数影响;结构形状主要受标准节宽度与拉索宽度两参数影响;结构刚度和稳定性受拉索初应力影响较大. 故将以上参数作为优化设计变量. 为了使优化结果满足模块化要求且便于加工与安装,优化过程采用离散的拓扑设计变量,只考虑5种典型的斜杆布置形式与2种横隔布置形式. 由于标准节中拉耳位置固定,拉索端部实际位置根据“拉索端部近似高度”就近取为架体上预装拉耳的位置.
图 3
2.2.3. 约束条件
约束条件是指在优化过程中为保证结构的安全性与适用性,对结构的变形、应力、稳定性等施加的各种限制. 对于临时转播塔结构,约束条件包括应力约束、变形约束,长细比约束和稳定性约束.
1) 应力约束条件.
式中:q1为单位长度的覆冰重力荷载,b为基本覆冰厚度,d1为圆截面构件的直径,α1为与直径有关的覆冰厚度修正系数,α2为覆冰厚度的高度递增系数,γ为覆冰重度,qa为单位面积的覆冰重力荷载.
式中:wk为风荷载标准值;w0为基本风压;μz为风压高度变化系数;μs为风荷载体形系数;βz为风振系数,按规范[23]计算;B为覆冰时风荷载增大系数.
在承载能力极限状态下,各构件的等效应力不得超过强度设计值;在正常使用极限状态下,各杆件的等效应力不得超过强度标准值,表达式如下:
式中:σi为第i个构件的等效应力,[σ]为容许应力.
2) 变形约束条件.
依据高耸结构设计标准[23],在风荷载为主的标准组合作用下,结构的水平位移角不得超过限值.
式中:Δu为塔顶水平位移,H为结构总高度.
3) 长细比约束条件.
式中:λi为第i根杆件的长细比;[λ]为容许长细比,对于立柱,[λ]=150,对于斜杆、横杆和横隔,[λ]=180.
4) 稳定性约束条件.
依据钢结构设计标准[26],临时转播塔结构中各类杆件须满足稳定性约束条件.
式中:
式中:φx、φy为对强轴x-x和弱轴y-y的轴心受压构件整体稳定系数;φbx、φby为均匀弯曲的受弯构件整体稳定性系数,取1.0;Mx、My为所计算构件段范围内对强轴和弱轴的最大弯矩设计值;Wx、Wy为对强轴和弱轴的毛截面模量;η为调整系数;βmx、βmy为弯矩作用平面内的等效弯矩系数;βtx、βty为弯矩作用平面外的等效弯矩系数.
3. 改进浮点数编码遗传算法
为了提升FGA算法的计算效率与搜索能力,通过引入初始替换、初始大种群、末位替换、差异化与自适应遗传算子等5种优化策略,提出改进浮点数编码遗传算法(IFGA). 该算法使用由11个浮点数构成的染色体表示转播塔结构的11个设计变量,各变量的取值范围见表1.
3.1. 适应度函数
在遗传算法中以适应度的大小来评定个体的优劣程度. 直接取目标函数值作为适应度,对不满足约束条件的个体,其适应度赋大值. 适应度函数的表达式如下:
式中:M(X)为结构的总质量,单位为t.
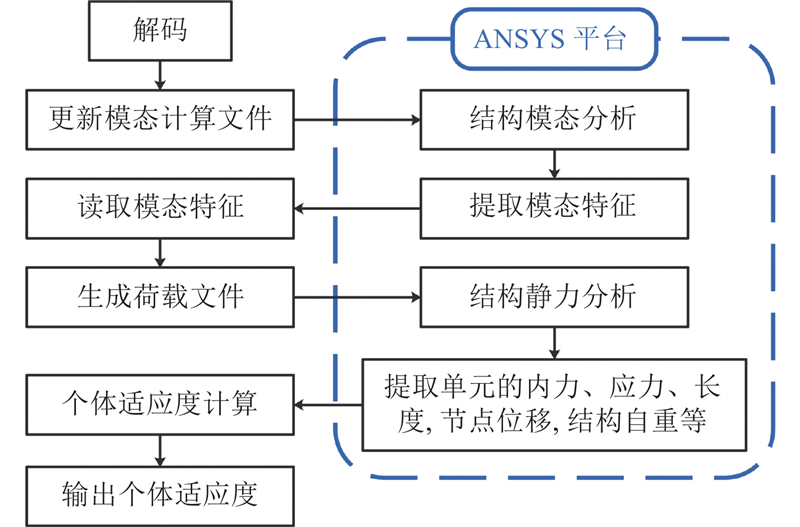
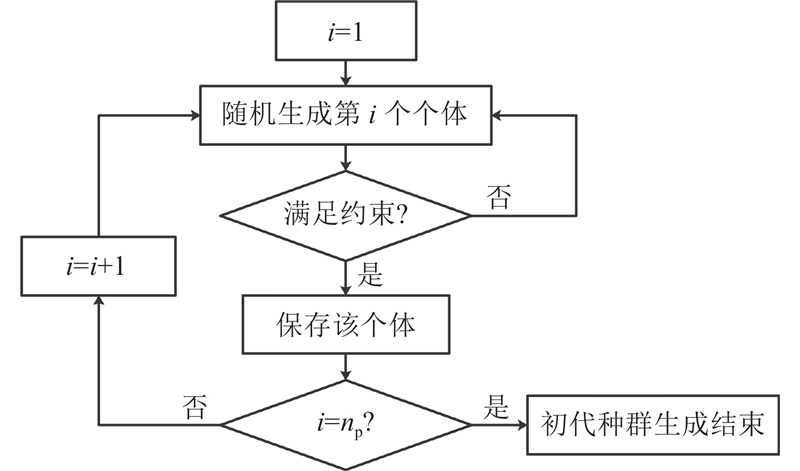
适应度函数的计算流程见图4.
图 4
3.2. 种群初始化
种群规模对遗传算法的全局搜索能力有显著影响,对于FGA算法,一般取设计变量的5~10倍[27],本研究的种群规模取80.
3.2.1. 初始大种群
扩大初始种群规模可以增加初始种群中个体的分布范围,提升遗传算法的全局搜索能力,从而能够以较小的计算成本避免遗传算法陷入局部最优解,且能够加速遗传算法的收敛过程. 遗传算法的初始种群规模不宜小于设计变量的10倍[27]. 本研究的初始种群规模取200.
3.2.2. 初始替换策略
图 5
3.3. 末位替换策略与差异化策略
研究[29]表明,遗传算法在迭代过程中,种群的所有个体会逐渐趋于一致,从而导致算法过早收敛并陷入局部最优解. 为了避免算法的早熟性收敛现象,引入末位替换策略与差异化策略. 在新种群生成后,删除种群中适应度最差的个体并重新生成新个体,以拓宽算法的搜索空间. 而后,计算每个个体与最优个体之间以及与相邻个体之间的差异度,删除差异度低于阈值的个体并重新生成新个体,以保证种群的多样性,避免陷入局部最优解. 个体差异度的表达式如下:
式中:D1(j)为第j个个体与最优个体的差异度;D2(j)为第j与第j−1个个体的差异度;Xj、Xj−1分别为第j和第j−1个个体的基因型;Xbest为最优个体的基因型;Δ为各基因取值范围组成的向量,Δ=[δ1, δ2, ···, δ11];[D]为差异度阈值,本研究取0.01.
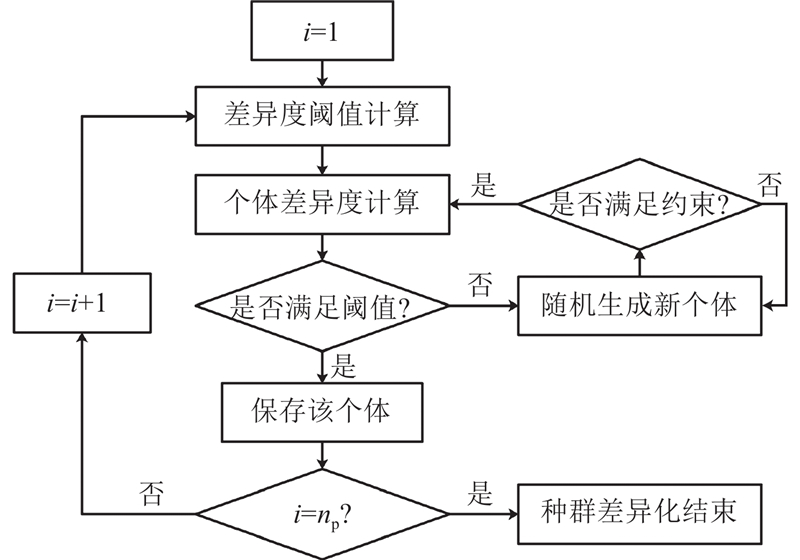
种群差异化流程见图6.
图 6
3.4. 遗传算子的选择
采用轮盘赌选择算子,个体被选中的概率与适应度值成反比.
为了使交叉算子的搜索范围能够覆盖整个解空间,选用扩展均匀算数交叉算子. 交叉概率的推荐取值为Pc=0.50~1.00[30],本研究取Pc=0.85. 亲代个体交叉前随机生成与染色体等长的二进制串(q1,q2,
式中:
采用均匀变异算子. FGA算法中变异概率的推荐取值为Pm=
3.5. 自适应的交叉、变异和差异化算子
遗传算法中交叉算子的伸缩系数、变异算子的变异概率和差异化算子的差异度阈值通常取定值. 进化初期过低的伸缩系数、变异概率和差异度阈值难以扩大算法的搜索空间,会使算法发生早熟性收敛;而进化后期过高的伸缩系数、变异概率和差异度阈值会破坏过多优质个体,使算法趋于随机搜索难以收敛. 因此,难以找到对不同进化阶段的所有个体都合适的伸缩系数、变异概率和差异度阈值.
引入自适应遗传策略,采用进化代数与适应度值作为控制变量来调整伸缩系数、变异概率和差异度阈值. 进化初期加剧种群的交叉、变异与差异化过程,加大较差个体的交叉幅度、变异概率与差异度;进化后期抑制种群的交叉、变异与差异化程度,减小优良个体的交叉幅度、变异概率与差异度. 算法得以在探索更广区域的同时维持当前的收敛方向,从而加快收敛速度,提高计算效率. 自适应的伸缩系数、变异概率和差异度阈值的表达式如下:
式中:αcmax、αcmin为考虑适应度影响的伸缩系数上、下限,αmmax、αmmin为考虑适应度影响的变异概率上、下限,αdmax、αdmin为考虑适应度影响的差异度阈值上、下限,βcmax、βcmin为考虑进化代数影响的伸缩系数上、下限,βmmax、βmmin为考虑进化代数影响的变异概率上、下限,βdmax、βdmin为考虑进化代数影响的差异度阈值上、下限,fˊ为参与交叉的两个体中较小的适应度,f为变异个体的适应度,favg为种群平均适应度,fmax为种群最大适应度,t为当前进化代数,T为总进化代数. 本研究取αcmax=0.55, αcmin=0.20, αmmax=0.10, αmmin=0.03, αdmax=0.020, αdmin=0.002, βcmax=1.0, βcmin=0.3, βmmax=1.0, βmmin=0.5, βdmax=1.0, βdmin=0.5.
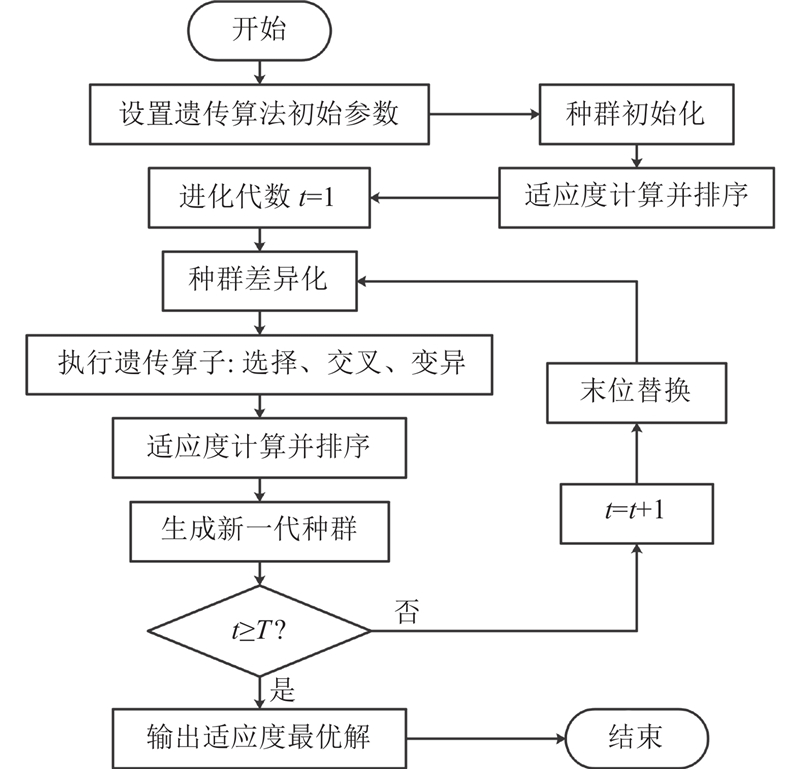
IFGA算法的计算流程见图7.
图 7
4. 优化设计实例与分析
4.1. 优化设计系统
基于模块化临时转播塔结构的综合优化方法,构建该类结构的优化设计系统. 如图8所示,系统分参数定义、设计计算、结果输出3个模块. 用户按照要求在参数定义模块输入实际工程的使用要求与设计条件,设计计算模块会自动完成模块会化临时转播塔结构的方案设计与优化,结果输出模块输出符合设计要求且经济性良好的建议设计方案及各参数的优化历程曲线,从而能够以较快的速度完成临时转播塔结构方案的设计,显著提升设计效率.
图 8
4.2. 工程概况
模块化临时转播塔的建造地点位于河北省张家口市,塔顶设备高度为100 m,拉索选用多束1×7-15.2-1860型预应力钢绞线. 地面粗糙度为B类,基本风压按50 a重现期取为0.55 kN/m2,基本覆冰厚度取10 mm. 依据当地气象数据取结构最大升温为30 ℃,最大降温为−50 ℃.
4.3. 算法性能分析
为了检验所提IFGA算法的计算效率、寻优能力及对结构优化问题的适用性,进行临时转播塔结构优化的对比试验. 采用算法运行过程中个体适应度的总求解次数衡量该算法的计算成本,通过分析不同算法的收敛曲线评价该算法的全局寻优能力.
4.3.1. 改进策略的有效性分析
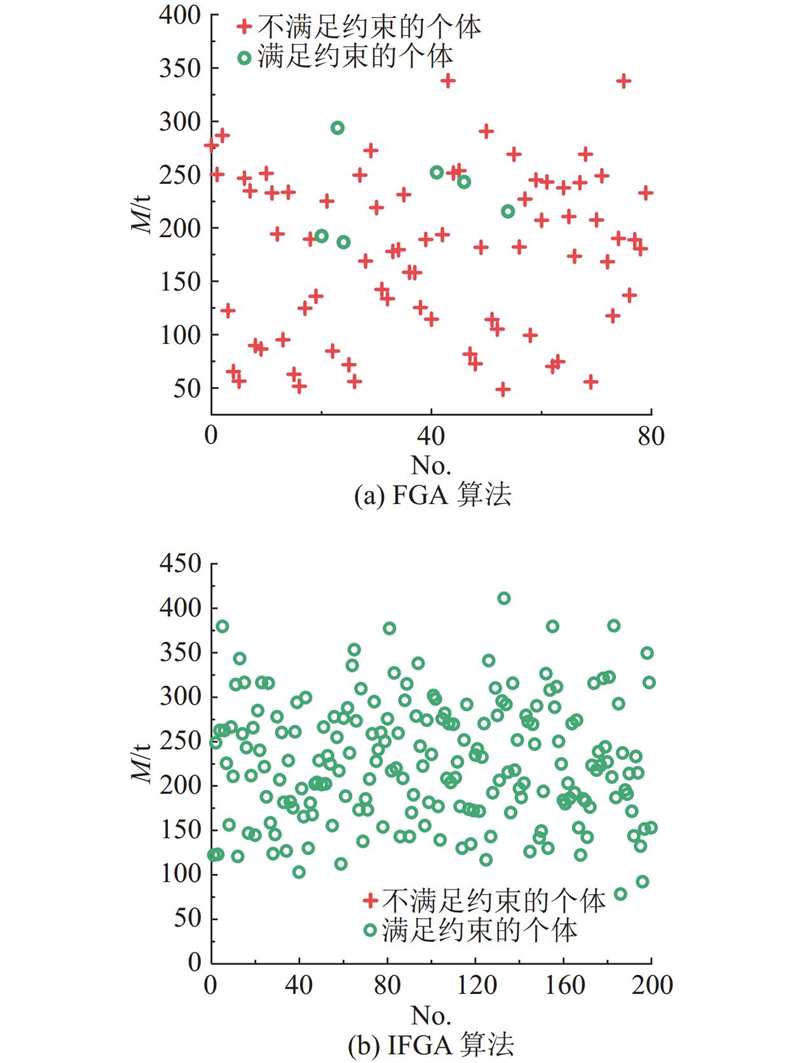
改进前后遗传算法的初始种群分布如图9所示. 图中,No.为个体编号. 针对结构优化问题,FGA算法随机生成的初始种群中仅有7.5%的个体满足约束条件,种群缺乏多样性,限制了算法的全局搜索能力. IFGA算法由于引入了初始大种群策略和初始替换策略,初始种群的个体数量更多且100%满足约束条件,能够更为均匀地覆盖整个解空间,种群多样性良好,从而可以有效避免局部收敛现象的发生.
图 9
图 9 改进前后遗传算法的初始种群
Fig.9 Initial population of genetic algorithms before and after improvement
表 3 不同策略遗传算法的优化结果与计算成本
Tab.3
| 算法名称 | S | M/t |
| FGA | 40.42 | |
| RGA | 38.42 | |
| LRGA | 37.22 | |
| LRSGA | 36.44 | |
| LRSDGA | 33.80 | |
| IFGA | 32.77 |
图 10
图 10 不同策略遗传算法的进化历程
Fig.10 Evolutionary process of GAs with different strategies
由表3可知,在结构轻量化方面,各改进策略均可以改善算法的优化结果,均有助于提高FGA算法的搜索能力. IFGA算法的优化效果最为显著,其用钢质量相较于FGA算法降低了18.9%. 同时,引入改进策略后FGA算法的计算成本明显增加,这是由于初始替换策略、初始大种群策略、末位替换策略与差异化策略扩大了算法的搜索范围,从而增加了算法对解空间中不同个体的求解次数. 自适应遗传算子适当减弱了进化后期对种群多样性的约束,从而减少了维持种群多样性所需的求解次数,提高了算法的计算效率. 这表明本研究提出的IFGA算法具有较好的计算效率与全局寻优能力.
由图10可知,在引入改进策略后,算法的收敛速度明显加快,寻优能力显著增强. 初始替换策略与初始大种群策略的引入提高了初始种群的多样性,拓展了进化初期算法的搜索范围,提升了算法的全局搜索能力,加快了收敛速度;但算法的过早收敛现象仍然存在,在进化中后期种群的多样性过低,算法容易陷入局部收敛. 引入末位替换策略与种群差异化策略后,进化中后期种群的多样性维持在较高水平,拓展了算法的搜索范围,加快了进化中期的收敛速度;但在进化后期维持较高的种群多样性,会增加算法的计算成本,削弱算法的局部搜索能力,导致种群难以在最优解域收敛,所得优化结果是与最优解偏差较大的近似值. 引入自适应遗传算子后,适当减小了进化后期较优个体的交叉幅度、变异概率和差异度,缩小了算法的搜索范围,提高了算法的局部开发能力和计算效率,使优化结果更加准确. IFGA算法的寻优能力和计算效率明显优于FGA算法,更适合在复杂实际工程中的应用.
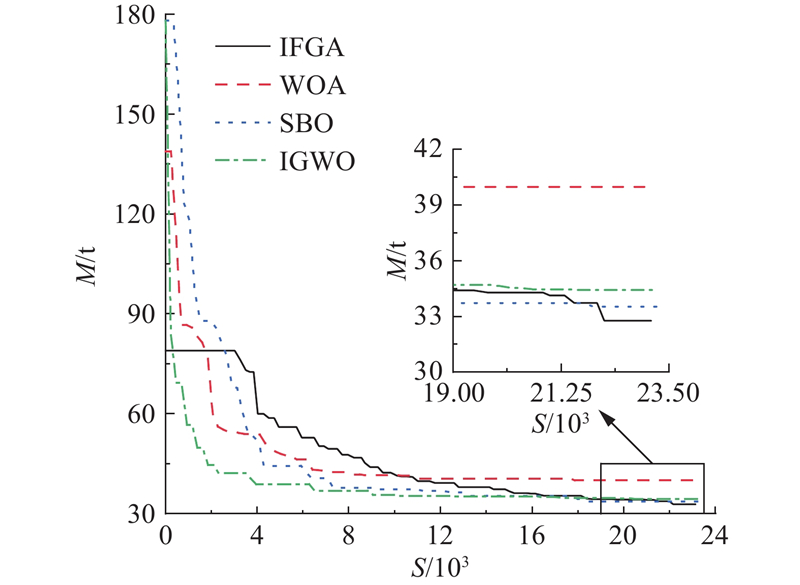
4.3.2. 与其他优化算法对比
表 4 不同算法的优化结果与计算成本
Tab.4
| 算法名称 | S | M/t |
| IFGA | 32.77 | |
| WOA | 40.00 | |
| SBO | 33.54 | |
| IGWO | 34.43 |
图 11
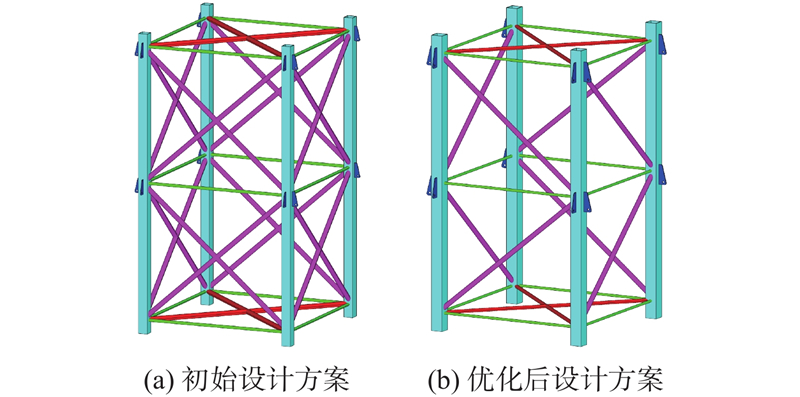
4.4. 结构轻量化效果分析
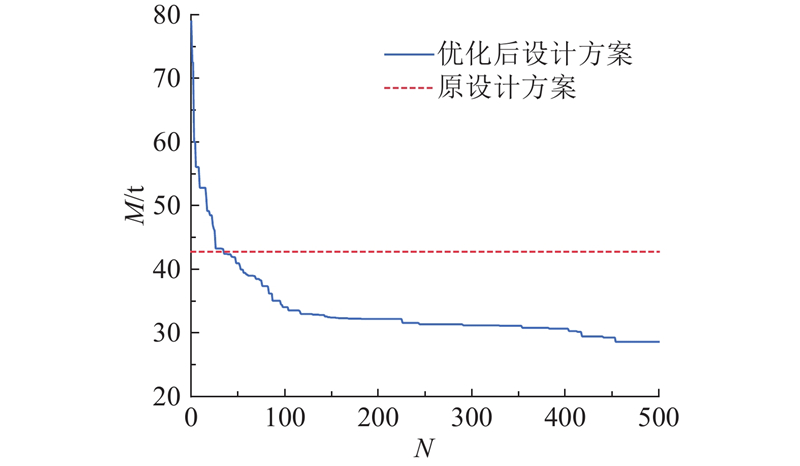
优化过程中结构总质量的进化历程如图12所示. 在进化初期,算法的寻优主要集中于对整个解空间的探索,评价了多样化的设计方案,最优个体的适应度得以迅速减小. 在进化后期,算法进入开发阶段,此阶段内整个种群逐渐向最优个体所标定的方向收敛,直至寻找到一个最优的设计方案. 算法经过500代进化后趋于收敛,所得最优设计方案的总用钢质量为28.579 t,相较于初始设计方案总用钢质量减少了33.2%.
图 12
表 5 优化前后设计方案的质量变化
Tab.5
| 构件类型 | M1/t | M2/t | Δ/% | Q/% |
| 立柱 | 24.341 | 21.311 | −12.45 | 21.36 |
| 横杆 | 3.123 | 1.240 | −60.30 | 13.27 |
| 斜杆 | 8.401 | 2.329 | −72.28 | 42.80 |
| 横隔 | 2.163 | 1.153 | −46.68 | 7.12 |
| 拉索 | 4.737 | 2.546 | −46.26 | 15.45 |
| 结构 | 42.766 | 28.579 | −33.17 | — |
图 13
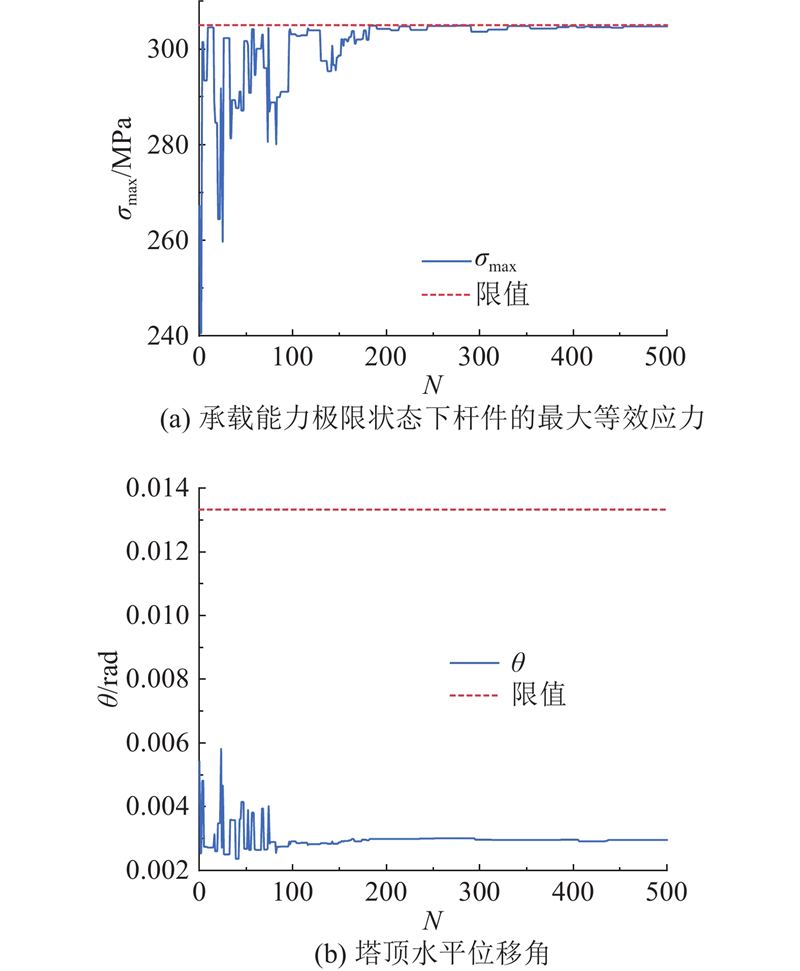
4.5. 约束条件影响分析
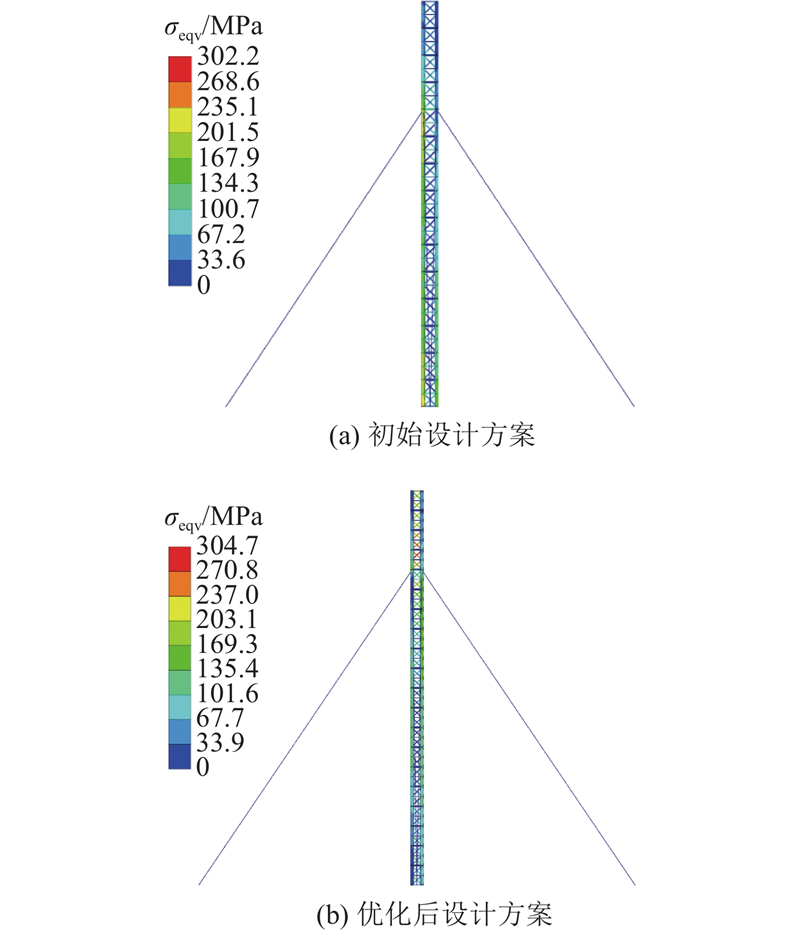
优化过程中承载能力极限状态下杆件最大等效应力
图 14
优化前后承载能力极限状态下临时转播塔结构中各杆件的等效应力
图 15
4.6. 主要设计参数
表 6 优化前后结构设计变量的对比
Tab.6
| 设计变量 | x1/mm | x2/mm | x3/mm | x4/mm | x5 | x6/m |
| 优化前 | 200 | 66 | 80 | 80 | 6 | 3.4 |
| 优化后 | 189 | 42 | 59 | 60 | 3 | 2.5 |
| 设计变量 | x7/m | x8/m | x9 | x10 | x11/MPa | — |
| 优化前 | 50.0 | 74.6 | 2 | 2 | 150 | — |
| 优化后 | 54.3 | 79.8 | 1 | 2 | 186 | — |
5. 结 论
设计模块化临时转播塔结构,建立该结构的参数化有限元模型,结合5种改进策略提出改进浮点数编码遗传算法(IFGA). 考虑模块化临时转播塔结构的形状、尺寸、杆件布置形式及拉索初应力,基于IFGA算法提出该类结构的综合优化方法. 通过在工程实例中的应用,验证了所提方法的有效性.
(1)本研究设计的模块化临时转播塔结构力学性能好、用钢质量少,建立的参数化有限元模型能够反映结构的真实力学性能.
(2)初始替换策略、初始大种群策略、末位替换策略及差异化策略能够扩大算法的搜索范围避免发生早熟性收敛现象,自适应遗传策略可提高算法的局部搜索能力和计算效率,各改进策略具有一定的协作互补性. 在临时转播塔结构的轻量化问题上,IFGA算法的优化结果相较于FGA算法节省用钢18.9%;相较于鲸鱼算法、学校算法及改进灰狼算法能够更为有效地摆脱停滞,以更低的计算成本实现临时转播塔结构的优化设计.
(3)所提出的综合优化方法能够同时优化临时转播塔的杆件布置形式、构件截面尺寸、结构形状及拉索初应力,考虑了算法迭代过程中设计参数改变引起的风荷载变化. 优化后结构的力学性能指标满足规范要求,且拉索与水平地面夹角为55.77°,与规范推荐值相近,证明了该方法的合理性.
(4)通过应用本研究提出的优化设计方法,模块化临时转播塔结构在确保安全的前提下,总用钢质量相较于初始设计方案减少了33.2%,显著提高了设计方案的经济性和节能性,验证了优化设计方法的有效性.
参考文献
Considerations for the structural analysis and design of wind turbine towers: a review
[J].DOI:10.1016/j.rser.2020.110447 [本文引用: 3]
On the structural response of a tall hybrid onshore wind turbine tower
[J].DOI:10.1016/j.proeng.2017.09.535 [本文引用: 2]
Design optimization of wind turbine tower with lattice-tubular hybrid structure using particle swarm algorithm
[J].DOI:10.1002/tal.1281 [本文引用: 2]
变截面构架式风力发电塔架 GA 优化
[J].
GA optimization for variable cross section frame wind turbine
[J].
Meta-heuristic algorithms to truss optimization: Literature mapping and application
[J].DOI:10.1016/j.eswa.2021.115197 [本文引用: 1]
Solution of structural and mathematical optimization problems using a new hybrid swarm intelligence optimization algorithm
[J].DOI:10.1016/j.advengsoft.2018.11.004 [本文引用: 2]
Object-oriented optimization approach using genetic algorithms for lattice towers
[J].DOI:10.1061/(ASCE)0887-3801(2004)18:2(162) [本文引用: 1]
A comparative study on optimum design of multi-element truss structures
[J].DOI:10.12989/scs.2016.22.3.521 [本文引用: 1]
Improved GWO algorithm for optimal design of truss structures
[J].DOI:10.1007/s00366-017-0567-1 [本文引用: 2]
Sizing and layout optimization of truss structures with artificial bee colony algorithm
[J].DOI:10.1016/j.istruc.2021.01.016 [本文引用: 1]
Structural optimization of lattice steel transmission towers
[J].DOI:10.1016/j.engstruct.2016.03.005 [本文引用: 1]
Computer software for analysis and design optimization of power transmission structures by simulated annealing and sensitivity analysis
[J].DOI:10.1007/s00366-020-01022-x [本文引用: 1]
Geometric optimisation analysis of steel–concrete hybrid wind turbine towers
[J].DOI:10.1016/j.istruc.2021.08.036 [本文引用: 1]
Topology optimisation of lattice telecommunication tower and performance-based design considering wind and ice loads
[J].DOI:10.1016/j.istruc.2020.08.010 [本文引用: 1]
A procedure for the size, shape and topology optimization of transmission line tower structures
[J].DOI:10.1016/j.engstruct.2015.12.005 [本文引用: 1]
Sizing, layout and topology design optimization of truss structures using the Jaya algorithm
[J].DOI:10.1016/j.asoc.2017.10.001 [本文引用: 1]
Structural optimization of transmission towers using a novel genetic algorithm approach with a variable length genome
[J].DOI:10.1016/j.engstruct.2021.112306 [本文引用: 1]
输电塔结构离散变量优化设计方法
[J].DOI:10.6052/j.issn.1000-4750.2015.02.0102 [本文引用: 1]
Discrete variable optimal design method of transmission tower structure
[J].DOI:10.6052/j.issn.1000-4750.2015.02.0102 [本文引用: 1]
The mosaic of metaheuristic algorithms in structural optimization
[J].DOI:10.1007/s11831-022-09773-0 [本文引用: 1]
Improved Shuffled Jaya algorithm for sizing optimization of skeletal structures with discrete variables
[J].DOI:10.1016/j.istruc.2020.11.008
Quantum teaching-learning-based optimization algorithm for sizing optimization of skeletal structures with discrete variables
[J].DOI:10.1016/j.istruc.2021.03.046 [本文引用: 1]
Integrated structural optimisation of offshore wind turbine support structures based on finite element analysis and genetic algorithm
[J].DOI:10.1016/j.apenergy.2017.05.009 [本文引用: 3]
基于改进遗传算法的钢-混组合式风电机组塔架优化设计研究
[J].
Design optimization of steel-concrete hybrid wind turbine tower based on improved genetic algorithm
[J].
A systematic literature review of adaptive parameter control methods for evolutionary algorithms
[J].
Gradual distributed real-coded genetic algorithms
[J].DOI:10.1109/4235.843494 [本文引用: 2]
浮点数编码遗传算法变异概率的选取
[J].
Selection of mutation probability of floating-point number code genetic algorithm
[J].
The whale optimization algorithm
[J].DOI:10.1016/j.advengsoft.2016.01.008 [本文引用: 1]
School based optimization algorithm for design of steel frames
[J].DOI:10.1016/j.engstruct.2018.05.085 [本文引用: 1]