过去研究表明,采用移动车辆加载的方法可以有效提高桥梁影响线的识别效率[8],这一领域的研究已经引起广泛关注. Obrien等[9]基于影响系数的基本概念和车致桥梁响应分析,采用矩阵法成功实现了桥梁影响线的识别. Ieng[10]利用极大似然估计法提高对影响线的识别精度,在多次测试中表现良好. 在考虑车辆荷载的情况下,桥梁响应包含静态和动态成分,其中动态成分容易受到车速、路面不平度和噪声影响而产生扰动,是影响线识别精度的主要影响因素. 陈志为等[11]为了解决影响线测试中路面不平度和动力效应静力因素引入正则化方法,以消除不合理波动对于影响线的二维拓展——影响面识别问题. 王宁波等[12]采用多项式分段拟合的方法去除桥梁振动的干扰,从而实现对影响线的提取. Yan等[13]从概率频域的角度提出利用静力响应传递比函数法识别影响线. Mustafa等[14]利用低通滤波技术提出桥梁响应的动态成分,从而提高桥梁影响线的识别精度. Khuc等[15]通过迭代逼近的方法成功将影响线识别拓展到宽桥的影响面识别. 此外,周宇等[16-17]从数学模型的角度证明了影响线的解析表达和可识别性.
为了克服这类方法在桥梁影响线识别中的不足,提出结合变分模态分解(variational mode decomposition,VMD)[20]和分段多项式截断奇异值分解(piecewise polynomial truncated singular value decomposition,PPTSVD)[21]的新型桥梁影响线识别方法. 该方法通过VMD将桥梁响应分解为多个固有模态函数(intrinsic mode functions,IMFs),并通过调整截断频率提取低阶IMFs的准静态成分,从而捕捉桥梁的动态响应特征. PPTSVD技术被应用于从准静态响应中识别桥梁影响线,并针对噪声和扰动进行优化,解决了反问题中的不适定性问题. 这一方法结合了VMD和PPTSVD的特点,提供新的框架来改进桥梁影响线识别的过程.
1. 车桥耦合系统
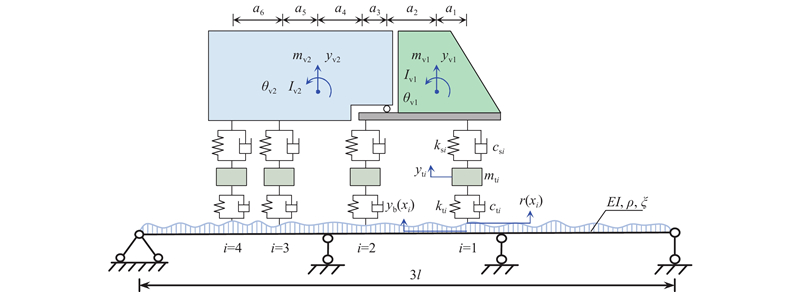
如图1所示为车桥耦合模型示意图. 图中,
图 1
所用车辆为单辆四轴车,其前部车体和后部车体被简化为刚体,两者通过铰接连接. 由于铰接的存在,两车体仅有3个自由度,即前部车体的转动以及后部车体的竖向平动和转动. 车辆悬挂和轮胎悬挂被简化为弹簧阻尼器,车轴质量被简化为1个具有竖向平动自由度的刚体,整个车辆总共有7个自由度.
车桥耦合系统的动力方程如下:
式中:
2. 影响线识别理论
2.1. 变分模态分解
桥梁在行驶车辆作用下产生的位移或应变存在不稳定的动态波动,导致这类桥梁的响应不能直接用于桥梁影响线识别,须提前提取出桥梁的准静态响应. 本研究提出利用VMD算法提取桥梁的准静态响应. VMD假设将桥梁动态的原信号
式中:
VMD将各阶IMF定义为调幅调频的窄带宽信号,其表达式如下:
式中:
通过Hilbert变换,能够将实信号
式中:
在信号中混入一个中心频率为
进而可利用以下公式估计子信号的带宽:
VMD基于2个假设构建目标函数:1)最小化各子信号的带宽之和;2)确保各子信号相加的总和等于原信号. 基于这2个假设,目标函数可以定义为
式(7)为一个带有约束的泛函,通过引入拉格朗日乘子,可将该问题转化为一个无约束的最优化问题,其形式如下:
式中:
可应用交替方向乘子法迭代求解式(8),在第
式中:
如式(9)所示信号的中心频率的表达式如下:
须指出的是,每一次迭代完成后都须更新拉格朗日乘子,第
式中:
判定迭代收敛的条件如下:
式中:
式中:
基于上述理论,可从原始信号中分解出指定阶数的IMF,每个IMF包含一个中心频率,通过设置截止频率,可以筛选出低于该截止频率的IMF. 将这些低阶IMF叠加在一起,即可得到桥梁的准静态响应.
2.2. 分段多项式截断奇异值分解
桥梁影响线与桥梁响应之间可建立如下数学关系:
式中:
式中:
首先对矩阵
式中:
通过截取奇异值矩阵分解中前
式中:
式中:
上述内容总结了本研究提出的方法的所有技术过程,其实施路径如图2所示.
图 2
3. 数值案例
数值案例的桥梁模型为如图1所示的三跨连续梁桥,每跨长度
本研究中影响线的识别误差[24]定义如下:
式中:
3.1. 分解精度
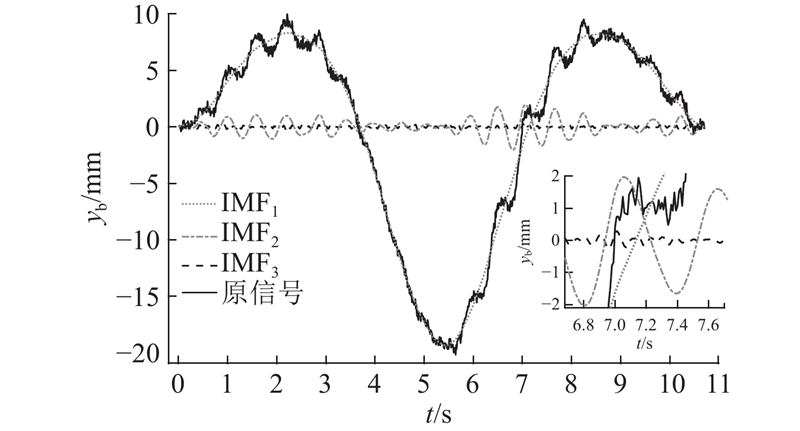
VMD分解得到的每一个IMF都携带有中心频率fc的信息,通过设定截断频率,可以筛选出中心频率低于截断频率的IMF,并在时域上将这些筛选出的IMF叠加,即可得到桥梁的准静态响应. 以如图3所示的桥梁位移为例,为了便于展示,设定仅将原信号分解成3个IMF,每个IMF的中心频率分别为0.13、1.75、13.68 Hz. 图中,
图 3
图 3 桥梁位移的固有模态函数比较
Fig.3 Comparison of intrinsic mode functions of bridge displacement
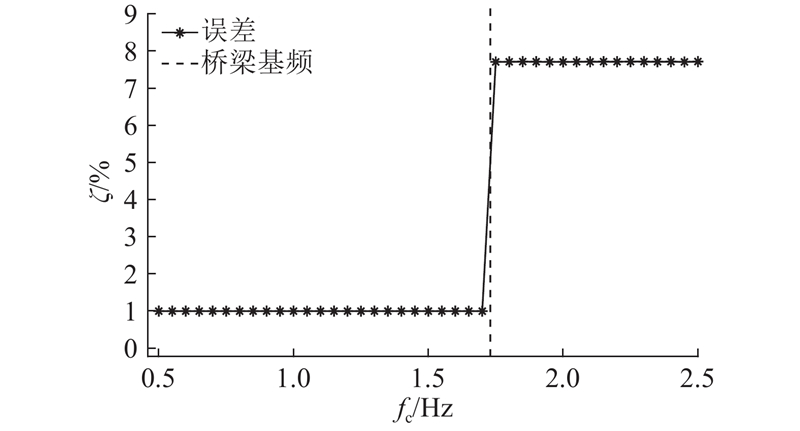
为了探究截止频率的合理取值,分析不同截止频率下的准静态响应分解误差,结果如图4所示. 可以看出,当截止频率取在桥梁基频附近时,分解误差产生了突变. 因为当截止频率大于桥梁基频时,分解结果中将引入桥梁位移中的第1阶振动信号,导致分解结果不准确. 因此,截止频率应小于桥梁基频,同时应避免在桥梁基频附近取值,以保证所提方法能准确地剔除基频信号. 本研究建议截止频率为0.5倍桥梁基频.
图 4
图 4 变分模态分解的截止频率分析
Fig.4 Analysis of cutoff frequency for variational mode decomposition
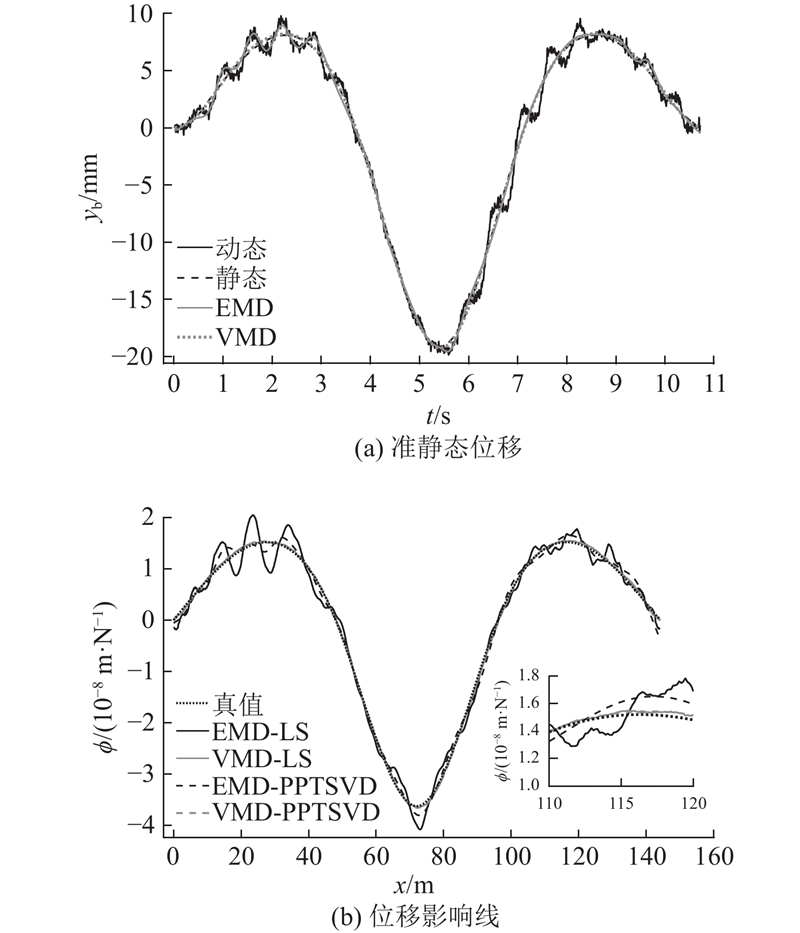
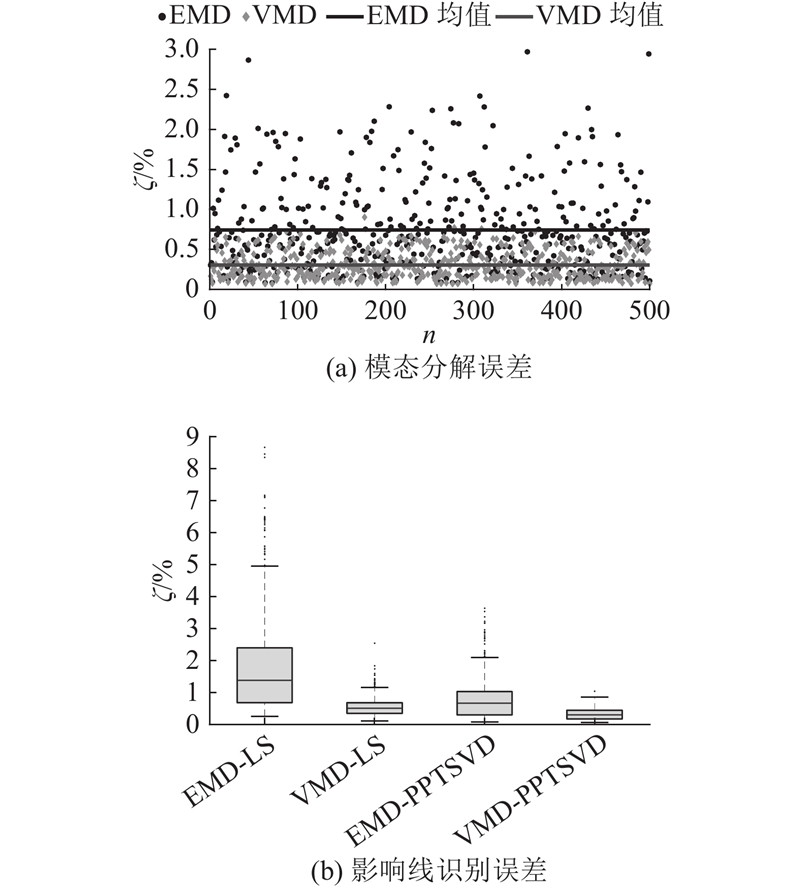
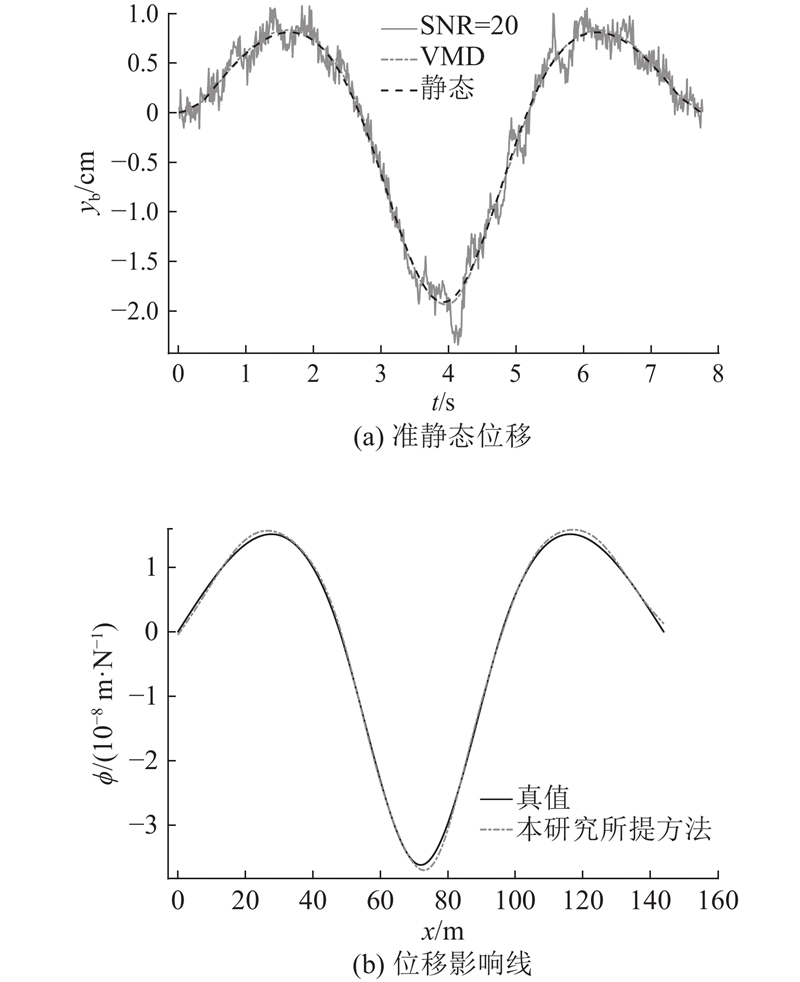
为了进一步验证VMD的分解精度,如图5(a)所示展示了VMD与EMD的对比结果,发现两者均能准确地从桥梁位移中提取出桥梁的准静态位移. 然而,EMD的结果在局部位置存在细微的波动,特别是在跨中和边缘部位. EMD和VMD的提取误差分别为0.79%和0.49%. 如图5(b)所示展示了4种方法识别影响线的结果,分别为EMD-LS、VMD-LS、EMD-PPTSVD和VMD-PPTSVD,识别误差分别为1.39%、0.81%、1.00%、0.56%. 由于EMD提取的桥梁准静态位移包含更大的误差,因此基于EMD的影响线识别结果精度也更差. VMD分解算法表现出更好的精度,因此其识别出来的影响线更为准确. 此外,基于PPTSVD的算法相较于最小二乘方法的结果更光滑且精度更高.
图 5
图 5 不同方法识别影响线的结果对比
Fig.5 Results comparison of different methods for identifying influence line
图 6
3.2. 路面不平度的影响
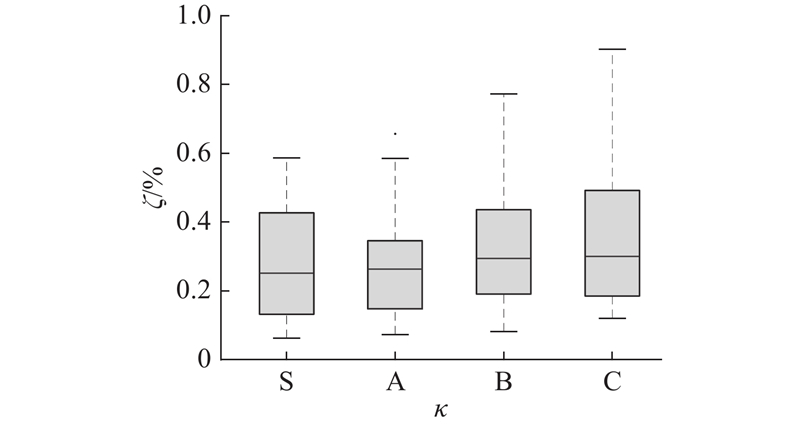
如图7所示展示了在不同路面等级下识别出的影响线误差. S到C级的误差中位数分别为0.26%、0.28%、0.31%和0.33%. 即使在C级路面情况下,所提出的方法识别出的影响线误差仍然保持在小于1.00%的水平,表明所提方法能够有效克服路面不平度对识别结果的影响.
图 7
3.3. 车速的影响
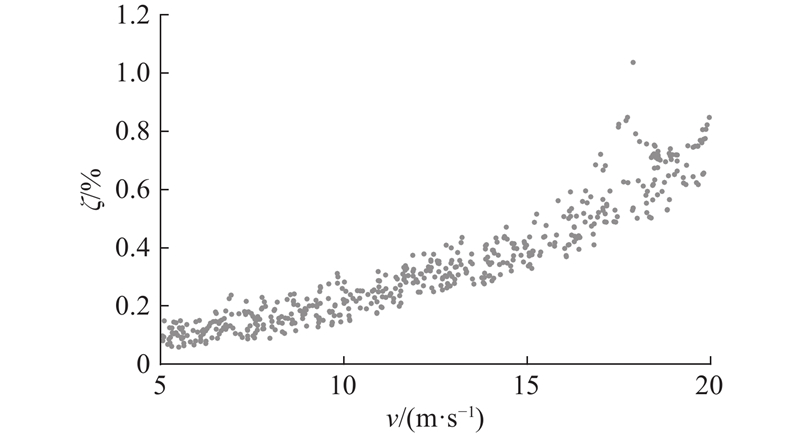
在测试的500组工况中,每组工况的车速在5~20 m/s均匀随机抽取,如图8所示展示了所有工况中识别误差与车速之间的关系. 由于车桥耦合系统的动态效应,影响线识别精度会表现出随机性,这导致误差最大值并不是出现在速度最大的时候. 总体而言,随着车速的增加,识别误差也呈现增加的趋势,但误差依然处于较低的水平,最大误差约为1.04%.
图 8
3.4. 噪声的影响
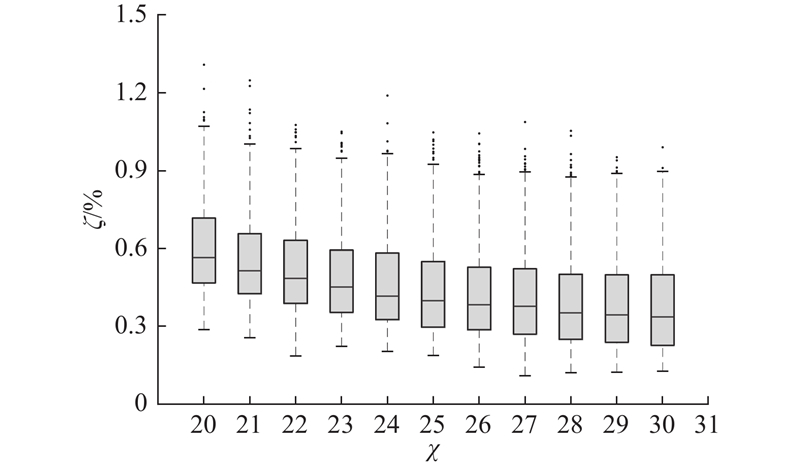
本研究分析了不同信噪比对识别结果的影响,设定信噪比
图 9
图 10
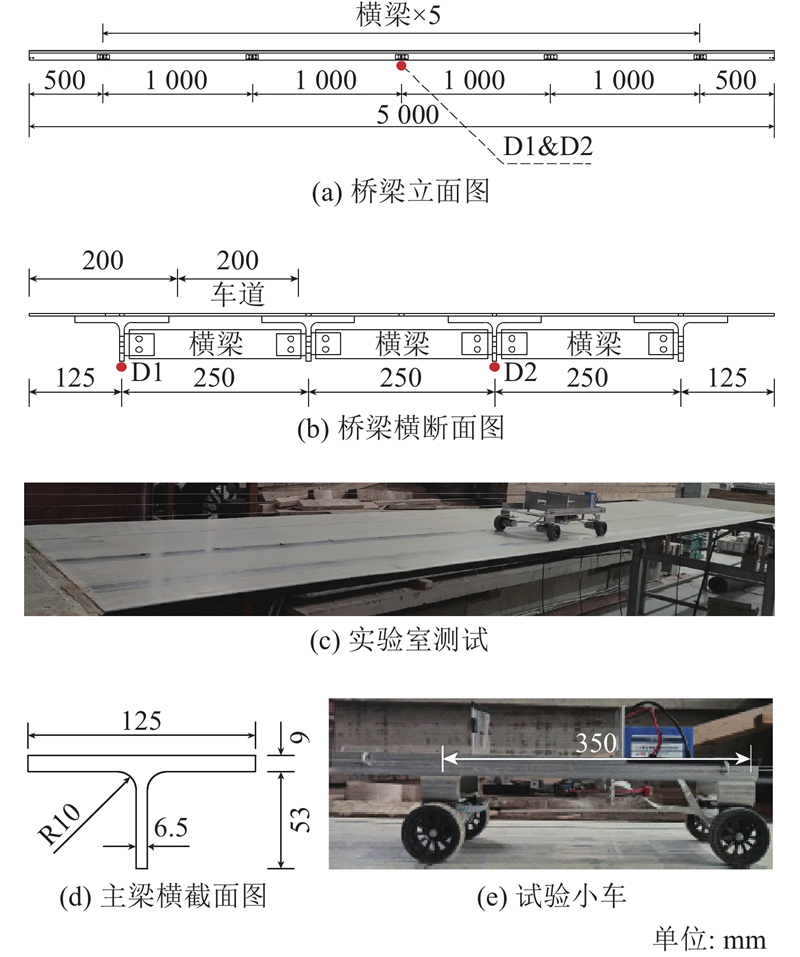
4. 实验室试验
图 11
在桥梁测试过程中,车辆以不同的速度穿过桥梁,测量到的响应如图12所示. 不同速度下的位移响应序列长度不一样,为了便于对比,采用归一化时长
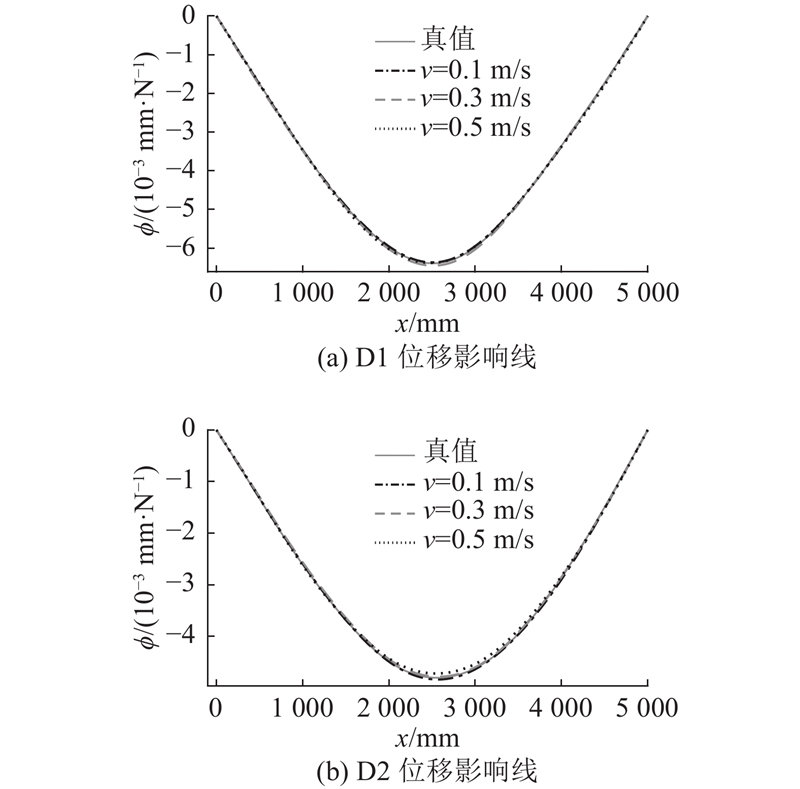
图 12
图 13
表 1 影响线识别误差
Tab.1
| 测点 | |||
| v =0.1 m/s | v =0.3 m/s | v =0.5 m/s | |
| D1 | 0.44 | 0.89 | 1.26 |
| D2 | 0.56 | 1.11 | 2.23 |
5. 结 论
(1)相较于经典的经验模态分解和最小二乘方法,VMD-PPTSVD方法能更有效地提取桥梁准静态响应并克服扰动成分的影响,稳定性和适应性较强,具有更高的影响线识别精度.
(2)VMD-PPTSVD在面对不同等级路面时均表现出精确的识别精度,即便在C级路面下,识别误差的最大值仅约为1.00%.
(3)随着车速的增加,VMD-PPTSVD的识别精度略有下降,但最大误差仅约为1.04%.
(4)随着信噪比的降低,VMD-PPTSVD的识别精度轻微下降,其在应对噪声干扰时表现出较强的鲁棒性,当SNR=20时,最大识别误差为1.24%.
(5)本研究所提的识别影响线方法须中断交通,研究正常通行状态下的桥梁影响线识别将是下一步的研究方向.
参考文献
Three-dimensional analysis of train-rail-bridge interaction problems
[J].DOI:10.1076/vesd.36.1.1.3567 [本文引用: 1]
基于车致桥梁响应和L1正则化的损伤识别研究
[J].DOI:10.3969/j.issn.1001-7372.2021.04.005
Bridge damage detection based on the moving-vehicle-induced response and L1 regularization
[J].DOI:10.3969/j.issn.1001-7372.2021.04.005
公路车-桥耦合振动的理论和应用研究进展
[J].DOI:10.3969/j.issn.1001-7372.2018.07.003
Research progress in theory and applications of highway vehicle-bridge coupling vibration
[J].DOI:10.3969/j.issn.1001-7372.2018.07.003
基于VMD和DBN的非线性结构模型参数识别
[J].
Parametric recognition of nonlinear structural model based on VMD and DBN
[J].
Multiscale modeling and model updating of a cable-stayed bridge. II: model updating using modal frequencies and influence lines
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000723
Weigh-in-motion system using instrumented bridges
[J].
Load-carrying capacity evaluation of girder bridge using moving vehicle
[J].DOI:10.1016/j.engstruct.2020.111645 [本文引用: 1]
Calculating an influence line from direct measurements
[J].DOI:10.1680/bren.2006.159.1.31 [本文引用: 1]
Bridge influence line estimation for bridge weigh-in-motion system
[J].
基于正则化与 B 样条曲线的桥梁影响线识别方法
[J].
Bridge influence line identification method based on regularization and B-spline curves
[J].
基于桥梁动力响应的应变影响线提取
[J].
Extraction of strain influence line of bridge from dynamic responses
[J].
A new probabilistic frequency domain approach for influence line extraction from static transmissibility measurements under unknown moving loads
[J].DOI:10.1016/j.engstruct.2020.110625 [本文引用: 1]
An investigation of bridge influence line identification using time-domain and frequency-domain methods
[J].DOI:10.1016/j.istruc.2021.05.082 [本文引用: 1]
Structural identification using computer vision-based bridge health monitoring
[J].
变截面悬链线无铰拱应变影响线的解析解
[J].DOI:10.7511/jslx20210425002 [本文引用: 1]
Practical analytical expression to strain influence line of varying cross section catenary fixed arch
[J].DOI:10.7511/jslx20210425002 [本文引用: 1]
结构影响线识别: 反问题可识别性分析与降维贝叶斯不确定性量化
[J].DOI:10.6052/j.issn.1000-4750.2021.07.0574 [本文引用: 1]
Structural influence line identification: inverse problem identifiability analysis and reduced-dimension Bayesian uncertain quantification
[J].DOI:10.6052/j.issn.1000-4750.2021.07.0574 [本文引用: 1]
Bridge influence line identification based on regularized least-squares QR decomposition method
[J].DOI:10.1061/(ASCE)BE.1943-5592.0001458 [本文引用: 1]
Bridge influence line identification from structural dynamic responses induced by a high-speed vehicle
[J].
Variational mode decomposition
[J].DOI:10.1109/TSP.2013.2288675 [本文引用: 1]
基于PPTSVD的桥梁移动荷载识别
[J].
Identification of dynamic axle loads on bridge based on PPTSVD
[J].
On the numerical modelization of moving load beam problems by a dedicated parallel computing fem implementation
[J].
Fatigue life evaluation of bridge stay cables subject to monitoring traffic and considering road roughness
[J].DOI:10.1016/j.engstruct.2023.116572 [本文引用: 1]
A comparative study of vehicle-bridge interaction dynamics with 2D and 3D vehicle models
[J].DOI:10.1016/j.engstruct.2023.116493 [本文引用: 1]
A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components
[J].DOI:10.1016/j.ymssp.2011.02.002 [本文引用: 1]