1. 数学模型与求解
1.1. 模型示意图与基本假设
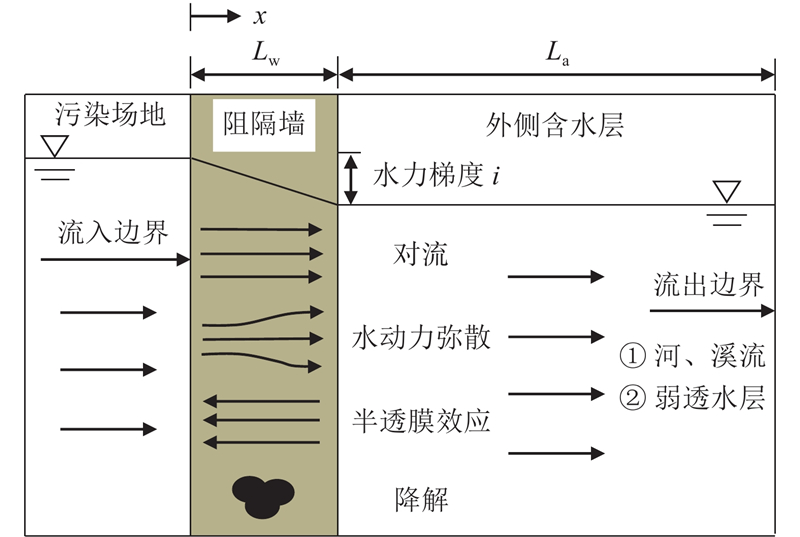
数学模型如图1所示. 竖向阻隔墙和含水层的厚度分别为Lw和La. 水平坐标x向右为正,其坐标轴原点位于污染场地与阻隔墙的界面处. 阻隔墙处的流入边界采用常质量浓度边界,对于外侧含水层的流出边界,考虑2种典型情况,分别为①河流或溪流,②弱透水层,对应Dirichlet边界条件和Nuemann边界条件.
图 1
1.2. 控制方程
式中:ρw (x, t)、ρa (x, t)分别为阻隔墙内部和含水层中位置x处t时刻孔隙流体中污染物的质量浓度,ω为阻隔墙的半透膜效率系数(也叫化学渗透效率系数),vs,w和vs,a分别为阻隔墙和含水层中的渗流速度,Dw和Da分别为污染物在阻隔墙和含水层中的水动力弥散系数,λw和λa分别为污染物在阻隔墙和含水层中的衰减因子,kw为阻隔墙的渗透系数,R为通用气体常数,T为热力学温度,M为污染物的摩尔质量,ne,w为阻隔墙的有效孔隙率,γw为孔隙流体的容重,Rd,w和Rd,a分别为污染物在阻隔墙和含水层中的阻滞因子.
Dw和Da可以表示为有效扩散系数和机械弥散系数之和[20],即
式中:De,w和De,a分别为污染物在阻隔墙和含水层中的有效扩散系数,Dm,w和Dm,a分别为对应的机械弥散系数.
De,w和De,a可以通过自由扩散系数和曲折因子确定,而在考虑半透膜效应时,溶质扩散受一定程度的限制,表示如下[21]:
式中:τw和τa分别为阻隔墙和含水层的曲折因子,取值为0~1.0;D0为污染物在自由溶液中的扩散系数.
Dm,w和Dm,a可以表示为渗流速度和弥散度的乘积,即
式中:αw和αa分别为阻隔墙和含水层的弥散度. Gelhar等[22]根据大量的现场观测数据,总结得到弥散度与含水层尺寸的经验关系为
衰减因子λw和λa,即一阶降解速率常数,可由下式[23]确定:
渗流速度vs,b和vs,a可由达西流速va和有效孔隙率ne计算得到.
式中:va为水的达西流速,ne,a为含水层的有效孔隙率,i为水力梯度.
阻滞因子Rd,w和Rd,a可以由Henry定律以及有效孔隙率和不可流动流体孔隙率确定[24]:
式中:ni,w和ni,a分别为阻隔墙和含水层的不可流动流体孔隙率,且有nw = ni,w+ne,w和na = ni,a+ne,a,其中nw和na分别为阻隔墙和含水层的总孔隙率;ρs,w和ρs,a分别为阻隔墙和含水层的干密度;Kd,w和Kd,a分别为污染物在阻隔墙和含水层的分配系数.
污染物迁移控制方程(1)、(2)的初始条件为
式中:Fw (x)和Fa (x)为空间坐标x的函数.
阻隔墙-含水层系统的流入边界条件为
式中:ρ0为污染物源质量浓度.
对于阻隔墙-含水层系统的流出边界条件,考虑以下2种典型情况:
根据阻隔墙和含水层界面的浓度连续性和质量通量连续性,可得
阻隔墙外侧的污染物质量通量为
阻隔墙外侧的污染物累积流出质量为
1.3. 有限差分法的求解
由于考虑半透膜效应的影响,污染物迁移控制方程中的化学渗透项为变系数项,导致很难求得封闭解析解. 选择有限差分法,计算污染物在阻隔墙-含水层系统中的质量浓度分布、质量通量和污染物累积流出质量. 由于阻隔墙和含水层之间的厚度一般差距较大,采用不同空间步长的差分格式分析污染物在不同层间的迁移过程,而时间步长保持一致.
将式(1)、(2)在[xm-1, xm+1]×[tn, tn+1]上使用有限差分法展开,在第n+1个时间步的第m个计算单元中的解更新为
2. 模型验证
2.1. 与解析解的对比(双层土、无半透膜效应)
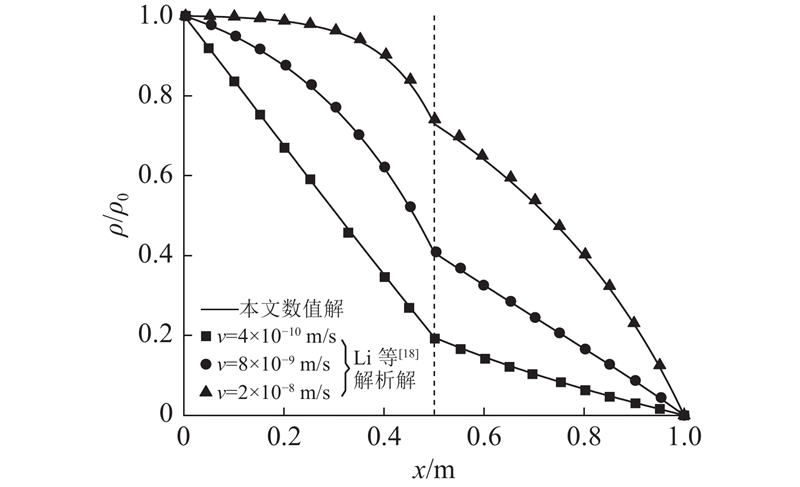
Li等[18]提出有限厚度的双层多孔介质中考虑对流和扩散的溶质运移一维解析解,研究常质量浓度、常质量通量及其组合的多种边界条件. 采用该解析解,验证本文数值解的正确性. 假定2个土层的厚度均为0.5 m,有效孔隙率分别为0.4和0.6,阻滞因子分别为2.0和4.0. 一阶降解常数假设为零. 2个土层的扩散系数分别为5×10−9和1×10−8 m2/s,整个系统的达西流速选用几个典型值(即4×10−10、8×10−9和2×10−8 m/s). 由于Li等[18]无法考虑半透膜效应,采用半透膜效率系数ω = 0. 入口边界处的溶质质量浓度固定为1 mg/L,出口边界处选择零质量浓度边界. 整个系统采用零质量浓度的初始条件. 将溶质运移时间设为2 a.
图 2
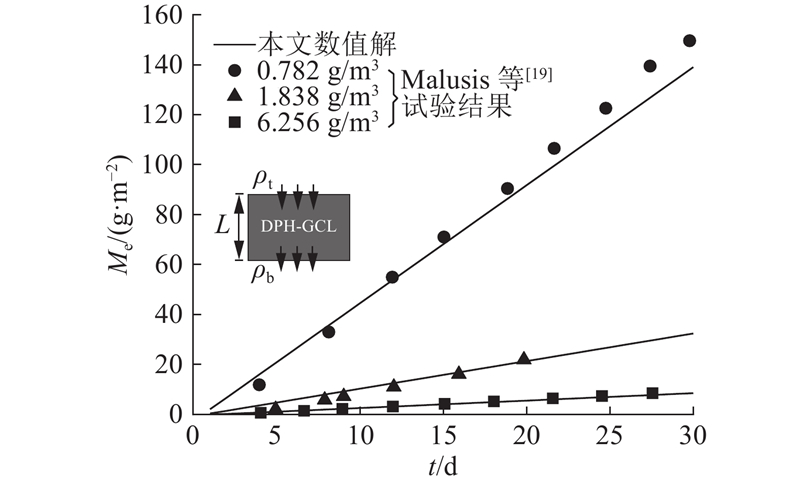
2.2. 与试验对比(单层土、考虑半透膜效应)
表 1 Malusis等[19]开展的半透膜试验的相关参数
Tab.1
| 试验 编号 | ρ0/ (g·m−3) | ρt/ (g·m−3) | ρb/ (g·m−3) | L/ mm | n | k/ (10−12 m·s−1) | De /(10−10 m2·s−1) |
| 试验1 | 0.782 | 0.719 | 0.031 | 5.6 | 0.64 | 1.1 | 0.45 |
| 试验2 | 1.838 | 1.615 | 0.125 | 5.0 | 0.60 | 2.0 | 0.75 |
| 试验3 | 6.256 | 5.411 | 0.575 | 4.9 | 0.62 | 0.75 | 0.92 |
图 3
2.3. 与COMSOL软件的对比(双层土、考虑半透膜效应)
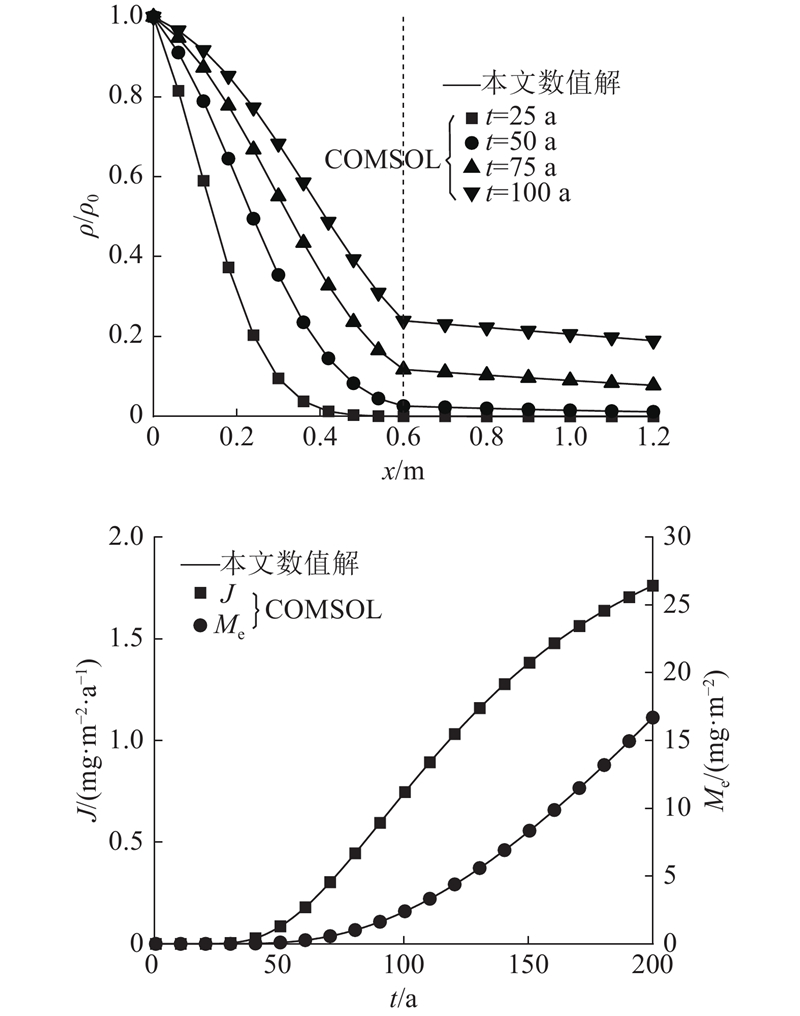
为了验证本文的数值解,使用有限元软件COMSOL Multiphysics 5.5建立阻隔墙-含水层模型. 假定该模型由0.6 m厚的土-膨润土阻隔墙和10 m厚的外侧含水层组成. 外侧含水层的流出边界条件为零质量浓度边界. 选用污染场地中常见的重金属铅离子作为特征污染物. 根据文献[4]的报道,假设铅离子在污染场地中的源质量浓度固定为0.1 mg/L. 土-膨润土墙和含水层的半透膜效率系数分别为0.28[25]和0. 土-膨润土墙的有效孔隙率和总孔隙率分别为0.4和0.5,含水层的有效孔隙率和总孔隙率分别为0.45和0.55. 将水力梯度设为1.0. 铅离子摩尔质量M为207.2 g/mol,通用气体常数R为8.314 J/(mol·K),绝对温度T为293.15 K. 表2给出污染物运移参数和阻隔墙-含水层系统的材料参数. 表中,τ为曲折因子,vs为渗流速度,α为弥散度,Kd为分配系数,ρs为干密度,D0为自由扩散系数,γw为流体容重,t1/2为半衰期.
表 2 污染物的迁移参数和阻隔墙-含水层系统的材料参数
Tab.2
图 4
图 4 本文数值解与COMSOL软件的计算结果对比
Fig.4 Comparison between proposed numerical solution and numerical result of COMSOL
3. 参数分析
3.1. 阻隔墙半透膜效应的影响
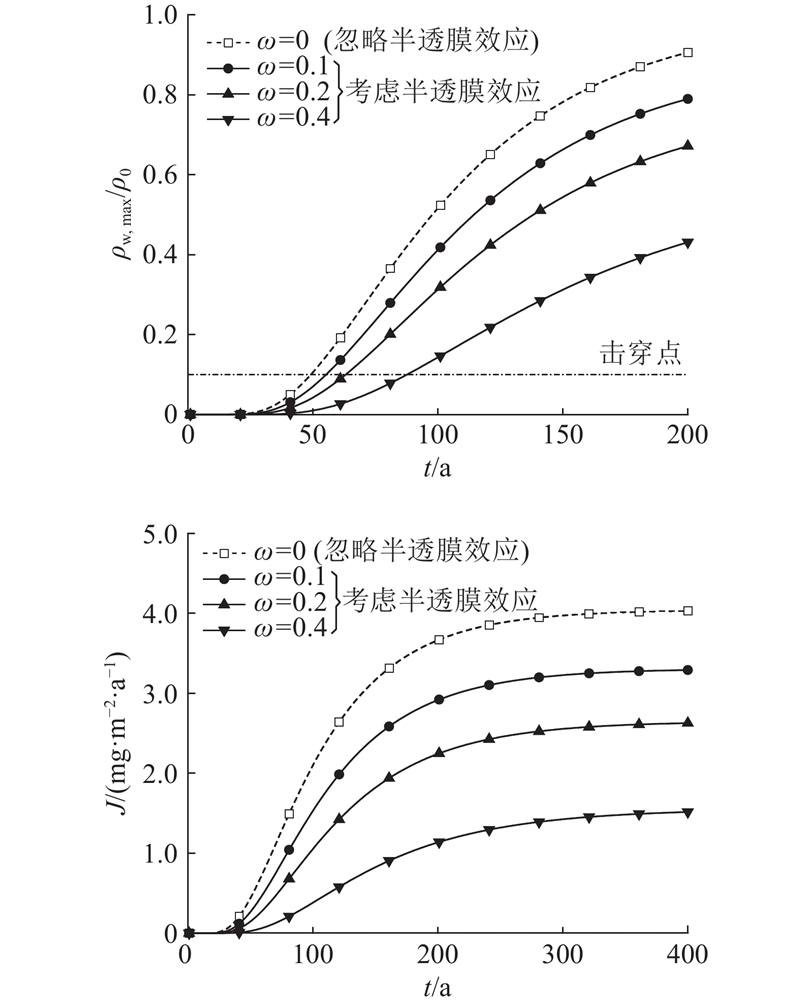
不同屏障材料对相同浓度下同一污染物的半透膜效率系数ω有较大差异,例如,对于浓度为3.9 mmol/L的KCl溶液,Yeo等[8]测得天然黏土回填料的ω为0.018~0.024,土-膨润土回填料的ω为0.118~0.166;Kang等[29]得到土工合成黏土衬垫的ω为0.427~0.680. 为了研究阻隔墙半透膜效应对铅离子运移过程的影响,选择4个不同的ω进行分析,分别为0(即不考虑半透膜效应)、0.1、0.2和0.4(取值范围参考文献[13]). 图5给出不同ω下阻隔墙出口边界处污染物最大质量浓度ρw,max与污染物源质量浓度ρ0的比值(即ρw,max/ρ0)和阻隔墙出口边界处的质量通量J随时间变化的曲线. 使用击穿时间tb来评估阻隔墙的服役性能,tb定义为阻隔墙出口边界处质量浓度达到某一限定值的时间. 根据世界卫生组织饮用水质量标准,取铅离子的击穿限值为0.01 mg/L,即图5(a)中击穿点为ρw,max/ρ0 = 0.1的时间. 图5表明,忽略半透膜效应将显著缩短污染物的击穿时间,增大污染物的质量通量,导致了阻隔墙防污性能的低估. 结果显示,相较于忽略半透膜效应,ω = 0.1、0.2和0.4时的击穿时间分别增加了12.2%、28.6%和79.6%,稳态污染物的质量通量分别降低了18.4%、34.7%和62.3%. 这是因为半透膜效应可以通过3种机制阻滞污染物运移,分别为超滤、化学渗透和限制溶质扩散[30],表现如下:1)将对流通量由vaρw减小至(1−ω)vaρw;2)化学渗透与对流和扩散的方向相反,因此减少了质量通量;3)污染物的有效扩散系数由τwD0减小至(1−ω)τwD0. 综上所述,半透膜效应显著减小了污染物穿过防污屏障的总通量,延长了击穿时间,忽略半透膜效应将较大程度地高估污染物的流出量并低估阻隔墙击穿时间.
图 5
图 5 阻隔墙半透膜效率系数对污染物相对质量浓度和质量通量的影响
Fig.5 Effect of membrane efficiency coefficient on relative mass concentration and mass flux of contaminant
3.2. 污染物源质量浓度的影响
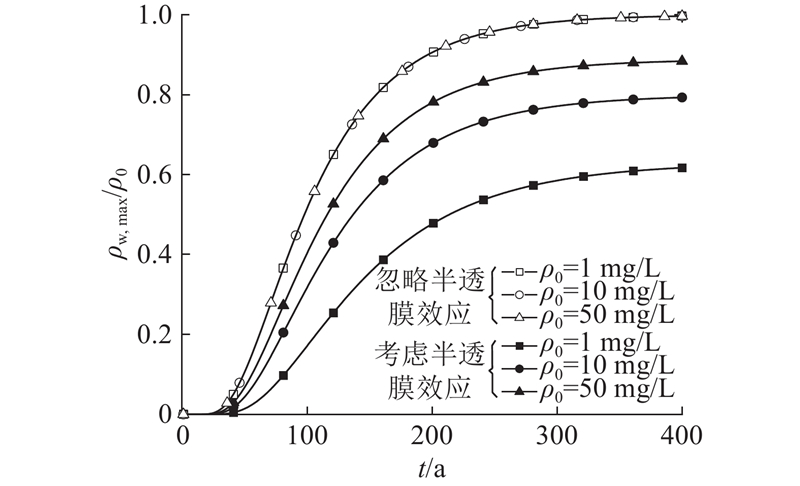
污染物质量浓度对半透膜效应的发挥和保持有较大的影响[10]. 为了定量研究污染物质量浓度的影响,分别取ρ0 = 1、10和50 mg/L(分别为《地下水环境质量标准》(GB/T 14848—2017)III类饮用水中铅离子质量浓度的100、1 000和5 000倍). 如图6所示为不同ρ0下ρw,max/ρ0随时间变化的曲线. 可知,当不考虑半透膜效应时,源质量浓度对污染物相对质量浓度没有影响,相对质量浓度曲线完全重叠;当考虑半透膜效应时,源质量浓度对相对质量浓度曲线有显著的影响,源质量浓度越大,则污染物迁移越快,达到相同相对质量浓度的时间越短. 例如,当ρw,max/ρ0均达到0.5时,ρ0 = 1 mg/L较ρ0 = 50 mg/L对应的时间增加了84.5%. 这一现象的原因是半透膜效率系数随源质量浓度的增大而减小,从而对污染物迁移的阻滞作用减小. 根据李双杰等[13]的半透膜试验结果可知,与ρ0 = 1、10和50 mg/L相对应的ω分别为0.36、0.20和0.11,因为质量浓度的增大压缩了黏土颗粒间的扩散双电层,使得溶质更容易通过半透膜的限制,当质量浓度足够大时,扩散双电层彻底失去对离子迁移的限制,半透膜效应完全消失. 当考虑半透膜效应对污染物运移过程的影响时,必须注意污染物质量浓度与半透膜效率系数之间的关系,当污染物质量浓度足够高时可以忽略半透膜效应的影响,具体数值应根据相关试验进行测定.
图 6
图 6 污染物源质量浓度对污染物相对质量浓度曲线的影响
Fig.6 Effect of contaminant source mass concentration on relative mass concentration of contaminant
3.3. 阻隔墙厚度的影响
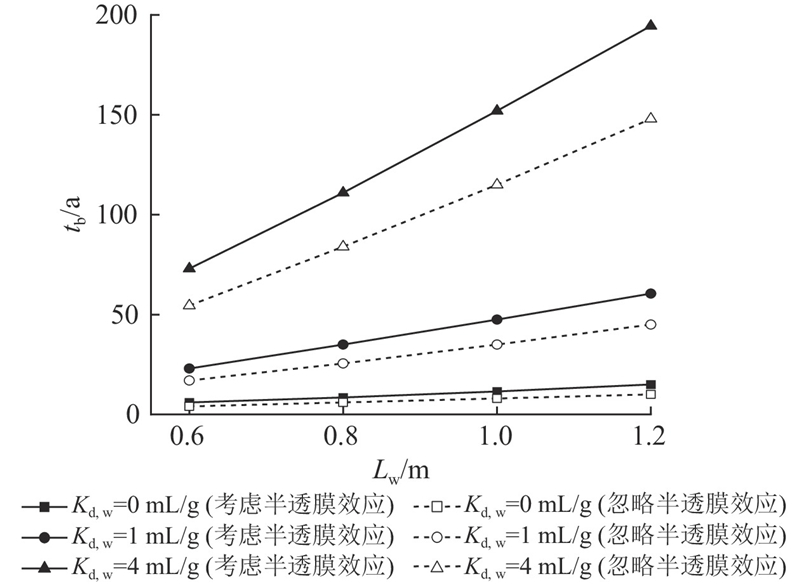
墙体厚度对污染物击穿阻隔墙的时间有重要影响. 图7给出阻隔墙厚度Lw对击穿时间tb的影响,考虑了铅离子分配系数Kd,w不同取值的情况. 结果显示,随着阻隔墙厚度的增加,击穿时间tb基本呈线性增长,考虑半透膜效应(ω = 0.28)的击穿时间比忽略该效应的tb更长. 考虑半透膜效应,当墙厚从0.6 m增加至1.2 m时,Kd,w = 1 mL/g工况的tb从23 a增加至61 a(因为阻隔墙越厚,运移路径越长). 此外,tb随着分配系数的增大而显著增加. 例如,当Kd,w由0增加至4 mL/g时,Lw = 0.6 m工况的tb从6 a增加至73 a(因为Kd,w越大,墙对污染物的阻滞因子越大,则迁移速率越低). 综上所述,增加阻隔墙厚度和增强吸附能力可以显著提高阻隔墙的阻滞能力,延长阻隔墙的击穿时间.
图 7
图 7 不同分配系数下阻隔墙厚度对污染物击穿时间的影响
Fig.7 Effect of thickness of cutoff wall on breakthrough time for various distribution coefficient
3.4. 阻隔墙渗透系数的影响
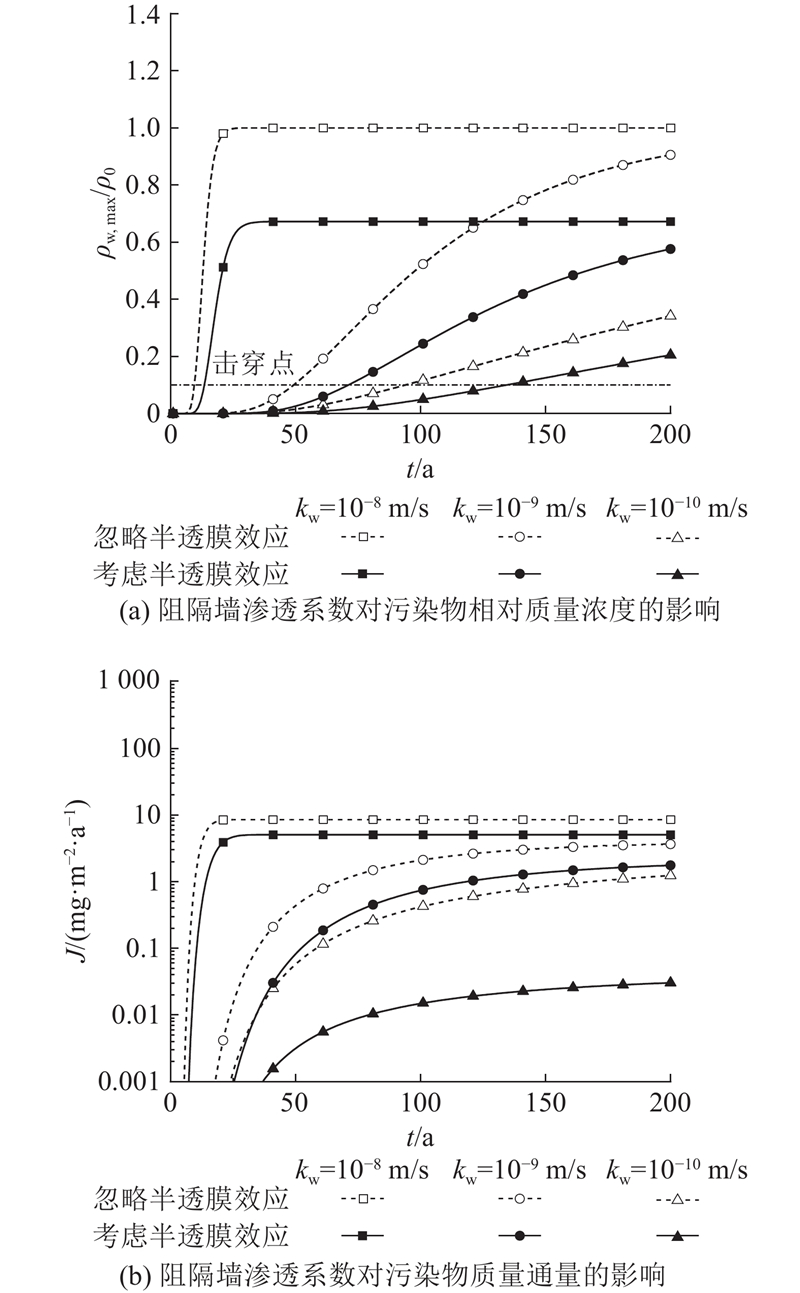
渗透系数是决定阻隔墙防污性能的重要指标. 阻隔墙材料的渗透系数一般要求不大于1×10−9 m/s,但阻隔墙在服役期间易产生性能劣化,导致渗透系数大幅上升. 为了研究阻隔墙渗透系数对铅离子运移的影响,选取3个渗透系数kw进行分析,分别为kw = 1×10−8、1×10−9和1×10−10 m/s. 不同kw对应的ρw,max/ρ0和J随时间的变化曲线如图8所示. 随着kw的减小,tb显著增加,污染物质量通量大幅减小. 考虑半透膜效应(ω = 0.28),当kw由1×10−9 m/s减小1个数量级至1×10−10 m/s时,tb从71 a增加至135 a(提高了90.1%),t = 200 a时的质量通量减少了2个数量级. 当kw增加1个数量级至1×10−8 m/s时,污染物迁移迅速达到稳态,tb从71 a减少至14 a(缩短了80.3%),t = 200 a时的质量通量增大了1.89倍. 这是因为渗透系数直接影响孔隙水渗流速率和污染物在阻隔墙中的对流通量. 此外,当渗透系数较小时,半透膜效应对降低质量通量具有更显著的作用. 例如,当kw由1×10−8 m/s减小至1×10−10 m/s时,t = 200 a时考虑半透膜效应的质量通量相较于忽略半透膜效应的降低比例由31.1%扩大至97.5%. 以上分析表明,渗透系数对击穿时间和污染物质量通量的影响显著,减小渗透系数有利于半透膜效应的发挥.
图 8
图 8 阻隔墙渗透系数对污染物相对质量浓度和质量通量的影响
Fig.8 Effect of hydraulic conductivity of cutoff wall on relative mass concentration and mass flux of contaminant
4. 结 论
(1)半透膜效应对阻隔墙-含水层系统中污染物的运移过程有显著影响,忽略半透膜效应将高估污染物的质量通量并低估污染物击穿时间. 计算结果表明,当考虑半透膜效应时,重金属铅离子击穿时间增加了12.2%~79.6%,质量通量减小了18.4%~62.3%. 当需要进行更准确的污染物迁移分析时,有必要考虑半透膜效应.
(2)增加阻隔墙厚度、减小渗透系数和提高吸附性能是提升阻隔墙防污性能的重要措施,能够显著延长阻隔墙的击穿时间. 当渗透系数由1×10−8 m/s减小至1×10−10 m/s时,击穿时间延长了8.6倍,质量通量减小了2个数量级. 此外,是否考虑半透膜效应的差异由31.1%增加至97.5%,即当渗透系数较小时,半透膜效应更显著,对降低污染物质量通量的作用更明显.
参考文献
Bentonite cut-off walls: solution for landfill remedial works
[J].DOI:10.1680/jenge.14.00022 [本文引用: 2]
污染物击穿防污屏障与地下水土污染防控研究进展
[J].
Review on penetration of barriers by contaminants and technologies for groundwater and soil contamination control
[J].
Design charts for contaminant transport through slurry trench cutoff walls
[J].DOI:10.1061/(ASCE)EE.1943-7870.0001253 [本文引用: 2]
An analytical model for contaminant transport in cut-off wall and aquifer system
[J].
A two-dimensional analytical model for organic contaminant transport in cutoff wall and aquifer system
[J].DOI:10.1002/nag.3179 [本文引用: 5]
Simulation of solute transport across low-permeability barrier walls
[J].
地下水渗流条件下土工膜复合隔离墙中有机污染物迁移研究
[J].
Migration of organic contaminants in composite geomembrane cut-off wall considering groundwater seepage
[J].
Membrane behavior of model soil-bentonite backfills
[J].DOI:10.1061/(ASCE)1090-0241(2005)131:4(418) [本文引用: 3]
Assessment of membrane and diffusion behavior of soil-bentonite slurry trench wall backfill consisted of sand and xanthan gum amended bentonite
[J].DOI:10.1016/j.jclepro.2022.132779
PAC改性膨润土/砂竖向阻隔屏障回填料化学渗透膜效应及扩散特性研究
[J].
Chemico-osmotic membrane behavior and diffusive properties of PAC amended bentonite/sand vertical cutoff wall backfills
[J].
氧化镁碱激发矿粉-膨润土-土竖向屏障材料阻隔铅污染物的化学渗透膜效应
[J].
Experimental study on chemico-osmotic membrane behaviors of reactive MgO-activated slag-bentonite backfill in vertical cutoff walls exposed to Pb-laden groundwater
[J].
Membrane behavior and diffusion properties of sand/ shmp-amended bentonite vertical cutoff wall backfill exposed to lead contamination
[J].DOI:10.1016/j.enggeo.2021.106037 [本文引用: 1]
Modelling the osmosis effect on solute migration through porous media
[J].DOI:10.1680/geot.2003.53.5.481 [本文引用: 2]
Explicit and implicit coupling during solute transport through clay membrane barriers
[J].DOI:10.1016/j.jconhyd.2003.12.002 [本文引用: 1]
Coupled solute transport through a polymer-enhanced bentonite
[J].DOI:10.1016/j.sandf.2022.101235 [本文引用: 1]
Analytical solutions for advective–dispersive solute transport in double-layered finite porous media
[J].
Membrane efficiency and diffusive tortuosity of a dense prehydrated geosynthetic clay liner
[J].DOI:10.1016/j.geotexmem.2016.05.006 [本文引用: 8]
Restricted salt diffusion in a geosynthetic clay liner
[J].DOI:10.1680/envgeo.13.00080 [本文引用: 1]
A critical review of data on field-scale dispersion in aquifers
[J].DOI:10.1029/92WR00607 [本文引用: 1]
An analytical model for one-dimensional diffusion of degradable contaminant through a composite geomembrane cut-off wall
[J].DOI:10.1016/j.jconhyd.2021.103845 [本文引用: 1]
A retardation factor considering solute transfer between mobile and immobile water in porous media
[J].DOI:10.1007/s10666-020-09726-6 [本文引用: 1]
Membrane behavior of bentonite-amended compacted clay towards Zn(II) and Pb(II)
[J].DOI:10.12989/mwt.2015.6.5.393 [本文引用: 1]
Lead adsorption and transport in loess-amended soil-bentonite cut-off wall
[J].DOI:10.1016/j.enggeo.2016.11.002 [本文引用: 1]
A two-dimensional analytical model for organic contaminants transport in a transition layer-cutoff wall-aquifer system
[J].
Consolidation enhanced membrane behavior of a geosynthetic clay liner
[J].DOI:10.1016/j.geotexmem.2011.07.002 [本文引用: 1]
Assessing the influence of chemico-osmosis on solute transport in bentonite membranes based on combined phenomenological and physical modeling
[J].DOI:10.3208/jgssp.v09.cpeg023 [本文引用: 1]