目前,针对静荷载作用下层状岩体稳定性的研究已相对完善[3-5]. 王伟等[6]通过开展不同层理面及围压组合下的力学测试,得到千枚岩强度劣化及变形特征. 张传庆等[7]综合考虑岩体参数、岩体类型及地应力环境等因素,建立围岩破坏形式的分类体系. 王孝健等[8]从力学出发,推导硬岩的线弹性变形及软岩的大变形解析解,推理得到不同围岩应力下岩体发生的破坏类型. 以上研究多是从静荷载进行分析,然而在隧道钻爆开挖的过程中,已开挖区围岩不仅承受着地应力的作用,还承受着开挖区带来的动力扰动[9-11]. 针对动力扰动的研究,多是借助SHPB试验进行展开. 李杨等[12]利用SHPB试验,分析不同层状复合岩体在冲击动力作用下的动态破坏特征及能量耗散区别. 周喻等[13]通过开展不同速率及加载方向的冲击试验,得到不同复合层状岩体的强度效果. 解北京等[14]利用分离式霍普金森杆,分析在静水压条件下煤岩的裂纹演化及破碎特征. 这些研究针对隧道断面整体结构的影响欠缺考虑,且多是从围岩变形的分析出发,无法了解静动力荷载对隧道断面围岩应力分布特征的影响,对于工程现场围岩结构的安全性判断应用局限性较大.
基于秘鲁圣加旺水电站引水隧洞的钻爆开挖工程,本文通过设计隧道围岩相似材料及模型试验,分析地应力静载条件下围岩变形场的分布特征,研究静荷载Q1、动荷载Q2及围岩倾角θ三大主要影响因素,通过LSDYNA分析层状岩体应力波的传播特性及围岩应力的分布特征. 通过正交试验分析不同因素对围岩峰值应力及二次平衡应力的敏感性,结合量纲分析推导得到多因素影响下的围岩应力预测模型,得到隧洞围岩在不同动、静荷载组合作用下的破坏类型及安全荷载控制范围,为现场施工提供参考.
1. 引水隧洞层状岩体的物理模型试验
1.1. 工程概况
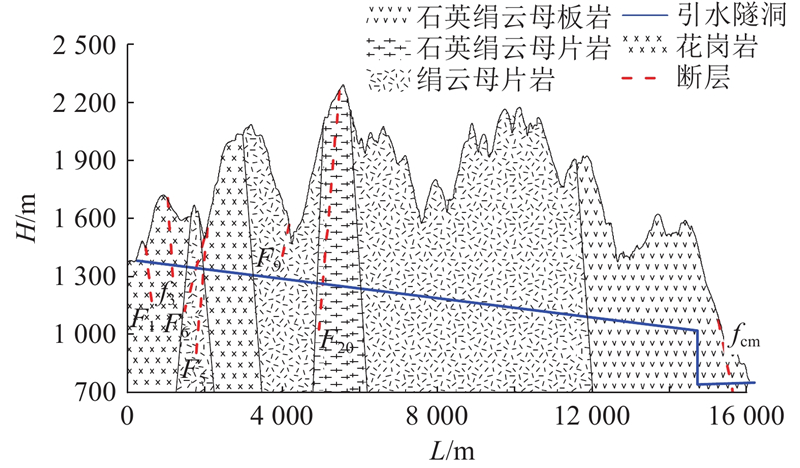
引水隧道地处秘鲁圣加旺河右岸山体中,隧道截面所处山体剖面高程H为751~2 292 m,线路总长L为16.12 km. 工程区内沟脊相间,山脉走势为305°~325°,地形完整性较差. 山体地形坡度为30°~45°. 隧洞断面为马蹄形,断面尺寸为5.7 m×5.7 m,隧洞周边围岩主要为花岗闪长岩、石英绢云母片岩及板岩,存在明显的层理特征,大致呈现45°倾斜,岩层层厚约为156 cm,隧洞线路穿越的地质环境如图1所示. 隧道线路以II、III级围岩为主,占总线路的72.8%,采用水压致裂法测得的工程现场地应力为6.19~12.80 MPa,测试深度为233.6~483.0 m,地应力测试区段见图1.
图 1
1.2. 物理模型的试验设计
由于现场岩样获取困难,通过相似材料进行缩尺实验成为较有效的方式之一. 从相似理论可知,模型试验应符合如下所示的相似准则:
式中:CG、CX、Cε、Cρ、CF及
以边界力、模型试验几何参数、岩体密度及单轴抗压强度为主要控制因素,选择水灰质量比为0.85、胶砂质量比为1∶6的配比制备相似材料,密度为2.007 g/cm3,单轴抗压强度为8.9 MPa,而工程岩体密度为2.024 g/cm3,单轴抗压强度为91.91 MPa,因此得到密度相似比Cρ = 1,抗压强度相似比
表 1 层状围岩静力变形的模型试验参数
Tab.1
| 参数类型 | (l×w)/m2 | ρ/(g·cm−3) | σc/MPa | h/cm | F/MPa |
| 实际值 | 5.7×5.7 | 2.024 | 91.91 | 156 | 6、8 |
| 计算值 | 0.57×0.57 | 2.024 | 9.191 | 15.6 | 0.6、0.8 |
| 试验值 | 0.57×0.57 | 2.007 | 8.900 | 15.6 | 0.6、0.8 |
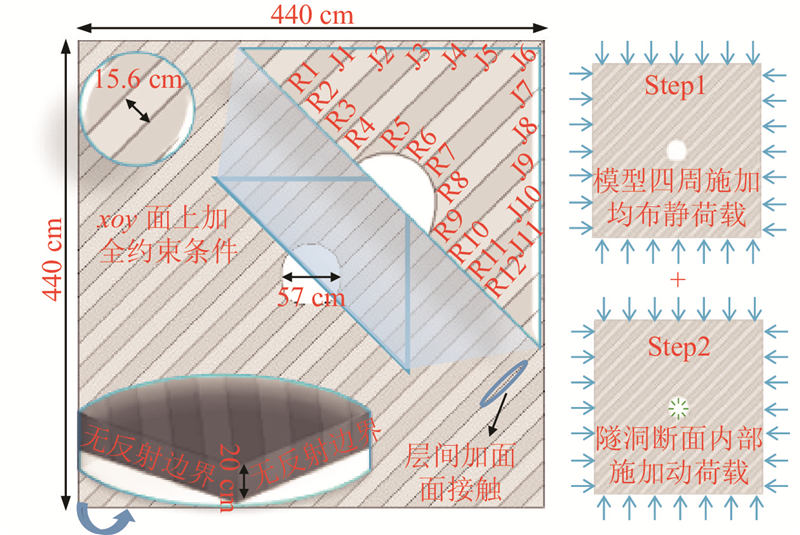
如图2所示,模型试验装置共包含4块铁片、6个液压器及1个反力架. 反力架用于提供支撑反力,液压千斤顶用于模拟地应力环境. 由于铁皮的硬度及强度均远大于相似材料,可以将液压器提供的集中荷载转换为均布荷载,其中下侧铁皮固定不动,其余三侧可移动. 为了更加符合实际工程的边界条件,在模型试验上方放置亚克力板,通过沙袋实现荷载的施加,用于约束轴向变形. 模型实验采用分层浇筑的方式,共布置8个双轴应变花. 围岩荷载按照0.6、0.8 MPa的顺序依次进行施加,利用DH3817F动静态应力应变测试分析系统采集并分析数据.
图 2
图 2 层状围岩静力变形的模型试验示意图
Fig.2 Model test diagram of static deformation of layered rock
1.3. 模型试验结果的分析
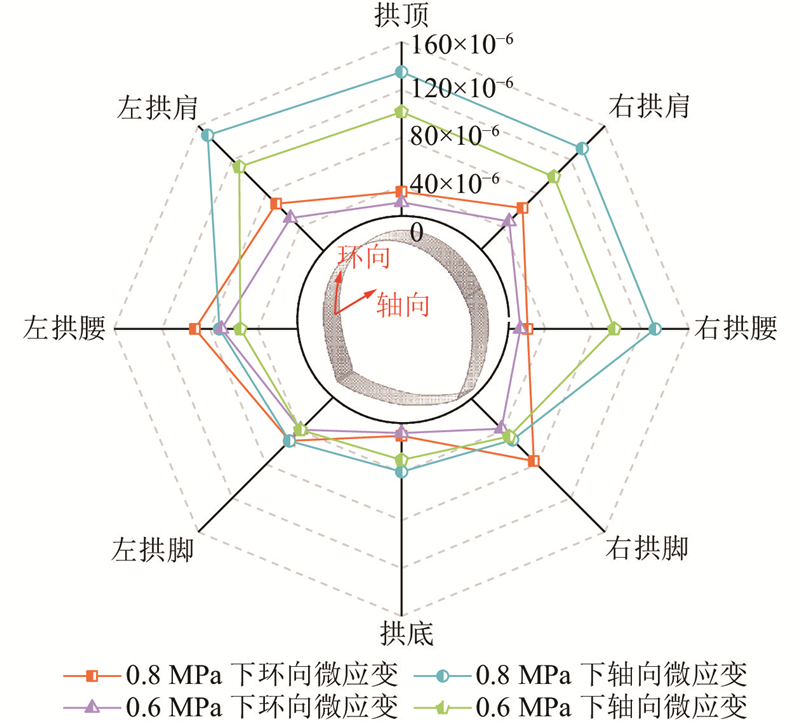
利用液压千斤顶缓慢加压至0.6 MPa,待应变数据稳定后再次加压至0.8 MPa,稳定后得到2个应力条件下隧道断面不同位置处的应变,如图3所示. 以沿着隧道筒体轴线方向为轴向,以环绕着筒体方向、圆周切线方向为环向,统计隧道断面上各监测点环向及轴向的应变分布特征,可以发现两者存在明显的区别. 其中环向微应变集中在拱肩、左拱腰及右拱脚,最大值为92.408×10−6,出现在左拱腰;轴向微应变集中在拱顶、拱肩及右拱腰,最大值为148.820×10−6,出现在左拱肩. 随着应力的增大,轴向及环向应变均不断增大,其中轴向应变整体上大于环向应变.
图 3
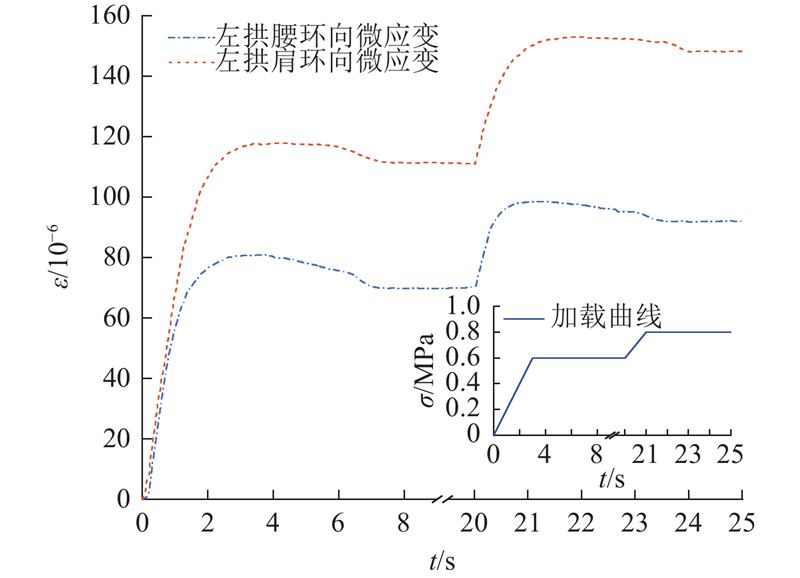
分别获取DHDAS动态信号采集分析系统得到的左拱腰环向应变曲线及左拱肩轴向应变曲线,利用origin进行去毛刺处理,如图4所示. 图中,ε为应变. 在0.6 MPa工况下的初始加载阶段,应变随着应力的增大而增大,其中左拱腰环向微应变最大达到81.257×10−6,左拱肩轴向微应变最大达到118.049×10−6,随着应力加载不再变化,受到围岩结构自稳性的作用,隧道断面监测点的应变逐步进入平衡状态,此时左拱腰环向微应变与左拱肩轴向微应变分别为70.246×10−6、111.64×10−6. 0.8 MPa工况下的应变变化特征与0.6 MPa工况基本一致.
图 4
2. 数值计算模型
2.1. 数值模型及材料参数
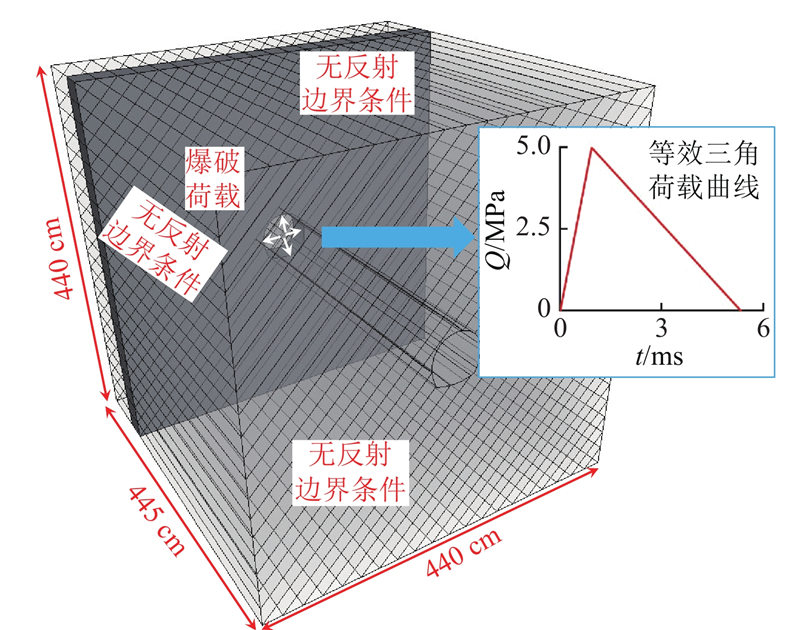
采用LS-DYNA进行数值模拟,由于物理缩尺模型试验未考虑支护措施,数值模型仅考虑地应力条件下毛洞的稳定状态. 根据圣维南原理可知,隧道开挖后的应力重分布仅发生在靠近洞室的一定范围内. 当围岩范围超出3倍洞径时,围岩尺寸对应力分布的影响可以忽略不计,因此,取数值模型尺寸为440 cm×440 cm×20 cm,隧道断面尺寸为57 cm×57 cm,层厚为15.6 cm. 模型计算共分为2个阶段:一是静力平衡阶段Step1,二是初始静力条件下的动力扰动阶段Step2. 在Step1阶段中,在模型四侧施加均布静荷载Q1(地应力模拟),采用*INTERFACE输出dynain文件,替代原有的k文件,该文件相当于赋予了动载计算的初始化应力条件,可以有效地实现应力条件下的模型计算[15]. 在Step2阶段中,Step1阶段的边界静荷载Q1保持恒定不变,在隧洞断面内部施加动力荷载Q2,通过*INCLUDE导入dynain文件,开展动力扰动过程的计算. 数值模型及计算流程可见图5.图中,R1~R12表示岩层编号,J1~J11表示层理编号. 2个阶段所用的模型是同一个,因此数值模型大小、材料参数及模型边界条件等均保持不变,其中隧道围岩四周设置无反射边界条件,隧道围岩前后侧设置全约束条件. 通过*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE在不同的岩层间施加面面接触[16],其中静摩擦系数FS为0.5,动摩擦系数FD为0.2,通过*damping对阻尼进行调用,设置模型阻尼比为0.035.
图 5
图 5 层状岩体隧道模型及计算流程
Fig.5 Tunnel model of layered rock and calculation flow chart
岩石材料采用有限元软件自带的3号材料模型*MAT_PLASTIC_KINEMATIC,该材料适用于各向异性和双向随动硬化模型,特别适用于梁、壳及实体单元. 岩体参数如下:密度为2.007 cm/s,弹性模量为3.856 GPa,单轴抗压强度为8.9 MPa.
2.2. 模型可靠性的验证
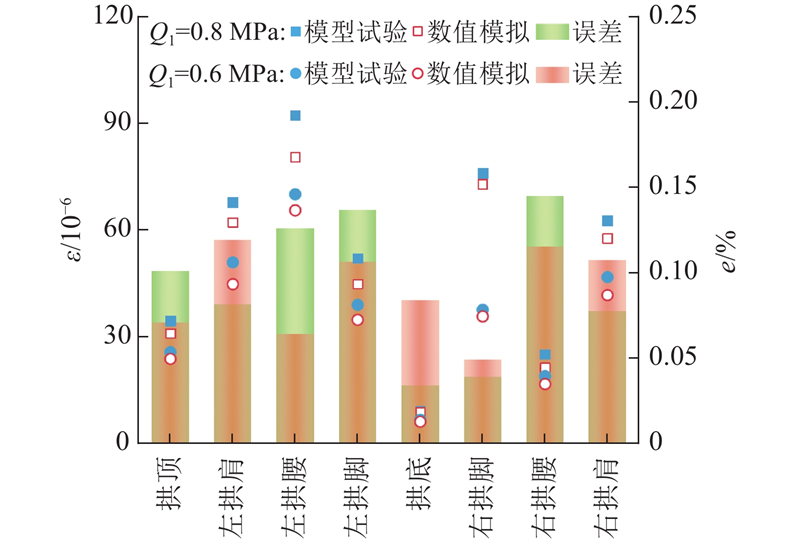
以0.6 MPa及0.8 MPa的静荷载工况为例,分别获取拱顶、拱肩、拱腰、拱脚及拱底的环向应变,并与物理模型试验测得的数据进行比较,结果如图6所示. 图中,e为误差. 数值模拟的结果整体上小于模型试验的结果,这是由于数值模拟忽略了围岩的不完整性及浇筑过程带来的误差,但是两者的数据以及应变分布特征基本一致,误差普遍小于15%,说明数值模拟方法及材料参数的设置具有一定的合理性及可靠性.
图 6
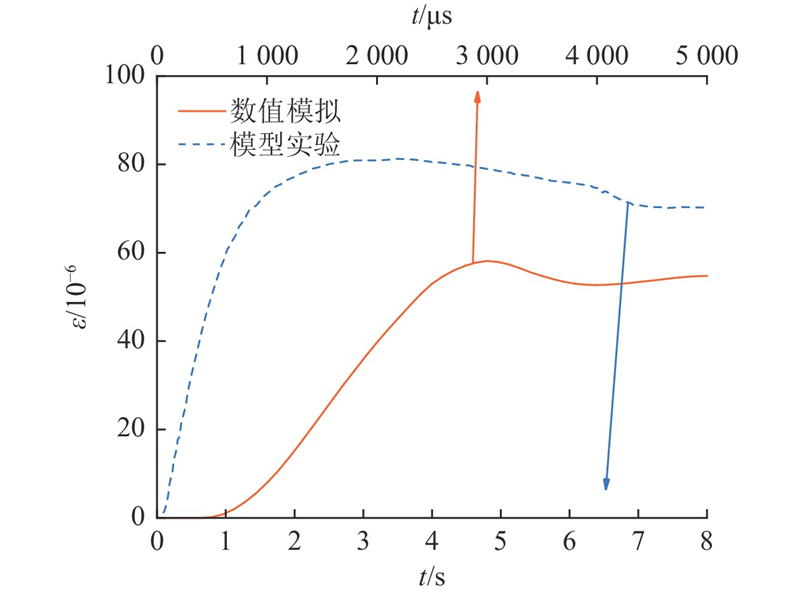
选取0.6 MPa的静荷载工况为研究对象,提取左拱腰单元的环向微应变曲线,并与模型试验获取的结果进行对比,见图7. 数值模拟与模型试验得到的应变曲线变化特征基本保持一致. 在应力加载期间,左拱腰环向微应变迅速上升. 在应力恒定不变后,应变经过轻微衰减后进入平衡状态. 平衡后数值模拟与模型试验得到的左拱腰环向微应变分别为70.246×10−6、65.715×10−6,两者误差为6.45%,说明利用数值模拟来进行拓展分析是合理、有效的.
图 7
图 7 数值模拟与模型试验的左拱腰应变曲线对比
Fig.7 Comparison of left hance’s strain curve between numerical simulation and model test
2.3. 动力荷载获取
2.3.1. 爆破模型
图 8
式中:p(t)为随时间变化的炮孔压力,pm为爆破荷载峰值压力,t为爆破荷载作用时间,tr为爆破荷载峰值压力对应的时间点,td为荷载作用时间.
对于多炮孔同时起爆,炮孔初始平均压力p0与等效弹性边界上的荷载峰值p1的计算如下:
式中:ρe为炸药密度,D为炸药爆速,γ为炸药等熵指数,dc为药包直径,db为炮孔直径,k为群孔起爆影响系数,r0为炮孔半径,r1为岩体粉碎区半径,r2为岩体破碎区半径,μ为岩体泊松比.
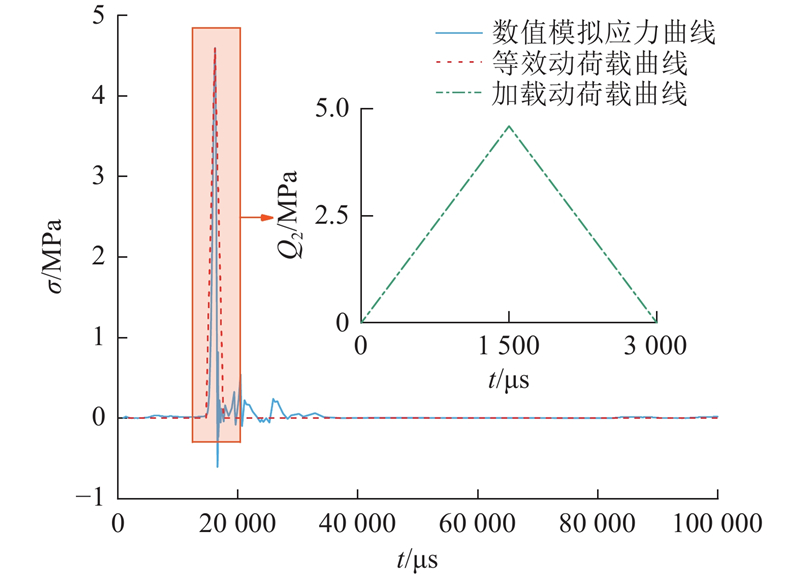
2.3.2. 动荷载曲线
图 9
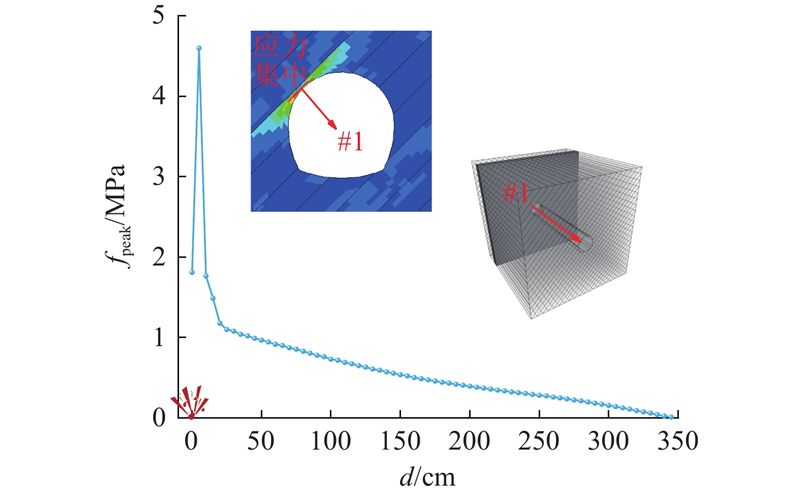
图 9 质点等效应力峰值与爆源距的关系
Fig.9 Relationship between peak particle equivalent stress and blast source distance
图 10
2.4. 数值模拟工况
探究Q1(地应力)、Q2(爆破扰动荷载)及岩层倾角θ三大因素,设置如表2所示的数值计算工况进行分析.
表 2 层状岩体隧道模型的数值计算工况
Tab.2
| 工况 | Q1/MPa | Q2/MPa | θ/(°) |
| I | 0.8 | 4.0 | 45 |
| II-1 | 0.6 | 4.5 | 45 |
| II-2 | 0.8 | 4.5 | 45 |
| II-3 | 1.0 | 4.5 | 45 |
| II-4 | 1.2 | 4.5 | 45 |
| II-5 | 1.4 | 4.5 | 45 |
| III-1 | 0.8 | 0.5 | 45 |
| III-2 | 0.8 | 1.5 | 45 |
| III-3 | 0.8 | 2.5 | 45 |
| III-4 | 0.8 | 3.5 | 45 |
| III-5 | 0.8 | 4.5 | 45 |
| IV-1 | 0.8 | 4.0 | 0 |
| IV-2 | 0.8 | 4.0 | 15 |
| IV-3 | 0.8 | 4.0 | 45 |
| IV-4 | 0.8 | 4.0 | 75 |
| IV-5 | 0.8 | 4.0 | 90 |
3. 动静荷载下的围岩应力分布特征
3.1. 层状岩体应力波传播特性
3.1.1. 静力过程
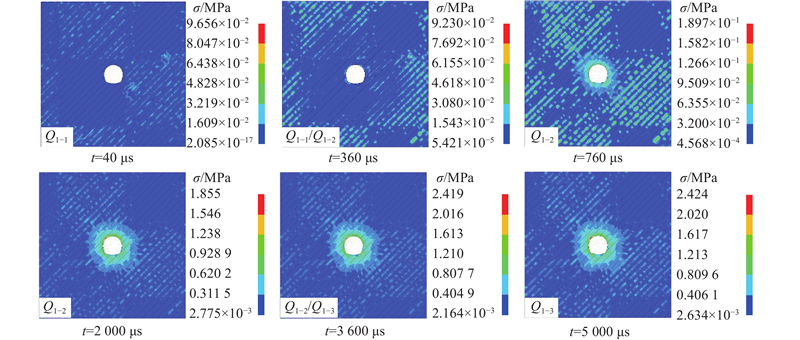
静力Q1加载的围岩应力发展可以划分为以下3个阶段. 1)应力传播阶段Q1-1,此时应力波仅在围岩内部传播,未传递到隧道断面,因此没有发生自由面导致的透反射现象. 2)应力集中阶段Q1-2,此时由于隧道断面的存在,应力波在自由面处发生透反射现象,出现应力集中. 3)静力平衡阶段Q1-3,由于自身结构的稳定性,随着应力的持续作用,围岩应力分布不再发生改变,进入平衡状态. 以Q1 = 0.8 MPa、Q2 = 4.0 MPa、θ = 45°的工况I为研究案例,得到静载条件下的围岩应力云图(见图11).
图 11
从图11可知,在围岩应力发展的不同阶段下应力分布特征存在明显区别,在应力传播阶段Q1-1,应力波主要在围岩间进行传递,受到层理结构的影响,围岩节理部分区域出现应力集中的现象,散点式分布. 当t = 360 μs时,隧道断面周边围岩开始出现应力集中,应力发展进入应力集中阶段Q1-2,随着静力荷载的增加,围岩应力不断增大. 当t = 2 000 μs时,静荷载不再增加,最大应力不断增大,但增长速率明显下降,直到t =
在弹性阶段,应力与应变的关系可以通过胡克定律来描述,如下所示:
式中:σ为应力,E为弹性模量.
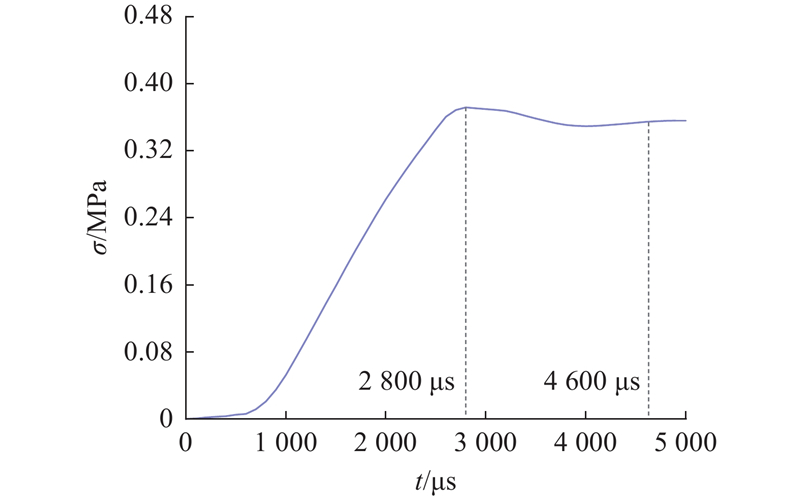
获取工况I中左拱腰单元的有效应力时程曲线,如图12所示,隧道断面左拱腰有效应力在2 800 μs内迅速增加,在4 600 μs左右进入平衡状态,静力平衡应力为0.301 MPa,有效应力变化特征与应变变化特征基本一致. 在0.8 MPa的静力作用下,通过模型试验得到的左拱腰应变为92.408×10−6,通过胡克定律计算得到左拱腰应力平衡值为0.356 MPa,数值模拟与模型试验所得的结果较接近.
图 12
图 12 工况I左拱腰处的有效应力时程曲线
Fig.12 Time travel curve of left haunch’s effective stress of in condition I
3.1.2. 动力扰动过程
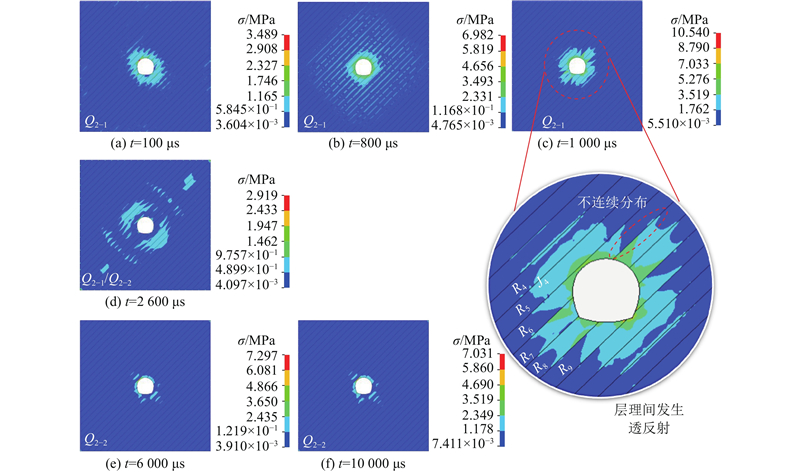
动力Q2加载的围岩应力发展可以划分为以下2个阶段. 1)动力作用阶段Q2-1,此时围岩受到静荷载和动荷载的共同作用. 2)静力二次平衡阶段Q2-2,此时动荷载施加结束,围岩在静力作用下发生二次平衡,重新进入稳定状态. 动力作用下的围岩应力云图如图13所示.
图 13
在动力作用阶段Q2-1,当动载作用起始时,如图13(a)所示,由于动荷载远远小于静荷载,围岩此时主要受到静荷载的作用,原始平衡状态基本保持不变. 图13(b)中,随着动荷载的不断增大,围岩应力平衡状态被打破,此时围岩主要受到动载的作用. 当t = 1 000 μs时,动载加载至最大值,峰值应力fmax为10.540 MPa,围岩受动力扰动的作用明显,由于围岩层理的存在,应力波不均匀地向四周扩散. 图13(c)中,岩层R5的应力波在层理J4处发生透反射,反射应力波沿着倾角方向在R5内扩散,透射波穿过层理J4进入岩层R4,该现象在R6、R7岩层中表现得更加明显,最终波阵面的整体形状发生较大改变,不再均匀分布. 当t = 2 600 μs时,围岩的应力发展进入静力二次平衡阶段Q2-2,此时动荷载与静荷载接近,围岩应力发展出现最小值,为2.919 MPa. 随着动荷载不断衰减,围岩开始主要受静载的作用,隧道断面周边的围岩开始出现应力集中的现象. 图13(e)、(f)中,围岩应力在t = 6 000 μs时进入稳定状态,二次平衡应力f为7.031 MPa,与静力平衡的结果相比,围岩应力提高了2.9倍. 这是由于动力扰动导致围岩结构受到二次破坏,围岩稳定性变差,加剧了应力集中,说明在隧道钻爆的施工过程中,注意爆破振动带给隧道已开挖区域的影响是保证隧道安全施工的关键.
3.2. 围岩应力的分布特征
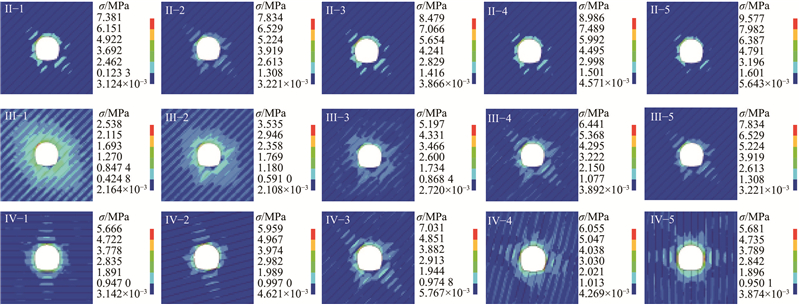
将II-1~5、III-1~5及IV-1~5等不同的参数工况作为研究对象,得到不同动载下的围岩应力云图(见图14),分析不同参数对围岩二次平衡应力f分布特征的影响.
图 14
图 14 不同影响因素下围岩二次平衡应力的分布特征
Fig.14 Distribution characteristics of secondary equilibrium stress of surrounding rock under different influencing factor
从图14可知,受到层理的影响,围岩应力云图存在不连续分布的特征. 动、静荷载对应力集中位置的影响较小,对应力数值的影响较大,围岩应力集中主要发生在左拱肩,这是由于该处所处对应层的围岩两端厚、中间薄,厚度不均导致应力集中更加明显. 动荷载对波阵面不连续分布特征的影响明显. 当动荷载较小时,岩体基本上不产生动态破坏,二次平衡应力的分布特征与静力平衡应力的分布特征较接近;当动荷载较大时,岩体受到动态扰动的破坏,岩体完整性降低,应力集中加剧,波阵面不连续分布的特征更加明显. 倾角对围岩二次平衡应力分布特征的影响明显,随着倾角的增大,隧道断面上半部分的应力集中位置由拱顶向左拱腰转移,而隧道断面下半部分的应力集中位置由拱底向右拱腰转移,2个应力集中点的连线与倾角方向基本上保持相互垂直. 为了分析不同影响因素与fmax、f的关系,统计各工况的应力,如图15所示.
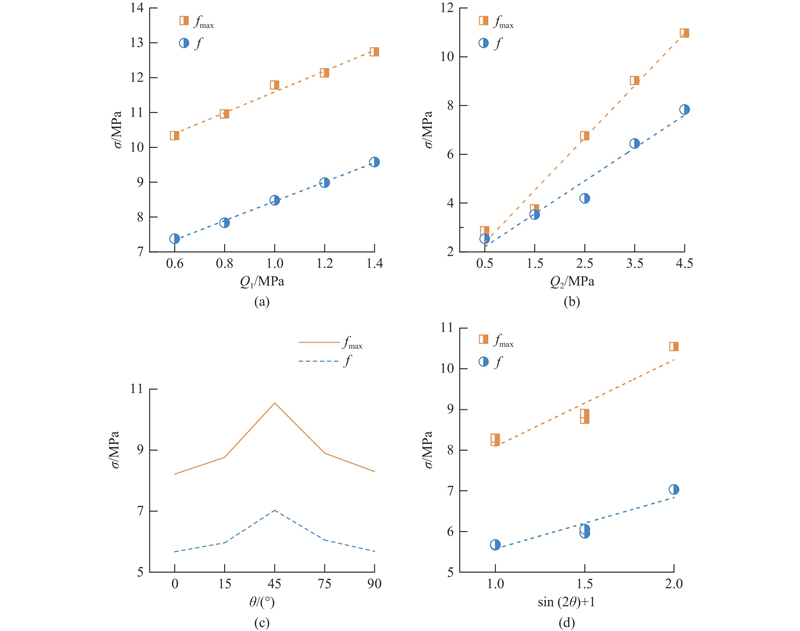
图 15
分析图15(a)、(b)可知,随着动、静荷载的增大,fmax与f不断增大,利用一次函数对不同动、静荷载条件下的fmax与f进行线性回归分析,拟合度R2均大于0.85,说明拟合效果较好,Q1、Q2与fmax及f均呈现正线性相关. 随着倾角的增大,fmax及f均呈现出先增大后减小的趋势,呈“∧”型分布,最大值出现在45°倾角. 对倾角进行基本数学转换,令g(θ) = sin (2θ)+1,并进行线性分析可知,g(θ)与fmax及f均呈现正线性相关.
4. 基于量纲分析法的层状围岩应力预测模型
4.1. 多因素正交试验设计
表 3 正交试验的模拟因素及水平
Tab.3
| 水平 | 因素 | |||
| Q1/MPa | Q2/MPa | θ/(°) | A | |
| 1 | 0.6 | 0.5 | 0 | 1 |
| 2 | 0.8 | 1.5 | 15 | 2 |
| 3 | 1.0 | 2.5 | 45 | 3 |
| 4 | 1.2 | 3.5 | 75 | 4 |
| 5 | 1.4 | 4.5 | 90 | 5 |
表 4 正交试验结果的统计
Tab.4
| 试验编号 | Q1/MPa | Q2/MPa | θ/(°) | A | f/MPa | fmax/MPa |
| 1 | 0.6 | 0.5 | 0 | 1 | 1.541 | 1.668 |
| 2 | 0.6 | 1.5 | 45 | 4 | 3.256 | 6.592 |
| 3 | 0.6 | 2.5 | 90 | 2 | 3.623 | 5.612 |
| 4 | 0.6 | 3.5 | 15 | 5 | 4.966 | 7.487 |
| 5 | 0.6 | 4.5 | 75 | 3 | 6.313 | 10.732 |
| 6 | 0.8 | 0.5 | 90 | 4 | 2.046 | 2.179 |
| 7 | 0.8 | 1.5 | 15 | 2 | 2.976 | 3.381 |
| 8 | 0.8 | 2.5 | 75 | 5 | 4.445 | 6.223 |
| 9 | 0.8 | 3.5 | 0 | 3 | 5.153 | 8.151 |
| 10 | 0.8 | 4.5 | 45 | 1 | 7.834 | 10.960 |
| 11 | 1.0 | 0.5 | 75 | 2 | 2.774 | 3.190 |
| 12 | 1.0 | 1.5 | 0 | 5 | 3.641 | 4.311 |
| 13 | 1.0 | 2.5 | 45 | 3 | 5.917 | 9.519 |
| 14 | 1.0 | 3.5 | 90 | 1 | 5.762 | 8.857 |
| 15 | 1.0 | 4.5 | 15 | 4 | 7.139 | 11.851 |
| 16 | 1.2 | 0.5 | 45 | 5 | 3.928 | 4.122 |
| 17 | 1.2 | 1.5 | 90 | 3 | 4.124 | 4.464 |
| 18 | 1.2 | 2.5 | 15 | 1 | 5.371 | 6.895 |
| 19 | 1.2 | 3.5 | 75 | 4 | 6.603 | 10.103 |
| 20 | 1.2 | 4.5 | 0 | 2 | 7.189 | 11.050 |
| 21 | 1.4 | 0.5 | 15 | 3 | 3.845 | 4.614 |
| 22 | 1.4 | 1.5 | 75 | 1 | 4.905 | 5.309 |
| 23 | 1.4 | 2.5 | 0 | 4 | 5.606 | 6.795 |
| 24 | 1.4 | 3.5 | 45 | 2 | 8.306 | 13.270 |
| 25 | 1.4 | 4.5 | 90 | 5 | 7.723 | 14.720 |
表 5 极差分析
Tab.5
| 指标 | 综合平均值 | Q1/MPa | Q2/MPa | θ/(°) | A |
| f | k1 | 3.940 | 2.827 | 4.626 | 5.083 |
| k2 | 4.491 | 3.780 | 4.859 | 4.973 | |
| k3 | 5.047 | 4.992 | 5.848 | 5.070 | |
| k4 | 5.443 | 6.158 | 5.008 | 4.930 | |
| k5 | 6.077 | 7.240 | 4.656 | 4.941 | |
| R | 2.137 | 4.413 | 1.222 | 0.153 | |
| fmax | k1 | 6.418 | 3.155 | 6.395 | 6.738 |
| k2 | 6.179 | 4.811 | 6.846 | 7.301 | |
| k3 | 7.546 | 7.009 | 8.893 | 7.496 | |
| k4 | 7.327 | 9.574 | 7.111 | 7.504 | |
| k5 | 8.942 | 11.863 | 7.166 | 7.373 | |
| R | 2.523 | 8.708 | 2.498 | 0.766 |
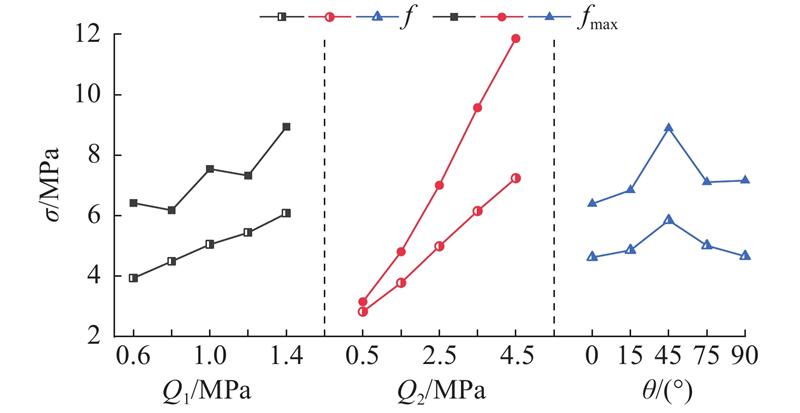
图 16
图 16 各参量边际均值的直观分布图
Fig.16 Visual distribution of marginal mean of each parameter
采用方差法分析各因素对试验指标的影响显著程度,结合F分布统计,将各因素的显著性水平划分为4个等级,即高显著影响、显著影响、影响不十分显著、无显著影响. 根据F的大小,按照显著性水平由高到低划分为F ≥ F1-0.01、F1-0.01 ≥ F ≥ F1-0.05、F1-0.05 ≥ F ≥ F1-0.1、F ≤ F1-0.1的4个区间,依次用“***”、“**”、“*”、“×”4种不同的标志来表示分析结果. 本研究中,F1-0.01(3,4) = 28.710,F1-0.05(3,4) = 9.12,F1-0.1(3,4) = 5.34,通过正交分析得到的结果如表6所示.
表 6 方差分析
Tab.6
| 指标 | 方差来源 | 偏差平方和 | 自由度 | 均方和 | F值 | 显著性 |
| f | Q1 | 13.708 | 4 | 3.427 | 24.833 | ** |
| Q2 | 62.835 | 4 | 15.709 | 113.833 | *** | |
| θ | 4.989 | 4 | 1.247 | 9.036 | * | |
| A | 0.550 | 4 | 0.138 | — | — | |
| fmax | Q1 | 23.945 | 4 | 5.986 | 5.527 | * |
| Q2 | 247.236 | 4 | 61.809 | 57.072 | *** | |
| θ | 18.069 | 4 | 4.517 | 4.171 | × | |
| A | 4.332 | 4 | 1.083 | — | — |
从表6可知,对于二次平衡应力,Q1为显著影响,Q2为高显著影响,倾角为影响不十分显著;对于峰值应力,Q1为影响不十分显著,Q2为显著影响,倾角为无显著影响. 三者对二次平衡应力及峰值应力的影响程度顺序均为静载>动载>倾角,与直观性分析所得的结果一致.
4.2. 模型推导
采用量纲分析法推导围岩应力预测模型,影响围岩应力的因素主要分为岩体参数、荷载参数及隧道参数3类,具体如表7所示.
表 7 影响因素及量纲
Tab.7
| 影响因素 | 量纲 | 影响因素 | 量纲 | |
| 二次平衡应力f | ML−1T−2 | 峰值应力fmax | ML−1T−2 | |
| 岩体密度ρ | ML−3 | 层间黏聚力φ | — | |
| 纵波波速v | LT−1 | 弹性模量E | ML−1T−2 | |
| 静荷载Q1 | ML−1T−2 | 动荷载Q2 | ML−1T−2 | |
| 倾角θ | — | 层厚H | L |
为了满足幂函数的基本要求,对θ进行数学变换,得到g(θ) = sin (2θ)+1. 由量纲分析白金汉定理(π定理)可知,围岩应力集中最值可以表示为
根据π定理,独立量纲取为ρ、Q1、sin (2θ)+1、H,则有如下无量纲数:
假设上述无量纲数满足如下关系:
将各个π值的含义代入式(7),可得
假设上述参量满足下述关系:
对于某一特定岩体下的隧道工程,岩体参数ρ、VP、E、φ及隧道等效半径R、层厚H均是确定的,属于已知常数,因此可以进一步简化为
式中:
同理得到峰值应力的预测模型如下:
4.3. 层状围岩的安全控制极限动静荷载
围岩在承受爆破扰动后,围岩应力经历了从应力平衡状态到动力扰动、最后应力二次平衡的发展状态,围岩的破坏状态与受力特征密切相关. 当冲击荷载或静力荷载过大时,围岩在强应力的挤压作用下发生破坏,形成受压破坏区;当冲击荷载或静力荷载较大时,虽然未造成围岩发生压破坏,但是超过了围岩抗拉强度,导致围岩发生拉破坏. 根据第一强度准则,得到围岩破坏准则:
基于正交试验结果,得到不同因素影响下的围岩应力预测模型,如下所示.
拟合得到的R2分别为0.938及0.907,说明拟合结果具有较好的可靠性.
图 17
图 17 不同动、静荷载下的围岩破坏特征
Fig.17 Failure characteristic of surrounding rock under different dynamic and static load
5. 结 论
(1)在地应力作用下,隧道围岩存在初始应力集中的现象. 在动荷载施加结束后,围岩应力二次平衡,应力整体增大,动力扰动对围岩稳定性的影响明显. 应力波在层理处发生透反射,导致应力波波阵面呈现不连续分布的特征.
(2)动静荷载与围岩峰值应力及二次平衡应力呈正线性相关,但不影响围岩应力集中的位置. 围岩峰值应力及二次平衡应力随着倾角增大呈现先增后减的变化,倾角对应力集中位置的影响显著.
(3)不同因素对围岩峰值应力及二次平衡应力的敏感性顺序均为动载>静载>倾角,其中动载对于围岩峰值应力及二次平衡应力分别为显著、高显著影响,静载对于围岩峰值应力及二次平衡应力的影响分别为不十分显著、显著,倾角对于围岩峰值应力及二次平衡应力的影响分别为不显著、不十分显著.
(4)基于应力预测模型及围岩动、静抗压(拉)强度,得到隧洞围岩在不同动、静荷载组合作用下的破坏类型. 当围岩倾角为90°(0°)、75°(15°)、60°(30°)及45°时,静荷载极限值分别为0.731、0.555、0.479及0.456 MPa,动荷载极限值分别为0.624、0.523、0.477及0.463 MPa.
参考文献
复杂开采条件下深部硬岩板裂化破坏试验与模拟研究进展和关键问题
[J].
Research progress and key issues of laboratory test and numerical simulation for slabbing failure in hard rock under complex mining conditions
[J].
不同煤柱尺寸条件下采动巷道层状底板稳定性分析与控制对策
[J].
Stability analysis and control strategy of layered floor of mining roadway under different coal pillar size
[J].
Analytical stress solution for cold region tunnels with unequal ground stress and support delay under different frost heave conditions of surrounding rock
[J].DOI:10.1016/j.coldregions.2022.103742 [本文引用: 1]
Analytical solution of frost heaving force and stress distribution in cold region tunnels under non-axisymmetric stress and transversely isotropic frost heave of surrounding rock
[J].DOI:10.1016/j.coldregions.2020.103117
不同加载速率下煤岩动力破坏特征实验研究
[J].
Experimental study on dynamic failure characteristics of coal and rock under different loading rates
[J].
层状千枚岩各向异性力学特性与脆性评价研究
[J].
Anisotropic mechanical properties and brittleness evaluation of layered phyllite
[J].
基于地应力水平评价的围岩潜在破坏模式研究
[J].
Study on potential failure modes of surrounding rock mass based on evaluation of geostress level
[J].
高地应力环境下地下工程围岩变形破坏的地质力学模式分析
[J].
Geomechanical model analysis of deformation and failure of surrounding rock in underground engineering under high ground stress environment
[J].
动载下层状复合岩石能量耗散及断裂特征研究
[J].
Numerical simulation of jointed rock mass blasting under different in-site stress conditions
[J].
深埋隧洞连续爆破开挖围岩应力演化规律
[J].
Stress evolution of surrounding rocks under continuous blasting of deep-buried tunnel
[J].
循环爆破荷载作用下小净距隧道围岩累积损伤特性研究
[J].
Research on cumulative damage characteristics of surrounding rock of small-clear distance tunnel under cycle blasting load
[J].
动载下层状复合岩石能量耗散及断裂特征研究
[J].
Energy dissipation and fracture characteristics of composite layered rock under dynamic load
[J].
动载下层状岩体力学特性试验与数值模拟
[J].
Test and numerical simulation for mechanical properties of laminated rock mass under dynamic loading
[J].
静水压下原生组合煤岩动力学破坏特征
[J].
Dynamic failure characteristics of primary coal-rock combination under hydrostatic pressure
[J].
初始应力下岩体爆破损伤特性及破裂机理
[J].
Blast-induced damage characteristics and fracture mechanism of rock mass under initial stress
[J].
软硬互层隧道稳定性分析及初期支护优化
[J].
Stability analysis and optimization of primary support on tunnel excavation with soft-hard interbed rock
[J].
Modeling study of cumulative damage effects and safety criterion of surrounding rock under multiple full-face blasting of a large cross-section tunnel
[J].DOI:10.1016/j.ijrmms.2021.104882 [本文引用: 1]
爆破振动对建(构)筑物影响数值计算模型及安全判据的研究
[J].
Study on numerical model and safety criterion of the influence of blasting vibration on buildings and structures
[J].
大断面隧道爆破作用下围岩动力响应特性与损伤效应研究
[J].
Study on dynamic response and damage effect of surrounding rock in large tunnel under blasting excavation
[J].
大型地下厂房开挖爆破振动动力响应数值模拟
[J].
Numerical simulation of dynamic response of large underground powerhouse subjected to blasting vibration
[J].