相较电磁开关阀动态特性直接检测法,基于模型的位移估计法、基于容腔压力变化的油压检测法和基于电气参数判断法等检测方式被相继提出,此类方法不依赖电磁开关阀的构型特征,可间接测量阀芯的运动状态. Zhong等[10]根据阀芯的力平衡方程算出电磁开关阀的临界启闭电流值,基于基尔霍夫定律得到该阀的临界启闭时间. 此时间识别精度取决于数理模型的建模精度,在非线性参数和外扰动影响下,电磁开关阀启闭时间的识别精度会降低. Kong等[11]通过阀前阀后油液的建压时间与掉压时间来检测电磁开关阀的动态性能,毫秒级的动态时间不仅对压力传感器本身的采集频率有极高的硬件要求,而且油压检测法无法避免密闭容腔的体积越大,油压变化滞后于电磁开关阀的实际响应时间越明显的问题. Rahman等[12]通过增量电感估计了阀芯具体位置,但是磁滞特性与电感变化梯度会加大估计的难度. 王文静[13]经测量线圈电流后,通过牛顿迭代法得到时变电感,并基于电感和阀芯位移的数学模型实现对电磁开关阀动态特性的软测量. 相比上述间接检测方式,基于电流特征识别法具有既简单且易测试的优点. Ahn等[14-16]的研究表明:电流曲线上的凸点、上拐点、凹点和下拐点依次对应电磁开关阀的开启滞后时间、开启运动时间、关闭滞后时间和关闭运动时间,这种检测方式在工程中被广泛用来快速判断电磁开关阀的动态特性. Yudell等[17]通过限制阀芯运动行程的方法来分析电磁开关阀各切换状态在电流曲线上的特征点,试验结果表明:凸点和凹点不能准确对应临界开启点和临界关闭点. 在此基础上,Gao等[18]建立一阶电流导数与阀芯运动状态的匹配关系,实现对电磁开关阀总启闭时间的识别. 但是,该研究对电流导数差分信号的滞后补偿存在较大的不确定非线性,影响了动态时间的识别精度. 此外,电磁开关阀的长时间启闭势必增加线圈温升,从而增大线圈电阻,进而影响电流导数法中的线圈电流及其导数变化趋势[19-20]. 因此,上述的间接检测方式依旧存在较大的测量偏差,无法精准检测电磁开关阀真实的动态特性.
本研究考虑电磁开关阀软磁材料的磁化特性,分析磁导率导数对该阀动态特性的影响规律,揭示线圈电流多阶导数曲线上的特征点与电磁开关阀临界启闭时刻、完全启闭时刻的匹配机理. 经与激光位移直接检测法比较后,得到基于时变温升工况的测量偏差,从而验证基于电流多阶导数特性检测法的可行性,最终实现对电磁开关阀动态特性高精度、无损检测.
1. 电磁开关阀结构与工作原理
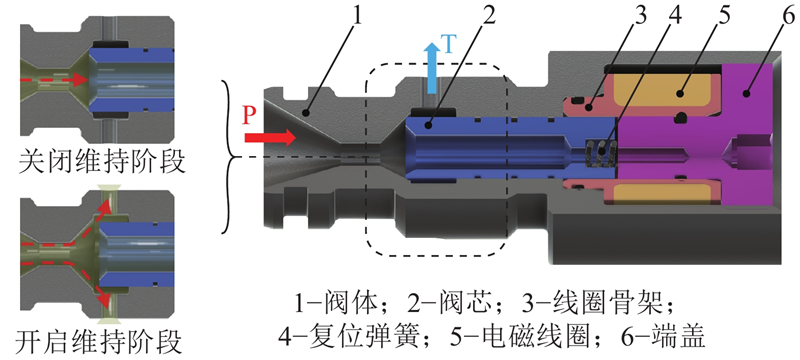
如图1所示,直通式二位二通常闭电磁开关阀由阀体、阀芯、线圈骨架、复位弹簧、电磁线圈和端盖组成,关键参数信息如下:线圈310匝、阀芯6.32 g、阀芯行程0.2 mm、初始气隙0.3 mm、弹簧弹性系数28.9 N/mm. 图中,P为进油口,T为出油口. 该阀的工作原理:当电磁线圈通电时,阀芯在电磁力的作用下克服弹簧力、液压力、摩擦力等其他阻尼力开始运动,此时P与T联通,电磁开关阀处于开启状态. 当电磁线圈失电时,激励的电磁力不足以维持电磁开关阀开启状态,阀芯向复位方向运动,此时电磁开关阀处于关闭状态,直至P与T断开.
图 1
2. 电磁开关阀数学建模
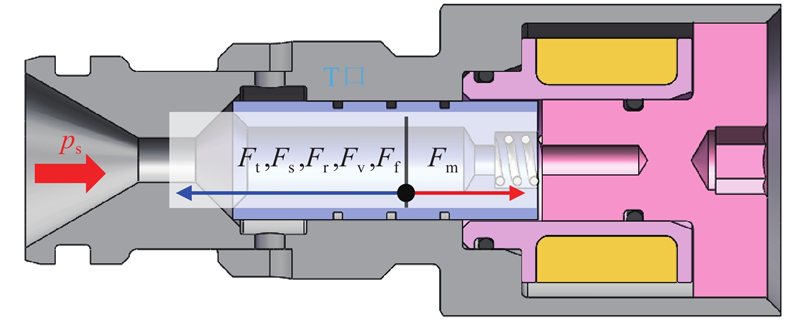
在电磁开关阀开启阶段,阀口随着阀芯的移动逐渐打开,此过程的阀芯受力分析如图2所示. 根据牛顿第二定律,阀芯的力平衡方程为
图 2
式中:m为阀芯质量,x为阀芯位移,Fm为电磁力,ps为进油口压力,A为进油口有效横截面积,Ft为瞬态液动力,Fs为稳态液动力,Fr为弹簧力,Fv为阻尼力,Ff为阀芯与阀体间的摩擦力.
式中:Cd为流量系数,Cv为流速系数,w为阀口梯度,Ld为油液阻尼长度,θ为射流角,ρ为油液密度,Ao为阀口过流面积,ΔpPT为P与T的压差.
式中:k为弹簧弹力系数,c为阻尼系数,
式中:tm1和tm0分别为电磁开关阀的开启运动时间和关闭运动时间. 当驱动电压加载至电磁线圈上时,电磁开关阀的电场数学模型为
式中:U为驱动电压,R为线圈电阻,L为线圈电感,I为线圈电流. 电磁开关阀启闭时会产生能量损耗,导致线圈温升,影响线圈电阻. 电阻模型为
式中:T(t)为电磁线圈的时变温度. 电磁线圈产生的磁动势及其电感导数特性分别表示为[21]
式中:Um为磁动势,N为线圈匝数,l为总磁路等效长度,H为磁场强度,δ0为初始气隙,μr为相对磁导率,表示软磁材料磁导率μc与空气磁导率μ0之比. 结合式(11)和式(12),考虑磁导率导数特性,线圈电感导数表达式为
将式(9)和式(10)代入式(13),考虑线圈电阻在时变温升工况下的变化规律,电磁开关阀电流导数、电感导数和阀芯运动速度之间的数学模型为
基于上述数学建模分析,得到如下结论. 1)在电磁开关阀启闭过程中,阀芯位移变化与软磁材料的磁导率变化直接影响线圈电感的导数特性. 2)结合线圈电流导数与线圈电感导数的耦合模型,电磁开关阀的启闭动态性能与电流导数特性相互关联.
3. 动态特性检测原理
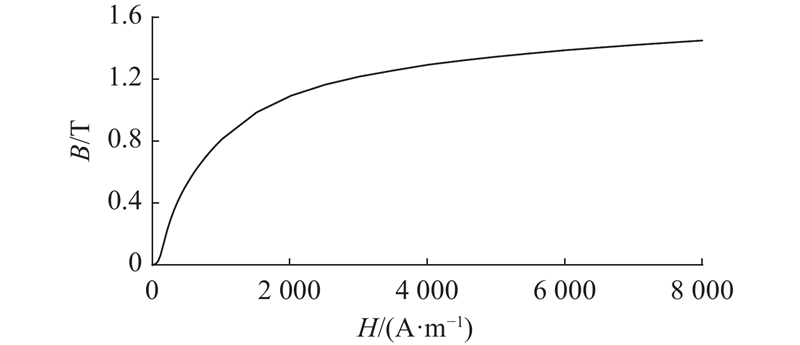
由理论分析的结论可知,软磁材料磁导率导数特性与电磁开关阀动态响应特性相关. 本研究电磁开关阀的关键部件材料均为软磁合金1J117,该类材料经送检测量的磁化曲线如图3所示,其中B为磁感应强度. 结合电磁开关阀启闭过程中的磁场强度变化范围,对磁化曲线求导,分别得到软磁材料的磁导率及其导数曲线,如图4所示. 该软磁合金的磁化特性在所选磁场强度变化范围内基本不受线圈温升的影响,本文忽略该影响因素. 阀芯在单周期启闭运动过程中的磁场强度基本介于90~250 A/m. 随着电磁开关阀开启,磁场强度随着线圈电流的上升而增大,此时磁导率导数主要呈现下降的趋势. 同理,在电磁开关阀关闭过程中,磁导率导数随着磁场强度的减小而增大.
图 3
图 3 电磁开关阀软磁材料的磁化曲线
Fig.3 Magnetization curve of soft magnetic materials for solenoid switching valve
图 4
图 4 软磁材料磁导率及其导数曲线
Fig.4 Magnetic permeability and its derivative curve of soft magnetic materials
图 5
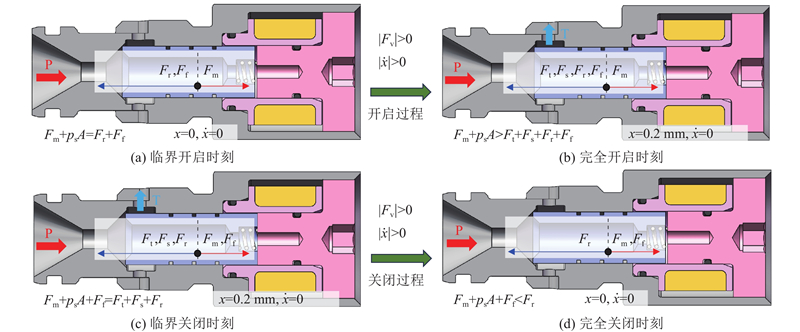
图 5 电磁开关阀在不同启闭时刻的受力分析
Fig.5 Force analysis of solenoid switching valve at different opening and closing moments
式中:td1和td0分别为开启滞后时间和关闭滞后时间,L1和L0分别为电磁开关阀在开启和关闭状态下的等效电感,Ii为线圈初始电流,I1和I0分别为临界开启电流和临界关闭电流. 开启运动时间为阀芯开始运动直至达到最大位移的变化时间,关闭运动时间为阀芯开始复位运动直至达到初始位置的变化时间,分别表示为
式中:xmax为阀芯最大位移,即阀芯行程.
3.1. 开启滞后阶段
当电磁开关阀从响应开启指令信号到临界开启时,阀芯位移及其速度均为零. 式(14)在该阶段的表达式为
在开始滞后阶段,电流一阶导数随着线圈电流和磁导率导数的增大而逐渐减小. 当激励的电磁力可以克服弹簧力与其他阻力时,阀芯处于临界开启状态. 在开启运动后,阀芯在高电压激励下加速运动,阀芯位移及其速度快速增大. 此时,电流导数必然呈现明显减小的趋势,但相较于整个电流一阶导数的数量级,该特征点的变化幅值不大. 为此在原有电流一阶导数的基础上求导,通过数量级的提升来增大对此变化幅值的辨识度,电流二阶导数曲线必然存在1个明显的凸点与电磁开关阀的临界开启瞬间对应.
3.2. 开启运动阶段
随着阀芯运动位移不断增大,当电磁开关阀完全开启时,阀芯速度瞬间降为零,式(14)在该阶段的表达式为
运动速度在碰撞时刻的突变性导致电流导数中分子部分瞬间增大,上升趋势明显,因此该曲线上必然存在1个凹点与电磁开关阀的完全开启时刻相互对应.
3.3. 关闭滞后阶段
采用单电压驱动控制策略验证本研究所提检测方法在时变温升下的有效性,该方法在电磁开关阀关闭阶段以零电压激励,故驱动电压为零. 随着线圈电流的减小和磁导率导数的增大,电流导数值随之增大,其曲线缓慢上升. 当电磁开关阀开始复位关闭时,阀芯在复位弹簧的作用下作加速运动,此时阀芯运动位移及速度值不为零,式(14)在该阶段的表达式为
式(21)分子上速度项的减小会明显增大电流导数曲线上升的趋势. 类比于开启滞后阶段,对该一阶电流导数进一步求导,基于电流二阶导数曲线上的上折点可以与电磁开关阀临界关闭时刻相互匹配.
3.4. 关闭运动阶段
阀芯撞击阀体的瞬间电磁开关阀完全关闭,阀芯运动速度突变为零. 式(14)在该阶段的表达式为
电流导数分子上速度项的突变性,导致该曲线存在明显下降的趋势,此时必然存在1个下折点与电磁开关阀完全关闭时刻相互匹配.
综上所述,电磁开关阀启闭过程涉及复杂的电-磁-机-热等多物理场耦合作用以及软磁材料的磁滞特性,本研究对基于电流多阶导数特性的检测原理进行定性地分析,得到如下结论. 1)开启电流导数曲线上的凸/凹点分别对应电磁开关阀的临界/完全开启时刻. 2)关闭电流导数曲线上的上/下折点分别匹配电磁开关阀的临界/完全关闭时刻.
4. 试验结果分析
图 6
图 6 电磁开关阀动态特性测试平台
Fig.6 Test platform for dynamic performance of solenoid switching valve
表 1 试验台的主要参数
Tab.1
| 仪器名称 | 型号 | 最大采样频率/(kS·s−1) |
| 激光位移传感器 | LK-G155 | 50 |
| 线圈电流数据采集卡 | NI 9227 | 50 |
| 阀芯位移数据采集卡 | NI 9205 | 250 |
4.1. 温升特性
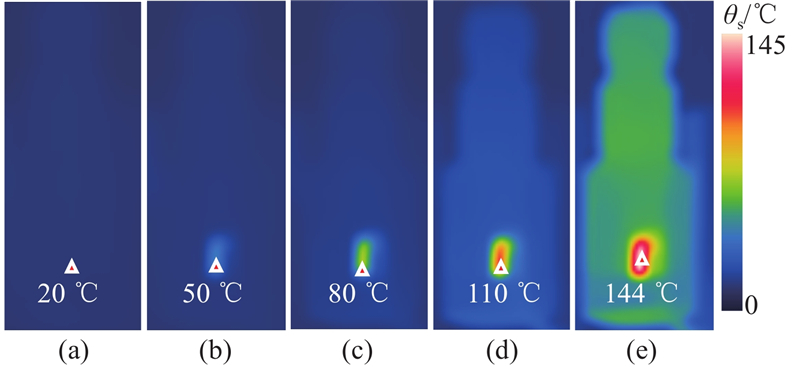
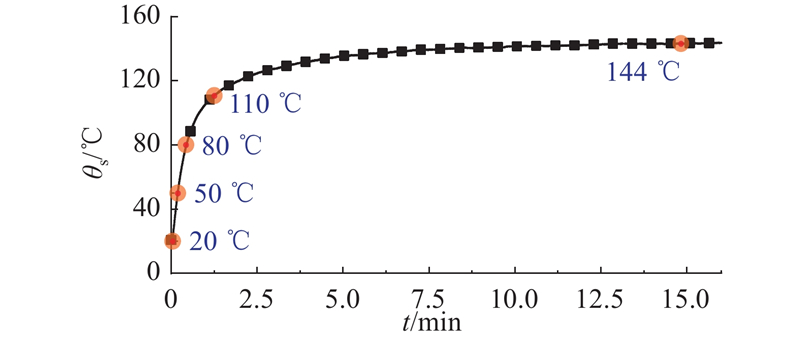
驱动频率为20 Hz的电磁开关阀温度分布如图7所示. 可以看出,电磁线圈不仅最先发热,其热成像也是整个阀温度最高区域. 随着启闭时间的增加,线圈温度随之上升. 经阀芯、端盖等部件热传导后,热量逐渐扩散至四周.
图 7
图 8
图 9
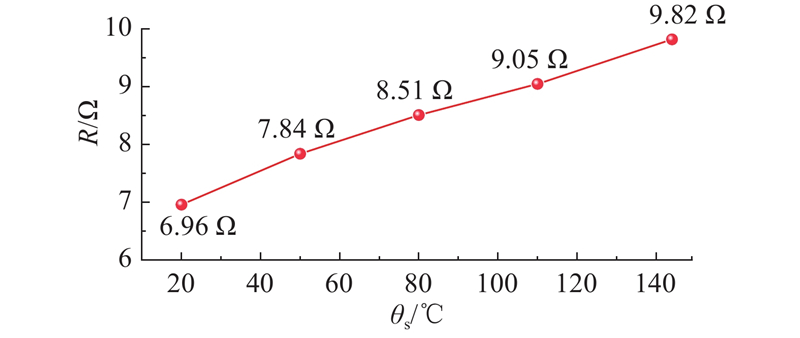
图 9 电磁线圈温升影响下的电阻变化
Fig.9 Resistance variation under temperature rising of solenoid’s coil
4.2. 启闭动态特性
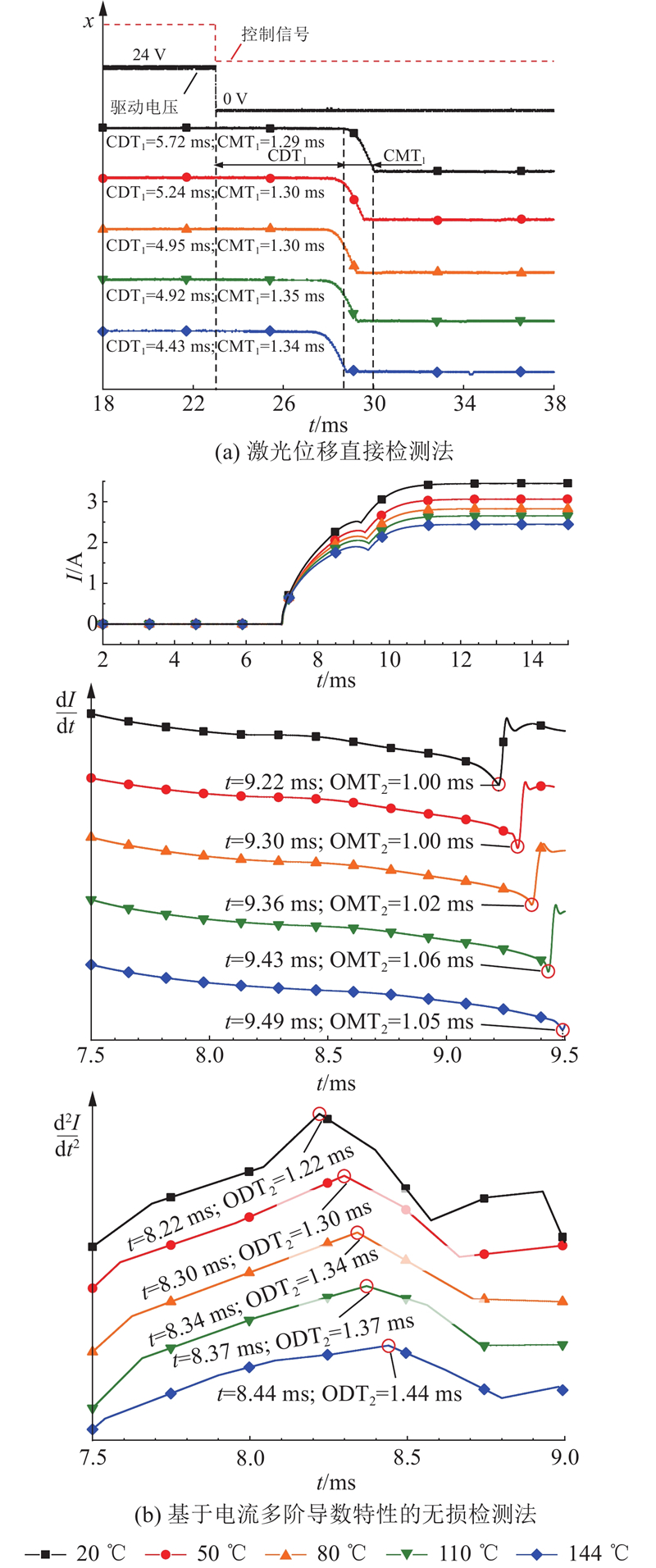
电磁开关阀在20 Hz控制单周期内的动态特性检测对比如图10和图11所示,控制信号开启指令和关闭指令分别在7 ms时刻和23 ms时刻触发. 激光位移直接检测法的结果如图10(a)和图11(a)所示,开启滞后时间随着线圈温度的上升而增加,从1.25 ms增大到1.43 ms;关闭滞后时间随之减小,从5.72 ms减小至4.43 ms. 原因是线圈温度越高,电阻越大,线圈电流的最大稳定值相应减小. 因此,在电磁开关阀关闭阶段,电流变化范围的减小能够提升该阀的关闭滞后性能. 基于电流多阶导数特性检测法的测量结果分别如图10(b)和图11(b)所示. 可以看出,电流一阶导数曲线及其二阶导数曲线均存在明显的特征点,不同曲线上的特征点类型与检测原理分析结果一致,验证了该方法理论定性分析的准确性. 随着电磁开关阀线圈温度的上升,电流一阶导数上的凹点后移,说明总开启时间逐渐增加,开启运动时间受时变温升的影响不大,最大变化差值为0.06 ms. 由电流二阶导数曲线中可以看出,开启滞后时间随着温度上升从1.22 ms增加至1.44 ms. 与开启过程相反,受到关闭滞后时间的影响,电磁开关阀的总关闭时间随着温度上升而减小,具体来看,从20 ℃的5.67 ms减小至144 ℃的4.37 ms.
图 10
图 10 电磁开关阀开启阶段的动态特性
Fig.10 Dynamic performance of solenoid switching valve in opening stage
图 11
图 11 电磁开关阀关闭阶段的动态特性
Fig.11 Dynamic performance of solenoid switching valve in closing stage
测量结果的偏差e计算式为
式中:tx为应用激光位移直接检测法的采集时间,ti为应用基于电流多阶导数检测法的识别时间. 2种方法测量的不同阶段动态时间和总启闭时间偏差如图12所示. 结果表明:最大测量偏差为80 ℃下的关闭运动时间,为3.08%,最小测量偏差为50 ℃下的总启闭时间,为0.11%. 线圈温升会影响线圈电流,对所提方法产生干扰. 经与激光位移直接检测结果比较可知,基于电流多阶导数特性检测法能够高精度且无损地测量电磁开关阀在启闭各阶段的动态特性,并检测动态特性受时变温升影响下的变化趋势.
图 12
图 12 电磁开关阀各阶段在不同温升条件下的测量偏差
Fig.12 Measurement deviation of solenoid switching valve at different stages under different temperature rise conditions
4.3. 连续启闭特性
电磁开关阀阀体的进油口直径仅为2 mm,导致激光无法照射到阀芯上,为此在对照方法中采用探针和金属片与阀芯相固连的方式. 如图13所示,虽然该方法能够直接检测到阀芯运动的动态过程,但增加了2.53%的阀芯运动质量,改变了原有的启闭动态特性.
图 13
图 13 电磁开关阀位移检测原理与质量实测
Fig.13 Displacement detection principle and mass measurement of solenoid switching valve
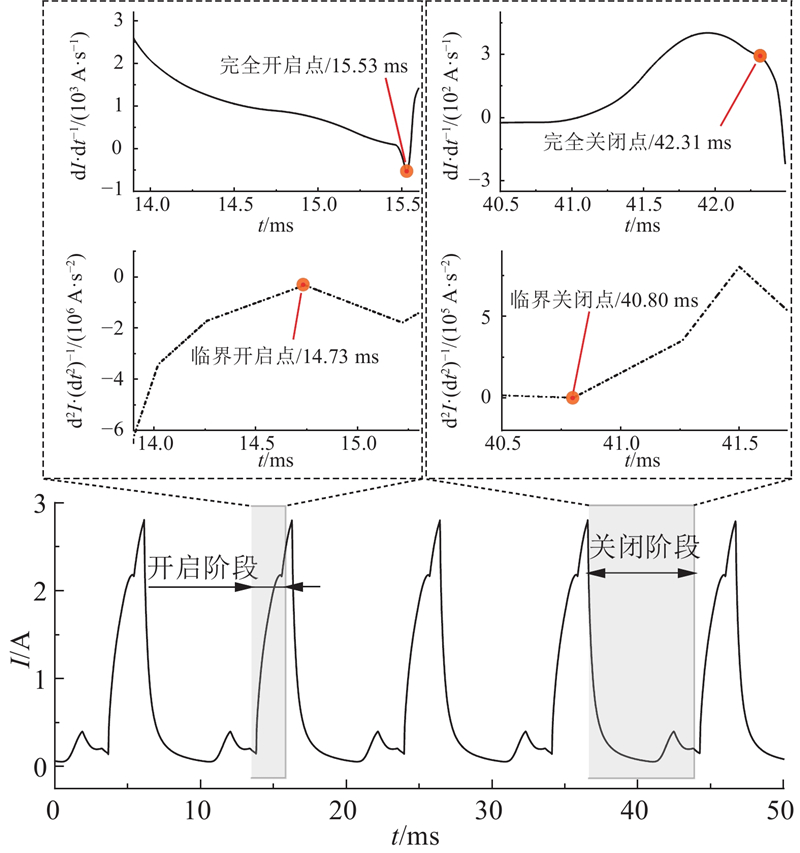
为了进一步验证基于电流多阶导数特性检测法的可行性,在50 Hz和100 Hz连续高频启闭的工况下测量电磁开关阀去除探针结构后的真实动态特性. 电磁开关阀在50 Hz连续启闭下的动态特性如图14所示,经对线圈电流多阶求导后,电流一阶、二阶曲线上的特征点依然明显,并与控制单周期内的电流导数变化趋势相一致. 其中临界启闭时刻分别为21.92 ms和29.86 ms,完全启闭时刻分别为22.77 ms和31.24 ms. 将连续驱动频率进一步提升至100 Hz,电磁开关阀的动态特性如图15所示. 为了防止各启闭周期的差异性,选取不同的控制单周期分别求导,得到开启动态特性和关闭动态特性. 检测结果表明:临界开启时刻和完全开启时刻依次为14.73 ms和15.53 ms,临界关闭时刻和完全关闭时刻依次为40.80 ms和42.31 ms. 为此,连续高频启闭下的电流导数曲线上依旧存在明显的特征点,且不受驱动频率的影响,充分验证了基于电流多阶导数特性检测法的可行性.
图 14
图 14 连续启闭动态特性(50 Hz驱动频率)
Fig.14 Continuous switching dynamic performance with 50 Hz driving frequency
图 15
图 15 连续启闭动态特性(100 Hz驱动频率)
Fig.15 Continuous switching dynamic performance with 100 Hz driving frequency
经红外热成像仪检测,电磁开关阀在100 Hz连续启闭下的热平衡温度为88 ℃,相较于50 Hz驱动工况下的100 ℃,降低了22 ℃,这是由于随着启闭频率的提升,单位时间内的电磁开关阀启闭次数增加,其切换动能也增大. 此时,随着等效开启状态和关闭状态维持时间的减小,其原有维持该状态的能量(热能)也降低. 因此,能量转化效率的提升减少了能量损耗,降低了连续启闭下的电磁线圈温升,减小了电磁开关阀的热平衡温度.
5. 结 语
本研究针对电磁开关阀由于结构特性和工装方式导致动态特性难以被直接检测的问题,提出基于电流多阶导数特性的无损检测方法,验证了所建数学模型的准确性,证明了所提方法在时变温升工况下的有效性与可行性. 根据上述研究结果得到如下结论:1)电磁开关阀启闭过程中的线圈温升特性会增大电阻,从而减小等效线圈电流,影响该阀的启闭动态特性;2)软磁合金的磁导率及其导数变化会直接影响线圈电感特性,导致线圈电流特性随之变化;3)所提方法能够精准测量电磁开关阀的临界/完全开启时刻和临界/完全关闭时刻,最大测量偏差为3.08%. 未来计划将所提方法应用于阀控系统中来实时感知每个电磁开关阀的工作状态,并配合高性能闭环控制算法来实现主机装备的高精度运动控制.
参考文献
Engineering research in fluid power: a review
[J].DOI:10.1631/jzus.A1500042 [本文引用: 1]
High-efficiency aircraft antiskid brake control algorithm via runway condition identification based on an on-off valve array
[J].
Investigation into the independent metering control performance of a twin spools valve with switching technology-controlled pilot
[J].DOI:10.1186/s10033-021-00616-w
Different boost voltage effects on the dynamic response and energy losses of high-speed solenoid valves
[J].DOI:10.1016/j.applthermaleng.2017.05.117 [本文引用: 1]
A novel equivalent continuous metering control with a uniform switching strategy for digital valve system
[J].DOI:10.1109/TMECH.2023.3247220 [本文引用: 1]
Development of high-speed on-off valves and their applications
[J].DOI:10.1186/s10033-021-00666-0
基于电流反馈的高速开关阀3电压激励控制策略
[J].
Three power sources excitation control strategy of high speed on/off valve based on current feedback
[J].
高速开关阀的研究现状
[J].DOI:10.3969/j.issn.1672-5581.2011.03.020 [本文引用: 1]
Advances on high-speed on-off valves
[J].DOI:10.3969/j.issn.1672-5581.2011.03.020 [本文引用: 1]
A vibration-based measurement method for dynamic characteristic of solenoid switching valve
[J].
Investigation into the adjustable dynamic characteristic of the high-speed/valve with an advanced pulsewidth modulation control algorithm
[J].DOI:10.1109/TMECH.2021.3131095 [本文引用: 2]
Dynamic performance of high speed solenoid valve with parallel coils
[J].DOI:10.3901/CJME.2014.0513.091 [本文引用: 1]
Position estimation in solenoid actuators
[J].DOI:10.1109/28.502166 [本文引用: 1]
Intelligent switching control of pneumatic actuator using on/off solenoid valves
[J].DOI:10.1016/j.mechatronics.2005.01.001 [本文引用: 1]
Energy-saving and performanceenhancing of a high speed on/off solenoid valve
[J].
Experimental analysis of new high-speed powerful digital solenoid valves
[J].DOI:10.1016/j.enconman.2010.12.032 [本文引用: 1]
Predicting solenoid valve spool displacement through current analysis
[J].DOI:10.1080/14399776.2015.1068549 [本文引用: 1]
Identification of critical moving characteristics in high speed on/off valve based on time derivative of the coil current
[J].
Dynamic performance and temperature rising characteristic of a high-speed on/off valve based on pre-excitation control algorithm
[J].DOI:10.1016/j.cja.2023.04.005 [本文引用: 1]